1 Introduction

Piezoelectric stage (PS) is an electromechanical device which produces motion in one degree of freedom and is operated by piezoceramic actuators (PCAs). These piezoceramic actuators have well positional accuracy with sub-nanometer resolution, highly stable with large blocking force and fast response with in milliseconds; therefore, they are extensively used in the applications of micro- or nano-positioning systems like space antenna applications [1], lithography systems [2], sensors applications [3], energy harvesting [4], micromechanical systems [5] and micro-robotics [6]. The PCAs produced nonlinearity into a PS system because of hysteresis and piezoceramic polarization, while hysteresis is the response for the input voltage with output displacement that highly destroy the positional accuracy of PS systems [7, 8]. Therefore, in nano-positioning applications, the hysteresis must be suppressed for high accuracy. Hence, precise modeling is still the challenging task for researchers. In order to cancel out the nonlinear hysteresis effect, an inverse compensation is introduced to the PS system. The nonlinear hysteresis model is categorized as operator-based hysteresis model [9] and differential systems-based hysteresis model [10]. The common model of differential systems used to explain the hysteresis of PS contains the Duhem model [11], Backlash model [12] and Bouc–Wen model [13]. The operator-based hysteresis model contains Prandtl–Ishlinskii model, [14] Krasnosel’skii–Pokrovkii model, [15] and Preisach model [16].

The recent, relevant, reported studies for electro-vibro dynamic hysteresis modeling of piezostage actuator (PSA) in different applications include a feedforward control methodology of dynamic hysteresis inverse classic Preisach model [17], and proportional-integral-derivative control [18] is proposed for PSA. Interval type-2 fuzzy system based on gradient optimization is presented for hysteresis modeling and feedforward control of the PSA [19]. The design of hysteresis by autoregressive exogenous neural network for is presented in order to enhance the performance accuracy of PSA for vibrations of helicopter vibrations [20]. Another approach for hysteresis compensation based on adaptive control of single neuron is proposed to dynamically control the PSA input by utilizing the combination of supervised learning and Hebb learning rules [21]. A self-tuning neural network control approach is offered to apprehend the system accuracy by tracking PSA uncertainties and nonlinear hysteresis [22]. A slide mode controller based on Prandtl-Ishlinskii model is introduced [23]. Another dynamic delay Prandtl–Ishlinskii model is presented to characterize the dynamic and asymmetrical features of PSA in order to suppress the hysteresis effect [24]. Lee et al. presented finite-time integral terminal sliding mode and time-delayed estimation approaches in order to achieve fast, accurate, and robust force tracking performance [25]. The Elman neural network-based dynamic hysteretic operator is used to alter the multi-valued mappings of hysteresis [26]. A polynomial-based disturbance fractional-order model is presented to describe the intricate PSA hysteresis effect that considerably suppressed hysteresis nonlinearity over a wide bandwidth [27]. A tracking control Pneumatic muscle PSA is presented, based on echo state Gaussian process and nonlinear predictive control model for lower limb exoskeleton [28]. Moreover, the recurrent neural network-based inversion model is introduced to compensate the nonlinearities of PSA in order to get a high-accuracy, broadband and less computational complexity [29].

1.1 Related study

Different researchers present different approaches in order to optimize the system parameters of this nonlinear effect of input and output displacements. The particle swarm optimization (PSO) method is used to optimize the nonlinearity of Dahl model, Duhem model, generalized Duhem and Bouc-Wen hysteresis models [11]. The parameter identification of Duhem model is employed by genetic algorithm as well as clonal selection algorithm [30]. For Bouc-Wen hysteresis model accuracy, the least square method has also been used [31]. Transitional Markov chain Monte Carlo approach is exploited to optimize the parameters of Bouc–Wen model [32]. Improved artificial bee colony algorithm is presented in order to identify hysteresis parameters [33]. Furthermore, the optimization of nonlinear effect of piezo actuator for Bouc-Wen hysteresis model has been performed by hybrid adaptive differential evolution [34]. Hence, the Bouc-Wen hysteresis model is commonly adaptive technique to model the hysteresis of PS systems as only one auxiliary differential system is essential to explain the behavior of hysteresis.

Numerical methods focused on soft computing paradigm are commonly used to solve various problems of differential systems [35, 36]. Some recently published studies of paramount significance contain solution of mathematical model for Painlevé-II representing the dynamics of nonlinear optics [37], nonlinear Bratu’s equation arising in electrically conducting solid models [38, 39], reactive transport system of soft tissue [40], Van-der-Pol oscillatory nonlinear systems [41, 42], convergent/convergent fluidic flow systems [43, 44], thin-film flow studies [45, 46], combustion theory [47], nonlinear circuit theory models [48, 49], astrophysics [50], mathematical models involving Carbon nanotubes [51], heartbeat dynamic models [52], dusty plasma [53], HIV infection spread models [54], atomic physics [55, 56], piezoelectric transducer modeling [57], wind power [58, 59], load dispatch problem [60], financial models [61, 62], nonlinear fractional dynamic modeling with Riccati fractional differential equations (FrDEs) [63, 64] and Bagley–Torvik FrDEs [65].

1.2 System model: Bouc–Wen model for hysteresis modeling of piezoelectric actuator

The nano-position moving stage excited by piezo actuator (PA) is graphically demonstrated in Fig. 1. By applying an input voltage x on the piezoelectric stack, the elongation is formed in the stack due to piezoelectric effect, which exerts force on the sliding mass m and caused essential displacement d. The unsymmetrical relationship between this output displacement and applied voltage is the hysteresis loop that can be described by Bouc-Wen model. The standard Bouc-Wen model (BWM) is first presented by Bouc in 1967 [66] where the hysterical act of external applied force and output displacement is numerically expressed in form of function; then, in 1976 the generalized version of this function is proposed by Wen. This model comprises of two equations, the nonlinear first-order state equation and the linear output equation of input and state signals. It can be demonstrated in numerous variety of hysteresis behavior depending on the selection of parameters. The electromechanical expression for dynamic hysteresis model of piezo actuator can be described in Eqs. (1) and (2).

$$ m\;\ddot{d}(t) + c\;\dot{d}(t) + k\;{\text{d}}(t) = k(\delta x(t) - h(t)), $$
(1)
$$\begin{aligned} & \dot{h}(t) = \alpha \delta \dot{x}(t) - \beta \left|{\dot{x}(t)}\right|h(t)\left|{h(t)}\right|^{n - 1} \\ & \quad - \gamma \dot{x}(t)\left|{h(t)}\right|^{n} , \\ \end{aligned}$$
(2)
Fig. 1
figure 1

System model

Full size image

where x signifies the input voltage, d is the output displacement, t indicates time variable, c is the damping coefficient, h denotes hysteresis, k represents stiffness coefficient and δ symbolize the piezoelectric coefficient. The parameters α, β, γ and n are the magnitude and shape control variables of hysteresis, where α, β and γ control the basic shape, while order n is responsible for the sharpness and smoothness of the hysteresis loop that switch the response from elastic to plastic. The values of all these model parameters are given in Table 1.

Table 1 Piezo actuator settings
Full size table

1.3 Problem statement and significance

The enriched importance of piezoelectric actuator attracts different researchers to implement numerous techniques to observe the dynamics of system, but the soft computing technique has not been exhaustively examined for the analysis of Bouc–Wen hysteresis model. The main objective of this investigation is to exploit soft computing paradigm through the ability of Levenberg–Marquardt backpropagated neural networks (LMB-NNs) to solve the differential system representing in Eqs. (1–2). The proposed LMB-NNs can be a good alternative to be exploited for Duhem model, Dahl model and Prandtl–Ishlinskii model.

1.4 Contribution and innovative insights

The creative elements of the designed computing infrastructure are briefly illustrated as:

  • Novel application of neuro-heuristic technique based on Levenberg–Marquardt backpropagated neural networks (LMB-NNs) is presented to study the Bouc–Wen hysteresis model for piezostage actuator.

  • The dataset of Bouc–Wen hysteresis model is created by exploiting the strength of Adam numerical solver for training, testing and validation purpose.

  • The efficacy of the scheme is validated by variation in applied input voltage signals to piezostage actuator model on accuracy through performance metrics based on mean squared error, error histogram illustrations, as well as regression analyses.

  • Apart from the proven competence of precise solution, other valued key characteristics of the scheme are sound procedures, smooth execution, fast steady convergence, reliability and extensibility.

1.5 Organization

The rest of the paper is organized as follows: Sect. 2 narrates methodology based on supervised neural network employed for solving the hysteresis modeling of piezoelectric actuator. In Sect. 3, outcomes with necessary interpretation are narrated, while concluding inferences are listed in Sect. 4.

2 Methodology

In this section, the methodology is presented that consists of the three parts. Initially, the creation of data set by Adams numerical method, then formulation of LMB-NNs and finally the performance indices is discussed. The graphical abstract of design methodology is represented in Fig. 2. The steps of our proposed work are demonstrated in algorithms 1.

Fig. 2
figure 2

Graphical abstract of proposed methodology

Full size image

2.1 Adams numerical method

Adams numerical approach for first-order system is written as:

$$ \frac{{{\text{d}}y}}{{{\text{d}}x}} = f(x,y), $$
(3)
$$ Y_{l + 1} = y_{l} + \int\limits_{{t_{l} }}^{{t_{l + 1} }} {\frac{{{\text{d}}y}}{{{\text{d}}x}}} {\text{d}}t = y_{l} + \int\limits_{{t_{l} }}^{{t_{l + 1} }} {f(y,t){\text{d}}t} , $$
(4)

where y signifies output of linear first-order ordinary differential equation, x represents the input value, \(Y_{l + 1}\) symbolize the first-order interpolation iterative approach, and t denotes the time interval.

Adams methods are based on the principle of approximating the integral within the interval (tl, tl+1) with a polynomial. There are two kinds of Adams methods, the explicit and the implicit types. The Adams–Bashforth (AB) methods are called the explicit type, and the Adams–Moulton (AM) methods are called the implicit type. The AB and AM methods of the first order are essentially the methods of forward and backward Euler. The second-order versions of these methods are very common (obtained by using a linear interpolant). In Eq. (5), the second-order Adams–Bashforth (AB2) method is described.

$$ Y_{l + 1} = y_{l} \, + \,\frac{q}{2}(3f(y_{l} ,\,t_{l} \; - \,f(y_{l - 1} ,t_{l - 1} )) $$
(5)

where q is the step interval. The Adams–Moulton second order (AM2) is an implicit method, also referred to as the trapezoidal principle given below:

$$ Y_{l + 1} = y_{l} \, + \,\frac{q}{2}(f(y_{l + 1} ,\,t_{l + 1} \; + \,f(y_{l} ,t_{l} )) $$
(6)

2.2 Levenberg–Marquardt backpropagation method

In 1944, Kenneth Levenberg and Donald Marquardt developed the Levenberg–Marquardt algorithm, that exploits the strength of steepest decent method (SDM) and the Gauss–Newton method (GNM). Due to the hereditary convergent efficiency of GNM and of SDM stability, the algorithm is robust. The minimum function F(x) is initially determined in the LM algorithm as:

$$ F(x) = \sum\limits_{i = 1}^{l} {\left( {\frac{{\left( {f_{i} (x)} \right)^{2} }}{2}} \right)} , $$
(7)

while J represents Jacobian of the function and the LM method proceed as:

$$ (J_{a}^{{\text{T}}} J_{a} + \lambda_{a} I)p_{a} = - J_{a}^{{\text{T}}} f_{a} , $$
(8)

where \(\lambda_{l}\) represents positive scalar values, I stands for identity matrix, and p is downhill step. The updated rule for weights in LBM-NNs algorithm is given as:

$$ w_{a + 1} = w_{a} - (J_{a}^{{\text{T}}} J_{a} + \lambda_{a} I)^{ - 1} J_{a} e_{a} , $$
(9)

Here ea and wa are error and weight vector, respectively.

The convergence rate of the LM algorithm is higher than both GNM and SDM. LM algorithms have two feasible alternatives for the path of the algorithm at each iteration. At the same time, it can handle several parameters.

figure b

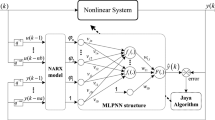
Artificial neural networks are composed of a series of linked units called artificial neurons. A signal can be transmitted to another neuron through each synapse between neurons. The state of neurons can easily be expressed by entries generally real number between [0, 1]. Neurons are usually arranged into layers’ structure with different types of transformation functions. On their inputs, different layers can perform different types of transformations. In this methodology, 20 to 100 hidden layers were used in order to achieve the desire output. The basic structure of proposed neural network is shown in Fig. 3. Here, a Levenberg–Marquardt backpropagation algorithm-based neural network is presented to optimize the Bouc–Wen hysteresis model of piezostage actuator graphically shown in Fig. 4.

Fig. 3
figure 3

Structure of supervised neural network

Full size image
Fig. 4
figure 4

Levenberg–Marquardt backpropagation

Full size image

2.3 Performance indices

The performance of our proposed work has been illustrated by regression analysis, error histogram, curve fitting and mean square error.

2.3.1 Regression analysis

Regression analysis is a powerful form of statistics that help to analyze the relationship of interest between two or more variables. Although there are several forms of regression analysis, they all analyze the effect of independent variables over dependent variables. It is most commonly used for forecasting and prediction, where its application overlaps greatly with the field of machine learning. The regression method helps to confidently decide which variables matter most, the relationship between these variables and which variable can be ignored. Regression model shows that Yi is a function of Xi and ς, with ei which represents a random statistical noise as given in Eq. (10).

$$ Y_{i} = f(X_{i} ,\;\varsigma )\; + \;e_{i} . $$
(10)

2.3.2 Error histogram

Error histogram shows the differences between predicted values and targeted values obtained after training a feedforward deep neural network. Since these error values show how expected values vary from the target values, they may also be negative. Bins represent the vertical bars on the graph, and y-axis denotes number samples from given dataset. Zero line on graph corresponds to the zero error.

2.3.3 Mean square error

The mean square error (MSE) of an estimator is used in statistics to calculate the average error squares, i.e., the average square difference between the expected values and the real value. It can be used as a loss function in order to analyze the model performance. The mathematical expression of MSE is shown in Eq. (11).

$$ {\text{MSE}} = \frac{1}{s}\sum\limits_{i = 1}^{s} {(Y_{i} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y}_{i} )^{2} } , $$
(11)

where s is the number of sample data points, \(Y\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y}\) are true output and estimated output. The error can be obtained from the difference of estimated and true output values.

3 Results and discussion

In this section, dynamic hysteresis model of piezo actuator using proposed LBM-NNs is presented with numerical and graphical illustrations of outcomes. Results are presented for all three cases of dynamic hysteresis model of piezo actuator by variation of input voltage signal as per following details.

The solution of dynamic hysteresis model of piezo stage actuator is presented by taking following three cases:

3.1 Case 1: piezoelectric actuator model with type 1 input

In this case study, dynamics of Bouc-Wen hysteresis model is represented in Eqs. (1) and (2) for piezostage actuator with given initial conditions presented by choosing type 1 input voltage signal in \(t \in \left[ {0,10} \right]\). The initial conditions are:

$$ d(0) = 0,\quad d^{{\prime }} (0) = 0,\quad h(0) = 0. $$

The type 1 input voltage signal is shown in Eq. (12).

$$ x(t) = 5{\text{e}}^{ - 0.1t} \left( {\sin (6\pi t{\text{e}}^{ - 0.346t} - 1.5) + 1} \right),\; $$
(12)

Using Eq. (12), the updated Bouc-Wen hysteresis model for piezoelectric actuator is given in Eqs. (13–14).

$$ \left( \begin{gathered} m\ddot{d}(t) + c\dot{d}(t) + kd(t) + kh(t) \hfill \\ - 5\delta k{\text{e}}^{ - 0.1t} \left( {\sin \left( {6\pi t{\text{e}}^{ - 0.346t} - 1.5} \right) + 1} \right) \hfill \\ \end{gathered} \right) = 0, $$
(13)
$$ \begin{aligned} & \dot{h}(t) = \left( {\alpha \delta - \gamma \left| {h(t)} \right|^{n} } \right)\left( \begin{gathered} - 5{\text{e}}^{ - 0.1t} \left( { - 6\pi {\text{e}}^{ - 0.346t} + 6.522t{\text{e}}^{ - 0.346t} } \right) \hfill \\ \cos \left( {1.5 - 6\pi t{\text{e}}^{ - 0.346t} } \right) - 0.5{\text{e}}^{ - 0.1t} \left( {1 - \sin \left( {1.5 - 6\pi t{\text{e}}^{ - 0.346t} } \right)} \right) \hfill \\ \end{gathered} \right) \\ & \quad - \beta \left| { - 5{\text{e}}^{ - 0.1t} \left( \begin{gathered} - 6\pi {\text{e}}^{ - 0.346t} \hfill \\ + 6.522t{\text{e}}^{ - 0.346t} \hfill \\ \end{gathered} \right)\cos \left( \begin{gathered} 1.5 \hfill \\ - 6\pi t{\text{e}}^{ - 0.346t} \hfill \\ \end{gathered} \right) - 0.5{\text{e}}^{ - 0.1t} \left( {\left( {1 - } \right.\,\sin \left( \begin{aligned} 1.5 \hfill \\ - 6\pi t{\text{e}}^{ - 0.346t} \hfill \\ \end{aligned} \right)} \right)} \right|h(t)\left|{h(t)}\right|^{n - 1} . \\ \end{aligned} $$
(14)

3.2 Case 2: Piezoelectric actuator model with type 2 input

In this case study, a type 2 input voltage signal for time \(t \in \left[ {0,10} \right]\) is shown in Eq. (15) chosen for the dynamic of BWM of piezoelectric actuator described in Eqs. (16–17).

$$ x(t) = 5{\text{e}}^{ - 0.13t} \left( {\cos (3\pi t{\text{e}}^{ - 0.09t} - 3.15) + 1} \right)\;, $$
(15)
$$ \left( \begin{gathered} m\ddot{d}(t) + c\dot{d}(t) + kd(t) + kh(t) \hfill \\ - 5\delta k{\text{e}}^{ - 0.13t} \left( {\cos \left( {3\pi t{\text{e}}^{ - 0.09t} - 3.15} \right) + 1} \right) \hfill \\ \end{gathered} \right) = 0, $$
(16)
$$ \begin{aligned} \dot{h}(t) & = \left( {\alpha \delta - \gamma \left| {h(t)} \right|^{n} } \right)\left( { - 0.65{\text{e}}^{ - 0.13t} \left( \begin{gathered} 1 + \cos \left( {3.15 - 3{\text{e}}^{ - 0.09t} \pi t} \right) \hfill \\ - 5{\text{e}}^{ - 0.13t} \left( \begin{gathered} - 3{\text{e}}^{ - 0.09t} \pi \hfill \\ + 0.84823{\text{e}}^{ - 0.09t} t \hfill \\ \end{gathered} \right)\sin \left( {3.15 - 3{\text{e}}^{ - 0.09t} \pi t} \right) \hfill \\ \end{gathered} \right)} \right) \\ & \quad { - \beta }\left| { - 0.65{\text{e}}^{ - 0.13t} \left( {1 + \cos \left( \begin{gathered} 3.15 - \hfill \\ 3{\text{e}}^{ - 0.09t} \pi t \hfill \\ \end{gathered} \right)} \right) - 5{\text{e}}^{ - 0.13t} \left( \begin{gathered} - 3{\text{e}}^{ - 0.09t} \pi + \hfill \\ 0.84823{\text{e}}^{ - 0.09t} t \hfill \\ \end{gathered} \right)\sin \left( \begin{gathered} 3.15 - \hfill \\ 3{\text{e}}^{ - 0.09t} \pi t \hfill \\ \end{gathered} \right)} \right|h(t){}\left|{h(t)}\right|^{n - 1} . \\ \end{aligned} $$
(17)

3.3 Case 3: Piezoelectric actuator model with type 3 input

In this case study, a type 3 signal in \(t \in \left[ {0,10} \right]\) shown in Eq. (18) is selected as an input signal of piezoelectric actuator in order to determine the dynamics of Bouc-Wen hysteresis model.

$$ x(t) = 5 + 3.4{\text{e}}^{ - 0.24t} \left( {\cos 2\pi t} \right), $$
(18)

Now Eqs. (1) and (2) turn in the form of Eqs. (19–20).

$$ \left( \begin{gathered} m\ddot{d}(t) + c\dot{d}(t) + kd(t) + kh(t) \hfill \\ - 5\delta k + 3.4{\text{e}}^{ - 0.24t} k\delta \left( {\cos 2\pi t} \right) \hfill \\ \end{gathered} \right) = 0, $$
(19)
$$ \dot{h}(t) = \left( \begin{gathered} \alpha \delta - \hfill \\ \gamma \left| {h(t)} \right|^{n} \hfill \\ \end{gathered} \right)\left( \begin{gathered} - 21.3628{\text{e}}^{ - 0.24t} \sin \left( {2\pi t} \right) \hfill \\ - 0.816{\text{e}}^{ - 0.24t} \cos \left( {2\pi t} \right) \hfill \\ \end{gathered} \right) - \,\upbeta \left| \begin{gathered} - 21.3628{\text{e}}^{ - 0.24t} \sin \left( {2\pi t} \right) \hfill \\ - 0.816{\text{e}}^{ - 0.24t} \cos \left( {2\pi t} \right) \hfill \\ \end{gathered} \right|h(t)\left|{h(t)}\right|^{n - 1} . $$
(20)

Initially, the dataset for all three cases was created with Adams numerical method by using ‘NDSolver’ in Mathematica platform. Different datasets for each analysis were created with step size 0.1 in order to find the solution of dynamic Bouc-Wen hysteresis model with supervised neural network. The datasets for all three cases with different input signals for selected twenty points with step size 0.5 are numerically represented in Table 2. The number of data points created for each case is 101 with step size 0.1. Furthermore, these datasets were imported into MATLAB for implementation of SNN where 90% of data points is used for training the model, 5% is for testing, and leftover 5% is used for validation purpose of obtained results. Performance analysis for all three cases of proposed dynamic hysteresis model of piezo actuator are numerically shown in Table 2, where the hidden layer neurons were kept 20, 50 and 100 according to achieve better performance. The best observed performance value for case 1 is 8.3166E−05 in 786th epoch, for case 2 is 0.024098 in 134th epoch and for case 3 is 3.2433E−04 in 329th epoch. The values of step size (Mu), gradient and mean square error (MSE) are also shown in table. To verify the model accuracy, the MSE is used that has shown optimal values for all three cases. The MSE values of training, testing and validation of proposed model for case 1 are 1.073e−06, 0.4945 and 6.227e−06, respectively. The case 3 shows minimum MSE value for testing of system that is 4.767e−04 with step size (Mu) of 1.0E−08 in 329th epoch as compared to other two cases.

Table 2 Datasets of displacement (mm) for all three scenarios
Full size table

The obtained results are also graphically shown in form of performance analysis, regression analysis of training, testing and validation, curve fitting of output displacement and model error and histogram. The performance analysis of dynamic hysteresis piezo actuator for all three cases is graphically illustrate in Fig. 5 where the MSE values are plot against each epoch for training, validation and testing of model. The best MSE value is achieved at case 1 for validation that is 8.31E−05 at 786 epoch. The gradient, Mu and validation check at 786 epochs are also graphically shown. The best line for case 1 is observed near 10−4, for case 2 is around 10−2 and for case 3 is closed to 10−3. These graphs show that for all cases the accurate MSE value is taken; however, a bit degradation in performance of model for testing and validation is observed due to un-biasness, while the training provides best values in all graphs although during validation and testing process the target at input were not defined. The algorithm stability is shown by state estimation due to Mu. The state estimation of proposed model is actually the step size (Mu), gradient and validation check at each epoch shown in Fig. 5; here, the gradient is used to find another vector at each epoch during training. The Mu represents the step size of used algorithm, and the term validation check is generalized measure of the model. The convergence results for smaller Mu of all three cases are shown by these graphs; however, the best convergence is observed in case 3 where the Mu value is 1E−08 at 329 epoch.

Fig. 5
figure 5

Comparison of performance and training states of input signals

Full size image

The regression analysis of dynamic hysteresis piezo stage actuator for training, testing and validation are graphically demonstrated in Fig. 6; here, the prediction and forecasting are graphically demonstrated. It shows that the value of regression (R) is achieved approximately 1 for all three cases, which determines the closed correlation between the targets and the output vectors.

Fig. 6
figure 6

Regression Analysis of training, testing and validation for all scenarios

Full size image

In order to find accuracy of dynamic hysteresis model of piezo actuator, the fitness graphs are plotted. And hence the error of all three cases is found. Input signals, model hysteresis, training states of fitness graphs and errors of dynamic hysteresis piezo stage model for case 1 are shown in Fig. 7, that of case 2 are shown in Fig. 8 and that of case 3 are shown in Fig. 9, respectively.

Fig. 7
figure 7

Case 1: curve fitting: a output displacement curve fitting, b input signal 1, c hysteresis loop

Full size image
Fig. 8
figure 8

Case 2: curve fitting a output displacement curve fitting, b input signal 2, c hysteresis loop

Full size image
Fig. 9
figure 9

Case 3: a Output displacement curve fitting, b input signal, c hysteresis loop

Full size image

Further analysis is performed through histogram where the error is plot verses instances for all data points including training, testing and validation with 20 bins. The histogram for all three case is shown in Fig. 10. Most data points are observed to converge toward a zero error line with less extreme values. On the left side of the target line, the negative error is plotted, while the positive error is plotted on the right side. In case 1, the targeted zero error line occurred at − 0.1 where it falls into the bin; in case 2, the zero error falls into the bin at 0.035, and in case 3, the zero error line lies at − 0.003 on error axis (Table 3).

Fig. 10
figure 10

Error histogram for all three cases

Full size image
Table 3 Performance analysis for all three cases of proposed piezo actuator model
Full size table

4 Conclusion

In this research work, an neurocomputing heuristics is presented to model differential equations of nonlinear Bouc-Wen hysteresis model and optimized with the LMB-NNs. The dataset of piezostage actuator is created by Adams numerical method. Various experiments based on variation of input voltage signal for actuation of piezostage actuator model are conducted in order to validate, train and test the system. A neural networks approach for nonlinear hysteresis modeling of piezoelectric actuator has exposed remarkable, efficient and stable results with highest accuracy in terms of mean squared error, regression analyses and error histogram. The best testing result is obtained in case 3 where the MSE value is 4.767e−04. The best performance is 8.3166E−05 which is achieved by case 1 with step size 1.0E−07 in 786 epochs. The minimum error is shown by case 3 where the zero error line lies on − 0.004.

The proposed neurocomputing intelligence algorithm can be a good alternative to be implemented on renewed applications in broad fields [67,68,69,70,71,72,73].