1 Introduction

Due to the wide range of advanced engineering applications of nonhomogeneous submicron structures, studying the various aspects of their characteristics is of the great importance in modern engineering. Besides the experimental and atomistic modeling methods which have difficulties to perform and are computationally expensive, the continuum mechanics-based approach provides an acceptable and dominant method in this regard. The classical continuum theory due to lack of consideration the two important characteristics of submicron structures, called surface and small-scale effects, is not able to estimate an accurate response of such structures.

In submicron structures, the equilibrium conditions of atoms in exposure to a free surface are different from those inside since the surface-to-volume ratio is high. In other words, the energy of surface atoms is different from the bulk atoms. This feature that is known as surface effects is a significant factor in the investigation of submicron structures. In order to incorporate the surface effects into the mechanical analysis of submicron structures using the continuum mechanics-based approach, Gurtin and Murdoch [1, 2] presented the surface elasticity theory. On the basis of this theory, the surface layers are modeled as a two-dimensional membrane with zero thickness and different material properties from the bulk section and are perfectly adhered to the underlying bulk section without slipping. Their achievement has been widely used in nanoplates [3,4,5] and nanobeams [6,7,8,9,10] studies, and it has been shown that surface properties broadly affect the mechanical behavior of submicron structures.

Lee and Chang [11] examined the effects of surface on the natural frequency using nonlocal Timoshenko beam theory. They demonstrated while the nonlocal effect is not considered in the model, the result has no difference from those of modified Timoshenko beam theory. Lei et al. [12] analyzed the effects of surface on the free vibration of double-walled carbon nanotubes by employing nonlocal Timoshenko beam theory. The influence of the surface elasticity modulus and residual surface stress on the natural frequency is investigated in this research. Zhang et al. [13] studied the effects of surface stress on the natural frequency of nanobeams with use of a modified continuum model. Their results displayed that surface elasticity and surface density have exponential relations with surface layer thickness. Therefore, surface relaxation and surface reconstruction can impose, respectively, surface elasticity and residual surface stresses. Ghadiri et al. [14] took into account surface effects and thermal environment for analyzing the nonlinear forced vibration behavior of a nanobeam by Euler–Bernoulli theory. They proved that when the residual surface stress and temperature increase, the jump phenomenon delays.

Rouhi et al. [15] detected free vibration of nanoshells by using first-order shear deformation theory (FSDT) and surface elasticity theory of Gurtin–Murdoch. They have examined the influences of residual surface stress, surface elasticity modulus and surface mass density on responses. In another work [16], they analyzed the nonlinear vibration of a cylindrical nanoshell considering the effects of surface by Gurtin–Murdoch method and von Kármán’s equation, to illustrate that the responses of Gurtin–Murdoch and classical theories are significantly different from each other.

Nanthakumar et al. [17] have applied the surface properties to the shape and topology optimization of nanostructures using Gurtin–Murdoch surface elasticity theory and coupling of the extended finite element method (XFEM) and the level set method. They presented a general formulation that can be used for different materials so long as their surface properties are known.

Small-scale effects as another important feature in submicron structures are the influence of inter-molecular or inter-atomic interactions [18] and can be taken into account in the continuum mechanics-based approach by the size-dependent theories. There are two main theories of this type that are the nonlocal [19, 20] and gradient elasticity [21,22,23,24,25] theories which, respectively, model the two entirely different effects called stiffness softening and stiffness enhancement phenomena in the submicron structures. In the nonlocal theory, it is supposed that the stress at a point is not only a function of strains at that point, but also a function of strains at all the other points within the body [26, 27]. The size-dependent parameter in this theory is the nonlocal parameter and considers the long-range cohesive inter-molecular or inter-atomic forces [27]. The gradient elasticity theories by the material length scale size-dependent parameter make it possible that the higher-order deformations and stiffness enhancement phenomenon which cannot be predicted by the nonlocal theory, are to be included. In these theories, instead of modeling the material as a collection of points, it is modeled as atoms with higher-order deformations and the constitutive equations consist of strain gradient terms [28]. It can be realized that to assess the true small-scale effects on the mechanical analysis of submicron structures, both stiffness softening and stiffness enhancement phenomena need to be modeled simultaneously. To this end, nonlocal strain gradient theory (NSGT) has been presented recently [27] by combining the local and nonlocal sections of fundamental relations. According to this method, the stress due to submicron scales is considered in both nonlocal stress and pure strain gradient stresses [25]. Lim et al. [27] extracted NSGT equations by employing the thermodynamic principles; consequently, the higher-order nonlocal and the nonlocal gradient length parameters were accounted in small-scale effects studies. Many researchers have been fascinated by the utilizations of NSGT in vibrational behavior of nanobeams [28,29,30,31]. Ghorbani et al. [32] calibrated the nonlocal and material length scale parameters of carbon nanotubes by comparing the results of molecular dynamics simulation and NSGT. They have reported between the size-dependent parameters, nonlocal parameter has the most significant effect on the natural frequency. Mohammadi et al. [33] analyzed the vibrational behavior of a cylindrical shell by applying the NSGT. It is concluded from this study that the strain gradient and nonlocal theories can obtain the highest and smallest natural frequencies, respectively, and the NSGT resultants set somewhere in between. Also, in another research, utilizing the NSGT and molecular dynamics simulation, Mohammadi et al. [34] calibrated the size-dependent parameters of a fluid-conveying CNT. Decreasing the nonlocal parameter through the enhancement of flow velocity is reported in this research. The influences of size-dependent parameter on the critical flow rate and natural frequency of single-walled carbon nanotube exerting the cylindrical shell theory and NSGT, were examined by Mahinzare et al. [35]. Using the Gurtin–Murdoch and nonlocal strain gradient theories, Ghorbani et al. [36] investigated the submicron scale effects on the natural frequency of nanoshells. A new analysis that can be made in the determination of size-dependent parameters and studying the effects of these parameters on the mechanical behavior of submicron structures is the uncertainty analysis. To perform this analysis, one can find a useful software framework in Ref. [37].

Functionally graded materials (FGMs) establish a class of nonhomogeneous materials which can be made in a way that their thermo-mechanical behavior varies along a particular direction. Zidi et al. [38] examined the bending of a FGM plate embedded in two parameters Pasternak foundation and under thermo-hydro-mechanical loading. They used four variable refined plate theory and obtained the nondimension stresses and displacements for plates with the metal-ceramic mixture in their study. Kandasamy et al. [39] conducted research on thermal buckling and free vibration of FG plates and shells. In some other works [40, 41], vibration behavior of CNT-reinforced FGM cylindrical shell was investigated in the thermal environment. These researches observed the effect of different parameters such as FG gradient index, CNTs distribution and their volume fraction. In addition, FGMs have some applications in submicron structures such as MEMs, NEMs, and atomic force microscopes [42,43,44,45]. Therefore, studying the vibration analysis and structural stability must be considered in their mechanical design.

From the literature mentioned above, surface and small-scale effects are the two significant characteristics in submicron structures which must be considered in the investigation of the mechanical behavior of submicron structures utilizing continuum mechanics based approach. Also, NSGT is a recently proposed general theory which models both stiffness softening and stiffness enhancement phenomena of small-scale effects simultaneously. The requirement to provide the model for the vibration analysis of FG nanoshell with surface and small-scale effects based on Gurtin–Murdoch surface elasticity theory and NSGT, motivates us to conduct present study. In this study, for the first time, the effects of surface properties, size-dependent parameters and FG gradient index on the natural frequency of a FG cylindrical shell are investigated utilizing the theories of Gurtin–Murdoch and nonlocal strain gradient. The model presented in this study can be used as a basic model in the study of the effects of external loads such as thermal, visco-elastic medium and hygro-thermal on the vibration behavior of FG nanoshell.

2 Mathematical modeling

In this section, the process of extracting the governing motion equations and the related boundary conditions (B.Cs) of a FG cylindrical nanoshell is presented. To this end, utilizing the FSDT and surface elasticity theory of Gurtin–Murdoch, the classical constitutive equations will be achieved, and then, by calculating nonclassical constitutive equations based on the NSGT and using Hamilton’s principle, the corresponding equations will be extracted. At the end of the section, the solution procedure will be discussed.

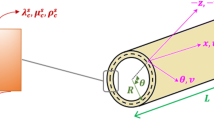
Figure 1 represents a shell with the thickness h, mean radius R, and length L, which is considered in curvilinear coordinates (r, θ, z). The desired nanoshell contains the bulk section with effective material properties of elastic modulus E (z), Poisson’s ratio \( \nu \left( z \right) \) and mass density \( \rho \left( z \right) \); and two thin surface layers with surface properties of elastic modulus \( E^{s \pm } \), Poisson’s ratio \( \nu^{s \pm } \), mass density \( \rho^{s \pm } \), and residual surface stress \( \tau^{s \pm } \). The (+) and (−) superscripts are related to the upper and bottom thin surfaces, respectively. It is supposed that the effective material properties vary continuously through the thickness (z−) direction as follows [46]:

$$ P(z) = P^{ + } V^{ + } (z) + P^{ - } V^{ - } (z) $$
(1)

where P(z), P± and V± are the effective material properties (E (z), \( \nu \left( z \right) \) and, \( \rho \left( z \right) \)), constituents properties (\( E^{ \pm } , \upsilon^{ \pm } \) and \( \rho^{ \pm } \)) and volume fractions, respectively. According to the power law function, the volume fractions can be stated as:

$$ V^{ + } (z) = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} , { }V^{ - } (z) = 1 - V^{ + } (z), \, \frac{h}{2} \le z \le \frac{h}{2} $$
(2)

in which k is the FG gradient index and shows the material properties distribution through the thickness of the shell. By inserting Eq. (2) into Eq. (1), the following effective material properties can be concluded:

$$ {\begin{aligned} E(z) & = \left( {E^{ + } - E^{ - } } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + E^{ - } \\ \upsilon (z) & = \left( {\upsilon ^{ + } - \upsilon ^{ - } } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + \upsilon ^{ - } \\ \rho (z) & = \left( {\rho ^{ + } - \rho ^{ - } } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + \rho ^{ - } \\ \end{aligned}} $$
(3)
Fig. 1
figure 1

Schematic illustration of a FG cylindrical nanoshell

Full size image

2.1 First-order shear deformation shell model

In this model, the components of displacement field will be considered as Eq. (4) where \( (u_{x} ,u_{\theta } ,u_{z} ) \) are the displacements at any point of the shell along the (x, θ, z); (u, v, w) are the middle surface displacements along the (x, θ, z) and \( \psi_{x} \) and \( \psi_{\theta } \) exhibit the total angular rotations of the middle surface normals around the θ and x-axis, respectively.

$$ {\begin{aligned} u_{x} (x,\theta ,z,t) = u(x,\theta ,t) + z\psi_{x} (x,\theta ,t) \hfill \\ u_{\theta } (x,\theta ,z,t) = v(x,\theta ,t) + z\psi_{\theta } (x,\theta ,t) \hfill \\ u_{z} (x,\theta ,z,t) = w(x,\theta ,t) \hfill \\ \end{aligned}} $$
(4)

According to this equation and with the assumption of small displacements, the corresponding strain tensor components are obtained as follows [15]:

$$ {\begin{aligned} & \varepsilon_{xx} = \frac{\partial u}{\partial x} + z\frac{{\partial \psi_{x} }}{\partial x} = \varepsilon_{xx}^{0} + z\kappa_{xx} ;\quad \gamma_{xz} = \psi_{x} + \frac{\partial w}{\partial x} \\ & \varepsilon_{\theta \theta } = \frac{1}{R}\left( {\frac{\partial v}{\partial \theta } + w} \right) + \frac{z}{R}\frac{{\partial \psi_{\theta } }}{\partial \theta } = \varepsilon_{\theta \theta }^{0} + z\kappa_{\theta \theta } ;\quad \gamma_{\theta z} = \psi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R} \\ & \gamma_{x\theta } = \left( {\frac{1}{R}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x}} \right) + z\left( {\frac{1}{R}\frac{{\partial \psi_{x} }}{\partial \theta } + \frac{{\partial \psi_{\theta } }}{\partial x}} \right) = \gamma_{x\theta }^{0} + z\kappa_{x\theta } \\ \end{aligned}} $$
(5)

The classical constitutive equations of the bulk section can be expressed in terms of Lamé parameters \( \lambda = \upsilon E/1 - \upsilon^{2} \) and \( \mu = E/2(1 + \upsilon ) \) as:

$$ \varvec{\sigma}= 2\mu\varvec{\varepsilon}+ \lambda {\mathbf{tr}}\left(\varvec{\varepsilon}\right)\varvec{I} $$
(6)

where \( \varvec{\sigma} \), \( \varvec{\varepsilon} \), \( {\mathbf{tr()}} \), and \( \varvec{I} \) are the classical stress tensor, strain tensor, trace function, and identity matrix, respectively. In FSDT it is assumed that the normal stress \( \sigma_{zz} \) is negligible, thus, Eq. (6) leads to the constitutive equations as:

$$ {\begin{aligned} \sigma_{xx} = \left( {\lambda + 2\mu } \right)\varepsilon_{xx} + \lambda \varepsilon_{\theta \theta } \hfill \\ \sigma_{\theta \theta } = \left( {\lambda + 2\mu } \right)\varepsilon_{\theta \theta } + \lambda \varepsilon_{xx} \hfill \\ \sigma_{x\theta } = \mu \gamma_{x\theta } , \, \sigma_{\theta z} = \mu \gamma_{\theta z} , \, \sigma_{xz} = \mu \gamma_{xz} \hfill \\ \end{aligned}} $$
(7)

2.2 The Gurtin–Murdoch surface elasticity theory

To consider the surface effects, the stresses on the two thin surfaces \( S^{ + } \) (\( z = h/2 \)) and \( S^{ - } \) (\( z = - h/2 \)) which, respectively, denoted by \( \tau_{\beta i}^{ + } \) and \( \tau_{\beta i}^{ - } \), satisfy the equilibrium conditions of Gurtin–Murdoch theory [1, 2] as,

$$ \begin{aligned} & \tau_{\beta i,\beta }^{ + } - \sigma_{iz}^{ + } = \rho^{s + } \ddot{u}_{i}^{ + } \quad {\text{at}}\;z = h/2\quad i = R,\theta ,z ;\;\beta = R,\theta \\ & \tau_{\beta i,\beta }^{ - } + \sigma_{iz}^{ - } = \rho^{s - } \ddot{u}_{i}^{ - } \quad {\text{at}}\;z = - h/2 \\ \end{aligned} $$
(8)

where \( \sigma_{iz}^{ + } \) and \( \sigma_{iz}^{ - } \) are the bulk section stresses at \( S^{ + } \) and \( S^{ - } \) surfaces, respectively, and ui are the components of displacement field. Based on the Gurtin–Murdoch surface elasticity theory, the constitutive equations in the surface layers are expressed as [15]:

$$ \begin{aligned} & \sigma_{\alpha \beta }^{s \pm } = \tau^{s \pm } \delta_{\alpha \beta } + \left( {\tau^{s \pm } + \lambda^{s \pm } } \right)\varepsilon_{\gamma \gamma } \delta_{\alpha \beta } + 2\left( {\mu^{s \pm } - \tau^{s \pm } } \right)\varepsilon_{\alpha \beta } + \tau^{s \pm } u_{\alpha ,\beta }^{s \pm } ;\quad (\alpha ,\beta ,\gamma ) = x,\theta \\ & \sigma_{\alpha z}^{s \pm } = \tau^{s \pm } u_{z,\alpha }^{s \pm } \\ \end{aligned} $$
(9)

where \( \sigma_{\alpha \beta }^{s \pm } \) are the surface stresses and \( \delta_{\alpha \beta } \) is Kronecker delta. Also, \( \lambda^{s} \) and \( \mu^{s} \) are surface Lamé parameters. According to this equation, it can be concluded that:

$$ \begin{aligned} & \sigma_{xx}^{s \pm } = \tau^{s \pm } + \left( {\lambda^{s \pm } + 2\mu^{s \pm } } \right)\varepsilon_{xx} + \left( {\tau^{s \pm } + \lambda^{s \pm } } \right)\varepsilon_{\theta \theta } ,\quad \sigma_{\theta x}^{s \pm } = \mu^{s \pm } \gamma_{\theta x} - \tau^{s \pm } \left[ {\frac{1}{R}\frac{\partial u}{\partial \theta } + \frac{z}{R}\frac{{\partial \psi_{x} }}{\partial \theta }} \right] \\ & \sigma_{\theta \theta }^{s \pm } = \tau^{s \pm } + \left( {\lambda^{s \pm } + 2\mu^{s \pm } } \right)\varepsilon_{\theta \theta } + \left( {\tau^{s \pm } + \lambda^{s \pm } } \right)\varepsilon_{xx} - \tau^{s \pm } \frac{w}{R} ,\quad \sigma_{xz}^{s \pm } = \tau^{s \pm } \frac{\partial w}{\partial x} \\ & \sigma_{x\theta }^{s \pm } = \mu^{s \pm } \gamma_{x\theta } - \tau^{s \pm } \left[ {\frac{\partial v}{\partial x} + z\frac{{\partial \psi_{\theta } }}{\partial x}} \right] ,\quad \sigma_{\theta z}^{s \pm } = \frac{{\tau^{s \pm } }}{R}\frac{\partial w}{\partial \theta } \\ \end{aligned} $$
(10)

As mentioned earlier, in the FSDT the normal stress \( \sigma_{zz} \) is negligible; but this assumption is not able to satisfy the equilibrium equation of surface elasticity theory [Eq. (8)]. To solve this contradiction, different distribution of \( \sigma_{zz} \) through the thickness is introduced [47, 48] among which the cubically distribution is proposed for structures with varying material properties such as FGM [48]. Using this distribution and the expression related to the i = z in Eq. (8), \( \sigma_{zz} \) is then obtained as:

$$ \begin{aligned} \sigma_{zz} & = f\left( z \right)\left( {\sigma_{zz}^{s + } - \sigma_{zz}^{s - } } \right){ + }\frac{1}{2}\left( {\sigma_{zz}^{s + } + \sigma_{zz}^{s - } } \right) \\ & \quad { = }f\left( z \right)\left[ {\left( {\tau^{s + } + \tau^{s - } } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{{R^{2} }}\left( {\tau^{s + } + \tau^{s - } } \right)\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \left( {\rho^{s + } + \rho^{s - } } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right] \\ & \quad \quad { + }\frac{1}{2}\left[ {\left( {\tau^{s + } - \tau^{s - } } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{{R^{2} }}\left( {\tau^{s + } - \tau^{s - } } \right)\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \left( {\rho^{s + } - \rho^{s - } } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right] \\ \end{aligned} $$
(11)

where \( f\left( z \right) = \frac{2z}{h}\left( {\frac{{z^{2} }}{{h^{2} }} - \frac{3}{4}} \right) \). So, the normal stresses \( \sigma_{xx} \) and \( \sigma_{\theta \theta } \) in Eq. (7) are modified as:

$$ \begin{aligned} \sigma_{xx} & = \left( {\lambda + 2\mu } \right)\varepsilon_{xx} + \lambda \varepsilon_{\theta \theta } + \frac{\lambda }{2\mu }\sigma_{zz} \\ \sigma_{\theta \theta } & = \left( {\lambda + 2\mu } \right)\varepsilon_{\theta \theta } + \lambda \varepsilon_{xx} + \frac{\lambda }{2\mu }\sigma_{zz} \\ \end{aligned} $$
(12)

Thus, the classical force resultants \( \tilde{N}_{ij}^{c} \), bending moments \( \tilde{M}_{ij}^{c} \) and shear forces \( \tilde{Q}_{ij}^{c} \) incorporating the surface effects can be deduced as follows:

$$ \begin{aligned} \tilde{N}_{xx}^{c} & = \int\limits_{ - h/2}^{h/2} {\sigma_{xx} dz} + \sigma_{xx}^{s + } + \sigma_{xx}^{s - } \, \Rightarrow \, \tilde{N}_{xx}^{c} = A_{11}^{*} \varepsilon_{xx}^{0} + A_{12}^{*} \varepsilon_{\theta \theta }^{0} + B_{11}^{*} k_{xx} + B_{12}^{*} k_{\theta \theta } + \left( {\tau^{s + } + \tau^{s - } } \right) \\ & \quad + a_{1} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) - a_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} \\ \tilde{N}_{\theta \theta }^{c} & = \int\limits_{ - h/2}^{h/2} {\sigma_{\theta \theta } dz} + \sigma_{\theta \theta }^{s + } + \sigma_{\theta \theta }^{s - } \, \Rightarrow \, \tilde{N}_{\theta \theta }^{c} = A_{11}^{*} \varepsilon_{\theta \theta }^{0} + A_{12}^{*} \varepsilon_{xx}^{0} + B_{11}^{*} k_{\theta \theta } + B_{12}^{*} k_{xx} + \left( {\tau^{s + } + \tau^{s - } } \right) \\ & \quad + a_{1} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{a_{1} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - a_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} - \left( {\tau^{s + } + \tau^{s - } } \right)\frac{w}{R} \\ \tilde{N}_{x\theta }^{c} & = \int\limits_{ - h/2}^{h/2} {\sigma_{x\theta } dz} + \frac{1}{2}\left( {\sigma_{x\theta }^{s + } + \sigma_{x\theta }^{s - } + \sigma_{\theta x}^{s + } + \sigma_{\theta x}^{s - } } \right) \, \Rightarrow \, \tilde{N}_{x\theta }^{c} = A_{66}^{*} \gamma_{x\theta }^{0} + B_{66}^{*} k_{x\theta } \\ \tilde{M}_{xx}^{c} & = \int\limits_{ - h/2}^{h/2} {\sigma_{xx} zdz} + \frac{h}{2}\left( {\sigma_{xx}^{s + } - \sigma_{xx}^{s - } } \right) \, \Rightarrow \, \tilde{M}_{xx}^{c} = B_{11}^{*} \varepsilon_{xx}^{0} + B_{12}^{*} \varepsilon_{\theta \theta }^{0} + D_{11}^{*} k_{xx} + D_{12}^{*} k_{\theta \theta } \\ & \quad + \frac{h}{2}\left( {\tau^{s + } - \tau^{s - } } \right) + b_{1} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) - b_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} \\ \tilde{M}_{\theta \theta }^{c} & = \int\limits_{ - h/2}^{h/2} {\sigma_{\theta \theta } zdz} + \frac{h}{2}\left( {\sigma_{\theta \theta }^{s + } - \sigma_{\theta \theta }^{s - } } \right) \, \Rightarrow \, \tilde{M}_{\theta \theta }^{c} = B_{11}^{*} \varepsilon_{\theta \theta }^{0} + B_{12}^{*} \varepsilon_{xx}^{0} + D_{11}^{*} k_{\theta \theta } + D_{12}^{*} k_{xx} \\ & \quad + \frac{h}{2}\left( {\tau^{s + } - \tau^{s - } } \right) + b_{1} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) - b_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} - \frac{h}{2}\left( {\tau^{s + } - \tau^{s - } } \right)\frac{w}{R} \\ \tilde{M}_{x\theta }^{c} & = \int\limits_{ - h/2}^{h/2} {\sigma_{x\theta } zdz} + \frac{h}{2}\left( {\sigma_{x\theta }^{s + } - \sigma_{x\theta }^{s - } + \sigma_{\theta x}^{s + } - \sigma_{\theta x}^{s - } } \right) \, \Rightarrow \, \tilde{N}_{x\theta }^{c} = B_{66}^{*} \gamma_{x\theta }^{0} + D_{66}^{*} k_{x\theta } \\ Q_{xz}^{c} & = \kappa_{s} A_{66} \gamma_{xz} ,\quad Q_{\theta z}^{c} = \kappa_{s} A_{66} \gamma_{\theta z} ,\quad Q_{xz}^{{s{\text{ c}}}} = \left( {\tau^{s + } + \tau^{s - } } \right)\frac{\partial w}{\partial x} ,\quad Q_{\theta z}^{{s{\text{ c}}}} = \left( {\tau^{s + } + \tau^{s - } } \right)\frac{1}{R}\frac{\partial w}{\partial \theta } \\ \end{aligned} $$
(13)

where \( \kappa_{s} = 5/6 \) is the shear correction factor [49]. The defined coefficients in this equation are presented in “Appendix”. This equation will be used in extracting the governing motion equations and B.C. in terms of displacement field components.

2.3 Nonlocal strain gradient theory

As mentioned in the introduction section, Lim et al. [27] proposed the NSGT that contains two independent material size-dependent parameters, nonlocal parameter \( \xi \) and material length scale parameter l, which are associated with the nonlocal [20] and pure strain gradient theories [25], respectively. The NSGT general stress tensor, t, is explained as:

$$ \varvec{t} =\varvec{\sigma}- \nabla\varvec{\sigma}^{{\left( {\mathbf{1}} \right)}} $$
(14)

where \( \nabla \) is the gradient operator. Also, \( \varvec{\sigma} \) and \( \varvec{\sigma}^{{\left( {\mathbf{1}} \right)}} \) are the nonlocal stress tensors of zeroth and higher order and are defined as follows [50]:

$$ (1 - \zeta^{2} {\nabla }^{2} )\varvec{\sigma}= \varvec{C:\varepsilon } $$
(15)
$$ (1 - \zeta^{2} {\nabla }^{2} )\varvec{\sigma}^{(1)} = l^{2} \varvec{C:}{\nabla }\varvec{\varepsilon} $$
(16)

in which \( \varvec{\varepsilon} \), \( {\mathbf{\nabla }}\varvec{\varepsilon} \) and \( \varvec{C} \) denote the strain tensor, strain gradient tensor and fourth-order elasticity tensor, respectively, and \( \nabla^{2} \) is the Laplacian operator. Using Eqs. (15), (16) and (14), the constitutive equation of NSGT can be then obtained. The index notation of this equation is as follows:

$$ \begin{aligned} (1 - \zeta^{2} \nabla^{2} )t_{ij} & = C_{ijkl} \varepsilon_{kl} - l^{2} \delta_{mn} C_{ijkl} \varepsilon_{kl,mn} \, \Rightarrow \\ (1 - \zeta^{2} \nabla^{2} )t_{ij} & = C_{ijkl} (1 - l^{2} \nabla^{2} )\varepsilon_{kl} \, \Rightarrow \, \\ (1 - \zeta^{2} \nabla^{2} )t_{ij} & = (1 - l^{2} \nabla^{2} )\sigma_{ij}^{c} \\ \end{aligned} $$
(17)

Here \( \sigma_{ij}^{c} \) is the classical stress tensor. The governing motion equations and boundary conditions will be derived by computing the strain and kinetic energies and then using Hamilton’s principle. According to this principle, the variation of the energy of system in the time domain must be set equal to zero. In the absence of work done by external forces, this principle is formulated as follows:

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {\left( {\varPi_{T} - \varPi_{s} } \right) \, } dt = 0 $$
(18)

Here \( \delta \) is the variation operator, and, \( \varPi_{T} \) and \( \varPi_{s} \) indicate the kinetic and potential energies, respectively. According to the NSGT, the strain energy is expressed as [51]:

$$ \varPi_{s} = \frac{1}{2}\iiint\limits_{V} {\left( {\sigma_{ij} \varepsilon_{ij} + \sigma_{ijm}^{\left( 1 \right)} \varepsilon_{ij,m} } \right){\text{d}}V} $$
(19)

This equation can be rewritten in the following form using the divergence theorem:

$$ \begin{aligned} \varPi_{s} & { = }\frac{1}{2}\iiint\limits_{V} {\left( {\sigma_{ij} - \sigma_{ijm,m}^{\left( 1 \right)} } \right)\varepsilon_{ij} {\text{d}}V} + \frac{1}{2}\iint\limits_{A} {\sigma_{ijm}^{\left( 1 \right)} }\varepsilon_{ij} {\text{d}}An_{x} \\ & { = }\frac{1}{2}\iiint\limits_{V} {t_{ij} \varepsilon_{ij} {\text{d}}V} + \frac{1}{2}\iint\limits_{A} {\sigma_{ijm}^{\left( 1 \right)} }\varepsilon_{ij} {\text{d}}An_{x} \\ \end{aligned} $$
(20)

where \( n_{x} \) is the unit vector perpendicular to cross-section area and \( {\text{d}}A = R{\text{d}}\theta {\text{d}}z \). By defining the nonclassical force resultants \( \tilde{N}_{ij} ,\tilde{N}_{ij}^{\left( 1 \right)} \), bending moments \( \tilde{M}_{ij} ,\tilde{M}_{ij}^{\left( 1 \right)} \) and shear forces \( \tilde{Q}_{ij} \), \( \tilde{Q}_{ij}^{\left( 1 \right)} \) based on their counterpart in classical form as

$$ \begin{aligned} \left\{ \begin{aligned} \begin{array}{*{20}c} {\tilde{N}_{xx} ,\tilde{N}_{xx}^{(1)} } \\ {\tilde{N}_{\theta \theta } ,\tilde{N}_{\theta \theta }^{(1)} } \\ {\tilde{N}_{x\theta } } \\ \end{array} \hfill \\ \, \tilde{N}_{x\theta }^{(1)} \hfill \\ \end{aligned} \right\} & = \int\limits_{ - h/2}^{h/2} {\left\{ \begin{aligned} \begin{array}{*{20}c} {t_{xx} ,\sigma_{xx}^{(1)} } \\ {t_{\theta \theta } ,\sigma_{\theta \theta }^{(1)} } \\ {t_{x\theta } } \\ \end{array} \hfill \\ \, \sigma_{x\theta }^{(1)} \hfill \\ \end{aligned} \right\}{\text{d}}z} + \left\{ \begin{aligned} \, \begin{array}{*{20}c} {t_{xx}^{s + } + t_{xx}^{s - } ,\sigma_{xx}^{{s + { (1)}}} + \sigma_{xx}^{{s + { (1)}}} } \\ {t_{\theta \theta }^{s + } + t_{\theta \theta }^{s - } ,\sigma_{\theta \theta }^{{s + { (1)}}} + \sigma_{\theta \theta }^{{s - { (1)}}} } \\ {0.5\left( {t_{x\theta }^{s + } + t_{x\theta }^{s - } + t_{\theta x}^{s + } + t_{\theta x}^{s - } } \right)} \\ \end{array} \hfill \\ 0.5\left( {\sigma_{x\theta }^{{s + { (1)}}} + \sigma_{x\theta }^{{s - { (1)}}} + \sigma_{\theta x}^{{s + { (1)}}} + \sigma_{\theta x}^{{s - { (1)}}} } \right) \hfill \\ \end{aligned} \right\} \\ \left\{ \begin{aligned} \begin{array}{*{20}c} {\tilde{M}_{xx} ,\tilde{M}_{xx}^{(1)} } \\ {\tilde{M}_{\theta \theta } ,\tilde{M}_{\theta \theta }^{(1)} } \\ {\tilde{M}_{x\theta } } \\ \end{array} \hfill \\ \, \tilde{M}_{x\theta }^{(1)} \hfill \\ \end{aligned} \right\} & = \int\limits_{ - h/2}^{h/2} {\left\{ \begin{aligned} \begin{array}{*{20}c} {t_{xx} ,\sigma_{xx}^{(1)} } \\ {t_{\theta \theta } ,\sigma_{\theta \theta }^{(1)} } \\ {t_{x\theta } } \\ \end{array} \hfill \\ \, \sigma_{x\theta }^{(1)} \hfill \\ \end{aligned} \right\}z{\text{d}}z + \frac{h}{2}\left\{ \begin{aligned} \, \begin{array}{*{20}c} {t_{xx}^{s + } - t_{xx}^{s - } ,\sigma_{xx}^{{s + { (1)}}} - \sigma_{xx}^{{s + { (1)}}} } \\ {t_{\theta \theta }^{s + } - t_{\theta \theta }^{s - } ,\sigma_{\theta \theta }^{{s + { (1)}}} - \sigma_{\theta \theta }^{{s - { (1)}}} } \\ {0.5\left( {t_{x\theta }^{s + } - t_{x\theta }^{s - } + t_{\theta x}^{s + } - t_{\theta x}^{s - } } \right)} \\ \end{array} \hfill \\ 0.5\left( {\sigma_{x\theta }^{{s + { (1)}}} - \sigma_{x\theta }^{{s - { (1)}}} + \sigma_{\theta x}^{{s + { (1)}}} - \sigma_{\theta x}^{{s - { (1)}}} } \right) \hfill \\ \end{aligned} \right\}} \\ \left\{ {\begin{array}{*{20}c} {\tilde{Q}_{xz} ,\tilde{Q}_{xz}^{(1)} } \\ {\tilde{Q}_{\theta z} ,\tilde{Q}_{\theta z}^{(1)} } \\ {\tilde{Q}_{xz}^{s} ,\tilde{Q}_{xz}^{{s{ (1)}}} } \\ {\tilde{Q}_{\theta z}^{s} ,\tilde{Q}_{\theta z}^{{s{ (1)}}} } \\ \end{array} } \right\} & = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {t_{xz} ,\sigma_{xz}^{(1)} } \\ {t_{\theta z} ,\sigma_{\theta z}^{(1)} } \\ {t_{xz}^{s + } + t_{xz}^{s + } ,\sigma_{xz}^{{s + { (1)}}} + \sigma_{xz}^{{s + { (1)}}} } \\ {t_{\theta z}^{s + } + t_{\theta z}^{s + } ,\sigma_{\theta z}^{{s + { (1)}}} + \sigma_{\theta z}^{{s + { (1)}}} } \\ \end{array} } \right\}{\text{d}}z} \\ \end{aligned} $$
(21)

the strain energy can be written as

$$ \begin{aligned} \varPi_{s} & = \frac{1}{2}\int\limits_{A} {\left\{ \begin{aligned} \tilde{N}_{xx} \varepsilon_{xx}^{0} + \tilde{N}_{\theta \theta } \varepsilon_{\theta \theta }^{0} + \tilde{N}_{x\theta } \gamma_{x\theta }^{0} + \tilde{M}_{xx} \kappa_{xx} + \tilde{M}_{\theta \theta } \kappa_{\theta \theta } + \tilde{M}_{x\theta } \kappa_{x\theta } \hfill \\ { + }\tilde{Q}_{xz} \gamma_{xz} + \tilde{Q}_{\theta z} \gamma_{\theta z} { + }\tilde{Q}_{xz}^{s} \frac{\partial w}{\partial x} + \tilde{Q}_{\theta z}^{s} \frac{1}{R}\frac{\partial w}{\partial \theta } \hfill \\ \end{aligned} \right\}{\text{d}}s} \\ & \quad { + }\frac{1}{2}\int {\left\{ \begin{aligned} \tilde{N}_{xx}^{(1)} \varepsilon_{xx}^{0} + \tilde{N}_{\theta \theta }^{(1)} \varepsilon_{\theta \theta }^{0} + \tilde{N}_{x\theta }^{(1)} \gamma_{x\theta }^{0} + \tilde{M}_{xx}^{(1)} \kappa_{xx} + \tilde{M}_{\theta \theta }^{(1)} \kappa_{\theta \theta } + \tilde{M}_{x\theta }^{(1)} \kappa_{x\theta } \hfill \\ { + }\tilde{Q}_{xz}^{(1)} \gamma_{xz} + \tilde{Q}_{\theta z}^{(1)} \gamma_{\theta z} { + }\tilde{Q}_{xz}^{{s{ (1)}}} \frac{\partial w}{\partial x} + \tilde{Q}_{\theta z}^{{s{ (1)}}} \frac{1}{R}\frac{\partial w}{\partial \theta } \hfill \\ \end{aligned} \right\}R{\text{d}}\theta n_{x} } \\ \end{aligned} $$
(22)

where \( {\text{d}}s = R{\text{d}}\theta {\text{d}}x \). It should be noted that in Eq. (21) the terms with (\( s \pm \)) superscripts are related to the surface stresses.

The kinetic energy of the system can be expressed as:

$$ \begin{aligned} \varPi_{T} & = \frac{1}{2}\int\limits_{s} {\int\limits_{ - h/2}^{h/2} {\rho \left[ {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{\theta } }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} } \right]{\text{d}}z} {\text{d}}s} \\ & \quad + \frac{1}{2}\int\limits_{{s^{ + } }} {\rho^{s + } } \left[ {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{\theta } }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} } \right]{\text{d}}s^{ + } \\ & \quad { + }\frac{1}{2}\int\limits_{{s^{ - } }} {\rho^{s - } } \left[ {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{\theta } }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} } \right]{\text{d}}s^{ - } \\ \end{aligned} $$
(23)

By inserting Eq. (4) into Eq. (23), the kinetic energy takes the form of:

$$ \varPi_{T} = \frac{1}{2}\int\limits_{s} {\left\{ \begin{aligned} I_{0}^{*} \left[ {\left( {\frac{\partial u}{\partial t}} \right)^{2} + \left( {\frac{\partial v}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right] + 2I_{1}^{*} \left[ {\left( {\frac{\partial u}{\partial t}} \right)\left( {\frac{{\partial \psi_{x} }}{\partial t}} \right) + \left( {\frac{\partial v}{\partial t}} \right)\left( {\frac{{\partial \psi_{\theta } }}{\partial t}} \right)} \right] \hfill \\ + I_{2}^{*} \left[ {\left( {\frac{{\partial \psi_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial \psi_{\theta } }}{\partial t}} \right)^{2} } \right] \hfill \\ \end{aligned} \right\}{\text{d}}s} $$
(24)

where

$$ {\begin{aligned} & I_{0}^{*} = \int\limits_{ - h/2}^{h/2} \rho {\text{d}}z + \left( {\rho^{s + } + \rho^{s - } } \right) ,\quad I_{0}^{*} = \int\limits_{ - h/2}^{h/2} {\rho z} {\text{d}}z + \frac{h}{2}\left( {\rho^{s + } - \rho^{s - } } \right) \\ & I_{2}^{*} = \int\limits_{ - h/2}^{h/2} {\rho z^{2} } {\text{d}}z + \frac{{h^{2} }}{4}\left( {\rho^{s + } + \rho^{s - } } \right) \\ \end{aligned}} $$
(25)

By substituting Eqs. (22) and (24) in Eq. (18) and calculating the first variation, the equations of motion can be derived as:

$$ \begin{aligned} & \delta u:\quad \frac{\partial }{\partial x}\left( {\tilde{N}_{xx} } \right) + \frac{1}{R}\frac{\partial }{\partial \theta }\left( {\tilde{N}_{x\theta } } \right) = I_{0}^{*} \frac{{\partial^{2} u}}{{\partial t^{2} }} \\ & \delta v:\quad \frac{1}{R}\frac{\partial }{\partial \theta }\left( {\tilde{N}_{\theta \theta } } \right) + \frac{\partial }{\partial x}\left( {\tilde{N}_{x\theta } } \right) + \frac{1}{R}Q_{\theta z} = I_{0}^{*} \frac{{\partial^{2} v}}{{\partial t^{2} }} \\ & \delta w:\quad \frac{\partial }{\partial x}\left( {\tilde{Q}_{xz} + \tilde{Q}_{xz}^{s} } \right) + \frac{1}{R}\frac{\partial }{\partial \theta }\left( {\tilde{Q}_{\theta z} + \tilde{Q}_{\theta z}^{s} } \right) - \frac{1}{R}\tilde{N}_{\theta \theta } = I_{0}^{*} \frac{{\partial^{2} w}}{{\partial t^{2} }} \\ & \delta \psi_{x} :\quad \frac{\partial }{\partial x}\left( {\tilde{M}_{xx} } \right) + \frac{1}{R}\frac{\partial }{\partial \theta }\left( {\tilde{M}_{x\theta } } \right) - \tilde{Q}_{xz} = I_{2}^{*} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} \\ & \delta \psi_{\theta } :\quad \frac{1}{R}\frac{\partial }{\partial \theta }\left( {\tilde{M}_{\theta \theta } } \right) + \frac{\partial }{\partial x}\left( {\tilde{M}_{x\theta } } \right) - \tilde{Q}_{z\theta } = I_{2}^{*} \frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }} \\ \end{aligned} $$
(26)

and B.Cs as:

$$ {\begin{aligned} & \delta u = 0\quad {\text{or}}\quad \tilde{N}_{xx} - \frac{1}{R}\frac{{\partial \tilde{N}_{x\theta }^{(1)} }}{\partial \theta } = 0 ,\quad \delta \frac{\partial u}{\partial x} = 0\quad {\text{or}}\quad \tilde{N}_{xx}^{(1)} = 0 \\ & \delta v = 0\quad {\text{or}}\quad \tilde{N}_{x\theta } - \frac{1}{R}\frac{{\partial \tilde{N}_{\theta \theta }^{(1)} }}{\partial \theta } - \frac{{\tilde{Q}_{\theta z}^{(1)} }}{R} = 0 ,\quad \delta \frac{\partial v}{\partial x} = 0\quad {\text{or}}\quad \tilde{N}_{x\theta }^{(1)} = 0 \\ & \delta w = 0\quad {\text{or}}\quad \tilde{Q}_{xz} + \tilde{Q}_{xz}^{s} + \frac{{\tilde{N}_{\theta \theta }^{(1)} }}{R} - \frac{1}{R}\frac{{\partial \tilde{Q}_{\theta z}^{(1)} }}{\partial \theta } - \frac{1}{R}\frac{{\partial \tilde{Q}_{\theta z}^{s \, (1)} }}{\partial \theta } = 0 \\ & \delta \frac{\partial w}{\partial x} = 0\quad {\text{or}}\quad \tilde{Q}_{xz}^{(1)} + \tilde{Q}_{xz}^{s \, (1)} = 0 \\ & \delta \psi_{x} = 0\quad {\text{or}}\quad \tilde{M}_{xx} - \frac{1}{R}\frac{{\partial \tilde{M}_{x\theta }^{(1)} }}{\partial \theta } + \tilde{Q}_{xz}^{(1)} = 0 ,\quad \delta \frac{{\partial \psi_{x} }}{\partial x} = 0\quad {\text{or}}\quad \tilde{M}_{xx}^{(1)} = 0 \\ & \delta \psi_{\theta } = 0\quad {\text{or}}\quad \tilde{M}_{x\theta } - \frac{1}{R}\frac{{\partial \tilde{M}_{\theta \theta }^{(1)} }}{\partial \theta } + \tilde{Q}_{\theta z}^{(1)} = 0 ,\quad \delta \frac{{\partial \psi_{\theta } }}{\partial x} = 0\quad {\text{or}}\quad \tilde{M}_{x\theta }^{(1)} = 0 \\ \end{aligned}} $$
(27)

According to Eq. (17) which is actually the relation between the nonclassical and classical stresses, and Eq. (15), it can be concluded that

$$ (1 - \zeta^{2} \nabla^{2} )\left\{ \begin{aligned} \tilde{N}_{ij} \hfill \\ \tilde{M}_{ij} \hfill \\ \tilde{Q}_{ij} \hfill \\ \end{aligned} \right\} = (1 - l^{2} \nabla^{2} )\left\{ \begin{aligned} \tilde{N}_{ij}^{c} \hfill \\ \tilde{M}_{ij}^{c} \hfill \\ \tilde{Q}_{ij}^{c} \hfill \\ \end{aligned} \right\} $$
(28)
$$ (1 - \zeta^{2} \nabla^{2} )\left\{ \begin{aligned} \tilde{N}_{ij}^{\left( 1 \right)} \hfill \\ \tilde{M}_{ij}^{\left( 1 \right)} \hfill \\ \tilde{Q}_{ij}^{\left( 1 \right)} \hfill \\ \end{aligned} \right\} = l^{2} \frac{\partial }{\partial x}\left\{ \begin{aligned} \tilde{N}_{ij}^{c} \hfill \\ \tilde{M}_{ij}^{c} \hfill \\ \tilde{Q}_{ij}^{c} \hfill \\ \end{aligned} \right\} $$
(29)

By applying Eqs. (28) and (29) in Eqs. (26) and (27) and using Eq. (13), the governing motion equations and B.Cs can be extracted in terms of components of displacement field (i.e., u, v, w, \( \psi_{x} \) and \( \psi_{\theta } \)).

2.4 The solution procedure

The extracted governing equations are solved using the generalized differential quadrature (GDQ) method. This method was presented by Shu and Richards [52] and Shu [53] as an extension of the differential quadrature (DQ) method [54, 55]. According to this method, the mth order derivative at a grid point coordinate xi along the x-direction, \( f_{x}^{\left( m \right)} \left( {x_{i} } \right) \), is given as:

$$ f_{x}^{\left( m \right)} \left( {x_{i} } \right) = \sum\limits_{j = 1}^{N} {C_{ij}^{\left( m \right)} f\left( {x_{j} } \right)} ,\quad \, i = 1,2, \ldots ,N $$
(30)

where N is the number of grid points along the x-direction, and \( C_{ij}^{\left( m \right)} \) are the weighting factors of mth order derivative. In the GDQ method, the weighting factors of the first-order derivative can be computed without any restriction in the choice of the number of grid points as follows [56]:

$$ \begin{aligned} & C_{ij}^{\left( 1 \right)} = \frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}} ,\quad i,j = 1,2, \ldots ,N\;{\text{and}}\;i \ne j \\ & C_{ii}^{\left( 1 \right)} = - \sum\limits_{j = 1,i \ne j}^{N} {C_{ij}^{\left( 1 \right)} } ,\quad i = j \\ \end{aligned} $$
(31)

where

$$ M\left( {x_{i} } \right) = \prod\limits_{j = 1,i \ne j}^{N} {\left( {x_{i} - x_{j} } \right)} $$
(32)

For the mth order derivative, the weighting factors will be calculated considering the recurrence formula as follows:

$$ \begin{aligned} & C_{ij}^{\left( m \right)} = m\left( {C_{ij}^{\left( 1 \right)} C_{ij}^{{\left( {m - 1} \right)}} - \frac{{C_{ij}^{{\left( {m - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right) ,\quad \, j \ne i ,\; 2\le m \le N - 1 \\ & C_{ii}^{\left( m \right)} = - \sum\limits_{j = 1,i \ne j}^{N} {C_{ij}^{\left( m \right)} } ,\quad \, j = i \\ \end{aligned} $$
(33)

The distribution of grid points plays an important role in the acceptable performance of the DQ/GDQ method. In this paper, Chebyshev–Gauss–Lobatto as a nonuniform distribution is utilized which determines the coordinates of grid points as follows:

$$ x_{i} = \frac{1}{2}\left[ {1 - \cos \left( {\frac{i - 1}{N - 1}\pi } \right)} \right] ,\quad i = 1,2, \ldots N $$
(34)

To solve the governing equations, the following solutions are assumed for the components of displacement field:

$$ \left\{ \begin{array}{l} u(x,\theta ,t) \\ v(x,\theta ,t) \\ w(x,\theta ,t) \\ \psi_{x} (x,\theta ,t) \\ \psi_{\theta } (x,\theta ,t) \\ \end{array} \right\} = \sum\limits_{n = 1}^{\infty} \left\{ \begin{array}{l} U_{n} (x)\,\cos \,(n\theta )e^{i\omega t} \\ V_{n} (x)\,\,\sin \,(n\theta )e^{i\omega t} \\ W_{n} (x)\,\cos \,(n\theta )e^{i\omega t} \\ \varPsi_{nx} (x)\,\cos \,(n\theta )e^{i\omega t} \\ \varPsi_{n\theta} (x)\,\sin \,(n\theta )e^{i\omega t} \\ \end{array} \right\} $$
(35)

Here \( U, V, W,\Psi _{x} ,\, {\text{and}}\,\Psi _{\theta } \) denote the vibration amplitudes. Also, n and \( \omega \) exhibit the circumferential wave number and the natural frequency of nanoshell, respectively. By inserting Eq. (35) into the governing equations and related B.Cs and then employing the GDQ method, the following general relation is achieved:

$$ \left( {\left[ K \right] + \left[ M \right]\omega^{2} } \right)\left\{ {\begin{array}{*{20}c} U \\ V \\ W \\ {\varPsi_{x\,} } \\ {\varPsi_{\theta } } \\ \end{array} } \right\} = 0 $$
(36)

in which K and M are the stiffness and mass matrixes, respectively. Finally, by calculating the eigenvalues of the above equation, natural frequencies will be predicted.

At the end of this subsection, it should be mentioned that in addition to the finite element based solution methods in solving the governing equations, recently, new solution methods [57, 58] based on neural networks and machine learning have presented which can be used in this regard.

3 Numerical results and discussion

In the current section, results of the proposed FG nanoshell will be analyzed. The bulk and surfaces material properties of this nanoshell are illustrated in Table 1. Also, the dimensionless nonlocal and material length scale parameters are supposed to be \( \zeta /h = 50 \) and l/h = 10, respectively. It should be noted that for simplicity, different theories of the classical continuum, nonlocal, strain gradient and nonlocal strain gradient are displayed as Classic, Nonlocal, SG and NSGT, respectively.

Table 1 Bulk and surfaces material properties [48]
Full size table

3.1 Convergence and stability

In order to investigate the convergence and stability of the GDQ method in different theories and B.Cs with and without consideration of surface effects, the dimensionless natural frequency of a FG cylindrical nanoshell for the various number of grid points are listed in Table 2. The dimensionless natural frequency is given by:

$$ {{\Omega}} = \omega R\sqrt {\rho^{ + } /E^{ + } } $$
(37)

It is observed that in all cases for simply supported (SS) B.Cs and the case of with surface effects for clamped (CC) B.Cs, convergence occurs in the minimum number of grid points, i.e., 13. Beside, SG theory without surface effects and clamped B.Cs requires the maximum number of grid points (i.e., 21) for convergence. Also, it can be concluded that the surface effects have led to the enhancement of the stability and the rate of convergence of the responses. The geometric properties of the presented shell model are h = 0.3 nm, R/h = 10, L/R = 20, \( \zeta /h = 50 \), l/h = 10, k = 2.

Table 2 Convergence of the dimensionless natural frequency \( {{\Omega}} = \omega R\sqrt {\rho^{ + } /E^{ + } } \) for a FG cylindrical shell (h = 0.3 nm, R/h = 10, L/R = 20, \( \zeta /h = 50 \), l/h = 10, k = 2)
Full size table

3.2 Comparison of results

In Table 3, results of the natural frequency for a simply supported FG cylindrical macroshell are compared with those obtained by Loy et al. [59] for various FG gradient index and the thickness-to-radius ratio. The upper and inner surfaces of this shell consist of Nickel (\( E^{ + } = 205.098\,{\text{GPa}} \), \( \nu^{ + } = 0.31 \), \( \rho^{ + } = 8900\,{\text{kg/m}}^{3} \)) and stainless steel (\( E^{ + } = 207.788\,{\text{GPa}} \), \( \nu^{ + } = 0.317756 \), \( \rho^{ + } = 8166\,{\text{kg/m}}^{3} \)), respectively. From this table, the results of this study are in excellent accord with those given by Loy et al. [59]. For another validation of the present study, as tabulated in Table 4 for different values of the nonlocal parameter and the thickness-to-radius ratio, a simply supported homogeneous nonlocal cylindrical shell model provides a good agreement with Alibeigloo and Shaban [60]. The observed difference between the results is due to the fact that in Ref. [60] the three-dimensional elasticity theory is used to investigate the vibration of the nanoshell. Here, the shell has the properties of \( E = 1.06\,{\text{TPa}} \), \( \nu = 0.3 \), \( \rho = 2300\,{\text{kg/m}}^{3} \), \( R = 2.32\,{\text{nm}} \), and \( L/R = 5 \). Notice that for comparison study, the surface effects have been ignored.

Table 3 Comparison of the natural frequency \( \tilde{\omega } = \omega /2\pi \) for a simply supported FG cylindrical macro shell (m = n = 1 and L/R = 20)
Full size table
Table 4 Comparison of the dimensionless natural frequency \( {{\Omega}} = \omega R\sqrt {\rho /E} \) for a simply supported homogeneous cylindrical nanoshell based on the nonlocal theory (m = n = 1 and L/R = 5)
Full size table

3.3 Effect of surface properties

The aim of this subsection is establishing a comprehensive study on the effects of surface properties on the dimensionless natural frequency. To this end, a clamped and a simply supported homogenous cylindrical nanoshell based on the NSGT with properties of h = 0.3 nm, R/h = 10, \( \zeta /h = 50 \), l/h = 10 are considered. Figures of this subsection include two parts (a) and (b) which are, respectively, related to the clamped and simply supported B.Cs.

The effects of surface elastic properties of \( \lambda^{s} \) and \( \mu^{s} \) are discussed at first. The positive values of these parameters have the concept of enhancing the stiffness of the whole structure, and the negative values have the sense of reducing it. Therefore, due to the direct relationship between the frequency and the stiffness of structure, compared to the zero values of these properties, their positive and negative values have led to the increase and decrease in the frequency, respectively. This effect is visible in Figs. 2 and 3 in which the variation of frequency versus length-to-radius ratio is plotted in different values of \( \lambda^{s} \) and \( \mu^{s} \), respectively.

Fig. 2
figure 2

Variation of the dimensionless natural frequency \( {{\Omega}} \) with length-to-radius ratio L/R for different values of surface elastic property \( \lambda^{s} \)-homogenous cylindrical nanoshell. a Clamped and b simply supported B.Cs (h = 0.3 nm, R/h = 10, \( \zeta /h = 50 \), l/h = 10)

Full size image
Fig. 3
figure 3

Variation of the dimensionless natural frequency \( {{\Omega }} \) with length-to-radius ratio L/R for different values of surface elastic property \( \mu^{s} \)-homogenous cylindrical nanoshell. a Clamped and b simply supported B.Cs (h = 0.3 nm, R/h = 10, \( \zeta /h = 50 \), l/h = 10)

Full size image

From the comparative investigation of the influence of these two surface elastic properties on the frequency, as it can be seen in Figs. 2 and 3, the \( \mu^{s} \) property is more effective than the \( \lambda^{s} \) in this regard. Also, the negative values of \( \lambda^{s} \) make more changes to the frequency than the positive values of this property, while this behavior is not significant for the \( \mu^{s} \). Another remarkable conclusion from these figures is the reduction of the surface elastic properties effect on the frequency by increasing the ratio of length to radius and convergence of the results to the frequency which is close to the frequency of without considering these surface properties. So, it can be concluded that by increasing the ratio of length to radius, and in fact by increasing the size of the structure, these properties can be ignored.

Next investigation is about the effect of surface mass density \( \rho^{s} \) on the frequency. As illustrated in Fig. 4, given that the consideration of surface mass density leads to an increase in the density of structure, the frequency reduces through the enhancement of this property. This behavior can be interpreted in such a way that considering the surface mass density makes the structure more flexible. This reduction in frequency does not occur at a constant rate. It means that with a gradual increase in surface mass density, the variation of frequency decreases. Also, the same behavior to the surface elastic properties can be seen by increasing the ratio of length to radius, i.e., diminution of the effect of surface mass density on the frequency and approaching the frequency to the case of without surface mass density.

Fig. 4
figure 4

Variation of the dimensionless natural frequency \( {{\Omega}} \) with length-to-radius ratio L/R for different values of surface mass density \( \rho^{s} \)-homogenous cylindrical nanoshell. a Clamped and b simply supported B.Cs (h = 0.3 nm, R/h = 10, \( \zeta /h = 50 \), l/h = 10)

Full size image

In order to examine the effect of the surface residual stress \( \tau^{s} \), the variation of the dimensionless natural frequency versus the ratio of length to radius for different values of the surface residual stress is plotted in Fig. 5. This figure shows that the positive surface residual stress, in the sense of tensile stress, leads to an increase in frequency. This increase goes on with an almost constant rate by enhancing the surface residual stress. About the effect of the ratio of length to radius, contrary to the behavior of other surface properties that their effect declines by increasing this ratio, for the surface residual stress, its effect decreases to a certain value of the ratio of length to radius and then remains constant. This certain ratio depends on the amount of surface residual stress so that the increase in the surface residual stress reduces this ratio. In fact, the surface residual stress has caused that the independence of the frequency from the ratio of length to radius occurs in a lower ratio. Moreover, it can be observed that the influence of surface residual stress is more pronounced in simply supported B.Cs. In other words, the influence of surface residual stress increases for the softer boundary conditions and it means that besides the geometric parameters and the value and sign of surface properties, the B.Cs also play a role in the influence of surface residual stress on the frequency. For surface elastic and surface mass density properties, there is no significant distinction between the results of different B.Cs.

Fig. 5
figure 5

Variation of the dimensionless natural frequency \( {{\Omega}} \) with length-to-radius ratio L/R for different values of surface residual stress \( \tau^{s} \)-homogenous cylindrical nanoshell. a Clamped and b simply supported B.Cs (h = 0.3 nm, R/h = 10, \( \zeta /h = 50 \), l/h = 10)

Full size image

From the comparative analysis, one can find that among the surface properties, the effects of surface residual stress are relatively the major ones.

3.4 Effect of surface and FG gradient index

In this subsection, the dimensionless natural frequency of a clamped and simply supported FG cylindrical shell has been presented based on the various continuum mechanics theories including classical (Classic) (\( \zeta /h = 0 \), l/h = 0), nonlocal (Nonlocal) (\( \zeta /h = 50 \), l/h = 0), strain gradient (SG) (\( \zeta /h = 0 \), l/h = 10) and nonlocal strain gradient (NSGT) (\( \zeta /h = 50 \), l/h = 10), with consideration of the surface effects and without them. According to Fig. 6 and also Tables 5 and 6, by comparing the results of different theories, the greatest and smallest frequency will be achieved by employing the strain gradient and nonlocal theories, respectively. Indeed, nonlocal and strain gradient theories due to the modeling the softening and stiffening phenomena, respectively, predict the more and less frequency in comparison with classical theory. The nonlocal strain gradient theory by applying both phenomena simultaneously computes the frequency between the frequency of nonlocal and strain gradient theories whose value depends on the values of nonlocal and material length scale size-dependent parameters. This behavior is observed in both cases of with and without the consideration of surface effects. As indicated in Fig. 6, in the case of without surface effects, by increasing the length-to-radius ratio the difference between the frequency of different theories decreases and at higher ratios, the effect of this ratio has declined and the frequency will reach an almost constant value. On the other hand, consideration of surface effects causes that this difference remains constant and does not change with the variation of length-to-radius ratio. Moreover, the frequency independence from the length-to-radius ratio occurs at the lower ratios.

Fig. 6
figure 6

Variation of the dimensionless natural frequency \( {{\Omega}}\) with length-to-radius ratio L/R for different continuum mechanics theories-FG cylindrical nanoshell. a Clamped and b simply supported B.Cs (h = 0.3 nm, R/h = 10, \( \zeta /h = 50 \), l/h = 10, k = 2)

Full size image
Table 5 Effect of length-to-radius ratio L/R and surface properties on the dimensionless natural frequency \( {{\Omega}} \) of FG cylindrical nanoshell in different continuum mechanics theories and B.Cs (h = 0.3 nm, R/h = 10, k = 2, \( \zeta /h = 50 \), l/h = 10)
Full size table
Table 6 Effect of FG gradient index k and surface effects on the dimensionless natural frequency \( {{\Omega}}\) of FG cylindrical nanoshell in different continuum mechanics theories and B.Cs (h = 0.3 nm, R/h = 10, L/R = 20, \( \zeta /h \) = 50, l/h = 10)
Full size table

According to the results of the previous subsection, it can be concluded that the observed behavior in the case of with surface effects is due to the surface residual stress property and as expressed before, surface residual stress is the most influential surface property on the frequency.

To more accurately investigate the influence of surface effects on the frequency of the proposed FG shell model in different length-to-radius ratios, the values of dimensionless frequency in length-to-radius ratios of 10 and 50, for different continuum theories, B.Cs and with and without surface effects are shown in Table 5. An overall conclusion from this table is that the difference between the frequency of with and without surface effects is more prominent at lower value of length-to-radius ratio and for the high ratio this difference drastically reduced. Therefore, it can be said that considering surface effects at lower length-to-radius ratio is critical for correctly predicting the behavior of nanoscale systems and it is not enough to just modeling these systems based on the nonclassical continuum size-dependent theories. Next interesting result in this table is about the frequency of length-to-radius ratio of 50 in simply supported B.Cs and with surface effects, in which its value is equal to the results of clamped B.Cs. In other words, in the high length-to-radius ratio, when surface effects are considered, the frequency is independent of B.Cs. This behavior is observed in all four theories. At the low ratios, being larger the clamped frequency from simply supported frequency is valid. Moreover, by comparing the frequency of with and without surface effects, it can be deduced that its ratio follows an almost constant value in all four theories, which means that the influence of surface effects on the frequency is independent of the type of continuum mechanics theories. Also, it is seen that consideration of surface effects reduces and enhances the frequency at length-to-radius ratios 10 and 50, respectively. It is worth noting that, as discussed in the previous subsection, the influence of surface effects on the frequency depends on the geometry and both value and sign of surface properties, so, increasing and/or decreasing influence of surface effects on frequency are not general results.

About the FG gradient index effect, as depicted in Table 6, an enhancement of this parameter increases the frequency in all continuum mechanics theories and types of with and without the consideration of surface effects. Also, from this table it can be realized that surface properties decrease the effect of FG gradient index. In other words, surface properties decrease the rate of frequency changes relative to FG gradient index. This behavior is less pronounced in strain gradient theory as compared to other theories.

4 Conclusion

In this paper, by applying the Gurtin–Murdoch surface elasticity theory and NSGT, surface effects on the natural frequency of a FG cylindrical nanoshell were investigated. It is observed that with increasing the surface elastic properties and residual surface stress, the frequency increases and surface mass density reduces the frequency, and among the surface properties, the surface residual stress has the most effect on the frequency. Also, except the surface residual stress, the effect of other surface properties decreases through the enhancement of the length-to-radius ratio. The difference between the frequency of with and without surface effects is more prominent at lower values of length-to-radius ratio and for the high ratio this difference drastically reduced. In the high length-to-radius ratio, when surface effects are considered, the frequency is independent of the boundary conditions. Generally, in addition to the sign and the value of surface properties, geometric parameters also play a role in the influence of surface properties on the natural frequency. Also, surface properties decline the rate of frequency changes relative to FG gradient index. This behavior is less pronounced in strain gradient theory as compared to other theories. Another noticeable result was that utilizing the strain gradient and nonlocal theories, the greatest and smallest frequency could be predicted, respectively, and the results of NSGT fall somewhere in between. Given the importance of natural frequency as an inherent property and design criteria, the results of the present study can be useful in precise prediction and properly design of the micro/nanoscale equipment.