1 Introduction

Physical and EM properties of combination of new materials are always interesting. One of the most important topics in the physics and EM theories is the polarization [1]. It is a specification of transverse EM waves and has wide range of applications such as: liquid crystal display [2], antennas radiation [3], satellite links [4] and optical structures [1]. Many scientists have worked to change the polarization of the EM wave in presence of novel structures like: ferromagnetic [5, 6], anisotropic metamaterials [7] and chiral medium [8,9,10]. Rotation of polarization occurred in optically active materials such as chiral medium [11]. Chiral medium exhibits circular birefringence and different phase velocities for the left circularly polarized (LCP) and the right circularly polarized (RCP) fields. Also, chiral medium has been a state of the art in physics [12, 13] and electromagnetic theory like: EM scattering [14,15,16,17], the reflection and transmission coefficients of the interferences of dielectric-chiral [18] and chiral-dielectric [19]. Time harmonic dependency is assumed as \( \exp \left( { - j\omega t} \right) \), and it is implicit throughout this investigation.

A chiral medium can be expressed by the following constitutive relation [18]:

$$ {\mathbf{D}} = \varepsilon {\mathbf{E}} + j\gamma {\mathbf{B}} $$
(1)
$$ {\mathbf{H}} = j\gamma {\mathbf{E}} + {{\mathbf{B}} \mathord{\left/ {\vphantom {{\mathbf{B}} \mu }} \right. \kern-0pt} \mu } $$
(2)

Here \( \mu \left( { = \mu_{0} \mu_{r} } \right),\,\,\varepsilon \left( { = \varepsilon_{0} \varepsilon_{r} } \right) \) and \( \gamma \) are permeability, permittivity and chirality of the chiral medium, respectively. Also, E, H, D and B are electric field intensity, magnetic field intensity, electric flux density and magnetic flux density, respectively.

Two waves propagate in the chiral medium [18]: right and left circularly polarized (RCP and LCP) waves. The wave number for the RCP wave is expressed as:

$$ h_{1} = \omega \mu \gamma + \left( {\omega^{2} \mu^{2} \gamma^{2} + k^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} $$
(3)

and the one for the LCP wave is:

$$ h_{2} = - \omega \mu \gamma + \left( {\omega^{2} \mu^{2} \gamma^{2} + k^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} $$
(4)

where

$$ k = \omega \sqrt {\mu \varepsilon } $$
(5)

The total electric field in the chiral medium is summation of the RCP and the LCP fields. Intrinsic impedance of the chiral medium is equal to \( \eta = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu \varepsilon }} \right. \kern-0pt} \varepsilon }} \). The two phenomena of optical rotatory dispersion (ORD) and circular dichroism (CD) are found when an EM plane wave with linear polarization travels through a suspension of chiral molecules [11]. ORD is called as rotation of the plane of polarization of the transmitted plane wave with respect to that of the incident plane wave, while CD is defined as the differential absorption of the left and the right circularly polarized plane waves inside the chiral medium [11]. In this paper, closed-form formulas for reflection and transmission coefficients and also Brewster angles are calculated for geometry of interface of two different chiral media. Generally, the reflection and transmission coefficients are very important [20, 21] to help us to predict and understand the behavior of EM waves [22, 23]. Closed-form equations are analytical and fast [24]; being fast [25,26,27] and analytical [28, 29] have been among the most important and interesting features in scientific and engineering studies.

2 Geometry and theoretical derivation

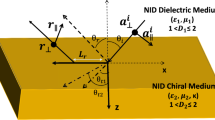
The geometry of the problem is shown in Fig. 1, where upper half space \( \left( {y > 0} \right) \) is filled by chiral medium 1 and the lower one \( \left( {y < 0} \right) \) by chiral medium 2. A plane wave is traveling through upper medium and makes incidence with the interface of the two chiral media. The problem will be solved for incident RCP and LCP waves. In Fig. 1, the red square dot and the green round dot refer to the incident RCP and LCP waves, respectively. Also, the subscripts \( {\rm X} \) and \( c \) refer to the cross- and co-polarized components of the incident field, respectively.

Fig. 1
figure 1

Geometry of the problem

Full size image

The incident fields are RCP and LCP fields as follows; so \( i = 1,\,\,2 \) where \( i = 1 \) refers to RCP and \( i = 2 \) refers to LCP.

$$ {\mathbf{E}}_{1}^{\text{inc}} = P_{1} \left( { - j\sin \phi_{1} \,\hat{a}_{x} + j\cos \phi_{1} \,\hat{a}_{y} + \,\hat{a}_{z} } \right)\exp ( - jh_{1u} (x\cos \phi_{1} + y\sin \phi_{1} )) $$
(6)
$$ {\mathbf{E}}_{2}^{\text{inc}} = P_{2} \left( {j\sin \phi_{2} \hat{a}_{x} - j\cos \phi_{2} \hat{a}_{y} + \hat{a}_{z} } \right)\exp ( - jh_{2u} (x\cos \phi_{2} + y\sin \phi_{2} )) $$
(7)

Here \( P_{1} \), \( \phi_{1} \), \( P_{2} \) and \( \phi_{2} \) are the amplitude and incident angle of the incident RCP and LCP fields, respectively. The subscript \( u \) refers to the upper chiral medium. The reflected fields to the upper half space are expressed as

$$ {\mathbf{E}}_{1}^{r} = \varGamma_{1} \left( {j\sin \phi_{r1} \,\hat{a}_{x} + j\cos \phi_{r1} \,\hat{a}_{y} + \,\hat{a}_{z} } \right)\exp ( - jh_{1u} (x\cos \phi_{r1} - y\sin \phi_{r1} )) $$
(8)
$$ {\mathbf{E}}_{2}^{r} = \varGamma_{2} \left( { - j\sin \phi_{r2} \,\hat{a}_{x} - j\cos \phi_{r2} \,\hat{a}_{y} + \,\hat{a}_{z} } \right)\exp ( - jh_{2u} (x\cos \phi_{r2} - y\sin \phi_{r2} )) $$
(9)

where \( \phi_{r1} \) and \( \phi_{r2} \) are the angles of the reflected RCP and LCP fields. Also, the transmitted fields to the chiral medium 2 are stated as below

$$ {\mathbf{E}}_{1}^{t} = T_{1} \left( { - j\sin \phi_{t1} \,\hat{a}_{x} + j\cos \phi_{t1} \,\hat{a}_{y} + \,\hat{a}_{z} } \right)\exp ( - jh_{1l} (x\cos \phi_{t1} + y\sin \phi_{t1} )) $$
(10)
$$ {\mathbf{E}}_{2}^{t} = T_{2} \left( {j\sin \phi_{t2} \,\hat{a}_{x} - j\cos \phi_{t2} \,\hat{a}_{y} + \,\hat{a}_{z} } \right)\exp ( - jh_{2l} (x\cos \phi_{t2} + y\sin \phi_{t2} )) $$
(11)

Here \( l \) denotes the lower half space; while \( \phi_{t1} \) and \( \phi_{t2} \) are the angles of the transmitted RCP and LCP fields. The coefficients \( \varGamma_{1} ,\,\,\varGamma_{2} ,\,\,T_{1} \) and \( T_{2} \) are the unknown amplitudes that will be determined by applying boundary conditions. The boundary conditions of the proposed geometry are

$$ E_{x}^{\text{total}} \left| {_{{y_{a} = 0^{ + } }} } \right. = E_{x}^{\text{total}} \left| {_{{y_{a} = 0^{ - } }} } \right. $$
(12)
$$ E_{z}^{\text{total}} \left| {_{{y_{a} = 0^{ + } }} } \right. = E_{z}^{\text{total}} \left| {_{{y_{a} = 0^{ - } }} } \right. $$
(13)
$$ H_{x}^{\text{total}} \left| {_{{y_{a} = 0^{ + } }} } \right. = H_{x}^{\text{total}} \left| {_{{y_{a} = 0^{ - } }} } \right. $$
(14)
$$ H_{z}^{\text{total}} \left| {_{{y_{a} = 0^{ + } }} } \right. = H_{z}^{\text{total}} \left| {_{{y_{a} = 0^{ - } }} } \right. $$
(15)

As mentioned before, the problem is solved separately for incident RCP and LCP fields. When the incident field is \( {\mathbf{E}}_{1}^{\text{inc}} \): to satisfy Eq. (12), Eqs. (6), (8)–(11) are applied and the following relation is produced.

$$ - P_{1} \sin \phi_{1} + \varGamma_{11} \sin \phi_{r1} - \varGamma_{21} \sin \phi_{r2} + T_{11} \sin \phi_{t1} - T_{21} \sin \phi_{t2} = 0 $$
(16)

where \( \varGamma_{11} ,\,\,\varGamma_{21} ,\,\,T_{11} \) and \( T_{21} \) are \( \varGamma_{1} ,\,\,\varGamma_{2} ,\,\,T_{1} \) and \( T_{2} \) when the excitation is \( {\mathbf{E}}_{1}^{\text{inc}} \). Also, the angles \( \phi_{r1} \), \( \phi_{r2} \), \( \phi_{t1} \) and \( \phi_{t2} \) are as below

$$ \phi_{\delta \beta } = \cos^{ - 1} \left( {\frac{{h_{\begin{subarray}{l} 1u \\ 2 \end{subarray} } \cos \phi_{\begin{subarray}{l} 1 \\ 2 \end{subarray} } }}{{h_{\beta \kappa } }}} \right);\,\delta = r,\,t;\,\beta = 1,\,2;\,\kappa = \left\{ {\begin{array}{*{20}c} {u;} & {{\text{for}}\;\delta = r} \\ {l;} & {{\text{for}}\;\delta = t} \\ \end{array} } \right. $$
(17)

where the upper and the lower subscripts are related to the incident RCP and LCP waves, respectively. The boundary condition of Eq. (13) is satisfied similar to satisfying of Eq. (12) and results in

$$ P_{1} + \varGamma_{11} + \varGamma_{21} - T_{11} - T_{21} = 0 $$
(18)

Applying Eq. (14) leads to

$$ - \eta_{l} \sin \phi_{1} P_{1} + \eta_{l} \sin \phi_{r1} \varGamma_{11} + \eta_{l} \sin \phi_{r2} \varGamma_{21} + \eta_{u} \sin \phi_{t1} T_{11} + \eta_{u} \sin \phi_{t2} T_{21} = 0 $$
(19)

The following relation is obtained using the continuity of \( H_{z} \) on the interface (Eq. (15)).

$$ \eta_{l} P_{1} + \eta_{l} \varGamma_{11} - \eta_{l} \varGamma_{21} - \eta_{u} T_{11} + \eta_{u} T_{21} = 0 $$
(20)

The analytical solution of the set of Eqs. (16) and (18)–(20) leads to involved mathematical manipulation; finally, the following closed-form formulas are obtained for the four unknown coefficients.

$$ \varGamma_{21} = P_{1} \left[ {\begin{array}{*{20}l} {\sin \phi_{t1} \left( {\frac{{\eta_{l} + \eta_{u} }}{2}} \right)\left( {L_{1} - \frac{{L_{3} }}{{\eta_{u} }}} \right) - \sin \phi_{t2} \left( {\frac{{\eta_{l} - \eta_{u} }}{2}} \right)} \hfill \\ {\left( {L_{1} + \frac{{L_{3} }}{{\eta_{u} }}} \right) - \sin \phi_{1} \left( {\eta_{l} L_{1} - L_{3} } \right)} \hfill \\ \end{array} } \right] \div \left[ {L_{1} L_{4} - L_{2} L_{3} } \right] $$
(21)

where

$$ L_{1} = \sin \phi_{t1} \left( {\frac{{\eta_{l} + \eta_{u} }}{{2\eta_{u} }}} \right) + \sin \phi_{t2} \left( {\frac{{\eta_{l} - \eta_{u} }}{{2\eta_{u} }}} \right) + \sin \phi_{r1} $$
(22)
$$ L_{2} = \sin \phi_{t1} \left( {\frac{{\eta_{l} - \eta_{u} }}{{2\eta_{u} }}} \right) + \sin \phi_{t2} \left( {\frac{{\eta_{l} + \eta_{u} }}{{2\eta_{u} }}} \right) + \sin \phi_{r2} $$
(23)
$$ L_{3} = \sin \phi_{t1} \left( {\frac{{\eta_{l} + \eta_{u} }}{2}} \right) - \sin \phi_{t2} \left( {\frac{{\eta_{l} - \eta_{u} }}{2}} \right) + \eta_{l} \sin \phi_{r1} $$
(24)
$$ L_{4} = \sin \phi_{t1} \left( {\frac{{\eta_{l} - \eta_{u} }}{2}} \right) - \sin \phi_{t2} \left( {\frac{{\eta_{l} + \eta_{u} }}{2}} \right) - \eta_{l} \sin \phi_{r2} $$
(25)

and

$$ \varGamma_{11} = P_{1} \left[ {\begin{array}{*{20}l} {\sin \phi_{t1} \left( {\frac{{\eta_{l} + \eta_{u} }}{2}} \right)\left( {L_{2} - \frac{{L_{4} }}{{\eta_{u} }}} \right) - \sin \phi_{t2} \left( {\frac{{\eta_{l} - \eta_{u} }}{2}} \right)} \hfill \\ {\left( {L_{2} + \frac{{L_{4} }}{{\eta_{u} }}} \right) - \sin \phi_{1} \left( {\eta_{l} L_{2} - L_{4} } \right)} \hfill \\ \end{array} } \right] \div \left[ {L_{1} L_{4} - L_{2} L_{3} } \right] $$
(26)
$$ T_{21} = \left[ {\varGamma_{21} \left( {\eta_{l} + \eta_{u} } \right) - \left( {\eta_{l} - \eta_{u} } \right)\left( {P_{1} + \varGamma_{11} } \right)} \right] \div 2\eta_{u} $$
(27)
$$ T_{11} = P_{1} + \varGamma_{11} + \varGamma_{21} - T_{21} $$
(28)

Now, the problem is solved for incident LCP field. Substituting Eqs. (7)–(11) in Eq. (12) leads to

$$ \sin \phi_{2} P_{2} + \varGamma_{12} \sin \phi_{r1} - \varGamma_{22} \sin \phi_{r2} + T_{12} \sin \phi_{t1} - T_{22} \sin \phi_{t2} = 0 $$
(29)

Here \( \varGamma_{12} ,\,\,\varGamma_{22} ,\,\,T_{12} \) and \( T_{22} \) are equal to \( \varGamma_{1} ,\,\,\varGamma_{2} ,\,\,T_{1} \) and \( T_{2} \) when the incident field is \( {\mathbf{E}}_{2}^{inc} \). Equation (13) is satisfied similar to Eq. (12); the following equation is obtained.

$$ P_{2} + \varGamma_{12} + \varGamma_{22} - T_{12} - T_{22} = 0 $$
(30)

Applying the boundary condition of Eq. (14) leads to

$$ - \eta_{l} \sin \phi_{2} P_{2} + \eta_{l} \sin \phi_{r1} \varGamma_{12} + \eta_{l} \sin \phi_{r2} \varGamma_{22} + \eta_{u} \sin \phi_{t1} T_{12} + \eta_{u} \sin \phi_{t2} T_{22} = 0 $$
(31)

Finally, satisfying Eq. (15) results in

$$ - \eta_{l} P_{2} + \eta_{l} \varGamma_{12} - \eta_{l} \varGamma_{22} - \eta_{u} T_{12} + \eta_{u} T_{22} = 0 $$
(32)

Similar to the process of the derivations of Eqs. (21)–(28), the unknown coefficients \( \varGamma_{12} ,\,\,\varGamma_{22} ,\,\,T_{12} \) and \( T_{22} \) are determined.

$$ \varGamma_{22} = \frac{{j\eta_{u} P_{2} }}{{\left[ {L_{1} L_{4} - L_{2} L_{3} } \right]}}\left[ {\begin{array}{*{20}l} {\sin \phi_{t1} \left( {\frac{{\eta_{l} - \eta_{u} }}{2}} \right)\left( {L_{1} - \frac{{L_{3} }}{{\eta_{u} }}} \right) - \sin \phi_{t2} \left( {\frac{{\eta_{l} + \eta_{u} }}{2}} \right)} \hfill \\ {\left( {L_{1} + \frac{{L_{3} }}{{\eta_{u} }}} \right) + \sin \phi_{2} \left( {\eta_{l} L_{1} + L_{3} } \right)} \hfill \\ \end{array} } \right] $$
(33)
$$ \varGamma_{12} = j\eta_{u} P_{2} \left[ {\begin{array}{*{20}l} {\sin \phi_{t1} \left( {\frac{{\eta_{l} - \eta_{u} }}{2}} \right)\left( {L_{2} - \frac{{L_{4} }}{{\eta_{u} }}} \right) - \sin \phi_{t2} \left( {\frac{{\eta_{l} + \eta_{u} }}{2}} \right)} \hfill \\ {\left( {L_{2} + \frac{{L_{4} }}{{\eta_{u} }}} \right) + \sin \phi_{2} \left( {\eta_{l} L_{2} + L_{4} } \right)} \hfill \\ \end{array} } \right] \div \left[ {L_{1} L_{4} - L_{2} L_{3} } \right] $$
(34)
$$ T_{22} = \left[ {\left( {\eta_{l} + \eta_{u} } \right)\left( {P_{2} + \varGamma_{22} } \right) - \varGamma_{12} \left( {\eta_{l} - \eta_{u} } \right)} \right] \div 2\eta_{u} $$
(35)
$$ T_{12} = P_{2} + \varGamma_{12} + \varGamma_{22} - T_{22} $$
(36)

In the next section, the effects of the incident angles and the chirality parameters of the two media are studied.

3 Brewster angle

As shown in the previous section, the reflection and transmission coefficients are functions of the constitutive parameters of the two chiral media. Now, one may ask is there an incident angle which no energy reflects from the interface (definition of Brewster angle). Based on our knowledge, there has not been any formulation for Brewster angle related to the geometry of Fig. 1, yet, because no closed-form formulas have been calculated for the reflected and transmitted fields.

If there are no closed-form formulas for the coefficients, the Brewster angle is not determined.

After determining the closed-form formulas and many mathematical manipulations, the Brewster angle is occurred under the following conditions for the incident RCP and LCP fields (see Table 1).

Table 1 The conditions for the Brewster angle in case of the two incident fields
Full size table

where \( - 1 < \eta_{l} \gamma_{2} < 1 \); and \( \varepsilon_{1} ,\,\,\mu_{1} ,\,\,\gamma_{1} \) and \( \eta_{u} \) are the permittivity, the permeability, the chirality parameter and the intrinsic impedance of the upper medium, respectively; also \( \varepsilon_{2} ,\,\,\mu_{2} ,\,\,\gamma_{2} \) and \( \eta_{l} \) are the permittivity, the permeability, the chirality parameter and the intrinsic impedance of the lower medium, respectively. Please note: the permittivity and the permeability of each medium should have a same sign. It is notable that the mentioned point is referred to double positive (DPS) and double negative (DNG) media. The Brewster angle is so applicable for the geometry of Fig. 1, particularly, for determining the chirality of a chiral medium and also concealing the lower medium electromagnetically because for any incident angle there is no reflected wave. These works can be done using the degrees of freedom presented in Table 1. For example, consider a chiral medium with unknown chirality; and it is so important to determine its chirality for a specific application like medicine [30, 31]. This chiral medium can be set as the lower medium in the geometry of Fig. 1 and a RCP or LCP field travels to the interface. Then, the parameters of Table 1 should be varied until no wave reflects. When there is no reflected field, the chirality of the lower medium is obtained easily using the formulas of Table 1. The case of concealing the lower medium can be done similar to the previous case.

4 Results and discussion

In this section, the influences of the chirality, permittivity, incident angle and permeability on the normalized reflected electric field are studied. It is notable that FEM is applied in order to validate the results.

Figure 2 depicts the effects of the chirality of the upper medium on the normalized reflected electric field for the incident RCP and LCP waves. By increasing the \( \eta_{u} \gamma_{1} \), the reflected field decreases for grazing incident angles in case of the both incident fields; but when the angle of incidence gets away from the grazing angles, the reflected field increases by enhancement of the \( \eta_{u} \gamma_{1} \) for incident LCP field, and the variation of the \( \eta_{u} \gamma_{1} \) has almost no effect for incident RCP field. Also the results obtained by FEM are in a very good agreement with the results of the proposed formulations.

Fig. 2
figure 2

The normalized reflected electric field versus incident angle for \( \varepsilon_{r2} = 6 \), \( \varepsilon_{r1} = 2 \) and \( \eta_{l} \gamma_{2} = 0.5 \); The incident field is: a RCP field b LCP field

Full size image

Figure 3 shows the normalized reflected electric field for different values of \( \varepsilon_{1} \) for the both incident fields. Generally, increasing the \( \varepsilon_{1} \) leads to decreasing the reflected field for the incident RCP and LCP fields; but the amount of the decrease for the incident LCP field is more than the one for the incident RCP field. Please note that the results computed by the presented closed-form formulas correspond completely with the results of FEM.

Fig. 3
figure 3

The normalized reflected electric field versus incident angle for \( \varepsilon_{r2} = 6 \), \( \eta_{u} \gamma_{1} = 0.2 \) and \( \eta_{l} \gamma_{2} = 0.5 \); the incident field is: a RCP field b LCP field

Full size image

The relations presented in Table 1 are used to calculate the Brewster angles for the both incident fields and different values of the constitutive parameters. Let us define parameters “a” and “\( \tau \)” as \( {{\mu_{1} } \mathord{\left/ {\vphantom {{\mu_{1} } {\mu_{2} }}} \right. \kern-0pt} {\mu_{2} }} \) and \( {{1 - \left( {{{\mu_{2} } \mathord{\left/ {\vphantom {{\mu_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right)\gamma_{2}^{2} } \mathord{\left/ {\vphantom {{1 - \left( {{{\mu_{2} } \mathord{\left/ {\vphantom {{\mu_{2} } {\varepsilon_{2} }}} \right. \kern-0pt} {\varepsilon_{2} }}} \right)\gamma_{2}^{2} } {1 - \left( {b,d} \right)_{1}^{2} }}} \right. \kern-0pt} {1 - \left( {b,d} \right)_{1}^{2} }} \), respectively, where \( b \) and \( d \) are used for the incident RCP and LCP waves, respectively. It is obvious that various permeabilities result in different values of the parameter “a”. In order to validate the formulas of Table 1, the normalized reflected electric field is computed and compared with FEM in Fig. 4 for different values of the permittivities and permeabilities that result in various values of “a” (I:\( \mu_{2} = 1 \), \( \mu_{1} = 2 \Rightarrow a = 2 \), \( \varepsilon_{2} = 2 \); II:\( \mu_{2} = 2.5 \), \( \mu_{1} = - 7.5 \Rightarrow a = - 3 \), \( \varepsilon_{2} = 1.5 \)). According to Table 1, the values of I and II leads to zero reflection for \( \varepsilon_{1} = 4\tau \) and \( \varepsilon_{1} = - 4.5\tau \), respectively, in case of incident RCP and LCP fields and all angles of incidence. It is notable that in Fig. 4 the amount of \( \eta_{u} \gamma_{1} \) is calculated using Table 1. It is shown that the values of I result in zero reflection for \( \varepsilon_{1} = 4\tau \), all incident angles and the both incident fields (Fig. 4a); also zero reflection occurs for \( \varepsilon_{1} = - 4.5\tau \), all angles of incidence and the both incident fields in case of values of II. The equality between the results of the formulas of Table 1 and FEM confirms that the formulas are accurate and reliable.

Fig. 4
figure 4

The normalized reflected electric field versus \( \varepsilon_{1} \) for: a \( \mu_{2} = 1 \), \( \mu_{1} = 2 \) and \( \varepsilon_{2} = 2 \) b \( \mu_{2} = 2.5 \), \( \mu_{1} = - 7.5 \) and \( \varepsilon_{2} = 1.5 \)

Full size image

Figure 5 illustrates the reflected electric field from the interface in case of incident RCP and LCP fields for \( \mu_{1} = 2 \), \( \mu_{2} = 1 \), \( \varepsilon_{2} = 2 \) and different \( \eta_{l} \gamma_{2} \). Please note that the chirality of the upper chiral medium can be obtained using Table 1. It is observed that for various \( \eta_{l} \gamma_{2} \), the reflected wave is equal to zero for only one value of \( \varepsilon_{1} \) that is determined using Table 1\( \left( {\varepsilon_{1} = a\varepsilon_{2} \mathop{\longrightarrow}\limits[{\varepsilon_{2} = 2}]{a = 2}\varepsilon_{1} = 4\tau } \right) \) for all the incident angles which is indicated by black arrow.

Fig. 5
figure 5

The normalized reflected electric field versus incident angle and \( \varepsilon_{1} \div \tau \) for \( \mu_{1} = 2 \), \( \mu_{2} = 1 \) and \( \varepsilon_{2} = 2 \); the incident field is: a RCP field, \( \eta_{l} \gamma_{2} = 0.2 \) b LCP field, \( \eta_{l} \gamma_{2} = 0.2 \) c RCP field, \( \eta_{l} \gamma_{2} = - 0.8 \) d LCP field, \( \eta_{l} \gamma_{2} = - 0.8 \)

Full size image

The amount of the reflected field for another values of the permittivities and the permeabilities \( \left( {\mu_{1} = - 3,\;\mu_{2} = - 1.5,\;\varepsilon_{2} = - 2.5} \right) \) that lead to the same value of \( a \) \( \left( {a = 2} \right) \) of Fig. 5 are used in calculation of Fig. 6 for the two incident fields and different values of the chirality of the lower medium. It is shown that the reflected field exists for all the incident angles and all the permittivities of the upper medium, except for \( \varepsilon_{1} = - 5\tau \) (Table 1: \( \left. {\varepsilon_{1} = a\varepsilon_{2} \mathop{\longrightarrow}\limits[{\varepsilon_{2} = - 2.5}]{a = 2}\varepsilon_{1} = - 5\tau } \right) \).

Fig. 6
figure 6

The normalized reflected electric field versus incident angle and \( \varepsilon_{1} \div \tau \) for \( \mu_{1} = - 3 \), \( \mu_{2} = - 1.5 \) and \( \varepsilon_{2} = - 2.5 \); the incident field is: a RCP field, \( \eta_{l} \gamma_{2} = 0.35 \) b LCP field, \( \eta_{l} \gamma_{2} = 0.35 \) c RCP field, \( \eta_{l} \gamma_{2} = - 0.5 \) d LCP field, \( \eta_{l} \gamma_{2} = - 0.5 \)

Full size image

In Fig. 7, the effects of the incident angles and \( \varepsilon_{1} \) on the reflected field for RCP and LCP excitation fields and different \( \eta_{l} \gamma_{2} \) are studied. Where \( \mu_{1} = 3 \), \( \mu_{2} = - 1 \), \( \varepsilon_{2} = - 0.5 \). It is observed that as mentioned in Table 1, only one value of \( \varepsilon_{1} \) \( \left( {\varepsilon_{1} = a\varepsilon_{2} \mathop{\longrightarrow}\limits[{\varepsilon_{2} = - 0.5}]{a = - 3}\varepsilon_{1} = 1.5\tau } \right) \) results in zero RCS or Brewster angles (zero reflection) for all the incident angles and the both excitations.

Fig. 7
figure 7

The normalized reflected electric field versus incident angle and \( \varepsilon_{1} \div \tau \) for \( \mu_{1} = 3 \), \( \mu_{2} = - 1 \) and \( \varepsilon_{2} = - 0.5 \); the incident field is: a RCP field, \( \eta_{l} \gamma_{2} = 0.99 \) b LCP field, \( \eta_{l} \gamma_{2} = 0.99 \) c RCP field, \( \eta_{l} \gamma_{2} = - 0.25 \) d LCP field, \( \eta_{l} \gamma_{2} = - 0.25 \)

Full size image

Figure 8 shows the behavior of the reflected electric field versus the permittivity of the upper medium and the incident angles in case of the both excitations for \( \mu_{1} = - 7.5 \), \( \mu_{2} = 2.5 \), \( \varepsilon_{2} = 1.5. \) It is shown that there is no reflected field for all the incident angles—this is zero RCS—and various \( \eta_{l} \gamma_{2} \) when the permittivity of the upper medium is equal to \( - 4.5\tau \) \( \left( {\varepsilon_{1} = a\varepsilon_{2} \mathop{\longrightarrow}\limits[{\varepsilon_{2} = 1.5}]{a = - 3}\varepsilon_{1} = - 4.5\tau } \right) \).

Fig. 8
figure 8

The normalized reflected electric field versus incident angle and \( \varepsilon_{1} \div \tau \) for \( \mu_{1} = - 7.5 \), \( \mu_{2} = 2.5 \) and \( \varepsilon_{2} = 1.5 \); the incident field is: a RCP field, \( \eta_{l} \gamma_{2} = 0.01 \) (b) LCP field, \( \eta_{l} \gamma_{2} = 0.01 \) c RCP field, \( \eta_{l} \gamma_{2} = - 0.95 \) d LCP field, \( \eta_{l} \gamma_{2} = - 0.95 \)

Full size image

5 Conclusion

In this paper, the analytical closed-form formulas for the reflection and transmission coefficients are presented when a RCP or LCP field travels to the interface of two chiral media. After obtaining the formulas, we are able to find conditions that result in no reflected field or Brewster angles. The conditions are presented for the both incident fields. Also the influences of the chirality of the lower medium, the permittivity and the permeability of the media on the reflected electric field are studied. The conditions of Brewster angles are applied to calculate the reflected electric field for different values of the parameters of the problem. Also, the presented investigation is validated using FEM.