Calculating the indoor radon flux from construction materials and soil

Abstract

A theoretical method is used to calculate the radon exhalation and flux from the walls of a room and the soil to the living space in the room. The calculations are based on the Fick’s laws to describe the radon diffusion through the walls and in the soil. In both cases, the diffusion is considered as one-dimension along the direction to the inside of the room. Under some conditions, the three-dimensional diffusion has to be taken into account. A comparison between the one- and three-dimensional descriptions is discussed, and hence the radon areal release rate from a wall and that from a construction material sample are formulated and related. Consequent indoor radon concentrations and inhalation doses are represented. The effect of the radon release from the construction materials on calculating the gamma dose rate in a room is studied.

1 Introduction

Radon is a radioactive noble gas with no color, smell or taste. It is created in the natural decay series of ²³⁵U, ²³²Th and ²³⁸U, with radium as its parent radionuclide. Radon isotopes have short half-lives. The long-lived one, ²²²Rn (usually known as just radon), which has a half-life of 3.82 days, comes from the ²³⁸U series. Another one from the ²³⁸U series is ²¹⁸Rn, which has a half-life of 35 ms. The ²³⁵U series gives ²¹⁹Rn with 3.96 s half-life. The second longest half-life is for the isotope ²²⁰Rn which comes from the ²³²Th series. It is usually known as thoron (Tn), and it has a half-life 55.6 s. In spite of the short half-lives of the radon isotopes, they are always present around us because of their continuous creation by the extremely long-lived naturally occurred uranium and thorium radioactive decay series. The half-lives of ²³⁵U, ²³⁸U and ²³²Th are about 0.70, 4.47 and 14.10 billion years, respectively. Their decay chains end with stable lead isotopes.

Since radon is a gas, it can easily be released from construction materials and soil and build up in our living space. In contrast to radon as a gas, its daughters are solids and can stick to surfaces. Therefore, inhalation of radon and its short-lived daughters could result in their sedimentation in the respiratory system and lungs. They expose the cells there to radiation, thus boosting the hazard of having a lung cancer. In fact, radon is considered in some countries as the second leading cause of lung cancer after smoking [1,2,3,4,5,6,7,8]. In the USA, for example, radon causes about 21 thousand deaths of lung cancer every year [8]. Further, almost 3 thousand out of this death toll happen among individuals who are not smokers. Actually, according to the United States Environmental Protection Agency, radon is the main reason of lung cancer for non-smokers. It is therefore very important to study the main sources of indoor radon and the main factors that control its flux.

2 Radon release from the walls of a room

To study the exhalation process of radon from a wall, we exploit the Fick’s second law in describing the diffusion of radon through the wall. If C(x,t) denotes the radon concentration in the interspaces (pores) of the construction material (Bq m⁻³), $\lambda = \ln \left( 2 \right)/\lambda_{1/2}$ is the radon decay constant (s⁻¹), $g$ is the radon production rate per unit volume of the pores (Bq m⁻³ s⁻¹), $D$ is the radon diffusion coefficient (m² s⁻¹), $\lambda_{1/2}$ is the half-life of radon, x is the position across the wall in the direction toward the living space of the room and t is the time (s), then Fick’s second law describing the radon diffusion takes the form

$$ \frac{{\partial C\left( {x,t} \right)}}{\partial t} = D\frac{{\partial^{2} C\left( {x,t} \right)}}{{\partial x^{2} }} + g - \lambda C\left( {x,t} \right) . $$

(1)

In the steady state, $C$ varies with the position only and not with the time. In this case, the solution of Eq. (1) can take the form

$$ C\left( x \right) = B + A \cosh \left( {\frac{x}{l}} \right) , $$

(2)

where $A$ and $B$ are some constants that can be found by imposing the suitable boundary conditions and $l = \sqrt {D/\lambda }$ is the radon diffusion length. Because now the concentration does not depend on the time, Eq. (1) becomes zero, which gives the value of the constant $B = g/\lambda$. The constant A can be found by applying the approximation that the radon concentration can be taken as zero on the face of the wall, because it is actually very small compared to that inside the wall. If the center of the wall is taken as the origin of the x-axis, then this boundary condition means that $C\left( L \right) = 0$, where L is the half width of the wall. Applying this in Eq. (2) gives $A = - B/{ \cosh }\left( {L/l} \right)$. Therefore, Eq. (2) now becomes

$$ C\left( x \right) = \left( {1 - \frac{{{ \cosh }\left( {x/l} \right)}}{{{ \cosh }\left( {L/l} \right)}}} \right)\frac{g}{\lambda } . $$

(3)

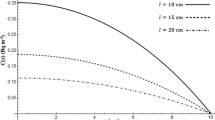
The change of the radon concentration across the wall, as described by Eq. (3), is shown in Fig. 1. This is demonstrated for different diffusion lengths; 10, 15 and 20 cm. The wall is assumed to have a width of 20 cm. It can be seen from the figure that the concentration starts as a maximum at the middle of the wall and then diminishes monotonically toward the edge of the wall until it vanishes on its face. We can also see from the curves that the shorter the diffusion length the larger the radon concentration. The gross radon concentration in the wall, $a_{Rn} \left( x \right)$, is obtained by adding the concentration in the pores, C, and that of the non-emanated radons (in the grains)

$$ a_{Rn} \left( x \right) = \left( {1 - \frac{{\cosh \left( {x/l} \right)}}{{\cosh \left( {L/l} \right)}}} \right)a\eta + \left( {1 - \eta } \right)a , $$

(4)

where C is converted to Bq kg⁻¹ by multiplying by the factor $p/\rho$, where $p$ is the porosity (dimensionless) of the construction material and $\rho$ is its density (kg m⁻³). The radon areal exhalation rate from the wall, $R_{w}$ (Bq m⁻² s⁻¹), is defined as [9]

$$ R_{w} = \left| { - pD\frac{dC\left( x \right)}{dx}} \right|_{x = L} , $$

(5)

which upon using Eq. (3) gives

$$ R_{w} = pgl\tanh \left( {\frac{L}{l}} \right) . $$

(6)

Fig. 1

Dependence of the radon concentration in the pores of a material on the position inside a wall. The origin of the x-axis is at the center of the wall, which has a width 20 cm. The displayed three curves are for diffusion lengths 10, 15 and 20 cm from top to bottom, respectively. The concentration is given in terms of $\frac{g}{\lambda }$

Since the radon production rate per unit volume of the pores is just

$$ g = \frac{ a \eta \lambda \rho }{p} , $$

(7)

where $\eta$ is the radon emanation factor (dimensionless) and $a$ is the radium radioactivity concentration (Bq kg⁻¹), then Eq. (6) takes the form

$$ R_{w} = a \eta \lambda \rho l\tanh \left( {\frac{L}{l}} \right). $$

(8)

The type of the construction material is a basic factor that controls the radon exhalation rate. For most types, the radon diffusion length is much longer than the half width of the wall ($l \gg L$) [10]. Therefore, Eq. (8) can be approximated by replacing tanh $\left( {L/l} \right)$ by $L/l$

$$ R_{w} = L a \eta \lambda \rho , $$

(9)

with independence on the radon diffusion coefficient. In this case, most of the emanated radon atoms will be released. Nevertheless, for some few types of the construction materials, the radon diffusion length is much shorter than the half width of the wall ($l \ll L$). For those types, Eq. (8) can be approximated by replacing tanh $\left( {L/l} \right)$ by 1

$$ R_{w} = l a \eta \lambda \rho , $$

(10)

with direct dependence on the radon diffusion length.

3 Radon flux from the soil

The radon flux to the inside of a room can also be found from Eq. (5) if the radon concentration in the soil is available. This can be gotten by again using Eq. (1) but after including the advection term to account for the possible soil softness and the fact that there could be a flow of water (vapor) [11]. This leads to the general one-dimensional transport equation

$$ \frac{{\partial C\left( {x,t} \right)}}{\partial t} = D\frac{{\partial^{2} C\left( {x,t} \right)}}{{\partial x^{2} }} - v\frac{{\partial C\left( {x,t} \right)}}{\partial x} - \lambda .C\left( {x,t} \right) + g , $$

(11)

where $v$ is the radon advection speed (m s⁻¹) in the soil, and of course all the symbols in the equation are now describing the soil. A solution in the steady state can be put in the form

$$ C\left( x \right) = C_{o1} e^{ - wx} + C_{o2} e^{{\left( {\frac{v}{D} + w} \right)x}} + C_{f} , $$

(12)

where the constants $C_{o1}$ and $C_{o2}$ are to be calculated by using the suitable boundary conditions, and the constant $C_{f} = \eta \rho a/p$ gives the expected level of saturation for the radon concentration. The $w$ parameter is obtained by solving the equation

$$ Dw^{2} + vw - \lambda = 0 , $$

(13)

which comes when substitute Eq. (12) in Eq. (11), and so is given by

$$ w = \sqrt {\left( {\frac{v}{2D}} \right)^{2} + \frac{\lambda }{D}} - \frac{v}{2D} . $$

(14)

If we consider the downward of the soil as the positive x direction, with the origin on the surface, then imposing the boundary conditions

$$ C\left( 0 \right) = 0 $$

(15)

and

$$ \left| {\frac{dC}{dx}} \right|_{x \to \infty } = 0 , $$

(16)

will lead to $C_{o2}$ = 0 and $C_{o1} = - C_{f}$. Therefore, the radon concentration in the soil becomes

$$ C\left( x \right) = C_{f} \left( { 1 - e^{ - wx} } \right) , $$

(17)

where the values of the $C_{f}$ and w parameters can be estimated by fitting Eq. (17) to the experimental data. The radon release rate per unit area of the soil can be obtained from Eq. (5) with using Eq. (17). As an example of fitting Eq. (17) to experimental data, we consider ref [12]. If we try to fit Eq. (17) to the data in the figure labeled 2a in ref [12], we find a trend like that shown in Fig. 2. It means that Eq. (17) can represent the data partly down to 130 cm depth where the radon concentration begins saturation. The data rise again after that temporary saturation. If we look carefully at the data, we can notice that this behavior is going to happen again around the depth 217 cm. This would imply that the soil could be depicted as composed of three layers, with each of them having its own characteristics. To use Eq. (17) to describe such a type of soils, we consider the following adjustments. The concentrations in the three layers will be given by

$$ C_{1} \left( x \right) = C_{f1} \left( {1 - e^{{ - w_{1} x}} } \right) , $$

(18)

$$ C_{2} \left( x \right) = C_{f2}^{a} + C_{f2}^{b} \left( {1 - e^{{ - w_{2} \left( {x - x_{12} } \right)}} } \right) $$

(19)

and

$$ C_{3} \left( x \right) = C_{f3}^{a} + C_{f3}^{b} \left( {1 - e^{{ - w_{3} \left( {x - x_{23} } \right)}} } \right) , $$

(20)

where

$$ C_{f2}^{a} + C_{f2}^{b} = C_{f2} , $$

(21)

and

$$ C_{f3}^{a} + C_{f3}^{b} = C_{f3} $$

(22)

are the expected saturation levels for the radon concentration in the second and third layers, respectively, $x_{12}$ is the boundary between the first and the second layers and $x_{23}$ is the boundary between the second and third layers. The boundary conditions will be

$$ C_{1} \left( 0 \right) = 0 , $$

(23)

$$ \left| {\frac{{dC_{3} }}{dx}} \right|_{x \to \infty } = 0 , $$

(24)

$$ C_{1} \left( {x_{12} } \right) = C_{2} \left( {x_{12} } \right) $$

(25)

and

$$ C_{2} \left( {x_{23} } \right) = C_{3} \left( {x_{23} } \right) . $$

(26)

Therefore, the radon concentration in the soil is

$$ C\left( x \right) = \left\{ {\begin{array}{*{20}l} {C_{1} \left( x \right) = C_{f1} \left( {1 - e^{{ - w_{1} x}} } \right) ,} & {0 \le x \le x_{12} } \\ {C_{2} \left( x \right) = C_{f2}^{a} + C_{f2}^{b} \left( {1 - e^{{ - w_{2} \left( {x - x_{12} } \right)}} } \right) ,} & {x_{12} \le x \le x_{23} } \\ {C_{3} \left( x \right) = C_{f3}^{a} + C_{f3}^{b} \left( {1 - e^{{ - w_{3} \left( {x - x_{23} } \right)}} } \right) , } & {x_{23} \le x } \\ \end{array} } \right. $$

(27)

where the values of the parameters $w_{1}$, $w_{2}$, $w_{3}$, $C_{f1}$, $C_{f2}^{a}$, $C_{f2}^{b}$, $C_{f3}^{a}$ and $C_{f3}^{b}$ are to be estimated by fitting Eq. (27) to the experimental data. By doing the fitting process on the data in Fig. 2, we get the curve shown in Fig. 3. The boundaries are x₁₂ = 130 cm and x₂₃ = 217 cm, and the parameters of Eq. (27) are

$$ \left. {\begin{array}{*{20}l} { w_{1} = 0.010\,{\text{cm}}^{ - 1} } \\ {w_{2} = 0.018\,{\text{cm}}^{ - 1} } \\ { w_{3} = 0.010\,{\text{cm}}^{ - 1} } \\ {C_{f1} = 19000 \frac{\text{Bq}}{{{\text{m}}^{3} }}} \\ {C_{f2}^{a} = 13822 \frac{\text{Bq}}{{{\text{m}}^{3} }}} \\ {C_{f2}^{b} = 15100 \frac{\text{Bq}}{{{\text{m}}^{3} }}} \\ {C_{f3}^{a} = 25768 \frac{\text{Bq}}{{{\text{m}}^{3} }}} \\ {C_{f3}^{b} = 18100 \frac{\text{Bq}}{{{\text{m}}^{3} }}} \\ \end{array} } \right\} $$

(28)

Fig. 2

Radon concentration in soil (the solid curve) as given by Eq. (17), assuming a single layer, in comparison with the experimental data taken from Ref. [12]

Fig. 3

Radon concentration in soil as given by Eq. (27), assuming a three-layer description

Figure 3 demonstrates the potential of the model for describing the radon concentration in the soil. The values of the parameters in Eq. (28) could be claimed to be almost unique because we could not find another set of values that can give a better fitting. Only the parameters describing the third layer ($x_{23} \le x$) could be argued as the data there are few. To demonstrate the model’s efficiency further, we compare it with other models [12]. This is shown in Fig. 4 where some models of one-, two- and three-layer descriptions are drawn with the experimental data. It is clear that the curve in Fig. 3 matches the experimental data very well compared to those in Fig. 4. This indicates that the presented model for describing the radon concentration in soil, with its formulations and dividing $C_{f}$ to two terms (Eqs. (21) and (22)), can fully fit the data. The division of $C_{f}$ to two terms is extremely useful in making the function flexible.

Fig. 4

Radon concentration in soil described by the approach of ref [12] using one-, two- and three-layer assumptions; Fig. 2a in ref [12]

By looking at Eq. (27), it may seem at first glance that the model involves many parameters; however, this is not true. This is because each layer should be considered alone, which means that there is just a couple of parameters for the first layer, and just three parameters for any layer after that. Once these parameters have been estimated, some important characteristics can be calculated for the distribution and transport of radon in the soil. For example, using w, we calculate the radon diffusion length $l = 1/w$ and the radon diffusion coefficient

$$ D = \frac{\lambda }{{w^{2} }} , $$

(29)

and then the radon advection speed is calculated from Eq. (14). Radon saturated concentrations are found from Eqs. (28), (21) and (22), and the corresponding depths can be gotten from Fig. 3.

4 Exposure to radon

The radon inhalation dose is given by [13]

$$ I = C_{in} . F.O.d , $$

(30)

where d is the dose conversion factor (nSv Bq⁻¹ m³), F is a parameter designating the degree of equilibrium between radon and its short-lived daughters (typically 0.4 for radon and 0.1 for thoron [14, 15]), O is the ratio of the indoor hours by the total hours of the year (known as the indoor occupancy factor) and $C_{in}$ is the radon indoor concentration (Bq m⁻³) due to exhalation [15]

$$ C_{in} = \frac{R.A}{r.V} , $$

(31)

where V and A are the volume and area of the room, respectively, R is the radon areal exhalation rate and r is the ventilation rate in the room (typically ~ 0.63 h⁻¹ [13, 15,16,17]).

The radon areal exhalation rate (R) in Eq. (31) is often taken as the one evaluated experimentally, which is usually carried out by using a sample of the construction material. However, this is disputable. Realistically, the radon areal release rate has to be the one evaluated from the walls of the room (not from the construction material sample). This is because in the experimental work, the radon flow is usually measured from the entire faces of the construction material sample; however, technically, the only direction of flow that matters is the one across the width of the wall to the living space. Any other direction has no importance if we want to estimate the indoor radon concentration. Additionally, for the radon flowing along the other directions, it is almost sure that it will decay before reaching the faces of the wall. Furthermore, even if the experimental work considers just one face of the sample, the radon areal release rate actually depends on the geometry and dimensions of the sample. Even for the wall, the radon release rate depends on the width of the wall. To see how much it could be different, evaluating the radon areal release rate from a construction material sample and from a wall, we compare the theoretical description of the radon diffusion in both cases. The one for a wall has been already done above, and so now we consider the case of a construction material sample.

5 Radon release from a construction material sample

If we consider the construction material sample to be a parallelepiped with edges 2L₁, 2L₂, and 2L₃ along the x, y and z directions, respectively, then a diffusion in the three-dimension described by Fick’s second law will be

$$ \frac{{\partial C\left( {x,y,z,t} \right)}}{\partial t} = D\left[ {\frac{{\partial^{2} C\left( {x,y,z,t} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} C\left( {x,y,z,t} \right)}}{{\partial y^{2} }} + \frac{{\partial^{2} C\left( {x,y,z,t} \right)}}{{\partial z^{2} }}} \right] + g - \lambda C\left( {x,y,z,t} \right), $$

(32)

where the center of the sample is taken as the origin. A solution in the steady state is

$$ C\left( {x,y,z} \right) = Q \cdot { \cosh }\left( {\frac{{\left( {x + y + z} \right)}}{\sqrt 3 l}} \right) + \frac{g}{\lambda } , $$

(33)

where $Q$ is a constant that can be determined by using boundary conditions like in the case of a wall, i.e., the concentrations are considered zero at the faces of the sample. Putting $C\left( {L_{1} ,0, 0} \right) = 0$ on the face $x = L_{1}$ gives

$$ Q_{x} = \frac{{ - \frac{g}{\lambda }}}{{{ \cosh }\left( {\frac{{L_{1} }}{\sqrt 3 l}} \right)}} , $$

(34)

where $Q_{x}$ is the value of $Q$ along the x-axis. The pertinent concentration along the x-axis will be

$$ C_{x} = \left( {1 - \frac{{{ \cosh }\left( {\frac{x}{{\sqrt {3 } l}}} \right)}}{{{ \cosh }\left( {\frac{{L_{1} }}{{\sqrt {3 } l}}} \right)}}} \right) \frac{g}{\lambda } . $$

(35)

For the other two faces $y = L_{2}$ and $z = L_{3}$, we will have

$$ Q_{y} = \frac{{ - \frac{g}{\lambda }}}{{{ \cosh }\left( {\frac{{L_{2} }}{\sqrt 3 l}} \right)}} , $$

(36)

$$ Q_{z} = \frac{{ - \frac{g}{\lambda }}}{{{ \cosh }\left( {\frac{{L_{3} }}{\sqrt 3 l}} \right)}}, $$

(37)

$$ C_{y} = \left( {1 - \frac{{{ \cosh }\left( {\frac{y}{{\sqrt {3 } l}}} \right)}}{{{ \cosh }\left( {\frac{{L_{2} }}{{\sqrt {3 } l}}} \right)}}} \right) \frac{g}{\lambda } $$

(38)

and

$$ C_{z} = \left( {1 - \frac{{{ \cosh }\left( {\frac{z}{{\sqrt {3 } l}}} \right)}}{{{ \cosh }\left( {\frac{{L_{3} }}{{\sqrt {3 } l}}} \right)}}} \right) \frac{g}{\lambda } , $$

(39)

where ($Q_{y}$, $C_{y}$) and ($Q_{z}$, $C_{z}$) have the same definitions like ($Q_{x}$, $C_{x}$) but along the y and z axes, respectively. The radon areal release rates are

$$ R_{x} = \left| { - pD\frac{{dC_{x} }}{dx}} \right|_{{x = L_{1} }} = \frac{p D g}{\sqrt 3 \lambda l}\tanh \left( {\frac{{L_{1} }}{\sqrt 3 l}} \right) = \frac{a \eta \lambda \rho l}{\sqrt 3 } \tanh \left( {\frac{{L_{1} }}{\sqrt 3 l}} \right) , $$

(40)

$$ R_{y} = \left| { - pD\frac{{dC_{y} }}{dy}} \right|_{{y = L_{2} }} = \frac{p D g}{\sqrt 3 \lambda l}\tanh \left( {\frac{{L_{2} }}{\sqrt 3 l}} \right) = \frac{a \eta \lambda \rho l}{\sqrt 3 } \tanh \left( {\frac{{L_{2} }}{\sqrt 3 l}} \right) $$

(41)

and

$$ R_{z} = \left| { - pD\frac{{dC_{z} }}{dz}} \right|_{{z = L_{3} }} = \frac{p D g}{\sqrt 3 \lambda l}\tanh \left( {\frac{{L_{3} }}{\sqrt 3 l}} \right) = \frac{a \eta \lambda \rho l}{\sqrt 3 } \tanh \left( {\frac{{L_{3} }}{\sqrt 3 l}} \right) . $$

(42)

In Eqs. (40), (41) and (42), the factor $\sqrt 3$ is manifested as an important number in the radon release rates from the construction material sample. The significance of that factor becomes clearer if we divide the radon release rate from a wall, Eq. (8), by those from the construction material sample, Eqs. (40), (41) and (42)

$$ \frac{{R_{w} }}{{R_{x} }} = \frac{{\sqrt 3 { \tanh }\left( {\frac{L}{l}} \right)}}{{{ \tanh }\left( {\frac{{L_{1} }}{\sqrt 3 l}} \right)}} , $$

(43)

$$ \frac{{R_{w} }}{{R_{y} }} = \frac{{\sqrt 3 { \tanh }\left( {\frac{L}{l}} \right)}}{{{ \tanh }\left( {\frac{{L_{2} }}{\sqrt 3 l}} \right)}} $$

(44)

and

$$ \frac{{R_{w} }}{{R_{z} }} = \frac{{\sqrt 3 { \tanh }\left( {\frac{L}{l}} \right)}}{{{ \tanh }\left( {\frac{{L_{3} }}{\sqrt 3 l}} \right)}} , $$

(45)

with an average

$$ R_{w/xyz} = \frac{1}{3}\left( {\frac{{R_{w} }}{{R_{x} }} + \frac{{R_{w} }}{{R_{y} }} + \frac{{R_{w} }}{{R_{z} }}} \right) . $$

(46)

To examine how much the radon release rate of a construction material sample differs from that of a wall, we show some graphs of the relative rate, Eq. (46), changing with the radon diffusion length, for different typical sets of the sample’s dimensions and the wall’s width. The obtained curves are displayed in Figs. 5, 6, 7 and 8. The figures show that the radon release rate from a wall is larger than that from a construction material sample by not less than a factor of $\sqrt 3$ (≈ 1.73). By looking into the graphs carefully, one can see that $R_{w/xyz}$ could easily reach a value of 10, depending on the dimensions of the sample, the width of the wall and the magnitude of the radon diffusion length. This demonstrates that if the radon exhalation rate is obtained by using a construction material sample, it could be significantly underestimated, and of course, the radon indoor concentration and inhalation doses would be as well.

Fig. 5

Radon areal release rate from a wall relative to that from the construction material sample considered as a cube with edge 10 cm (L₁ = L₂ = L₃ = 5 cm). The x-axis is the radon diffusion length. The width of the wall is considered 20 cm (L = 10 cm)

Fig. 6

Radon areal release rate from a wall relative to that from the construction material sample considered as a cube with edge 20 cm (L₁ = L₂ = L₃ = 10 cm). The x-axis is the radon diffusion length. The width of the wall is considered 20 cm (L = 10 cm)

Fig. 7

Radon areal release rate from a wall relative to that from the construction material sample considered as a parallelepiped with edges 6, 10 and 12 cm (L₁ = 3 cm, L₂ = 5 cm and L₃ = 6 cm). The x-axis is the radon diffusion length. The width of the wall is considered 20 cm (L = 10 cm)

Fig. 8

Radon areal release rate from a wall relative to that from the construction material sample considered as a parallelepiped with edges 10, 10 and 14 cm (L₁ = 5 cm, L₂ = 5 cm and L₃ = 7 cm). The x-axis is the radon diffusion length. The width of the wall is considered 30 cm (L = 15 cm)

6 Effect of radon release from construction materials on the gamma-radiation dose rate

Because normally walls are not sealed or covered by special wrapping that can prevent radon from releasing, the equilibrium in the ²³⁸U radioactive decay series is usually not satisfied. This causes an escape of a number of gamma lines that were supposed to share in the indoor gamma dose due to the ²³⁸U decay series existing in the construction materials. At the same time, the radon release results in a reduction in the concentration of radon and its short-lived progenies in the construction material. To a good degree of approximation, the reduced gamma dose rate from the construction materials could be accounted for by calculating it using the radon concentration inside the walls instead of that of the radium. This is well justified knowing that the majority of the radiation from the ²³⁸U series is due to the short-lived progenies of radon. Equation (4) gives the total radon concentration inside a wall, which can be put in the form

$$ a_{Rn} \left( x \right) = \left( {1 - F_{Rn} \frac{{L \cosh \left( {x/l} \right)}}{{l \sinh \left( {L/l} \right)}}} \right)a , $$

(47)

where $F_{Rn}$ is a factor that gives the percentage of radon atoms exhale from the wall with respect to the whole number created inside the wall per second. It is known as the radon release factor and is therefore given by

$$ F_{Rn} = \frac{{R_{w} }}{a \lambda \rho L} = \frac{l}{L}\eta \tanh \left( {\frac{L}{l}} \right) . $$

(48)

Equation (47) clarifies that the term $F_{Rn} \frac{{L { \cosh }\left( {x/l} \right)}}{{l { \sinh }\left( {L/l} \right)}}$ makes the radon concentration inside the wall less than that of radium. As stated above, for most types of the construction materials, the radon diffusion length is much larger than the half width of the wall ($l \gg L$), which means that ${ \sinh }\left( {L/l} \right)$ and ${ \cosh }\left( {x/l} \right)$ can be approximated by $L/l$ and 1, respectively, and accordingly Eq. (47) is set into a very simple and practical form independent of $x$

$$ a_{Rn} = a\left( {1 - F_{Rn} } \right) , $$

(49)

or

$$ a_{Rn} /a = \left( {1 - F_{Rn} } \right) . $$

(50)

From the definition of the radon release factor, we have 0 ≤ $\left( {1 - F_{Rn} } \right)$ ≤ 1. Therefore, Eq. (50) tells us that the radon concentration in the construction material is less than that of the radium by a factor of $\left( {1 - F_{Rn} } \right)$. Therefore, to approximately find the true (reduced) gamma dose rate, caused by non-equilibrium in the ²³⁸U decay series, all we have to do is perform the calculations normally assuming an existence of equilibrium, namely with using the measured radium activity concentration, and then in the end we just multiply the result with the factor $\left( {1 - F_{Rn} } \right)$. It is obvious from Eq. (50) that if radon exhalation is somehow prevented, namely if $F_{Rn}$ disappeared, then $a_{Rn}$ and $a$ will be the same, i.e., secular equilibrium is attained.

7 Conclusion

Fick’s diffusion second law has been applied to describe the radon diffusion through construction materials and soil. This scheme is used to calculate the radon indoor release rates from walls and ground. Using a one-dimensional diffusion description, the radon areal exhalation rate from a wall has been calculated. Comparing that to a three-dimensional diffusion from a construction material sample, the latter is found to be smaller than the former by at least a factor of ~ 1.7. In some cases, the differing factor could reach an order of magnitude (10). From practical point of view, this study suggests that the radon surface release rate to be calculated from walls and not from material samples, or otherwise the ways of measuring the radon exhalation rates from construction material samples have to be reconsidered.

A one-dimensional radon diffusion has also been applied to describe the radon diffusion through a soil to the indoor of a room. The general transport equation, including advection, has been solved to formulate the radon concentration inside the soil. The obtained form is found to be applicable to describe monotonic radon concentrations, but for non-monotonic ones the form has to be modified. Suggesting some modifications, the theoretical form has been fitted successfully to experimental data. Assuming a multi-layer description of the soil, the proposed method predicts that some soils are constructed of several layers, with each one has its own characteristics of radon distribution and transport.

Using the radon diffusion description across the walls, a simple way of estimating the decreased gamma absorbed rate has been suggested. The dose rate could be estimated roughly by using the radon concentration inside the walls instead of the radium concentration. This leads to a final simple and convenient form that does not require any repetition of previously calculated dose rates. All the dose rates that were calculated assuming a secular equilibrium in the uranium series are to be multiplied by a correction factor $\left( {1 - F_{Rn} } \right)$, where $F_{Rn}$ is the measured radon release factor of the construction material.