Introduction

Radon is a colorless, odorless and tasteless radioactive noble gas. Its creation in the 235U, 232Th and 238U natural decay chains comes from the decay of radium. The most interesting radon isotope, 222Rn, which is usually referred to as just radon, comes from the 238U series and has 3.82 d half-life. The other isotopes have relatively much shorter half-lives. 218Rn, for example, which also comes from the 238U decay chain, has a 35 ms half-life. 219Rn and 220Rn, which come from the 235U and 232Th decay chains, have half-lives of 3.96 s and 55.6 s, respectively. Despite their small half-lives, radon isotopes have a continuous existence due to their constant production in the natural decay chains of uranium and thorium that have enormous half-lives.

As a gas, radon can exhale from materials around us and spread in the air. Its progenies, however, are solids and can therefore accumulate on surfaces. Accordingly, when radon and its progenies are inhaled, they could deposit on the airways and the lungs. The cells there are then irradiated and could develop cancer [1,2,3,4,5,6,7,8,9]. Therefore, it is very vital to examine the indoor radon major sources and the main parameters controlling its flow. This is the main objective of this study, where a plain theoretical model is offered to easily estimate the radon exhalation rates from walls and soil. The radon indoor concentration and inhalation doses are then formulated. The main parameters affecting the indoor radon flow are talked about. For completion of the picture, a critical calculation of the radon exhalation rate from construction material samples is presented, and the effect of radon release on calculating the gamma indoor dose is discussed.

Exhalation of radon from a wall

Fick’s second law is used to describe the radon diffusion in a wall. This reads

$$ \frac{{\partial C\left( {x,t} \right)}}{\partial t} = D\frac{{\partial^{2} C\left( {x,t} \right)}}{{\partial x^{2} }} + g - \lambda C\left( {x,t} \right), $$
(1)

where \( C\left( {x,t} \right) \) is the radon concentration (Bq/m3) in the pores of the building material, \( D \) is the radon diffusion coefficient (m2/s), \( x \) is the distance from the center of the wall to the indoor direction, \( g \) is the radon creation rate per unit size of the pores (Bq/m3/s) and \( \lambda \) is the radon decay constant (s−1). Assuming a steady state, where the concentration is only a position dependent, Eq. (1) has the solution

$$ C\left( x \right) = B + A\; cosh\left( {\frac{x}{l}} \right), $$
(2)

where \( l = \sqrt {D/\lambda } \) is the radon diffusion length and the constants \( A \) and \( B \) are to be obtained by applying some boundary conditions. Considering the radon concentration as almost zero on the wall’s surface, we find that \( A = - B/{ \cosh }\left( {L/l} \right) \) with \( B = g/\lambda \), where \( L \) is the wall half-thickness. Equation (2) is then

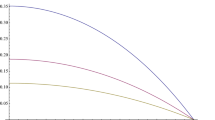
$$ C\left( x \right) = \left( {1 - \frac{{{ \cosh }\left( {x/l} \right)}}{{{ \cosh }\left( {L/l} \right)}}} \right)\frac{g}{\lambda }. $$
(3)

The behavior of Eq. (3) is demonstrated in Fig. 1 for some values of the diffusion length. In the figure one can see that the concentration has its largest value at the center of the wall and it decreases smoothly until it becomes zero at the surface. It is clear in the figure that the concentration is higher with smaller diffusion length. Now, to obtain the total radon concentration, \( a_{Rn} \left( x \right) \), we just add the interspaces concentration, Eq. (3), to the radon concentration inside the grains (non-emanated)

$$ a_{Rn} \left( x \right) = \left( {1 - \frac{{{ \cosh }\left( {x/l} \right)}}{{{ \cosh }\left( {L/l} \right)}}} \right)a\upeta + \left( {1 -\upeta} \right)a, $$
(4)

where C has been multiplied by \( {\raise0.7ex\hbox{$p$} \!\mathord{\left/ {\vphantom {p\uprho}}\right.\kern-0pt} \!\lower0.7ex\hbox{$\uprho$}} \) to convert it to Bq/kg, with \( p \) being the porosity of the building material that has a density \( \uprho \) (kg/m3) and a radium radioactivity concentration \( a \) (Bq/kg) and \( \upeta \) is the radon emanation factor.

Fig. 1
figure 1

Change of interspaces radon concentration with position, Eq. (3). \( x = 0 \) is in the middle of the wall, which has a thickness 20 cm. The \( y \)-axis is in terms of \( (g /\lambda ) \)

Full size image

The radon surface release rate \( \left( {{\text{Bq/m}}^{2} / {\text{s}}} \right) \) from a wall is [10]

$$ R_{w} = \left| { - pD\frac{dC\left( x \right)}{dx}} \right|_{x = L} , $$
(5)

which, by inserting Eq. (3), becomes

$$ R_{w} = pgl\tanh \left( {\frac{L}{l}} \right). $$
(6)

The time rate of change of the radon atoms in the pores, N, within an element of volume \( \Delta V \) is [11]

$$ \frac{dN}{dt} = - \lambda N + \eta \, \rho \,a\,\Delta V, $$
(6a)

and the radon concentration in the pores (C) within the same element of volume is related to N by

$$ C = \frac{\lambda N}{p \Delta V}, $$
(6b)

with a rate of change

$$ \frac{dC}{dt} = \frac{\lambda }{p \Delta V} \frac{dN}{dt}, $$

which, using Eqs. (6a) and (6b), becomes

$$ \frac{dC}{dt} = - \frac{{\lambda^{2} N}}{p\Delta V} + \frac{\eta \,\rho \,a \lambda }{p} = - \lambda C + g. $$

The term \( \lambda C \) is the sink term due to the decay of radon while the term

$$ g = \frac{\eta \,\rho \,a \lambda }{p}, $$
(7)

is the source (production) term due to the emanated radon atoms. These are the two terms added as correction terms to \( D\frac{{\partial^{2} C\left( {x,t} \right)}}{{\partial x^{2} }} \) in the one-dimension Fick’s second law, Eq. (1), to account for the fact that radon is a radioactive gas that decays after being created from the decay of radium. Using Eqs. (7), (6) takes the form

$$ R_{w} = a\,\upeta\,\lambda \,\uprho\,l\;{ \tanh }\left( {\frac{L}{l}} \right). $$
(8)

Equation (8) informs us that the type of the building material is a basic factor that affects the radon release rate. For the majority of the known building material types we have \( l \gg L \) [12]. In such a case, the greater part of the emanated radon atoms will be exhaled, and Eq. (8), after simplified by approximating \( { \tanh }\left( {L/l} \right) \) by \( L/l \), will have no dependence on \( l \)

$$ R_{w} = L\,a\,\upeta\,\lambda \,\varvec{\rho}, $$
(9)

nevertheless, for other small number of building materials we have \( l \ll L \). In that case, Eq. (8), after simplified by approximating \( { \tanh }\left( {L/l} \right) \) by unity, will have just a straight dependence on \( l \)

$$ R_{w} = l\,a\,\upeta\,\lambda \,\uprho. $$
(10)

Flow of radon from soil

Radon exhalation from a soil can also be gotten from Eq. (5) provided the soil radon concentration is known. This can be found by again solving Eq. (1) after adding the advection term

$$ \frac{{\partial C\left( {x,t} \right)}}{\partial t} = D\frac{{\partial^{2} C\left( {x,t} \right)}}{{\partial x^{2} }} - v\frac{{\partial C\left( {x,t} \right)}}{\partial x} - \lambda .C\left( {x,t} \right) + g, $$
(11)

where now all the parameters and variables are for the soil case, with \( v \)\( \left( {\text{m/s}} \right) \) the radon advection speed. The steady state solution is

$$ C\left( x \right) = C_{o1} e^{{\frac{1}{2}\left( {\frac{v}{D} - K} \right)x}} + C_{o2} e^{{\frac{1}{2}\left( {\frac{v}{D} + K} \right)x}} + C_{f} , $$
(12)

where the constants \( C_{o1} \) and \( C_{o2} \) are to be obtained by applying some boundary conditions, and the constant

$$ C_{f} = \frac{\eta \,\rho \,a}{p}, $$
(13)

is the saturated radon concentration. The parameter \( K \) is given by

$$ K = \sqrt {\frac{{v^{2} }}{{D^{2} }} + 4\frac{\lambda }{D}} . $$
(14)

Taking the +ve x-direction vertically down the soil surface \( (x = 0) \), and applying the boundary conditions

$$ C\left( 0 \right) = 0, $$
(15)
$$ \left| {\frac{dC}{dx}} \right|_{x \to \infty } = 0, $$
(16)

gives \( C_{o2} = 0\; {\text{and}}\; C_{o1} = - C_{f} \). Equation (12) then becomes

$$ C\left( x \right) = C_{f} \left( { 1 - e^{ - wx} } \right), $$
(17)

where we define the parameter

$$ w = \frac{1}{2}\left( {K - \frac{v}{D}} \right), $$
(17a)

as the reciprocal of the radon migration length. It can be noticed that if the advection process is ignored and we set \( v = 0 \) in Eq. (17a), we just get the previous equation for the radon diffusion length, \( l = \frac{1}{w} = \sqrt {D/\lambda } \), mentioned above following Eq. (2). The parameters \( C_{f} \;{\text{and}}\; w \) can be evaluated by adjusting Eq. (17) to experimental data. For some experimental data, let us consider those in Fig. 2a of Ref. [13], which is for a soil composed of clay and sand with different composition percentages. These percentages vary both horizontally and vertically down the soil surface. By roughly adjusting Eq. (17) to the data, we get the curve shown in Fig. 2. This obviously shows that Eq. (17) can describe the data in part. Having a careful look at the data in Fig. 2, one can notice that they could fully be described by having three successive curves like the one shown. This would suggest a 3-layer structure of the soil. To describe these types of soils, Eq. (17) has to be modified and split

$$ C_{1} \left( x \right) = C_{f1} \left( {1 - e^{{ - w_{1} x}} } \right), $$
(18)
$$ C_{2} \left( x \right) = C_{f2}^{a} + C_{f2}^{b} \left( {1 - e^{{ - w_{2} \left( {x - x_{12} } \right)}} } \right) $$
(19)

and

$$ C_{3} \left( x \right) = C_{f3}^{a} + C_{f3}^{b} \left( {1 - e^{{ - w_{3} \left( {x - x_{23} } \right)}} } \right), $$
(20)

where

$$ C_{f2}^{a} + C_{f2}^{b} = C_{f2} $$
(21)

and

$$ C_{f3}^{a} + C_{f3}^{b} = C_{f3} $$
(22)

are the saturated radon concentrations of layer 2 and layer 3, respectively. \( x_{12} \) is the border between layer 1 and layer 2, while \( x_{23} \) is the border between layer 2 and layer 3. The saturation levels are split into two terms to make the function more flexible to the fitting process. It should be noticed that Eqs. (18), (19) and (20) satisfy Eq. (11) provided that for each layer \( Dw^{2} + vw - \lambda = 0 \), which upon solved for \( w \) will again give Eq. (17a). The boundary conditions for the three layers are

$$ C_{1} \left( 0 \right) = 0, $$
(23)
$$ \left| {\frac{{dC_{3} }}{dx}} \right|_{x \to \infty } = 0, $$
(24)
$$ C_{1} \left( {x_{12} } \right) = C_{2} \left( {x_{12} } \right) $$
(25)

and

$$ C_{2} \left( {x_{23} } \right) = C_{3} \left( {x_{23} } \right). $$
(26)
Fig. 2
figure 2

Soil radon concentration, Eq. (17), considering the soil as a single layer. The experimental data (the dots) are from Ref. [13]

Full size image

The first boundary condition assumes, as in the case of a wall, that the radon concentration is negligible on the surface compared to the inside of the soil. The second boundary condition ensures a stability in the radon concentration in the third layer, assuming no new layer after that. The third and fourth boundary conditions ensure the continuity in the radon concentrations through the soil.

In summary, the soil radon concentration is

$$ C\left( x \right) = \left\{ {\begin{array}{*{20}l} {C_{1} \left( x \right) = C_{f1} \left( {1 - e^{{ - w_{1} x}} } \right),} \hfill & {0 \le x \le x_{12} } \hfill \\ {C_{2} \left( x \right) = C_{f2}^{a} + C_{f2}^{b} \left( {1 - e^{{ - w_{2} \left( {x - x_{12} } \right)}} } \right),} \hfill & {x_{12} \le x \le x_{23} } \hfill \\ {C_{3} \left( x \right) = C_{f3}^{a} + C_{f3}^{b} \left( {1 - e^{{ - w_{3} \left( {x - x_{23} } \right)}} } \right),} \hfill & {x_{23} \le x} \hfill \\ \end{array} } \right. $$
(27)

where the parameters \( w_{1} \), \( w_{2} \), \( w_{3} \), \( C_{f1} \), \( C_{f2}^{a} \), \( C_{f2}^{b} \), \( C_{f3}^{a} \) and \( C_{f3}^{b} \) are to be obtained by adjusting Eq. (27) to the data. Each of the three concentrations satisfies the transport equation, Eq. (11), with the pertinent characteristics. For example, in the first layer, substituting \( C_{1} \left( x \right) \) in Eq. (11) we have

$$ D_{1} w_{1}^{2} + v_{1} w_{1} - \lambda = 0, $$
$$ g_{1} = \lambda C_{f1} = \frac{{\eta_{1} \rho_{1} a_{1} \lambda }}{{p_{1} }}, $$
$$ K_{1} = \sqrt {\frac{{v_{1}^{2} }}{{D_{1}^{2} }} + 4\frac{\lambda }{{D_{1} }}} , $$
$$ w_{1} = \frac{1}{2}\left( {K_{1} - \frac{{v_{1} }}{{D_{1} }}} \right), $$

for the second layer, substituting \( C_{2} \left( x \right) \) in Eq. (11) we have

$$ D_{2} w_{2}^{2} + v_{2} w_{2} - \lambda = 0, $$
$$ g_{2} = \lambda \left( {C_{f2}^{a} + C_{f2}^{b} } \right) = \lambda C_{f2} = \frac{{\eta_{2} \;\rho_{2} \; a_{2} \;\lambda }}{{p_{2} }}, $$
$$ K_{2} = \sqrt {\frac{{v_{2}^{2} }}{{D_{2}^{2} }} + 4\frac{\lambda }{{D_{2} }}} , $$
$$ w_{2} = \frac{1}{2}\left( {K_{2} - \frac{{v_{2} }}{{D_{2} }}} \right), $$

and for the third layer, substituting \( C_{3} \left( x \right) \) in Eq. (11) we have

$$ D_{3} w_{3}^{2} + v_{3} w_{3} - \lambda = 0, $$
$$ g_{3} = \lambda \left( {C_{f3}^{a} + C_{f3}^{b} } \right) = \lambda C_{f3} = \frac{{\eta_{3} \;\rho_{3} \;a_{3} \;\lambda }}{{p_{3} }}, $$
$$ K_{3} = \sqrt {\frac{{v_{3}^{2} }}{{D_{3}^{2} }} + 4\frac{\lambda }{{D_{3} }}} , $$
$$ w_{3} = \frac{1}{2}\left( {K_{3} - \frac{{v_{3} }}{{D_{3} }}} \right). $$

Now with the considered data here, and taking the borders as approximately \( x_{12} = 130\;{\text{cm}}\;{\text{and}}\;x_{23} = 217\;{\text{cm}} \), we get the results shown in Fig. 3 with the following parameters

$$ \left. {\begin{array}{*{20}l} {w_{1} = 0.010\; {\text{cm}}^{ - 1} ,\;w_{2} = 0.018\; {\text{cm}}^{ - 1} ,\;w_{3} = 0.010\; {\text{cm}}^{ - 1} } \hfill \\ {C_{f1} = 19000\; {\text{Bq/m}}^{3} } \hfill \\ {C_{f2}^{a} = 13822\; {\text{Bq/m}}^{3} ,\;C_{f2}^{b} = 15100\;{\text{Bq/m}}^{3} } \hfill \\ {C_{f3}^{a} = 25768 \;{\text{Bq/m}}^{3} ,\;C_{f3}^{b} = 18100\;{\text{Bq/m}}^{3} } \hfill \\ \end{array} } \right\} $$
(28)
Fig. 3
figure 3

Soil radon concentration, Eq. (27), considering the soil as a triple layer

Full size image

The numbers in Eq. (28) can be considered as the most trusted set of parameters to describe the soil. Among other suggested sets the one shown in Eq. (28) has the best fitting according to the least squares method. This can be seen in Fig. 3 which displays the ability of the model in characterizing the radon concentration in soil. The last layer however has a little data, the thing that can raise some dispute about its truthfulness. To show further the merit of the model we compare it to some other theoretical results [13] displayed here in Fig. 4. Those calculations also assume a multi-layer soil description [13]. This comparison manifests the model’s efficiency in fully fitting the experimental data. It should however be noticed that this model is designed basically to describe those types of soils, such as the one studied here in Fig. 3, where the radon concentrations show a non-monotonic behavior.

Fig. 4
figure 4

Soil radon concentration, methods of Ref. [13]. Figure 2a in the reference

Full size image

Having the parameters of Eq. (28), several interesting features for the soil radon can be set. For instance, the radon migration length and diffusion coefficient

$$ l = \frac{1}{w}\quad {\text{and}}\quad D = \frac{\lambda }{{w^{2} }}, $$
(29)

and using Eq. (17a) the radon advection speed can be found. Equations (28), (21) and (22) can be used to find the saturation levels, the depths of which can be obtained from Fig. 3.

Radon inhalation

To calculate the inhalation dose, we first need to know the indoor radon concentration \( ({\text{Bq/m}}^{3} ) \). This is given by [14]

$$ C_{in} = \frac{R \cdot A}{r \cdot V}, $$
(30)

where \( A\; {\text{and}}\; V \) are the room’s surface area and volume, respectively, \( r \) is the rate of ventilation and \( R \) is the radon surface release rate. Equation (30) reflects the main factors that affect the indoor radon variation and distribution. As expected [15, 16], increasing the room’s rate of ventilation decreases the indoor radon concentration. Another factor is the dimensions and style of the room [15,16,17,18]. Some important factors are embedded in the radon release rate, \( R \), like the type of the construction material and all of its parameters. In addition, factors like the seasons, the air’s vapor saturation level and the air quality in general can also affect the indoor radon variation and distribution [15,16,17,18]. Radon inhalation dose is expressed as [19]

$$ I = C_{in} \cdot F.O.d, $$
(31)

where \( d \) is the dose conversion factor \( \left( {{\text{nSv}} \cdot {\text{m}}3 / {\text{Bq}}} \right) \), \( O \) is the indoor occupancy factor and \( F \) is the magnitude of equilibrium among radon and its progenies.

To evaluate the indoor radon concentration, the measured radon release rates are usually used in Eq. (30). These measurements are performed on samples of the building materials. However, from technical point of view, this may need to be re-examined. The reason for this is that in experiment, the outflow of radon from all surfaces of the sample is taken into account; however, one may think that, when a wall is built of that material, only the inner surface of the wall is important if we want to assess the indoor radon concentration. Still, even if the experiment measures only one surface of the sample, this cannot correct for the fact that the radon release rate varies with the sample’s size and shape. To shed more light on that argument, we shall calculate the radon release rate from a material sample and compare it with that from a wall.

Exhalation of radon from a sample of the building material

To account for the flow of radon from different surfaces, we use the Fick’s second law of diffusion in the 3-dimension case. Taking the sample as a cuboid with dimensions \( 2L_{1 } , \;2L_{2 } \;{\text{and}}\;2L_{3 } \) along the axes \( x, \;y\; {\text{and}}\;z, \) respectively, we have

$$ \frac{{\partial C\left( {x,y,z,t} \right)}}{\partial t} = D\left[ {\frac{{\partial^{2} C\left( {x,y,z,t} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} C\left( {x,y,z,t} \right)}}{{\partial y^{2} }} + \frac{{\partial^{2} C\left( {x,y,z,t} \right)}}{{\partial z^{2} }}} \right] + g - \lambda C\left( {x,y,z,t} \right), $$
(32)

where the origin of the axes is the central point of the sample. The steady state solution is

$$ C\left( {x,y,z} \right) = Q \cdot { \cosh }\left( {\frac{{\left( {x + y + z} \right)}}{\sqrt 3 l}} \right) + \frac{g}{\lambda } , $$
(33)

where \( Q \) is a constant. As in the case of a wall, the radon concentrations are assumed to be zero on the sample’s surfaces. Applying this on the center of the surface \( x = L_{1} , \) namely, \( C\left( {L_{1} ,0, 0} \right) = 0, \) gives

$$ Q_{x} = \frac{{ - \frac{g}{\lambda }}}{{{ \cosh }\left( {\frac{{L_{1} }}{\sqrt 3 l}} \right)}} , $$
(34)

where \( Q_{x} \) is \( Q \) along the \( x \)-axis. The concentration along the \( x \)-axis is

$$ C_{x} = \left( {1 - \frac{{{ \cosh }\left( {\frac{x}{{\sqrt {3 } l}}} \right)}}{{{ \cosh }\left( {\frac{{L_{1} }}{{\sqrt {3 } l}}} \right)}}} \right) \frac{g}{\lambda }. $$
(35)

Applying the boundary conditions on the surfaces \( y = L_{2} \;{\text{and}}\;z = L_{3} , \) we similarly get

$$ Q_{y} = \frac{{ - \frac{g}{\lambda }}}{{{ \cosh }\left( {\frac{{L_{2} }}{\sqrt 3 l}} \right)}}, $$
(36)
$$ C_{y} = \left( {1 - \frac{{{ \cosh }\left( {\frac{y}{{\sqrt {3 } l}}} \right)}}{{{ \cosh }\left( {\frac{{L_{2} }}{{\sqrt {3 } l}}} \right)}}} \right) \frac{g}{\lambda }, $$
(37)
$$ Q_{z} = \frac{{ - \frac{g}{\lambda }}}{{{ \cosh }\left( {\frac{{L_{3} }}{\sqrt 3 l}} \right)}}, $$
(38)
$$ C_{z} = \left( {1 - \frac{{{ \cosh }\left( {\frac{z}{{\sqrt {3 } l}}} \right)}}{{{ \cosh }\left( {\frac{{L_{3} }}{{\sqrt {3 } l}}} \right)}}} \right) \frac{g}{\lambda }. $$
(39)

The radon release rates will be

$$ R_{x} = \left| { - pD\frac{{dC_{x} }}{dx}} \right|_{{x = L_{1} }} = \frac{p D g}{\sqrt 3 \lambda l}\tanh \left( {\frac{{L_{1} }}{\sqrt 3 l}} \right) = \frac{{a\,\upeta\,\lambda \,\uprho\,l}}{\sqrt 3 } { \tanh }\left( {\frac{{L_{1} }}{\sqrt 3 l}} \right), $$
(40)
$$ R_{y} = \left| { - pD\frac{{dC_{y} }}{dy}} \right|_{{y = L_{2} }} = \frac{p D g}{\sqrt 3 \lambda l}\tanh \left( {\frac{{L_{2} }}{\sqrt 3 l}} \right) = \frac{{a\,\upeta\,\lambda \,\uprho\,l}}{\sqrt 3 }\tanh \left( {\frac{{L_{2} }}{\sqrt 3 l}} \right), $$
(41)
$$ R_{z} = \left| { - pD\frac{{dC_{z} }}{dz}} \right|_{{z = L_{3} }} = \frac{p D g}{\sqrt 3 \lambda l}\tanh \left( {\frac{{L_{3} }}{\sqrt 3 l}} \right) = \frac{{a\,\upeta\,\lambda \,\uprho\,l}}{\sqrt 3 } { \tanh }\left( {\frac{{L_{3} }}{\sqrt 3 l}} \right), $$
(42)

where, as can be seen, the number \( \sqrt 3 \) plays a key role in differing the sample’s rates from the wall’s rate, Eq. (8). To sense the difference, we divide both rates

$$ \frac{{R_{w} }}{{R_{x} }} = \frac{{\sqrt 3 { \tanh }\left( {\frac{L}{l}} \right)}}{{{ \tanh }\left( {\frac{{L_{1} }}{\sqrt 3 l}} \right)}}, $$
(43)
$$ \frac{{R_{w} }}{{R_{y} }} = \frac{{\sqrt 3 { \tanh }\left( {\frac{L}{l}} \right)}}{{{ \tanh }\left( {\frac{{L_{2} }}{\sqrt 3 l}} \right)}}, $$
(44)
$$ \frac{{R_{w} }}{{R_{z} }} = \frac{{\sqrt 3 { \tanh }\left( {\frac{L}{l}} \right)}}{{{ \tanh }\left( {\frac{{L_{3} }}{\sqrt 3 l}} \right)}}, $$
(45)

with average

$$ R_{w/xyz} = \frac{1}{3}\left( {\frac{{R_{w} }}{{R_{x} }} + \frac{{R_{w} }}{{R_{y} }} + \frac{{R_{w} }}{{R_{z} }}} \right). $$
(46)

The change of \( R_{w/xyz} \) with the radon diffusion length is shown in Figs. 5, 6, 7 and 8 for different sets of \( L,\;L_{1} ,\; L_{2} \;{\text{and}}\; L_{3} \). It can be seen from the figures that the wall’s rate is higher than the sample’s rate by a factor of at least 1.73 \( (\sqrt 3 ) \). It is also clear from the figures that, depending on the set of values \( l, L, L_{1} , L_{2} {\text{and}} L_{3} , \) both rates could easily differ from each other by a factor of 10. This indicates that estimating the radon release rates from the materials’ samples could lead to a significant underestimation of the radon indoor concentrations and inhalation doses.

Fig. 5
figure 5

The ratio \( R_{w/xyz} \), Eq. (46), between radon surface exhalation rate from a wall and that from a sample of the building material in the form of a cuboid with \( L_{1} = L_{2} = L_{3} = 5\;{\text{cm}} \), as a function of the radon diffusion length. The wall’s thickness is \( 20\; {\text{cm}} \)

Full size image
Fig. 6
figure 6

The ratio \( R_{w/xyz} \), Eq. (46), between radon surface exhalation rate from a wall and that from a sample of the building material in the form of a cuboid with \( L_{1} = L_{2} = L_{3} = 10\; {\text{cm}} \), as a function of the radon diffusion length. The wall’s thickness is \( 20 \;{\text{cm}} \)

Full size image
Fig. 7
figure 7

The ratio \( R_{w/xyz} \), Eq. (46), between radon surface exhalation rate from a wall and that from a sample of the building material in the form of a cuboid with \( L_{1} = 3,\; L_{2} = 5,\; L_{3} = 6\;{\text{cm}} \), as a function of the radon diffusion length. The wall’s thickness is \( 20 \;{\text{cm}} \)

Full size image
Fig. 8
figure 8

The ratio \( R_{w/xyz} \), Eq. (46), between radon surface exhalation rate from a wall and that from a sample of the building material in the form of a cuboid with \( L_{1} = 5,\; L_{2} = 5,\; L_{3} = 7\;{\text{cm}} \), as a function of the radon diffusion length. The wall’s thickness is \( 30\; {\text{cm}} \)

Full size image

Impact of radon exhalation from walls on calculating the indoor gamma absorbed-dose

Most of the radiation due to the \( {}_{{}}^{238} {\text{U}} \) decay chain is by radon’s short-lived daughters. Therefore, radon release from walls results in a reduction in the indoor gamma absorbed-dose from the building materials. It also results in a non-equilibrium in the 238U chain and a reduced concentration of radon and its short-lived daughters inside the walls. A suggested approximate way to assess the reduced gamma dose is to perform the calculations with replacing the radium concentration by the reduced radon concentration inside the walls [20]. This concentration, as given by Eq. (4), can be expressed as

$$ a_{Rn} \left( x \right) = \left( {1 - F_{Rn} \frac{{L \cosh \left( {x/l} \right)}}{{l \sinh \left( {L/l} \right)}}} \right)a, $$
(47)

where \( F_{Rn} \) is the radon release factor which is the fraction of radon atoms released from the wall out of the total ones produced per second inside the wall

$$ F_{Rn} = \frac{{R_{w} }}{{a \lambda \uprho L}} = \frac{l}{L}\upeta\tanh \left( {\frac{L}{l}} \right). $$
(48)

By approximating \( { \cosh }\left( {x /l} \right) \) by 1 and \( { \sinh }\left( {L /l} \right) \) by \( L /l \), which is quite acceptable since \( l \gg L \) for most types of building materials, Eq. (47) becomes

$$ a_{Rn} = a\left( {1 - F_{Rn} } \right), $$
(49)

with no dependence on position. Using this form to calculate the corrected gamma dose rate means that all we have to do is just multiply the previously calculated dose rate by the factor \( \left( {1 - F_{Rn} } \right) \). It should be noticed in Eq. (49) that if radon stopped to release from the walls, namely \( F_{Rn} = 0 \), then as expected \( a_{Rn} = a \), which would mean that the decay chain is in equilibrium.

The radon release factor is used for not only studying the gamma dose rate but for studying the radon indoor concentration as well. It is important, therefore, to discuss further the different parameters that affect the radon release rate. As can be seen from Eq. (8), the most important and direct parameters are the density of the building material, the radium content, the radon emanation factor and the radon diffusion length. The wall’s thickness also influences the radon release rate. Another parameter is the percentage of water vapor in the pore spaces inside the material. This is because the distance travelled by the recoiled radon atoms upon creation is pretty much controlled by the amount of water vapor between the grains. Another important parameter that affects the radon release rate is painting and coating the walls. This can have strong effect depending on the types of paints and coatings used.

Conclusion

Radon concentrations inside walls and ground have been studied using Fick’s second law of diffusion. In both cases, a 1-dimension diffusion description is used, with including the advection process in the soil case. The resulting indoor radon flow and indoor radon concentration have been formulated. The soil radon concentration form has been successfully adjusted to some experimental data. The radon exhalation rate from a building material sample has been calculated based on a 3-dimension diffusion description, and the obtained formula has been compared to radon exhalation rate from a wall. A big difference between the two cases could be expected, depending on the radon diffusion length, the wall’s thickness and the sample’s dimensions. In other words, by using the radon exhalation rate from a building material sample to estimate the radon indoor concentration, a significant underestimation of the latter could happen.

Gamma indoor absorbed-dose rate, due to building materials, becomes less by the release of radon from the walls. An approximate way to calculate the corrected gamma dose has been proposed. It is built on the above description of radon diffusion in walls, and it suggests using the radon concentration inside the walls in calculating the gamma dose rate, instead of using the radium concentration. The method is very simple and it just requires a multiplication of a correction factor; \( (1 - F_{Rn} ) \), where \( F_{Rn} \) is the observed radon release factor. An experimental verification for that method is yet to be performed. It should be noted that, although the analyses in this paper have been focusing on the radon \( {}_{{}}^{222} {\text{Rn}} \), due to its relatively much larger half-life than those of the other radon isotopes, the formulations in this paper are valid for other radon isotopes.