1 Introduction

A research of the thermodynamic properties is significant in the understanding of the specific behavior of real gases for various pressure and temperature ranges [1, 2]. The leading work of VDW in 1873 caused the generation of new equations of state to investigate the thermal properties of gases [3]. Therefore, researchers have suggested many of equations of state for the determination of the thermal properties of fluids [4, 5]. The equations of state such as Soave–Redlich–Kwong [6], Redlich–Kwong [7], Beattie–Bridgeman [8] and the Peng–Robinson [9] have been used commonly for the study of fluid systems. The virial equation of state that defines thermal properties such as speed of sound, entropy, enthalpy and heat capacity at constant pressure for gases is one of these equations. The virial equation of state consists of the second, third, fourth virial coefficients, etc. The virial coefficients are important because there are strong relations between the interactions of the molecules in pairs, triplets, and so on [10]. The virial coefficients ensure a precious way to knowledge of the intermolecular forces since they depend on intermolecular interaction energy and temperature [10, 11]. Therefore, we preferred the virial coefficients which are suitable for calculating the HP and SS of used gases accurately for the industrial field in this work. The sufficient methods are presented for the second and third virial coefficients; however, precise determination of the fourth virial coefficient for different intermolecular potentials has not been completed yet [12]. Therefore, many researchers have proposed a lot of methods for the evaluation of fourth virial coefficient accurately. Katsura has tried to calculate the FVC over square well potential by utilization of Fourier transforms [13]. Also, Boys and Shavitt have calculated the FVC for Lennard-Jones (12-6) potential approximately by using the method based on Gaussian functions [14]. Barker and Monaghan have calculated the FVC over Lennard-Jones (12-6) and square well potentials by using Legendre polynomial expansion procedure [15]. But the FVC of different intermolecular potentials has not been calculated precisely and accurately so far. Nowadays, it is still quite difficult to determine the FVC and thermodynamic properties analytically according to the FVC [15,16,17,18,19].

We have suggested a new approach in this study for the computation of the HC and SS of real gases using the approach for the FVC over Lennard-Jones (12-6) potential. To our knowledge, this work is the initial approximation to the computation of HC at constant pressure and SS for real gases by FVC over Lennard-Jones (12-6) potential. This theoretical study strongly benefits the evaluation of HC at constant pressure and SS of real gases. Note that the obtained results are in a satisfactory agreement with the existing numerically evaluated data.

2 Definition and expressions of FVC and HC at constant pressure and SS

The FVC is given by

$$ D\left( T \right) = D_{1} \left( T \right) + D_{2} \left( T \right) + D_{3} \left( T \right), $$
(1)

where the quantities \( D_{1} \left( T \right) \), \( D_{2} \left( T \right) \) and \( D_{3} \left( T \right) \) can be written in the following forms [12, 15]:

$$ D_{1} \left( T \right) = - \frac{{3N_{A}^{3} }}{8}\iiint {f\left( {r_{12} } \right)}\;f\left( {r_{14} } \right)f\left( {r_{23} } \right)f\left( {r_{34} } \right)\text{d}r_{2} \text{d}r_{3} \text{d}r_{4} , $$
(2)
$$ D_{2} \left( T \right) = - \frac{{3N_{A}^{3} }}{4}\iiint {f\left( {r_{12} } \right)}\;f\left( {r_{13} } \right)f\left( {r_{14} } \right)f\left( {r_{23} } \right)f\left( {r_{34} } \right)\text{d}r_{2} \text{d}r_{3} \text{d}r_{4} , $$
(3)
$$ D_{3} \left( T \right) = - \frac{{N_{A}^{3} }}{8}\iiint {f\left( {r_{12} } \right)}\;f\left( {r_{13} } \right)f\left( {r_{14} } \right)f\left( {r_{23} } \right)f\left( {r_{24} } \right)f\left( {r_{34} } \right)\text{d}r_{2} \text{d}r_{3} \text{d}r_{4} . $$
(4)

Here, \( f\left( {r_{ij} } \right) = \left( {e^{{{{u(r_{ij} )} \mathord{\left/ {\vphantom {{u(r_{ij} )} {k_{\text{B}} T}}} \right. \kern-0pt} {k_{\text{B}} T}}}} - 1} \right) \) is Mayer function [12]. In Eqs. (2)–(4), angular coordinates are expressed as follows:

$$ \eta_{ij} = \cos \theta_{ij} , $$
(5)
$$ r_{ij}^{2} = r_{li}^{2} + r_{lj}^{2} - 2r_{li} r_{lj} \cos \theta_{ij} , $$
(6)
$$ \cos \left( {\theta_{ij} } \right) = \cos \left( {\theta_{ik} } \right)\cos \left( {\theta_{lj} } \right) + \sin \left( {\theta_{ik} } \right)\sin \left( {\theta_{lj} } \right)\cos \vartheta . $$
(7)

By substituting Eqs. (5)–(7) into Eqs. (2)–(4) and considering Lennard-Jones (12-6) potential, we obtain the following formulae:

$$ \begin{aligned} D_{1} \left( T \right) & = - 6\pi^{2} b_{0}^{3} \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {r_{12}^{2} \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{B} }}\left( {\left( {\frac{\sigma }{{r_{12} }}} \right)^{12} - \left( {\frac{\sigma }{{r_{12} }}} \right)^{6} } \right)}} - 1} \right)\;} } } } }\\ &\quad\quad r_{13}^{2} \;r_{14}^{2} \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{B} }}\left( {\left( {\frac{\sigma }{{r_{14} }}} \right)^{12} - \left( {\frac{\sigma }{{r_{14} }}} \right)^{6} } \right)}} - 1} \right) \\ & \quad \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{B} }}\left( {\left( {\frac{\sigma }{{\sqrt {r_{12}^{2} + r_{13}^{2} - 2r_{12} r_{13} \eta_{23} } }}} \right)^{12} - \left( {\frac{\sigma }{{\sqrt {r_{12}^{2} + r_{13}^{2} - 2r_{12} r_{13} \eta_{23} } }}} \right)^{6} } \right)}} - 1} \right)\\ &\quad\quad\left( {e^{{ - \frac{4\varepsilon }{{T\;k_{B} }}\left( {\left( {\frac{\sigma }{{\sqrt {r_{14}^{2} + r_{13}^{2} - 2r_{14} r_{13} \eta_{34} } }}} \right)^{12} - \left( {\frac{\sigma }{{\sqrt {r_{14}^{2} + r_{13}^{2} - 2r_{14} r_{13} \eta_{34} } }}} \right)^{6} } \right)}} - 1} \right) \\ & \quad {\text{d}}r_{12} {\text{d}}r_{13} {\text{d}}r_{14} {\text{d}}\eta_{23} {\text{d}}\eta_{34} \\ \end{aligned} $$
(8)
$$ \begin{aligned} D_{2} \left( T \right) & = - 12\pi^{2} b_{0}^{3} \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {r_{12}^{2} \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{r_{12} }}} \right)^{12} - \left( {\frac{\sigma }{{r_{12} }}} \right)^{6} } \right)}} - 1} \right)} } } } }\\ &\quad r_{13}^{2} \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{r_{13} }}} \right)^{12} - \left( {\frac{\sigma }{{r_{13} }}} \right)^{6} } \right)}} - 1} \right)r_{14}^{2} \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{r_{14} }}} \right)^{12} - \left( {\frac{\sigma }{{r_{14} }}} \right)^{6} } \right)}} - 1} \right) \\ & \quad \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{\sqrt {r_{13}^{2} + r_{12}^{2} - 2r_{13} r_{12} \eta_{23} } }}} \right)^{12} - \left( {\frac{\sigma }{{\sqrt {r_{13}^{2} + r_{12}^{2} - 2r_{13} r_{12} \eta_{23} } }}} \right)^{6} } \right)}} - 1} \right)\\ &\quad\left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{\sqrt {r_{12}^{2} + r_{14}^{2} - 2r_{12} r_{14} \eta_{24} } }}} \right)^{12} - \left( {\frac{\sigma }{{\sqrt {r_{12}^{2} + r_{14}^{2} - 2r_{12} r_{14} \eta_{24} } }}} \right)^{6} } \right)}} - 1} \right) \\ & \quad {\text{d}}r_{12} {\text{d}}r_{13} {\text{d}}r_{14} {\text{d}}\eta_{23} {\text{d}}\eta_{24} \\ \end{aligned} $$
(9)
$$ \begin{aligned} D_{3} \left( T \right) & = - \pi^{2} b_{0}^{3} \int\limits_{0}^{\infty } \int\limits_{0}^{\infty } \int\limits_{0}^{\infty } \int\limits_{ - 1}^{1} \int\limits_{ - 1}^{1} \int\limits_{0}^{2\pi } r_{12}^{2} \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{r_{12} }}} \right)^{12} - \left( {\frac{\sigma }{{r_{12} }}} \right)^{6} } \right)}} - 1} \right)\\ &\quad r_{13}^{2} \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{r_{13} }}} \right)^{12} - \left( {\frac{\sigma }{{r_{13} }}} \right)^{6} } \right)}} - 1} \right)r_{14}^{2} \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{r_{14} }}} \right)^{12} - \left( {\frac{\sigma }{{r_{14} }}} \right)^{6} } \right)}} - 1} \right) \\ & \quad \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{\sqrt {r_{12}^{2} + r_{14}^{2} - 2r_{12} r_{14} \eta_{24} } }}} \right)^{12} - \left( {\frac{\sigma }{{\sqrt {r_{12}^{2} + r_{14}^{2} - 2r_{12} r_{14} \eta_{24} } }}} \right)^{6} } \right)}} - 1} \right)\\ &\quad \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{\sqrt {r_{13}^{2} + r_{14}^{2} - 2r_{13} r_{14} \eta_{34} } }}} \right)^{12} - \left( {\frac{\sigma }{{\sqrt {r_{13}^{2} + r_{14}^{2} - 2r_{13} r_{14} \eta_{34} } }}} \right)^{6} } \right)}} - 1} \right) \\ & \quad \left( {e^{{ - \frac{4\varepsilon }{{T\;k_{\text{B}} }}\left( {\left( {\frac{\sigma }{{\sqrt {r_{12}^{2} + r_{13}^{2} - 2r_{12} r_{13} \left( {\eta_{24} \eta_{34} + \sqrt {1 - \eta_{24}^{2} } \sqrt {1 - \eta_{34}^{2} } \cos \vartheta } \right)} }}} \right)^{12} - \left( {\frac{\sigma }{{\sqrt {r_{12}^{2} + r_{13}^{2} - 2r_{12} r_{13} \left( {\eta_{24} \eta_{34} + \sqrt {1 - \eta_{24}^{2} } \sqrt {1 - \eta_{34}^{2} } \cos \vartheta } \right)} }}} \right)^{6} } \right)}} - 1} \right) \\ & \quad {\text{d}}r_{12} {\text{d}}r_{13} {\text{d}}r_{14} {\text{d}}\eta_{24} {\text{d}}\eta_{34} {\text{d}}\vartheta \\ \end{aligned} $$
(10)

where \( b_{0} = {{2\pi N_{\text{A}} \sigma^{3} } \mathord{\left/ {\vphantom {{2\pi N_{\text{A}} \sigma^{3} } 3}} \right. \kern-0pt} 3} \). Note that the deviations from the ideal behavior are efficiently described by the second virial coefficient at low densities, but higher virial coefficients must be considered at higher densities [20]. Therefore, the HC and SS of gases may be expressed with the fourth virial coefficient approximately as follows [12, 21, 22], respectively:

$$ C_{\text{P}} - C_{\text{P}}^{0} = - \frac{1}{{4R^{4} }}\left( {\frac{P}{T}} \right)^{3} D\left( T \right), $$
(11)
$$ u^{2} = \frac{\gamma RT}{M}\left( {1 + 2\left( {\frac{P}{RT}} \right)^{3} \frac{{\left( {1 + \gamma } \right)}}{\gamma }D\left( T \right)} \right), $$
(12)

where \( D\left( T \right) \) is the fourth virial coefficient and \( \gamma = {{C_{\text{P}} } \mathord{\left/ {\vphantom {{C_{\text{P}} } {C_{\text{V}} }}} \right. \kern-0pt} {C_{\text{V}} }} \) is the heat capacity ratio. The symbol small zero \( \left( {^{0} } \right) \) expresses the property of gas in its ideal state in Eqs. (11)–(12). We have suggested a new approach for calculating heat capacity at constant pressure and speed of sound according to the fourth virial coefficient by substituting Eq. (1) into Eqs. (11)–(12).

3 Numerical results and discussion

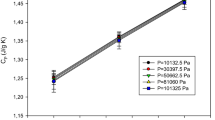
A new approach to calculate the HC at constant pressure and SS for real gases using the FVC is presented. The utility approach for calculating HC and SS of gases is proposed, and it can be applied to any gases. We made some mathematical transformations on the fourth virial coefficient to make it numerically solvable. Equations (11)–(12) have been evaluated using the numerical method. This work is the first approach to the calculation of HC at constant pressure and SS for real gases by FVC over Lennard-Jones (12-6) potential, as far as we know. The Lennard-Jones (12-6) parameters for gases of Ar, SF6 and SiH4 are given in Table 1 [24,25,26]. The Mathematica 7.0 software system has been used to compute the HC at constant pressure and SS. The obtained results are given for HC at constant pressure and SS of gases of Ar, SF6 and SiH4 in Tables 2, 3 and 4. The calculation results of Eqs. (11)–(12) have been compared with those obtained by literature data [2, 22, 23, 27, 28]. The results are in well agreement with the existing literature at a varying temperature ranging from 90 to 800 K and at a varying pressure ranging between 0.09 and 100.7 atm [2, 23]. The standard deviation is given for the sound of speed and heat capacities of Ar, SF6 and SiH4 in Tables 2, 3, 4, 5, 6 and 7. The obtained results of the HC at constant pressure for gases of Ar, SF6 and SiH4 are compared with theoretical data [22, 23, 27, 28]. The calculated results of SS for gases Ar, SF6 and SiH4 are compared with theoretical and experimental data [2, 22, 23, 27]. It is well known that the real gases begin to switch into the liquid phase at low temperatures and high pressures. Therefore, as seen in Tables 2, 4 and 6, the computation results of the heat capacities by using the FVC deviate a little from literature data at high pressures and low temperatures [22, 27, 28]. Also, as the pressure increases at a constant temperature, the agreement between the obtained calculation results for SS and the experimental data is demonstrated in Table 5. As seen from Tables 2, 3, 4, 5, 6 and 7, note that the FVC is implemented at the private temperature and pressure ranges that molecule indicates the gas behavior. As known, the deviations from the ideal behavior at low densities are efficiently expressed by the second virial coefficient; however, higher virial coefficients are taken into regard at higher densities. One of the advantages of this work is the utilization of the FVC for the accepted formulae of HC and SS for gases at higher densities. Therefore, the established formulae for the FVC to calculate HC and SS are suitable in the arbitrary range of values of parameters. As seen from the calculation results, the suggested approach displays good results in various ranges of parameters. Therefore, the calculation results obtained from this work will be beneficial for a different perspective of industry and technology.

Table 1 Parameters of Lennard-Jones (12-6) potential
Full size table
Table 2 Comparative results of heat capacity at constant pressure of Ar
Full size table
Table 3 Comparative results of speed of sound of Ar
Full size table
Table 4 Comparative results of heat capacity at constant pressure of SF6
Full size table
Table 5 Comparative results of speed of sound of SF6
Full size table
Table 6 Comparative results of heat capacity at constant pressure and of SiH4
Full size table
Table 7 Comparative results of speed of sound of SiH4
Full size table

4 Conclusion

A new approach has been proposed in this study to calculate the HC at constant pressure and SS of real gases at different temperature and pressure ranges using the fourth virial coefficient. As seen from the results, the present theoretical approximation is general and provides a useful guidance for a correct assessment of the other thermal properties of gases.