1 Introduction

Quantum correlations (QCs) are seen as necessary and influential phenomena in quantum information technology. Numerous QCs can be described as a kind of nonlocal correlation between two or more quantum subsystems [1]. QCs are considered the main source of quantum cryptography, teleportation and quantum metrology in quantum information processing [2,3,4]. The main aim of these processes is to generate entangled states between subsystems that are not possible with a classical resource. The QD is another kind of correlation that depends on mutual quantum information. The QD is more general than entanglement and can be nonzero for separable mixed states [5,6,7]. Generally, it is difficult to evaluate the QD due to the problem of optimization. For the special case of qubit systems in the X-form state, the QD can be evaluated analytically [8,9,10].

In the framework of parameter estimation theory, various attempts have been made to discover quantifiers of QCs for quantum subsystems. In this regard, the QFI has been employed to detect atom-field entanglement [11,12,13,14]. The relationship between the QFI and atom-field entanglement in the absence and presence of decoherence has been studied [15, 16]. The flow of QFI was introduced to detect the non-Markovianity in open systems [17]. Additionally, the QFI for Markovian and non-Markovian dynamics of a two-level atomic system driven by the phase noise of a laser beam was examined [18]. Recently, the characterization of QCs via local QFI was considered [19]. Also, the question of “does large QFI imply Bell correlations?” has been answered [20]. The property of QFI continuity, that is, that two close states with close first derivatives have close QFI, has been demonstrated [21].

A main research direction in quantum information technology is generalization based on the type of interaction between quantum systems. Under this consideration, the studied models provide new physical situations and have become more realizable. The JC model was extended based on atomic motion, which was quantized as the motion of the center of mass of an atom, and the vibrational motion was quantized. The properties of entanglement of a three-two level atom and the field mode in Fock have also been investigated [22]. The sudden death and birth phenomena of entanglement between two atoms have been discovered [23]. The effect of time-dependent coupling on QCs between a pair of atoms and the field mode of power-law potentials has also been examined [24].

The QD attempts to capture quantum aspects of correlations beyond entanglement [5, 25], and there exist separable states that return a nonzero value of QD. These correlations have several advantages in the theoretical and experimental domain. For example, some interesting applications of QD in quantum computation [26,27,28,29], state merging [30, 31], remote state preparation [32] and open quantum systems representation [33] have been reported. Recently, the dynamics of super QD and QD teleportation in the JCM have been discussed [34]. Moreover, the relation between quantum coherence and geometric QD has been explored [35]. The sudden death and sudden birth of QD have also been investigated [36]. Furthermore, the properties of Rènyi discord have been studied for two-independent dimer systems coupled to two correlated Fermi-spin environments under non-Markovian conditions [37]. However, these studies do not consider the case of time-varying coupling on the evolution of QD and other correlations and its link with the quantum Fisher information. To the best of our knowledge, this manuscript is the first to study the effect of the time-dependent effect on quantum discord, classical correlation and quantum Fisher information.

In this paper, we examine the dynamic behavior of some important measures of QCs of a nonidentical qubit-field system with and without time-varying coupling under the dissipation effect. We explore the influence of the time variation of the coupling terms on the quantifiers when the qubits are immersed in a vacuum. We show the relationship among QD, CC, qubit-qubit entanglement and QFI in the absence and presence of the dissipation effect during the time evolution.

This paper is organized in the following order. The basic equations and relations in the system under consideration are given in Sect. 2. The different kinds of correlations based on the evolution of concurrence and QD are presented in Sect. 3. Section 4 shows the dynamical properties of the QFI with respect to the main parameters of the model. The main conclusion is presented in Sect. 5.

2 Model of the qubit-field in two separate JC nodes

Recently, considerable effort has been exerted in the investigation of different types of atom-field interactions [38, 39]. Here, we present a model of two separate JC nodes with a nonidentical qubit-field system as

$$\begin{aligned} \frac{{\hat{H}}}{\hbar }= & {} {\hat{H}}_{A}+{\hat{H}}_{B}=\sum \limits _{j=1}^{2}\left\{ \omega _{j}{\hat{b}}_{j}^{\dag }{\hat{b}}_{j}+\frac{\Omega _{j}}{2}\hat{\sigma }_{z}^{(j)}-i\frac{\gamma _{j}}{2}{\hat{\sigma }}_{+}^{(j)}{\hat{\sigma }} _{-}^{(j)}\right. \nonumber \\&\left. \frac{{}}{{}}+g_{j}\left( {\hat{\sigma }}_{+}^{(j)}{\hat{b}}_{j}+\hat{ \sigma }_{-}^{(j)}{\hat{b}}_{j}^{\dag }\right) \right\} ,\ \ \ \ \end{aligned}$$
(1)

where \(\ \hbar =1\) and the two qubits are represented by the atomic operators \({\hat{\sigma }}_{z}^{(j)}\), \({\hat{\sigma }}_{+}^{(j)}\) and \({\hat{\sigma }}_{-}^{(j)}\) for the jth qubit donated by A for \(j=1\) and B for \(j=2\). The atomic operators are defined in terms of the atomic basis as \(\left| \uparrow \right\rangle \left\langle \uparrow \right| -\left| \downarrow \right\rangle \left\langle \downarrow \right| \), \(\left| \uparrow \right\rangle \left\langle \downarrow \right| \) and \(\left| \downarrow \right\rangle \left\langle \uparrow \right| \). The optical field is represented by the annihilation (creation) operator \({\hat{b}}_{j}\)(\( {\hat{b}}_{j}^{\dag }\)), with the jth field mode. The values \(g_{j}\) are the coupling coefficients between the jth qubit and the localized field, and we set \(g_{1}=g_{2}=g\).

We assume the field modes are initially in their vacuum states and the two qubits are initially in the maximally entangled states

$$\begin{aligned} |v(0)\rangle =\frac{1}{\sqrt{2}}\left[ \exp (i\beta )\left| \uparrow \right\rangle \left\langle \uparrow \right| +\left| \downarrow \right\rangle \left\langle \downarrow \right| \right] \otimes |0_{1}0_{2}\rangle . \end{aligned}$$
(2)

In the context of quantum state estimation, Eq.(2) is the optimal input state after the phase gate operation \(\beta \) for the two-qubit systems interacting with two fields in the vacuum state.

At any time \(|v(t)\rangle =\exp \left\{ -i({\hat{H}}_{A}+{\hat{H}}_{B})t\right\} |v(0)\rangle \), where \([{\hat{H}}_{A},{\hat{H}}_{B}]=0\). Thus, we have

$$\begin{aligned}&\exp \left\{ -i{\hat{H}}_{A}t\right\} |n,\uparrow \rangle =C(t)|n,\uparrow \rangle +S(t)|n+1,\downarrow \rangle , \end{aligned}$$
(3)
$$\begin{aligned}&\exp \left\{ -i{\hat{H}}_{A}t\right\} |n+1,\downarrow \rangle =S(t)|n,\uparrow \rangle -C(t)|n+1,\downarrow \rangle . \end{aligned}$$
(4)

In the case of time-dependent coupling, we have \(|v(t)\rangle =\exp \left\{ i\int _{0}^{t}{\hat{H}}(\tau )d\tau \right\} |v(0)\rangle \), and after some calculations for the field in the vacuum state, one can obtain

$$\begin{aligned}&C(t)=\left\{ \cos (G(t)\sqrt{1-\gamma ^{2}})-\frac{\gamma }{\sqrt{1-\gamma ^{2}}}\cos (G(t)\sqrt{1-\gamma ^{2}})\right\} e^{-\gamma t}, \end{aligned}$$
(5)
$$\begin{aligned}&S(t)=\frac{-ie^{-\gamma t}}{\sqrt{1-\gamma ^{2}}}\sin (G(t)\sqrt{1-\gamma ^{2}}). \end{aligned}$$
(6)

The target of this work is to examine the effect of constant and time-dependent coupling between each qubit j and vacuum field defined as

$$\begin{aligned} G(t)=\left\{ \begin{array}{ll} gt&{}\quad \text { for }g_{j}=\text {const. } \\ g\sin (t)&{}\quad \text { for }g_{j}(t)=\cos (t)\\ g(1-\cos (t))&{}\quad \text { for }g_{j}(t)=\sin (t) \end{array} \right. \end{aligned}$$
(7)

Therefore, by tracing out two field modes, the resulting two-qubit state is obtained in the form X-state as

$$\begin{aligned} \varrho _{AB}(t)=tr_{1,2}\left( |v(t)\rangle \left\langle v(t)\right| \right) =\left[ \begin{array}{llll} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \varrho _{22} &{}\quad \varrho _{23} &{}\quad 0 \\ 0 &{}\quad \varrho _{32} &{}\quad \varrho _{33} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \varrho _{44} \end{array} \right] \end{aligned}$$

3 Quantum and classical correlations

The entanglement transfer between the subsystem has useful applications in quantum computing and quantum information technology [23, 40, 41]. Moreover, the creation of entangled states for many subsystems also has interesting applications. The most famous suitable model for discussing quantum and classical correlations is a model of the interaction between the field and the TQs. The QD is a main measure of QCs between the two qubits, and the concurrence is a measure of the first and second qubit entanglement defined as [42]

$$\begin{aligned} C_{AB}=\max \{0,\lambda _{1}-\lambda _{2}-\lambda _{3}-\lambda _{4}\}, \end{aligned}$$
(8)

where \(\lambda _{j}\) defines the eigenvalues in decreasing order of \(\varrho _{AB}{\tilde{\varrho }}_{AB}\) and \({\tilde{\varrho }}_{AB}\) is defined as

$$\begin{aligned} {\tilde{\varrho }}_{AB}=(\sigma _{Y}\otimes \sigma _{Y})\varrho _{AB}^{*}(\sigma _{Y}\otimes \sigma _{Y}), \end{aligned}$$
(9)

where \(\varrho _{AB}^{*}\) denotes the conjugate of \(\varrho _{AB}\) and \( \sigma _{Y}\) is the Pauli operator. The qubits A and B are in a pure state as \(C_{AB}=0\), but \(C_{AB}=1\) indicates that the qubits are in a maximally entangled state.

Here, we employ the von Neumann entropy to quantify the two qubits and two vacuum field entanglements defined by [43, 44]

$$\begin{aligned} S(\varrho _{AB})=-tr\{\varrho _{AB}\ln (\varrho _{AB})\}. \end{aligned}$$
(10)

Equation (10) can be written in terms of the eigenvalues of \(\varrho _{AB}\) and the atomic density \(\varphi _{j}\)

$$\begin{aligned} S(\varrho _{AB})=-\sum _{j=1}^{4}\varphi _{j}\ln (\varphi _{j}). \end{aligned}$$
(11)

Let us assume \(\{\theta ^{j}\}\) is the set of local measurements on a subsystem, which leads to the following density matrix

$$\begin{aligned} \varrho _{AB}^{j}=\frac{1}{p^{j}}(I\otimes \theta ^{j})\varrho _{AB}(I\otimes \theta ^{j}), \end{aligned}$$
(12)

such that

$$\begin{aligned} p^{j}=tr[(I\otimes \theta ^{j})\varrho _{AB}(I\otimes \theta ^{j})], \end{aligned}$$
(13)

representing the probability of measuring the jth state. The bipartite system is considered a conditional density operator, the conditional entropy is given by

$$\begin{aligned} S(\varrho _{AB}|\{\theta ^{j}\})=\sum _{j}p^{j}S(\varrho _{AB}), \end{aligned}$$
(14)

and the total correlation (TC) corresponding to the difference between the partial von Neumann entropy and the quantum mutual information is obtained as

$$\begin{aligned} \text {TC}(\varrho _{AB}|\{\theta ^{j}\})=S(\varrho _{A})-S(\varrho _{AB}|\{\theta ^{j}\}). \end{aligned}$$
(15)

The CC is the maximal amount of information in a subsystem after performing the local measurements and is defined as

$$\begin{aligned} \text {CC}(\varrho _{AB}|\{\theta ^{j}\})=S(\varrho _{A})-\min _{\{\theta ^{j}\}}[S(\varrho _{AB}|\{\theta ^{j}\})]. \end{aligned}$$
(16)

Therefore, the QD, which measures the quantum correlation in bipartite systems [45, 46], takes the following form,

$$\begin{aligned} D_{AB}=\text {TC}(\varrho _{AB})-\text {CC}(\varrho _{AB}). \end{aligned}$$
(17)
Fig. 1
figure 1

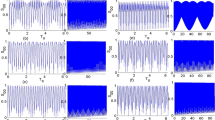
The evolution of the quantum discord \(D(\rho =\varrho )\) (solid red line), concurrence \(C_{AB}\) (dashed blue), and classical correlation \(\text {CC}(\varrho )\) (dashed-dotted black line) for the constant coupling between the qubits and vacuum fields (i.e., \( g_{A}(t)=g_{B}(t)=g\)). a The case in the absence of the dissipation effect (i.e., \(\gamma _{A}/g=\gamma _{B}/g=0\)) and b the case in the presence of the dissipation effect (i.e., \(\gamma _{A}= \gamma _{B}=0.1g\))

Full size image

We first study the time evolution of the three kinds of correlations of the two qubits in the absence of time-varying coupling \(g_{A}(t)=g_{B}(t)=g\), with and without the dissipative effect. The time evolution of the correlations for the initial Bell states in the case of \(\gamma _{A}/g=\gamma _{B}/g=0\) and \(\gamma _{A}/g=\gamma _{B}/g\ne 0\) is plotted in Fig. 1. As shown in Fig 1a, the correlations exhibit oscillations that are described by a periodic function during the evolution in the absence of dissipation. The three correlations show sudden death and birth phenomena that do not occur simultaneously within the interaction time. Moreover, the concurrence and classical correlation are less than the QD with the same maximum and minimum values during the evolution. Nevertheless, this result is not generally true since the correlations are three different quantities and there is no proportionate ordering among them. From Fig. 1b, we observe that the presence of the dissipative effect decreases the correlations during the evolution. The amount of the three correlations of the two qubits decreases with an increase in the decay terms \(\gamma _{j}\) in the Hamiltonian. The extent of the decrease in the concurrence and QD is less than that in the classical correlation during the dynamic process. Moreover, for some intervals of time, the entanglement tends to zero, where the two qubits are still discordant.

Fig. 2
figure 2

The same as Fig. 1 but the qubits-field coupling is a function of time as \(g_{A}(t)=g_{B}(t)=g\cos (t)\)

Full size image
Fig. 3
figure 3

The same as Fig. 1 but the qubits-field coupling is a function of time as \(g_{A}(t)=g_{B}(t)=g\sin (t)\)

Full size image

The time evolution of the three correlations for the JCM has been studied in previous works. Here, we consider time-varying coupling between the qubits and the fields and explore the realistic dynamics of these correlations under the dissipative effect, which has not previously been reported. In Fig. 2, we show the effects of the time-varying \( g_{A}(t)=g_{B}(t)=g\cos (t)\) on the dynamic behavior of the three correlations with and without the dissipation effect. The behavior of the three correlations is similar to that shown in Fig. 1. Moreover, the presence of the time-varying coupling leads to avoidance of the sudden death and sudden birth phenomena in the absence of the dissipative effect. On the other hand, the behavior of the correlations is affected by the choice of the time coupling, as shown in Fig. 3 for the case of \(g_{A}(t)=g_{B}(t)=g \sin (t)\). Therefore, control of the time-varying coupling in the interaction between the qubits and the field can help to enhance and stabilize the degree of correlation between the qubits during the evolution.

4 Quantum Fisher information

The Fisher information is defined in terms of the distribution function \(h_{ {\hat{\varphi }}}(x)\) as [47, 48]

$$\begin{aligned} I_{{\hat{\varphi }}}=\int \frac{1}{h_{{\hat{\varphi }}}(x)}\left( \frac{\partial h_{{\hat{\varphi }}}(x)}{\partial {\hat{\varphi }}}\right) ^{2}\mathrm{d}x\text {,} \end{aligned}$$
(18)

where \({\hat{\varphi }}\) is the estimator of the parameter. QFI is the quantum modification of the Fisher information and is defined in terms of the symmetric logarithmic derivative (SLD). If we consider the phase shift \({\hat{\varphi }}=\beta \), then the SLD can be obtained from the density matrix of the two-qubit in terms of , which is given by [11, 16]

$$\begin{aligned} \frac{\partial \varrho _{AB}(\beta ,t)}{\partial \beta }=\frac{1}{2} \{\varrho _{AB}(\beta ,t)D(\beta ,t)+D(\beta ,t)\varrho _{AB}(\beta ,t)\} \end{aligned}$$
(19)

Hence, the QFI for the phase shift parameter \(\beta \) is given by [11]

$$\begin{aligned} F_{Q}(t)=tr(\varrho _{AB}(\beta ,t)D(\beta ,t)^{2}) \end{aligned}$$
(20)

within the qubit density operator \(\varrho _{AB}(\beta ,t)\) and the SLD.

Fig. 4
figure 4

The dynamics of the QFI in terms of the phase shift estimator parameter \(\beta \) for different types of time-dependent qubit-field coupling, where the solid blue line is for \(g_{A}(t)=g_{B}(t)=g\), the dashed red line is for \(g_{A}(t)=g_{B}(t)=g\cos (t) \) and the dashed-dotted black line is for \(g_{A}(t)=g_{B}(t)=g\sin (t)\). a The case of the absence of the dissipation effect (i.e., \(\gamma _{A}/g=\gamma _{B}/g=0\) ) and b the presence of the dissipation effect (i.e., \(\gamma _{A}= \gamma _{B}=0.1g\))

Full size image

Now, the main interest is to examine the dynamic behavior of the QFI under the effect of time-varying coupling for the interaction term between the qubit and the field with and without the dissipative effect. We compare the influence of different parameters h_i on the evolution of the QFI. The blue line is for \(g_{A}(t)=g_{B}(t)=g\), the dashed-red line is for \( g_{A}(t)=g_{B}(t)=g\cos (t)\), dashed-black line is for \(g_{A}(t)=g_{B}(t)=g \sin (t)\). Figure 4a shows the dynamic behavior of the function \(F_{Q}(t)\) in terms of the scaled time for \(g_{j}=0\). The QFI function exhibits oscillation as a periodic function with an amplitude that depends on the parameter \(g_{j}\). This indicates that the enhancement and preservation of the QFI may occur through control of the interaction coupling strength of the whole system. Moreover, we can obtain a monotonic correlation between the QFI and quantum correlations in this case. Figure 4b shows the time evolution of the function \(F_{Q}\) versus time in the presence of the dissipative effect. The precision of the parameter estimation of the atom is highly sensitive to the dissipative environment. Interestingly, the dissipative effect causes a destructive effect on the amount of QFI during the evolution. The decay speed of the QFI is strictly dependent on the choice of parameter \(g_{j}\). Moreover, the local maximum values of function \( F_{Q}\) decrease gradually during the time evolution and the decrease rate of these maximal values depends on parameter \(g_{j}\). As time increases, the dissipative effect in the system interaction restrains the quantum effects of the qubit system and the value of function \(F_{Q} \) saturates to its lower level, with inaccurate estimation of parameter \(\beta \). On the other hand, the presence of time-varying coupling destroys the monotonic relation between the functions QFI and correlations during the dynamic evolution. The results show that appropriate preparation of the atom-field clearly improves the estimation enhancement realized by JCM under the dissipative effect, which may provide new perspectives to the field of quantum metrology.

5 Conclusion

In summary, we have considered two separate Jaynes–Cummings nodes with an nonidentical qubit-field system in the presence of the dissipation effect. We have investigated the dynamic behavior of the quantum discord, classical correlation, qubit-qubit entanglement, and quantum Fisher information. We have explored the influence of the time variation of the coupling terms on the quantifiers when the qubits are immersed in a vacuum. We have demonstrated the time evolution of the three kinds of correlations of the two qubits in the absence and presence of time-varying coupling. Moreover, we have shown how the presence of the dissipative effect leads to a decrease in the correlations during the evolution. Finally, we investigated the dynamic behavior of the quantum Fisher information under the effect of time-varying coupling with and without the dissipative effect. We found that enhancement and preservation of the quantum Fisher information may occur through control of the interaction coupling strength of the whole system. Moreover, we can obtain a monotonic correlation between the quantum Fisher information and quantum correlations in the absence of time-varying coupling, whereas the presence of time-varying coupling damages this monotonic relation.