Internal resonance analysis of a fluid-conveying tube resting on a nonlinear elastic foundation

Abstract

This study used a fluid-conveying nonlinear beam and a nonlinear spring to simulate the vibration of a fluid-conveying tube placed on an elastic foundation. The centripetal force and tangential force of fluid acting on the tube wall were considered. In this paper, Hamilton’s principle is used to derive the equation for the nonlinear flow-structure coupled motion, where the method of multiple scales is used to derive the frequency response of each mode under the fixed point (steady state), and the amplitude of each mode is used to examine internal resonance. This study added (tuned mass dampers) TMDs of different masses, spring constants and damping coefficients at different locations in the system to observe the effect of the shock absorber in avoiding the internal resonance of the flow-structure coupled system and reducing the vibration of the system. Poincaré map, maximum amplitude contour plots, and basin of attraction are used to analyze and compare the system to verify the correctness of our theory. The stability of the system is analyzed by changing the flow velocity of the fluid. The results show that under a certain combination of elastic foundation spring constants and flow speeds, the 1:3 internal resonance between the first and third modes of the main system will occur. In addition, the stability range of any case will increase significantly after TMD is added, indicating that TMD plays an important role.

1 Introduction

Fluid-conveying tubes are widely used in the engineering sector, such as air conditioner and offshore oil-conveying pipes, and can even simulate the aorta in the human body. As this system has the possibility of coupling the vibration between fluid and solid, the topic of the fluid-conveying tube has been widely discussed. Paidoussis et al. [1, 2] used the Bernoulli–Euler beam as the theoretical model to study the dynamic characteristics of the fluid-conveying tube. Blevins [3] gave a comprehensive overview of flow-induced vibration, while this paper gives a detailed description of the phenomena of vortex-induced vibration, meaning Galloping and Flutter. Based on the Bernoulli–Euler beam, Semler et al. [4] used the large deformations of the beam to derive the geometric nonlinear motion equation of the fluid-conveying tube. Zhang et al. [5] studied the vibration of the fluid-conveying tube, deduced the matrix equation of dynamic equilibrium by using the Lagrange principle, and used Eulerian and Fictitious loads to study the concept of kinematic correction to analyze the vibration. Reddy and Wang [6] used the theoretical model of a fluid-conveying beam to simulate the vibration of a fluid-conveying tube, meaning a nonlinear Bernoulli–Euler beam and a nonlinear Timoshenko beam were used to derive the equations of motion of the fluid-conveying beam of the two theories, respectively, and their results provided a method to simulate pipe vibration with the theoretical model of the nonlinear beam.

The vibration of the fluid-conveying tube and flow-induced wall vibration plays an important role in medical research. In addition to deteriorating elastin in the vascular wall, prolonged vibration may damage vascular smooth muscle, resulting in vascular dilatation; if the dilatation area is wider, the aneurysm may change permanently [7]. In addition, in the murmur-producing areas of arteries, changes in the elasticity of arterial walls are accompanied by poststenotic dilation. Boughner and Roach [8] found that low-frequency vibration in vascular murmurs caused changes in the properties of vascular walls. However, there was no literature regarding the relationship between the radial and axial vibrations of arterial wall and blood flow until 2000, when Sunagawa et al. [9] simultaneously measured the radial and axial vibrations and blood flow velocity of the arterial wall using ultrasonic beams, and the data they obtained on vascular wall vibration are beneficial to the diagnosis of the upper carotid artery. These studies have found that there is an important correlation between the elasticity of the arterial wall and the pressure on the arterial wall.

The vibration of nonlinear systems has always played an important role in the study of vibration, as internal resonance (I.R.) is a unique phenomenon in nonlinear systems; when the natural frequencies of different modes with the same degree of freedom have integer multiple relations with each other, the high modes of the excitation system will produce higher amplitudes in the low modes [10]. In a nonlinear system, the internal resonance is caused by the transfer of energy from the high mode of excitation to the low mode of nonexcitation, which triggers the low mode to produce a larger amplitude than the high mode, and this phenomenon may cause unpredictable damage to the system. Nayfeh et al. [11] studied the effects of various nonlinear external forces on I.R. The double-beam system, as considered by Palmeri and Adhikari [12], is composed of two slender beams connected by Winkler-type springs as the inner layer; they used the Galerkin-type method to study the transverse vibration of the double-deck beam system, and the obtained numerical results validated the accuracy and versatility of the method. Sedighi et al. [13] studied the nonlinear vibration of cantilever beams under preloaded nonlinear cubic spring boundary conditions, where the He’s Parameter Expanding Method (HPEM) was used to obtain the exact solution for the dynamic behavior in this system, and the results demonstrated that series expansions with one term are sufficient to obtain an accurate solution. Nayfeh and Pai [14] proposed many linear and nonlinear beam models to simulate practical applications, as well as various methods for the analysis of nonlinear systems, such as the average method and the method of multiple scales (MOMS). In addition, Nayfeh and Balachandran [15] illustrated the definitions of various stabilities in nonlinear systems, as well as the methods for judging the stability of various systems, which are of great reference value to the stability analysis of this system.

Merely changing the location of the damper can reduce vibration, without the need to change the damper itself; for example, Wang and Kuo [16] discussed a hinged-free linear Euler–Bernoulli beam resting on a nonlinear elastic foundation and found that placing a DVA with appropriate mass could prevent internal resonance and suppress vibrations in the beam. Wang and Lu [17] reported that, in a system with a hinged-hinged nonlinear beam resting on a nonlinear elastic foundation, 1:3 I.R. occurs within the 1st and 3rd modes when the ratio of the elastic modulus of the foundation to that of the beam is $9\pi ^{4}$. Wang and Liang [18] investigated the damping effects of vibration absorbers with a lumped mass on a hinged-hinged beam and found that this kind of vibration absorber is able to mitigate vibrations in mechanical and civil engineering structures on an elastic foundation. This shows that changing the position, mass, spring constant, or damping coefficient of the TMD or DVA is also feasible approaches to preventing I.R. and reducing vibrations. Wang et al. [19] also found that when the $m_{\mathrm {D}}k$ of the TMD shock absorber is a certain value ($m_{\mathrm {D}}k =0.0475$), the best vibration reduction effect can be obtained, and this characteristic still exists when the location of the TMD ($l_{\mathrm {D}})$ is adjusted. In this study, TMD was added to the flow-structure coupled system to try to avoid I.R. and achieve the best effect of vibration reduction by changing the parameters of TMD.

In this paper, Hamilton’s principle is used to derive the equation for the nonlinear flow-structure coupled motion, where the method of multiple scales (MOMS) is used to derive the frequency response of each mode under the fixed point (steady state), and the amplitude of each mode is used to examine I.R. This study mounted TMDs of different masses in different locations on beams, in order to determine whether their fixed point plots can avoid I.R. and reduce the amplitude. In addition, we used the 3D maximum amplitude contour plot (3D MACP) to comprehensively identify the best TMD vibration reduction combination (including mass, position, spring constant, and the damping coefficient of TMD) for the flow-structure coupled system and verified the correctness of the results with numerical simulation. This study analyzed the effects of different flow velocities and TMD parameters on the I.R. of the entire system and used the Floquet theory to analyze the stability of the flow-structure coupled system. Based on the criterion of Floquet multipliers (F.M.), we drew the basin of attraction plots of the system to explore the stability of the fluid delivery system at different flow rates and after TMD was added.

2 Establishment and analysis of the theoretical model

2.1 Establishment of the fluid-conveying tube system

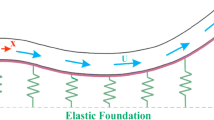
Figure 1 shows the schematic diagram of a fluid-conveying tube system. We put the system on an elastic foundation, which can be used to simulate the water-cooled heat sink pipeline system, the offshore oil pipeline, submarine cable, micro-electromechanical system, or the vibration model of the human aorta. A laminar flow with no circulation or vortex in the pipe was considered. So we assumed that a nonviscous fluid flows in a pipe at the velocity of v and considered that the main body was affected by the distribution force. We added a damping ring to the pipe, which can be simulated by a tuned mass damper (TMD), in order to reduce the vibration, and took the fluid-conveying nonlinear beam to simulate the model of the fluid-conveying tube, and then, used a nonlinear spring to simulate the elastic foundation, and the relevant coordinate system and boundary conditions are detailed in Fig. 2. Among them, $m_{b}$ is beam mass/unit length, $A_{b}$ is the cross-sectional area of the beam, E is Young’s modulus, $I_{b}$ is the moment of inertia, $k_{w}$ and $B_{w}$ are the linear and nonlinear spring constants of the elastic foundation, respectively, $m_{D}$ is the mass of the additional TMD, $f_{s}$ is the spring constant of the additional TMD, and $g_{s}$ is the damping coefficient of the additional TMD. This study took an element of a nonlinear beam for analysis, as shown in Fig. 3, which assumed the elastic beam bend at slight angle $\theta$ after deformation, and considered the effects of the centripetal force and tangential force of the fluid acting on the pipe wall. Among them, u and w are the deformation of the elastic beam in the x and y directions, respectively, $m_{f}$ is the mass of fluid per unit length, and $\rho$ is the radius of the curvature of the beam.

Fig. 1

Schematic diagram of a fluid-conveying tube system

Fig. 2

Fluid-conveying nonlinear beam coordinate system and boundary conditions

Fig. 3

Element of a fluid-conveying nonlinear beam system

2.2 Derivation of the equation of motion for the nonlinear flow-structure coupled system

First, this study considered the nonlinear Bernoulli–Euler beam and defined $\kappa =\frac{1}{\rho }=\frac{\partial \theta }{\partial x}=\frac{\partial ^{2}w}{\partial x^{2}}$ as the curvature of the beam. Based on the relationship between von Kármán nonlinear strain ($\eta )$ and deformation (u, w), we can obtain that the nonlinear strain of the beam is $\eta =\frac{\partial u}{\partial x}+\frac{1}{2}(\frac{\partial w}{\partial x})^{2}+y(\frac{\partial ^{2}w}{\partial x{ }^{2}})=\eta _{0} +y\eta _{1}$, in which $\eta _{{0}} =\frac{\partial u}{\partial x}+\frac{1}{2}(\frac{\partial w}{\partial x})^{2}$ is the tensile strain of the beam, $\eta _{1} =(\frac{\partial ^{2}w}{\partial x^{2}})$ is the bending strain of the beam, and y is the cross-sectional coordinate system of the beam. In this study, Hamilton’s principle is used to derive the equation of motion for the flow-structure coupled system, and its kinetic energy (T) is, as follows:

(1)

The first integral term is the kinetic energy of the beam, the second integral term is the kinetic energy of the fluid $y\frac{\partial ^{2}w}{\partial t\partial x}=y\frac{\partial \theta }{\partial t}=y\omega$, and is the relative velocity of the fluid and the beam, in which the velocity is $v=Y\sin \omega t$. The potential energy (U) of the system is:

$$\begin{aligned} U= & {} \int _0^l \left( \frac{1}{2}EA_{b} \eta ^{2}\right) {\mathrm{d}}x+\int _0^l {[-qw} +m_{f} v^{2}\frac{\partial ^{2}w}{\partial x^{2}}(w\cos \theta -u\sin \theta )\nonumber \\&+m_{f} {\dot{v}}(u\cos \theta +w\sin \theta )]{\mathrm{d}}x. \end{aligned}$$

(2)

Considering the hypothesis that angle $\theta$ is a small angle, the relative velocity of the fluid and the beam can be expressed as:

(3)

Then, we further assumed that the variability ( ${\dot{u}}$ and ${\dot{w}})$ of the beam deformed in u and w directions is very small relative to flow speed (v). After we neglected it, we obtained the following equation:

(4)

Based on Hamilton’s principle: $\int _0^T {\delta (T-U} ){\mathrm{d}}t=0$, after the variation of Eq. (1), the following results are obtained:

$$\begin{aligned} \int _0^T {\delta T{\mathrm{d}}} t= & {} \int _0^T {\int _0^l {m_{f} (} v-({v}'{w}'w+vw{w}'')){\mathrm{d}}x{\mathrm{d}}t\delta v} -\int _0^T {\int _0^l {[m_{b} } {\ddot{u}}]{\mathrm{d}}x{\mathrm{d}}t\delta u}\nonumber \\&-\int _0^T {\int _0^l {[m_{b} } {\ddot{w}}-(m_{b} +m_{f} )y^{2}{{\ddot{w}}}''+m_{f} (v{v}'{w}'+v^{2}{w}'')]{\mathrm{d}}x{\mathrm{d}}t\delta w}\nonumber \\&+\Bigg \{\int _0^l {m_{b} } ({\dot{u}}\delta u){\mathrm{d}}x\vert _{0}^{T} +\int _0^l {m_{b} } \left( y^{2}{{\dot{w}}}'\frac{\partial \delta w}{\partial x}\right) {\mathrm{d}}x\vert _{0}^{T} -\int _0^T {m_{b} } (y^{2}{{\ddot{w}}}'\delta w){\mathrm{d}}t\vert _{0}^{l}\nonumber \\&+\int _0^l {m_{b} } ({\dot{w}}\delta w){\mathrm{d}}x\vert _{0}^{T} +\int _0^l {m_{f} } \left( y^{2}{{\dot{w}}}'\frac{\partial \delta w}{\partial x}\right) {\mathrm{d}}x\vert _{0}^{T} -\int _0^T {m_{f} } (y^{2}{{\ddot{w}}}'\delta w){\mathrm{d}}t\vert _{0}^{l}\nonumber \\&+\int _0^T {m_{f} v{w}'\delta vw{\mathrm{d}}t\vert _{0}^{l} +} \int _0^l {m_{f} } v{w}'\delta w{\mathrm{d}}x\vert _{0}^{T} \Bigg \}. \end{aligned}$$

(5)

Similarly, by the variation of Eq. (2), we can obtain the following:

$$\begin{aligned} \int _0^T {\delta U} dt= & {} \int _0^T {\int _0^l {m_{f} ({\dot{v}}-v^{2}{w}''{w}')} {\mathrm{d}}x{\mathrm{d}}t\delta u} -EA_{b} \int _0^T {\int _0^l {({u}''+{w}'{w}'')} {\mathrm{d}}x{\mathrm{d}}t\delta u} \nonumber \\&+\int _0^T {\int _0^l {m_{f} {\dot{v}}{w}'{\mathrm{d}}x{\mathrm{d}}t\delta w} } +\int _0^T {\int _0^l {m_{f} v^{2}{w}''{\mathrm{d}}x{\mathrm{d}}t\delta w} } +\int _0^T {\int _0^l {-q{\mathrm{d}}x{\mathrm{d}}t\delta w} } \nonumber \\&-EA_{b} \int _0^T {\int _0^l {({u}''{w}'+{u}'{w}''+\frac{3}{2}{w}''{w}'^{2}-y^{2}w^{iv}){\mathrm{d}}x{\mathrm{d}}t\delta w} } \nonumber \\&+\Bigg \{\int _0^T {EA_{b} } {u}'\delta u{\mathrm{d}}t\vert _{0}^{l} +\int _0^T {EA_{b} } {u}'{w}'\delta w{\mathrm{d}}t\vert _{0}^{l} +\int _0^T {EA_{b} } y^{2}{w}''\delta {w}'{\mathrm{d}}t\vert _{0}^{l} \nonumber \\&+\int _0^T {EA_{b} } \frac{1}{2}{w}'^{3}\delta w{\mathrm{d}}t\vert _{0}^{l} +\int _0^T {EA_{b} } \frac{1}{2}{w}'^{2}\delta u{\mathrm{d}}t\vert _{0}^{l} -\int _0^T {EA_{b} } y^{2}{w}'''\delta w{\mathrm{d}}t\vert _{0}^{l} \Bigg \}.\nonumber \\ \end{aligned}$$

(6)

Based on Hamilton’s principle, we can obtain the following coupling equations of motion for the fluid-conveying nonlinear beam system:

$$\begin{aligned}&m_{b} {\ddot{u}}-EA_{b} ({u}''+{w}'{w}'')+m_{f} {\dot{v}}-m_{f} v^{2}{w}''{w}'=0, \end{aligned}$$

(7)

$$\begin{aligned}&m_{b} {\ddot{w}}-(I_{m_{b} } +I_{m_{f} } ){{\ddot{w}}}''+EI_{b} w^{iv}-EA_{b} ({u}''{w}'+{u}'{w}''+\frac{3}{2}{w}''{w}'^{2}) \nonumber \\&\quad +m_{f} (v{v}'{w}'+2v^{2}{w}''+{\dot{v}}{w}')-q=0. \end{aligned}$$

(8)

Equations (7) and (8) are the coupling equations of motion of the system in the u and w directions, respectively. To simplify the symbols, we defined $(\;)'$ as the space differential and $\mathop {(\;)}\limits ^{\bullet }$ as the time differential. Among them, $EI_{b} =EA_{b} y^{2}$ is the flexural rigidity of the beam; $I_{m_{b} } =m_{b} y^{2}$ and $I_{m_{f} } =m_{f} y^{2}$ are moment of inertia of the beam and fluid, respectively. At this time, we added the structural damping terms $\mu _{u} {\dot{u}}$, $\mu _{w} {\dot{w}}$ of the elastic beam and the nonlinear elastic foundation $k_{w} w+B_{w} w^{3}$ of the support system. Based on Newton’s method, the coupling equations of motion can be expressed, as follows:

$$\begin{aligned}&m_{b} {\ddot{u}}+\mu _{u} {\dot{u}}-EA_{b} ({u}''+{w}'{w}'')+m_{f} {\dot{v}}-m_{f} v^{2}{w}''{w}'=0, \end{aligned}$$

(9)

$$\begin{aligned}&m_{b} {\ddot{w}}-(I_{m_{b} } +I_{m_{f} } ){{\ddot{w}}}''+\mu _{w} {\dot{w}}+EI_{b} w^{iv}-EA_{b} \left( {u}''{w}'+{u}'{w}''+\frac{3}{2}{w}''{w}'^{2}\right) \nonumber \\&\quad +m_{f} (v{v}'{w}'+2v^{2}{w}''+{\dot{v}}{w}')+k_{w} w+B_{w} w^{3}-q=0. \end{aligned}$$

(10)

To facilitate the writing of equations, this study used the same symbols as the dimensional equation of motion to express the dimensionless equations of motion. After dimensionless transformation of Eqs. (9) and (10), we obtained:

$$\begin{aligned}&{\ddot{u}}+\mu _{u} {\dot{u}}-({u}''+{w}'{w}'')+M{\dot{v}}-Mv^{2}{w}'{w}''=0, \end{aligned}$$

(11)

$$\begin{aligned}&{\ddot{w}}-{\bar{I}}{{\ddot{w}}}''+\mu _{w} {\dot{w}}+\omega ^{2}w^{iv}-\left( {u}''{w}'+{u}'{w}''+\frac{3}{2}{w}''{w}'^{2}\right) \nonumber \\&\quad +M(v{v}'{w}'+2v^{2}{w}''+{\dot{v}}{w}')+k_{w} w+B_{w} w^{3}-qe^{i\Omega \tau }=0. \end{aligned}$$

(12)

The dimensionless definition of the coefficients is shown in “Appendix A,” where M is the ratio of the fluid mass to the elastic beam mass, $\omega$ is the ratio of transverse to the axial natural frequency of the elastic beam, ${\bar{I}}$ is the moment of inertia, and $\Omega$ is the frequency of external force. Both ends of the elastic beam are hinged, and the dimensionless boundary conditions are, as follows:

$$\begin{aligned} u(0,\tau )= & {} 0,\;u(1,\tau )=0,\nonumber \\ w(0,\tau )= & {} 0,\;{w}'' (0,\tau )=0,\;w(1,\tau )=0,\;{w}'' (1,\tau )=0. \end{aligned}$$

(13)

To simplify the problem, we assumed that the flow velocity (v) of the fluid is a uniform flow field, and that the elastic beam is transformed into a steady state in the u direction. Therefore, Eqs. (11) and (12) can be replaced by:

$$\begin{aligned}&{u}''+{w}'{w}''-M{\dot{v}}+Mv^{2}{w}'{w}''=0, \end{aligned}$$

(14)

$$\begin{aligned}&{\ddot{w}}-{\bar{I}}{{\ddot{w}}}''+\mu _{w} {\dot{w}}+\omega ^{2}w^{iv}-\left( {u}''{w}'+{u}'{w}''+\frac{3}{2}{w}''{w}'^{2}\right) \nonumber \\&\quad +M(2v^{2}{w}''+{\dot{v}}{w}')+k_{w} w+B_{w} w^{3}-qe^{i\Omega \tau }=0. \end{aligned}$$

(15)

From Eq. (14), we can obtain the following relations.

$$\begin{aligned} {u}''=(-Mv^{2}-1){w}'{w}''+M{\dot{v}}. \end{aligned}$$

(16)

After integrating Eq. (16), the results are expressed, as follows:

$$\begin{aligned} {u}'= & {} -\frac{1}{2}(Mv^{2}+1)({w}')^{2}+M{\dot{v}}x+c_{1} (\tau ),\nonumber \\ u= & {} -\frac{1}{2}(Mv^{2}+1)\int _0^x {({w}')^{2}} {\mathrm{d}}x+\frac{1}{2}M{\dot{v}}x^{2}+c_{1} (\tau )x+c_{2} (\tau ). \end{aligned}$$

(17)

By substituting boundary conditions Eq. (13) into Eq. (17), we can obtain:

$$\begin{aligned} c_{2} (\tau )=0; \quad c_{1} (\tau )=\frac{1}{2}(Mv^{2}+1)\int _0^1 {({w}')^{2}} {\mathrm{d}}x-\frac{1}{2}M{\dot{v}}. \end{aligned}$$

(18)

Then, Eqs. (16–18) are substituted into Eq. (15). We further assumed that the velocity of the fluid is a steady state; thus, the equation of motion of the flow-structure coupling system can be simplified to the equation of motion of the w-direction vibration, as follows:

$$\begin{aligned}&{\ddot{w}}-{\bar{I}}{{\ddot{w}}}''+\mu _{w} {\dot{w}}+\omega ^{2}w^{iv} +\frac{3}{2}Mv^{2}{w}''{w}'^{2}-\frac{1}{2}Mv^{2}{w}''\int _0^1 {({w}')^{2}} {\mathrm{d}}x-\frac{1}{2}{w}''\int _0^1 {({w}')^{2}} {\mathrm{d}}x\nonumber \\&+2Mv^{2}{w}''+k_{w} w+B_{w} w^{3}-qe^{i\Omega \tau }=0. \end{aligned}$$

(19)

At this time, we added TMD to the main system, which can be regarded as the concentrated load acting on the elastic beam, and its effect on the elastic beam can be expressed as: $\{g_{s} [{\dot{w}}(x,t)-{\dot{W}}_{D} (t)]+$$f_{s} [w(x,t)-W_{D} (t)]\}\delta [x-l_{D} ]$. To simplify the symbols, we used the same symbols as the dimensional equations of motion to represent the variables. Based on Newton’s method, the dimensionless equation of motion of the fluid-conveying elastic beam with TMD is obtained, as follows:

$$\begin{aligned}&{\ddot{w}}-{\bar{I}}{{\ddot{w}}}''+\mu _{w} {\dot{w}}+\omega ^{2}w^{iv} +\frac{3}{2}Mv^{2}{w}''{w}'^{2}-\frac{1}{2}Mv^{2}{w}''\int _0^1 {({w}')^{2}} {\mathrm{d}}x-\frac{1}{2}{w}''\int _0^1 {({w}')^{2}} {\mathrm{d}}x \nonumber \\&\quad +2Mv^{2}{w}''+\{g_{s} ({\dot{w}}-{\dot{W}}_{D} )+f_{s} (w-W_{D} )\}\delta [x-l_{D} ]+k_{w} w+B_{w} w^{3}-qe^{i\Omega \tau }=0.\nonumber \\ \end{aligned}$$

(20)

The equation of motion of the TMD added to the elastic beam can also be obtained by Newton’s method:

$$\begin{aligned} {\bar{m}}_{D} {\bar{W}}_{D}^{**} (\tau )-{\bar{f}}_{s} [{\bar{w}}({\bar{x}},\tau )-{\bar{W}}_{D} (\tau )]-{\bar{g}}_{s} [{\bar{w}}^{*}({\bar{x}},\tau )-{\bar{W}}_{D}^{*} (\tau )]=0. \end{aligned}$$

(21)

Equation (21) is a dimensionless TMD equation of motion; for the dimensionless definition of the coefficients, please refer to “Appendix A”; among them, ${\bar{m}}_{D}$ is the mass of dimensionless TMD, and ${\bar{f}}_{s}$ and ${\bar{g}}_{s}$ are the spring constant and damping coefficient of dimensionless TMD, respectively.

2.3 Comparing the framework of this model with relevant research

To verify the correctness of the flow-structure coupling motion equation, as deduced by this study, the structure of this model was compared with the related research. Nayfeh and Pai [14] used Newton’s 2$^{\mathrm {nd}}$ law, meaning the coordinate transformation of Euler’s angle and Taylor series expansion, in order to obtain the complete equations of the motion of nonlinear beams. Assuming that Nayfeh and Pai [14] did not consider the high number of beams or confine the beams to planar 2D motion, the derived nonlinear beam equation can be rewritten, as follows:

$$\begin{aligned}&m{\ddot{{\bar{u}}}}-EA{{\bar{u}}}''=EA\left( \frac{1}{2}{{\bar{w}}}'^{2} -{{\bar{u}}}'{{\bar{w}}}'^{2}\right) '+EI\left[ {{{\bar{w}}}'\left( {{{\bar{w}}}'''-{{\bar{u}}}'''{{\bar{w}}}'-2{{\bar{u}}}''{{\bar{w}}}'' -3{{\bar{u}}}'{{\bar{w}}}'''} \right) } \right] ^{\prime },\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned}&m{\ddot{{\bar{w}}}}-j_{3} {{\ddot{{\bar{w}}}}}''+EI{\bar{w}}^{iv}=EA({{\bar{u}}}'{{\bar{w}}}' -{{\bar{u}}}'^{2}{{\bar{w}}}'+\frac{1}{2}{{\bar{w}}}'^{3})^{\prime }\nonumber \\&\quad +EI\left[ {{\bar{u}}}'{{\bar{w}}}'''+\left( {{{\bar{u}}}'{{\bar{w}}}'} \right) ''-\left( {{{\bar{u}}}'^{2}-{{\bar{w}}}'^{2}} \right) {{\bar{w}}}'''-{{\bar{u}}}'\left( {{{\bar{u}}}'{{\bar{w}}}'} \right) ''-\left( {{\bar{u}}}'^{2}{{\bar{w}}}'-\frac{1}{3}{{\bar{w}}}'^{3}\right) ''\right] ^{\prime }+{\bar{F}}.\nonumber \\ \end{aligned}$$

(23)

Ignoring the coupling rotary term of u and w in Eqs. (22) and (23), and ignoring that ${\bar{uw}}$ is higher than the coupling term of cubic, it can be expressed as:

$$\begin{aligned}&m{\ddot{{\bar{u}}}}-EA\left[ {{\bar{u}}}''+EA\left( \frac{1}{2}{{\bar{w}}}'^{2} \right) '\right] =0, \end{aligned}$$

(24)

$$\begin{aligned}&m{\ddot{{\bar{w}}}}-j_{3}{{\ddot{{\bar{w}}}}}''+EI{\bar{w}}^{iv}-EA\left( {{\bar{u}}}'{{\bar{w}}}' +\frac{1}{2}{{\bar{w}}}'^{3}\right) ^{\prime }-{\bar{F}}=0. \end{aligned}$$

(25)

On the contrary, in Eqs. (11) and (12), as deduced by this study, if the structural damping, elastic foundation, and the influence of fluid are neglected, the nonlinear beam equation can be obtained, as follows:

$$\begin{aligned}&{\ddot{u}}-({u}''+{w}'{w}'')=0, \end{aligned}$$

(26)

$$\begin{aligned}&{\ddot{w}}-{\bar{I}}{{\ddot{w}}}''+\omega ^{2}w^{iv}-({u}''{w}'+{u}'{w}''+\frac{3}{2}{w}''{w}'^{2})-qe^{i\Omega \tau }=0. \end{aligned}$$

(27)

After comparison, it is found that Eqs. (24) and (25), as deduced by Nayfeh and Pai [14], are consistent with Eqs. (26) and (27), as deduced by this study; thus, the correctness of the nonlinear beam equation deduced by this study can be verified.

We also referred to the equation of motion of the fluid-conveying beam, as derived by Reddy and Wang [6]. Reddy and Wang [6] assumed that the main beam is a nonlinear Bernoulli–Euler beam and considered the tangential force and centripetal force of the fluid acting on the pipe wall. The fluid-conveying nonlinear beam equation is derived, as follows:

$$\begin{aligned}&(m_{p} +m_{f} ){\ddot{u}}_{0} -E_{p} A_{p} ({u}''_{0} +{w'}_{0} {w}''_{0} )+m_{f} {\dot{v}}-m_{f} v{w'}_{0} ({{\dot{w}}'}_{0} +v{w}''_{0})=0, \end{aligned}$$

(28)

$$\begin{aligned}&(m_{p} +m_{f} ){\ddot{w}}_{0} -(\hat{{I}}_{p} +\hat{{I}}_{f} ){{\ddot{w}}}''_{0} +E_{p} I_{p} w_{0}^{iv} -E_{p} A_{p} ({u}''_{0} {w'}_{0} +{u'}_{0} {w}''_{0} +\frac{3}{2}{w}''_{0} {{w}'}_{0}^{2} )\nonumber \\&\quad +m_{f} (2v{\dot{{w'}}}_{0} +v^{2}{w}''_{0} +{\dot{v}}{w'}_{0} )-m_{f} v[{\dot{u}}_{0} {w}''_{0} +{w'}_{0} ({\dot{w}}_{0} {w}''_{0} +{{\dot{u}}'}_{0} )]=q. \end{aligned}$$

(29)

Regarding the fluid-conveying nonlinear beam of this study, it is assumed that the variability (${\dot{u}}$ and ${\dot{w}})$ relative velocity v of the beam, as deformed in u and w directions, is very small; thus, it is ignored. If the structural damping and elastic foundation are further ignored, eqs. (11 and 12) can be expressed as follows:

$$\begin{aligned}&{\ddot{u}}-({u}''+{w}'{w}'')+M{\dot{v}}-Mv^{2}{w}'{w}''=0, \end{aligned}$$

(30)

$$\begin{aligned}&{\ddot{w}}-{\bar{I}}{{\ddot{w}}}''+\omega ^{2}w^{iv}-({u}''{w}'+{u}'{w}''+\frac{3}{2}{w}''{{w}'}^{2}) +M(v{v}'{w}'+2v^{2}{w}''+{\dot{v}}{w}')=qe^{i\Omega \tau }.\nonumber \\ \end{aligned}$$

(31)

After comparing eqs. (28 and 29) and eqs. (30 and 31), it can be found that, if the coupling terms of v and ${\dot{u}}_{0} \& {\dot{w}}_{0} (m_{f} v{w'}_{0} {{\dot{w}}'}_{0} , 2m_{f} v{\dot{{w}'}}_{0}$ and $m_{f} v[{\dot{u}}_{0} {w}''_{0} +{w'}_{0} ({\dot{w}}_{0} {w}''_{0} +{{\dot{u}}'}_{0} )])$ in eqs. (28 and 29) are eliminated, the results are similar to those of eqs. (30 and 31), as deduced by this study; therefore, the correctness of the equation of the motion of the fluid-conveying nonlinear elastic beam, as deduced by this study, can be verified again.

In comparing with the typical existing theoretical researches, Chen [20] studied a simply supported pipe model with conveying fluid. He investigated the stability of this pipe with constant mean flow velocity superimposed on a time-varying component. Only linear model was assumed, and the effects of bending and curvature of the beam were not considered in his work. Rahmati et al. [21] proposed a method for investigating probabilistic stability of pipes conveying fluid. The conveying pipe was resting on an elastic foundation. The divergence instability of this pipe with uncertain flow velocity was analyzed. However, the spring constant effect of the elastic foundation on the conveying beam was not studied. The unique nonlinear property of internal resonance was not considered in their work. In the present study, a nonlinear model of fluid-conveying beam resting on an elastic foundation was proposed. The centripetal force and tangential force of fluid acting on the beam were considered. In comparing with the existing theories, this nonlinear flow-induced beam model is not only a novel work in physics but also application on medical research and engineering problems.

2.4 Method of multiple scales

This study adopted MOMS to analyze the frequency response and fixed points of the nonlinear equation, which involved dividing the time scale into fast and slow timescales. Suppose $T_{0}=\tau$ is the fast-time term, $T_{1}=\varepsilon ^{2}\tau$ is the slow-time term, and $W(x,\tau ,\varepsilon )=\varepsilon W_{0} (x,T_{0} ,T_{1} ....)+\varepsilon ^{3}W_{1} (x,T_{0} ,T_{1} ....)$, where $\varepsilon$ is the timescale of small disturbances and is a minimum value. MOMS is a technique used for small perturbations. This study considered weak damping and nonlinearity. Under the assumptions of small perturbations and weak nonlinear vibrations, we scaled the dimensionless damping coefficient ($\mu )$ and the other nonlinear terms in the order of $\varepsilon ^{2}$. Since $\varepsilon$ is the minimum value, we ignored the influence of higher-order terms, such as $\varepsilon ^{{5}}\,,\varepsilon ^{{7}}\ldots$ on the system. Then the order of $\mu _{w}$, $f_{s}$, $g_{s}$ is $\varepsilon ^{2}$, and the order of uniformly distributed external forces is assumed to be $\varepsilon ^{3}$ for analysis. Based on these assumptions and with the expansion of $W(x,\tau ,\varepsilon )$ in the order of $\varepsilon$ and $\varepsilon ^{3}$, the damping coefficient ($\mu )$, the nonlinear terms, and the external force are collected in the same order of $\varepsilon ^{3}$ The time-scaled equation can be obtained as follows:

$$\begin{aligned}&\left( \varepsilon \frac{\partial ^{{2}}w_{0} }{\partial T_{0}^{2} }+\varepsilon ^{{3}}\frac{\partial ^{{2}}w_{1} }{\partial T_{0}^{2} }+{2}\varepsilon ^{{3}}\frac{\partial ^{{2}}w_{0} }{\partial T_{0} \partial T_{1} }\right) -{\bar{I}}\left( \varepsilon \frac{\partial ^{2}{w}''_{0} }{\partial T_{0}^{2} }+\varepsilon ^{3}\frac{\partial ^{2}{w}''_{1} }{\partial T_{0}^{2} }+2\varepsilon ^{3}\frac{\partial ^{2}{w}''_{0} }{\partial T_{0} \partial T_{1} }\right) \nonumber \\&\quad +\varepsilon ^{2}\mu _{w} \left( \varepsilon \frac{\partial w_{0} }{\partial T_{0} }+\varepsilon ^{{3}}\frac{\partial w_{1} }{\partial T_{0} }+\varepsilon ^{{3}}\frac{\partial w_{0} }{\partial T_{1} }\right) +\omega ^{2}\left( \varepsilon w_{0}^{iv} +\varepsilon ^{3}w_{1}^{iv} \right) \nonumber \\&\quad +\frac{3}{2}Mv^{2}\left( \varepsilon {w}''_{0} +\varepsilon ^{3}{w}''_{1} \right) (\varepsilon ^{2}{{w}'}_{0}^{2})\nonumber \\&\quad -\frac{1}{2}(Mv^{2}+1)(\varepsilon {w}''_{0} +\varepsilon ^{3}{w}''_{1} )\int _0^1 {(\varepsilon {w'}_{0} )^{2}} dx+\Bigg \{\varepsilon ^{2}g_{s} (\varepsilon \frac{\partial w_{0} }{\partial T_{0} }+\varepsilon ^{3}\frac{\partial w_{1} }{\partial T_{0} }+\varepsilon ^{3}\frac{\partial w_{0} }{\partial T_{1} }\nonumber \\&\quad -\varepsilon \frac{\partial W_{D} }{\partial T_{0} }-\varepsilon ^{3}\frac{\partial W_{D} }{\partial T_{1} })+\varepsilon ^{2}f_{s} (\varepsilon w_{0} +\varepsilon ^{3}w_{1} -\varepsilon W_{D} )\Bigg \}\delta (x-l_{D} )\nonumber \\&\quad +2Mv^{2}(\varepsilon {w}''_{0} +\varepsilon ^{3}{w}''_{1} )+k_{w} (\varepsilon w_{0} +\varepsilon ^{3}w_{1} )+B_{w} (\varepsilon w_{0} )^{3}-\varepsilon ^{3}qe^{i\Omega \tau }=0. \end{aligned}$$

(32)

Among them, the term consisting of $\varepsilon ^{1}$ is:

$$\begin{aligned} \frac{\partial ^{2}w_{0} }{\partial T_{0}^{2} }-{\bar{I}}\frac{\partial ^{2}{w}''_{0} }{\partial T_{0}^{2} } +\omega ^{2}w_{0}^{iv} +2Mv^{2}{w}''_{0} +k_{w} w_{0} =0. \end{aligned}$$

(33)

The term consisting of $\varepsilon ^{3}$is:

$$\begin{aligned}&\frac{\partial ^{2}w_{1} }{\partial T_{0}^{2} }-{\bar{I}}\frac{\partial ^{2}{w}''_{1} }{\partial T_{0}^{2} } +\omega ^{2}w_{1}^{iv} +2Mv^{2}{w}''_{1} +k_{w} w_{1} =\nonumber \\&\quad -2\frac{\partial ^{2}w_{0} }{\partial T_{0} \partial T_{1} }+2{\bar{I}}\frac{\partial ^{2}{w}''_{0} }{\partial T_{0} \partial T_{1} }-\mu _{w} \frac{\partial w_{0} }{\partial T_{0} }-\frac{3}{2}Mv^{2}{w}''_{0} {{w}'}_{0}^{2}+\frac{1}{2}(Mv^{2}+1){w}''_{0} \int _0^1 {({w'}_{0} )^{2}} {\mathrm{d}}x\nonumber \\&\quad -\left[ g_{s} \left( \frac{\partial w_{0} }{\partial T_{0} }-\frac{\partial W_{D} }{\partial T_{0} }\right) +f_{s} (w_{0} -W_{D} )\right] \delta (x-l_{D} ) -B_{w} w_{0}^{3}+qe^{i\Omega \tau }. \end{aligned}$$

(34)

The corresponding boundary conditions of the equations for $\varepsilon ^{1}$ and $\varepsilon ^{3}$ are, as follows:

$$\begin{aligned}&\varepsilon ^{1}:w_{{0}} (0,\tau )=0,\;{w}''_{{0}} (0,\tau )=0,\;w_{{0}} (1,\tau )=0,\;{w}''_{{0}} (1,\tau )=0,\nonumber \\&\varepsilon ^{3}:w_{{1}} (0,\tau )=0,\;{w}''_{{1}} (0,\tau )=0,\;w_{{1}} (1,\tau )=0,\;{w}''_{{1}} (1,\tau )=0. \end{aligned}$$

(35)

Based on the separation of variable and boundary conditions, we can obtain the characteristic equation of Eq. (33),

$$\begin{aligned} \sin \gamma l=0. \end{aligned}$$

(36)

Among them, the eigenvalues are $\gamma _{n} =\frac{n\pi }{l},\;n=1,2,3...$, and the mode shape is

$$\begin{aligned} \phi _{n} (x)=\sin \gamma _{n} x. \end{aligned}$$

(37)

The subscript n represents each mode.

3 Analysis of resonance in systems

3.1 Equation for the nonlinear flow-structure coupled motion without TMD

We first discussed the phenomenon of nonlinear vibration in the main body without TMD, in order to analyze the vibration of the nonlinear beam in the absence of a damper, and found the target of vibration reduction. After removing TMD from the beam system, we obtain the following equation:

$$\begin{aligned}&{\ddot{w}}-{\bar{I}}{{\ddot{w}}}''+\mu _{w} {\dot{w}}+\omega ^{2}w^{iv} +\frac{3}{2}Mv^{2}{w}''{w}'^{2}-\frac{1}{2}Mv^{2}{w}''\int _0^1 {({w}')^{2}} {\mathrm{d}}x-\frac{1}{2}{w}''\int _0^1 {({w}')^{2}} {\mathrm{d}}x\nonumber \\&+2Mv^{2}{w}''+k_{w} w+B_{w} w^{3}-qe^{i\Omega \tau }=0. \end{aligned}$$

(38)

The boundary condition of the hinged-hinged beam is:

$$\begin{aligned} w(0,\tau )=0,\;{w}'' (0,\tau )=0,\;w(1,\tau )=0,\;{w}'' (1,\tau )=0. \end{aligned}$$

(39)

The dimensionless definition of its coefficients can be found in “Appendix A.”

3.2 Analysis of internal resonance conditions

This study adopted MOMS and gave the equations for $\varepsilon ^{1}$and $\varepsilon ^{3}$.

The term consisting of $\varepsilon ^{1}$is:

$$\begin{aligned} \frac{\partial ^{2}w_{0} }{\partial T_{0}^{2} }-{\bar{I}}\frac{\partial ^{2}{w}''_{0} }{\partial T_{0}^{2} } +\omega ^{2}w_{0}^{iv} +2Mv^{2}{w}''_{0} +k_{w} w_{0} =0. \end{aligned}$$

(40)

The term consisting of $\varepsilon ^{3}$is:

$$\begin{aligned}&\frac{\partial ^{2}w_{1} }{\partial T_{0}^{2} }-{\bar{I}}\frac{\partial ^{2}{w}''_{1} }{\partial T_{0}^{2} } +\omega ^{2}w_{1}^{iv} +2Mv^{2}{w}''_{1} +k_{w} w_{1} = -2\frac{\partial ^{2}w_{0} }{\partial T_{0} \partial T_{1} }+2{\bar{I}}\frac{\partial ^{2}{w}''_{0} }{\partial T_{0} \partial T_{1} } \nonumber \\&-\mu _{w} \frac{\partial w_{0} }{\partial T_{0} }-\frac{3}{2}Mv^{2}{w}''_{0} {{w}'}_{0}^{2}+\frac{1}{2}(Mv^{2}+1){w}''_{0} \int _0^1 {({w'}_{0} )^{2}} {\mathrm{d}}x -B_{w} w_{0}^{3}+qe^{i\Omega \tau }. \end{aligned}$$

(41)

The boundary conditions of the corresponding equations for $\varepsilon ^{1}$and $\varepsilon ^{3}$are, as follows,

$$\begin{aligned} \varepsilon ^{1}:w_{{0}} (0,\tau )=0,\;{w}''_{{0}} (0,\tau )=0,\;w_{{0}} (1,\tau )=0,\;{w}''_{{0}} (1,\tau )=0,\nonumber \\ \varepsilon ^{3}:w_{{1}} (0,\tau )=0,\;{w}''_{{1}} (0,\tau )=0,\;w_{{1}} (1,\tau )=0,\;{w}''_{{1}} (1,\tau )=0. \end{aligned}$$

(42)

To explore the conditions for the generation of I.R. by a vibrating body, we must first determine the conditions under which $k_{w}$ can cause I.R. First, we define:

$$\begin{aligned} w_{0} =\sum \limits _{n=1}^\infty {\xi _{0n} (\tau )\phi _{n} (x)} ,\;\;w_{1} =\sum \limits _{n=1}^\infty {\xi _{1n} (\tau )\phi _{n} (x)} . \end{aligned}$$

(43)

Substituting Eq. (43) into Eq. (40) composed of $\varepsilon ^{1}$ and Eq. (41) composed of $\varepsilon ^{3}$, we can obtain the order of $\varepsilon ^{1}$:

$$\begin{aligned} \sum \limits _{n=1}^\infty {(\phi _{n} -{\bar{I}}{\phi }''_{n} ){\ddot{\xi }}_{0n} } +\sum \limits _{n=1}^\infty {(\omega ^{2}\phi _{n} ^{iv}+2Mv^{2}{\phi }''_{n} +k_{w} \phi _{n} )\xi _{0n} } =0. \end{aligned}$$

(44)

the order of $\varepsilon ^{3}$:

$$\begin{aligned}&\sum \limits _{n=1}^\infty ( \phi _{n} -{\bar{I}}{\phi }''_{n} ){\ddot{\xi }}_{1n} +\sum \limits _{n=1}^\infty ( \omega ^{2}\phi _{n} ^{iv}+2Mv^{2}{\phi }''_{n} +k_{w} \phi _{n} )\xi _{1n} =\nonumber \\&\quad -2\frac{\partial ^{2}}{\partial T_{0} \partial T_{1} }\sum \limits _{n=1}^\infty {\xi _{0n} } \phi _{n} +2{\bar{I}}\frac{\partial ^{2}}{\partial T_{0} \partial T_{1} }\sum \limits _{n=1}^\infty {\xi _{0n} } {\phi }''_{n} -\mu _{w} \sum \limits _{n=1}^\infty {{\dot{\xi }}_{0n} } \phi _{n}\nonumber \\&\quad -\frac{3}{2}Mv^{2}\sum \limits _{n,j,k=1}^\infty {\xi _{0n} } \xi _{0j} \xi _{0k} {\phi }''_{n} {\phi '}_{j} {\phi '}_{k}\nonumber \\&\quad +\frac{1}{2}(Mv^{2}+1)\sum \limits _{n,j,k=1}^\infty {\xi _{0n} } \xi _{0j} \xi _{0k} {\phi }''_{n} \int _0^1 {{\phi '}_{j} } {\phi '}_{k} {\mathrm{d}}x -B_{w} \sum \limits _{n,j,k=1}^\infty {\xi _{0n} } \xi _{0j} \xi _{0k} \phi _{n} \phi _{j} \phi _{k} +qe^{i\Omega \tau }.\nonumber \\ \end{aligned}$$

(45)

Fig. 4

Relation schema between the natural frequency ratio and spring constant ($k_{w})$

By using the orthogonal method, the following dynamic equations are obtained by multiplying Eqs. (44) and (45) by $\phi _{m} (x)$ and integrating them at 0~$l (l=$1).

$$\begin{aligned}&{\ddot{\xi }}_{0m} {+}\frac{(\gamma _{m}^{4} \omega ^{2}-2Mv^{2}\gamma _{m}^{2} {+}k_{w} )}{(1{+}{\bar{I}}\gamma _{m}^{2} )}\,\xi _{0m} {=}0, \end{aligned}$$

(46)

$$\begin{aligned}&{\ddot{\xi }}_{1m} {+}\frac{(\gamma _{m}^{4} \omega ^{2}-2Mv^{2}\gamma _{m}^{2} {+}k_{w} )}{(1+{\bar{I}}\gamma _{m}^{2} )}\,\xi _{1m} {=} -\frac{2}{(1+{\bar{I}}\gamma _{m}^{2} )}\frac{\partial ^{2}}{\partial T_{0} \partial T_{1} }\xi _{0m} -\frac{2{\bar{I}}\gamma _{m}^{2} }{(1+{\bar{I}}\gamma _{m}^{2} )}\frac{\partial ^{2}}{\partial T_{0} \partial T_{1} }\,\xi _{0m}\nonumber \\&\quad -\frac{\mu _{w} }{(1+{\bar{I}}\gamma _{m}^{2} )}{\dot{\xi }}_{0m} -\frac{3Mv^{2}}{2(1+{\bar{I}}\gamma _{m}^{2} )\int _0^1 {\phi _{m}^{2} {\mathrm{d}}x} }\int _0^1 {\phi _{m} {\phi }''_{n} {\phi '}_{j} {\phi '}_{k} {\mathrm{d}}x\sum \limits _{n,j,k=1}^\infty {\xi _{0n} \xi _{0j} \xi _{0k} } }\nonumber \\&\quad +\frac{(Mv^{2}+1)}{2(1+{\bar{I}}\gamma _{m}^{2} )\int _0^1 {\phi _{m}^{2} {\mathrm{d}}x} }\int _0^1 {\phi _{m} {\phi }''_{n} {\mathrm{d}}x} \int _0^1 {{\phi '}_{j} {\phi '}_{k} {\mathrm{d}}x} \sum \limits _{n,j,k=1}^\infty {\xi _{0n} } \xi _{0j} \xi _{0k}\nonumber \\&\quad -\frac{B_{w} }{(1+{\bar{I}}\gamma _{m}^{2} )\int _0^1 {\phi _{m}^{2} {\mathrm{d}}x} }\int _0^1 {\phi _{m} \phi _{n} \phi _{j} \phi _{k} {\mathrm{d}}x} \sum \limits _{n,j,k=1}^\infty {\xi _{0n} } \xi _{0j} \xi _{0k} +\frac{\int _0^1 {\phi _{m} dx} }{(1+{\bar{I}}\gamma _{m}^{2} )\int _0^1 {\phi _{m}^{2} } \,dx}qe^{i\Omega \tau }_{\mathrm {.}}\nonumber \\ \end{aligned}$$

(47)

From Eq. (46), we can determine that the natural frequency of the flow-structure coupled system is, as follows:

$$\begin{aligned} \omega _{m} =\left[ {\frac{(\gamma _{m}^{4} \omega ^{2}-2Mv^{2}\gamma _{m}^{2} +k_{w} )}{(1+{\bar{I}}\gamma _{m}^{2} )\,}} \right] ^{\frac{1}{2}}, m=1, 2, 3\ldots \end{aligned}$$

(48)

The relation schema between the natural frequency ratio of each mode of the system and spring constant ($k_{w})$ of the elastic foundation can be obtained by Eq. (48). As shown in Fig. 4, when the frequency ratio of different modes is an integer, I.R. may occur. We discussed several representative conditions; when $k_{w}=$65.7, $\omega _{1} :\omega _{2} =1:{2}, k_{w}=$80.7, $\omega _{1} :\omega _{3} =1:{3}$, and $k_{w}=$315, $\omega _{1} :\omega _{3} =1:{2}$, I.R. may occur in the system. However, in Eq. (47), we found that the right side of the equal sign contains only the first and second power terms of $\xi$, which means that there will be no coupling terms between the modes when the frequency ratio of different modes is 1:2; thus, even if the frequency is an integer ratio, there will be no I.R and there is no energy transfer between the modes. Therefore, analysis is only required to determine whether I.R. occurs when the frequency ratio of the first mode to the third mode is 1:3.

3.3 Analysis of the frequency response in the system

Figure 4 shows that the 1st mode and 3rd mode may have the I.R. phenomena of 1:3; therefore, this study discusses the 1st mode and 3rd mode. First, we assume $\xi _{0m} (\tau )=B_{m} (T_{1} )e^{-i\varsigma _{m} }e^{i\omega _{m} T_{0} }+{\bar{B}}_{m} (T_{1} )e^{i\varsigma _{m} }e^{-i\omega _{m} T_{0} }$ and substitute it into Eq. (47) to obtain the following equation:

$$\begin{aligned}&{\ddot{\xi }}_{1m} +\omega _{m}^{2} \xi _{1m} =\nonumber \\&\quad -A_{m} \left( {i\omega _{m} {B'}_{m} (T_{1} )e^{-i\varsigma _{m} }e^{i\omega _{m} T_{0} }-i\omega _{m} {{\bar{B}}'}_{m} (T_{1} )e^{i\varsigma _{m} }e^{-i\omega _{m} T_{0} }+\omega _{m} {\varsigma '}_{m} \xi _{0m} } \right) +F_{m} qe^{i\Omega \tau }\nonumber \\&-\beta _{m} \left( {i\omega _{m} B_{m} (T_{1} )e^{-i\varsigma _{m} }e^{i\omega _{m} T_{0} }-i\omega _{m} {\bar{B}}_{m} (T_{1} )e^{i\varsigma _{m} }e^{-i\omega _{m} T_{0} }} \right) \nonumber \\&-C_{m} \Bigg [\int _0^1 {\phi _{m} \phi _{n} \phi _{j} \phi _{k} {\mathrm{d}}x} \sum \limits _{n,j,k=1}^\infty {(B_{n} (T_{1} )e^{-i\varsigma _{n} }e^{i\omega _{n} T_{0} }+{\bar{B}}_{n} (T_{1} )e^{i\varsigma _{n} }e^{-i\omega _{n} T_{0} })} \nonumber \\&(B_{j} (T_{1} )e^{-i\varsigma _{j} }e^{i\omega _{j} T_{0} }+{\bar{B}}_{j} (T_{1} )e^{i\varsigma _{j} }e^{-i\omega _{j} T_{0} })(B_{k} (T_{1} )e^{-i\varsigma _{k} }e^{i\omega _{k} T_{0} }+{\bar{B}}_{k} (T_{1} )e^{i\varsigma _{k} }e^{-i\omega _{k} T_{0} })\Bigg ] \nonumber \\&\quad -D_{m} \Bigg [\int _0^1 {\phi _{m} {\phi }''_{n} {\phi '}_{j} {\phi '}_{k} {\mathrm{d}}x} \sum \limits _{n,j,k=1}^\infty {(B_{n} (T_{1} )e^{-i\varsigma _{n} }e^{i\omega _{n} T_{0} }+{\bar{B}}_{n} (T_{1} )e^{i\varsigma _{n} }e^{-i\omega _{n} T_{0} })} \nonumber \\&(B_{j} (T_{1} )e^{-i\varsigma _{j} }e^{i\omega _{j} T_{0} }+{\bar{B}}_{j} (T_{1} )e^{i\varsigma _{j} }e^{-i\omega _{j} T_{0} })(B_{k} (T_{1} )e^{-i\varsigma _{k} }e^{i\omega _{k} T_{0} }+{\bar{B}}_{k} (T_{1} )e^{i\varsigma _{k} }e^{-i\omega _{k} T_{0} })\Bigg ] \nonumber \\&\quad +E_{m} \Bigg [\int _0^1 {\phi _{m} {\phi }''_{n} {\mathrm{d}}x} \int _0^1 {{\phi '}_{j} {\phi '}_{k} {\mathrm{d}}x} \sum \limits _{n,j,k=1}^\infty {(B_{n} (T_{1} )e^{-i\varsigma _{n} }e^{i\omega _{n} T_{0} }+{\bar{B}}_{n} (T_{1} )e^{i\varsigma _{n} }e^{-i\omega _{n} T_{0} })} \nonumber \\&(B_{j} (T_{1} )e^{-i\varsigma _{j} }e^{i\omega _{j} T_{0} }+{\bar{B}}_{j} (T_{1} )e^{i\varsigma _{j} }e^{-i\omega _{j} T_{0} })(B_{k} (T_{1} )e^{-i\varsigma _{k} }e^{i\omega _{k} T_{0} }+{\bar{B}}_{k} (T_{1} )e^{i\varsigma _{k} }e^{-i\omega _{k} T_{0} })\Bigg ].\nonumber \\ \end{aligned}$$

(49)

For the definition of the relevant coefficients, please refer to “Appendix B.” In addition to analyzing the frequency response of the system and drawing the fixed point plots, we assume that the uniform distributed harmonic force is in the following form:

$$\begin{aligned} q_{m} e^{i\Omega \tau }=q_{m} e^{i(\omega _{m} +\varepsilon ^{2}\sigma )T_{0} }=q_{m} (e^{i\varepsilon ^{2}\sigma T_{0} }e^{i\omega _{m} T_{0} })=q_{m} e^{i\sigma T_{1} }e^{i\omega _{m} T_{0} }. \end{aligned}$$

(50)

If the solving procedure continues, terms containing the factors of the system frequencies (or harmonics) appear on the right-hand side of Eq. (49). Terms such as these are called secular terms. Because of the secular terms, the solution of Eq. (49) increases without bound as t increases. The time scale of $\xi _{1}$ does not provide a small correction to time scale of $\xi _{0}$. For the first mode ($m=$1), the secular terms should choose the harmonics of $\omega _{1}$ and $\omega _{{3}} -2\omega _{1}$. For the third mode ($m=$3), the secular terms should choose the harmonics of $\omega _{3}$ and $3\omega _{1}$. After selecting the secular terms, we can obtain the solvability condition by setting them to zero. This study discusses whether there is an I.R. phenomenon in the external excitation in the fixed-point plot. Assuming that the external force excites the first mode ($q_{1} e^{i\Omega \tau }=q_{1} e^{i\sigma T_{1} }e^{i\omega _{1} T_{0} })$, we multiply the secular terms of the first mode by $e^{i\varsigma _{1} }$ and set ${\Gamma }_{B} =3\varsigma _{{1}} -\varsigma _{{3}}$. In addition, in order to find the frequency response of the system in the fixed points (steady state), we set ${{\Gamma }'}_{A} =\sigma +{\varsigma '}_{{1}} =0\;\;\Rightarrow \;\;{\varsigma '}_{{1}} =-\sigma$, ${{\Gamma }'}_{B} =3{\varsigma '}_{{1}} -{\varsigma '}_{{3}} =0\;\Rightarrow \;{\varsigma '}_{{3}} =-3\sigma$, and $\frac{\partial B_{1} }{\partial T_{1} }=\frac{\partial B_{3} }{\partial T_{1} }=0$, and substitute the solvability condition, then the square sum of the real and imaginary parts of the first mode is:

$$\begin{aligned}&\left\{ {A_{1} \left( {\omega _{1} \sigma B_{1} } \right) -C_{1} \left( {3B_{1}^{2} {\bar{B}}_{1} \int _0^1 {\phi _{1}^{4} {\mathrm{d}}x} +6B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1}^{2} \phi _{3}^{2} {\mathrm{d}}x} +3{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) } \right. \nonumber \\&\quad +E_{1} \left( {3B_{1}^{2} {\bar{B}}_{1} \int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x} \int _0^1 {{{\phi }'}_{1}^{2} {\mathrm{d}}x} +2B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{3}^{2} } {\mathrm{d}}x} } \right. \nonumber \\&\quad +4B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x}\nonumber \\&\quad +{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{{\phi }'}_{1}^{2} } {\mathrm{d}}x} \left. {+2{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} } \right) \nonumber \\&\quad -D_{1} \left( {3B_{1}^{2} {\bar{B}}_{1} \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} +2B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{3}^{2} {\mathrm{d}}x} +4B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{3} {\phi '}_{1} {\mathrm{d}}x} } \right. \nonumber \\&\quad \left. {\left. {+{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} +2{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x} } \right) } \right\} ^{2}\nonumber \\&\quad +\left\{ {-\beta _{1} \left( {\omega _{1} B_{1} } \right) -C_{1} \left( {3{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) } \right. \nonumber \\&\quad +E_{1} \left( {{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} +2{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} } \right) \nonumber \\&\quad \left. {-D_{1} \left( {{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} +2{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x} } \right) } \right\} ^{2}=F_{1}^{2} q_{1}^{2} .\quad \end{aligned}$$

(51)

If we multiply the secular terms of the third mode by $e^{i\varsigma _{3} }$, then the real part is:

$$\begin{aligned}&3A_{3} \left( {\omega _{3} \sigma B_{3} } \right) -C_{3} \left( {3B_{3}^{2} {\bar{B}}_{3} \int _0^1 {\phi _{3}^{4} {\mathrm{d}}x} +6B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{1}^{2} \phi _{3}^{2} {\mathrm{d}}x} +B_{1}^{3} \cos \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) \nonumber \\&+E_{3} \left( {3B_{3}^{2} {\bar{B}}_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\mathrm{d}}x} \int _0^1 {{\phi '}_{3}^{2} {\mathrm{d}}x} +2B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} } \right. \nonumber \\&\left. {+4B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} +B_{1}^{3} \cos \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} } \right) \nonumber \\&-D_{3} \left( {3B_{3}^{2} {\bar{B}}_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\phi '}_{3}^{2} {\mathrm{d}}x} +2B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right. +4B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{3} {\phi '}_{1} {\mathrm{d}}x} \nonumber \\&\left. {+B_{1}^{3} \cos \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right) =0. \end{aligned}$$

(52)

The imaginary part is:

$$\begin{aligned}&-\beta _{3} \left( {\omega _{3} B_{3} } \right) -C_{3} \left( {B_{1}^{3} \sin \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) \nonumber \\&-D_{3} \left( {B_{1}^{3} \sin \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right) +E_{3} \left( {B_{1}^{3} \sin \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} } \right) =0.\nonumber \\ \end{aligned}$$

(53)

We used the numerical method to solve eqs. (51-53) and drew the response charts of the system’s amplitude $B_{{1}}$ and $B_{\mathrm {3}}$ and fine-tuning frequency “$\sigma$” (fixed-point plot), in order to observe whether there is an I.R. phenomenon.

Similarly, if the third mode ($q_{3} e^{i\Omega \tau }=q_{3} e^{i\sigma T_{1} }e^{i\omega _{3} T_{0} })$ is excited by an external force, the real part of the first mode is:

$$\begin{aligned}&\frac{A_{1} }{3}\left( {\omega _{1} \sigma B_{1} } \right) -C_{1} \left( {3B_{1}^{2} {\bar{B}}_{1} \int _0^1 {\phi _{1}^{4} {\mathrm{d}}x} +6B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1}^{2} \phi _{3}^{2} {\mathrm{d}}x} +3{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) \nonumber \\&\quad +E_{1} \left( {3B_{1}^{2} {\bar{B}}_{1} \int _0^1 {\phi _{1} {\phi }''_{1} dx} \int _0^1 {{\phi '}_{1}^{2} {\mathrm{d}}x} +2B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{1} dx\int _0^1 {{\phi '}_{3}^{2} } {\mathrm{d}}x} } \right. \nonumber \\&\quad +4B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x}\nonumber \\&\quad +{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} \left. {+2{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} } \right) \nonumber \\&\quad -D_{1} \left( {3B_{1}^{2} {\bar{B}}_{1} \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} +2B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{3}^{2} {\mathrm{d}}x} +4B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{3} {\phi '}_{1} {\mathrm{d}}x} } \right. \nonumber \\&\quad \left. {+{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} +2{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x} } \right) =0. \end{aligned}$$

(54)

The imaginary part is:

$$\begin{aligned}&-\beta _{1} \left( {\omega _{1} B_{1} } \right) -C_{1} \left( {3{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) \nonumber \\&{+}E_{1} \left( {{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} +2{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} } \right) \nonumber \\&{-}D_{1} \left( {{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} +2{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x} } \right) =0. \end{aligned}$$

(55)

Then, to eliminate the time-related terms, we added the square of the real part and the imaginary part of the third mode to obtain:

$$\begin{aligned}&\left\{ {A_{3} \left( {\omega _{3} \sigma B_{3} } \right) -C_{3} \left( {3B_{3}^{2} {\bar{B}}_{3} \int _0^1 {\phi _{3}^{4} {\mathrm{d}}x} +6B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{1}^{2} \phi _{3}^{2} {\mathrm{d}}x} +B_{1}^{3} \cos \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) } \right. \nonumber \\&\quad +E_{3} \left( {3B_{3}^{2} {\bar{B}}_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\mathrm{d}}x} \int _0^1 {{\phi '}_{3}^{2} {\mathrm{d}}x} +2B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} } \right. \nonumber \\&\quad \left. {+4B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} +B_{1}^{3} \cos \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} } \right) \nonumber \\&\quad -D_{3} \left( {3B_{3}^{2} {\bar{B}}_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\phi '}_{3}^{2} {\mathrm{d}}x} +2B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right. +4B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{3} {\phi '}_{1} {\mathrm{d}}x}\nonumber \\&\quad \left. {\left. {+B_{1}^{3} \cos \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right) } \right\} ^{2}\nonumber \\&\quad +\left\{ {-\beta _{3} \left( {\omega _{3} B_{3} } \right) -C_{3} \left( {B_{1}^{3} \sin \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) -D_{3} \left( {B_{1}^{3} \sin \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right) } \right. \nonumber \\&\quad \left. {+E_{3} \left( {B_{1}^{3} \sin \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} } \right) } \right\} ^{2}=F_{3}^{2} q_{3}^{2} . \end{aligned}$$

(56)

eqs. (54-56) could be solved numerically. We drew the Fixed-point plot of the system’s amplitude $B_{\mathrm {1}}$ and $B_{\mathrm {3}}$ and the tuned frequency “$\sigma$,” in order to observe whether there is internal resonance.

3.4 Analysis of internal resonance

Figure 5 shows the Fixed-point plot of each mode under different $k_{w}$ values for the beam’s third mode is excited. The horizontal axis is the tuned frequency, and the vertical axis is the beam’s dimensionless amplitude. Figure 5 shows that when $k_{w}=80.7$, the frequency response of the first mode has the largest amplitude (0.01462), as compared with other $k_{w}$ values (0.01459 for $k_{w}=$25 and 0.01052 for $k_{w}=$300), while the frequency response of the third mode has the smallest amplitude (0.05124 for $k_{w}=$80.7, 0.06396 for $k_{w}=$25 and 0.076632 for $k_{w}=$300). The results show that when $k_{w}=80.7$, although the amplitude of the third mode is larger than that of the first mode, there is energy transfer between the first mode and the third mode, which represents the generation of weak internal resonance in the system under this condition, and Fig. 4 shows the reference index.

Fig. 5

Fixed-point plots of each mode under different $k_{w}$s for the third mode are excited (no TMD). a$k_{w}=80.7$, 1st mode, b$k_{w}=25$, 1st mode, c$k_{w}=300$, 1st mode, d$k_{w}=80.7$, 3rd mode, e$k_{w}=25$, 3rd mode, f$k_{w}=300$, 3rd mode

4 Systematic analysis of TMD

4.1 Theoretical model of TMD

The research of Sect. 3 analyzed the energy exchange between the first and the third modes of the main structure, which leads to the generation of weak I.R.; thus, this study adds shock absorbers to the first and third modes of the system and analyzes the vibration reduction effects. The TMD equation is, as follows:

$$\begin{aligned} m_{D} {\ddot{W}}_{D} (\tau )-f_{s} \left[ \sum \limits _{n=1}^\infty {w_{n} (x,\tau )-W_{D} (\tau )} \right] -g_{s} \left[ \sum \limits _{n=1}^\infty {{\dot{w}}_{n} (x,\tau )-{\dot{W}}_{D} (\tau )} \right] =0. \end{aligned}$$

(57)

Since TMD is regarded as an external force of the main body equation of motion, we first discuss the displacement of TMD ($W_{D})$ and, then, substitute it into Eq. (34). If we set $n=$1 and $n=$3 in Eq. (57), then Eq. (57) expands, as follows:

$$\begin{aligned}&m_{D} {\ddot{W}}_{D} (\tau )-f_{s} [\phi _{1} (x_{D} )\xi _{1} (\tau )+\phi _{3} (x_{D} )\xi _{3} (\tau )-W_{D} (\tau )]\nonumber \\&\quad -g_{s} [\phi _{1} (x_{D} ){\dot{\xi }}_{1} (\tau )+\phi _{3} (x_{D} ){\dot{\xi }}_{3} (\tau )-{\dot{W}}_{D} (\tau )]=0. \end{aligned}$$

(58)

Now, according to Eq. (33), we can assume that the solutions of $\xi _{10}$ and $\xi _{30}$ are:

$$\begin{aligned}&\xi _{10} =B_{1} e^{-i\varsigma _{1} }e^{i\omega { }_{1}T_{0} }+{\bar{B}}_{1} e^{i\varsigma _{1} }e^{-i\omega { }_{1}T_{0} },\nonumber \\&\xi _{30} =B_{3} e^{-i\varsigma _{3} }e^{i\omega { }_{3}T_{0} }+{\bar{B}}_{3} e^{i\varsigma _{3} }e^{-i\omega { }_{3}T_{0} }. \end{aligned}$$

(59)

Substitute its solution to Eq. (58) and assume that the solution is:

$$\begin{aligned} W_{D} =H_{1} e^{-i\varsigma _{1} }e^{i\omega _{1} T_{0} }+{\bar{H}}_{1} e^{i\varsigma _{1} }e^{-i\omega _{1} T_{0} }+H_{3} e^{-i\varsigma _{3} }e^{i\omega _{3} T_{0} }+{\bar{H}}_{3} e^{i\varsigma _{3} }e^{-i\omega _{3} T_{0} }. \end{aligned}$$

(60)

Then, we can obtain:

$$\begin{aligned} H_{1}= & {} B_{1} \frac{\phi _{1} (x_{D} )(f_{s} +i\omega _{1} g_{s} )}{(f_{s} +i\omega _{1} g_{s} )-m_{D} \omega _{1}^{2} }, \quad {\bar{H}}_{1} ={\bar{B}}_{1} \frac{\phi _{1} (x_{D} )(f_{s} -i\omega _{1} g_{s} )}{(f_{s} -i\omega _{1} g_{s} )-m_{D} \omega _{1}^{2} },\nonumber \\ H_{3}= & {} B_{3} \frac{\phi _{3} (x_{D} )(f_{s} +i\omega _{3} g_{s} )}{(f_{s} +i\omega _{3} g_{s} )-m_{D} \omega _{3}^{2} }, \quad {\bar{H}}_{3} ={\bar{B}}_{3} \frac{\phi _{3} (x_{D} )(f_{s} -i\omega _{3} g_{s} )}{(f_{s} -i\omega _{3} g_{s} )-m_{D} \omega _{3}^{2} },\nonumber \\ W_{D}= & {} H_{1} e^{-i\varsigma _{1} }e^{i\omega _{1} T_{0} }+{\bar{H}}_{1} e^{i\varsigma _{1} }e^{-i\omega _{1} T_{0} }+H_{3} e^{-i\varsigma _{3} }e^{i\omega _{3} T_{0} }+{\bar{H}}_{3} e^{i\varsigma _{3} }e^{-i\omega _{3} T_{0} }. \end{aligned}$$

(61)

After the rationalization of Eq. (61), we can obtain:

$$\begin{aligned} H_{1}= & {} \phi _{1} (x_{D} )\left( {\frac{-f_{s} B_{1} m_{D} \omega _{1}^{2} +g_{s}^{2} B_{1} \omega _{1}^{2} +f_{s}^{2} B_{1} }{m_{D}^{2} \omega _{1}^{4} -2f_{s} m_{D} \omega _{1}^{2} +g_{s}^{2} \omega _{1}^{2} +f_{s}^{2} }{+}i\frac{-g_{s} B_{1} m_{D} \omega _{1}^{3} }{m_{D}^{2} \omega _{1}^{4} -2f_{s} m_{D} \omega _{1}^{2} +g_{s}^{2} \omega _{1}^{2} +f_{s}^{2} }} \right) ,\nonumber \\ {\bar{H}}_{1}= & {} \phi _{1} (x_{D} )\left( {\frac{-f_{s} {\bar{B}}_{1} m_{D} \omega _{1}^{2} +g_{s}^{2} {\bar{B}}_{1} \omega _{1}^{2} +f_{s}^{2} {\bar{B}}_{1} }{m_{D}^{2} \omega _{1}^{4} -2f_{s} m_{D} \omega _{1}^{2} +g_{s}^{2} \omega _{1}^{2} +f_{s}^{2} }{+}i\frac{g_{s} {\bar{B}}_{1} m_{D} \omega _{1}^{3} }{m_{D}^{2} \omega _{1}^{4} -2f_{s} m_{D} \omega _{1}^{2} +g_{s}^{2} \omega _{1}^{2} +f_{s}^{2} }} \right) ,\nonumber \\ H_{3}= & {} \phi _{3} (x_{D} )\left( {\frac{-f_{s} B_{3} m_{D} \omega _{3}^{2} +g_{s}^{2} B_{3} \omega _{3}^{2} +f_{s}^{2} B_{3} }{m_{D}^{2} \omega _{3}^{4} -2f_{s} m_{D} \omega _{3}^{2} +g_{s}^{2} \omega _{3}^{2} +f_{s}^{2} }{+}i\frac{-g_{s} B_{3} m_{D} \omega _{3}^{3} }{m_{D}^{2} \omega _{3}^{4} -2f_{s} m_{D} \omega _{3}^{2} +g_{s}^{2} \omega _{3}^{2} +f_{s}^{2} }} \right) ,\nonumber \\ {\bar{H}}_{3}= & {} \phi _{3} (x_{D} )\left( {\frac{-f_{s} {\bar{B}}_{3} m_{D} \omega _{3}^{2} +g_{s}^{2} {\bar{B}}_{3} \omega _{3}^{2} +f_{s}^{2} {\bar{B}}_{3} }{m_{D}^{2} \omega _{3}^{4} -2f_{s} m_{D} \omega _{3}^{2} +g_{s}^{2} \omega _{3}^{2} +f_{s}^{2} }{+}i\frac{g_{s} {\bar{B}}_{3} m_{D} \omega _{3}^{3} }{m_{D}^{2} \omega _{3}^{4} -2f_{s} m_{D} \omega _{3}^{2} +g_{s}^{2} \omega _{3}^{2} +f_{s}^{2} }} \right) .\nonumber \\ \end{aligned}$$

(62)

Now, Eq. (62) is substituted into Eq. (34) and orthogonalized to obtain:

$$\begin{aligned}&{\ddot{\xi }}_{1m} +\omega _{m}^{2} \,\xi _{1m} =-A_{m} \left( {\frac{\partial ^{2}}{\partial T_{0} \partial T_{1} }\xi _{0m} } \right) -\beta _{m} {\dot{\xi }}_{0m} -C_{m} \left( {\int _0^1 {\phi _{m} \phi _{n} \phi _{j} \phi _{k} {\mathrm{d}}x} \sum \limits _{n,j,k=1}^\infty {\xi _{0n} } \xi _{0j} \xi _{0k} } \right) \nonumber \\&\quad -D_{m} \left( {\int _0^1 {\phi _{m} {\phi }''_{n} {\phi '}_{j} {\phi '}_{k} {\mathrm{d}}x\sum \limits _{n,j,k=1}^\infty {\xi _{0n} \xi _{0j} \xi _{0k} } } } \right) \nonumber \\&\quad +E_{m} \left( {\int _0^1 {\phi _{m} {\phi }''_{n} {\mathrm{d}}x} \int _0^1 {{\phi '}_{j} {\phi '}_{k} {\mathrm{d}}x} \sum \limits _{n,j,k=1}^\infty {\xi _{0n} } \xi _{0j} \xi _{0k} } \right) \nonumber \\&\quad -Q_{m} g_{s} \left( {\phi _{m}^{2} (x_{D} ){\dot{\xi }}_{0m} -\phi _{m} (x_{D} ){\dot{W}}_{D} } \right) -Q_{m} f_{s} \left( {\phi _{m}^{2} (x_{D} )\xi _{0m} -\phi _{m} (x_{D} )W_{D} } \right) +F_{m} qe^{i\Omega \tau }. \end{aligned}$$

(63)

The definitions of the coefficients are detailed in “Appendix B.” Thus, we can obtain the beam dynamic equation with TMD.

4.2 Frequency response analysis of the beam system with TMD

As previously assumed, the equation of uniformly distributed external forces is expressed as $q_{m} e^{i\Omega \tau }=q_{m} e^{i(\omega _{m} +\varepsilon ^{2}\sigma )T_{0} }=q_{m} (e^{i\varepsilon ^{2}\sigma T_{0} }e^{i\omega _{m} T_{0} })=q_{m} e^{i\sigma T_{1} }e^{i\omega _{m} T_{0} }$. For the first mode $m =$ 1 (1st mode), the secular terms should choose the harmonics as $\omega _{1}$ and $\omega _{{3}} -2\omega _{1}$. For the third mode $m=3$ (3rd mode), the secular terms should choose the harmonics as $\omega _{3}$ and $3\omega _{1}$. When secular terms are selected, the solvability condition can be obtained by setting them to zero. Similar to Sect. 3, this study discussed the cases of the first mode and the third mode excited by external force, respectively, in order to determine the numerical solution and draw the fixed-point plot, and to observe whether the weak I.R. can be effectively avoided or the amplitude of the system can be reduced by adding the shock absorber. To simplify the layout, we omitted the calculation details of the equation and list only the sorted results. Assuming that the external force excites the first mode ($q_{1} e^{i\Omega \tau }=q_{1} e^{i\sigma T_{1} }e^{i\omega _{1} T_{0} })$, the square sum of the real and imaginary parts of the first mode is:

$$\begin{aligned}&\left\{ {A_{1} \left( {\omega _{1} \sigma B_{1} } \right) -C_{1} \left( {3B_{1}^{2} {\bar{B}}_{1} \int _0^1 {\phi _{1}^{4} {\mathrm{d}}x} +6B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1}^{2} \phi _{3}^{2} {\mathrm{d}}x} +3{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) } \right. \nonumber \\&\quad +E_{1} \left( {3B_{1}^{2} {\bar{B}}_{1} \int _0^1 {\phi _{1} {\phi }''_{1} dx} \int _0^1 {{\phi '}_{1}^{2} {\mathrm{d}}x} +2B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{3}^{2} } {\mathrm{d}}x} } \right. \nonumber \\&\quad +4B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} \nonumber \\&\quad +{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} \left. {+2{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} } \right) \nonumber \\&\quad -D_{1} \left( {3B_{1}^{2} {\bar{B}}_{1} \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} +2B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{3}^{2} {\mathrm{d}}x} +4B_{1} B_{3} {\bar{B}}_{3} \int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{3} {\phi '}_{1} {\mathrm{d}}x} } \right. \nonumber \\&\quad \left. {+{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} +2{\bar{B}}_{1}^{2} B_{3} \cos \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x} } \right) \nonumber \\&\quad -Q_{1} g_{s} \phi _{1}^{2} (x_{D} )\left( {\frac{-g_{s} B_{1} m_{D} \omega _{1}^{4} }{m_{D}^{2} \omega _{1}^{4} -2f_{s} m_{D} \omega _{1}^{2} +g_{s}^{2} \omega _{1}^{2} +f_{s}^{2} }} \right) \nonumber \\&\quad \left. {-Q_{1} f_{s} \phi _{1}^{2} (x_{D} )\left[ {B_{1} -\left( {\frac{-f_{s} B_{1} m_{D} \omega _{1}^{2} +g_{s}^{2} B_{1} \omega _{1}^{2} +f_{s}^{2} B_{1} }{m_{D}^{2} \omega _{1}^{4} -2f_{s} m_{D} \omega _{1}^{2} +g_{s}^{2} \omega _{1}^{2} +f_{s}^{2} }} \right) } \right] } \right\} ^{2}\nonumber \\&\quad +\left\{ {-\beta _{1} \left( {\omega _{1} B_{1} } \right) -C_{1} \left( {3{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) } \right. \nonumber \\&\quad -D_{1} \left( {{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} +2{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x} } \right) \nonumber \\&\quad +E_{1} \left( {{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} +2{\bar{B}}_{1}^{2} B_{3} \sin \left( {\Gamma _{B} } \right) \int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} } \right) \nonumber \\&\quad -Q_{1} g_{s} \phi _{1}^{2} (x_{D} )\left[ {\omega _{1} B_{1} -\left( {\frac{-f_{s} B_{1} m_{D} \omega _{1}^{3} +g_{s}^{2} B_{1} \omega _{1}^{3} +f_{s}^{2} B_{1} \omega _{1} }{m_{D}^{2} \omega _{1}^{4} -2f_{s} m_{D} \omega _{1}^{2} +g_{s}^{2} \omega _{1}^{2} +f_{s}^{2} }} \right) } \right] \nonumber \\&\left. {-Q_{1} f_{s} \phi _{1}^{2} (x_{D} )\left( {\frac{g_{s} B_{1} m_{D} \omega _{1}^{3} }{m_{D}^{2} \omega _{1}^{4} -2f_{s} m_{D} \omega _{1}^{2} +g_{s}^{2} \omega _{1}^{2} +f_{s}^{2} }} \right) } \right\} ^{2}=F_{1}^{2} q_{1}^{2}. \end{aligned}$$

(64)

The real part of the third mode is:

$$\begin{aligned}&3A_{3} \left( {\omega _{3} \sigma B_{3} } \right) -C_{3} \left( {3B_{3}^{2} {\bar{B}}_{3} \int _0^1 {\phi _{3}^{4} {\mathrm{d}}x} +6B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{1}^{2} \phi _{3}^{2} {\mathrm{d}}x} +B_{1}^{3} \cos \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) \nonumber \\&\quad +E_{3} \left( {3B_{3}^{2} {\bar{B}}_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\mathrm{d}}x} \int _0^1 {{\phi '}_{3}^{2} {\mathrm{d}}x} +2B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} } \right. \nonumber \\&\quad \left. {+4B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1} {\phi '}_{3} } {\mathrm{d}}x} +B_{1}^{3} \cos \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} } \right) \nonumber \\&\quad -D_{3} \left( {3B_{3}^{2} {\bar{B}}_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\phi '}_{3}^{2} {\mathrm{d}}x} +2B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right. +4B_{1} {\bar{B}}_{1} B_{3} \int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{3} {\phi '}_{1} {\mathrm{d}}x}\nonumber \\&\quad \left. {+B_{1}^{3} \cos \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right) -Q_{3} g_{s} \phi _{3}^{2} (x_{D} )\left( {\frac{-g_{s} B_{3} m_{D} \omega _{3}^{4} }{m_{D}^{2} \omega _{3}^{4} -2f_{s} m_{D} \omega _{3}^{2} +g_{s}^{2} \omega _{3}^{2} +f_{s}^{2} }} \right) \nonumber \\&\quad -Q_{3} f_{s} \phi _{3}^{2} (x_{D} )\left[ {B_{3} -\left( {\frac{-f_{s} B_{3} m_{D} \omega _{3}^{2} +g_{s}^{2} B_{3} \omega _{3}^{2} +f_{s}^{2} B_{3} }{m_{D}^{2} \omega _{3}^{4} -2f_{s} m_{D} \omega _{3}^{2} +g_{s}^{2} \omega _{3}^{2} +f_{s}^{2} }} \right) } \right] =0. \end{aligned}$$

(65)

The imaginary part is:

$$\begin{aligned}&-\beta _{3} \left( {\omega _{3} B_{3} } \right) -C_{3} \left( {B_{1}^{3} \sin \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right) \nonumber \\&-D_{3} \left( {B_{1}^{3} \sin \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right) +E_{3} \left( {B_{1}^{3} \sin \left( {-\Gamma _{B} } \right) \int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{1}^{2} } {\mathrm{d}}x} } \right) \nonumber \\&-Q_{3} g_{s} \phi _{3}^{2} (x_{D} )\left[ {\omega _{3} B_{3} -\left( {\frac{-f_{s} B_{3} m_{D} \omega _{3}^{3} +g_{s}^{2} B_{3} \omega _{3}^{3} +f_{s}^{2} B_{3} \omega _{3} }{m_{D}^{2} \omega _{3}^{4} -2f_{s} m_{D} \omega _{3}^{2} +g_{s}^{2} \omega _{3}^{2} +f_{s}^{2} }} \right) } \right] \nonumber \\&-Q_{3} f_{s} \phi _{3}^{2} (x_{D} )\left( {\frac{g_{s} B_{3} m_{D} \omega _{3}^{3} }{m_{D}^{2} \omega _{3}^{4} -2f_{s} m_{D} \omega _{3}^{2} +g_{s}^{2} \omega _{3}^{2} +f_{s}^{2} }} \right) =0. \end{aligned}$$

(66)

The analysis method of the third mode ($q_{3} e^{i\Omega \tau }=q_{3} e^{i\sigma T_{1} }e^{i\omega _{3} T_{0} })$ of external force excitation is similar to that of the first mode of excitation; thus, it is not necessary to elaborate here. This study solved the solvability condition equations numerically and drew the fixed-point plot of the system’s amplitude $B_{\mathrm {1}}$, $B_{\mathrm {3}}$ and the tuned frequency “$\sigma$,” in order to observe the effect of the damper on the system. In addition, we comprehensively analyzed the various parameters of TMD and, then, used the 3D maximum amplitude plots (3D MAPs) and maximum amplitude contour plots (MACPs) to conclude the best combination of TMD, and the results are discussed in Sect. 7.

5 Effects of different parameters on the system

5.1 Analysis of internal resonance

The I.R. is a unique property in the nonlinear system. The unexcited mode may have higher amplitude than the excited mode, if the I.R. is triggered. This study focuses on the parameters to trigger the I.R. on the flow-induced vibration system. The flow velocity (v) is the main factor to trigger the I.R. and make system unstable. The moment of inertia (${\bar{I}})$, the ratio of transverse to the axial natural frequency of the elastic beam ($\omega )$, and the spring constants of the elastic foundation ($k_{w})$ would also affect the system natural frequencies. We changed v, ${\bar{I}}$, and $\omega$ of the flow field to observe the amplitudes of the vibration system. The results are presented in Tables 1, 2, and 3, where Tables 1, 2, and 3 are drawn for ${\bar{I}}=0.01$, ${\bar{I}}=0.05$, and ${\bar{I}}=0.1$. The three tables are all analyzed for different flow velocities in the flow field. Based on the simplicity of the layout, we only list $v=0.5$, 0.7, and 0.9 for each table. In addition, each elastic constant $k_{w}$ in Tables 1, 2, and 3 is the corresponding value when the frequency ratio of the first and third modes of the system is 1:3, while Amp. represents the maximum amplitude of the first and third modes of the exciting system in the third mode. Tables 1, 2, and 3 show that the amplitude of the flow-structure coupled system increased slowly with the increase of flow velocity. In addition, by drawing the fixed-point plots in Tables 1, 2, and 3, we found that flow velocities $v=0.7$, $\omega =$ 0.5 and $k_{w}=113.1$, $\omega =0.8$ and $k_{w}=285.3$, $\omega =1.0$ and $k_{w}=444.0$ would cause internal resonance of the main system, such as case (B-1)–(B-3) of Table 1 (marked by (*)), which represent that the system is in the state of energy exchange between high and low harmonic modes when the velocity of the flow field is 0.7. This I.R. case will cause mechanical components to vibrate in an unexpected harmonic mode and may even affect the stability of the structure.

Table 1 Effects of different parameters on the system (${\bar{I}}=0.01)$

Table 2 Effects of different parameters on the system (${\bar{I}}=0.05)$

Table 3 Effects of different parameters on the system (${\bar{I}}=0.1)$

5.2 Frequency response analysis of the beam system with TMD

To reduce the vibration and avoid the internal resonance of the main system, we added TMD to case (B-1)–(B-3) when the flow velocity was $v =0.7$, as shown in Table 1. This study used MOMS to solve the equation and drew the fixed-point plot of the system’s amplitude $B_{\mathrm {1}}$, $B_{\mathrm {3}}$ and fine-tuning frequency “$\sigma$,” to observe the effect of the damper on the system. In addition, we comprehensively analyzed the various parameters of TMD and, then, used 3D MAPs and MACPs to conclude the best combination of TMD, and the results are discussed in Sect. 7.

6 Analysis of system stability

This section discusses the effects of TMD dampers on system stability. In Eq. (20) for the flow-structure coupled motion with the TMD system, we considered the different fluid velocities (v) and used the Floquet theory to analyze the stability of the system. The Floquet theory applies the Floquet transition matrix to the state variables at beginning and end of one period. The eigenvalues of the Floquet transition matrix are shown to be exponentials occurring in Floquet’s form of the initial value solution. This study used the 4th-order Runge–Kutta method to find the Floquet transient matrix of the system with a shock absorber and obtained the eigenvalue ($\Lambda )$ of the matrix. Let $\Lambda =a+ib$ and the flow-induced system’s eigenvalue is $\eta =\frac{\ln \sqrt{a^{2}+b^{2}} }{T}+i(\frac{1}{T}\tan ^{-1}\frac{b}{a}+\frac{2n\pi }{T})$, where T is the period of the system. The stability criteria are defined by the Floquet multipliers (F.M.) and F.M. $= \sqrt{a^{2}+b^{2}}$. When all F.M. < 1, the system is stable; when all F.M. > 1, the system is unstable. If some F.M. > 1 and some F.M. < 1, it can be called the unstable limit cycle of the saddle type, which means that the system has a saddle point, and it is still unstable. First, in order to analyze the stability of the system, we used the perturbation technique to assume that:

$$\begin{aligned} w=\sum \limits _{n=1}^\infty {(\xi _{n} +{\tilde{\xi }}_{n} )\phi _{n} }. \end{aligned}$$

(67)

Among them, $\xi _{n}$ is the equilibrium or periodic term, and ${\tilde{\xi }}_{n}$ represents the disturbant terms. This study substituted Eq. (67) into Eq. (20), made them orthogonal, and then, we expanded the dynamic equation according to each mode, as follows.

The first mode:

$$\begin{aligned}&{\ddot{{\tilde{\xi }}}}_{1} +\beta _{1} {\dot{{\tilde{\xi }}}}_{1} +\omega _{1}^{2} (\xi _{1} +{\tilde{\xi }}_{1} )+C_{1} \left[ {(\xi _{1} +{\tilde{\xi }}_{1} )^{3}\int _0^1 {\phi _{1}^{4} {\mathrm{d}}x} } \right. +(\xi _{3} +{\tilde{\xi }}_{3} )^{3}\int _0^1 {\phi _{1} \phi _{3}^{3} {\mathrm{d}}x}\nonumber \\&\quad +3(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} \left. {+3(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{1}^{2} \phi _{3}^{2} {\mathrm{d}}x} } \right] \nonumber \\&\quad +D_{1} \left[ {(\xi _{1} +{\tilde{\xi }}_{1} )^{3}\int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right. \nonumber \\&\quad +2(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x} +(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} \nonumber \\&\quad +2(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{3} {\phi '}_{1} {\mathrm{d}}x}\nonumber \\&\quad \left. {+(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{1} {\phi }''_{1} {\phi '}_{3}^{2} {\mathrm{d}}x+(\xi _{3} +{\tilde{\xi }}_{3} )^{3}\int _0^1 {\phi _{1} {\phi }''_{3} {\phi '}_{3}^{2} {\mathrm{d}}x} } } \right] \nonumber \\&\quad -E_{1} \left[ {(\xi _{1} +{\tilde{\xi }}_{1} )^{3}\int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x} \int _0^1 {{\phi '}_{1}^{2} dx} } \right. +2(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x} \int _0^1 {{\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x}\nonumber \\&\quad +(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x} \int _0^1 {{\phi '}_{1}^{2} {\mathrm{d}}x} +2(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x} \int _0^1 {{\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x}\nonumber \\&\quad \left. {+(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{1} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{3}^{2} {\mathrm{d}}x} } +(\xi _{3} +{\tilde{\xi }}_{3} )^{3}\int _0^1 {\phi _{1} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{3}^{2} } } {\mathrm{d}}x} \right] \nonumber \\&\quad +Q_{1} g_{s} (\phi _{1}^{2} (x_{D} ){\dot{{\tilde{\xi }}}}_{1} -\phi _{1} (x_{D} ){\dot{{\tilde{\xi }}}}_{D} )+Q_{1} f_{s} [\phi _{1}^{2} (x_{D} )(\xi _{1} +{\tilde{\xi }}_{1} )-\phi _{1} (x_{D} ){\tilde{\xi }}_{D} ]=F_{1} qe^{i\Omega \tau }. \end{aligned}$$

(68)

The third mode:

$$\begin{aligned}&{\ddot{{\tilde{\xi }}}}_{3} +\beta _{3} {\dot{{\tilde{\xi }}}}_{3} +\omega _{3}^{2} (\xi _{3} +{\tilde{\xi }}_{3} )+C_{3} \left[ {(\xi _{1} +{\tilde{\xi }}_{1} )^{3}\int _0^1 {\phi _{1}^{3} \phi _{3} {\mathrm{d}}x} } \right. +(\xi _{3} +{\tilde{\xi }}_{3} )^{3}\int _0^1 {\phi _{3}^{4} {\mathrm{d}}x}\nonumber \\&\quad +3(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{1}^{2} \phi _{3}^{2} {\mathrm{d}}x} \left. {+3(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{1} \phi _{3}^{3} {\mathrm{d}}x} } \right] \nonumber \\&\quad +D_{3} \left[ {(\xi _{1} +{\tilde{\xi }}_{1} )^{3}\int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{1}^{2} {\mathrm{d}}x} } \right. +2(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x} \nonumber \\&\quad +(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{3} {\phi }''_{3} {\phi '}_{1}^{2} {\mathrm{d}}x} +2(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{3} {\phi }''_{3} {\phi '}_{3} {\phi '}_{1} {\mathrm{d}}x}\nonumber \\&\quad \left. {+(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{3} {\phi }''_{1} {\phi '}_{3}^{2} {\mathrm{d}}x+(\xi _{3} +{\tilde{\xi }}_{3} )^{3}\int _0^1 {\phi _{3} {\phi }''_{3} {\phi '}_{3}^{2} {\mathrm{d}}x} } } \right] \nonumber \\&\quad -E_{3} \left[ {(\xi _{1} +{\tilde{\xi }}_{1} )^{3}\int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x} \int _0^1 {{\phi '}_{1}^{2} {\mathrm{d}}x} } \right. +2(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x} \int _0^1 {{\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x}\nonumber \\&\quad +(\xi _{1} +{\tilde{\xi }}_{1} )^{2}(\xi _{3} +{\tilde{\xi }}_{3} )\int _0^1 {\phi _{3} {\phi }''_{3} {\mathrm{d}}x} \int _0^1 {{\phi '}_{1}^{2} {\mathrm{d}}x} +2(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{3} {\phi }''_{3} {\mathrm{d}}x} \int _0^1 {{\phi '}_{1} {\phi '}_{3} {\mathrm{d}}x}\nonumber \\&\quad \left. {+(\xi _{1} +{\tilde{\xi }}_{1} )(\xi _{3} +{\tilde{\xi }}_{3} )^{2}\int _0^1 {\phi _{3} {\phi }''_{1} {\mathrm{d}}x\int _0^1 {{\phi '}_{3}^{2} {\mathrm{d}}x} } +(\xi _{3} +{\tilde{\xi }}_{3} )^{3}\int _0^1 {\phi _{3} {\phi }''_{3} {\mathrm{d}}x\int _0^1 {{\phi '}_{3}^{2} } } {\mathrm{d}}x} \right] \nonumber \\&\quad +Q_{3} g_{s} (\phi _{3}^{2} (x_{D} ){\dot{{\tilde{\xi }}}}_{3} -\phi _{3} (x_{D} ){\dot{{\tilde{\xi }}}}_{D} )+Q_{3} f_{s} [\phi _{3}^{2} (x_{D} )(\xi _{3} +{\tilde{\xi }}_{3} )-\phi _{3} (x_{D} ){\tilde{\xi }}_{D} ]=F_{3} qe^{i\Omega \tau }. \end{aligned}$$

(69)

The parameters of each coefficient are defined in “Appendix B,” and the dynamic equation of TMD is, as follows:

$$\begin{aligned}&m_{D} {\ddot{{\tilde{\xi }}}}_{D} -f_{s} [\phi _{1} (x_{D} )(\xi _{1} +{\tilde{\xi }}_{1} )+\phi _{3} (x_{D} )(\xi _{3} +{\tilde{\xi }}_{3} )-{\tilde{\xi }}_{D} ]\nonumber \\&\quad -g_{s} [\phi _{1} (x_{D} ){\dot{{\tilde{\xi }}}}_{1} +\phi _{3} (x_{D} ){\dot{{\tilde{\xi }}}}_{3} -{\dot{{\tilde{\xi }}}}_{D} ]=0. \end{aligned}$$

(70)

Based on the above analysis, we know that when $k_{w}=$ 80.7, there is a weak I.R. between the first and third modes of the system, and velocity v at this time is 0.01. When velocity v is 0.7, that is, under the parameter condition of case (B-1)–(B-3) in Table 1, the resonance phenomenon between the first and third modes of the main system will occur within 1:3. Stability analysis was carried out for different flow velocities in these two cases, and an attempt was made to determine the flow velocities that diverge from the system and stability after adding shock absorbers. The results are discussed in subsequent sections.

7 Results and discussion

7.1 Discussion on the effect of fluid flow velocity on the system

The purpose of this study is to use the fluid-conveying nonlinear beam as the main model to simulate the fluid-conveying tube system and, then, place the system on a nonlinear elastic foundation to discuss its flow-induced vibration. To analyze the effects of fluid on the tangential shear force and centripetal force on the tube wall, which are caused by velocity (v), we used $v =0$ to represent centripetal force and tangential force and used the increase of v to represent the increase of these two forces.

Table 4 Effect of fluid flow velocity on the system

Table 5 Damping effects of the TMD

First, we assumed that the velocity of the fluid is $v =0$, which means that the flow field is stationary in the pipe, and therefore, the pipe wall will not be affected by the tangential shear force or centripetal force produced by the fluid flow. We drew Table 4 to observe the amplitude change of the system with or without considering the shear force and centripetal force, and four examples are given for analysis and discussion. The first is when the elastic constant $k_{w}$ of the elastic foundation is 80.7, the system will produce weak I.R., and velocity v at this time is 0.01; the other three are cases of I.R., which have the parameter condition of cases (B-1)–(B-3) in Table 1, and velocity v at this time is 0.7. Then, we observed the amplitudes of the first and third modes of the four cases, respectively, where Amp. in Table 4 is the maximum amplitude of the first and third modes. Table 4 shows that the amplitudes of the first and third modes of the excitation system are larger when the tangential shear force and centripetal force are taken into account ($v\ne$0). It is worth noting that, in the case of weak I.R., although the amplitude difference between the first and third modes is not large when $v =0.01$ and $v =0$, this means that, even if the fluid velocity is not large, there will be energy exchange between the modes of the main system, which will lead to the generation of weak I.R. In addition, in the three cases (B-1)–(B-3) that occur in I.R., if the effect of tangential shear and centripetal force ($v=$0) is not considered, I.R. will not occur between the first and third modes of the system. This result also proves that the effect of fluid on the main system cannot be ignored.

7.2 Analysis of vibration reduction effects of the system with TMD

This section discusses the fluid-conveying elastic beam system with TMD, and analyzes the vibration reduction effects of TMD according to different mass ($m_{D})$, location ($l_{D})$, spring constant ($f_{s})$, and damping coefficient ($g_{s})$. We drew the 3DMAP and MACP by combining the vibration reduction results of various parameters, in order to observe and determine the best vibration reduction combination of TMD.

Fig. 6

3D MAPs of the 1st mode when the 1st mode is excited, a$g_{s}=0.1$, b$g_{s}=0.5$, (c) $g_{s}=0.9$

Fig. 7

3D MAPs of each mode when the 3rd mode is excited. a 1st mode, $g_{s}=0.1$, b 1st mode, $g_{s}=0.5$, c 1st mode, $g_{s}=0.9$, d 3rd mode, $g_{s}=0.1$, e 3rd mode, $g_{s}=0.5$, f 3rd mode, $g_{s}=0.9$

Fig. 8

MACPs of the 1st mode when the 1st mode is excited    ($f_{s}=9$), a$g_{s}=0.1$, b$g_{s}=0.5$, c$g_{s}=0.9$

Fig. 9

MACPs of the 3rd mode when the 3rd mode is excited    ($f_{s}=9$), a$g_{s}=0.1$, b$g_{s}=0.5$, c$g_{s}=0.9$

Using the solvability conditions of the excitation to the first mode and the third mode of the system, we drew fixed-point plots according to the different combinations of TMD parameters ($m_{D}$ = 0.02–0.1, $l_{D}= 0.0001$-0.5, $f_{s}= 1, 5, 9$, $g_{s}= 0.1, 0.5, 0.9$) and extracted their maximum amplitudes from each fixed-point plot, in order that we could clearly know the maximum amplitude of each mode when the system is affected by different TMD parameters. In addition, since the amplitude of the third mode is much smaller than that of the first mode when the first mode is excited, this study did not analyze the vibration reduction of the third mode when the first mode was excited. The results of vibration reduction are shown in Figs. 6 and 7. The 3D MAP easily shows the trend of overall vibration reduction, in which the x-axis is the mass of TMD, the y-axis is the position of TMD, and the z-axis is the maximum amplitude corresponding to x and y. In the figure, different amplitude intervals are divided by different colors: red indicates the higher amplitude interval, while blue indicates the lower amplitude interval, which represents the better effect of vibration reduction. Then, we compared and analyzed the 3D MAP (Fig. 6a–c) of the first mode when exciting the first mode. Figure 6 shows that, regardless of the value of the fixed $g_{s}$, the minimum amplitude of the first mode occurs when $f_{s}=$ 9. In addition, the minimum amplitude of the first mode occurs when TMD is placed at 0.5, and the greater the mass of the TMD, the better the vibration reduction effect. It is noteworthy that, when comparing the minimum amplitudes of each mode in Fig. 6, it is not found that the larger the $g_{s}$, the better the effect of vibration reduction for the first mode, but the best effect for the first mode occurs when $g_{s} = 0.1$. This trend also appears in the 3D MAP (Fig. 7a–c) of the first mode when the third mode is excited. In the 3D MAP (Fig. 7d–f) of the third mode when the third mode is disturbed, the minimum amplitude appears at $f_{s}= 9$. Detailed analysis of the different 3D MAP maps found that TMD has the smallest amplitude when placed at 0.2 and 0.5, but when placed at 0.5, its vibration reduction efficiency is better than 0.2. Although the effects of the three maps are not obvious at $f_{s}= 1$, it can be seen when $f_{s} = 5$ and $f_{s}= 9$. Comparison of the minimum amplitudes of Fig. 7d–f found that the third mode vibration reduction has the best effect when $g_{s}= 0.9$.

Although the 3D MAP can provide the general design concept of the shock absorber ($f_{s}$, $g_{s})$, it is difficult to see the optimal combination of TMD due to the numerous TMD parameters. Therefore, this study drew the MACP and analyzed the influence of TMD placement and mass on the system one by one. According to the results of the 3D MAP, we fixed $f_{s}= 9$, which has the best shock absorber effect, and selected different $g_{s}$ to draw its MACP, as shown in Figs. 8 and 9. Figure 8 is the MACP of the first mode when exciting mode 1, and Fig. 9 is the MACP of the third mode when exciting mode 3. Figure 8 shows that all three maps have the best vibration reduction effect when the TMD is placed at 0.5 and its mass is 0.1. After detailed comparison, it can be seen that, when $g_{s}= 0.1$, the lowest amplitude range (blue area) is obtained. It is obvious in Fig. 9 that when the mass of TMD is 0.1, it has the lowest amplitudes at 0.2 and 0.5, as compared with the other locations, but it can still be found that the amplitude range at 0.5 is smaller; therefore, the effect of vibration reduction here is the best. After comparing the three maps, it is clear that the lowest amplitude range (blue area) is found when $g_{s}= 0.9$. By analyzing the 3D MAP and MACP, we can conclude that the optimal TMD vibration reduction combination for the first mode is $m_{D}=0.1$, $l_{D}=0.5$, $f_{s}=9$, $g_{s}=0.9$, whereas the best combination is $m_{D}=0.1$, $l_{D}=0.5$, $f_{s}=9$, $g_{s}=0.9$ for the third mode. It is worth noting that no matter what combination of $f_{s}$ and $g_{s}$, when TMD is placed in the center of the elastic beam ($l_{D}=0.5$), the first mode can achieve the best effect of vibration reduction. However, the third mode has the smallest amplitude when TMD is placed at $l_{D}=0.2$ and 0.5, but has the best effect when $l_{D}=0.5$. The reason is that the maximum amplitude of the first mode shape of the elastic beam is 0.5, while the maximum amplitude of the third mode shape is 0.5 and close to 0.2 (about 0.16–0.18), as shown in Fig. 10. Therefore, the optimal vibration reduction effect can be achieved by placing TMD at the maximum amplitude of each mode. To observe and analyze the vibration reduction effects of the TMD under different conditions, we drew the results shown in Table 5, where Amp. (no TMD) is the maximum amplitude of each mode without additional TMD under different conditions, and Amp. (with TMD) is the maximum amplitude of each mode with additional TMD. The parameters of TMD are the combination of the best vibration reduction effects for each mode, while the “Effect” is expressed as a percentage of the vibration reduction effects for each mode under different cases. Table 5 shows that under any case, the vibration reduction effect for the first mode is greater than that of no TMD. In addition, by comparing with each other, it can be seen that the vibration reduction effect of the TMD for the first mode is greater than that for the third mode under any case.

Fig. 10

Mode shapes of a hinged-hinged beam

To further verify the correctness of the MACP plot, we used the 4th-order Runge–Kutta method to solve the perturbation equations in time domain (Eqs. 68–70) and then to verify the amplitude for a certain frequency response on the fixed-point plot to determine the credibility of the results of this study. For example, Fig. 11 shows the MACP plot for the first mode when exciting the first mode at $f_{s}=9$, $g_{s}=0.1$. This study chose two representative combinations to draw the fixed-point plots and time response plots for validation. The displacement of the time response plot is gradually stable with the increase of time. At this time, the average value of stability is consistent with the maximum amplitude of the corresponding fixed-point plot; for example, Fig. 12a, b can also be verified by the above fixed-point plot and time response plot. The results coincide with each other, which verifies that the accuracy of the proposed MACP is extremely high.

Fig. 11

MACPs of the 1st mode when the 1st mode is excited, ($f_{s}=9, g_{s}=0.1$) a Fixed-point and time response plots for $m_{D}=$0.1 and $l_{D}=$0.5. b Fixed-point and time response plots for $m_{D}=$0.08 and $l_{D}=$0.4

Fig. 12

MACPs of the 1st mode when the 3rd mode is excited, ($f_{s}=9$, $g_{s}=0.1$) a Fixed-point and time response plots for $m_{D}=0.1$ and $l_{D}=0.5$. b Fixed-point and time response plots for $m_{D}=0.04$ and $l_{D}=0.1$.

Fig. 13

Basin of attraction of the case of weak I.R. (no TMD) av = 0.01–0.075, bv = 0.065–0.076 (zoom)

Fig. 14

Basin of attraction of the case of weak I.R. (no TMD). av = 0.065–0.076 basin of attraction, bv = 0.07 basin of attraction, c Poincaré map of initial condition (2.0, $-0.6$), (stable), d Poincaré map of initial condition (2.0, $-0.8$), (unstable).

Fig. 15

Basin of attraction of the case of weak I.R. (with TMD) av = 0.065–0.076 basin of attraction, b$v=0.07$ basin of attraction, c Poincaré map of initial condition (0.4,2.4), (stable), d Poincaré map of initial condition (0.4,2.8), (unstable)

Fig. 16

Basin of attraction of the I.R. case B-1 (no TMD) av = 0.1–0.7 basin of attraction, b$v=0.6$ basin of attraction, c Poincaré map of initial condition ($-2.4$, 1.2) (stable), d Poincaré map of initial condition ($-1.2$, 1.2), (unstable)

Fig. 17

Basin of attraction of the I.R. case B-1 (with TMD) av = 0.1–0.7 basin of attraction, bv = 0.6 basin of attraction, c Poincaré map of initial condition ($-2.4$, 4.8), (stable), d Poincaré map of initial condition ($-2.4$, 6.0), (unstable)

7.3 Analysis of system stability

To observe the stability of the system under different initial conditions, the Floquet theory was used to discuss the cases of weak I.R. and cases (B-1)–(B-3) with internal resonance, as shown in Table 1. The corresponding dimensionless velocities are $v =0.01$ and $v =0.7$, respectively. We changed the different velocities (v) and used the judgment rule of F.M; if it is in a stable state, it will be expressed by a black dot, and if it is in an unstable state, it will not be marked, in order to draw the basin of attraction (BOA) plot and observe the stability of the system with a shock absorber. The BOA is a set of initial conditions leading to long-time dynamic motion that approaches to an attractor. The motion of the long-time behavior of a given system can be different depending on which basin of attraction the initial condition lies in. The BOA is a useful way to verify the nonlinear system’s stability for a different set of beam initial conditions. Based on flow velocity $v =0.01$, this study analyzed the stability of the system near this velocity and drew the corresponding 3D BOA plot, as shown in Fig. 13. Figure 13a is a BOA plot drawn from $v =$ 0.01 to 0.075 at 0.005 intervals. In Fig. 13a, it can be found that the change of the stability range of the system is not obvious at $v=$0.01 to 0.065, but begins to decrease sharply at $v =0.065$ to 0.075. We reduced the flow velocity interval to 0.001 and drew the BOA plot from $v=0.065$ to 0.076 to observe the changes, as shown in Fig. 13b. Figure 13b shows that the stability range of the system decreases with the increased flow velocity, and when the flow velocity is $v =0.076$, the system has no stability range. This shows that although this case triggers the energy exchange between the system modes and leads to the generation of weak I.R. when $v=0.01$, it does not mean that the system is in the most unstable state at this velocity. To verify the stability prediction of Fig. 13b, we chose the BOA plot at $v =0.07$ as an example and verified its stability range with the Poincaré map, as shown in Fig. 14. Figure 14b is a BOA plot when $v=0.07$, while Fig. 14c, d is the initial conditions of the stable area (2.0, -0.6) and the initial conditions of the unstable area (2.0, $-0.8$) when $v =0.07$, respectively. By observing Fig. 14c, it can be found that the Poincaré map of the stable region is in a stable state, while Fig. 14d shows a chaotic state. In addition, in order to analyze the effect of additional dampers on the stability of the system, we drew a BOA plot of a weak I.R. case with TMD at flow velocity $v =$ 0.065-0.076, as shown in Fig. 15. Comparing Fig. 14 with Fig. 15 shows that the stability range of the system increases obviously after adding TMD regardless of the flow velocity. By observing Fig. 15a, it also can be found that the system has a stable region even when $v =0.076$, meaning that TMD can reduce the amplitude, increase the stability of the system, and improve the divergence of the system. Similarly, to verify the accuracy of the BOA plot after TMD is added to the system, we also took the BOA plot at $v =0.07$ as an example and verified it with a Poincaré map, as shown in Fig. 15b–d. From Fig. 15c, d, it can be confirmed that the dotted block is indeed stable, while the white block is unstable.

In the stability analysis of I.R., we can take the case of Table 1 (B-1) as an example and draw its 3D BOA plot, as shown in Fig. 16. Figure 16a shows a BOA plot with velocity $v =0.1$-0.7, as drawn at intervals of 0.05. Figure 16a shows that the stability range decreases with the increased flow velocity, and the system has fully diverged when the flow velocity increases to $v =0.7$, meaning that the fluid-conveying tube system will produce I.R. when $v=0.7$, and the velocity is the diverge speed under this case. The BOA plot after adding TMD is shown in Fig. 17. Comparing Fig. 16a and Fig. 17a, we can see that the range of stability of the system increases under any flow velocity after adding TMD, and Fig. 17a shows that, even when$v=0.7$, there are local stable areas. The results confirm that TMD can increase the range of the stable area and the divergence speed of the system to a certain extent. In addition, for the verification of I.R. stability, we take the BOA plot at $v =0.6$ as an example in Fig. 16a, 17a and validate the initial conditions of the stable area and the unstable area in Figs. 16c, d and 17c, d, respectively. The results of the Poincaré map are consistent with the prediction of the BOA plot.

8 Conclusions

In this study, a fluid-conveying nonlinear beam is used as the main model to simulate the vibration of a fluid-conveying tube, and then, nonlinear spring support is used to simulate the system on an elastic foundation. The TMD is added to the system to determine the optimal vibration reduction combination of TMD by changing its mass, position, elastic constants, and damping coefficients. The flow-structure coupled system includes the phenomena of mutual coupling and internal resonance among modes; therefore, MOMS, fixed-point plots, Poincaré map, MACP, and basin of attraction are used to analyze and compare the system to verify the correctness of our theory. In addition to providing the vibration characteristics of the nonlinear flow-structure coupled system, the influence of TMD parameters on the whole system is analyzed, and the stability of the system is analyzed by changing the flow velocity of the fluid. Finally, the following conclusions are proposed for this study.

• 1. Under a certain combination of elastic foundation spring constants, taking $k_{w}=80.7$ as an example, the energy exchange between the first and third modes of the system will occur, and weak I.R. does exist in the fluid-conveying tube system. When $v=0.7$ and ${\bar{I}}=0.01$, and $\omega$$=0.5$ and $k_{w}=113.1$, $\omega =0.8$ and $k_{w}=285.3$ and $\omega =1$ and $k_{w}=444$, the 1:3 internal resonance between the first and third modes of the main system will occur.

• 2. The placement of TMD is very important for the vibration reduction effect of the system. If TMD is placed in the position with the maximum amplitude of the vibration mode of the elastic beam (e.g., 0.5l for the first mode, and 0.5l & near 0.2l for the third mode), the system will have the best vibration reduction effect. Relatively, if TMD is placed in the position where the vibration amplitude is the smallest (e.g., 0.0001l at the end point), there is no vibration reduction effect. Therefore, the optimal placement of TMD depends on the maximum amplitude of each mode shape.

• 3. This TMD can effectively avoid I.R. and suppress vibration for this fluid-conveying tube. In addition, for the first mode, the optimal combination of vibration reduction parameters is $m_{D}=0.1$, $l_{D}=0.5$, $f_{s}=9$, $g_{s}=0.1$, and $m_{D}=0.1$, $l_{D}=0.5$, $f_{s}=$ 9, $g_{s}=0.9$ for the third mode.

• 4. The influence of fluid on the vibration behavior of the main system should not be neglected; for example, when the tangential shear force and centripetal force acting on the tube wall are considered, the amplitude of the system is larger, and when velocity v of the fluid increases gradually, the amplitude of the flow-structure coupled system tends to increase.

• 5. In the stability analysis of weak I.R., it can be found that, although weak I.R. will be triggered when $v =0.01$, there is still a stable area in the system at this flow velocity, and the system will diverge completely when the flow velocity is increased to $v =0.076$. In the stability analysis of I.R., it is found that $v =0.7$ happens to be the divergent velocity of this case, which means that I.R. will occur at this velocity, and the system will diverge in an all-round manner. In addition, the stability range of any case will increase significantly after TMD is added, indicating that TMD plays an important role.

Appendices

Appendix A: Dimensionless definition of the coefficients

$$\begin{aligned} {\bar{u}}= & {} \frac{u}{l}, \quad {\bar{w}}=\frac{w}{l}, \quad \omega _{u} =\sqrt{\frac{EA_{b} }{m_{b} l^{2}}} , \quad \omega _{w} =\sqrt{\frac{EI_{b} }{m_{b} l^{4}}} , \quad {\bar{v}}=\frac{v}{\omega _{u} l}, \quad \tau =t\omega _{u} ,\\ {\bar{\mu }}_{u}= & {} \frac{\mu _{u} }{m_{b} \omega _{u} }, \quad {\bar{\mu }}_{w} =\frac{\mu _{w} }{m_{b} \omega _{u} }, \quad {\bar{k}}_{w} =\frac{k_{w} }{m_{b} \omega _{u}^{2} }, \quad {\bar{B}}_{w} =\frac{B_{w} l^{2}}{m_{b} \omega _{u}^{2} }, \\ {\bar{q}}= & {} \frac{q}{m_{b} l\omega _{u}^{2} }, \quad {\bar{I}}=\frac{(I_{m_{b} } +I_{m_{f} } )}{m_{b} l^{2}}, \quad M=\frac{m_{f} }{m_{b} } \quad {\bar{m}}_{D} =\frac{m_{D} }{m_{b} } {\bar{f}}_{s} =\frac{f_{s} }{m_{b} l\omega _{u}^{2} }, \quad {\bar{g}}_{s} =\frac{g_{s} }{m_{b} l\omega _{u} } \end{aligned}$$

Appendix B: Definition of the coefficients

$$\begin{aligned} A_{m}= & {} \frac{2+2{\bar{I}}\gamma _{m}^{2} }{1+{\bar{I}}\gamma _{m}^{2} }, \quad \beta _{m} =\frac{\mu _{w} }{1+{\bar{I}}\gamma _{m}^{2} }, \quad C_{m} =\frac{B_{w} }{(1+{\bar{I}}\gamma _{m}^{2} )\int _0^1 {\phi _{m}^{2} {\mathrm{d}}x} }, \\ D_{m}= & {} \frac{3Mv^{2}}{2(1+{\bar{I}}\gamma _{m}^{2} )\int _0^1 {\phi _{m}^{2} {\mathrm{d}}x} }\\ E_{m}= & {} \frac{(Mv^{2}+1)}{2(1+{\bar{I}}\gamma _{m}^{2} )\int _0^1 {\phi _{m}^{2} {\mathrm{d}}x} }, \quad F_{m} =\frac{\int _0^1 {\phi _{m} {\mathrm{d}}x} }{(1+{\bar{I}}\gamma _{m}^{2} )\int _0^1 {\phi _{m}^{2} } \,{\mathrm{d}}x}, \\ Q_{m}= & {} \frac{1}{(1+{\bar{I}}\gamma _{m}^{2} )\int _0^1 {\phi _{m}^{2} } \,{\mathrm{d}}x} \end{aligned}$$