1 Introduction

In cosmology, dark energy (DE) is an unknown form of energy which is hypothesized to constitute most of the space, leading to accelerate the expansion of Universe [1]. The most widely accepted hypotheses since the 1990s are based on observations that support the current DE [2] and show that the expansion of the Universe is accelerating. In quintessence models of DE, the observed acceleration of the scale factor is caused by the potential energy of a dynamic field, referred to as the quintessence field [3,4,5]. Quintessence differs from the cosmological constant since it can vary both in space and in time. In order for it not to clump and form structure like matter, the field must be very light so that it has a large Compton wavelength. Although there is no evidence of quintessence is yet available, it has been getting attention since the mystery on the accelerated expansion of Universe has not been resolved. The existence of the quintessence generally predicts a slightly slower acceleration of the expansion of Universe than the cosmological constant. Some scientists think that the best evidence for quintessence would come from violations of Einstein’s equivalence principle and variation of the fundamental constants in space or time. Moreover, scalar fields are considered as another forms of DE where broad types of scalar field models have been suggested, such as quintessence [6,7,8,9,10,11], phantom [12,13,14] , K-essence [15, 16] and quintom [17]. Scalar fields are predicted by the standard model of particle physics and string theory, but an analogous problem to the cosmological constant problem (or the problem of constructing models of cosmological inflation) occurs: Renormalization theory predicts that scalar fields should acquire large masses. (For details, a reader is referred to [18].) Recently, Cicciarella and Pieroni [19] have written an in-depth review of universality for quintessence and, moreover, discussed the application of inflation methods to models of quintessence. Detailed discussion has also been made for the quintessence that is non-minimally coupled with gravity.

On the other hand, the effect of quintessence on black holes (BHs) geodesics and the thermodynamics have received considerable attention in recent published papers. For example, Fernando [20] studied the null geodesics of Schwarzschild BH surrounded by quintessence (SBHSQ) and extracted some of the physical proprieties of the BH. Further, the null geodesics of Schwarzschild, Reissner–Nordström, Schwarzschild-de Sitter and Bardeen BHs surrounded by quintessence are investigated in [21]. In Ref. [22], the marginally stable circular orbits of a massive test particle are investigated in the geometry of the SBHSQ.

Our present paper is divided into two parts. In the first part, we derive the general formalism of the geodesics in the SBHSQ spacetime and study the effect of quintessence parameter on the timelike geodesics. Radial geodesics for massive particles are solved exactly. Study of the effective potential in radial motion shows that all radial orbits are unstable due to the presence of quintessence field. Circular timelike geodesics are also considered. All types of possible orbits in non-radial timelike geodesics are analyzed. We also determine the Lyapunov exponent and the effective force acting on the particle in the presence of quintessence field. In the second part of the paper, we evaluate the greybody factor and transmission probability of the SBHSQ. It is worth noting that semiclassical black holes emit thermal radiation: Hawking radiation [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59] . Such radiation, as seen by an asymptotic observer far outside the BH, differs from the original radiation near the horizon of the black hole by a redshift factor and the so-called greybody factor. (See for example [60, 61].) We then discuss the effect of quintessence on the greybody radiation and transformation probability. In fact, we derive the greybody factor with the help of transmission probability via the method of Miller–Good transformation [62]. To this end, we apply that particular transformation to the wave equation, which is nothing but the one-dimensional Schrödinger equation, and obtain the greybody factor.

Our paper is organized as follows: In Sect. 2, we introduce the SBHSQ spacetime. In Sect. 3, we derive the geodesic equations that give us a complete description of the motion of the particle in the geometry of SBHSQ. In addition, the radial and circular timelike geodesics for massive particles are investigated. In Sect. 4, we compute the Lyapunov exponent and effective force on the particle. Section 5 is devoted to the effective potential of massless scalar field. The Miller–Good transformation and greybody factor of SBHSQ are presented in Sects. 6 and 7, respectively. Finally, we make concluding remarks and discuss future work in Sect. 8.

2 Structure of SBHSQ

In this section, we consider the SBHSQ spacetime, which was introduced by Kiselev [63]. To this end, Kiselev assumed a spherically symmetric static gravitational field with the following energy–momentum tensor:

$$\begin{aligned} T_{t}^{t}=T_{r}^{r}=\rho _{q},\quad T_{\theta }^{\theta }=T_{\phi }^{\phi } =-\frac{\rho _{q}}{2}( 3w_{q}+1) , \end{aligned}$$
(1)

where \(w_{q}\) is the quintessence state parameter having a range \(-1<w_{q} <-\frac{1}{3}.\) The equation of the state for the quintessence field is given by

$$\begin{aligned} p_{q}=w_{q}\rho _{q},\quad \rho _{q}=-\frac{3cw_{q}}{2r^{3\left( 1+w_{q}\right) }}, \end{aligned}$$
(2)

where \(p_{q}\) is the pressure, \(\rho _{q}\) denotes the energy density and c stands for the positive normalization factor. To have an accelerated expansion of Universe, the quintessence pressure \(p_{q}\) must be negative. Furthermore, the matter energy density \(\rho _{q}\) must also be positive. Therefore, the normalization factor c must be positive for negative \(w_{q}\). The geometry of the SBHSQ is given by [63]

$$\begin{aligned} \text {d}s^{2}=-f\left( r\right) \text {d}t^{2}+f^{-1}(r)\text {d}r^{2}+r^{2}( \text {d}\theta ^{2}+\sin ^{2}\theta \text {d}\phi ^{2}) , \end{aligned}$$
(3)

where the metric function f(r) reads

$$\begin{aligned} f(r) =1-\frac{2M}{r}-\frac{c}{r^{3w_{q}+1}}, \end{aligned}$$
(4)

and M denotes the mass of the BH. One can compute the curvature of the above metric as follows:

$$\begin{aligned} R=2T_{\mu }^{\mu }=3cw_{q}\frac{1-3w_{q}}{r^{3\left( w_{q}+1\right) }}, \end{aligned}$$
(5)

which has a singularity at \(r=0\) if \(w_{q}\ne \{0,\frac{1}{3},-1\}\). Metric (3) satisfies all the required limits as boundary conditions; when \(c=0\), we recover the Schwarzschild BH (SBH), and when \(c\ne 0\) we have SBHSQ. Throughout this work, we shall concentrate on the special case \(w_{q} =-\frac{2}{3}.\) Hence,

$$\begin{aligned} f\left( r\right) =1-\frac{2M}{r}-cr. \end{aligned}$$
(6)

The metric of SBHSQ (3) with f(r) given in (6) has two horizons. For \(8Mc<1\), the inner (\(r_\mathrm{in}\)) and outer (\(r_\mathrm{out}\)) horizons are given by

$$\begin{aligned} r_\mathrm{in}= & {} \frac{1-\sqrt{1-8Mc}}{2c}, \end{aligned}$$
(7)
$$\begin{aligned} r_\mathrm{out}= & {} \frac{1+\sqrt{1-8Mc}}{2c}, \end{aligned}$$
(8)

where \(r_\mathrm{out}\) likes the horizon in Schwarzschild–de Sitter BH. It should be noted that the area between the two horizons is significant; therefore, in analyzing the motion of massive particles we also consider this region. It is worth noting that for \(8Mc>1,\) the metric does not have horizons (naked singularity case). On the other hand, when \(8Mc=1\) we have an extreme horizon. Figure 1 shows all three cases of possible horizons.

Fig. 1
figure 1

f(r) versus r graph for various values of the parameter c. The plots are governed by Eq. (6). Here, \(2M=1\)

Full size image

3 Geodesics of SBHSQ

In this section, we will derive the geodesic equations for massive particles in the geometry of SBHSQ. For a generic spacetime with a line element \(\text {d}s^{2}=g_{\mu \nu }\text {d}x^{\mu }\text {d}x^{\nu }\), the Lagrangian can be derived from

$$\begin{aligned} { L }=\frac{1}{2}g_{\mu \nu }\frac{\text {d}x^{\mu }}{\text {d}s}\frac{\text {d}x^{\nu }}{\text {d}s}, \end{aligned}$$
(9)

where s is an affine parameter along the geodesics. For the SBHSQ spacetime, the Lagrangian is

$$\begin{aligned} 2{ L }=-f(r) {\dot{t}}^{2}+f^{-1}(r) {\dot{r}}^{2}+r^{2}( {\dot{\theta }}^{2}+\sin ^{2}\theta {\dot{\phi }}^{2}) , \end{aligned}$$
(10)

in which a dot denotes a differentiation with respect to s. There are two conserved quantities, the energy E and the angular momentum \(\ell \) in \(\phi \) direction,

$$\begin{aligned} E= & {} \frac{\text {d}L}{\text {d}{\dot{t}}}=-\left( 1-\frac{2M}{r}-cr\right) {\dot{t}}, \end{aligned}$$
(11)
$$\begin{aligned} \ell= & {} \frac{\text {d}L}{\text {d}{\dot{\phi }}}=r^{2}\sin ^{2}\theta {\dot{\phi }}\text {.} \end{aligned}$$
(12)

Let us choose \(\theta =\pi /2\) and \(\overset{\cdot }{\theta }=0\) as the initial conditions. This means that the motion is restricted to the equatorial plane. Using the two constants of motion (11) and (12), the geodesics equation reduces to

$$\begin{aligned} \left( \frac{\text {d}r}{\text {d}\phi }\right) ^{2}=\frac{r^{4}}{\ell ^{2}}\left( E^{2}-\left( 1-\frac{2M}{r}-cr\right) \left( \epsilon +\frac{\ell ^{2}}{r^{2}}\right) \right) . \end{aligned}$$
(13)

We can obtain the r equation as a function of s and t, respectively,

$$\begin{aligned} \left( \frac{\text {d}r}{\text {d}s}\right) ^{2}= & {} E^{2}-\left( 1-\frac{2M}{r}-cr\right) \left( \epsilon +\frac{\ell ^{2}}{r^{2}}\right) , \end{aligned}$$
(14)
$$\begin{aligned} \left( \frac{\text {d}r}{\text {d}t}\right) ^{2}= & {} \frac{1}{E^{2}}\left( E^{2}-\left( 1-\frac{2M}{r}-cr\right) \left( \epsilon +\frac{\ell ^{2}}{r^{2}}\right) \right) \left( 1-\frac{2M}{r}-cr\right) ^{2}. \end{aligned}$$
(15)

Equations [(13)–(15)] give us a complete description of the motion of the particle. Here, \(\epsilon =1\) corresponds to timelike geodesics and \(\epsilon =0\) is for the null geodesics. We can obtain the effective potential by comparing Eq. (14) with the equation of motion for a unit mass test particle \(\frac{1}{2}\left( \frac{\text {d}r}{\text {d}s}\right) ^{2}+V_\mathrm{eff}( r) =\varepsilon _\mathrm{eff},\) where the effective energy is \(\varepsilon _\mathrm{eff}=\frac{1}{2}E^{2}.\) Hence, the effective potential is given by

$$\begin{aligned} V_\mathrm{eff}(r) =\frac{1}{2}\left( 1-\frac{2M}{r}-cr\right) \left( \epsilon +\frac{\ell ^{2}}{r^{2}}\right) . \end{aligned}$$
(16)

For a real classical region r is limited by the constraint \(\varepsilon _\mathrm{eff}\ge V_\mathrm{eff}(r) \). When introducing \(u=1/r\), we get the u-equation as follows:

$$\begin{aligned} \left( \frac{\text {d}u}{\text {d}\phi }\right) ^{2}=\frac{E^{2}}{\ell ^{2}}-\left( 1-2Mu-\frac{c}{u}\right) \left( \frac{\epsilon }{\ell ^{2}}+u^{2}\right) =P(u) . \end{aligned}$$
(17)

3.1 Radial timelike geodesics

First, we study the radial timelike geodesics corresponds to the motion of massive particles in zero angular momentum (\(\ell =0\)). Then, Eq. (14) becomes

$$\begin{aligned} \left( \frac{\text {d}r}{\text {d}s}\right) ^{2}=E^{2}-1+\frac{2M}{r}+cr. \end{aligned}$$
(18)

Choosing s to be the proper time \(\tau \), Eq. (18) can be rewritten as

$$\begin{aligned} \frac{\text {d}^{2}r}{\text {d}\tau ^{2}}=\frac{c}{2}-\frac{M}{r^{2}}. \end{aligned}$$
(19)

For radial timelike geodesics, the effective potential is given by

$$\begin{aligned} V_\mathrm{eff}(r) =\frac{1}{2}\left( 1-\frac{2M}{r}-cr\right) . \end{aligned}$$
(20)
Fig. 2
figure 2

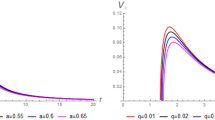
Behavior of \(V_\mathrm{eff}\) [Eq. (20)] for different values of normalization factor c. \(V_\mathrm{eff}\) falls with the increasing c. For increasing c, the radial paths become more unstable

Full size image

The evolution of the effective potential for the radial particles at different values of the normalization factor c is depicted in Fig. 2. Note that the horizons \(r_\mathrm{in}\) and \(r_\mathrm{out}\) are the intersection of \(V_\mathrm{eff}\) with the r-axis. We observe from Fig. 2 that the effective potentials curves are concave down and fall as the normalization factor c increases which implies that there are no stable orbits in SBHSQ. One can check from Eq. (20) that \(V_\mathrm{eff}\) has one maximum point only and no minimum points. Moreover, Fig. 2 shows that the radial motion of a massive particle is unbounded which means that the particle in SBHSQ can escape to infinity.

Let us consider the particle falling toward the center, under the attraction of gravity, from a finite distance \(r_{0}\) with zero initial velocity where the starting distance is related to the constant E by \(E^{2}=1-\frac{2M}{r_{0}}-cr_{0}.\) Making the change of variable \(r=r_{0}\cos ^{2}\eta /2\) and following the same steps in driving the timelike radial geodesic described by the test particle in SBH [64], we obtain

$$\begin{aligned} \tau&=\frac{2M}{\left( \frac{2M}{r_{0}}-cr_{0}\right) ^{3/2}}\tan ^{-1}\left[ \frac{\sqrt{2\left( \frac{2M}{r_{0}}-cr_{0}\right) }\sin (\eta /2)}{\sqrt{\left( \frac{2M}{r_{0}}-cr_{0}\right) \left( 1+\cos \eta \right) +2cr_{0}}}\right] \nonumber \\&\quad +\frac{\sqrt{\left( \frac{2M}{r_{0}}+cr_{0}\right) \left( 1+\cos \eta \right) +2cr_{0}}}{\sqrt{2}\left( \frac{2M}{r_{0}}-cr_{0}\right) } r_{0}\sin \left( \eta /2\right) . \end{aligned}$$
(21)
Fig. 3
figure 3

Particle fall into \(r=0\) singularity versus proper time in SBH (\(c=0\)) and SBHSQ (\(c=0.01\) and \(c=0.02\)). The fall apparently delays in the presence of quintessence field

Full size image

For \(c=0,\) the exact analytical expression (21) reduces to \(\tau =\sqrt{\frac{r_{0}^{3}}{8M}}\left( \eta +\sin \eta \right) \) which coincides with SBH case. To investigate the effect of quintessence matter on the timelike radial motion, we plot Eq. (21) in Fig. 3 and compare it with the SBH (without quintessence). From Fig. 3, it is observed that the quintessence field surrounding the Schwarzschild metric delays the particle following the timelike radial geodesics so that the particles reach the singularity slower than the SBH case.

3.2 Circular timelike geodesics

We shall study here the circular motion of massive test particle for the case \(\ell \ne 0\). From (17), we obtain the conditions of the occurrence of circular orbits, namely \(g\left( u=u_{c}\right) =0\) and \(g^{\prime }\left( u=u_{c}\right) =0\) in which \(r_{c}=\frac{1}{u_{c}}\) is the circular orbit of the particle. Hence,

$$\begin{aligned} \frac{E^{2}}{\ell ^{2}}-\left( 1-2Mu_{c}-\frac{c}{u_{c}}\right) \left( \frac{1}{\ell ^{2}}+u_{c}\right) =0, \end{aligned}$$
(22)

and

$$\begin{aligned} \frac{\text {d}}{\text {d}u}\left( \frac{E^{2}}{\ell ^{2}}-\left( 1-2Mu-\frac{c}{u}\right) \left( \frac{1}{\ell ^{2}}+u^{2}\right) \right) \left| _{u=u_{c} }\right. =0. \end{aligned}$$
(23)

Using the above conditions [Eqs. (22) and (23)], we can obtain the expressions for the energy E and the angular momentum \(\ell \) of the particle as

$$\begin{aligned} E^{2}= & {} \frac{2\left( u_{c}-2Mu_{c}-c\right) ^{2}}{u_{c}\left( 2u_{c} -6Mu_{c}-c\right) }, \end{aligned}$$
(24)
$$\begin{aligned} \ell ^{2}= & {} \frac{\left( 2Mu_{c}-c\right) }{u_{c}\left( 2u_{c}-6Mu_{c} -c\right) }. \end{aligned}$$
(25)

We notice from Eq. (24) that for a physical acceptable motion the constraint \(\left( 2u_{c}{-}6Mu_{c}{-}c\right) {>}0\) emerges naturally. Therefore,

$$\begin{aligned} r_{c\min }=\frac{1-\sqrt{1-6Mc}}{c}<r_{c} \end{aligned}$$
(26)
Fig. 4
figure 4

The difference between circular geodesics radii \(r_{c\min }\) and \(r_{h}\) is shown as a function of c

Full size image

To have a physical orbit, \(r_{c}>r_\mathrm{in}\) must hold. To justify this, we compare both radii [Eqs. (7)and(26)]; it is seen that \(r_{c\min }\) is larger so that \(r_{c\min }-r_\mathrm{in}=\frac{1+\sqrt{1-8Mc} -2\sqrt{1-6Mc}}{2c}>0\). In Fig. 4, we have plotted \(\left( r_{c\min }-r_\mathrm{in}\right) \) versus c; it is clear that \(\left( r_{c\min }-r_\mathrm{in}\right) \) is always positive and as c increases the circular geodesics approaches the horizon. Let us note that when \(c\rightarrow 0,\)\(r_{c\min }\rightarrow 3M\) we recover the radius of the unstable circular orbit of the SBH.

Fig. 5
figure 5

Angular momentum Eq. (25) behavior of a massive particle versus distance \(r_{c}\) for various c values. It is observed that all curves coincide at \(\frac{r_{c}}{M}=4\)

Full size image
Fig. 6
figure 6

Radial dependence of energy Eq. (24) of circular orbits around SBHSQ for different values of c

Full size image

The radial dependence of both \(\ell ^{2}\) (25) and \(E^{2}\) (24) of the test particle moving on circular orbits is shown in Figs. 5 and 6, respectively. It is seen from Fig. 5 that as \(r_{c}\rightarrow r_{c\min }\) the angular momentum goes to minus infinity. We also deduce from Eq. (25) and Fig. 5 that \(\frac{r_{c}}{M}=4\) is the only orbit in which irrespective to the value of c, \(\frac{\ell ^{2}}{M^{2}}=16\). However, Fig. 6 clearly shows that with the decrease in the quintessence parameter c, energy possesses a minimum value.

The effective potential in the circular timelike motion is given by

$$\begin{aligned} V_\mathrm{eff}( r) =\frac{1}{2}\left( 1-\frac{2M}{r}-cr\right) \left( 1+\frac{\ell ^{2}}{r^{2}}\right) . \end{aligned}$$
(27)
Fig. 7
figure 7

\(V_\mathrm{eff}\) for massive particles versus r for the Schwarzschild BH without quintessence \((c=0)\) and with quintessence \((c=0.01)\). The steeply falling potential barrier in SBHSQ explains why the orbits remain unbounded. Here, \(l^{2}=14\) and \(M=1\)

Full size image

To investigate the stability of the equilibrium circular motion of a massive test particle, we make a plot of Eq. (27) in Fig. 7. The figure represents the behavior of the effective potentials of SBHSQ and SBH, jointly. Both figures are concave down, and particles can escape to infinity for a given energy larger than the asymptotic value of \(V_\mathrm{eff}\). There are two main differences between the two curves, the stable orbits and the asymptotic behavior. There are no stable parts in the curve \(V_\mathrm{eff}\) for SBHSQ because of the steeply falling down, whereas the \(V_\mathrm{eff}\) of SBH has some stable parts and is asymptotically constant. We conclude that there are no stable circular orbits due to the presence of quintessence matter. A plot of \(V_\mathrm{eff}\) (27) with three energy levels for a particular value for \(\ell ^{2}=14,\)\(c=0.01\) and \(M=1\) is shown in Fig. 8. Since the relation \(\left( \frac{\text {d}r}{\text {d}s}\right) ^{2}+V_\mathrm{eff}( r) =E^{2}\), the motion of the particles (orbits) depends on the energy levels. To have a complete analytic description of different types of orbits, we will consider three cases according to different values of E. Separate cases are highlighted in the following:

Fig. 8
figure 8

The graph shows the relation of \(V_\mathrm{eff}\) with the energy E

Full size image
Fig. 9
figure 9

The graph shows the timelike geodesics for \(E_{1}=0.45>E_{c}\), with \({\mathrm {c}}=0.01\), \(l^{2}=14\) and \({\mathrm {M}}=1\). The orbit (blue) starts from larger distance and ends below \(r_\mathrm{in}\)

Full size image
Fig. 10
figure 10

The graph shows the timelike geodesics for \(E_{2}=0.4<E_{c}\), with \({\mathrm {c}}=0.01\), \(l^{2}=14\) and \({\mathrm {M}}=1\). The orbit (blue) starts from larger distance and escapes to infinity

Full size image
Fig. 11
figure 11

The graph shows the timelike geodesics for \(E=0.425=E_{c}\), with \({\mathrm {c}}=0.01\), \(l^{2}=14\) and \({\mathrm {M}}=1\). The orbit (blue) starts from larger distance, approaches the BH and merges to the circular orbit at \(r=r_{c}\)

Full size image

Case I The energy level \(E=E_{1}>E_{c}\) gives \(E^{2}-V_\mathrm{eff}(r) >0\) and \(\frac{\text {d}r}{\text {d}s}>0\); hence, if the particle starts its motion from larger r,  it will cross the \(r_\mathrm{in}\) and falls into the singularity. The corresponding orbit is shown in Fig. 9.

Case II The energy level \(E=E_{2}<E_{c}\) gives \(E^{2}-V_\mathrm{eff}(r) \ge 0\); here, we have two regions. if the particle starts its motion at \(r>r_{c.}\), it will fall to a minimum radius and escape to infinity. But if the particle starts the motion at \(r<r_{c}\), then it will fall into the black hole. An example to this case is shown in Fig. 10.

Case III The energy level \(E=E_{c}\) gives \(E^{2}-V_\mathrm{eff}\left( r\right) =0,\) and \(\frac{\text {d}r}{\text {d}s}=0\); hence, we have circular orbits. Because of the nature of the effective potential at \(r=r_{c.}\), the orbits are unstable. The corresponding orbit is shown in Fig. 11.

Using Eq. (17), we can obtain the circular orbit of a massive particle with unit mass at \(r_{c}=r_{\min }\) as

$$\begin{aligned} \left( \frac{\text {d}u}{\text {d}\phi }\right) ^{2}=\frac{E^{2}}{\ell ^{2}}-\left( 1-2Mu-\frac{c}{u}\right) \left( \frac{1}{\ell ^{2}}+u^{2}\right) . \end{aligned}$$
(28)

For \(\ell ^{2}=200,\) we have \(E^{2}=356.8143470=\left( 1-\frac{2}{r}-0.01r\right) \left( 1+\frac{200}{r^{2}}\right) \); hence, the minimum circular radius becomes \(r_{\min }=3.093402159\), while \(r_\mathrm{in}=2.041684766.\) Figure 12 shows the circular orbit of a massive particle at \(r_{c}=r_{\min }\).

Fig. 12
figure 12

The inner horizon and the minimum circular radius for the values \(l^{2}=200,\ {\mathrm {c}}=0.01\) and \({\mathrm {M}}=1\)

Full size image

It is possible to obtain a general solution to the equation of the orbits Eq. (28); hence,

$$\begin{aligned} \left( \frac{\text {d}u}{\text {d}\phi }\right) ^{2}=2Mu^{4}-u^{3}+\left( \frac{2M+c\ell ^{2}}{\ell ^{2}}\right) u^{2}+\left( \frac{E^{2}-1}{\ell ^{2}}\right) u+\frac{c}{\ell ^{2}}=P\left( u\right) . \end{aligned}$$
(29)

The geometry of the geodesics will depend on the roots of the function \(P\left( u\right) .\) For \(c\rightarrow 0,\) Eq. (29) reduces to \(P(u) =u^{4}-\left( \frac{1}{2M}\right) u^{3}+\left( \frac{1}{\ell ^{2}}\right) u^{2}+\left( \frac{E^{2}-1}{2M\ell ^{2}}\right) \) as expected; we recover the non-radial geodesics for the SBH. For \(u\rightarrow \mp \infty ,\)\(P( u) \rightarrow \infty .\) Also when \(u\rightarrow 0,\)\(P( u) \rightarrow \frac{c}{\ell ^{2}}.\) Therefore, P(u) definitely has one negative real root.

Equation (29) can be written as

$$\begin{aligned} \frac{\text {d}u}{\text {d}\phi }=\mp \sqrt{P\left( u\right) }, \end{aligned}$$
(30)

where P(u) is given by

$$\begin{aligned} P( u) =2M( u-u_{4}) ( u-u_{3}) ( u-u_{2})( u-u_{1}) . \end{aligned}$$
(31)

We will choose the “+” sign without lose of generality. When integrating Eq. (30), a relation between u and \(\phi \) in terms of Jacobi elliptic integral \({\mathcal {F}}(x,y)\) is obtained as

$$\begin{aligned} \phi =\frac{\sqrt{2}{\mathcal {F}}(x,y)}{\sqrt{M( u_{2}-u_{3})( u_{1}-u_{4}) }}+const, \end{aligned}$$
(32)

where

$$\begin{aligned} \sin x= & {} \sqrt{\frac{( u-u_{2})( u_{1}-u_{4}) }{( u-u_{1}) ( u_{2}-u_{4}) }}, \end{aligned}$$
(33)
$$\begin{aligned} y= & {} \frac{( u_{1}-u_{3}) ( u_{2}-u_{4}) }{( u_{2}-u_{3}) ( u_{1}-u_{4}) }, \end{aligned}$$
(34)
$$\begin{aligned} {\mathcal {F}}(x,y)= & {} \int _{0}^{x}\frac{\text {d}\lambda }{\sqrt{1-y\sin ^{2}\lambda }}. \end{aligned}$$
(35)

4 Lyapunov exponent and effective force

The Lyapunov exponent is a quantity that characterizes the rate of separation of infinitesimally close trajectories of the average rate at which nearby trajectories converge or diverge in the phase space. If the Lyapunov exponent is positive, then it implies a divergence between nearby trajectories, which means high sensitivity to initial conditions. To evaluate the Lyapunov exponent for the unstable timelike circular orbits, we use the expression derived by Cardoso et al. [65] as

$$\begin{aligned} \lambda&=\sqrt{\frac{-V_\mathrm{eff}^{\prime \prime }( r_{c}) }{2\overset{\cdot }{t}( r_{c}) ^{2}}} \end{aligned}$$
(36)
$$\begin{aligned}&=\sqrt{-\frac{c^{2}}{2}+\frac{6M^{2}}{r_{c}^{4}}-\frac{M}{r_{c}^{3}} -\frac{6Mc}{r_{c}^{2}}+\frac{3c}{2r_{c}}}. \end{aligned}$$
(37)
Fig. 13
figure 13

The Lyapunov exponent \(\lambda \) versus c with \(M=0.5\)

Full size image

The plot of the Lyapunov exponent \(\lambda \) as a function of c for the SBHSQ is shown in Fig. 13. We notice that the instability of the timelike circular orbits is more for the SBHSQ in comparison with SBH. To calculate the critical exponent for instability of orbits, we use [65]

$$\begin{aligned} \gamma =\frac{T_{\lambda }}{T}, \end{aligned}$$
(38)

where \(T_{\lambda }\) is the instability timescale given by \(T_{\lambda }=1/\lambda \) and the time period \(T=\left| \frac{2\pi r_{c}^{2}}{\ell }\right| \) (Eq. 12). Therefore, as the values of c increases, \(\lambda \) becomes smaller for the same critical exponent.

When we expand the effective potential (27), it looks like

$$\begin{aligned} V_\mathrm{eff}( r) =-\left( r+\frac{\ell ^{2}}{r}\right) c-\frac{2\ell ^{2}M}{r^{3}}+\frac{\ell ^{2}}{r^{2}}-\frac{2M}{r}+1. \end{aligned}$$
(39)

It is seen that the contribution to the effective potential from the quintessence matter is \(-\left( cr+\frac{c\ell ^{2}}{r}\right) \) compared to the SBH. We can also obtain the effective force on the particle as

$$\begin{aligned} F=-\frac{1}{2}\frac{\text {d}V_\mathrm{eff}\left( r\right) }{\text {d}r}=-\left( \frac{3M\ell ^{2} }{r^{2}}+M+\frac{c\ell ^{2}}{2}\right) \frac{1}{r^{2}}+\frac{\ell ^{2}}{r^{3} }+\frac{c}{2}. \end{aligned}$$
(40)
Fig. 14
figure 14

The graph shows the effective force F as a function of r

Full size image

The first terms in (40) are the attractive force acting on the particle since they are negative, while the last two terms are repulsive. The plot of Eq. (40) is shown in Fig. 14 in which \(\ell =2,\)\(M=1\), and \(c=0.08\). Consequently, we have \(r_\mathrm{in}=2.5,\)\(r_{c}=5\), and \(r_\mathrm{out}=10.\) and \(F=0\) at \(r=1.86728\). From this figure, we can deduce that there are no stable circular orbits for a massive particle and the force on the particle is positive for \(r>r_\mathrm{in}\) which implies that the force is repulsive. This result agrees with the observations in cosmology that the DE is associated with a repulsive force tending to accelerate the expansion of the Universe.

5 Effective potential of a massless scalar field

In this section, we derive the effective potential of a massless scalar field propagating in the geometry of SBHSQ. To this end, we first consider the Klein–Gordon equation [66]:

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu }\left( \sqrt{-g}g^{\mu \nu }\partial _{\nu }\right) \Psi =0, \end{aligned}$$
(41)

in which \(\sqrt{-g}=r^{2}\sin \theta \) for the metric (3). Thus, Eq. (41) reads

$$\begin{aligned} -\frac{1}{f}\partial _{t}^{2}\Psi +\frac{1}{r^{2}}\partial _{r}\left( r^{2}f\partial _{r}\right) \Psi +\frac{1}{r^{2}}\partial _{\theta }^{2}\Psi +\frac{\cos \theta }{r^{2}\sin \theta }\partial _{\theta }\Psi +\frac{1}{r^{2} \sin ^{2}\theta }\partial _{\phi }^{2}\Psi =0. \end{aligned}$$
(42)

Considering the symmetries of the SBHSQ spacetime, one can set the scalar field \(\Psi \) as

$$\begin{aligned} \Psi \left( t,r,\theta ,\phi \right) =\frac{{\mathcal {S}}\left( r\right) }{r}\exp \left( -i\omega t\right) Y_{lm}\left( \theta ,\phi \right) , \end{aligned}$$
(43)

where \(\exp \left( -i\omega t\right) \) represents the oscillating function and \(Y_{lm}\left( \theta ,\phi \right) \) is nothing but the spheroidal harmonics [67] (l: angular quantum number, m: magnetic quantum number). The radial part of the Klein–Gordon equation is obtained as follows:

$$\begin{aligned} \frac{f}{{\mathcal {S}}\left( r\right) }{\mathcal {S}}^{\prime \prime }\left( r\right) +\frac{f^{\prime }}{{\mathcal {S}}\left( r\right) }{\mathcal {S}} ^{\prime }\left( r\right) +\left\{ \frac{\omega ^{2}}{f}-\frac{f^{\prime }}{r}-\frac{\lambda }{r^{2}}\right\} =0, \end{aligned}$$
(44)

where \(\lambda =-l\left( l+1\right) \). When Eq. (44) is rewritten as

$$\begin{aligned} \frac{1}{{\mathcal {S}}\left( r\right) }\frac{\text {d}}{\text {d}r}\left( f\frac{\text {d}{\mathcal {S}}\left( r\right) }{\text {d}r}\right) +\left\{ \frac{\omega ^{2}}{f}-\frac{f^{\prime }}{r}-\frac{\lambda }{r^{2}}\right\} =0, \end{aligned}$$
(45)

and introducing the tortoise coordinate

$$\begin{aligned} \frac{\text {d}r_{*}}{\text {d}r}=\frac{1}{f\left( r\right) }, \end{aligned}$$
(46)

then, after some algebra, the one-dimensional Schrödinger equation is obtained as

$$\begin{aligned} \frac{\text {d}^{2}{\mathcal {S}}\left( r\right) }{\text {d}r_{*}^{2}}+\left( \omega ^{2}-V_\mathrm{eff}\right) {\mathcal {S}}\left( r\right) =0, \end{aligned}$$
(47)

where the effective radial potential in the Schrödinger-like wave equation (47) reads

$$\begin{aligned} V_\mathrm{eff}=\frac{f}{r}\left( f^{\prime }+\frac{\lambda }{r}\right) . \end{aligned}$$
(48)

6 Miller–Good transformation of SBHSQ

Greybody factor is one of the quantum quantities of a BH. In short, it is the fraction of Hawking radiation that can reach spatial infinity. In this section, we shall focus on the Miller–Good transformation method [62] to derive the greybody factor of the SBHSQ. The Miller–Good transformation generates a general bound on quantum transmission probabilities. In this method, a particular transformation is applied to the Schrödinger equation (47) in such a way that the effective potential (48) is modified in order to yield a better transmission probability for the Hawking quanta [68].

Defining the new radial function \({\mathcal {S}}\left( r\right) =\frac{\psi \left( r\right) }{\sqrt{f}},\) Eq. (47) can be rewritten in the following compact form:

$$\begin{aligned} \frac{\text {d}^{2}\psi \left( r\right) }{\text {d}r^{2}}+k^{2}\left( r\right) \psi \left( r\right) =0, \end{aligned}$$
(49)

where

$$\begin{aligned} k^{2}\left( r\right) =\left\{ \frac{\omega ^{2}}{f^{2}}-\frac{f^{\prime } }{rf} -\frac{\lambda }{r^{2}f}-\frac{f^{\prime \prime }}{2f}+\frac{f^{^{\prime }2} }{4f^{2}}\right\} . \end{aligned}$$
(50)

Considering the Miller–Good transformation method, we first apply the following special transformation:

$$\begin{aligned} \psi \left( r\right) =\frac{1}{\sqrt{R^{\prime }\left( r\right) }} \Psi \left[ R\left( r\right) \right] , \end{aligned}$$
(51)

in which R is the new position variable such that \(R\left( r\right) \) is an invertible function, which implies that \(\frac{\text {d}R\left( r\right) }{\text {d}r}\ne 0.\) Without loss of generality, one can assert \(\frac{\text {d}R\left( r\right) }{\text {d}r}>0\), whence also \(\frac{dr}{dR\left( r\right) }>0\). Thus, the derivatives of the new function (51) yield

$$\begin{aligned} \psi ^{\prime }\left( r\right)&=\sqrt{R^{\prime }\left( r\right) } \Psi _{R}\left( R\left( r\right) \right) -\frac{1}{2}\frac{R^{\prime \prime }\left( r\right) }{R^{\prime }\left( r\right) \sqrt{R^{\prime }\left( r\right) }}\Psi \left( R\left( r\right) \right) , \end{aligned}$$
(52)
$$\begin{aligned} \psi ^{\prime \prime }\left( r\right)&=R^{\prime }\left( r\right) \sqrt{R^{\prime }\left( r\right) }\Psi _{RR}\left( R\left( r\right) \right) -\frac{1}{2}\frac{R^{\prime \prime \prime }\left( r\right) }{R^{\prime }\left( r\right) \sqrt{R^{\prime }\left( r\right) }}\Psi \left( R\left( r\right) \right) \nonumber \\&\quad +\frac{3}{4}\frac{R^{\prime \prime 2}\left( r\right) }{R^{\prime 2}\left( r\right) \sqrt{R^{\prime }\left( r\right) }}\Psi \left( R\left( r\right) \right) , \end{aligned}$$
(53)

where \(\Psi _{R}\) indicates \(\frac{\text {d}\Psi }{\text {d}R}\). Thus, Eq. (51) recasts in

$$\begin{aligned} \Psi _{RR}\left( R\left( r\right) \right) +\left\{ \frac{k^{2}}{R^{\prime 2}\left( r\right) }+\frac{3}{4}\frac{R^{\prime \prime 2}\left( r\right) }{R^{\prime 4}\left( r\right) }-\frac{1}{2}\frac{R^{\prime \prime \prime }\left( r\right) }{R^{\prime 3}\left( r\right) }\right\} \Psi \left( R\left( r\right) \right) =0. \end{aligned}$$
(54)

Letting

$$\begin{aligned} K^{2}=\frac{1}{R^{\prime 2}\left( r\right) }\left\{ \frac{\omega ^{2}}{f^{2} }-\frac{f^{\prime }}{rf}-\frac{\lambda }{r^{2}f}-\frac{f^{\prime \prime }}{2f}+\frac{f \acute{} ^{2}}{4f^{2}}-\frac{1}{2}\frac{R^{\prime \prime \prime }\left( r\right) }{R^{\prime }\left( r\right) }+\frac{3}{4}\frac{R^{\prime \prime 2}\left( r\right) }{R^{^{\prime }2}\left( r\right) }\right\} , \end{aligned}$$
(55)

one can rewrite Eq. (54) as a new Schrödinger-like wave equation:

$$\begin{aligned} \Psi _{RR}+K^{2}\Psi =0. \end{aligned}$$
(56)

Namely, Schrödinger equation (51) expressed in terms of \(\psi \left( r\right) \) and \(k\left( r\right) \) has been transformed into a new Schrödinger equation in terms of \(\Psi \left( R\left( r\right) \right) \) and \(K\left( R\left( r\right) \right) \). Meanwhile, the following combination

$$\begin{aligned} \sqrt{R^{\prime }\left( r\right) }\left( \frac{1}{\sqrt{R^{\prime }\left( r\right) }}\right) ^{\prime \prime }=-\frac{1}{2}\frac{R^{\prime \prime \prime }\left( r\right) }{R^{\prime }\left( r\right) }+\frac{3}{4}\frac{R^{\prime \prime 2}\left( r\right) }{R^{\prime 2}\left( r\right) } \end{aligned}$$
(57)

is named as the “Schwarzian derivative” [69, 70]. Thus, K can be simplified as

$$\begin{aligned} K^{2}=\frac{1}{R^{^{\prime }2}\left( r\right) }\left\{ \frac{\omega ^{2} }{f^{2}}-\frac{f^{\prime }}{rf}-\frac{\lambda }{r^{2}f}-\frac{f^{\prime \prime } }{2f}+\frac{f^{\prime 2}}{4f^{2}}+\sqrt{R^{\prime }\left( r\right) }\left( \frac{1}{\sqrt{R^{\prime }\left( r\right) }}\right) ^{\prime \prime }\right\} . \end{aligned}$$
(58)

As we have mentioned above, the parameter \(R^{\prime }\left( r\right) \) must be positive. To this end, we choose another parameter as

$$\begin{aligned} j\left( r\right) \equiv R^{\prime }\left( r\right) ; \end{aligned}$$
(59)

with \(j\left( r\right) >0,\) we can then write

$$\begin{aligned} K^{2}=\frac{1}{j^{2}\left( r\right) }\left\{ \frac{\omega ^{2}}{f^{2}} -\frac{f^{\prime }}{rf}-\frac{\lambda }{r^{2}f}-\frac{f^{\prime \prime }}{2f}+\frac{f^{\prime 2}}{4f^{2}}-\frac{1}{2}\frac{j^{\prime \prime }\left( r\right) }{j\left( r\right) }+\frac{3}{4}\frac{j^{\prime 2}\left( r\right) }{j^{2}\left( r\right) }\right\} . \end{aligned}$$
(60)

Furthermore, setting

$$\begin{aligned} j\left( r\right) =\frac{1}{J^{2}\left( r\right) }, \end{aligned}$$
(61)

with \(J\left( r\right) >0,\) we get

$$\begin{aligned} j^{\prime }\left( r\right) =-\frac{2J^{\prime }\left( r\right) }{J^{3}\left( r\right) }, \qquad j^{\prime \prime }\left( r\right) =\frac{6J^{\prime 2}\left( r\right) }{J^{4}\left( r\right) }-\frac{2J^{\prime \prime }\left( r\right) }{J^{3}\left( r\right) }, \end{aligned}$$
(62)

and

$$\begin{aligned} K^{2}=J^{4}\left( r\right) \left\{ \frac{\omega ^{2}}{f^{2}}-\frac{f^{\prime }}{rf}-\frac{\lambda }{r^{2}f}-\frac{f^{\prime \prime }}{2f} +\frac{f^{\prime 2}}{4f^{2}}+\frac{J^{\prime \prime }\left( r\right) }{J\left( r\right) }\right\} . \end{aligned}$$
(63)

In the case of \(J=1,\) one can immediately observe that \(K^{2}\left( R\right) =k^{2}\left( r\right) \); therefore, both potentials [\(K^{2}\left( R\right) \) and \(k^{2}\left( r\right) \)] have the same transmission amplitudes and consequently the same transmission probability. The second probability is to find the relation between two parameters J and f such that we will have different potentials and whence different transmission probabilities. For the later case, one can get the transmission probability from the following definition [62]:

$$\begin{aligned} {\mathcal {T}}\ge \sec h^{2}\left\{ \int _{-\infty }^{+\infty }\wp \text {d}r\right\} , \end{aligned}$$
(64)

in which \(\wp \) is given by

$$\begin{aligned} \wp =\frac{\sqrt{\left( h^{\prime }\right) ^{2}+\left[ k^{2}-h^{2}\right] ^{2}}}{2h}, \end{aligned}$$
(65)

with \(h\left( r\right) >0.\) Let us redefine function \(\wp \) as \(\overset{\thicksim }{\wp }\) in order to show the difference between \(k\left( r\right) \) and \(K\left( R\right) \). Then, we have

$$\begin{aligned} {\mathcal {T}}\ge \sec h^{2}\left\{ \int _{-\infty }^{+\infty }\overset{\thicksim }{\wp }\text {d}R\right\} , \end{aligned}$$
(66)

where \(\overset{\thicksim }{\wp }\) is the function with respect to new transformation parameters and

$$\begin{aligned} \text {d}R=R^{\prime }\text {d}r=j\text {d}r, \end{aligned}$$
(67)

so that Eq. (66) is given by

$$\begin{aligned} {\mathcal {T}}\ge \sec h^{2}\left\{ \int _{-\infty }^{+\infty }\frac{\sqrt{\left( h_{R}\right) ^{2}+\left[ K^{2}-h^{2}\right] ^{2}}}{2h}\text {d}R\right\} . \end{aligned}$$
(68)

After substituting Eqs. (60) and (67) into Eq. (68) and further using \(h_{R}=\frac{\text {d}h}{\text {d}r}\frac{\text {d}r}{\text {d}R}\), one can obtain

$$\begin{aligned}&{\mathcal {T}}\ge \sec h^{2}\left\{ \int _{-\infty }^{+\infty }\frac{1}{2h}\right. \nonumber \\&\qquad \left. \times \sqrt{\left( \frac{h^{\prime }}{R^{\prime }}\right) ^{2}{+}\left[ \frac{1}{j^{2}}\left\{ \frac{\omega ^{2}}{f^{2}}{-}\frac{f^{\prime }}{rf} {-}\frac{\lambda }{r^{2}f}{-}\frac{f^{\prime \prime }}{2f} {+}\frac{f^{\prime 2}}{4f^{2} }{-}\frac{1}{2}\frac{j^{\prime \prime }\left( r\right) }{j\left( r\right) }{+}\frac{3}{4}\frac{j^{\prime 2}\left( r\right) }{j^{2}\left( r\right) }\right\} -h^{2}\right] ^{2}}j\text {d}r\right\} .\nonumber \\ \end{aligned}$$
(69)

As we have mentioned before \(R^{\prime }=j\), Eq. (69) recasts in

$$\begin{aligned}&T\ge \sec h^{2}\left\{ \int _{-\infty }^{+\infty }\frac{1}{2h}\right. \nonumber \\&\qquad \left. \times \sqrt{\left( h^{\prime }\right) ^{2}{+}\left[ \frac{1}{j}\left\{ \frac{\omega ^{2}}{f^{2}}{-}\frac{f^{\prime }}{rf}{-}\frac{\lambda }{r^{2}f} {-}\frac{f^{\prime \prime }}{2f}{+}\frac{f^{\prime 2}}{4f^{2}}{-}\frac{1}{2} \frac{j^{\prime \prime }\left( r\right) }{j\left( r\right) }{+}\frac{3}{4}\frac{j^{\prime 2}\left( r\right) }{j^{2}\left( r\right) }\right\} -jh^{2}\right] ^{2}}\text {d}r\right\} ,\nonumber \\ \end{aligned}$$
(70)

which gives us the first form of the improved bound with the condition of \(h\left( r\right) >0;\) then, \(j\left( r\right) >0,\) too. One can further improve the bound by transforming j to J as follows [62]:

$$\begin{aligned} \text {d}R=R^{\prime }\text {d}r=J^{-2}\text {d}r; \end{aligned}$$
(71)

therefore, the second form of the improved bound for the transmission probability is given by

$$\begin{aligned}&T\ge \sec h^{2}\left\{ \int _{-\infty }^{+\infty }\frac{1}{2h}\right. \nonumber \\&\qquad \left. \times \sqrt{\left( h^{\prime }\right) ^{2}+\left[ J^{2}\left\{ \frac{\omega ^{2}}{f^{2}}-\frac{f \acute{} }{rf}-\frac{\lambda }{r^{2}f}-\frac{f^{\prime \prime }}{2f}+\frac{f^{\prime 2} }{4f^{2}}+\frac{J^{\prime \prime }}{J}\right\} -\frac{h^{2}}{J^{2}}\right] ^{2}}\text {d}r\right\} . \end{aligned}$$
(72)

Here, we consider \(J_{\pm \infty }\ne 1\) with the help of \(h\left( +\infty \right) =h\left( -\infty \right) =\omega \) and then \(h^{\prime }=0\). So, one can write Eq. (72) as

$$\begin{aligned} {\mathcal {T}}\ge \sec h^{2}\left\{ \frac{1}{2\omega }\int _{-\infty }^{+\infty }\left[ J^{2}\left\{ \frac{\omega ^{2}}{f^{2}}-\frac{f \acute{} }{rf}-\frac{\lambda }{r^{2}f}-\frac{f \acute{} \acute{} }{2f}+\frac{f \acute{} ^{2}}{4f^{2}}+\frac{J^{\prime \prime }}{J}\right\} -\frac{\omega ^{2}}{J^{2} }\right] \text {d}r\right\} . \end{aligned}$$
(73)

Moreover, we assume that the first and second terms of the integral are equal to make Eq. (73) more expressive. To this end, we set

$$\begin{aligned} J^{2}=f, \end{aligned}$$
(74)

so then

$$\begin{aligned} f^{\prime }=2JJ^{\prime },\quad \text {and}\quad f^{\prime \prime }=2J^{\prime 2}+2JJ^{\prime \prime }. \end{aligned}$$
(75)

We finally compute the transmission probability of the SBHSQ as follows:

$$\begin{aligned} T\ge \sec h^{2}\left\{ -\frac{1}{2\omega }\int _{-\infty }^{+\infty }\left( \frac{2JJ^{\prime }}{r}+\frac{\lambda }{r^{2}}\right) \text {d}r\right\} . \end{aligned}$$
(76)

7 Greybody factor of SBHSQ

In this section, we shall focus on the greybody factor of Schwarzschild black hole surrounded by quintessence, namely the SBHSQ. Within a semiclassical approximation, greybody factors can be investigated by using the Schrödinger-like one-dimensional wave equation to study the field scattering by the BH background. Actually, with the help of this method, we will be able to define the transmission and reflection coefficients of the BH [62]. Here, we concentrate on Eqs. (48) and (60) to define two kinds of the greybody factors and compare the obtained results over their graphs. The formula of the general semi-analytic bounds for the greybody factors is given by

$$\begin{aligned} \sigma _{l}\left( \omega \right) \ge \sec h^{2}\left( \int _{-\infty } ^{+\infty }\wp \text {d}r_{*}\right) , \end{aligned}$$
(77)

where \(\wp \) is the dimensionless greybody factor:

$$\begin{aligned} \wp =\frac{\sqrt{\left( h^{\prime }\right) ^{2}+\left( \omega ^{2} -V_\mathrm{eff}-h^{2}\right) ^{2}}}{2h}, \end{aligned}$$
(78)

in which \(h^{\prime }\) implies the derivation with respect to r. By considering the conditions for h [h must be positive and \(h\left( +\infty \right) =h\left( -\infty \right) =\omega \)], we can simplify Eq. (78) as

$$\begin{aligned} \wp =\frac{1}{2\omega }V_\mathrm{eff}, \end{aligned}$$
(79)

by using the tortoise coordinate as \(\frac{\text {d}r_{*}}{\text {d}r}=\frac{1}{f\left( r\right) }\). Hence, greybody factor reads

$$\begin{aligned} \sigma _{l}\left( \omega \right) \ge \sec h^{2}\left( \frac{1}{2\omega } \int _{r_{h}}^{+\infty }V_\mathrm{eff}\frac{\text {d}r}{f\left( r\right) }\right) . \end{aligned}$$
(80)

After substituting the effective potential (48) and the derivative of the metric function into Eq. (80), we obtain

$$\begin{aligned} \sigma _{l}\left( \omega \right) \ge \sec h^{2}\left( \frac{1}{2\omega } \int _{r_{h}}^{+\infty }\left( \frac{2M}{r^{3}}-\frac{c}{r}+\frac{\lambda }{r^{2}}\right) \text {d}r\right) . \end{aligned}$$
(81)

But the result of Eq. (81) has a natural logarithm \(\left( \ln \right) \) term, which means that the greybody factor of SBHSQ is measureless. Namely, the method that we have followed is failed. To overcome this difficulty, we shall consider the Miller– Good transformation [62].To this end, let us rewrite Eq. (76) in the form of

$$\begin{aligned} {\mathcal {T}}\ge \sec h^{2}\left\{ -\frac{1}{2\omega }\int _{r_{h}}^{+\infty }\left( \frac{2M-cr^{2}+\lambda r}{r^{3}}\right) \frac{r\text {d}r}{r-2M-cr^{2} }\right\} , \end{aligned}$$
(82)

which can be rewritten as

$$\begin{aligned} {\mathcal {T}}\ge \sec h^{2}\left\{ \frac{1}{2\omega }\int _{r_{h}}^{+\infty }\left( 2M-cr^{2}+\lambda r\right) \left( \frac{1}{r^{4}}\right) \frac{\text {d}r}{c+\frac{2M}{r^{2}}-\frac{1}{r}}\right\} . \end{aligned}$$
(83)

By considering the following asymptotic expansion

$$\begin{aligned} \frac{1}{c+\frac{2M}{r^{2}}-\frac{1}{r}}\simeq \frac{1}{c}+\frac{1}{c^{2} r}+\frac{-\frac{2M}{c}+\frac{1}{c^{2}}}{cr^{2}}\ldots , \end{aligned}$$
(84)

we find (for the similar procedure, the reader is refereed to [71])

$$\begin{aligned} \sigma _{l}\left( \omega \right)\equiv & {} {\mathcal {T}}\ge \sec h^{2}\left\{ \frac{1}{2\omega }\left[ \frac{2M}{3cr_{h}^{3}}+\frac{2M}{4c^{2}r_{h}^{4} }+\frac{2M\left( \frac{1}{c^{2}}-\frac{2M}{C}\right) }{5cr_{h}^{5}}-\frac{1}{r_{h}}-\frac{1}{2cr_{h}^{2}}\right. \right. \nonumber \\&\qquad \qquad \qquad \qquad \left. \left. -\,\frac{-\frac{2M}{c}+\frac{1}{c^{2}}}{3r_{h}^{3}} +\frac{\lambda }{2cr_{h}^{2}}+\frac{\lambda }{3c^{2}r_{h}^{3}}+\frac{\lambda \left( -\frac{2M}{c}+\frac{1}{c^{2}}\right) }{4cr_{h}^{4}}\right] \right\} .\quad \end{aligned}$$
(85)

The above result represents the greybody factor of SBHSQ, which is obtained by the Miller–Good transformation. It is obvious that the specific form of the greybody factor depends on some parameters which are related to the potential barrier. This is indeed the case that gives the greybody factor in terms of the transmission coefficient corresponding to the potential barrier. The result obtained in Eq. (85) is depicted in Fig. 15.

Fig. 15
figure 15

\(\sigma _{l}\left( \omega \right) \) versus \(\omega \) graph. The plots are governed by Eq. (85). For different c values, the corresponding greybody factors are illustrated. The physical parameters for this plot are chosen as \(M=l=1\)

Full size image

8 Conclusion

In this article, we have investigated the effect of quintessence field on the timelike geodesic and Hawking radiation in the background of SBHSQ. To see the effect on the motion for timelike geodesics, we have analyzed the radial and non-radial geodesics. We have then obtained an exact solution for a test particle falling from rest toward the singularity. It is shown that due to the presence of quintessence field around the Schwarzschild BH, the particles are delayed along the timelike radial geodesics. An increase in quintessence parameter causes more delay for the falling time of the particles. In non-radial timelike geodesics, it is shown that there are no stable circular orbits. All possible motion of orbits, i.e., unstable circular orbits, radially plunge and fly-by types of orbits, are obtained. Moreover, we have calculated the effective force acting on massive particles. It is shown that the force is always repulsive, which agrees with the observations in cosmology that the DE is associated with a repulsive force tending to accelerate the expansion of the Universe. The Lyapunov exponent for the unstable timelike circular orbits, which gives the instability timescale for the geodesics of the particle, is discussed. We observed that the instability of the timelike circular orbits is more in the case of SBHSQ in comparison with the SBH.

For the thermal radiation analysis of the SBHSQ, we have used the Miller–Good transformation for obtaining the greybody factor. By this way, we have uncovered the effect of the quintessence parameter on the Hawking radiation, which could be detected by an observer at spatial infinity. We also supported our results with graphics. In particular, we have found that the decrease in normalization parameter (c) causes the greybody factor to rapidly approach one.

In the near future, we want to generalize our work for the spinning particles and for the rotating spacetimes. Thus, we want to examine the quintessence effect on the geodesics and Hawking radiation in more depth.