Abstract
In this paper, nonlinear differential equation for a longitudinal fin (LF) heat transfer with thermal conductivity and heat generation that depends on temperature is solved numerically by employing Runge–Kutta technique of fourth-order (RK4) featuring shooting technique and analytically via a new modified analytical technique called Duan–Rach method. The physical model of the heat transfer was utilized to examine the influences of the thermogeometric parameters, heat transfer rate and variable thermal conductivity on the temperature profile and efficiency of LF. The obtained outcomes show that the temperature profile of fin, heat transfer and the efficiency of the fin are considerably impacted by the fin factor of thermogeometric. The analytical outcomes by a new efficient algorithm are compared with the numerical computations of the RK4 featuring shooting techniques and various available literature outcomes to achieve the precision of the proposed technique. Obtained results show obviously the fidelity of the suggested approach.
Graphic abstract
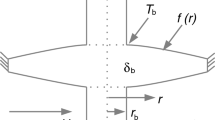
Flow model of longitudinal fin and the effect of thermogeometric parameter on dimensionless temperature distribution.

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fins are utilized to reinforce the transfer of heat among the basic surface and its convective, radiating or both in the surrounding medium. There have been considerable researches on the variable thermal factors conducted with fins working in transaction situations. The energy equilibrium has been developed for a differential fin component by Arslanturk [1]. The earned outcomes of nonlinear DE’s were dissolved by Adomian decomposition (ADM) method to assess the heat diffusion inside the fin. Coskun and Atay [2] utilized the variation iteration method (VIM) to investigate the convective proficiency of straight fins with thermal conductivity depending on temperature and made a comparison with ADM. From the findings of the finite element technique, he finished that VIM is a beneficial approach for the formulation and solution system compared to ADM, and the results earned by both techniques give rise to good results in the governing equation with sensible nonlinearity. Nevertheless, a high-order expression may be required with a highly nonlinear formulation. In order to resolve the same physical problem, Kulkarni and Joglekar [3] suggested a digital technology depended on minimization residue. The resulting nearby exact solution is utilized to measure the ailerons efficiency. If the thermal conductivity is unchanged, analytical methods validated the results. By contrast, when it is variable, they are supported by those of published literature. The suggested numerical method is reinforced by an excellent accord in every status. HAM (homotopy analysis method) to notice the effectiveness of convective rectal fins with variable thermal conductivity with temperature was investigated by Domairry and Fazeli [4]. The outcomes of HAM are examined with those of the precise solution and ADM which was studied by Arslanturk [1]. In dehumidifying environments, ADM was determined to assess the quality of a complete humid fin assembly [5]. To measure the leading force for the transfer of mass, a cubic equation among the moisture ratio of the saturated air and its temperature was adopted. The controlling equation of a fin structure is nonlinear with this relation. The execution parameters were provided as a function of various determination variables, namely efficiency of surface, and increment factor.
The inverse technique was analyzed by Das [6] for guessing the convective/conductive factor and the parameter of varying conductivity. The temperature distributions were determined from a forward/direct problem solution from a technique of decomposition relying on the Adomian framework. Aziz and Bouaziz [7] utilized the least-squares technique at the problem introduced by Aziz and Bouaziz [8], to achieve simple and precise terms for the thermal efficiency of a convective fin with a variable thermal conductivity; further, internal heat generation depends on temperature. The technique can be seen as a creative improvement in the optimal linearization (OLM) method. In this respect, many researchers have implemented numerical methods to resolve the nonlinear fin system. Certain of the related researches involving Duan et al. [9] addressed a temperature profile of a convective sequential fin with thermal conductivity depending on temperature utilizing MDM (modified decomposition method) as a new technique. Also, he expressed the efficiency of the fin with two parameters of a fin. These results make the parameter study of the heat transfer system significantly easier. In contrast, the undetermined ADM coefficients model has also been tested, but a temperature profile with any of the factors \( \beta \) and \( \psi \) has been found difficult to achieve. Utilizing an analytical technique named DTM (differential transformation method), an accurate and simple solution was provided by Poozesh et al. [10] for distribution of the convective–radiative oblong fins with varying thermal conductivities with temperature. A brief introduction of the definition of DTM was made, and the solutions of extremely nonlinear equations were then used. To verify the accuracy of the suggested technique, the data earned from DTM were compared to the findings of the numerical investigation.
The heat transfer rate in a fin with a longitudinal oblong shape with variable thermal conductivity with temperature and inner heat generation was conducted by Gangi et al. [11], utilizing FDM (finite difference method). Using 3D CFD (computation fluids dynamics) analysis and MATLAB DE’s solver, heat transfer features of a fin with variable thermal conductivity adopted on temperature were determined by Sevilgen et al. [12]. The calculations were carried out in two diverse cases with constant and linear functions for the property of thermal conductivity. The outcomes of the MATLAB and CFD were in excellent accord with the literature evidence. The nonlinear problem of fins has receipted substantial interest in last years for its practical implementations in heat exchangers, power breeders, semiconductors, solar thermal collectors and electronic devices [13]. With the support of MATLAB using fsolve, the constructed system of the nonlinear model resulting from discretization utilizing FDM was solved. The numerical outcomes were validated with a linear problem accurate solution. Fins are an effective solution for developing heat transfer among a hot surface to the surrounding medium [14].
Work on variable thermal conductivity and coefficient of heat transfer has been ongoing in the previous researches over the past few decades. The high nonlinear DE’s solutions were also constructed using various techniques [15,16,17,18]. The problem of the effect on the flow of MHD nanofluid through a nonlinear extending plate with a heat generation and chemically reactive species was discussed by Eid [19]. Unsteady flow of nanofluid past an extending wall in a porous material in the region of stagnation point was probed in [20] with chemical reaction. However, significant studies also involve thermal convection kinds of research with different approaches past various shapes [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. Dogonchi and Ganji [39] studied the DRA method to solve the flow equations of a power-law non-Newtonian liquid in an axisymmetric duct in a porous material. They provided a benchmarking with the numerical computations to check the precision. The time-dependent compressing flow of magnetic nanofluid among the endless parallel surfaces with radiation influence is examined by Dogonchi et al. [40] utilizing DRA. The DRA was utilized to analyze the heat transfer and a magnetohydrodynamic mixture nanofluid flow in a revolving system among two plates by Chamkha et al. [41]. Liu et al. [42] suggested a triangular longitudinal fin to improve the shell and tube solidification quality of the LHTES system. In addition, Kurşun [43] based his research on the thermal quality of the parabola receptor tube for the internal longitudinal fin with the straight and sinusoidal side layer. Gireesha et al. [44] presented Darcy’s hybrid nanofluid flow model, with the simultaneous effect of thermal radiation and natural convection, on porous longitudinal fin at a constant velocity. Sobamowo [45] compared an exact solution using Laplace transform with Galerkin finite element method of transient thermal behavior of convective-radiative cooling fin under convective conditions. Onyejekwe [46] probed a radial fin numerical solution using the boundary integral technique combined with domain discretification, with temperature-based thermal conductivity. Sobamowo et al. [47] implemented FVM with thermal dependent characteristics and internal heat generation to solve the problem of heat transfer in a longitudinal rectangular fin.
The originality of this research is the proposed new analytical algorithm of computation named Duan–Rach method (DRA). Thereafter, the proposed algorithm is tested by solving the nonlinear problem of LF heat transfer with thermal conductivity and heat generation depending on temperature. To accomplish the precision of the suggested technique, the findings were compared with the results earned by the numerical solution via RK4 featuring the shooting technique and other methods reported in the literature such as FVM, FDM and DTM.
2 Mathematical description
The thermal model development is focused on the study of the fin energy equilibrium. The analysis is done with some simplifying assumptions in mind [14]. The subsequent considerations have been made in model design.
- 1.
The heat flux in the fin remains constant with time and its temperature.
- 2.
The medium temperature around the fin is consolidated.
- 3.
Nothing is there of resisting to touch where the base of fin meets the primary surface.
- 4.
The fin’s base temperature is unified.
- 5.
The fin thicker is little compared with its length and width so that temperature differences via the thicker of the fin and the transfer of heat from the fin edges are tiny compared to the heat that leaves its sidelong surface.
According to previous considerations, an upright fin of thermal conductivity \( k\left( T \right) \) depends on temperature, variable internal heat source with temperature per unit volume \( Q\left( T \right) \), thickness \( \delta \), length \( L \) and downside, and upside surfaces are subjected to environmentally convective at ambient temperature \( T_{\infty } \) alternatively and fixed coefficient of heat transfer (\( h \)) as displayed in Fig. 1.
The \( x \) dimension refers to altitude coordinate which has its origin at the base of the fin and a positive direction from a base of the fin to a fin apex and thence expressed as next.
The heat conduction rate into the volume at x = heat conduction rate from the volume at \( x \)
The following equation mathematically expresses the thermal energy equilibrium:
namely,
when \( {\text{d}}x \to 0 \), Eq. (4) is reduced to Eq. (5)
where P is the fin perimeter and \( T_{\infty } \) is temperature of ambient. By using heat conduction equation from Fourier’s law:
here A is the fin sector area. From Eq. (6) into Eq. (5) we obtain:
For more simplification, Eq. (7) yields a governing DE of the fin taken the form:
so the corresponding boundary conditions are:
where \( T_{0} \) is the fin base temperature. The thermal conductivity and heat transfer rate are dependent on the temperature at numerous industrial implementations. Furthermore, the thermal characteristics based on the temperature and internal heat source are taken the form:
where the parameter \( \lambda \) is the thermal conductivity and \( \psi \) is internal heat generation. By using Eqs. (10) and (11) into Eq. (8), to obtain
by utilizing the next dimensionless transformations in Eq. (12) [14]:
where \( X \) is the nondimensional length, \( T_{b} \) is the fin base temperature, \( M \) is the nondimensional factor of the thermogeometric fin, \( Q \) is nondimensional heat transfer, \( \beta \) is a nonlinear parameter of thermal conductivity, and \( \gamma \) is nondimensional heat generation parameter. We obtain the nondimensional DE (Eq. 14) with the boundary conditions as follows:
with the related boundary conditions:
3 Characterization of the Duan–Rach (DRA) technique
Given the subsequent general nonlinear DE:
\( L = \frac{{{\text{d}}^{n} }}{{{\text{d}}x^{n} }} \) is the third-order operator of derivative, N is the nonlinear operator, and f is the input of system.
Related to the set of mixed boundary conditions of Dirichlet and Neumann:
By assuming \( L^{ - 1} \) is the operator of inverse that constitutes a n-fold integrate for the nth order of the operator of derivative L.
We take the inverse linear operator as:

where \( \zeta \) is a described value in the selected interval. Thus, we obtain:
Using the \( L^{ - 1} \) inverse operator on two sides of (16) results in:
By differentiating Eq. (19), therefore putting \( \eta = \eta_{2} \) and resolving \( u^{\prime\prime}\left( \zeta \right) \), one obtains:
Substituting from Eq. (21) into Eq. (20) produces:
The solution \( y \) of Eq. (1) can be built by the components sum determined by the next nonlinearity infinite series:
In addition, the following nonlinear definition is given as:
here \( A_{n} \)s are named as the polynomials of Adomian. The recursive equation that determines the polynomials of Adomian is obtained as follows:
The examined formula solution can be obtained as a form of infinite series by DRA recursive technique:
Now, we have the final solution:
4 Implementation of the Duan–Rach (DRA) method
In order to implement DRA technique, the linear and inverse operators are given by:
DEs of this problem (14) and (15), after applying Eq. (28), become:
where \( B \) is the nonlinear term. Operating with \( L_{1}^{ - 1} \) on Eq. (20) and after applying boundary conditions, we obtain:
where:
By putting \( \eta = 1 \) in Eq. (30), we have:
where \( \alpha \) is the parameter of fin shape and
Substituting Eq. (32) into Eq. (30) yields
where \( T_{0} \) is given by:
DRA method describes the solution terms as follows:
Finally, it is possible to express the approximate solution of the studied problem as:
Here the efficiency of fin \( e_{n} \) specified as the ratio between the rates of actual fin heat transfer and that which would be gained with a fin of constant temperature (the surface temperature of base) and is written as an integral:
5 Results and discussion
Heat transfer is a thermal engineering discipline which deals with thermal power generation, conversion and consumption among physical systems. You will experience any of the heat transfer procedure at every moment of your everyday life. Heat transfer is a wide scientific field, and therefore, numerous studies in various fields of heat transfer research are carried out every year. Between the common issues that are widely investigated, heat transfer from expanded fin holds out with its broad idea and quickly evolving implementations. The fins have been used extensively, particularly in thermal technology applications where cooling is important, to improve the rate of heat transfer from a hot surface. In addition to classic implementations like internal burning engines, heat exchangers and superchargers, fins also demonstrate efficiency in heat-exclusion schemes in cooling of electronic constituents and space vehicles.
For the various thermogeometric of a wall, thermal conductivity parameter and convective heat transfer parameter as depicted in Figs. 2, 3, 4 and 5, the nondimensional temperature profile decreases monotonously along the length of fin. The more heat the fin is connected, and the more thermal energy is transferred to the surrounding medium efficiently for high values in the factor of thermogeometric \( M \). The fin heat often flows along with a lower rate of temperature around the base region in the event of a minimal thermal loss from the fin point (isolation tip).
Figure 2 demonstrates that the changes in nondimensional temperature with nondimensional length along with the thermogeometric factor influence the straightened fin with an isolated tip. It is remarked that when the thermogeometric factor rises, the convective heat transfer (heat transfer rate) through the fin boosts, while the fin temperature becomes steeper (drops quicker). This leads to the high heat flow rate at the base that is reflected. The heat transfer ratio of convection to conduction at the fin base (\( h_{\text{b}} /K_{\text{b}} \)) increases. Therefore, the temperature through the fin declines, particularly at its tip, namely the end of tip temperature reduces as \( M \) rises. The profile has the highest gradient of temperature at \( M = 1.0 \), but the value derived from the lower thermal conductivity value is much higher than the other M values in the profiles. This shows that a low thermogeometric parameter value favors thermal performance or effectiveness since the goal is to reduce the temperature through the length of fin if the best-enabled perception for the \( T = T_{\text{b}} \) is found.
Figure 3 indicates the variance of the nondimensional temperature in the convective longitudinal fin with an isolated tip with a nondimensional length. The results of the thermogeometric \( M \) and thermal conductivity \( Q \) impacts on the nondimensional temperature profile are described in Fig. 4. It is apparent that from Fig. 4, as the thermogeometric factor improves, the heat transfer rate also rises through the fin and more heat is transported by conduction. This would increase the distribution of temperature in the fin, thus boosting the heat transfer.
Figures 4 and 5 show the influences of internal heat generation on the temperature profile. The fin temperature gradient declines with increasing the internal heat generation factor. This results in the increase in internal heat generation rate; the fin thermal performance reduces (Fig. 6) as a function of the nonlinear term. Nevertheless, the graphs report that the nondimensional temperature differences of the fin length rise with the change in the thermogeometric parameter.
Figure 7 displays the variation in the fin efficiency with the thermal conductivity coefficient. The performance of the fin increases with the rising thermal conductivity factor. On the other hand, this efficiency is shown to increase as the thermogeometric parameter decreases.
The analytical solution by DRA (Duan–Rach method) was validated when compared with the RK4 technique and with the well-known results in the literature view as outlined in Table 1 and Fig. 8. It can be seen that the DRA method is extremely precise and matches perfectly with the Runge–Kutta fourth order and other techniques in the above literature such as FVM, FDM and DTM.
Comparison between DRA technique and the results in [47] for \( T \) when \( B = 0.5,\;Q = 0.4 \) and \( \gamma = 0.6 \)
6 Conclusion
In this work, a new modified analytical technique called Duan–Rach method (DRA) was utilized to resolve the nonlinear DE of heat transfer in LF with variable thermal conductivity and internal heat generation depending on temperature. The actual outcomes were compared with those previously obtained findings using the numerical Runge–Kutta fourth-order method due to verification of the precision of the suggested technique. The analysis of the findings indicated an outstanding agreement between the analytical technique and the numerical outcomes. This technique allows us to define a solution for the calculation of undefined factors without using numerical methods.
Abbreviations
- DE’s:
-
Differential equations
- LF:
-
Longitudinal fin
- RK4:
-
Runge–Kutta method of fourth order
- DRA:
-
Duan–Rach method
- ADM:
-
Adomian decomposition method
- VIM:
-
Variation iteration method
- HAM:
-
Homotopy analysis method
- OLM:
-
Optimal linearization method
- MDM:
-
Modified decomposition method
- DTM:
-
Differential transformation method
- FVM:
-
Finite volume method
- CFD:
-
Computation fluids dynamics
References
C. Arslanturk, A decomposition method for fin efficiency of convective straight fins with temperature-dependent thermal conductivity. Int. Commun. Heat Mass Transf. 32, 831–841 (2005)
S.B. Coşkun, M.T. Atay, Fin efficiency analysis of convective straight fins with temperature dependent thermal conductivity using variational iteration method. Appl. Therm. Eng. 28, 2345–2352 (2008)
D.B. Kulkarni, M.M. Joglekar, Residue minimization technique to analyze the efficiency of convective straight fins having temperature-dependent thermal conductivity. Appl. Math. Comput. 215, 2184–2191 (2009)
G. Domairry, M. Fazeli, Homotopy analysis method to determine the fin efficiency of convective straight fins with temperature-dependent thermal conductivity. Commun. Nonlinear Sci. Numer. Simul. 14, 489–499 (2009)
B. Kundu, A. Miyara, An analytical method for determination of the performance of a fin assembly under dehumidifying conditions: a comparative study. Int. J. Refrig 32, 369–380 (2009)
R. Das, A simplex search method for a conductive–convective fin with variable conductivity. Int. J. Heat Mass Transf. 54, 5001–5009 (2011)
A. Aziz, M.N. Bouaziz, A least squares method for a longitudinal fin with temperature dependent internal heat generation and thermal conductivity. Energy Convers. Manage. 52(8–9), 2876–2882 (2011)
A. Aziz, M.N. Bouaziz, Simple and accurate solution for convective-radiative fin with temperature dependent thermal conductivity using double optimal linearization. Energy Convers. Manage. 51, 2776–2782 (2010)
J.-S. Duan, Z. Wang, S.-Z. Fu, T. Chaolu, Parametrized temperature distribution and efficiency of convective straight fins with temperature-dependent thermal conductivity by a new modified decomposition method. Int. J. Heat Mass Transf. 59, 137–143 (2013)
S. Poozesh, S. Nabi, M. Saber, S. Dinarvand, B. Fani, The efficiency of convective-radiative fin with temperature-dependent thermal conductivity by the differential transformation method. Res. J. Appl. Sci. Eng. Technol. 6(8), 1354–1359 (2013)
D.D. Gangi, A.S. Dogonchi, Analytical investigation of convective heat transfer of a longitudinal-fin with temperature-dependent thermal conductivity, heat transfer coefficient and heat generation. Int. J. Phys. Sci. 9(21), 466–474 (2014)
G. Sevilgen, A numerical analysis of a convective straight fin with temperature-dependent thermal conductivity. Therm. Sci. 21(2), 939–952 (2017)
I. Tabet, M. Kezzar, K. Touafeka, N. Bellel, S. Gheriebc, A. Khelifa, M. Adouanea, Adomian decomposition method and Padé approximation to determine fin efficiency of convective straight fins in solar air collector. Int. J. Math. Model. Comput. 5(4), 335–346 (2015)
M.G. Sobamowo, Analysis of convective longitudinal-fin with temperature-dependent thermal conductivity and internal heat generation. Alex. Eng. J. 56(1), 1–11 (2017)
F.M. Hady, F.S. Ibrahim, S.M. Abdel-Gaied, M.R. Eid, Influence of yield stress on free convective boundary-layer flow of a non-Newtonian nanofluid past a vertical plate in a porous medium. Mech. Sci. Technol. 25(8), 2043–2050 (2011)
F.M. Hady, F.S. Ibrahim, S.M. Abdel-Gaied, M.R. Eid, Boundary-layer non-Newtonian flow over a vertical plate in a porous medium saturated with a nanofluid. Appl. Math. Mech. Eng. Ed. 32(12), 1577–1586 (2011)
F.M. Hady, F.S. Ibrahim, S.M. Abdel-Gaied, M.R. Eid, Radiation effect on viscous flow of a nanofluid and heat transfer over a non-linearly stretching sheet. Nanoscale Res. Lett. 7, 229–242 (2012)
F.M. Hady, M.R. Eid, M.A. Ahmed, A nanofluid Flow in a non-linear stretching surface saturated in a porous medium with yield stress effect. Appl. Math. Inf. Sci. Lett. 2(2), 43–51 (2014)
M.R. Eid, Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation. J. Mol. Liq. 220, 718–725 (2016)
M.R. Eid, Time-dependent flow of water-NPs over a stretching sheet in a saturated porous medium in the stagnation-point region in the presence of chemical reaction. J. Nanofluids 6(3), 550–557 (2017)
M.R. Eid, S.R. Mishra, Exothermically reacting of non-Newtonian fluid flow over a permeable non-linear stretching vertical surface with heat and mass fluxes. Comput. Therm. Sci. 9(4), 283–296 (2017)
M.R. Eid, K.L. Mahny, Unsteady MHD heat and mass transfer of a non-Newtonian nanofluid flow of a two-phase model over a permeable stretching wall with heat generation/absorption. Adv. Powder Technol. 28(11), 3063–3073 (2017)
M.R. Eid, A. Alsaedi, T. Muhammad, T. Hayat, Comprehensive analysis of heat transfer of gold-blood nanofluid (Sisko-model) with thermal radiation. Results Phys. 7, 4388–4393 (2017)
M.R. Eid, K.L. Mahny, Flow and heat transfer in a porous medium saturated with a Sisko nanofluid over a non-linearly stretching sheet with heat generation/absorption. Heat Transfer-Asian Res. 47, 54–71 (2018)
M.R. Eid, K.L. Mahny, T. Muhammad, M. Sheikholeslami, Numerical treatment for Carreau nanofluid flow over a porous nonlinear stretching surface. Results Phys. 8, 1185–1193 (2018)
A. Wakif, Z. Boulahia, F. Ali, M.R. Eid, R. Sehaqui, Numerical analysis of the unsteady natural convection MHD Couette nanofluid flow in the presence of thermal radiation using single and two-phase nanofluid models for Cu–water nanofluids. Int. J. Appl. Comput. Math. 4, 81 (2018)
M.R. Eid, O.D. Makinde, Solar radiation effect on a magneto nanofluid flow in a porous medium with chemically reactive species. Int. J. Chem. React. Eng. 16(9), 20170212 (2018)
T. Muhammad, D. Lu, B. Mahanthesh, M.R. Eid, M. Ramzan, A. Dar, Significance of Darcy–Forchheimer porous medium in nanofluid through carbon nanotubes. Commun. Theor. Phys. 70, 361–366 (2018)
A.F. Al-Hossainy, M.R. Eid, M.S. Zoromba, Structural, DFT, optical dispersion characteristics of novel [DPPA-Zn-MR (Cl)(H2O)] nanostructured thin films. Mater. Chem. Phys. 232, 180–192 (2019)
A.F. Al-Hossainy, M.R. Eid, MSh Zoromba, SQLM for external yield stress effect on 3D MHD nanofluid flow in a porous medium. Phys. Scr. 94, 105208 (2019)
M.S. Zoromba, M. Bassyouni, M. Abdel-Aziz, A.F. Al-Hossainy, N. Salah, A. Al-Ghamdi, M.R. Eid, Structure and photoluminescence characteristics of mixed nickel–chromium oxides nanostructures. Appl. Phys. A 125(9), 642 (2019)
M. Kezzar, N. Boumaiza, I. Tabet, N. Nafir, Combined effects of ferromagnetic particles and magnetic field on mixed convection in the Falkner–Skan system using DRA. Int. J. Numer. Meth. Heat Fluid Flow 29(2), 814–832 (2019)
S. Lahmar, M. Kezzar, M.R. Eid, M.R. Sari, Heat transfer of squeezing unsteady nanofluid flow under the effects of an inclined magnetic field and variable thermal conductivity. Phys. A Stat. Mech. Appl. 540, 123138 (2019)
M.R. Eid, K. Mahny, A. Dar, T. Muhammad, Numerical study for Carreau nanofluid flow over a convectively heated nonlinear stretching surface with chemically reactive species. Phys. A Stat. Mech. Appl. 540, 123063 (2019)
M. Waqas, S. Jabeen, T. Hayat, M.I. Khan, A. Alsaedi, Modeling and analysis for magnetic dipole impact in nonlinear thermally radiating Carreau nanofluid flow subject to heat generation. Magn. Magn. Mater. 485, 197–204 (2019)
M. Waqas, S.A. Shehzad, T. Hayat, M.I. Khan, A. Alsaedi, Simulation of magnetohydrodynamics and radiative heat transport in convectively heated stratified flow of Jeffrey nanofluid. Phys. Chem. Solids 133, 45–51 (2019)
M. Waqas, Simulation of revised nanofluid model in the stagnation region of cross fluid by expanding-contracting cylinder. Int. J. Numer. Meth. Heat Fluid Flow 9(5), 1183–1191 (2019)
M. Waqas, M.I. Khan, T. Hayat, M.M. Gulzar, A. Alsaedi, Transportation of radiative energy in viscoelastic nanofluid considering buoyancy forces and convective conditions. Chaos Solit. Fract. 130, 109415 (2020)
A.S. Dogonchi, D. Ganji, Investigation of heat transfer for cooling turbine disks with a non-Newtonian fluid flow using DRA. Case Stud. Therm. Eng. 6, 40–51 (2015)
A. Dogonchi, K. Divsalar, D. Ganji, Flow and heat transfer of MHD nanofluid between parallel plates in the presence of thermal radiation. Comput. Methods Appl. Mech. Eng. 310, 58–76 (2016)
A.J. Chamkha, A. Dogonchi, D. Ganji, Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and Joule heating. AIP Adv. 9(2), 025103 (2019)
S. Liu, H. Peng, Z. Hu, X. Ling, J. Huang, Solidification performance of a latent heat storage unit with innovative longitudinal triangular fins. Int. J. Heat Mass Transfer 138, 667–676 (2019)
B. Kurşun, Thermal performance assessment of internal longitudinal fins with sinusoidal lateral surfaces in parabolic trough receiver tubes. Renew. Energy 140, 816–827 (2019)
B. Gireesha, G. Sowmya, M.I. Khan, H.F. Öztop, Flow of hybrid nanofluid across a permeable longitudinal moving fin along with thermal radiation and natural convection. Comp. Methods Prog. Biomed. 185, 105166 (2019)
M. Sobamowo, Finite element analysis of transient thermal performance of a convective-radiative cooling fin: effects of fin tip conditions and magnetic field. Res. Eng. Struct. Mater. 5(1), 43 (2019)
O.O. Onyejekwe, Simplified integral calculations for radial fin with temperature-dependent thermal conductivity. Appl. Math. Phys. 7(3), 513–526 (2019)
G.M. Sobamowo, B.Y. Ogunmola, G. Nzebuka, Finite volume method for analysis of convective longitudinal fin with temperature-dependent thermal conductivity and internal heat generation. Def. Diffus. Forum 374, 106–120 (2017)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kezzar, M., Tabet, I. & Eid, M.R. A new analytical solution of longitudinal fin with variable heat generation and thermal conductivity using DRA. Eur. Phys. J. Plus 135, 120 (2020). https://doi.org/10.1140/epjp/s13360-020-00206-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-020-00206-0