1 Introduction

The cavity optomechanical system offers a promising platform for investigating the interaction between light and mechanical oscillators [1, 2]. This interaction arises due to the radiation pressure acting between the mobile mirror and the cavity field within the cavity [3,4,5,6,7]. During the past two decades, cavity optomechanical systems have garnered significant interest, particularly in the realm of quantum information processing. They have been explored for various fascinating quantum tasks, such as achieving ground-state cooling of mechanical modes [8, 9], creating mechanical quantum superpositions [10], realizing entanglement between mechanical and optical modes in steady state [11,12,13], quantum measurement’s precision [14, 15] and gravitational-wave detectors [16, 17]. The exchange of quantum correlations among states within optomechanical systems holds great significance [18,19,20]. This importance stems primarily from the pivotal role that entanglement (non-separability) plays in enabling and augmenting quantum information processing, such as in the case of quantum teleportation [21]. Superdense coding [22], telecloning [23] and quantum cryptography [24].

Quantum entanglement represents a quantum property not present in classical physics [25]. This phenomenon is particularly notable in microscopic systems [26], acting as a non-local behavior of quantum correlations between spatially separated systems. The interaction between the system and its environment leads to the degradation of quantum correlations. In many studies of the entanglement of distant mechanical mirrors, squeezed light was used as an available resource in order to entangle the two distant mirrors [20, 27]. Recently, several approaches have been proposed to enhance quantum correlations in steady states among mechanical modes and to investigate the entanglement between two Fabry-Pérot cavities. One such method involves incorporating a parametric amplifier inside the cavities, as proposed in references [28,29,30], establishing a coupling between optical modes through the photon hopping process [31,32,33,34], and a coupling between mechanical modes through a phonon tunneling process [32, 35, 36], etc. Motivated by all these advanced results, we propose a system in which the optical modes are coupled by photon hopping and the mechanical modes are coupled by phonon tunneling. We also pumped the cavities with squeezed light, and inside the cavities, we injected a parametric amplifier. To find an appropriate choice between these two coupling strengths and to make entanglement more reliant against thermal effects in order to enhance quantum correlations, it is worth noting that the photon hopping process has been demonstrated to be a degrading factor for quantum correlations in optomechanical systems of this kind [32, 33]. The interaction between the system and its surrounding environment leads to the dissipation of quantum correlations, and under specific conditions, this phenomenon can manifest suddenly. This is referred to as entanglement sudden death (ESD) [37].This method, which combines the insertion of a parametric amplifier inside the cavities [28,29,30], couples the mechanical modes via phonon tunneling and connects the optical modes by photon hopping [31,32,33,34].

In this manuscript, we present a method for producing, enhancing, and assessing quantum entanglement between two mechanical modes within a dual Fabry-Pérot cavity optomechanical system, employing the rotating wave approximation (RWA). The two cavities are spatially separated, and each Fabry-Pérot cavity contains a parametric amplifier (PA) to enhance the entanglement of the mechanical resonators by generating squeezed light [38]. The generated entanglement is quantified by the logarithmic negativity. We show that the degree of shared entanglement among the mechanical resonators is affected by the temperature, the parameter of squeezed light and the gain of the PA. By analyzing the relationship between entanglement and coupling strengths, we discover that entanglement is strengthened within a certain range of values for the photon hopping process coupling strength but weakens as the photon tunneling coupling strength increases. Also, entanglement can be enhanced by adjusting the gain of the PA.

The paper’s structure is outlined as follows: In Sect. 2, we outline the model under consideration and give the expression of the Hamiltonian and the corresponding quantum Langevin equations for mechanical and optical modes. In Sect. 3, we introduced the EPR operators to obtain the covariance matrix in the steady state. In Sect. 4, we provide the explicit expression of logarithmic negativity used to quantify mechanical entanglement. Section 5 delves into the evolution of this measure for mechanical modes, considering various influencing factors. Ultimately, Sect. 6 presents the concluding remarks of the paper.

2 Model and dynamical equations

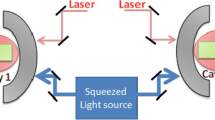
The system under consideration, as shown in Fig. 1, is composed of two spatially separated cavities; each of those cavities are consists of a movable mirror \((M_{j},j=1,2)\) and fixed mirror \((FM_{j},j=1,2) \). The cavities are driven by coherent laser sources and pumped by squeezed light. Optical modes \(c_{j}\) are coupled by a photon hopping process (PH), and mechanical modes \(a_{j}\) are coupled by a phonon tunneling process [36]. Inside each of the cavities, we have a parametric amplifier to generate squeezed light [38], and whose presence promotes optomechanical cooling [39].

Fig. 1
figure 1

a Schematics of two optomechanical cavities spatially separated. Both cavities are driven by coherent laser sources and pumped by squeezed light. Optical modes \(c_{j}\) (\(j=1,2\)) are coupled by a photon hopping process (PH), and mechanical modes \(a_{j}\) (\(j=1,2\)) are coupled by a phonon tunneling process. b The various coupling strengths in the system \(\beta \) are the coupling rate of phonon tunneling process, \(\alpha \) is the coupling force of photon hopping (PH), \(\mu _{j}\) represents the coupling between the jth mechanical mode and the optical mode, and each cavity has inside a parametric amplifier

Full size image

The Hamiltonian describing the system writes as

$$\begin{aligned} H= H_{Opm}+H_{Mm}+H_{In}+H_{Las}+H_{PA} +H_{\alpha }+H_{\beta }\nonumber \\ \end{aligned}$$
(1)

where \(H_{Mm}= \hbar \sum _{j=1}^{2} \omega _{{M}_{j}}a_{j}^{+}a_{j} \) and \(H_{Opm}= -\hbar \sum _{j=1}^{2} \Delta _{j}c_{j}^{+}c_{j}\) are the energy of mechanical and optical modes, respectively, and \(\Delta _j=\omega _{\ell _j}-\omega _{c_j}\) is the input-cavity detuning, \(\omega _{c_{j}}\) are the frequencies inside each cavity, the parameters \(\omega _{M_{j}}\) are the frequencies of movable mirror and \( \omega _{l_{j}}\) are the frequencies of the jth input field. The operators \(c_{j}(c_{j}^{+})\) and \(a_{j}(a_{j}^{+})\) represent the annihilation (creation) operators of the jth cavity optical modes and mechanical modes, respectively, they satisfy the following canonical commutation \(\left[ a_j, a_j^{+}\right] =1; \left[ c_j,c_j^{+}\right] =1\) \((j=1,2)\). \(H_{In}= -\hbar \sum _{j=1}^{2}\mu _{j}c_{j}^{+}c_{j}(a_{j}^{+}+a_{j})\) is the energy of optomechanical coupling via radiation pressure where \( \mu _{j}=\frac{\omega _{c_j}}{L_j} \sqrt{\frac{\hbar }{m_j \omega _{M_j}}}\) represents the coupling between the jth mechanical mode and the intensity of optical mode [1], \(L_j\) being the jth cavity length and \( m_{j}\) the jth mass of the movable mirror [1]. \(H_{Las}=\hbar \sum _{j=1}^{2}(c_{j}^{+}\upsilon _{j}\text {e}^{i\varphi _{j}}+c_{j}\upsilon _{j}\text {e}^{-i\varphi _{j}} )\) describes the energy of optical driving, with \( \varphi _{j}\) and \( \upsilon _{j}=\sqrt{\frac{2 \Gamma _j p_j}{\hbar \omega _{l_j}}}\) \((j=1,2)\) are, respectively, the phase and the amplitude of the input field where \(\Gamma _j\) is the jth cavity damping rate and \( p_j\) is the drive pump power of the jth laser. The terms \(H_{PA}= i\hbar \sum _{j=1}^{2}\lambda _{j}(\text {e}^{i \theta } c_{j}^{{+^{2}}}\text {e}^{-2i \omega _{ M_{j}}t}-\text {e}^{-i \theta } c_{j}^{{^{2}}}\text {e}^{2i \omega _{Mj}t})\) and \(H_{\alpha }= -\hbar \alpha (c_{1}^{+}c_{2}+c_{2}^{+}c_{1})\) express, respectively, the coupling between the optical modes inside the cavities, parametric amplifier and the photon hopping process where \(\alpha \) is the coupling strength of the phonon hopping process, \(\lambda _{j}\) and \( \theta _{j}\) are, respectively, the gain and the phase of the jth pump field driving the parametric amplifier which is related to the pump driving the PA. By doing this, the pump field driving the PA at frequency \( 2(\omega _{ M_{j}}+\omega _{ l_{j}}) \) interacts with the second-order nonlinear optical crystal, i.e., the signal and the idler have identical frequency \( (\omega _{ M_{j}}+\omega _{ l_{j}}) \) [28, 40]. The last term \(H_{\beta }= - \hbar \beta (a_{1}^{+}a_{2}+ a_{2}^{+}a_{1})\) is the energy of coupling between movable mirrors via photon tunneling process and \(\beta \) is the coupling force between the moving mirrors trough a phonon tunneling process. The dynamics of mechanical and the optical modes satisfy the following nonlinear Langevin equation, given by

$$\begin{aligned} \dot{a_1}= & {} -\left( \frac{\gamma _1}{2}+\textrm{i} \omega _{M_1}\right) a_1+\textrm{i} \mu _1 c_1^{+} c_1+\textrm{i} \beta a _{2}+\sqrt{\gamma _1} a_1^{i n} \nonumber \\ \end{aligned}$$
(2)
$$\begin{aligned} \dot{a_2}= & {} -\left( \frac{\gamma _2}{2}+\textrm{i} \omega _{M_2}\right) a_2+\textrm{i} \mu _2 c_2^{+} c_2+\textrm{i} \beta a _{1}+\sqrt{\gamma _2} a_2^{i n}\nonumber \\ \end{aligned}$$
(3)
$$\begin{aligned} \dot{c_1}= & {} -\left( \frac{\Gamma _1}{2}-\textrm{i} \Delta _1\right) c_1+\textrm{i} \mu _1 c_1\left( a_1^{+}+a_1\right) -\textrm{i} \vartheta _1 \textrm{e}^{\textrm{i} \varphi _1}\nonumber \\{} & {} +2 \lambda _1 \textrm{e}^{\textrm{i} \theta } c_1^{+} \textrm{e}^{-\textrm{i} 2 \omega _{M_1} t}+\textrm{i} \alpha c_2+\sqrt{\Gamma _1} c_1^{i n} \end{aligned}$$
(4)
$$\begin{aligned} \dot{c_2}= & {} -\left( \frac{\Gamma _2}{2}-\textrm{i} \Delta _2\right) c_2+ \textrm{i} \mu _2 c_2\left( a_2^{+}+a_2\right) -\textrm{i} \vartheta _2 \textrm{e}^{\textrm{i} \varphi _2}\nonumber \\{} & {} +2 \lambda _2 \textrm{e}^{\textrm{i} \theta } c_2^{+} \textrm{e}^{-\textrm{i} 2 \omega _{M_2} t}+\textrm{i}\alpha c_{1}+\sqrt{\Gamma _2} c_2^{i n} \end{aligned}$$
(5)

where \( \gamma _{j}\) is the dissipation rate of the jth movable mirror. The squeezed-vacuum operators \(c_j^{i n}\) and \( c_j^{{+}{i n}}\) verify the following nonzero correlations relations [41]

$$\begin{aligned} \begin{aligned}&\left\langle c_j^{i n }(t)c_j^{ {i n } {\dagger }}(t')\right\rangle = (\mathcal {R}+1)\delta (t-t') \\&\left\langle c_j^{{i n } {\dagger }} (t)c_j^{i n }(t')\right\rangle = \mathcal {R} \delta (t-t')\\&\left\langle c_j^{i n }(t)c_{j'}^{i n }(t')\right\rangle =\mathcal {V} \textrm{e}^{-\textrm{i} \omega _{M}(t+t')}\delta (t-t') \quad ;\quad \textrm{j} \ne \mathrm {j'} \\&\left\langle c_j^{{i n } {\dagger }} (t)c_{j'}^{{i n } {\dagger }} (t')\right\rangle =\mathcal {V} \textrm{e}^{\textrm{j} \omega _{M}(t+t')} \delta (t-t') \quad ; \quad \textrm{j} \ne \mathrm {j'} \end{aligned} \end{aligned}$$
(6)

where \(\mathcal {R}= \sinh ^{2}(r) \), \( \mathcal {V}= \sinh (r)\cosh (r)\) and r stands for the squeezing parameter characterizing the squeezed light. The terms \(a_j^{i n}\) represent the jth noise operators describing the coupling between the movable mirror and its own environment, and it can be presumed that the mechanical baths are Markovian, \(a_j^{i n}\) and \(a_j^{{i n}{\dagger }}\) has zero-mean value and we have [42, 43]

$$\begin{aligned} \begin{aligned}&\left\langle a_{j}^{in}(t) a_{j}^{{in}{\dagger }}\left( t^{\prime }\right) \right\rangle =\left( n_{{th}_{j}}+1\right) \delta \left( t-t^{\prime }\right) .\\&\left\langle a_{j}^{{in} {\dagger }}(t) a_{j}^{{in}{\dagger }}(t^{\prime }) \right\rangle =n_{{th}_{j}} \delta \left( t-t^{\prime }\right) \end{aligned} \end{aligned}$$
(7)

where \(n_{{th}_{j}}=\left[ \exp \left( \hbar \omega _{M_j} /\left( k_B T_j\right) \right) -1\right] ^{-1} \) is the photon number in the jth cavity, \(k_{B}\) is the Boltzmann constant. The nonlinear quantum Langevin equations are in general non-solvable analytically, for that we use the following linearization scheme \(\mathcal {T}_{j}=\left\langle \mathcal {T} _{j}\right\rangle + \delta \mathcal {T}_{j} \) where \(\mathcal {T}_{j}\) replace the two operators \( a_{j}\) and \(c_{j}\), \(\left\langle \mathcal {T} _{j}\right\rangle \) are the mean value in the steady state and \(\delta \mathcal {T}_{j}\) are the operators of fluctuation [20]. The values at steady-state are given by

$$\begin{aligned}{} & {} \left\langle a _{1}\right\rangle = \frac{\textrm{i}\mu _{1}\mathcal {I}_{2}|\left\langle c_{1}\right\rangle |^{2}-\beta \mu _{2}|\left\langle c_{2}\right\rangle |^{2}}{\mathcal {I}_{2}\mathcal {I}_{1}+\beta ^{2}} \quad ; \nonumber \\{} & {} \left\langle a _{2}\right\rangle = \frac{\textrm{i}\mu _{2}\mathcal {I}_{1}|\left\langle c_{2}\right\rangle |^{2}-\beta \mu _{1}|\left\langle c_{1}\right\rangle |^{2}}{\mathcal {I}_{1}\mathcal {I}_{2}+\beta ^{2}} \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \left\langle c _{1}\right\rangle = \frac{\textrm{i}\upsilon _{1}\mathcal {B}_{2}\textrm{e}^{\textrm{i}\varphi _{1}}+\alpha \upsilon _{2}\textrm{e}^{\textrm{i}\varphi _2}}{\mathcal {B}_{2}\mathcal {B}_{1}+\alpha ^{2}} \quad ;\nonumber \\{} & {} \left\langle c _{2}\right\rangle = \frac{\textrm{i}\upsilon _{2}\mathcal {B}_{1}\textrm{e}^{\textrm{i}\varphi _{2}}+\alpha \upsilon _{1}\textrm{e}^{\textrm{i}\varphi _1}}{\mathcal {B}_{1}\mathcal {B}_{2}+\alpha ^{2}} \end{aligned}$$
(9)

With \( \mathcal {I}_{j} = \textrm{i} \omega _{M_ j}+ \frac{\gamma _{j}}{2} \), \( \mathcal {B}_{j}= - \frac{\Gamma _{j}}{2}+ \textrm{i}\Delta _j^{\prime } \) (\(j=1,2\)) and \( \Delta _j^{\prime }=\Delta _j+\mu _j\left( \left\langle a _{j}^{+}\right\rangle + \left\langle a _{j}\right\rangle \right) \). We consider that the two cavities are identical, with equal temperature \(T_1=T_2=T \left( n_{t h_1}=n_{t h_2}=n_{t h}\right) \), and then \( \lambda _1=\lambda _2=\lambda \), \( \alpha _1=\alpha _2 = \alpha \), \( m_1=m_2= m\), \(\omega _{\ell _1}=\omega _{\ell _2}=\omega _{\ell }\), \(\omega _{c_1}=\omega _{c_2}=\omega _c\), \( \omega _{M_1}=\omega _{M_2}=\omega _M\), \( \Gamma _1=\Gamma _2=\Gamma \), \(\mathcal {B}_{1}= \mathcal {B}_{2}=\mathcal {B}\), \( \mathcal {I}_{1}= \mathcal {I}_{2}= \mathcal {I} \) and \(\gamma _1=\gamma _2=\gamma \). We noted that the many-photon optomechanical coupling within the jth cavity is defined as \(\mathcal {J}= \mu |\left\langle c \right\rangle |= \sqrt{\frac{2 \omega _{c}^{2}\Gamma P}{L^{2} m \omega _{M} \omega _{l}[ (\omega _M+ \alpha )^{2} + ( \frac{\Gamma ^{2}}{4}) ]}} \) [44]. To describe any given phase of the coherent drives, we employ the phase of the input laser as \(\varphi = - \arctan \left[ \frac{\Delta ^{'}+\alpha }{\Gamma }\right] \) so that \(\left\langle c \right\rangle = \mathrm {i|\left\langle c \right\rangle |}\) [38]. In result the linear Langevin equations is given by the following equations, in the limit \( |\left\langle c \right\rangle |\gg 1 \) as

$$\begin{aligned}{} & {} {\delta } \dot{a}_{j}=-\left( \textrm{i} \omega _{M}+\frac{\gamma }{2}\right) \delta a_{j}+\mathcal {J}\left( \delta c_{j}-\delta c_{j}^{+}\right) \nonumber \\{} & {} \quad \quad \,\, +\textrm{i}\beta \delta a_{n} +\sqrt{\gamma _{j}} a_{j}^{in} \quad ; \quad \textrm{j}\ne n \end{aligned}$$
(10)
$$\begin{aligned}{} & {} {\delta } \dot{c}_{j}=-\left( \frac{\Gamma }{2}-\textrm{i} \Delta ^{\prime }\right) \delta c_{j}-\mathcal {J} \left( \delta a_{j}^{+}+\delta a_{j}\right) + \textrm{i}\alpha \delta c_{n}\nonumber \\{} & {} \quad \quad \,\, +2 \lambda \textrm{e}^{\textrm{i} \theta } \delta c_j^{+} \textrm{e}^{-\textrm{i} 2 \omega _{M} t} +\sqrt{\Gamma } c_{j}^{in} \quad ; \quad \textrm{j}\ne n \end{aligned}$$
(11)

with \( \Delta ^{\prime }=\Delta +\mu \left( \left\langle a _{j}^{+}\right\rangle + \left\langle a _{j}\right\rangle \right) \) is the effective cavity detuning and which depends on the displacement of the mirrors resulting from the radiation pressure force. To consider slow fluctuations, we introduce the following transformations: \( \delta c_{j}(t)=\delta {\tilde{c}}_{j}(t) ~e^{i \Delta ^{\prime } t} and ~~~ \delta a_{j}(t)=\delta {\tilde{a}}_{j}(t)~ e^{-i \omega _{M}t} \), for the noise operators we have: \( {\tilde{c}}_j^{i n} \rightarrow \textrm{e}^{-\textrm{i} \Delta ^{\prime } t} c_j^{i n}\) and \( {\tilde{a}}_j^{i n} \rightarrow \textrm{e}^{\textrm{i}\omega _{{M}} {t}} a_j^{i n} \). Omitting the rapidly oscillating terms at \( \pm 2 \omega _{M}\), and assuming that the cavities are driven in the red sideband (\(\Delta ^{{\prime }}= -\omega _{M}\)). In the rotational wave approximation (RWA), i.e., in the limit where the mechanical frequency \(\omega _{M}\) is greater than the cavity decay rate (\(\omega _{M}\gg \Gamma \)) [44], the equations (10) and (11) became as follows

$$\begin{aligned} \delta \dot{{\tilde{a}}}_{j}{} & {} =-\frac{\gamma }{2} \delta {\tilde{a}}_{j}+\mathcal {J} \delta {{\tilde{c}}}_{j} +\textrm{i}\beta \delta {{\tilde{a}}}_{n} +\sqrt{\gamma } {\tilde{a}}_{j}^{in} \quad ; \quad j\ne n \nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned} \delta \dot{{\tilde{c}}}_{j}{} & {} =-\frac{\Gamma }{2} \delta {\tilde{c}}_{j}-\mathcal {J} \delta {{\tilde{a}}}_{j}+\textrm{i}\alpha \delta {{\tilde{c}}}_{n} \nonumber \\{} & {} \quad +2\lambda ( \cos {\theta } + \textrm{i} \sin {\theta } )\delta {\tilde{c}}_{j}^{+} +\sqrt{\Gamma } {\tilde{c}}_{j}^{in}; \quad j\ne n\qquad \end{aligned}$$
(13)

3 The steady state

The following EPR operators for the two mechanical and optical modes are introduced to obtain the covariance matrix

$$\begin{aligned} \delta {\tilde{Q}}_{a_{j}}= & {} \frac{\delta {\tilde{a}}_{j}^{+}+\delta {\tilde{a}}_{j}}{\sqrt{2}},\quad \delta {\tilde{P}}_{a_{j}}=\frac{\delta {\tilde{a}}_{j}-\delta {\tilde{a}}_{j}^{+}}{i \sqrt{2}}, \\ \delta {\tilde{Q}}_{c j}= & {} \frac{\delta {\tilde{c}}_{j}^{+}+\delta {\tilde{c}}_{j}}{\sqrt{2}},\quad \delta {\tilde{P}}_{c_{j}} =\frac{ \delta {\tilde{c}}_{j}- \delta {\tilde{c}}_{j}^{+}}{i \sqrt{2}},\ j = 1,2 \end{aligned}$$

So its possible to rewrite the two equations (12) and (13) as follows

$$\begin{aligned} \delta \dot{{\tilde{Q}}}_{a j} =-\frac{\gamma }{2} \delta {\tilde{Q}}_{a j}+\mathcal {J} \delta {\tilde{Q}}_{c j}-\beta \delta {\tilde{P}}_{a_ {n}}+\sqrt{\gamma } {\tilde{Q}}_{a j}^{\text {in }}; \quad j\ne n\nonumber \\ \end{aligned}$$
(14)
$$\begin{aligned} \delta \dot{{\tilde{P}}}_{a j}= & {} -\frac{\gamma }{2} \delta {\tilde{P}}_{a j}+\mathcal {J} \delta {\tilde{P}}_{c j}+\beta \delta {\tilde{Q}}_{a_ {n}}+\sqrt{\gamma } {\tilde{P}}_{a j}^{\text {in }}; \quad j\ne n \\ \delta \dot{{\tilde{Q}}}_{c_{j}}= & {} -\frac{\Gamma }{2} \delta {\tilde{Q}}_{c_{j}}-\mathcal {J} \delta {\tilde{Q}}_{a j}-\alpha \delta {\tilde{P}}_{c_ {n}}\\{} & {} +2 \lambda ( \cos {\theta }\delta {\tilde{Q}}_{c j}+ \sin {\theta }\delta {\tilde{P}}_{c j}) +\sqrt{\Gamma } {\tilde{Q}}_{c_{j}}^{\text {in }} \quad ; \quad j\ne n \end{aligned}$$
$$\begin{aligned}{} & {} \delta \dot{{\tilde{P}}}_{c_ {j}} =-\frac{\Gamma }{2} \delta {\tilde{P}}_{c_{j}}-\mathcal {J} \delta {\tilde{P}}_{a j}+\alpha \delta {\tilde{Q}}_{c_ {n}}\nonumber \\{} & {} -2 \lambda (\cos {\theta }\delta {\tilde{P}}_{c j}- \sin {\theta }\delta {\tilde{Q}}_{c j}) +\sqrt{\Gamma } {\tilde{P}}_{c_{j}}^{\text {in }}; \quad j\ne n\nonumber \\ \end{aligned}$$
(15)

where

$$\begin{aligned}{} & {} {\tilde{Q}}_{c_j}^{\textrm{in}}=\frac{{\tilde{c}}_j^{\mathrm {in^{+}} }+{\tilde{c}}_j^{\textrm{in}}}{\sqrt{2}}, \quad {\tilde{P}}_{c_j}^{\textrm{in}}=\frac{{\tilde{c}}_j^{\textrm{in}}-{\tilde{c}}_j^{\mathrm {in^{+}}}}{\textrm{i} \sqrt{2}},\nonumber \\{} & {} {\tilde{Q}}_{a_j}^{\textrm{in}}=\frac{{\tilde{a}}_j^{\mathrm {in^{+}}}+{\tilde{a}}_j^{\textrm{in}}}{\sqrt{2}}, \quad {\tilde{P}}_{a_j}^{\textrm{in}}=\frac{{\tilde{a}}_j^{\textrm{in}}-{\tilde{a}}_j^{\mathrm {in^{+}}}}{\textrm{i} \sqrt{2}}, \end{aligned}$$
(16)

One could write these equations in the following matrix form

$$\begin{aligned} \dot{\mathcal { Z}}(t)=\mathcal {Q} \mathcal {Z}(t)+\mathcal {Y}(t) \end{aligned}$$
(17)

with \(\mathcal {Z}(t)=(\delta {\widetilde{Q}}_{a_1}, \delta {\widetilde{P}}_{a_1}, \delta {\widetilde{Q}}_{a_2}, \delta {\widetilde{P}}_{a_2}, \delta {\widetilde{Q}}_{c_1}, \delta {\widetilde{P}}_{c_1}, \delta {\widetilde{Q}}_{c_2}, \delta {\widetilde{P}}_{c 2})^T\) and

$$\begin{aligned} \mathcal {Y}(t)= & {} \left( \sqrt{\gamma } {\widetilde{Q}}_{a_1}^{i n}, \sqrt{\gamma } {\widetilde{Y}}_{a_1}^{i n}, \sqrt{\gamma } {\widetilde{Q}}_{a_2}^{i n}, \sqrt{\gamma } {\widetilde{P}}_{a_2}^{i n}, \right. \\{} & {} \left. \sqrt{\Gamma } {\widetilde{Q}}_{c_1}^{i n}, \sqrt{\Gamma } {\widetilde{P}}_{c 1}^{i n}, \sqrt{\Gamma } {\widetilde{Q}}_{c_2}^{i n}, \sqrt{\Gamma } {\widetilde{P}}_{c 2}^{i n}\right) \end{aligned}$$

where \(\mathcal {Z}(t)\) is the quadrature vector and \(\mathcal {Y}(t)\) is the noise vector and the matrix \(\mathcal {Q}\) takes the following form

$$\begin{aligned} \mathcal {Q}=\left( \begin{array}{cccccccc} -\gamma / 2 &{}\quad 0 &{}\quad 0 &{}\quad -\beta &{}\quad \mathcal {J} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\gamma / 2 &{}\quad \beta &{}\quad 0 &{}\quad 0 &{}\quad \mathcal {J} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\beta &{}\quad -\gamma / 2 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathcal {J} &{}\quad 0 \\ \beta &{}\quad 0 &{}\quad 0 &{}\quad -\gamma / 2 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathcal {J} \\ -\mathcal {J} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\frac{\Gamma }{2}+2 \lambda \cos (\theta ) &{}\quad 2 \lambda \sin (\theta ) &{}\quad 0 &{}\quad - \alpha \\ 0 &{}\quad -\mathcal {J} &{}\quad 0 &{}\quad 0 &{}\quad 2 \lambda \sin (\theta ) &{}\quad -\frac{\Gamma }{2}-2 \lambda \cos (\theta ) &{}\quad \alpha &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad - \mathcal {J} &{}\quad 0 &{}\quad 0 &{}\quad -\alpha &{}\quad -\frac{\Gamma }{2}+2 \lambda \cos (\theta ) &{}\quad 2 \lambda \sin (\theta ) \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -\mathcal {J} &{}\quad \alpha &{}\quad 0 &{}\quad 2 \lambda \sin (\theta ) &{}\quad -\frac{\Gamma }{2}-2 \lambda \cos (\theta ) \end{array}\right) . \nonumber \\ \end{aligned}$$
(18)

The eigenvalues of matrix \(\mathcal {Q}\) have negative real parts which makes the system stable with the experimental parameters reported in reference [45]. This is in accordance with the Routh-Hurwitz criterion [46]. We can describe the system in the steady state by the Lyapunov equation [47]

$$\begin{aligned} \mathcal {Q} \eta +\eta \mathcal {Q}^T=-\Omega \end{aligned}$$
(19)

where \(\Omega \) is the stationary noise matrix: \(\Omega _{i j} \delta \left( t-t^{\prime }\right) =(1 / 2)\left\langle \mathcal {Y}(t)_i^{i n}(t) \mathcal {Y}(t)_j^{i n}\left( t^{\prime }\right) +\mathcal {Y}(t)_j^{i n}\left( t^{\prime }\right) \mathcal {Y}(t)_i^{i n}(t)\right\rangle \). \(\eta \) is the covariance matrix representing the system \(\eta _{i j}=(1 / 2)\left( \left\langle \mathcal {Z}_i(t) \mathcal {Z}_j\left( t^{\prime }\right) +\right. \right. \) \(\left. \left. \mathcal {Z}_j\left( t^{\prime }\right) \mathcal {Z}_i(t)\right\rangle \right) \).

\(\Omega \) take the following expression

$$\begin{aligned} \Omega =\left( \begin{array}{cccccccc} \gamma ^{\prime } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \gamma ^{\prime } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \gamma ^{\prime } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \gamma ^{\prime } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \Gamma ^{\prime } &{}\quad 0 &{}\quad \mathcal {V} \Gamma &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \Gamma ^{\prime } &{}\quad 0 &{}\quad -\mathcal {V} \Gamma \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathcal {V} \Gamma &{}\quad 0 &{}\quad \Gamma ^{\prime } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\mathcal {V} \Gamma &{}\quad 0 &{}\quad \Gamma ^{\prime }\end{array}\right) \nonumber \\ \end{aligned}$$
(20)

where \(\gamma ^{\prime }=\gamma \left( n_{th}+\frac{1}{2}\right) \) and \(\Gamma ^{\prime }=\Gamma \left( \mathcal {R}+\frac{1}{2}\right) \).

4 Quantum entanglement

This section summarizes the definition of logarithmic negativity used in this study to quantify quantum entanglement between the two mechanical modes. It is possible to evaluate the nonclassical correlations within the bipartite subsystem composed of moving mirrors M1 and M2 by using logarithmic negativity as a measure of entanglement. It is possible to simplify the global covariance matrix of the two mechanical modes in the following matrix

$$\begin{aligned} \sigma =\left( \begin{array}{cc} X &{}\quad Z \\ Z^T &{}\quad Y \end{array}\right) \end{aligned}$$
(21)

Let X and Y denote the covariance matrices of individual modes, each having dimensions \(2\times 2\). The \(2\times 2\) covariance matrix Z describes the correlation between the two mechanical subsystems. In the context of continuous variable (CV) systems, the logarithmic negativity \(E_{N}\) can be defined by [48,49,50]

$$\begin{aligned} E_{N} = \max \left[ 0,- ln(2\varrho ^{-})\right] \end{aligned}$$
(22)

where \(\varrho ^{-}\) is the smallest symplectic eigenvalue measuring the entanglement between the two mechanical modes, defined as follows

$$\begin{aligned} \varrho ^{-}=\bigg [\frac{\Psi -\sqrt{\Psi ^2-4 {\text {det}} \sigma }}{2}\bigg ]^{1/2} \end{aligned}$$
(23)

\(\Psi = {\text {det}} X + {\text {det}} Y- 2 {\text {det}} Z \) is a function of elements of symplectic of the simplified covariance matrix \(\sigma \). The system is separable when \(\varrho ^{-} > \frac{1}{2}\).

5 Results and discussion

We will discuss the steady-state quantum correlations of the two mechanical modes against various effects using the experimental values reported in [45]: Each movable mirror has a mas \(m= 145\) \(\textrm{ng}\) oscillates with frequency \(\omega _{m}= 2 \pi \times 947\times 10^{3} \) \(\textrm{Hz}\). The laser that drives the system possesses a power of \(p=11\) \(\textrm{mW}\). The cavity length and frequency are, respectively, \(L= 25\) \(\textrm{mm}\) and \(\omega _c=2 \pi \times 2.82\times 10^{14}\) \(\textrm{Hz}\), the laser frequency is \(\omega _{l}= 2 \pi \times 5.26 \times 10^{14} \) \(\textrm{Hz}\), \(\Gamma = 2 \pi \times 215 \times 10^{3}\) \(\textrm{Hz}\) and \(\gamma =2 \pi \times 140 \times 10^{3} \) \(\textrm{Hz}\).

Fig. 2
figure 2

The logarithmic negativity \(E_{mm}\) between the two mechanical modes as a function of temperature T for various values of the phonon tunneling rate \(\beta \), with \(r=1.5\), \(\theta =0\), \(\lambda =0.2\Gamma \) and \(\alpha =0.0015\Gamma \)

Full size image

In Fig. 2, we display how entanglement between the two mechanical modes changes with temperature for various values of the coupling rate \(\beta \). One can observe that for a fixed value of \(\beta \), the entanglement decreases as temperature increases due to decoherence phenomena [51]. The optimal value of T beyond which the entanglement disappears, decreases with increasing \(\beta \), and as the tunneling rate grows, the maximum value of entanglement decreases for a fixed temperature. This indicating that the tunneling rate degrades the entanglement as it mentioned in [32].

Fig. 3
figure 3

The logarithmic negativity \(E_{mm}\) between the two mechanical modes versus the gain \(\lambda \) of the degenerate parametric amplifier for different values of the temperature T, with \(r=3\), \(\theta =0\), \(\beta =0.0002\Gamma \) and \(\alpha =0.0015\Gamma \)

Full size image

We plot in Fig. 3 the entanglement between the two mechanical oscillators \(E_{mm}\) as a function of the gain \(\lambda \) of the parametric amplifier, considering different temperature values and for a fixed values of all other parameters. For fixed values of T, we notice that entanglement is enhanced with increasing the values of \( \lambda \) until it reaches its maximum value \(\lambda _{max}\), then, the entanglement decreases quickly with \(\lambda \) increasing. The gain \(\lambda \) is influenced by the number of photons present in the cavity. Thus, the increase in this number of photons leads to the emergence of thermal effects causing the phenomenon of decoherence [38]. This phenomenon causes the decay of quantum correlations, a topic that has been previously discussed in [30].

Fig. 4
figure 4

The logarithmic negativity \(E_{mm}\) of two mechanical modes as a function of the parameter r characterizing the squeezed light for various values of the gain \( \lambda \) of parametric amplifier, with \(T=0.2\), \(\theta =0\) mK, \(\beta =0.0002\Gamma \) and \(\alpha =0.0015\Gamma \)

Full size image

In Fig. 4, we present a plot showing the entanglement \(E_{mm}\) of mechanical modes as a function of the squeezing parameter r for various values of the gain \( \lambda \) of the parametric amplifier. This figure reveals that the creation of entanglement between movable mirrors requires a minimum value \(r_{min}\) of the parameter r, which is greater than zero (\(r_{min}>0\)). For a fixed value of \( \lambda \) the entanglement is achieved when r exceeds \(r_{min}\), and interestingly \(r_{min}\) increases with higher values of \( \lambda \), a phenomenon known as entanglement sudden birth [52]. Additionally, we observe that for a given value of \( \lambda \), the amount of entanglement increases as r increases until it reaches its maximum value, this occurrence can be attributed to the resonance phenomenon between the two movable mirrors [33]. However after reaching the maximum value, the entanglement decreases rapidly, this decrease, even when r increases, can be attributed to the diminishing effect of radiation pressure [31, 33]. Lastly, the plot in Fig. 4 demonstrates that the entanglement is affected by the value of the gain of the parametric amplifier. As expected, there exists a direct relationship between the generation of entanglement among mechanical modes, the gain of the parametric amplifier and the presence of squeezed light.

Fig. 5
figure 5

The density plot of bipartite bipartite entanglement between the two mechanical resonators as a function of coupling strength \(\alpha \) of the photon hopping (PH) and the gain \(\lambda \) of parametric amplifier. With \(r=2\), \(\theta =0\), \(T=0.02\) mK and \(\beta =0.002\Gamma \)

Full size image

We plot in Fig. 5, the entanglement \(E_{mm}\) between the two mechanical resonators as a function of coupling strength \(\alpha \) and the gain \(\lambda \). We remark that the entanglement decreases with increasing \( \lambda \) as already mentioned in Fig. 3. The magnitude of the stationary entanglement between the two mechanical modes improved only for a specific region of the \(\alpha \) values. This point highlights the significance of selecting an appropriate value of \(\alpha \) to enhance the quantum entanglement, as shown in [31].

For a value of \( \alpha \) almost larger than \(0.05\Gamma \), we observe that the entanglement decreases with the increase of \(\lambda \), until the sudden death of the entanglement [37].

We conclude, based on the previous findings, that the degree of shared entanglement among the mechanical resonators diminishes as the temperature T rises and increases for a particular interval of the gain \(\lambda \). Additionally, as r increases, so does the entanglement until it reaches a maximum value, after which it begins to diminish; this maximum value increases as the gain increases. By analyzing the relationship between entanglement and coupling strengths, we discover that entanglement is strengthened within a certain range of values for the photon hopping process coupling strength \(\alpha \), but weakens as the photon tunneling coupling strength \(\beta \) increases.

6 Conclusion

In conclusion, we have proposed a schematic of an hybrid optomechanical system to discuss the enhancement of entanglement between two movable mirrors (mechanical modes) in a double-cavity optomechanical system via squeezed-vacuum injection and intracavity squeezed light. The optical modes interact with each other via photon hopping, while the mechanical resonators are coupled through phonon tunneling. The two cavities are pumped by squeezed light and driven by coherent laser sources. We have proposed logarithmic negativity as a quantum measure to quantify quantum entanglement between the two mechanical modes. By adjusting the gain of the parametric amplifier, we successfully increased the entanglement for specified values of \(\lambda \). Also, we showed that the entanglement between the two movable mirrors is influenced by the rate of phonon tunneling; when the rate \(\beta \) increases, the entanglement decreases, indicating that the coupling rate of phonons degrades entanglement. In addition, entanglement can be improved by a convenient choice of coupling strength in the case of the photon hopping process. We have particularly witnessed two phenomena: entanglement in sudden birth and entanglement in sudden death.