1 Introduction

Entanglement is one of most astonishing features of quantum mechanics [1,2,3] and is at the heart of the large amount of applications in quantum information processing, such as quantum teleportation [4], superdense coding [5], telecloning [6] and quantum cryptography [7]. Logarithmic negativity is used as the witness of the entanglement between bipartite Gaussian mixed states [8, 9]. Quantum optomechanical systems involve basically the interaction between optical and mechanical modes via radiation pressure. This class of systems is a subject of a lot of interest in quantum correlations transfer between quantum states [10,11,12,13,14,15]. In this way, different works have considered the characterization of the entanglement transfer in optomechanical systems [16,17,18,19,20]. In addition, cavity optomechanics was also used in various applications in quantum information processing, especially in cooling the mechanical mode to their quantum ground states [21,22,23,24], generating mechanical quantum superpositions [25], realizing entanglement between mechanical and optical modes in steady state [26,27,28], enhancing precision measurements [29,30,31] and gravitational-wave detectors [32,33,34]. The biggest constraint of preserving entanglement is often attributed to the decoherence phenomenon produced when the quantum system interacts with its environment [35]. Furthermore, in optomechanical systems, the entanglement decreases quickly under the effect of certain parameters. This is called the phenomenon of entanglement sudden death (ESD) [36]. This phenomenon occurs when the entangled multipartite quantum system is placed in Markovian environments [37,38,39,40,41]. Alternatively, the entanglement can be generated suddenly. This is the phenomenon of entanglement sudden birth (ESB) [42]. The sudden death and the sudden birth of entanglement were phenomena discussed for continuous variable (CV) states which are suitable in quantum information protocols, from an experimental point of view in comparison with discrete variables states [43]. Besides, the Gaussian states play an important role in classes of the CV states [16, 17, 19, 44,45,46,47]. The role of the degenerate parametric amplification of squeezed light in enhancing the entanglement in an optomechanical system was discussed in [48]. Furthermore, recent studies have shown that when the parametric amplifier (PA) is placed inside the optomechanical cavity, the enhancement of entanglement in bipartite Gaussian states can be achieved. This is the main aim of the present work.

In this paper, we propose a scheme to generate and quantify the quantum correlations between two mechanical modes in a double Fabry–Pérot cavity optomechanical systems using the rotating wave approximation (RWA). The two cavities are separated in space and inside each Fabry–Pérot cavity is placed a parametric amplifier (PA). The PA is pumped at twice the frequency of the anti-Stokes sideband of the driving laser interacting with the movable mirrors. These two cavities are coupled to a two-mode squeezed light from spontaneous parametric down-conversion as shown in Fig. 1. We use the logarithmic negativity [8, 9] to quantify the amount of entanglement of two movable mirrors in adiabatic and nonadiabatic regimes of two-mode CV Gaussian mixed states. We show that the entanglement depends on the parameter amplifier gain, the bath temperature of the movable mirrors, the optomechanical cooperativity and the squeezing parameter. We show also that the entanglement in the adiabatic regime is more robust than in the nonadiabatic case.

The paper is organized as follows. In Sect. 2, the optomechanical system under consideration is introduced. The corresponding Hamiltonian and the associated Langevin equations for optical and mechanical modes are given. In Sect. 3, we employ the rotating wave approximation and we adopt a linearization procedure to solve the Langevin equations. In Sect. 4, we quantify the amount of quantum correlations between optical and mechanical modes. In particular, we analyze the enhancement of the entanglement between the mechanical modes in adiabatic and nonadiabatic regimes. Concluding remarks close this paper.

2 The optomechanical model

We consider two Fabry–Pérot cavities coupled to a common two-mode squeezed light from the output of a parametric down-conversion. Each cavity, composed by a fixed mirror (spatially transmitting) and the movable mirror \(M_j\) (\(j=1,2\)) (perfectly reflecting), contains inside a degenerate parametric amplifier (PA) and pumped by two sources of light coherent laser sources and squeezed light source as shown in Fig. 1. A degenerate PA is considered to produce squeezed light [49, 50].

Fig. 1
figure 1

Schematic of two identical Fabry–Pérot cavities coupled to a two-mode squeezed light from spontaneous parametric down-conversion and driven by coherent laser sources with amplitude \(\epsilon _{j}\) and the squeezed vacuum. The pump of the PA is not shown

Full size image

The Hamiltonian of the system in a rotating frame with \(\omega {_L}_j\) writes as

$$\begin{aligned} \mathcal {H}=\mathcal {H}_\mathrm{free}+\mathcal {H}_\mathrm{om}+\mathcal {H}_\mathrm{drive}+\mathcal {H}_\mathrm{oo}. \end{aligned}$$
(1)

The first term \(\mathcal {H}_\mathrm{free}=\hbar \sum _{j=1}^{2}[\omega _{M_{j}}b^{+}_{j}b_{j}+(\omega _{c_{j}}-\omega _{L_{j}})c^{+}_{j}c_{j}]\) is the free Hamiltonian describing the mechanical and optical modes, where \(\omega _{M_{j}}\), \(\omega _{c_{j}}\) and \(\omega _{L_{j}}\) are, respectively, the frequency of movable mirror, the frequency of jth cavity and the frequency of jth input field. We note by \(\Delta _{j}=\omega _{L_{j}}-\omega _{c_{j}}\) the input-cavity detuning. The annihilation and creation operators \(b_j\)(\(b_j^+\)) of movable mirrors satisfy the commutator relation \([b_j, b_j^+]=1\) (\(j=1,2\)), and the annihilation and creation operators \(c_j\)(\(c_j^+\)) of the cavity modes satisfy the commutator relation \([c_j, c_j^+]=1\) (\(j=1,2\)). The second term of Eq. (1) \(\mathcal {H}_\mathrm{om}=-\hbar \sum _{j=1}^{2} g_{j}c^{+}_{j}c_{j}(b^{+}_{j}+b_{j})\) describes the optomechanical interaction where \(g_j=\frac{\omega _{c_{j}}}{L_j}\sqrt{\frac{\hbar }{m_j\omega {_M}_j}}\) is the coupling of the mechanical mode with the intensity of optical mode [51], \(L_j\) is the jth cavity length and \(m_j\) is the jth mass of the movable mirror. The third term of Eq. (1) : \(\mathcal {H}_\mathrm{drive}=\hbar \sum _{j=1}^{2}(c^{+}_{j}\epsilon _{j}{{\,\mathrm{\text {e}}\,}}^{+\text {i}\phi _j}+c_{j}\epsilon _{j}{{\,\mathrm{\text {e}}\,}}^{-\text {i}\phi _{j}})\) describes the optical driving of the system, with \(\phi _j\) and \(\epsilon _j=\sqrt{\frac{2\kappa _j \mathcal {P}_j}{\hbar \omega {_L}_j}}\) (\(j=1,2\)) denoting, respectively, the phase and the input coherent field. The quantity \(\kappa _j\) is the jth cavity damping rate, and \(\mathcal {P}_j\) is the drive pump power of the jth laser. The last term of Eq. (1) \(\mathcal {H}_\mathrm{oo}=\text {i}\hbar \sum _{j=1}^{2}\lambda _j({{\,\mathrm{\text {e}}\,}}^{\text {i}\theta }c^{+2}_{j}{{\,\mathrm{\text {e}}\,}}^{-2\text {i}\omega {_M}_j t}-{{\,\mathrm{\text {e}}\,}}^{-\text {i}\theta }c^{2}_{j}{{\,\mathrm{\text {e}}\,}}^{2\text {i}\omega {_M}_j t})\) describes the coupling between the cavity field and the PA where \(\theta \) and \(\lambda _j\) are, respectively, the phase of the pump field driving the PA and the gain of the jth PA which is related to the pump driving the PA. In this way, the pump field driving the PA at frequency \(2(\omega {_M}_j+\omega {_L}_j)\) interacts with the second-order nonlinear optical crystal, i.e., the signal and the idler have identical frequency \(\omega {_M}_j+\omega {_L}_j\). The quantum Langevin equations are given by [17]

$$\begin{aligned} \dot{b_{j}}= & {} -\left( \text {i}\omega _{M_{j}}+\frac{\gamma _j}{2}\right) b_{j}+\text {i}g_{j}c^{+}_{j}c_{j} + \sqrt{\gamma _{j}}f_{j} \end{aligned}$$
(2)
$$\begin{aligned} \dot{c_{j}}= & {} -\left( \frac{\kappa _{j}}{2}-\text {i}\Delta _{j}\right) c_{j}+\text {i}g_{j}c_{j}(b^{+}_{j} + b_{j})-\text {i}\epsilon _{j}{{\,\mathrm{\text {e}}\,}}^{\text {i}\phi _{j}}+\,2\lambda _j{{\,\mathrm{\text {e}}\,}}^{\text {i}\theta }c_j^+{{\,\mathrm{\text {e}}\,}}^{-\text {i}2\omega _{M_{j}} t}\nonumber \\&+\,\sqrt{\kappa _{j}}c^{in}_{j} \end{aligned}$$
(3)

where \(\gamma _j\) is the dissipation rate of the jth movable mirrors, \(f_{j}\) and \(c^{in}_{j}\) are, respectively, the jth noise operator describing the coupling between mechanical mode and its own environment and the squeezed vacuum operator. For a large value of the mechanical quality factor, the mechanical baths can be assumed of Markovian type. The nonzero correlation function is given by [52, 53]

$$\begin{aligned} \langle f_{j}(t)f^{+}_{j}(t')\rangle= & {} (n_{th_j}+1)\delta (t-t') \end{aligned}$$
(4)
$$\begin{aligned} \langle f^{+}_{j}(t)f_{j}(t')\rangle= & {} n_{th_j}\delta (t-t') \end{aligned}$$
(5)

where the thermal baths phonons numbers in the jth cavity is \(n_{th_j}=\left[ {{\,\mathrm{\text {e}}\,}}^{\left( \frac{\hbar \omega _{M_{j}}}{k_{B} T_j}\right) }-1\right] ^{-1}\) with the Boltzmann constant \(k_\mathrm{B}\). The squeezed vacuum operators \(c^{in}_{j}\) and \(c^{in+}_{j}\) have nonzero correlations properties [54]

$$\begin{aligned} \langle c^{in}_{j}(t)c^{in+}_{j}(t')\rangle= & {} (\mathcal {N}+1)\delta (t-t') \end{aligned}$$
(6)
$$\begin{aligned} \langle c^{in+}_{j}(t)c^{in}_{j}(t')\rangle= & {} \mathcal {N}\delta (t-t') \end{aligned}$$
(7)
$$\begin{aligned} \langle c^{in}_{j}(t)c^{in}_{j'}(t')\rangle= & {} \mathcal {M}{{\,\mathrm{\text {e}}\,}}^{-\text {i}\omega _{M} (t+t')}\delta (t-t')\quad ;\quad j\ne j' \end{aligned}$$
(8)
$$\begin{aligned} \langle c^{in+}_{j}(t)c^{in+}_{j'}(t')\rangle= & {} \mathcal {M}{{\,\mathrm{\text {e}}\,}}^{\text {i}\omega _{M} (t+t')}\delta (t-t')\quad ;\quad j\ne j' \end{aligned}$$
(9)

where \(\mathcal {N}=\sinh ^2 r\) and \(\mathcal {M}=\sqrt{\mathcal {N}(\mathcal {N}+1)}\) with r is the squeezing parameter characterizing the squeezed light. (We consider \(\omega _{M}=\omega _{M_1}=\omega _{M_2}\).)

3 Linearization of quantum Langevin equations

The nonlinear quantum Langevin equations are in general non- solvable analytically. In this way, we use the scheme of linearization given in Ref. [48]

$$\begin{aligned} b_j=\langle b_j\rangle +\delta b_j{;}\quad c_j=\langle c_j\rangle +\delta c_j \end{aligned}$$
(10)

where \(\delta b_j\) and \(\delta c_j\) are the operators of fluctuations. \(\langle b_j\rangle \) and \(\langle c_j\rangle \) are the mean values of the operators, respectively, \(b_j\) and \(c_j\). The steady state of Eqs. (2) and (3) is written as

$$\begin{aligned} \langle c_j\rangle =\frac{\text {i}\epsilon _j {{\,\mathrm{\text {e}}\,}}^{\text {i}\phi _j}}{\frac{\kappa _j}{2}-\text {i}\Delta '_j}\quad ,\quad \langle b_j\rangle =\frac{\text {i}g_j |\langle c_j\rangle | ^2}{\frac{\gamma _j}{2}+\text {i}\omega _{M_{j}}} \end{aligned}$$
(11)

where \(\Delta '_j=\Delta _j+g_j(\langle b_j\rangle +\langle b_j\rangle ^*)\) is considered as the effective cavity detuning which depends on the displacement of the mirrors due to the radiation pressure force. Replacing \(b_j=\langle b_j\rangle +\delta b_j\) and \(c_j=\langle c_j\rangle +\delta c_j\) in Eqs. (2) and (3), we get

$$\begin{aligned} \dot{\delta b_{j}}= & {} -\left( \text {i}\omega _{M_{j}}+\frac{\gamma _j}{2}\right) \delta b_{j}+\mathcal {G}_{j}(\delta c_{j}-\delta c^+_{j}) + \sqrt{\gamma _{j}}f_{j} \end{aligned}$$
(12)
$$\begin{aligned} \dot{\delta c_{j}}= & {} -\left( \frac{\kappa _{j}}{2}-\text {i}\Delta '_{j}\right) \delta c_{j}-\mathcal {G}_{j}(\delta b^{+}_{j} + \delta b_{j})+2\lambda _j{{\,\mathrm{\text {e}}\,}}^{\text {i}\theta }\delta c_j^+{{\,\mathrm{\text {e}}\,}}^{-\text {i}2\omega _{M_{j}} t}+\sqrt{\kappa _{j}}c^{in}_{j}\nonumber \\ \end{aligned}$$
(13)

where \(\mathcal {G}_j=g_j |\langle c_j\rangle |\) is the many-photon optomechanical coupling inside the jth cavity. We have chosen \(\phi _j\), the phase of jth input laser, to be \(\phi _j=-\arctan \left( \frac{2\Delta '_j}{\kappa _j}\right) \), and we obtain \(\langle c_j\rangle =\text {i}|\langle c_j\rangle |\). Using the notations \(\delta c_j(t)=\delta \widetilde{c}_j (t){{\,\mathrm{\text {e}}\,}}^{\text {i}\Delta '_j t}\), \(\delta b_j (t)=\delta \widetilde{b}_j(t){{\,\mathrm{\text {e}}\,}}^{-\text {i}\omega _{M_j} t}\), \(\widetilde{c}^{in}_{j}={{\,\mathrm{\text {e}}\,}}^{-\text {i}\Delta '_j t}c^{in}_{j}\) and \(\widetilde{f}_{j}={{\,\mathrm{\text {e}}\,}}^{\text {i}\omega _{M_j} t}f_{j}\), Eqs. (12) and (13) give

$$\begin{aligned} \dot{\delta \widetilde{b}_{j}}= & {} -\frac{\gamma _j}{2} \delta \widetilde{b}_j + \mathcal {G}_j\left( \delta \widetilde{c}_j{{\,\mathrm{\text {e}}\,}}^{\text {i}(\Delta '_j+\omega _{M_j})t} - \delta \widetilde{c}_j^+{{\,\mathrm{\text {e}}\,}}^{-\text {i}(\Delta '_j-\omega _{M_j})t}\right) +\sqrt{\gamma _j}\widetilde{f}_{j} , \end{aligned}$$
(14)
$$\begin{aligned} \dot{\delta \widetilde{c}_{j}}= & {} -\frac{\kappa _j}{2}\delta \widetilde{c}_j-\mathcal {G}_j\left( \delta \widetilde{b}_j^+ {{\,\mathrm{\text {e}}\,}}^{-\text {i}(\Delta '_j-\omega _{M_j})t} +\delta \widetilde{b}_j{{\,\mathrm{\text {e}}\,}}^{-\text {i}(\Delta '_j+\omega _{M_j})t}\right) \nonumber \\&+\,2\lambda _j{{\,\mathrm{\text {e}}\,}}^{\text {i}\theta }\delta \widetilde{c}_{j}^+ +\sqrt{\kappa _j}\widetilde{c}^{in}_{j} . \end{aligned}$$
(15)

In the rotating wave approximation (RWA) [51, 55] (i.e., \(\omega _{M_j}\gg \kappa _j\)), the \(\Delta '_j\approx \Delta _j\), one can neglect the terms rotating at \(\pm 2\omega _{M_j}\). When the cavity is driven at the red sideband (\(\Delta '_j=-\omega _{M_j}\)), Eqs. (14) and (15) are written as

$$\begin{aligned} \dot{\delta \widetilde{b}_{j}}= & {} -\frac{\gamma _j}{2} \delta \widetilde{b}_j + \mathcal {G}_j\delta \widetilde{c}_j+\sqrt{\gamma _j}\widetilde{f}_{j} , \end{aligned}$$
(16)
$$\begin{aligned} \dot{\delta \widetilde{c}_{j}}= & {} -\frac{\kappa _j}{2} \delta \widetilde{c}_j - \mathcal {G}_j\delta \widetilde{b}_j+ {2\lambda _j\cos \theta \delta \widetilde{c}^+_{j}+2\text {i}\lambda _j\sin \theta \delta \widetilde{c}^+_{j}}+\sqrt{\kappa _j}\widetilde{c}^{in}_{j}. \end{aligned}$$
(17)

4 Steady-state entanglement

4.1 Adiabatic regime

Our aim in this subsection is to study the entanglement of two movable mirrors in adiabatic regime (i.e., where \(\kappa _j\gg \gamma _j, \mathcal {G}_j\)) [56], which is the case for mirrors with high-Q mechanical factor and weak effective optomechanical coupling. In this case, for \(\delta \dot{\widetilde{c}}_j=0\) the steady-state solution of Eq. (17) is given by

$$\begin{aligned} \delta \widetilde{c}_j=-\frac{\mathcal {G}_j\kappa _j}{2\left( \frac{\kappa _j^2}{4}-4\lambda _j^2\right) }\delta \widetilde{b}_j - \frac{2\mathcal {G}_j\lambda _j{{\,\mathrm{\text {e}}\,}}^{\text {i}\theta }}{\frac{\kappa _j^2}{4}-4\lambda _j^2}\delta \widetilde{b}^+_j + \frac{2\lambda _j{{\,\mathrm{\text {e}}\,}}^{\text {i}\theta }\sqrt{\kappa _j}}{\frac{\kappa _j^2}{4}-4\lambda _j^2} \widetilde{c}^{in+}_j + \frac{\kappa _j\sqrt{\kappa _j}}{2\left( \frac{\kappa _j^2}{4}-4\lambda _j^2\right) }\widetilde{c}^{in}_j . \end{aligned}$$
(18)

Inserting the steady-state solution (18) into Eq. (16), we have (with \(\theta =0\) and \(x_j=\lambda _j/\kappa _j\))

$$\begin{aligned} \delta \dot{\widetilde{b}}_j= & {} \frac{1}{1-16x^2_j}\left[ -\left( \frac{\gamma _j\kappa _j \left( 1-16x_j^2\right) +4\mathcal {G}^2_j}{2\kappa _j} \right) \delta \widetilde{b}_j - \frac{8\mathcal {G}_j^2x_j}{\kappa _j}\delta \widetilde{b}^+_j \right. \nonumber \\&\left. + \,{\frac{8\mathcal {G}_jx_j\sqrt{\kappa _j}}{\kappa _j}\widetilde{c}^{in+}_j + \frac{2\mathcal {G}_j\sqrt{\kappa _j}}{\kappa _j}\widetilde{c}^{in}_j }\right] + \sqrt{\gamma _j}\widetilde{f}_j \end{aligned}$$
(19)

By introducing the expressions of quadrature operators for two mechanical modes

$$\begin{aligned} \delta \widetilde{Q}_{b_j}= \frac{\delta \widetilde{b}_j^++\delta \widetilde{b}_j}{\sqrt{2}} \quad ,\quad \delta \widetilde{P}_{b_j}= \frac{\delta \widetilde{b}_j-\delta \widetilde{b}_j^+}{\text {i}\sqrt{2}} \end{aligned}$$
(20)

and

$$\begin{aligned} \delta \widetilde{Q}_{c_j}^{in}= & {} \frac{\delta \widetilde{c}^{in+}_j +\delta \widetilde{c}^{in}_j}{\sqrt{2}} \quad ,\quad \delta \widetilde{P}_{c_j}^{in}= \frac{\delta \widetilde{c}^{in}_j-\delta \widetilde{c}^{in+}_j}{\text {i}\sqrt{2}} , \end{aligned}$$
(21)
$$\begin{aligned} \delta \widetilde{Q}_{f_j}= & {} \frac{\widetilde{f}_j^++ \widetilde{f}_j}{\sqrt{2}} \quad ,\quad \delta \widetilde{P}_{f_j}= \frac{ \widetilde{f}_j- \widetilde{f}_j^+}{\text {i}\sqrt{2}} , \end{aligned}$$
(22)

equation (19) becomes in terms of the quadratures operators

$$\begin{aligned} \delta \dot{\widetilde{Q}}_{b_j}= & {} -\left( \frac{4\mathcal {G}_j^2+\gamma _j\kappa _j(1-4x_j)}{2\kappa _j(1-4x_j)}\right) \delta \widetilde{Q}_{b_j} + \widetilde{Q}^{in}_{b_j} \end{aligned}$$
(23)
$$\begin{aligned} \delta \dot{\widetilde{P}}_{b_j}= & {} -\left( \frac{4\mathcal {G}_j^2+\gamma _j\kappa _j(1+4x_j)}{2\kappa _j(1+4x_j)}\right) \delta \widetilde{P}_{b_j} + \widetilde{P}^{in}_{b_j} \end{aligned}$$
(24)

where \(\widetilde{Q}^{in}_{b_j}=\frac{2\mathcal {G}_j\sqrt{\kappa _j}}{\kappa _j(1-4x_j)} \delta \widetilde{Q}_{c_j}^{in} + \sqrt{\gamma _j}\delta \widetilde{Q}_{f_j}\) and \(\widetilde{P}^{in}_{b_j}=\frac{2\mathcal {G}_j\sqrt{\kappa _j}}{\kappa _j(1+4x_j)} \delta \widetilde{P}_{c_j}^{in} + \sqrt{\gamma _j}\delta \widetilde{P}_{f_j}\). Equations (23) and (24) take the following compact matrix form [57]

$$\begin{aligned} \dot{u}(t)=\mathcal {A}u(t)+\eta (t) \end{aligned}$$
(25)

with \(u^T(t)=(\delta \widetilde{Q}_{b_1},\delta \widetilde{P}_{b_1},\delta \widetilde{Q}_{b_2},\delta \widetilde{P}_{b_2})\), \(\eta ^T(t)=(\widetilde{Q}^{in}_{b_1},\widetilde{P}^{in}_{b_1},\widetilde{Q}^{in}_{b_2},\widetilde{P}^{in}_{b_2})\), yielding the formal solution

$$\begin{aligned} u(t)=M(t)u(0) + \int _0^t{\mathrm{d}s M(s)\eta (t-s)},\quad M(t)={{\,\mathrm{\text {e}}\,}}^{\mathcal {A} t} . \end{aligned}$$
(26)

For identical cavities, we consider that the two coherent sources have identical strength, and the thermal baths of two mechanical mirrors are at the same temperature \(T_1=T_2=T\) (\(n_{th_1}=n_{th_2}=n_{th}\)). Furthermore, \(m_1=m_2=m\), \(\omega _{c_1}=\omega _{c_2}=\omega _c\), \(\omega _{M_1}=\omega _{M_2}=\omega _M\), \(\kappa _1=\kappa _2=\kappa \), \(x_1=x_2=x\), \(\mathcal {G}_1=\mathcal {G}_2=\mathcal {G}\) and \(\gamma _1=\gamma _2=\gamma \). The matrix \(\mathcal {A}\) in (25) writes

$$\begin{aligned} \mathcal {A}= & {} {{\,\mathrm{\text {diag}}\,}}\left( -\frac{4\mathcal {G}^2+\gamma \kappa (1-4x)}{2\kappa (1-4x)},- \frac{4\mathcal {G}^2+\gamma \kappa (1+4x)}{2\kappa (1+4x)},-\frac{4\mathcal {G}^2 +\gamma \kappa (1-4x)}{2\kappa (1-4x)},\right. \nonumber \\&\left. -\,\frac{4\mathcal {G}^2+\gamma \kappa (1+4x)}{2\kappa (1+4x)}\right) , \end{aligned}$$
(27)

with \(x=\lambda /\kappa \). The system of the two mechanical modes is stable because all eigenvalues of the drift matrix \(\mathcal {A}\) are negative when \(x<0.25\) [58]. The covariance matrix \(\mathbb {V}\) of the system in the steady state is derived by making use of the Lyapunov equation [28, 59]

$$\begin{aligned} \mathcal {A}\mathbb {V}+\mathbb {V} \mathcal {A}^T=-\mathcal {L} \end{aligned}$$
(28)

where \(\mathcal {L}\) is the matrix of stationary noise correlations functions whose elements are defined by \( \mathcal {L}_{kl}\delta (t-t') =\frac{1}{2}(\langle \eta _k(t)\eta _l(t')+\eta _l(t')\eta _k(t)\rangle ) \). Explicitly, we have

$$\begin{aligned} \mathcal {L}= \begin{pmatrix} \mathcal {L}_1 &{} 0 &{} \mathcal {L}_{13} &{} 0 \\ 0 &{} \mathcal {L}_2 &{} 0 &{} -\mathcal {L}_{24} \\ \mathcal {L}_{13} &{} 0 &{} \mathcal {L}_1 &{} 0 \\ 0 &{} -\mathcal {L}_{24} &{} 0 &{} \mathcal {L}_2 \end{pmatrix} \end{aligned}$$
(29)

with \(\mathcal {L}_1=\frac{4\mathcal {G}^2(2\mathcal {N}+1)+\gamma \kappa (1-4x)^2(2n_{th}+1)}{2\kappa (1-4x)^2}\), \(\mathcal {L}_2=\frac{4\mathcal {G}^2(2\mathcal {N}+1)+\gamma \kappa (1+4x)^2(2n_{th}+1)}{2\kappa (1+4x)^2}\), \(\mathcal {L}_{13}=\frac{4\mathcal {M}\mathcal {G}^2}{\kappa (1-4x)^2}\) and \(\mathcal {L}_{24}=\frac{4\mathcal {M}\mathcal {G}^2}{\kappa (1+4x)^2}\). where \(\mathcal {N}=\sinh ^2 r\) and \(\mathcal {M}=\sqrt{\mathcal {N}(\mathcal {N}+1)}\). The explicit expressions of the nonvanishing matrix elements are given by

$$\begin{aligned} \mathbb {V}_{1}= & {} \frac{\mathcal {C}(1+2\mathcal {N})+(2n_{th}+1)(1-4x)^2}{2(1-4x)(\mathcal {C}+1-4x)}\quad ,\quad \nonumber \\ \mathbb {V}_{2}= & {} \frac{\mathcal {C}(1+2\mathcal {N})+(2n_{th}+1)(1+4x)^2}{2(1+4x)(\mathcal {C}+1+4x)} \end{aligned}$$
(30)
$$\begin{aligned} \mathbb {V}_{13}= & {} \frac{\mathcal {C}\mathcal {M}}{(1-4x)(\mathcal {C}+1-4x)}\quad ,\quad \mathbb {V}_{24} =\frac{\mathcal {C}\mathcal {M}}{(1+4x)(\mathcal {C}+1+4x)} \end{aligned}$$
(31)

The covariance matrix writes then as follows

$$\begin{aligned} \mathbb {V}_{(m_1m_2)} = \begin{pmatrix} \mathbb {V}_1 &{} 0 &{} \mathbb {V}_{13} &{} 0 \\ 0 &{} \mathbb {V}_2 &{} 0 &{} -\mathbb {V}_{24} \\ \mathbb {V}_{13} &{} 0 &{} \mathbb {V}_1 &{} 0 \\ 0 &{} -\mathbb {V}_{24} &{} 0 &{} \mathbb {V}_2 \end{pmatrix} . \end{aligned}$$
(32)

For \(x=0\) (i.e., \(\lambda =0\)), the covariance matrix \(\mathbb {V}_{(m_1m_2)}\) (32) gives the matrix obtained in [17, 60]. The optomechanical cooperativity \(\mathcal {C}\) is given by [51]

$$\begin{aligned} \mathcal {C}=\frac{4\mathcal {G}^2}{\gamma \kappa }=\frac{8\omega _{c}^2}{m\gamma \omega _{M}\omega _{L} L^2}\frac{\mathcal {P}}{\left[ \left( \frac{\kappa }{2}\right) ^2+\omega _{M}^2\right] } \end{aligned}$$
(33)

The covariance matrix (32) can be alternatively cast in the form

$$\begin{aligned} \mathbb {V}_{(m_1m_2)}\equiv \begin{pmatrix} \mathcal {S} &{} K \\ K^T &{} \mathcal {S} \end{pmatrix} . \end{aligned}$$
(34)

where \(\mathbb {S}= \begin{pmatrix} \mathbb {V}_1 &{} 0 \\ 0 &{} \mathbb {V}_2 \end{pmatrix}\) and \(K= \begin{pmatrix} \mathbb {V}_{13} &{} 0 \\ 0 &{} -\mathbb {V}_{24} \end{pmatrix}\) . In the case of CV system, the logarithmic negativity \(E_N\) is defined by [8, 9]

$$\begin{aligned} E_{N}=\max [0,-\ln (2\mu ^-)] \end{aligned}$$
(35)

and

$$\begin{aligned} \mu ^-= \sqrt{\frac{\Delta -\sqrt{\Delta ^2-4\det {\mathbb {V}_{(m_1m_2)}}}}{2}} \end{aligned}$$
(36)

where \(\Delta \) is \(\Delta =2(\det \mathcal {S}-\det \mathcal {K})\). The Gaussian state of two movable mirrors is entangled if \(\mu ^-<\frac{1}{2}\) (i.e., when \(E_N>0\)), which is equivalent to Simon’s criterion for Gaussian states [61]. According to the experimental data reported in [62], the movable mirrors oscillate with the frequency \(\omega _M/2\pi =947\times 10^3\) Hz, the mechanical damping rate \(\gamma /2\pi \)= 140 Hz and the mass \(m=\)145 ng. The cavity length is \(L=\)25 mm, and frequency of the cavity is \(\omega _c/2\pi =5.26\times 10^{14}\) Hz. The laser frequency \(\omega _L/2\pi =2.82\times 10^{14}\) Hz, the cavity damping rate \(\kappa =2\pi \times 215{,}000\) Hz, and drive laser power \(\mathcal {P}=11\) mW.

Fig. 2
figure 2

Logarithmic negativity \(E_N\) versus the temperature T of the thermal bath of the movable mirrors for different values of the gain \(\lambda \) and optomechanical cooperativity \(\mathcal {C}\) for \(r = 3\)

Full size image

In Fig. 2, we have plotted the logarithmic negativity \(E_N\) between the two movable mirrors as a function of the temperature T of the thermal bath of the movable mirrors for different values of the gain \(\lambda \) and optomechanical cooperativity \(\mathcal {C}\) while keeping all other parameters fixed. In the absence of the PA (\(\lambda =0\)), this figure shows that the entanglement decreases quickly until it vanishes (\(E_N=0\), i.e., two movable mirrors are separable) when the temperature increases. This situation was already reported in [17, 19], and this can be explained by the phenomenon of entanglement sudden death (ESD) [36]. We notice that when \(x=\lambda /\kappa \) increases, the entanglement appears robust against thermal effect, i.e., the entanglement transfer from two-mode squeezed light to mechanical mode is enhanced in the presence of PA. For example, for \(\mathcal {C}=32\) the negativity is zero (\(E_N=0\)) when \(T=0.75\) mK for \(x=0\) while negativity \(E_N\) vanishes \(E_N=0\) when \(T=0.93\) mK for \(x=0.15\). Moreover, entanglement increases when the optomechanical cooperativity increases, i.e., the augmentation of \(\mathcal {C}\) is due to the many-photon optomechanical coupling. Thus, the entanglement of two movable mirrors increases as shown in Fig. 2 under the influence of decoherence effects [35]. For instance, for \(x=0.15\) the negativity \(E_N=0\) when \(T=0.93\) mK and \(\mathcal {C}=32\), while the negativity \(E_N=0\) when \(T=1.4\) mK and \(\mathcal {C}=50\).

Fig. 3
figure 3

Logarithmic negativity \(E_N\) versus the squeezing parameter r for various values of the gain \(\lambda \) (\(\lambda =x\kappa \)) and the temperature T of the thermal bath of the movable mirrors in a, b. The negativity logarithmic \(E_N\) versus the gain \(\lambda \) for various values of the squeezing parameter r and the temperature T of the thermal bath of the movable mirrors in c, d for \(\mathcal {C}=32\)

Full size image

In Fig. 3a. b,the logarithmic negativity \(E_N\) between mechanical modes versus the squeezing parameter r for various values of the gain \(\lambda \) (with \(x=\lambda /\kappa \)) and the temperature T of the thermal bath of the movable mirrors is plotted keeping all other parameters fixed. This figure shows that the entanglement between two movable mirrors appears suddenly for \(r>r_\mathrm{min}\) (\(r_\mathrm{min}\) is a minimum value of r, with \(E_N=0\) for \(r<r_\mathrm{min}\)). This phenomenon can be explained by so-called entanglement sudden birth [42]. Moreover, the entanglement increases when r increases for different values of \(\lambda \) as shown in this figure. In this way, when \(\lambda >0\) (i.e., the presence of PA), the entanglement of two movable mirrors is directly related to the value of the squeezing parameter, i.e., there is a value of r for which the entanglement is enhanced in comparison with the situation where \(\lambda =0\) (absence of the PA). Furthermore, we remark that this special value of r which enhances the stationary entanglement decreases under thermal effect. This is due obviously to the decoherence effects [35]. For example, for \(r=4\) and \(x=0.20\) the negativity \(E_N=1.8\) for \(T= 0.2\) mK while the negativity \(E_N\approx 1.15\) for \(T= 0.4\) mK. We notice that the presence of the PA provides entanglement more robustness against thermal effect. This is due to the role of PA in generating the squeezed light which leads to increase the optomechanical coupling, and this is related to quantum correlation shared between two movable mirrors.

In Fig. 3c, d, we plot the logarithmic negativity \(E_N\) versus the gain \(\lambda \) for various values of the squeezing parameter r and the temperature T of the thermal bath of the movable mirrors. We notice that for \(r=3\), the entanglement still increases with increasing values of x until it achieves a maximum value and then decreases quickly until vanishes (i.e., the quantum correlations decay monotonically). Moreover, it is observed that the maximum value of \(E_N\) (\(E_N=1.8\)) is the attained when \(r=3\) when \(T=0.2\) mK and \(E_N=1.3\) when \(T=0.4\) mK for \(x=0.25\) .

4.2 Nonadiabatic regime

To get the explicit expression of degree of freedom of mechanical and optical modes in nonadiabatic regime, we consider the EPR-type quadrature operators correspond to the two subsystems

$$\begin{aligned} \delta \widetilde{Q}_{c_j}= \frac{\delta \widetilde{c}_j^+ +\delta \widetilde{c}_j}{\sqrt{2}}\quad ,\quad \delta \widetilde{P}_{c_j}= \frac{\delta \widetilde{c}_j-\delta \widetilde{c}_j^+}{\text {i}\sqrt{2}} \quad ;\quad j=1 , 2 \end{aligned}$$
(37)

Equations (16) and (17) become

$$\begin{aligned} \delta \dot{\widetilde{Q}}_{b_j}= & {} -\frac{\gamma }{2}\delta \widetilde{Q}_{b_j}+\mathcal {G}\delta \widetilde{Q}_{c_j}+\sqrt{\gamma }\delta \widetilde{Q}_{f_j}\quad ;\quad j=1 , 2 \end{aligned}$$
(38)
$$\begin{aligned} \delta \dot{\widetilde{P}}_{b_j}= & {} -\frac{\gamma }{2}\delta \widetilde{P}_{b_j}+\mathcal {G}\delta \widetilde{P}_{c_j}+\sqrt{\gamma }\delta \widetilde{P}_{f_j}\quad ;\quad j=1 , 2 \end{aligned}$$
(39)
$$\begin{aligned} \delta \dot{\widetilde{Q}}_{c_j}= & {} -\frac{\kappa }{2}\delta \widetilde{Q}_{c_j}-\mathcal {G}\delta \widetilde{Q}_{b_j}+2\lambda \cos (\theta )\delta \widetilde{Q}_{c_j}+2\lambda \sin (\theta )\delta \widetilde{P}_{c_j}\nonumber \\&+\,\sqrt{\kappa }\delta \widetilde{Q}_{c_j}^{in}\quad ;\quad j=1 , 2 \end{aligned}$$
(40)
$$\begin{aligned} \delta \dot{\widetilde{P}}_{c_j}= & {} -\frac{\kappa }{2}\delta \widetilde{P}_{c_j}-\mathcal {G}\delta \widetilde{P}_{b_j}-2\lambda \cos (\theta )\delta \widetilde{P}_{c_j}+2\lambda \sin (\theta )\delta \widetilde{Q}_{c_j}\nonumber \\&+\,\sqrt{\kappa }\delta \widetilde{P}_{c_j}^{in}\quad ;\quad j=1 , 2 \end{aligned}$$
(41)

with

\(u^T(t)=(\delta \widetilde{Q}_{b_1},\delta \widetilde{P}_{b_1},\delta \widetilde{Q}_{b_2},\delta \widetilde{P}_{b_2},\delta \widetilde{Q}_{c_1},\delta \widetilde{P}_{c_1},\delta \widetilde{Q}_{c_2},\delta \widetilde{P}_{c_2})\) and

\(\eta ^T(t)=(\sqrt{\gamma }\delta \widetilde{Q}_{f_1},\sqrt{\gamma }\delta \widetilde{P}_{f_1},\sqrt{\gamma }\delta \widetilde{Q}_{f_2},\sqrt{\gamma }\delta \widetilde{P}_{f_2},\sqrt{\kappa }\delta \widetilde{Q}_{c_1}^{in},\sqrt{\kappa }\delta \widetilde{P}_{c_1}^{in},\sqrt{\kappa }\delta \widetilde{Q}_{c_2}^{in},\sqrt{\kappa }\delta \widetilde{P}_{c_2}^{in})\)

where

$$\begin{aligned} \mathcal {A}= \begin{pmatrix} -\frac{\gamma }{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathcal {G} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\frac{\gamma }{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathcal {G} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -\frac{\gamma }{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathcal {G} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -\frac{\gamma }{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathcal {G} \\ -\mathcal {G} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\frac{\kappa }{2}+2\lambda \cos (\theta ) &{}\quad 2\lambda \sin (\theta ) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\mathcal {G} &{}\quad 0 &{}\quad 0 &{}\quad 2\lambda \sin (\theta ) &{}\quad -\frac{\kappa }{2}-2\lambda \cos (\theta ) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -\mathcal {G} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\frac{\kappa }{2}+2\lambda \cos (\theta ) &{}\quad 2\lambda \sin (\theta ) \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -\mathcal {G} &{}\quad 0 &{}\quad 0 &{}\quad 2\lambda \sin (\theta ) &{}\quad -\frac{\kappa }{2}-2\lambda \cos (\theta ) \end{pmatrix}\nonumber \\ \end{aligned}$$
(42)

Since all eigenvalues of the drift matrix \(\mathcal {A}\) are negative only if \(16\mathcal {G}^2-(-\kappa +\gamma +4\lambda )^2>0\) and \(4\lambda <\kappa +\gamma \), the system under study is stable [58]. The matrix of stationary noise correlations, whose elements are explicitly given by [19]

$$\begin{aligned} \mathcal {L}= \begin{pmatrix} \gamma ' &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \gamma ' &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \gamma ' &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \gamma ' &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \kappa ' &{}\quad 0 &{}\quad \mathcal {M}\kappa &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \kappa ' &{}\quad 0 &{}\quad -\mathcal {M}\kappa \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \mathcal {M}\kappa &{}\quad 0 &{}\quad \kappa ' &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\mathcal {M}\kappa &{}\quad 0 &{}\quad \kappa ' \end{pmatrix} \end{aligned}$$
(43)

where \(\gamma '=\gamma (n_{th}+\frac{1}{2})\) and \(\kappa '=\kappa (\mathcal {N}+\frac{1}{2})\). \(\mathbb {V}\) is a Gaussian state [see Eqs. (28), (42) and (43)] which can be characterized by a \(8\times 8\) covariance matrix. The elements of covariance matrix \(\mathbb {V}\) in the basis \((\delta \widetilde{Q}_{b_1},\delta \widetilde{P}_{b_1},\delta \widetilde{Q}_{b_2},\delta \widetilde{P}_{b_2})\) are characterized by the \(4\times 4\) covariance matrix \(\mathbb {V}_{(m_1m_2)}\) [see Eq. (32)] between the two movable mirrors in nonadiabatic regime (i.e., when \(\gamma \) and \(\kappa \) are comparable). The nonvanishing matrix elements write (with \(\theta =0\))

$$\begin{aligned} \mathbb {V}_{11}= & {} \frac{\mathcal {C}[(1+2n_{th})\frac{\gamma }{\kappa }+1+2\mathcal {N}]+(1+2n_{th})(1-4x)\left( \frac{\gamma }{\kappa }+1-4x\right) }{2(\mathcal {C}+1-4x)\left( \frac{\gamma }{\kappa }+1-4x\right) } \end{aligned}$$
(44)
$$\begin{aligned} \mathbb {V}_{22}= & {} \frac{\mathcal {C}[(1+2n_{th})\frac{\gamma }{\kappa }+1 +2\mathcal {N}]+(1+2n_{th})(1+4x)\left( \frac{\gamma }{\kappa }+1+4x\right) }{2(\mathcal {C} +1+4x)\left( \frac{\gamma }{\kappa }+1+4x\right) } \end{aligned}$$
(45)
$$\begin{aligned} \mathbb {V}_{13}= & {} \frac{\mathcal {C}\mathcal {M}}{(\mathcal {C}+1-4x) \left( \frac{\gamma }{\kappa }+1-4x\right) }\quad ,\quad \mathbb {V}_{42}=-\frac{\mathcal {C}\mathcal {M}}{(\mathcal {C}+1+4x) \left( \frac{\gamma }{\kappa }+1+4x\right) }\nonumber \\ \end{aligned}$$
(46)

For \(x=0\) (i.e., \(\lambda =0\)), these matrix elements of covariance matrix \(\mathbb {V}_{(m_1m_2)}\) reduce to the ones obtained elements published in Refs [17,18,19]. On the other hand, when \(\kappa \gg \gamma , \mathcal {G}\), the matrix elements of \(\mathbb {V}_{(m_1m_2)}\) coincide with those obtained for adiabatic regime [see Eqs. (30) and (31)].

Fig. 4
figure 4

Plots of the logarithmic negativity \(E_N\) versus the optomechanical cooperativity \(\mathcal {C}\) in adiabatic regime and in the nonadiabatic regime for \(\gamma /\kappa = 0.01\) and 0.02, with \(r=3\) and the gain \(\lambda =0.15\times \kappa \)

Full size image

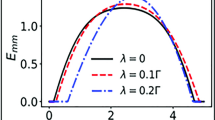
In Fig. 4, we plot the stationary entanglement between the two movable mirrors in the adiabatic and nonadiabatic regimes versus the optomechanical cooperativity \(\mathcal {C}\) for different values of the temperature T of the thermal bath of the movable mirrors. The entanglement production, usually called in the literature the sudden birth of entanglement, requires a minimal value of the cooperativity. This minimal value for adiabatic regime is small than the minimal value from which the entanglement is produced in the nonadiabatic case. Furthermore, in the nonadiabatic regime, the results reported in Fig. 4 show that the minimal value of the cooperativity, to produce entanglement in the system, increases with increasing values of the ratio \(\gamma /\kappa \). This can be explained by the dissipation effects which prevent the transfer of entanglement from the optical to mechanical modes. In fact, in the adiabatic regime \(\gamma \) is smaller than \(\kappa \) (\(\kappa \gg \gamma \)) which means that the movable mirror of each cavity remains in its cooling state in contrast with nonadiabatic regime. This explains why the production of entanglement in adiabatic regime occurs for small values of \(\mathcal {C}\) in comparison with nonadiabatic case. Finally, we notice that the thermal effects increase the minimal values of the cooperativity from which the entanglement can be generated.

Fig. 5
figure 5

Plots of the logarithmic negativity \(E_N\) versus the gain \(\lambda \) in adiabatic regime and nonadiabatic regimes for \(\gamma /\kappa = 0.001\), 0.002, 0.01 and 0.02, with \(r=3\) and the optomechanical cooperativity \(\mathcal {C}=30\)

Full size image

In Fig. 5, we plot the stationary entanglement between the two movable mirrors in the adiabatic and nonadiabatic regimes versus the gain \(\lambda \) for various values of the temperature T of the thermal bath of the movable mirrors and the values of \(\gamma /\kappa \). For \(T=0.2\) mK, the entanglement enhances until it achieves its maximal value and starts to decrease with increasing values of \(\lambda \), when \(\gamma /\kappa =\) 0.001 and 0.002 as shown in Fig. 5a. Moreover, the comparison between Fig. 5a, b shows the degradation of the entanglement under thermal effects (decoherence phenomenon). It must be noticed that increasing temperature does not affect the enhancement of the amount of entanglement between the two mechanical modes in adiabatic as well as nonadiabatic regime. In Figs. 5c, d, we give the behavior of the entanglement for \(\gamma /\kappa = 0.01\) and \(\gamma /\kappa = 0.02\). We notice that when we increase the values of \(\gamma /\kappa \), the enhancement of entanglement is observed in the adiabatic regime. However, in the nonadiabatic, we observe that the entanglement decreases monotonically versus the parameter \(x=\lambda /\kappa \).

5 Conclusion

In summary, we have proposed a theoretical scheme to enhance the entanglement of two movable mirrors of two specially separated cavities using rotating wave approximation in adiabatic and nonadiabatic regimes. Each cavity has inside the parametric amplifier (PA), pumped by two light sources squeezed, coherent and coupled to a common two-mode squeezed light from spontaneous parametric down-conversion. We have discussed the behavior of stationary entanglement with and without PA inside the two cavities. The physical parameters characterizing the optomechanical system under consideration are taken from the recently reported results of [62]. We have observed the phenomenon of decoherence, entanglement sudden birth and sudden death. We have shown that the entanglement depends crucially on the temperature T of the thermal bath of the movable mirrors, squeezed parameter, optomechanical cooperativity and the gain of the PA \(\lambda \). Moreover, we have shown that the squeezing of the cavity field produced by the PA can be transferred to the movable mirror. In this sense, the PA inside the optomechanical cavity enhances the entanglement of two movable mirrors. In the adiabatic regime, we have shown that when \(\lambda >0\), the entanglement increases with the optomechanical cooperativity and the optomechanical cooperativity allows more entanglement transfer from the optical modes. Moreover, we have found that the value of squeezing parameter influences the enhancement of the generation of stationary entanglement. Indeed, we have also discussed that the transfer of entanglement from the squeezing of the cavity field to the movable mirror in the nonadiabatic regime (realistic regime) is less important than in the adiabatic regime. Finally, our proposal scheme to enhance the entanglement transfer can present interest for applications in quantum information processing and communication.