1 Introduction

In a coincidence experiment, a projectile of momentum \(\varvec{k}_0\) and energy \(E_0\) impinges on a target atom and ionizes it. The ejected electron and scattered projectile are detected with their angles and energies resolved. If the spins were also determined, we would have a quantum mechanically complete experiment, but even if the spins are not known, such a measurement is kinematically complete and is ideal for exploring subtle few body collisional effects which would be swamped by more robust interactions in less differential measurements. Coincidences studies have contributed greatly to our understanding of few body atomic collisions, and much has been learned about the subtleties of the interactions in collisions between photons, ions and electrons with atomic and molecular target (see for example [1]). More recent pioneering work using antimatter projectiles, see e.g., [2,3,4,5], has opened up the possibility of performing complementary experiments which could effectively isolate competing interactions which cannot be separately detected in an experiment with a single projectile. Our concern in this paper is the electron and positron impact ionization of neutral atoms, with a particular focus on exploring the inclusion of post-collisional interactions (pci’s) in the description of these collisions. We will use the distorted wave Born approximation (DWBA) approach and look to modify it to take some account of post-collisional effects. The use of multiplicative corrections the Gamov factor [6, 7], and the Ward–Macek factor [8, 9] as well as the classical correction method [10, 11] are considered. The major concern with the classical correction approach is the freedom it gives in choosing the size of the collision complex. Our approach is to fix this for the electron impact ionization of hydrogen where the TDCS is well-understood and then with no free parameters study positron impact of hydrogen and then electron and positron collisions with argon targets.

2 Theory

2.1 Kinematics

Fig. 1
figure 1

General kinematics of a coincidence measurement. The fast incoming projectile has momentum \(\varvec{k}_0\) and energy \(E_0\) and comes in at an angle \(\Phi \) with respect to the plane in which the two final state particles are detected at angles \(\theta _f,\theta _s\) with respect to the projection of the incoming direction on their plane

Full size image

The momentum vectors of the scattered projectile, \(\varvec{k}_f\), and the ejected electron, \(\varvec{k}_s\), form a plane, and thus we can define all possible kinematics by the set (\(k_0,k_f,k_s,\Phi ,\theta _f,\theta _s\)), where \(\Phi \) defines the angle \(\varvec{k}_0\) makes to the plane of detection. The “gun angle” \(\Phi =0{}^{\circ }\) corresponds to coplanar geometry, and \(\Phi =90{}^{\circ }\) to perpendicular plane geometry. In this paper, we will be exclusively concerned with coplanar asymmetric geometry where the scattered projectile has a greater momentum than the ejected. The convention we adopt is that the “slow” particle is detected at an angle \(\theta _s\) measured in a clockwise direction with respect to the projection of the incoming direction on the plane, while the “fast” particle is detected at an angle \(\theta _f\) measured in the anti-clockwise direction (see Figure 1). In this geometry, the triple differential cross section (TDCS) is presented as a function of \(\theta _s\) for fixed \(\theta _f,k_f,k_s\)

2.2 Distorted wave and first born approximation

2.2.1 Electron scattering

The DWBA method refers to an approach which encompasses a range of approximations. The key features are that the projectile-electron interaction occurs once, and the wavefunctions of the incoming and outgoing electrons are calculated in “distorting potentials”. The general theory for including distorting potentials is given in [12]. There is quite a deal of freedom in the choice of these potentials, typically the potentials represent elastic scattering in the static-exchange potentials of the atom or ion, but other effects such as target polarization have been included [13, 14] to good effect.

The DWBA has been applied to electron impact ionization for quite some time, the first detailed account being given by [15]. The version we use here is, in essential features, the same with some refinements. For a full discussion of the approximation, its strengths, weaknesses and our computational implementation, see [1, 16, 17]. For the electron impact ionization of the n, l orbital of an inert gas atom, the TCDS, after summing over all final and averaging over all initial spin states, is given by:

$$\begin{aligned} \frac{d^3{\sigma ^{DWBA}}}{d\Omega _f d\Omega _s dE}= & {} 2(2\pi )^4\frac{k_1 k_2}{k_0}\nonumber \\&\sum \limits _{m=-l}^{l}[|f_{nlm}|^2+|g_{nlm}|^2-{\Re }{\textit{e}}{(f_{nlm}^*g_{nlm})}]\nonumber \\ \end{aligned}$$
(1)

where

$$\begin{aligned} f_{nlm}(\varvec{k}_f,\varvec{k}_s)= & {} \langle \chi ^-(\varvec{k}_f,\varvec{r}_f)\chi ^-(\varvec{k}_s,\varvec{r}_s)|\nonumber \\&\frac{1}{\Vert \varvec{r}_f-\varvec{r}_s\Vert }|\chi _0^+(\varvec{ k}_0,\varvec{r}_f)\psi _{nlm}(\varvec{r}_s)\rangle ,\nonumber \\ g_{nlm}(\varvec{k}_f.\varvec{k}_s)= & {} \langle \chi ^-(\varvec{k}_f,\varvec{r}_s)\chi ^-(\varvec{k}_s,\varvec{r}_f)|\nonumber \\&\frac{1}{\Vert \varvec{r}_f-\varvec{r}_s\Vert }|\chi _0^+(\varvec{ k}_0,\varvec{r}_f)\psi _{nlm}(\varvec{r}_s)\rangle , \end{aligned}$$
(2)

\(\chi _0^+\) is the distorted wave calculated in the static-exchange potential of the atom and \(\chi ^-\) is the distorted wave calculated in the static-exchange potential of the ion, orthogonalized to \(\psi _{nlm}\). These are normalized to a delta function i. e. 

$$\begin{aligned} \langle \chi ^\pm (\varvec{k},\varvec{r})|\chi ^\pm (\varvec{k'},\varvec{r})\rangle =\delta (\varvec{k-k'}). \end{aligned}$$
(3)

In our DWBA calculations, the full non-local exchange potential is not used to calculate the elastic scattering but rather a localized version [16, 18,19,20,21] is employed. Its use greatly simplifies the static exchange calculations in that one needs only solve differential equations rather than integro-differential equations. Because we treat each of the exiting electrons as moving in the field of a spin \(\frac{1}{2}\) ion, there is an inherent ambiguity in the choice of exchange potential in the final channels, we could chose it to be singlet or triplet [16, 22]. For most energies, there is little or no difference between results calculated with the singlet or triplet potentials [16, 21]

Both the singlet and triplet local exchange potential which depends on the static potential \(V_{static}({\varvec{r}})\) and the radial probability density \(\alpha ({\varvec{r}})\). The triplet term is alway real but if

$$\begin{aligned} \frac{1}{2}k^2-V_{static}({\varvec{r}}) <2\alpha ^2({\varvec{r}}) \end{aligned}$$
(4)

the singlet potential can become complex. For a detailed discussion of where this problem arises and how is dealt with in our code, see [16].

The atomic wave function plays an explicit role in (2) and implicitly in the calculation of the static exchange potentials. For most energies and kinematics, the TDCS is not overly sensitive to wavefunction effects in calculating the static-exchange potentials. However for (e, 2e) on argon at an impact energy of 200eV, there is evidence of an unexpected sensitivity [23, 24] clearly seen in the absolute size of the cross section. In our calculations, we will use the Hartree–Fock orbitals given in [25].

For atomic hydrogen, some of the same ambiguity occurs in the incident channel. This ambiguity can be partly avoided if we follow ([16]) and take

$$\begin{aligned} \frac{d^3{\sigma ^{DWBA}}}{d\Omega _f d\Omega _s dE} =\frac{(2\pi )^4k_fk_s}{k_0}\left[ \frac{3}{4}|f^t-g^t|^2+\frac{1}{4}|f^s+g^s|^2\right] \nonumber \\ \end{aligned}$$
(5)

with the direct and exchange amplitudes calculated using the singlet (s) or triplet (t) static-exchange potentials of the atom. Let us consider the special case of the DWBA where the incident and fast scattered electrons are replaced by plane waves

$$\begin{aligned} \chi ^-(\varvec{k}_f,\varvec{r}_f)\rightarrow & {} \frac{1}{(2\pi )^{3/2}}e^{i\varvec{k}_f.\varvec{r}_f}\nonumber \\ \chi ^-(\varvec{ k}_0,\varvec{r}_f)\rightarrow & {} \frac{1}{(2\pi )^{3/2}}e^{i\varvec{ k}_0.\varvec{r}_f} \end{aligned}$$
(6)

and exchange is neglected everywhere. In this case, the static potential of the ion is just the Coulomb potential of the proton and (5) reduces to the regular first Born approximation (FBA). The TDCS for the first Born approximation is symmetric about the direction of momentum transfer and a deviation from this is a clear signal that there are pre- or post-collisional effects which invalidates the choice of plane waves for the incident and scattered particle.

The DWBA neglects electron capture, and post-collisional interaction between the scattered projectile and the ejected electron. For the kinematics considered here, we can safely neglect the capture contribution [16] but not pci. In our earlier work [9, 26, 27], we used the distorted wave Born approximation (DWBA) and tried to take some account of pci by using a Gamow factor \(N_{e^-e^-}\) [6, 12]

$$\begin{aligned} \frac{d^3{\sigma ^{PCI}}}{d\Omega _1 d\Omega _2 dE}=N_{e-e-}\frac{d^3{\sigma ^{DWBA}}}{d\Omega _1 d\Omega _2 dE}\end{aligned}$$
(7)

where

$$\begin{aligned} N_{e-e-} =\frac{\gamma }{e^{\gamma }-1 } \end{aligned}$$
(8)

with

$$\begin{aligned} \gamma =\frac{2\pi }{\Vert {\varvec{k}_f-\varvec{k}_s}\Vert }. \end{aligned}$$
(9)

The Gamov factor is related to the analytic ansatz approximation of Brauner, Briggs and Klar [28]. The essence of the BBK approximation is to assume that the full three-body wavefunction could be approximated by three two-body wavefunctions corresponding to the three final state particles all independently acting in pairs. The approach has the appealing advantage of treating each two body system in a symmetric way. The \(N_{e^-e^-}\) factor comes from the Coulomb wave representing the two-body interaction between the two outgoing electrons [29, 30]. The BBK approximation tends to give a reasonable representation of the shape of the TDCS but unfortunately yields only a poor representation of the absolute size of the cross section and is difficult to apply to multi-electron targets[31, 32]. Nevertheless the \(N_{e^-e^-}\) factor tends to give the dominant angular behavior of the TDCS at low energies and it does correctly force the cross section to go to zero when \(\varvec{k}_f=\varvec{k}_s\). A modified version of the \(N_{e^-e^-}\) factor has been put forward by Ward and Macek [33] in an attempt to restore the normalization. In a number of earlier calculations, including our own [34], the Ward–Macek factor, \(M_{e^-e^-}\), was used. In their original derivation Ward and Macek assumed that at threshold, both exiting particles (electrons in their case) preferentially moved at \(180{}^{\circ }\) to each other which is consistent with the Wannier model for threshold electron impact ionization. This will not apply in the positron case, indeed intuitively one would expect \(\Phi _{fs}=0{}^{\circ }\) to be favored with the ejected electron partially screening the positron-nuclear repulsion. Furthermore, we know [27] that the \(DWBA+M_{e^-e^-}\) gives poor agreement with the absolute experiments of [35, 36] at 1eV and 2eV above threshold for the electron impact ionization of helium. The \(N_{e^-e^-}\) factors destroy the normalization consequently our primary focus here is on understanding what contributes to the shape of the cross section. In [27] \(N_{e^- e^-}\) was chosen to be unity when \(\Theta _{sf}=180{}^{\circ }\), i. e. the co-linear case. With this choice, one gets very good agreement between the DWBA and the absolute data in symmetric geometries [27].

2.2.2 Positron scattering

The DWBA TDCS equations look similar to (1) and (2), except that in this case, there is no exchange amplitude \(g_{nlm}\), and the distorted waves \(\chi _0^+(\mathbf{k}_0, \mathbf{r}_1)\) and \(\chi ^- (\mathbf{k}_1, \mathbf{r}_1)\) for the positron are generated in the static potential which is the minus of the static potential for electron impact. The distorted wave \(\chi ^-(\mathbf{k}_2, \mathbf{r}_2)\) for the slow ejected electron is orthogonalized to the bound state. There is now no longer any ambiguity in the choice of exchange potential. The ground state of our targets is spin singlet (\(S=0\)), and therefore, the ejected electron wave function must be calculated in the singlet static-exchange potential.

To estimate pci, we now change the sign of \(\gamma \) in (8).

$$\begin{aligned} N_{e+e-} =\frac{\gamma }{1-e^{-\gamma } } \end{aligned}$$
(10)

We still have the problem of choosing a normalization. Once again we could assume that when \(\Theta _{fs}=180{}^{\circ }\), the pci effects are minimal and normalize \(N_{e^+e^-}=1\) at the point. This is not ideal but is probably the best one can do. An undesirable feature is that in the symmetric geometry where \(k_f=k_s\) \(N_{e^-e^-}\rightarrow 0\) as \(\Theta _{fs}\rightarrow 0\), \(N_{e^+e^-}\) goes to infinity [9].

2.3 Classical correction

The idea of using a “pure classical” correction to account for pci was first proposed by Popov [10] and further developed by Klar and his collaborators [11]. Our assumption is that the classical correction can usefully be applied in a macroscopic region between the detector and a “reaction zone” of atomic dimension. In the region outside the reaction zone, we will assume that the fast scattered particle is essentially free, while the slow ejected electron moves in a Coulomb field of unit charge, i. e. the same condition as in the FBA.

The approach of [11] which we are following is a mixture of classical Hamiltonian dynamics and “perturbation” theory. Polar position and momentum coordinates

$$\begin{aligned} r_i,p_i= & {} \dot{r}_i,\\\theta _i, L_i= & {} r_i^2\dot{\theta _i} \end{aligned}$$

are taken as the generalized coordinates; then, the classical Hamiltonian for the escape of scattered projectile and ejected electron from the reaction zone is

$$\begin{aligned} H= & {} \frac{1}{2}\left( p_f^2+p_s^2+\frac{L_f^2}{r_f^2}+\frac{L_s^2}{r_s^2}\right) \nonumber \\&-V_f({r_f})-V_s(r_s)+\frac{(-1)^n}{r_{sf}}.\nonumber \\ V_s(r_s)= & {} V(r_s)\nonumber \\ V_f(r_f)= & {} {(-1)^n}V(r_f) \end{aligned}$$
(11)

where

$$\begin{aligned} V(r_i)\rightarrow \frac{1}{r_i} , r_i\rightarrow \infty \end{aligned}$$

\(p_i\) are the radial momenta, \(L_i\) are the angular momenta of the detected particles, \(i=s,f\)

$$\begin{aligned} n= {\left\{ \begin{array}{ll} 0&{} \text {if projectile is } e^-\\ +1&{} \text {if projectile is } e^+ \end{array}\right. } \end{aligned}$$
(12)

In the classical region, it is assumed, to first order, that outside the reaction zone, the scattered projectile can be treated as a free particle, and the ejected electron is elastically scattered in the field of the ion which because of screening this reduces to simply the coulomb potential

$$\begin{aligned} V(r)=\frac{1}{r}. \end{aligned}$$

Classically, this would correspond to

$$\begin{aligned} E_f= & {} \frac{1}{2}\left[ p_f^2+\frac{L_f^2}{r_f^2}\right] \nonumber \\ E_s= & {} \frac{1}{2}\left[ p_s^2+\frac{L_s^2}{r_s^2}\right] -V_s(r_s) \end{aligned}$$
(13)

being constants of the motion. The basic idea behind the classical correction is to assume that the DWBA approximation gives a good representation of the TDCS inside a “small” reaction zone but from the boundary of the reaction zone to the detector, it is assumed that the pci interactions, though small, are sufficient to affect the shape and size of the cross section at the detector which is assumed to be located at infinity. For example, if the energy of the fast electron, \(E_f\), is different from that at the reaction zone, then the symmetry about the direction of momentum transfer will be broken, and there will be an apparent shift in the position of the binary and recoil peaks [12]. If we treat \(E_s,E_f\) in (13) not as constants but as functions of time, then the energies at \(t=0\) is related to that that at \(t=\infty \) by

$$\begin{aligned} E_i(\infty ) - E_i(0)= & {} \int _0^\infty \dot{E}_idt\nonumber \\ \Rightarrow E_i(0)= & {} E_i(\infty )-\int _0^\infty \dot{E}_idt \end{aligned}$$
(14)

Now let us look for a “perturbative” approximation where to the lowest order, \(\theta _i\) is constant. We assume that to this order

$$\begin{aligned} r_f(t)= & {} r_f(0)+k_f t\nonumber \\ k_f= & {} \sqrt{2E_f(\infty )} \end{aligned}$$
(15)

and for the slow electron, its radial orbit is the solution of

$$\begin{aligned} \frac{1}{2}\dot{r}_s^2 -V(r_s)= & {} \frac{1}{2}k_s^2\nonumber \\ k_s= & {} \sqrt{2E_s(\infty )} \end{aligned}$$
(16)

Assuming that the angle between the exiting particles is

$$\begin{aligned} \chi =\theta _i+\theta _f, \end{aligned}$$

we can write

$$\begin{aligned} E_f(0)= & {} E_f(\infty )+(-1)^nV(r_f(0)) \nonumber \\&+(-1)^{n+1}\int _0^\infty dt\, \dot{r}_f r_{sf}^{-3}(r_f-r_s\cos \chi ),\nonumber \\ \end{aligned}$$
(17)

and in the same way,

$$\begin{aligned} E_s(0)= & {} E_s(\infty ) +(-1)^{n+1}\int _0^\infty dt \,\dot{r}_s r_{sf}^{-3}(r_s-r_f\cos \chi )\nonumber \\ \end{aligned}$$
(18)
Fig. 2
figure 2

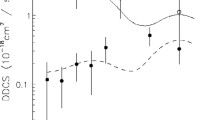
Triple differential cross section for the electron impact ionization of atomic hydrogen. \(E_0=250eV, E_s=5eV,\theta _f=3{}^{\circ }\). Experiment:[37], error bars show estimated 15% absolute error. Theory: red dotted line: FBA; dashed green line: \(\hbox {FBA}+M_{e^-e^-}\); black dashed-double dotted line: \(\hbox {FBA}+N_{e^- e^-}\); solid blue line: FBA+ classical correction,

Full size image

Now we can, as in [11], write

$$\begin{aligned} \theta _i(0)= & {} \theta _i(\infty )-\int _0^\infty dt\dot{\theta _i}(t)\nonumber \\ \dot{\theta }_i= & {} \frac{\partial H}{\partial L_i}\\= & {} \frac{L_i}{r_i^2}; \end{aligned}$$
(19)

then following the same approach as in ([11]), it follows that

$$\begin{aligned} \theta _i(0)= & {} \theta _i(\infty )+(-1)^{n+3}\int _0^\infty \frac{dt}{r_i^2}\nonumber \\&\int _0^tdt'\frac{r_s r_f\sin (\chi )}{[r_s^2+r_f^2-2r_s r_f\cos (\chi )]^{3/2} }\nonumber \\= & {} \theta _i(\infty )+(-1)^{n+3}\int _0^\infty \frac{dt}{r_i^2}\nonumber \\&\int _0^tdt'\frac{r_s r_f\sin (\chi )}{[r_s^2+r_f^2-2r_s r_f\cos (\chi )]^{3/2} }\nonumber \\= & {} \theta _i(\infty )+(-1)^{n+3}\sin (\chi )\int _0^\infty \frac{dt}{r_i^2}\nonumber \\&\int _0^tdt'\frac{r_s r_f}{[r_s^2+r_f^2-2r_s r_f\cos (\chi )]^{3/2} } \end{aligned}$$
(20)

To get an equivalent equation to equation (19) in [11], we change the order of integration and integrate over the same region of space in both double integrals. An undesirable feature of the classical correction approach is that we do not have an a priori method for choosing \(r_f(0)\) and \(r_s(0)\). The approach adopted here is to fix them by comparison with the best available data both experimental and theoretical for electron scattering from atomic hydrogen and then use the same values both for the positron ionization under the same conditions and then for the \((e^{\pm },e^{\pm }e^-)\) on argon in equivalent kinematics.

3 Results

3.1 Hydrogen target

3.1.1 Electron scattering

Fig. 3
figure 3

A comparison for the \(N_{e^-e^+}\) and \(N_{e^-e^-}\) factors as a function of \(\theta _s\) for \(E_f=231.4\;eV,E_s=5\, eV, \theta _f=3{}^{\circ }\) \(N_{e^+e^-}\) given by solid blue line, \(N_{e^+e^-} \) by the red dashed line

Full size image
Fig. 4
figure 4

Triple differential cross section for the electron/positron impact ionization of atomic hydrogen. \(E_0=250eV, E_s=5eV,\theta _f=3{}^{\circ }\). Red dotted curve FBA; classically corrected: \(e^-\) solid blue line; \(e^+\) green dashed

Full size image

Let us first consider the \((e^-,2e^-)\) results for atomic hydrogen where the TDCS is well-understood. Ehrhardt and collaborators [37] have produced highly accurate experimental data with which the coupled pseudo-state calculations of [22, 31] as well as the Eikonal Born series calculations of [38] agree. The coupled pseudo-state calculation is as close to a complete numerical treatment of the problem as one can hope. Its validity has been confirmed not only by the excellent agreement with experiment, but also by other large scale calculations, see for example [39]. However, its very completeness makes it difficult to extract an understanding of how different physical mechanisms contribute, and it is currently applicable only to the lightest of atoms. It is possible to place a \(15\%\) error estimate on the absolute size of the measured cross sections [37, 40]. As our basic case study, we will consider the electron impact ionization of hydrogen for an impact energy of 250eV, where the fast scattered electron is detected at \(\theta _f=3{}^{\circ }\) and \(E_s=5eV\); in these kinematics, there is only a small difference between the DWBA and FBA approximations [15, 16]. In Fig. 2, the experimental results of [37] are compared with the first Born approximation, together with the three pci correction techniques, the multiplication by \(N_{e^-e^-}\) and \(M_{e^-e^-}\), together with a classical corrected version with \(r_f(0)=2.8, r_s(0)=0.5\). The first Born is symmetric about the direction of momentum transfer. The experiment and the more sophisticated theories[22, 38, 39] yield a TDCS with a binary peak that is reduced and shifted toward larger angles and a recoil peak that is enhanced and shifted by an even larger amount also toward larger angles. Both the multiplicative approximations of pci have a shape that is similar to the FBA, and while the binary peak is somewhat reduced, the recoil remains too small. This behavior is not surprising when we consider Fig. 3. Both \(N_{e^+e^-}\) and \(N_{e^-e^-}\) are functions of \(\Vert \varvec{k}_f-\varvec{k}_s\Vert \) and in the current kinematics \(k_f>>k_s\); consequently, there is only a small change in both as we vary \(\theta _s\). In contrast to the more dramatic variation seen in symmetric geometries [9], \(N_{e^-e^-}\) takes its maximum value when \(\Theta _{fs}=180{}^{\circ }\) and its minimum when \(\Theta _{fs}=0{}^{\circ }\). In positron case, \(N_{e^+e^-}\) is maximal when \(\Theta _{fs}\) is close to zero and minimal when \(\Theta _{fs}=180{}^{\circ }\). The classically corrected approximation gives a better agreement with experiment, with the binary peak reduced and rotated to larger angles and the recoil peak enhanced and rotated to smaller angles. The positions of the binary and recoil peaks using the FBA with classical correction are in agreement with those given by the Eikonal Born series calculations tabulated in [38], and the ratio of binary maximum to recoil maximum is also in close accord. These results encourages in the belief that we have something of the character of the pci contained in our calculations.

3.1.2 Positron scattering

In Fig. 4, the classically corrected results are shown for exactly the same kinematics for both electron and positron impact ionization. The factors \(r_f(0),r_s(0)\) are the same for both calculations. These are the values used to give good agreement with experiment for the electron case, i. e. \(r_f(0)=2.8\) a.u. , \( r_s(0)=0.5 \) a.u. In the absence of pci, the first Born approximation is the same for both electron and positron scattering. The effect of pci is to reduce the binary maximum of the electron scattering and rotate it toward larger angles but in the positron case, the binary peak is enhanced and rotated toward smaller angles. The recoil peak is greatly diminished for positron impact and increased for electron impact.

Fig. 5
figure 5

PCI effects at \(E_0=250 eV\) on hydrogen, the scattered particle is detected at \(\theta _f=3{}^{\circ }\) with an energy of \(E_f=232.4 eV\). Plotted is (a) energy shift for the scattered projectile, b energy shift for the ejected electron, c bending of the trajectory for the scattered electron, d bending of the trajectory for the ejected electron, against the observation angle \(\theta _s=\theta _s(\infty )\). The blue solid curve is for an electron impact. The green dashed curve corresponds to a positron impact

Full size image
Fig. 6
figure 6

TDCS for electron and positron impact ionization of Argon(3p): green dashed dotted:DWBA(electron impact); black dotted:DWBA(electron)+\(N_{e^-e^-}\) ; red dashed: DWBA(positron); blue solid line:DWBA(positron)+\(N_{e^+e^-}\)

Full size image

In Fig. 4, we plot the energy shifts and the bending of the trajectories of the scattered particle and the ejected electron. Shown are results for both electron and positron impact. In each case, the trajectories of the ejected electron mirrors the positron. For positron impact, if the ejected electron accelerates, then for for electron impact, it is de-accelerated. If one particle trajectory is rotated clockwise, then the other is rotated anti-clockwise.

3.2 Argon

In the realm of \(e^+/e^-\) measurements, argon is most frequently used target [4, 5, 9, 26, 34, 41] and we will study it here. In order to use the methods developed above, we need to determine the size of the classical region, i.e., to fix \(r_s(0)\) and \(r_f(0)\). We can make the reasonable assumption that the spatial extension of the collision complex is proportional to the scattered particle’s velocity. The binding energy of the 3p electron in argon is a mere 2.2eV greater than hydrogen; thus, by increasing the impact energy to 252.2eV, we keep \(k_f\) and \(k_s\) unchanged from the hydrogen case. We can also look to the “size” of the atoms. Clementi and colleagues [42] have calculated the atomic radii of all the atoms in the first six rows of the periodic table. We considered the possibility of scaling the hydrogen \(r_s(0)\) by the ratio of the atomic radii which gives a value of \(r_s(0)\) of approximately 0.65. We fixed \(r_f(0) =2.8\) a.u. and considered values of \(r_s(0)\) between 0.5 au.and 0.65 a.u and found only a relatively small variation in the shape of the cross sections. In the calculations presented here, we use \(r_f(0)=2.8\) a.u. and \(r_s(0)=0.5\) a.u. In the DWBA calculation, the incoming and fast outgoing particle is assumed to be moving in the static-exchange (static in the positron case) of the atom and the ejected to be moving the singlet static-exchange potential of the ion.

The results shown in Fig. 6 correspond to the regular DWBA with and without \(N_{e^{\pm },e^-}\). All four results are very similar in shape and are more or less symmetric about the direction of momentum transfer \(\theta _q=49{}^{\circ }\)

In Fig. 7, we show the regular DWBA calculations for electron and positron impact together with the respective DWBA calculations with the inclusion of pci via the classical correction method. For electron impact, the binary peak is reduced and rotated away from the binary direction to larger angles, while the recoil peak is significantly enhanced. For positron impact, the binary peak is increased and rotated toward smaller angle, while the recoil peak is reduced.

Fig. 7
figure 7

TDCS for electron and positron impact ionization of Argon(3p) \(E_0=252.2 eV, E_s=5eV \theta _f=3{}^{\circ }\): DWBA solid orange; DWBA+ classical correction, dashed blue. a electron impact; b positron impact; c a comparison of the TDCS for electron/positron impact ionization of argon, \(E_0=252.2 eV\), \(E_s=5 eV, \theta _f=3{}^{\circ }\): Purple dashed curve electron, red dotted curve positron)

Full size image

In Fig. 7 c, comparison of the triple differential cross sections for electron and positron impact ionization calculated in the DWBA with pci included via the classical correction is shown.

Very recently, Du Bois and deLucio [5] have published results in kinematics very similar to ours. In particular, they give results for \(e^+/e^-\) on Argon at an impact energy of 200eV. The ejected electron energies are varied for a range from 2.6 to 19eV with \(\theta _f\) fixed at \(2{}^{\circ },3{}^{\circ }\) or \(4{}^{\circ }\). The qualitative features of these results are similar to ours. We plan a careful study of these experimental results.

4 Conclusions

The multiplicative approach to including post-collisional interactions has provided valuable insights in very symmetric geometries [6, 7, 27] but it largely fails in the low-to-intermediate energy asymmetric kinematics, considered here giving little improvement over a pci-free distorted wave Born calculation. The classical correction method developed here is more successful, giving at the least the gross features of the complementary \(e^+,e^-\) studies. Indeed the preliminary results presented here would appear to suggest that at least as far as the shape is concerned, the TDCS is far more sensitive to pci effects than to other more subtle few body effects, such as exchange. This study also suggests that pci can be well-represented classically in the macroscopic region between the collision complex and the detector. In this work, the spatial extent of the collision complex was empirically determined for the electron impact ionization of hydrogen and once so determined applied to predict the shape of the TDCS for positron impact and then for both positron and electron impact ionization of argon. The general shape and relative behavior of the argon cross sections are in qualitative agreement with very recent experimental work [5]. We hope to return to a more detailed comparison in the near future.