Storage and retrieval of nonlinear surface plasmon polariton solitons via electromagnetically induced transparency in a metal–dielectric–metal waveguide

Abstract

We propose a scheme to realize storage and retrieval of symmetric and antisymmetric nonlinear surface plasmon polaritons (SPPs) solitons via electromagnetically induced transparency (EIT) in a metal–dielectric–metal (MDM) waveguide. The dielectric is chosen as ladder-type three-level atoms with incoherent pumping. We find that the Ohmic loss of both symmetric and antisymmetric modes in the system can be totally compensated under EIT condition but with different incoherent pumps. The transparency window becomes wider for the symmetric mode, but deeper for the antisymmetric mode, when incoherent pumping exists. We also show that in nonlinear propagation regime, a huge enhancement of Kerr nonlinearity of the symmetric and antisymmetric SPPs can be obtained, and gain-assisted ($1+1$)-dimensional symmetric and antisymmetric subluminal SPPs solitons can be produced, stored and retrieved with high efficiency and stability. At last, we study the strategies to optimize the optical memory for the two modes. Our study may have promising applications in light information processing and transmission at nanoscale level based on MDM waveguides.

Graphical abstract

1 Introduction

Storage and retrieval of evanescent waves in confinement systems via electromagnetically induced transparency (EIT) has been one of the hotspots in micro/nano-optics recently, because of its practical application potentials [1, 2]. Due to the enhancement of the interaction between the evanescent waves and the coherent mediums in such systems, the storage efficiency and fidelity would be greatly improved [3, 4].

Various schemes have been proposed to realize high efficiency storage and retrieval of optical pluses in micro/nanostructure waveguide systems experimentally or theoretically [5,6,7]. And up to now, research on storage of optical pluses is not limited in the linear region [8], and it has been extended to the nonlinear region [9, 10].

In 2014, Xue et al. studied the mechanism of the light storage in a cylindrical waveguide with core of normal refractive index material and cladding of negative refractive index metamaterial [11]. In 2015, Gouraud et al. filled high-density cold atomic gas around the nanofiber to realize the storage of the evanescent waves in the nanofiber [12]. In the same year, Sayrin et al. demonstrated that nanofiber-based EIT optical memory in tapered optical fibers with a nanofiber waist [13]. In 2020, Zhou et al. theoretically investigated the optical memory in a nanofiber system via EIT in nonlinear region [14]. In 2017, Xu et al. investigated the nonlinear solitons memory in the atomic gas filled in a kagome-structured hollow-core photonic crystal fiber (HC-PCF) [15]. In 2018, Su et al. studied linear surface polariton (SP) memory in a $\Lambda$-type three-level quantum emitters doped at a metal–dielectric interface through numerical simulation, and improved the efficiency and fidelity of the linear SP memory by using a weak microwave field [16]. In 2020, Li et al. stored light in an ensemble of cold atoms inside an HC-PCF using an EIT process to studied the quantum memory of hollow core photonic crystal fiber [17]. In 2019, Shou et al. proposed a scheme to realize slow-light soliton beam splitters by using a tripod-type four-level atomic system [18]. However, it seems that storage and retrieval of nonlinear SPPs have not arisen enough attention of researchers.

Thus, we propose a scheme to realize storage and retrieval of SPPs solitons [19] in the metal–dielectric–metal (MDM) waveguide structure via the EIT effect. MDM waveguides are common waveguide structures [20,21,22], which is simple and easy to manufacture [23, 24]. In 2016, Walasik et al. developed two methods to calculate the stationary nonlinear solutions in one-dimensional plasmonic slot waveguides made of a finite-thickness nonlinear dielectric core surrounded by metal regions [25, 26], and the results show that nonlinear SPPs solitons can exist in the MDM waveguide. In addition, there are two propagation modes of SPPs, symmetric (short range) mode and antisymmetric (long range) mode [27, 28], in the MDM waveguides, which also provide a good platform for our research on the storage and retrieval of both modes SPPs solitons, together with their optimize strategies.

In this work, the dielectric is chosen as ladder-type three-level atoms with incoherent pumping. In the linear region, we obtain that the Ohmic loss of both symmetric and antisymmetric modes in the system can be totally compensated under EIT condition but with different incoherent pumps. In the nonlinear region, we show that a huge enhancement of Kerr nonlinearity of the symmetric and antisymmetric SPPs can be obtained, and a gain-assisted ($1+1$)-dimensional symmetric and antisymmetric subluminal SPPs solitons can be produced, stored and retrieved with high efficiency and stability. At last, we study the strategies to optimize the optical memory for the two modes. This work may have certain applications in micro/nanoscale quantum information processing.

The article is arranged as follows. In Sect. 2, the theoretical model and method are described. In Sect. 3, the linear propagation characteristics of the two propagation modes are discussed. In Sect. 4, the storage and retrieval of SPPs solitons are studied under nonlinear characteristics. Finally, the last section summarizes the main results of this work.

2 Model

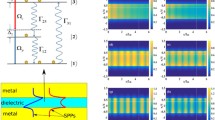
The model under study is shown in Fig. 1a. The system is composed of a three-layer waveguide, and the upper and lower layers are composed of metal, i.e., metal/dielectric/metal (MDM) waveguide. Assuming that they extend indefinitely in the y direction $({|z|\ge {d}/{2}})$, the permittivity and permeability of the metal are $\varepsilon _{2}$ and $\mu _{2}$, and are given by the Drude model in optical region [29]. The middle part is composed of dielectric $(|z|<{d}/{2})$, which is chosen as a cold atomic gas with a three-level ladder-type energy excitation diagram. The permittivity and permeability of this part are $\varepsilon _{1}$ and $\mu _{1}$.

Fig. 1

a MDM three-layer waveguide model structure. The intermediate layer is chosen as a cold atomic gas ensemble. The two curves in the figure represent the distribution of TM modes SPPs magnetic field in the y direction, including symmetric mode and antisymmetric mode. b Energy state structure and excitation diagram of a three-level ladder-type system. $\omega _{c}$ coupled state $|2\rangle$ and state $|3\rangle$, $\omega _{p}$ coupled state $|1\rangle$ and state $|2\rangle$. $\varGamma _{ij}\; (i, j= 1,2,3)$ is the spontaneous emission rate from state $|j\rangle$ to energy state $|i\rangle$, $\varGamma _{31}$ corresponds to incoherent pumping, and $\Delta _{2}$ and $\Delta _{3}$ are the single- and two-photon detunings, respectively

Since the electric field in the y direction cannot accumulate charge under continuous conditions at the interface between metal and dielectric, TE waves cannot propagate in the MDM waveguide, thus, we only consider TM mode in our work. Under the continuous condition of tangential electric field ${\mathbf {E}}$ and normal electric displacement vector ${\mathbf {D}}$, we can solve the Maxwell equations, and obtain the expressions for the electric field and the dispersion relationship of symmetric mode and antisymmetric mode, which are shown in Appendix 1.

For convenience, we assume the input probe light and control light propagate along the x direction, and the expression of the electric field can be expressed as:

$$\begin{aligned} {\mathbf {E}}({\mathbf {r}},t)={\mathbf {E}}_{p}+{\mathbf {E}}_{c}=\sum _{l=p,c}{\mathcal{E}_l(x,t){\mathbf {u}}_l(z)e^{i(k_lx-\omega _lt)}}+\mathrm{c.c.},\nonumber \\ \end{aligned}$$

(1)

where ${\mathcal {E}}_{l}(x,t)$ is the slowvary envelope function of the light field, ${\mathbf {u}}_l(z)$ is the fundamental mode distribution function, and $k_{l}=k(\omega _{l})$ is propagation constant. Under electric-dipole approximation and rotating-wave approximations (RWA), the Hamiltonian of the system in the interaction picture reads [30]

$$\begin{aligned} {\hat{H}}_\mathrm{int}=- & {} \hbar \sum _{j=1}^3\Delta _j|j\rangle \langle j|-\hbar [\zeta _p(z)e^{i\theta _p}\varOmega _p|2\rangle \langle 1|\nonumber \\+ & {} \zeta _c(z)e^{i\theta _c}\varOmega _c|3\rangle \langle 2 |+\mathrm{h.c.}], \end{aligned}$$

(2)

where $\zeta _{c}(z)={{\mathbf {e}}}_{23}\cdot {{\mathbf {u}}}_{c}(z), \zeta _{p}(z)={{\mathbf {e}}}_{12}\cdot {{\mathbf {u}}}_{p}(z)$ are mode functions of the control field and probe field, respectively. The Rabi frequency of the probe field and control field are defined as $\varOmega _{p}={{{{\mathcal {E}}}}_{p}|{{\mathbf {p}}}_{21}|}/{\hbar }, \varOmega _{c}={{{{\mathcal {E}}}}_{c}|{{\mathbf {p}}}_{32}|}/{\hbar }$. ${{\mathbf {p}}}_{ij}=|p_{ij}|{{\mathbf {e}}}_{ij}$ is the electric-dipole transition matrix element, ${\mathbf {e}}_{ij}$ is the unit vector of the electric-dipole moment from state $|j\rangle$ to state $|i\rangle$. Under the interaction picture, the equation describing the motion of the system can be expressed as [31]

$$\begin{aligned} i\hbar \left( \frac{\partial }{\partial t}+\varGamma \right) \sigma =\big [{\hat{H}}_\mathrm{int},\sigma \big ], \end{aligned}$$

(3)

where $\sigma$ is a $3\times 3$ density matrix, $\varGamma$ is a $3\times 3$ relaxation matrix with spontaneous emission and dephasing. The Bloch equation of the ladder atomic system in the MDM waveguide is presented in Appendix 5.

The propagation of the probe field and control field follows Maxwell equationss

$$\begin{aligned} \nabla ^2{\mathbf {E}}-\frac{1}{c^{2}}\frac{\partial ^2{\mathbf {E}}}{\partial t^2}=\frac{1}{\varepsilon _0c^2}\frac{\partial ^2{\mathbf {P}}}{\partial t^2}, \end{aligned}$$

(4)

where ${\mathbf {P}}={\mathcal {N}}\{{\mathbf {p}}_{12}\sigma _{21}\mathrm{exp}[i(k_{p}x-\omega _pt)] +{\mathbf {p}}_{23}\sigma _{32}\mathrm{exp}[i(k_{c}x-\omega _ct)]+c.c.\}$ is the electric polarization intensity of the system, and ${\mathcal {N}}$ represents the number density of the atoms.

Under the slowly varying envelope and mean-field approximation, the Maxwell equation describing the envelope of light field can be written as [30]

$$\begin{aligned} i\left( \frac{\partial }{\partial x}+\frac{n_1^2}{cn_\mathrm{eff}}\frac{\partial }{\partial t}\right) \varOmega _{p}e^{i\theta _{p}}+\kappa _{12}\langle \sigma _{21}\rangle =0, \end{aligned}$$

(5)

where $n_\mathrm{eff}=ck_p/\omega _p$ is the effective refractive index of the probe field. $\kappa _{12}={{\mathcal {N}}\omega _l|{{\mathbf {p}}}_{12}|^2}/{2\hbar \varepsilon _0cn_\mathrm{eff}}$ is the coupling constant describing the interaction between the atomic gas and the probe field. The expectation operator $\langle \rangle$ is defined as $\langle \Psi (z)\rangle \equiv {\int _{-\infty }^{+\infty }\hbox {d}z\zeta _{p}^*(z)\Psi (z)}/{\int _{-\infty }^{+\infty }\hbox {d}z|\zeta _{p}(z)|^2}$.

3 Linear properties of SPPs in MDM waveguide

3.1 Base state

We use the multiscale method in singular perturbation theory to solve the Maxwell–Bloch (MB, Eqs. (3) and (4)) equations step by step [32]. The density matrix element and the Rabi frequency of the probe field are expanded as $\sigma _{ij}=\sum _l\epsilon ^l\sigma _{ij}^{(l)}\ (l=0,1,2,3)$, $\varOmega _p=\sum _l\epsilon ^l\varOmega ^{(l)}_{p}\ (l=1,2,3)$, and all the physical quantities on the right side of the equation are functions of the multiple scales variable $x_{l}=\epsilon ^{l}x(l=0,1,2)$, $t_{l}=\epsilon ^{l}t(l=0,1)$. The base state of the system when there is no probe field, i.e., the initial state of the system, can be solved from the zeroth-order solution of the MB equation

$$\begin{aligned} \sigma _{11}^{(0)}=\frac{i\varGamma _{12}\varGamma _{23}|d_{32}|^2+|\zeta _c(z)\varOmega _ce^{i\theta _c}|^2(d_{32}-d_{32}^*)\varGamma _{12}}{i\varGamma |d_{32}|^2+|\zeta _c(z)\varOmega _ce^{i\theta _c}|^2(d_{32}-d_{32}^*)(\varGamma _{12}+2\varGamma _{31})},\nonumber \\ \end{aligned}$$

(6)

where $\varGamma =\varGamma _{12}\varGamma _{23}+\varGamma _{23}\varGamma _{31}+\varGamma _{12}\varGamma _{31}$,$\sigma _{33}^{(0)}=1-(\sigma _{11}^{(0)}+\sigma _{22}^{(0)})$,$\sigma _{22}^{(0)}=\varGamma _{31}\sigma _{11}^{(0)}/{\varGamma _{12}}$,$\sigma _{32}^{(0)}=\zeta _c(z)\varOmega _c(\sigma _{33}^{(0)}-\sigma _{22}^{(0)})e^{i\theta _c}/{d_{32}}$. When there is no incoherent pumping in the system (i.e., $\varGamma _{31}$ $=0$), particles are only occupy on state $|1\rangle$. When we provide an incoherent pumping to the system (i.e., $\varGamma _{31}\ne 0$), a partial number of atoms will be pumped to state $|2\rangle$ (i.e., $\sigma _{22}^{(0)}\ne 0$), which means that the probe field will obtain an effective gain.

3.2 Linear dispersion relation and slow light effect

The first-order solution of $\sigma _{ij}$ by using the multiscale method read

$$\begin{aligned}&\varOmega _p^{(1)}=Fe^{i\theta }, \end{aligned}$$

(7)

$$\begin{aligned}&\sigma _{21}^{(1)}=\frac{D_1}{D}\zeta _p(z)\varOmega _p^{(1)}e^{i\theta _p}, \end{aligned}$$

(8)

$$\begin{aligned}&\sigma _{31}^{(1)}=\frac{D_2}{D}\zeta _p(z)\varOmega _p^{(1)}e^{i\theta _p}, \end{aligned}$$

(9)

where $\theta =K(\omega )x_0-\omega t_0$ and F is an envelope function to be determined, depending on the slow variable $z_{1},z_{2},t_{1}$. $D=(\omega +d_{21})(\omega +d_{31})-|\zeta _{c}(z)\varOmega _ce^{i\theta _{c}}|^2$, $D_1=(\omega +d_{31})(\sigma _{22}^{(0)}-\sigma _{11}^{(0)})-\zeta ^*_{c}(z)\varOmega _c^*\sigma _{32}^{(0)}e^{-i\theta _c^{*}}$, $D_2=(\omega +d_{21})\sigma _{32}^{(0)}-(\sigma _{22}^{(0)}-\sigma _{11}^{(0)})\zeta _{c}(z)\varOmega _ce^{i\theta _{c}}$, $\sigma _{11}^{(1)}=\sigma _{22}^{(1)}=\sigma _{33}^{(1)}=\sigma _{32}^{(1)}=0$.

The linear dispersion relation of SPPs interacting with the atoms is expressed as

$$\begin{aligned} K(\omega )=\frac{\omega }{c}\frac{n_1^2}{n_\mathrm{eff}}+\kappa _{12}\left\langle \frac{D_1}{D}\zeta _p(z)\right\rangle . \end{aligned}$$

(10)

Fig. 2

Linear dispersion diagram of SPPs in MDM waveguide. a, b The relation between the linear absorption $\mathrm{Im}(K)$ of SPPs in symmetric mode and antisymmetric mode of frequency shift $\omega$, respectively. c, d The relation between the linear dispersion $\mathrm{Re}(K)$ of SPPs in symmetric mode and antisymmetric mode of frequency shift $\omega$, respectively. In panel a–d, red solid line and blue dashed line correspond to $\varGamma _{31}=0.5~\varGamma$ and $\varGamma _{31}=0$, respectively

Figure 2 shows the linear absorption $\mathrm{Im}(K)$ and dispersion relation $\mathrm{Re}(K)$ as function of frequency shift $\omega$. The blue dashed correspond the system with $\varGamma _{31}=0$, and the red solid lines correspond to the system with $\varGamma _{31}=0.5~\varGamma$. In Fig. 2a, b, when the system has the incoherent pumping, a transparent window is generated at the center frequency $\omega =0$ due to the quantum interference in the system. At this point, the probe field of the system is strongly inhibited, the system gain benefit and the EIT effect is enhanced. Comparing with antisymmetric mode, the transparent window at the center frequency of the symmetric mode is wider, thus, under the same condition the EIT effect is enhanced in symmetric mode. The transparent window at the center frequency of the antisymmetric mode is deeper, thus, the active gain is easier to obtain for the antisymmetric mode. Those results will strongly affect system parameters during the storage of SPPs. Figure 2c, d shows that the slope of the curve near the center frequency is larger and the group velocity is lower of system with incoherent pumping. When inputting incoherent pumping into the system, the group velocity changes more obviously for the symmetric mode comparing with the antisymmetric mode.

Fig. 3

a, b The group velocity $V_g$ as a function of frequency shift $\omega$ for the symmetric mode and antisymmetric mode, respectively. In panel a, b, red solid line and blue dashed line curve correspond to the system with $\varGamma _{31}=0.5~\varGamma$ and $\varGamma _{31}=0$, respectively. Shown in the inset figures are zoomed near the center frequency $\omega =0$

The group velocity is given by $V_{g}=\mathrm{Re}[\partial K_p/\partial \omega ]^{-1}$, and the detailed expression reads

$$\begin{aligned} V_{g}=\mathrm{Re}\left[ \frac{1}{c}\frac{n_{1}^{2}}{n_\mathrm{eff}}+k_{12}\frac{D_{2}\zeta _{c}^{*}\varOmega _{c}^{*}e^{-i\theta _{c}^{*}}-(\omega +d_{31})D_{1}}{D^{2}}\right] ^{-1}.\nonumber \\ \end{aligned}$$

(11)

Figure 3a (Fig. 3b) shows the group velocity $V_g$ as a function of frequency shift $\omega$ for the symmetric (antisymmetric) mode. The red solid line shows the group velocity of the system with $\varGamma _{31}=0.5\varGamma$, and the blue dashed line shows the group velocity of the system with $\varGamma _{31}=0$. The results show that the group velocity decreases at the central frequency when incoherent pumping is provided to the system for the symmetric mode. However, the group velocity is almost constant for the antisymmetric mode. The conclusions obtained are consistent with Fig. 2c, d.

The parameters used in this section are: $d=200$ nm, $\mu _{1}=\mu _{2}=1, \varepsilon _{1}=1, \varepsilon _{2}=-29.25+0.57i, \lambda =780$ nm, $\varGamma _{12}=6\times 10^{6}~\mathrm{s^{-1}}, \varGamma _{23}=1\times 10^{3}~\mathrm{s^{-1}},\varOmega _{c}=3\times 10^{8}~\mathrm{s^{-1}},\varGamma _{31}=3\times 10^{6}~\mathrm{s^{-1}}$. The matal is chosen as silver, and the cold atom gas ensemble is chosen as $^{87}{Rb}$, the energy levels are [12]$, |1\rangle =|5S_ {1/2},F=2\rangle ,|2\rangle =|5P_{3/2},F=3\rangle ,|3\rangle =|60S_{1/2}\rangle$. In symmetric mode $k=(18.46+0.031i)\times 10^{4}~\mathrm {cm}^{-1}$, in antisymmetric mode $k=(12.40+0.070i)\times 10^{4}~\mathrm {cm}^{-1}$.

4 Storage and retrieval of SPPs solitons in the MDM waveguide

4.1 Ultraslow optical solitons for EIT memory

In this section, we will focus on the nonlinearity of the system. The divergence-solvable conditions of second-order approximation is: $i[\partial F/\partial z_1+\partial F/(V_g\partial t_1)]=0$. The solvable condition in the third-order probe yields the nonlinear equation approximation is $i\partial F/\partial z_2-K_2\partial ^2 F/2\partial t_1^2-W|F|^2Fe^{-2{\bar{\alpha }}z_2}=0$. The second-order solutions of MB equations are given in Appendix 5. Combining the solvable conditions and envelope equations, the nonlinear envelop equation for probe light propagation is obtained

$$\begin{aligned} i\left( \frac{\partial }{\partial z}+\alpha \right) U-\frac{K_2}{2}\frac{\partial ^2}{\partial \tau ^2}U-W|U|^2U=0, \end{aligned}$$

(12)

with $\alpha =\mathrm{Im}[K(\omega =0)], U=\epsilon Fe^{-\alpha z}, \tau =t-x/V_{g}$, the complex group velocity dispersion of the probe field being $K_{2}=\partial ^{2}K(\omega )/\partial \omega ^2$, the probe file self-phase modulation coefficient W is given by

$$\begin{aligned} W=&\kappa _{12}\left\langle \frac{(\omega +d_{31})(a_{11}^{(2)}-a_{22}^{(2)})+\zeta _c^*(z)\varOmega _c^*e^{-i\theta _c^*}a_{32}^{(2)}}{D}\right. \nonumber \\&\left. \times \zeta _p(z)|\zeta _p(z)e^{i\theta _p}|^2\right\rangle . \end{aligned}$$

(13)

In general, the coefficients in Eq. (12) are complex. The stable propagation of SPPs needs to satisfy the low absorption of probe light, and balance of the dispersion and nonlinearity. Therefore, in order to make SPPs propagate stably over long distances, we need to find a set of parameters such that the real part of each term in Eq. (12) is much larger than the imaginary part. Ignoring the imaginary part of the equation, nonlinear Schrödinger equation (NLSE) in the dimensionless form is obtained

$$\begin{aligned} i\frac{\partial u}{\partial s}+\frac{\partial ^2u}{\partial \sigma ^2}+2|u|^2u=0, \end{aligned}$$

(14)

where we introduce the dimensionless variables $u=U/U_{0}$, $\sigma =\tau /\tau _{0}$,$s=-x/2L_{D}$. Here, $L_D=\tau _0^2/{{\tilde{K}}_2}$ is typical dispersion length of the system, $\tau _{0}$ is typical time scale, $L_{N}=1/({\tilde{W}}|U_{0}|^{2})$ is typical nonlinearity length. When the dispersion and nonlinear effects are balanced $(L_{D}=L_{N})$, the typical half Rabi frequency $U_0=(1/\tau _0)\sqrt{{\tilde{K}}_2/{\tilde{W}}}$. ${\tilde{K}}_{2}$ and ${\tilde{W}}$ is the real part of $K_{2}$ and W, respectively.

There are various soliton solutions in the nonlinear Schrödinger equation (NLSE). We choose a bright soliton solution, operation in the original parameter variables, the form of the soliton solution can be expressed as $u=\mathrm{sech}(\sigma )\exp (is)$, which can be expressed in the form of half Rabi frequency as

$$\begin{aligned} \varOmega _p(x,t)=\frac{1}{\tau _0}\sqrt{\frac{{\tilde{K}}_2}{{\tilde{W}}}}\mathrm{sech}\left[ \frac{1}{\tau _0}(\tau \!-\!\frac{x}{{\tilde{V}}_g})\right] \exp \left[ i{\tilde{K}}_0x\!+\!i\frac{x}{2L_D}\right] .\nonumber \\ \end{aligned}$$

(15)

In order to make the real part of coefficients much larger than the imaginary part in Eq. (12), the parameters selected above analyse are as follows: In symmetric mode, $\varGamma _{31}=0, \Delta _{2}=1\times 10^{7}~\mathrm {s^{-1}}, \Delta _{3}=-3\times 10^{5}~\mathrm {s^{-1}}.$ Then, we obtain $K_{2}=(1.5+0.4i)\times 10^{-11}~\mathrm {cm^{-1}s^{-2}}, W=(-3.6+0.01i)\times 10^{-16}~\mathrm {cm^{-1}s^{-2}}, L_{A}=1/|\alpha |=3~\mathrm {cm}, L_{D}=\tau _{0}^{2}/{\tilde{K}}_{2}=0.02~\mathrm {cm}.$ In antisymmetric mode, $\varGamma _{31}=0, \Delta _{2}=-1.67\times 10^{6}~\mathrm {s^{-1}}, \Delta _{3}=1.8\times 10^{5}~\mathrm {s^{-1}}.$ Then, we obtain $K_{2}=(-2.7+0.45i)\times 10^{-11}~\mathrm {cm^{-1}s^{-2}}, W=(7.6+0.02i)\times 10^{-17}~\mathrm {cm^{-1}s^{-2}}, L_{A}=1/|\alpha |=5~\mathrm {cm}, L_{D}=0.013~\mathrm {cm}.$ In the symmetric mode and the antisymmetric mode, the selected parameters make the real part of these complex numbers much larger than the imaginary part. In addition, the absorption length $L_{A}$ is also much larger than the typical nonlinearity length $L_{D}$.

4.2 Storage and retrieval of SPPs solitons

In this subsection, we use numerical methods to explore the storage and retrieval of SPPs solitons in the MDM waveguide. To realize ultraslow SPPs solitons storage and retrieval process, we need to simplify the MB equations into the effective MB equation, which is given in Appendix 5. By switching-off and switching-on of the control field, the storage process can be obtained. The control field is a function of time, which can be expressed in the form of half Rabi frequency as follows:

$$\begin{aligned} \varOmega _c(0,t)= & {} \varOmega _{c0}\left\{ 1-\frac{1}{2}\cdot \tanh \left[ \frac{t-T_\mathrm{off}}{T_\mathrm{s}}\right] \right. \nonumber \\&+\left. \frac{1}{2}\cdot \tanh \left[ \frac{t-T_\mathrm{on}}{T_\mathrm{s}}\right] \right\} , \end{aligned}$$

(16)

where $T_\mathrm{off}$ and $T_\mathrm{on}$ are times of switching-off and switching-on of the control field, respectively. The adiabatic parameter $T_\mathrm{s}$ represents the switching time of the control field. According to the dark state polaritons theory, the ultraslow soliton during storage can be expressed as:

$$\begin{aligned}&\varOmega _p(x,t)\approx \nonumber \\&\!\!\!\left\{ \!\!\! \begin{array}{c} \frac{A}{\tau _{0}}\sqrt{\frac{\widetilde{K_{2}}}{\widetilde{W}}} \mathrm {sech}[\frac{1}{\tau _{0}}(\tau -\frac{x}{\widetilde{V}_{g}})] \exp [i\widetilde{K_{0}}x+i\frac{x}{2L_{D}}],t<T_\mathrm{off} \\ 0,T_\mathrm{off}<t<T_\mathrm{on} \\ \!\frac{B}{\tau _{0}}\!\sqrt{\frac{\widetilde{K_{2}}}{\widetilde{W}}} \mathrm {sech}[\frac{1}{\tau _{0}}(\tau \!\!-\!\!\frac{x}{\widetilde{V}_{g}}\!\!-\!\!T_\mathrm{D})] \exp [i\widetilde{K_{0}}x\!+\!i\frac{x}{2L_{D}}\!+\!i\phi _0],t\!>\!T_\mathrm{on}\nonumber \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(17)

with A and B are constants connected to the initial condition, $\phi _{0}$ is a constant phase factor.

In order to explore the storage effect of optical soliton, we defined storage efficiency $\eta$ and fidelity $J^{2}$

$$\begin{aligned} \eta= & {} \frac{\int _{-\infty }^{+\infty }|\varOmega _p(L,t)|^2\text {d}t}{\int _{-\infty }^{+\infty }|\varOmega _p(x=0,t)|^2\text {d}t}, \end{aligned}$$

(18)

$$\begin{aligned} J^2= & {} \frac{|\!\int _{\!-\!\infty }^{\!+\!\infty }\varOmega _p(x\!=\!0,t)\cdot \varOmega _s(x\!=\!L,t\!+\!T_\mathrm{D}')\text {d}t\!|^2}{\int _{-\infty }^{\!+\!\infty }|\!\varOmega _p(x\!\!=\!\!0,t)|^2\text {d}t\cdot \int _{\!-\!\infty }^{\!+\!\infty }|\varOmega _p(x\!\!=\!\!L,t+T_\mathrm{D}')|^2\text {d}t},\nonumber \\ \end{aligned}$$

(19)

with $\eta$ characterize the energy loss of the output pulse, $J^{2}$ characterize the degree of waveform overlap in light pulses. The fidelity of light pulse storage is represented by $\eta J^{2}$.

The numerical calculation used the following physical parameters: for symmetric mode, $\varOmega _{c0}=6\times 10^{6}~\mathrm {s^{-1}}=\varGamma _{12}, \varGamma _{23}=3.2\times 10^{3}~\mathrm {s^{-1}}, \Delta _{2}=1\times 10^{7}~\mathrm {s^{-1}}, \Delta _{3}=-3\times 10^{5}~\mathrm {s^{-1}}, \tau _{0}=6\times 10^{-7}~\mathrm {s}, T_{off}=2.5~\tau _{0}, T_{on}=10~\tau _{0}$; for antisymmetric mode, $\varOmega _{c0}=1\times 10^{7}~\mathrm {s^{-1}},\varGamma _{12}=6\times 10^{6}~\mathrm {s^{-1}}, \varGamma _{23}=3.2\times 10^{3}~\mathrm {s^{-1}}, \Delta _{2}=-1.67\times 10^{6}~\mathrm {s^{-1}}, \Delta _{3}=1.8\times 10^{5}~\mathrm {s^{-1}}, \tau _{0}=6\times 10^{-7}~\mathrm {s}, T_{off}=3~\tau _{0}, T_{on}=13~\tau _{0}$. The other parameters of the cold atomic gas used in this subsection is the same as the previous subsection. In the process of numerical simulation, the initial form of the probe field is $\varOmega _{p0}\cdot \mathrm {sech}[1.763t/\tau _0]$, Eq. (16) gives the form of the control field.

Fig. 4

Time evolution of $|\varOmega _{p}\tau _{0}|$ and $|\varOmega _{c}\tau _{0}|$ as functions of x and t for EIT memory process in MDM waveguide system. a–c are temporal and spatial evolution of $|\varOmega _c\tau _0|$ and $|\varOmega _p\tau _0|$ for symmetric mode. a Storage and retrieval of a weak pulse with input pulse $\varOmega _{p}(0,t)\tau _0=0.6\mathrm {sech}[1.763t/\tau _0]$; b Storage and retrieval of a soliton pulse with input pulse $\varOmega _{p}(0,t)=1.36\mathrm {sech}[1.763t/\tau _0]$; c Storage and retrieval of a strong pulse with input pulse $\varOmega _{p}(0,t)=2.1\mathrm {sech}[1.763t/\tau _0]$. d–f are temporal and spatial evolution of $|\varOmega _c\tau _0|$ and $|\varOmega _p\tau _0|$ for antisymmetric mode. d Storage and retrieval of a weak pulse with input pulse $\varOmega _{p}(0,t)\tau _0=\mathrm {sech}[1.763t/\tau _0]$; e Storage and retrieval of a soliton pulse with input pulse $\varOmega _{p}(0,t)=2\mathrm {sech}[1.763t/\tau _0]$; f Storage and retrieval of a strong pulse with input pulse $\varOmega _{p}(0,t)=2.7\mathrm {sech}[1.763t/\tau _0]$

Figure 4 shows time evolution of $|\varOmega _{p}\tau _{0}|$ and $|\varOmega _{c}\tau _{0}|$ as functions of x and t in three optical memory processes. The signal pulse is launched into the waveguide at $x=0$ and readout at $x=0.65~\mathrm{mm}$ after a 6 $\mu s$ storage and retrieval process. Temporal and spatial evolution of $|\varOmega _c\tau _0|$ and $|\varOmega _p\tau _0|$ for (a), (b), (c) symmetric mode, and (d), (e), (f) antisymmetric mode.

Figure 4a–c shows temporal and spatial evolution of $|\varOmega _c\tau _0|$ and $|\varOmega _p\tau _0|$ for symmetric mode. Figure 4a shows the result of optical memory process for a weak probe pulse, where $\varOmega _{p}(0,t)\tau _0=0.6\mathrm {sech}[1.763t/\tau _0]$. In this situation, the linear dispersion effect in the system is strong and dominant. The light pulse is deformed during storage, and the probe pulse width broadened. The storage efficiency in this simulation is $\eta \approx 68\%$ and the memory fidelity is $\eta J^2\approx 60\%$. Figure 4b shows the result of optical memory process for a weak nonlinear probe pulse, where $\varOmega _{p}(0,t)\tau _0=1.36\mathrm {sech}[1.763t/\tau _0]$. In this case, the linear dispersion effect and the nonlinear effect in the system are balanced. The probe pulse is transformed into a sharp soliton before closing the control field, and is stored in the atomic medium after closing the control field. When the control light field is turned on again, the probe pulse continues to propagate forward in the form of a soliton. The storage efficiency in this simulation is $\eta \approx 75\%$, and the memory fidelity is $\eta J^2\approx 73\%$. Figure 4c shows the result of optical memory process for a strong probe pulse, where $\varOmega _{p}(0,t)\tau _0=2.1\mathrm {sech}[1.763t/\tau _0]$. For such a probe field, the system is nonlinearity dominant. The signal pulse has a significant distortion after storage, and some new peaks are generated. Storage efficiency and fidelity are not ideal, $\eta \approx 73\%, \eta J^2\approx 62\%$.

Figure 4d–f are temporal and spatial evolution of $|\varOmega _c\tau _0|$ and $|\varOmega _p\tau _0|$ for antisymmetric mode. Figure 4d shows the result of optical memory process for a weak probe pulse, where $\varOmega _{p}(0,t)\tau _0=\mathrm {sech}[1.763t/\tau _0]$. Similar to the case of the symmetric mode, the system is dispersion dominant. In this case, the storage efficiency is $\eta \approx 67\%$, and a low memory fidelity $\eta J^2\approx 60\%$. Figure 4e shows the result of optical memory process for a weak nonlinear probe pulse, where $\varOmega _{p}(0,t)\tau _0=2\mathrm {sech}[1.763t/\tau _0]$. The nonlinearity balancing the dispersion, so that a stable propagating SPPs soliton is formed. In this case, the storage efficiency improves to $\eta \approx 75\%$, and the memory fidelity improves to $\eta J^2\approx 73\%$. Figure 4f shows the result of optical memory process for a strong probe pulse, where $\varOmega _{p}(0,t)\tau _0=2.7\mathrm {sech}[1.763t/\tau _0]$. The strong nonlinearity not only causes an low efficiency $\eta \approx 70\%$, an low memory fidelity $\eta J^2\approx 56\%$.

From the above results, we can see that stable propagating SPPs soliton can be formed for both symmetric mode and antisymmetric mode, and both the optical soliton memory has a relatively high stability and efficiency, but with different parameters region. Next, we will explore the influencing factors of the optical soliton memory by changing the input signal amplitude $|\varOmega _{p0}\tau _0|$ and input control field amplitude $|\varOmega _{c0}\tau _0|$ to improve the stability and efficiency of the optical soliton memory.

Figure 5a, b illustrate the memory fidelity $\eta J^2$ as a function of $|\varOmega _{p0}\tau _0|$ and $|\varOmega _{c0}\tau _0|$ for symmetric mode and antisymmetric mode, respectively. Figure 5a shows there are two band regions where the memory fidelity is higher than 80%. The memory fidelity is gradually decreasing at the periphery of the frequency band. In the two higher fidelity band regions, the amplitude of the control field $|\varOmega _{c0}\tau _0|$ is similar, and the probe amplitude $|\varOmega _{p0}\tau _0|$ is quite different. Fig. 5b shows there is a band regions where the memory fidelity is higher than 80%. Similar to the case of the symmetric mode, near the band the memory fidelity decay quickly. In the band region, the amplitude of control field $|\varOmega _{c0}\tau _0|$ is relatively large and we can obtain a relatively high memory fidelity even if we vary signal amplitude $|\varOmega _{p0}\tau _0|$ in a wide range.

Fig. 5

Optimizing of MDM waveguide optical memory. The memory fidelity $\eta J^2$ as a function of input signal amplitude $|\varOmega _{p0}\tau _0|$ and input control field amplitude $|\varOmega _{c0}\tau _0|$ for a symmetric mode and b antisymmetric mode

5 Conclusion

In summary, we propose a scheme to realize storage and retrieval of symmetric and antisymmetric nonlinear SPPs solitons via EIT in a MDM waveguide. The atoms interacting with SPPs have a ladder-type three-level excited configuration with incoherent pumping. In the linear regime, we obtain that the Ohmic loss of both symmetric and antisymmetric modes in the system can be totally compensated under EIT condition but with different incoherent pumps. The transparency window becomes wider for the symmetric mode, but deeper for the antisymmetric mode, when incoherent pumping exists. We also show that in nonlinear propagation regime a huge enhancement of Kerr nonlinearity of the symmetric and antisymmetric SPPs can be obtained, and a gain-assisted ($1+1$)-dimensional symmetric and antisymmetric subluminal surface polaritonic solitons can be produced, stored and retrieved with high efficiency and stability. In the end, we study the strategies to optimize the optical memory for the two modes. Our study are helpful for practical applications in quantum information processing, and building future high-performance optical quantum information networks.

Appendices

Appendix

A The electric field expressions and dispersion relation

The electric field expression of symmetric propagation mode:

$$\begin{aligned}&{\mathbf {E}}({\mathbf {r}},t)\nonumber \\&~~=\left\{ \begin{array}{lcl} (k{\mathbf {e}}_z\!-\!ik_{z2}{\mathbf {e}}_x)\frac{\varepsilon _1}{k\varepsilon _2} \cosh (k_{z1}\frac{d}{2})e^{\!-\!k_{z2}(z\!-\!\frac{d}{2})\!+\!i(kx\!-\!\omega _lt)},\!z>\frac{d}{2}\\ \big [\cosh (k_{z1}z){\mathbf {e}}_z\!+\!\frac{ik_{z1}}{k} \sinh (k_{z1}z){\mathbf {e}}_x\big ]e^{i(kx\!-\!\omega _lt)},\!-\!\frac{d}{2}\!<\!z\!<\!\frac{d}{2}\\ (k{\mathbf {e}}_z\!+\!ik_{z2}{\mathbf {e}}_x)\frac{\varepsilon _1}{k\varepsilon _2} \cosh (k_{z1}\frac{d}{2})e^{k_{z2}(z\!+\!\frac{d}{2})\!+\!i(kx-\omega _lt)},\!z\!<\!-\frac{d}{2}.\nonumber \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(20)

The electric field expression of antisymmetric propagation mode:

$$\begin{aligned}&{\mathbf {E}}({\mathbf {r}},t)\nonumber \\&~~=\left\{ \begin{array}{lcl} (k{\mathbf {e}}_z\!\!-\!\!ik_{z2}{\mathbf {e}}_x)\frac{\varepsilon _1}{k\varepsilon _2} \sinh (k_{z1}\frac{d}{2})e^{\!-\!k_{z2}(z\!-\!\frac{d}{2})\!+\!i(kx-\omega _lt)},\!z\!>\!\frac{d}{2}\\ \big [\sinh (k_{z1}z){\mathbf {e}}_z\!+\!\frac{ik_{z1}}{k} \cosh (k_{z1}z){\mathbf {e}}_x\big ]e^{i(kx\!-\!\omega _lt)},\!\!-\!\frac{d}{2}\!<\!z\!<\!\frac{d}{2}\\ \!\!-\!(k{\mathbf {e}}_z\!\!+\!\!ik_{z2}{\mathbf {e}}_x)\frac{\varepsilon _1}{k\varepsilon _2} \sinh (k_{z1}\frac{d}{2})e^{k_{z2}(z\!+\!\frac{d}{2})\!+\!i(kx\!-\!\omega _lt)},\!z\!<\!-\frac{d}{2}.\nonumber \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(21)

The dispersion relation of symmetric mode

$$\begin{aligned} \varepsilon _1k_{z2}+\varepsilon _2k_{z1}\tanh \left( k_{z1}\frac{d}{2}\right) =0. \end{aligned}$$

(22)

The dispersion relation of antisymmetric mode

$$\begin{aligned} \varepsilon _1k_{z2}+\varepsilon _2k_{z1}\coth \left( k_{z1}\frac{d}{2}\right) =0, \end{aligned}$$

(23)

where $k_{zl}^2=k^2-({\omega _l}/{c})^2\varepsilon _{l}$ is the wave number, and ${\mathbf {e}}_{x,y,z}$ is the unit vector in the x, y, z directions.

B Bloch equations

$$\begin{aligned} i\left( \frac{\partial }{\partial {t}}+\varGamma _{31}\right) \sigma _{11}- & {} i\varGamma _{12}\sigma _{22}+\zeta _p^*(z)\varOmega _p^*\sigma _{21}e^{-i\theta _p^*}\nonumber \\- & {} \zeta _p(z)\varOmega _p\sigma _{21}^*e^{i\theta _p}=0,\nonumber \\ i\left( \frac{\partial }{\partial {t}}+\varGamma _{12}\right) \sigma _{22}- & {} i\varGamma _{23}\sigma _{33}+\zeta _p(z)\varOmega _p\sigma _{21}^*e^{i\theta _p}\nonumber \\+ & {} \zeta _c^*(z)\varOmega _c^*\sigma _{32}e^{-i\theta _c^*}-\zeta _p^*(z)\varOmega _p^*\sigma _{21}^*e^{-i\theta _p^*}\nonumber \\- & {} \zeta _c(z)\varOmega _c\sigma _{32}^*e^{i\theta _c}=0,\nonumber \\ i\left( \frac{\partial }{\partial {t}}+\varGamma _{23}\right) \sigma _{33}- & {} i\varGamma _{31}\sigma _{11}+\zeta _c(z)\varOmega _c\sigma _{32}^*e^{i\theta _c}\nonumber \\- & {} \zeta _c^*(z)\varOmega _c^*\sigma _{32}^*e^{-i\theta _c^*}=0,\nonumber \\ \left( i\frac{\partial }{\partial {t}}+d_{21}\right) \sigma _{21}+ & {} \zeta _c^*(z)\varOmega _c^*\sigma _{31}e^{-i\theta _c^*}\nonumber \\+ & {} \zeta _p(z)\varOmega _pe^{i\theta _p}(\sigma _{11}-\sigma _{22})=0,\nonumber \\ \left( i\frac{\partial }{\partial {t}}+d_{31}\right) \sigma _{31}- & {} \zeta _p(z)\varOmega _p\sigma _{32}e^{i\theta _p}\nonumber \\+ & {} \zeta _c(z)\varOmega _c\sigma _{21}e^{i\theta _c}=0,\nonumber \\ \left( i\frac{\partial }{\partial {t}}+d_{32}\right) \sigma _{32}- & {} \zeta _p^*(z)\varOmega _p^*\sigma _{31}e^{-i\theta _p^*}\nonumber \\+ & {} \zeta _c(z)\varOmega _ce^{i\theta _c}(\sigma _{22}-\sigma _{33})=0,\nonumber \\ \end{aligned}$$

(24)

where $d_{21}=\Delta _2+i\gamma _{21},d_{31}=\Delta _3+i\gamma _{31}$ and $d_{32}=\Delta _3-\Delta _2+i\gamma _{32}$. $\gamma _{ij}=(\varGamma _i+\varGamma _j)/2$ is the decoherence probability of the system.

C Second-order solutions of MB equations

$$\begin{aligned} \sigma _{11}^{(2)}= & {} \left\{ \left[ -i\varGamma _{23}{+}2|\zeta _c(z)\varOmega _ce^{i\theta _c}|^2\left( \frac{1}{d_{32}}{-}\frac{1}{d_{32}^*}\right) \right] \right. \nonumber \\&\left. \times \left( \frac{D_1^*}{D^*}{-}\frac{D_1}{D}\right) +i\varGamma _{12}\varOmega _c(\frac{\zeta _c^*(z)e^{-i\theta _c^*}}{d_{32}}\frac{D_2}{D}-c.c)\right\} \nonumber \\&/\left\{ \left( \varGamma _{23}\varGamma _{12}+\varGamma _{23}\varGamma _{31}+\varGamma _{31}\varGamma _{12}\right) \right. \nonumber \\&\left. {+}i(\varGamma _{12}{+}2\varGamma _{31})|\zeta _c(z)\varOmega _ce^{i\theta _c}|^2\left( \frac{1}{d_{32}}{-}\frac{1}{d_{32}^*}\right) \right\} \nonumber \\&\times |\zeta _p(x)e^{i\theta _p}|^2|F|^2e^{-2{\bar{\alpha }}z_2}\nonumber \\= & {} a_{11}^{(2)}|\zeta _p(z)e^{i\theta _p}|^2|F|^2e^{-2{\bar{\alpha }}z_2},\nonumber \\ \sigma _{22}^{(2)}= & {} \frac{\varGamma _{31}a_{11}^{(2)}+i\left( \frac{D_1^*}{D^*}-\frac{D_1}{D}\right) }{\varGamma _{12}}\times |\zeta _p(z)e^{i\theta _p}|^2|F|^2e^{-2{\bar{\alpha }}z_2}\nonumber \\= & {} a_{22}^{(2)}|\zeta _p(z)e^{i\theta _p}|^2|F|^2e^{-2{\bar{\alpha }}z_2},\nonumber \\ \sigma _{32}^{(2)}= & {} \frac{\left[ \frac{D_2}{D}{-}\zeta _c(z)\varOmega _c\left( 2a_{22}^{(2)}{+}a_{11}^{(2)}\right) \right] }{d_{32}}\nonumber \\&{\times }|\zeta _p(z)e^{i\theta _p}|^2|F|^2e^{-2{\bar{\alpha }}z_2}\nonumber \\= & {} a_{32}^{(2)}|\zeta _p(z)e^{i\theta _p}|^2|F|^2e^{-2{\bar{\alpha }}z_2},\nonumber \\ \sigma _{21}^{(2)}= & {} i\frac{D_2\zeta _c^*(x)\varOmega _c^*e^{-i\theta _c^*}-D_1(\omega +d_{31})}{D^2}\zeta _p(z)\frac{\partial F}{\partial t_1}e^{i\theta }e^{i\theta p}\nonumber \\= & {} a_{21}^{(2)}\zeta _p(z)\frac{\partial F}{\partial t_1}e^{i\theta }e^{i\theta p},\nonumber \\ \sigma _{31}^{(2)}= & {} -\frac{1}{\zeta _c^*(z)\varOmega _c^*e^{-i\theta _c^*}}\left[ i\frac{D_1}{D}+(\omega +d_{21})a_{21}^{(2)}\right] \nonumber \\&\zeta _p(z)\frac{\partial F}{\partial t_1}e^{i\theta }e^{i\theta _p}\nonumber \\= & {} a_{31}^{(2)}\zeta _p(z)\frac{\partial F}{\partial t_1}e^{i\theta }e^{i\theta _p}, \end{aligned}$$

(25)

where $\sigma _{33}^{(2)}=-(\sigma _{11}^{(2)}+\sigma _{22}^{(2)}), \theta =K(\omega )z_0-\omega t_0.$

D Effective MB equations

Taking the transformation ${\tilde{\sigma }}_{jj}(z,t)=\langle \sigma _{jj}(\rho ,\theta ,z,t)\rangle$, ${\tilde{\sigma }}_{31}$ (z, t)=$\langle \sigma _{31}(\rho ,\theta ,z,t)\rangle$, ${\tilde{\sigma }}_{21}(z,t)=\sigma _{21}(\rho ,\theta ,z,t)/\zeta _{c}(\rho ,\theta )$, ${\tilde{\sigma }}_{32}$ (z, t)=$\sigma _{32}(\rho ,\theta ,z,t)/\zeta _{c}(\rho ,\theta )$, then the MB equations reduce to effective MB equations

$$\begin{aligned} i\left( \frac{\partial }{\partial t}+\varGamma _{31}\right) {\tilde{\sigma }}_{11}- & {} i\varGamma _{12}{\tilde{\sigma }}_{22}+\varrho _{p1}\varOmega _{p}^{*}{\tilde{\sigma }}_{21}\nonumber \\- & {} \varrho _{p1}\varOmega _{p}{\tilde{\sigma }}_{21}^{*}=0,\nonumber \\ i\left( \frac{\partial }{\partial t}+\varGamma _{12}\right) {\tilde{\sigma }}_{22}- & {} i\varGamma _{23}{\tilde{\sigma }}_{33}+\varrho _{p1}\varOmega _{p}{\tilde{\sigma }}_{21}^{*}+\varrho _{c}\varOmega _{c}^{*}{\tilde{\sigma }}_{32}\nonumber \\- & {} \varrho _{p1}\varOmega _{p}^{*}{\tilde{\sigma }}_{21}-\varrho _{c}\varOmega _{c}{\tilde{\sigma }}_{32}^{*}=0,\nonumber \\ i\left( \frac{\partial }{\partial t}+\varGamma _{23}\right) {\tilde{\sigma }}_{33}- & {} i\varGamma _{31}{\tilde{\sigma }}_{11}+\varrho _{c}\varOmega _{c}{\tilde{\sigma }}_{32}^{*}-\varrho _{c}\varOmega _{c}^{*}{\tilde{\sigma }}_{32}=0,\nonumber \\ \left( i\frac{\partial }{\partial t}+d_{21}\right) {\tilde{\sigma }}_{21}+ & {} \varOmega _{c}^{*}{\tilde{\sigma }}_{31}+\varrho _{p2}\varOmega _{p}({\tilde{\sigma }}_{11}-{\tilde{\sigma }}_{22})=0,\nonumber \\ \left( i\frac{\partial }{\partial t}+d_{31}\right) {\tilde{\sigma }}_{31}- & {} \varrho _{p1}\varOmega _{p}{\tilde{\sigma }}_{32}+\varrho _{c}\varOmega _{c}{\tilde{\sigma }}_{21}=0,\nonumber \\ \left( i\frac{\partial }{\partial t}+d_{32}\right) {\tilde{\sigma }}_{32}- & {} \varrho _{p2}\varOmega _{p}^{*}{\tilde{\sigma }}_{31}+\varOmega _{c}({\tilde{\sigma }}_{22}-{\tilde{\sigma }}_{33})=0,\nonumber \\ \end{aligned}$$

(26)

with $\varrho _{p1}=\langle \zeta _c(z)\cdot \zeta _p(z)\rangle$, $\varrho _{p2}=\langle \zeta _p(z)/\zeta _c(z)\rangle$, $\varrho _{c}=\langle |\zeta _c(z)|^2\rangle$.