A study of cylindrically symmetric solutions in $f(R, \phi , X)$ theory of gravity

Abstract

In this article, we aim to investigate some cylindrically symmetric solutions in a very well known modified theory named as $f(R, \phi , X)$ theory of gravity, where the terms R, $\phi$ and X are clarified as Ricci Scalar, scalar potential, and kinetic term respectively. For this purpose, we consider the cylindrically symmetric space-time to discuss the cylindrical solutions in some realistic regions. We further discuss six distinct cases of exact solutions using the field equations of $f(R, \phi , X)$ modified theory of gravity. Furthermore, we set some suitable values of $U_0$ and $\alpha$ in $f(R, \phi , X)=R+\alpha R^2 - V(\phi )+ X$ for the investigation of well-known Levi–Civita and cosmic string solutions. The Energy conditions are also investigated for all different cases and observed that null energy conditions are violated, which is the indication of the existence of cylindrical wormholes.

1 Introduction

According to the Big bang theory, a massive blast from a single point of uncountable density was the reasoning behind the existence of our universe. From that stage of matter, it is expanding at an accelerating rate [1,2,3]. The reason defined beyond this accelerating expansion is some kind of matter and energy known as Dark Matter (DM) and Dark Energy (DE) [4,5,6,7,8,9,10,11]. In 1905, Albert Einstein provided a very different approach to explain this phenomenon which is named as “Special Theory of Relativity” (STR). Then in 1915, he provided “General Theory of Relativity” (GTR) which is the mixture of STR and the laws of gravity proposed by Isaac Newton [12]. These two theories depend upon a condition: All physics laws will be independent of the inertial frame of references. It means that they produce the same result in different places as STR and GTR are failed to explain cosmic expansion properly. Therefore, different modified theories are presented to create different ways for researchers to reveal the important facts about the accelerating expansion. Some of these theories are f(R), f(R, T), f(G), f(G, T) and f(R, G), where R is the Ricci scalar, G is the Gauss-Bonnet (GB) term and T is the trace of energy-momentum tensor [13,14,15,16,17,18,19,20].

In cosmology, the study of cylindrical symmetry provided different opportunities to get some realistic results. The static cylindrically symmetric vacuum solutions in Weyl coordinates studied by Azadi et al. in f(R) theory of gravity [21]. In Riemannian geometry, Cogliati presented different terms: Schouten, Levi–Civita, and the notation of parallelism [22]. To explain the interior and exterior space-time of a model of cosmic strings, Linet [23] presented a set of static metrics with cylindrical symmetry. Lian [24] found the cylindrically symmetric and static vacuum solutions of Einstein’s field equation with cosmological constant $\Lambda$. The cylindrically symmetric solutions of the $(2+1)$-dimensional nonlinear $\sigma$ model discussed by using the inverse scattering method have been discussed by Mikhailov, and Yarimchuk [25]. Shamir and Zahid investigated the exact solutions of cylindrically symmetric space-time in the background of f(R) theory of gravity. Sharif and Zaeem [27] explained the structure scalars for self-gravitating cylindrically symmetric change the anisotropic fluid. In the case of stationary cylindrical space-time, the existence of Einstein–Maxwell dilation and fluid system has been discussed by Klepac and Horskey [28].

Moreover, cylindrically symmetric results in f(R, G) theory of gravity are discussed by Shamir and Zia [29]. The existence of static solutions to the cylindrically symmetric Einstein–Vlasov system has been proved by Fajallborg [30] and sowed that the matter cylinder in two of the three spatial dimensions has finite extension. Momeni and Miraghaei [31] investigated the exact solution for the massless cylindrically symmetric scalar field in general relativity. Azadi et al. [32] studied the static cylindrically symmetric vacuum solutions in Weyl coordinates in the context of the metric f(R) theories of gravity. This paper constructs the exact solutions corresponding to different f(R) models. Momeni [33] obtained a two-parameter family of exact solutions which contains a cosmological constant and proved that in f(R) gravity the constant curvature solution in cylindrically symmetric cases is only one member of the most generalized Tian family in General relativity. Houndjo et al. [34] investigated the static cylindrically symmetric vacuum solutions in Weyl coordinates in the framework of f(T) theory of gravity, where T is the torsion scalar. Houndjo et al. [35] also presented the detailed cylindrically symmetric solutions for a type of Gauss-Bonnet gravity and derived the full system of field equations, and showed that there exist seven families of exact solutions for three forms of viable modes. Momeni et al. [36] investigated the cylindrical solutions in mimetic gravity and noticed that Kasner’s family of exact solutions needs to be reconsidered under this type of modified gravity. Delice [37] discussed the static cylindrically symmetric vacuum solutions with a cosmological constant in the framework of the Brans–Dicke theory.

Motivated from all the above work, we are interested in exploring cylindrically symmetric solutions in $f(R,\phi , X)$ modified theory of gravity. Bahamonde et al. [38] discussed the most generalized and extended form of the theory of gravity named as $f(R, \phi , X)$ modified gravity. This theory contains a wide range of known dark energy and modified gravity models, for instance, f(R) gravity models or Galileons. In particular, several cosmological solutions are studied within the framework of these theories, specific solutions that can provide cosmic acceleration at late times, and even the exact $\Lambda$CDM evolution. Shamir and Malik considered this theory and investigated some exact solutions using the different equations of state parameters [39]. Bahamonde, along with his collaborators [40] investigated new exact spherically symmetric solutions in $f(R,\phi , X)$ modified gravity by Noether’s symmetry approach. Recently, Shamir et al. [41] discussed the wormhole solutions in the background of $f(R, \phi , X)$ modified gravity. The same Authors [42] also investigated non-commutative wormhole geometry in the said gravity. Bahamonde et al. [43] discussed the minimally and non-minimally curvature-coupled scalar-tensor theory and studied the occurrence of accelerating universe versus decelerating. Furthermore, by using the same theory, some thought-provoking topics have been discussed in [44,45,46,47,48,49,50,51,52,53].

The considerations of spherically symmetric spacetime in finding the solution has been a task by many theoretical astrophysicists. However, the non-spherically objects, like cylindrical metric, axially symmetric, etc, are also seen to be the ingredients of our cosmos. Handling axially symmetric spacetime (with both non-diagonal terms) in this modified gravity is an ardent task. In view of this, we have considered cylindrical spacetime in the analysis. Such a mathematical may be used to analyze cosmological filaments as well as cosmic webs. For the present manuscript, we aim to find realistic regions for studying some cylindrically symmetric solutions in $f(R, \phi , X)$ theory of gravity. We are inspired to discuss the cylindrical solutions in the $f(R,\phi , X)$ theory of gravity. To the best of our knowledge, this is so far the first attempt to investigate the cylindrical solutions in $f(R,\phi , X)$ gravity. The rest of the manuscript is planned as follows:

• In Sect. 2, we defined the formation of field equations in $f(R, \phi , X)$ modified gravity.

• Section 3 deals with the $f(R, \phi , X)$ theory of gravity model and discusses six different cases by considering the different metric potentials in each case.

• Energy conditions along with their graphical behavior for all six cases are investigated in Sect. 3.

• In Sect. 4 and 4, we deal with the Levi–Civita (LC) solutions and cosmic string solutions in $f(R, \phi , X)$ modified gravity.

• In the last section, we have some conclusions regarding the findings of our work.

2 Basic formulism in $f(R, \phi , X)$ modified gravity

The worthwhile transformation of extended theories of gravity is suggested using $R, \phi , X$ defined as Ricci Scalar, scalar potential, and kinetic term, respectively. We consider the action as

$$\begin{aligned} S= \int d^4x \sqrt{-g} \left[ L_m + \frac{1}{2k^{2}}f(R,\phi ,X)\right] , \end{aligned}$$

(1)

where lagrangian matter is denoted by $L_m = L_m(g, \psi )$ ($\psi$ denotes matter fields) and g is the determinant of metric tensor $g_{\mu \nu }$. Here, the value of X is defined as

$$\begin{aligned} X(\phi ) = -\frac{1}{2}[\partial ^{\alpha }\phi \partial _{\alpha }\phi ]\xi . \end{aligned}$$

(2)

The parameter $\xi$ is defined in Eq. (2) based on the conditions that: if we set $\xi =1$ it will imply to the canonical scalar field, and if we set $\xi =-1$ then it will imply to a non-canonical scalar field. In this study, we used $(\xi =1)$ canonical scalar field. For simplicity, we used $\lambda ^2 \equiv 8\pi G$ and $f\equiv f(R,\phi , X)$. We have our field equation if we vary Eq. (1) concerning the metric tensor as follows

$$\begin{aligned}&HG_{\mu \nu }-\frac{1}{2}(f-RH) g_{\mu \nu }-\nabla _{\mu }\nabla _{\nu }H+g_{\mu \nu }\nabla _{\alpha }\nabla ^{\alpha }H\nonumber \\&\quad -\frac{\xi }{2}F(\nabla _{\mu }\phi ) ( \nabla _{\nu }\phi )=\lambda ^2T_{\mu \nu }, \end{aligned}$$

(3)

where, Eq. (3) represents a partial differential equation of order four. Also, $H\equiv \frac{\partial f}{\partial {R}}$, $F\equiv \frac{\partial f}{\partial {X}}$ and the expression $\nabla _{\mu }$ is define as the covariant derivative. In similar fashion, by varying Eq. (1) with respect to $\phi$ we will get Klein–Gordon equation as defined below

$$\begin{aligned} \nabla _{\mu }(F\nabla ^{\mu }\phi )+\xi f_{\phi }=0, \end{aligned}$$

(4)

where, $f_\phi \equiv \frac{\partial f}{\partial {\phi }}$. In our present work, we considered the following stress-energy-momentum tensor for ordinary matter $T_{\mu \nu }^{(mat.)}$

$$\begin{aligned} T_{\mu \nu }^{(mat.)}=\frac{1}{2}[\rho e^{2\psi }, p_{r}e^{2\chi -2\psi }, p_{\phi }e^{-2\psi } \zeta ^{2}, p_{z} e^{2\chi -2\psi }]. \end{aligned}$$

(5)

The terms $\rho$, $p_{r}$ and $p_{\phi }$ and $p_{z}$ in Eq. (5) are used for energy density and pressure terms respectively. We will discuss cylindrically symmetric solutions under the consideration of matter distribution. In this regard, we picked up the cylindrically symmetric line element as follows

$$\begin{aligned} d{s}^{2}=\frac{dt^{2}}{e^{-2\psi (r)}}-\frac{dr^{2}+dz^{2}}{e^{2(\psi (r)-\chi (r))}}-\frac{\zeta ^{2}d{\phi }^{2}}{e^{2\psi }}, \end{aligned}$$

(6)

where, $\psi =\psi (r),~\chi =\chi (r)$ and $\zeta ^{2}=\zeta ^{2}(r)$. The Ricci scalar corresponding to that metric tensor is defined as

$$\begin{aligned} R=2e^{(2\psi -2\chi )} \left[ \frac{\zeta ''}{\zeta }-\frac{\psi '\zeta '}{\zeta }-\psi ''+\psi '^{2}+\chi '' \right] . \end{aligned}$$

(7)

We can get the expressions for energy density and pressure terms by substituting Eqs. (2), (5) and (6) in Eq. (3) as bellow

$$\begin{aligned}&-2e^{(2\psi -2\chi )}f''_{R}+2e^{(2\psi -2\chi )} \left( 3\psi '-2\chi '-\frac{\zeta '}{\zeta }\right) f'_{R}\nonumber \\&\quad +2e^{(2\psi -2\chi )}\left( \psi ''-2\chi ''+\frac{\psi '\zeta '}{\zeta }\right) f_{R}-f=\lambda ^{2}\rho , \end{aligned}$$

(8)

$$\begin{aligned}&2e^{(2\psi -2\chi )}\left( -3\psi '+3\chi '+\frac{\zeta '}{\zeta }\right) f'_{R}\nonumber \\&\quad +2e^{(2\psi -2\chi )}\left( \psi ''-\chi ''+\frac{\psi '\zeta '}{\zeta } +\frac{\chi '\zeta '}{\zeta }-2\psi '^{2} -\frac{\zeta ''}{\zeta }\right) \nonumber \\&\quad \times f_{R}-e^{(2\psi -2\chi )}\xi f_{X}\phi '^{2}+f=\lambda ^{2}p_{r}, \end{aligned}$$

(9)

$$\begin{aligned}&2e^{(2\psi -2\chi )}f''_{R}+2e^{(2\psi -2\chi )}(2\chi '-\psi ')f'_{R}\nonumber \\&\quad +2e^{(2\psi -2\chi )} \left( \psi ''-\frac{\zeta ''}{\zeta }+\frac{\psi '\zeta '}{\zeta }\right) f_{R}+f=\lambda ^{2}p_{\phi }, \end{aligned}$$

(10)

$$\begin{aligned}&2e^{(2\psi -2\chi )}f''_{R}+2e^{(2\psi -2\chi )}\left( \chi '-\psi '+\frac{\zeta '}{\zeta }\right) f'_{R}\nonumber \\&\quad +2e^{(2\psi -2\chi )}\left( \psi ''-\chi ''-\frac{\zeta '\chi '}{\zeta }+\frac{\zeta '\psi '}{\zeta }\right) f_{R}\nonumber \\&\quad +f=\lambda ^{2}p_{z}, \end{aligned}$$

(11)

where Eqs. (8)–(11) are the mathematical terms for the energy density, radial pressure, azimuthal pressure, and axial pressure. The terms involved in these equations are mathematically defined as: metric parameters [$\psi (r)$, $\chi (r)$, $\zeta (r)$] and functions $(f, f_{X}, f_{\phi })$ along their radial derivatives involving different unknowns. It’s worth mentioning here that the prime represents the derivative w.r.t the r. It is observable that Eqs. (8)–(11) are non-linear differential equations in nature. We used the $f(R, \phi , X)$ modified gravity model to find their explicit form for further calculation and graphical analysis. In the coming sections, we will consider their explicit form by putting the $f(R, \phi , X)$ model and showing their graphical behavior for six cases by considering different values of unknowns in them.

3 Graphical analysis and physical aspects with $f(R,\phi ,X)$ modified gravity model

In this section firstly we consider the following model

$$\begin{aligned} f(R,\phi ,X)=\eta (R)- V(\phi ) + X. \end{aligned}$$

(12)

In order to reconstruct some particular solutions, we are considering the following

$$\begin{aligned} \eta (R)=R+\alpha R^2, \end{aligned}$$

(13)

where $\eta$ is a constant free parameter with the appropriate dimensions, this gravitational action is a very well-known one in the literature, as it is capable of reproducing inflation, and it shows exponential growth for early-time cosmic expansion [54]. For our current analysis, we further choose $V(\phi )=U_0 \phi ^m$, where $U_0$ and m are any real numbers. Moreover, scalar field $\phi$ term can be calculated through [55]

$$\begin{aligned} \phi \equiv \phi (r)=a_{0}(b_{0} r^{-1})^{\sigma _{1}},\quad r\ne 0 \end{aligned}$$

(14)

where  $a_{0}$, $b_{0}$ and d are any arbitrary real numbers. Substituting the model defined (12) in Eqs. (8)–(11), we get

$$\begin{aligned}&-4\eta e^{(2\psi -2\chi )}R''+4\eta e^{(2\psi -2\chi )} \left( 3\psi '-2\chi '-\frac{\zeta '}{\zeta } \right) R'\nonumber \\&\quad +2e^{(2\psi -2\chi )}\left( \psi ''-2\chi '' +\frac{\psi '\zeta '}{\zeta }\right) (1+2\eta R)\nonumber \\&\quad -R(1+\eta R) - X+ V(\phi )=\lambda ^{2}\rho , \end{aligned}$$

(15)

$$\begin{aligned}&4\eta e^{(2\psi -2\chi )}\left( -3\psi '+3\chi '+\frac{\zeta '}{\zeta }\right) R'\nonumber \\&\quad +2e^{(2\psi -2\chi )}\left( \psi ''-\chi ''+\frac{\psi '\zeta '}{\zeta }+\frac{\chi '\zeta '}{\zeta }-2\psi '^{2}-\frac{\zeta ''}{\zeta }\right) \nonumber \\&\quad \times (1+2\eta R)-e^{2\psi -2\chi }\xi \phi '^{2}\nonumber \\&\quad +R(1+\eta R)+ X- V(\phi )=\lambda ^{2}p_{r}, \end{aligned}$$

(16)

$$\begin{aligned}&4\eta e^{(2\psi -2\chi )}R''+4\eta e^{(2\psi -2\chi )}(2\chi '-\psi ')R'\nonumber \\&\quad +2e^{2\psi -2\chi }\left( \psi ''-\frac{\zeta ''}{\zeta }+\frac{\psi '\zeta '}{\zeta }\right) (1+2\eta R)\nonumber \\&\quad +R(1+\eta R) + X- V(\phi )=\lambda ^{2}p_{\phi }, \end{aligned}$$

(17)

$$\begin{aligned}&4\eta e^{(2\psi -2\chi )}R''+4\eta e^{(2\psi -2\chi )}\left( \chi '-\psi '+\frac{\zeta '}{\zeta }\right) R'\nonumber \\&\quad +2e^{(2\psi -2\chi )}\left( \psi ''-\chi ''-\frac{\zeta '\chi '}{\zeta }+\frac{\zeta '\psi '}{\zeta }\right) (1+2\eta R)\nonumber \\&\quad +R(1+\eta R) \nonumber + X\nonumber \\&\quad -V(\phi )=\lambda ^{2}p_{z}. \end{aligned}$$

(18)

Fig. 1

The graphical behavior of energy density (MeV/fm$^{3})$, $p_{r}$ (MeV/fm$^{3})$, $p_{\phi }$ (MeV/fm$^{3})$ and $p_{z}$ (MeV/fm$^{3})$ can be seen in this panel. CASE (A)

Fig. 2

Here, we shows variation of $(\rho +p_{r})$ (MeV/fm$^{3})$, $(\rho +p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$. CASE (A)

These Eqs. (15)–(18) help us to discuss the behavior of energy conditions. For our current work, we use $\psi \equiv \psi (r)$, $\chi \equiv \chi (r)$ and $\zeta \equiv \zeta (r)$.

3.1 Analysis of energy conditions

This section involves a discussion about the energy conditions and especially null energy conditions. We will do analysis related to all energy conditions for the specific six cases. Our focus is on NEC because violation of NEC may lead to the existence of cylindrical wormholes. For cylindrically symmetric solutions, the following energy conditions are defined as

• Null Energy Condition (NEC)             $\rho \geqslant -p_{n}$,

• Weak Energy Condition (WEC)           $\rho \ge 0$,   $\rho \ge -p_{n}$,

• Strong Energy Condition (SEC)           $\rho \ge -p_{n}$,   $\rho \ge -3p_{n}$,

• Dominant Energy Condition (DEC)      $\rho -|p_{n}|>0$.

In the above relation, the term $p_{n}$ represents the term $p_{r}$, $p_{\phi }$ and $p_{z}$ for $n=1$, $n=2$ and $n=3$ respectively.

Case (A)

In this case, we have done our calculations by using the following metric potentials

$$\begin{aligned}&\psi (r)=ln[\zeta (r)+A_{0}r],\nonumber \\&\chi (r)=ln[\zeta (r)],\nonumber \\&\zeta (r)=B_{0}+C_{0}r,\quad m=1, \end{aligned}$$

(19)

where $A_{0},~B_{0}$ and $C_{0}$ are arbitrary constants. Substituting these metric potentials in Eqs. (15)–(18), we get

Fig. 3

This panel shows the behavior of $(\rho +3p_{r})$ (MeV/fm$^{3})$, $(\rho +3p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +3p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. CASE (A)

Fig. 4

These figures shows the behavior of $(\rho -p_{r})$ (MeV/fm$^{3})$, $(\rho -p_{\phi })$ (MeV/fm$^{3})$ and $(\rho -p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. CASE (A)

$$\begin{aligned} \rho&= K^{-6}J^{-2}[2 B \left( A_0 \left( C_0 r-B_0\right) +C_0 K\right) \nonumber \\&\quad \times \left( A_0 \left( B_0+2 C_0 r\right) \right. \nonumber \\&\quad \left. +2 C_0 K\right) (12 A_0 B_0 C_0 \eta K+4 A_0^2 B_0 \eta M\nonumber \\&\quad +K^4)-J(24 A_0^2 B_0^2 C_0 \eta B \left( A_0 \left( 5 B_0+9 C_0 r\right) \right. \nonumber \\&\quad \left. +9 C_0 K\right) )]-k^{-8}[k^{4}(2 A_0 B_0 \left( A_0 M+3 C_0 K\right) )\nonumber \\&\quad +4 A_0^2 B_0^2 \eta \left( A_0 M+3 C_0 K\right) {}^2+k^{2}(32 A_0 B_0 C_0^2 \eta B\nonumber \\&\quad \times \left( A_0 \left( 4 B_0+9 C_0 r\right) +9 C_0 K\right) )]+N, \end{aligned}$$

(20)

$$\begin{aligned} p_{r}&= n^2 r^{2 n-2} B+k^{-8}[k^{4}(2 A_0 B_0 \left( A_0 M+3 C_0 K\right) )\nonumber \\&\quad +4 A_0^2 B_0^2 \eta \left( A_0 M+3 C_0 K\right) {}^2]-2 A_0 B_0 Bk^{-6}J^{-2}\nonumber \\&\quad \times [(A_0 (3 B_0+5 C_0 r)+5 C_0 K) (12 A_0 B_0 C_0 \eta K \nonumber \\&\quad +4 A_0^2 B_0 \eta M+K^4 )-4 C_0 \eta (A_0 (3 B_0-C_0 r)\nonumber \\&\quad -C_0 K) (A_0 (5 B_0+9 C_0 r)+9 C_0 K)]-N, \end{aligned}$$

(21)

$$\begin{aligned} p_{\phi }&= [-K(2 A_0 B B_0 (A_0+C_0) (12 A_0 B_0 C_0 \eta K \nonumber \\&\quad +4 A_0^2 B_0 \eta M+K^4))+J(8 A_0 B B_0 C_0 \eta \nonumber \\&\quad \times (A_0 (B_0-C_0 r)-C_0 K) (A_0 (5 B_0+9 C_0 r)\nonumber \\&\quad +9 C_0 K))]k^{-6}J^{-2}\nonumber \\&\quad +[k^{4}(2 A_0 B_0 (A_0 M+3 C_0 K))\nonumber \\&\quad +4 A_0^2 B_0^2 \eta (A_0 M+3 C_0 K){}^2\nonumber \\&\quad +k^{2}(32 A_0 B B_0 C_0^2 \eta (A_0 (4 B_0+9 C_0 r)\nonumber \\&\quad +9 C_0 K))]k^{-8}-N, \end{aligned}$$

(22)

$$\begin{aligned} p_{z}&= [-K(2 A_0 B B_0 (A_0+C_0) (12 A_0 B_0 C_0 \eta K\nonumber \\&\quad +4 A_0^2 B_0 \eta M+K^4))+J(8 A_0 B B_0 C_0 \eta \nonumber \\&\quad \times (A_0 (B_0-C_0 r)-C_0 K) (A_0 (5 B_0+9 C_0 r)\nonumber \\&\quad +9 C_0 K))]k^{-6}J^{-2} +[k^{4}(2 A_0 B_0 (A_0 M+3 C_0 K))\nonumber \\&\quad +4 A_0^2 B_0^2 \eta (A_0 M+3 C_0 K){}^2\nonumber \\&\quad +k^{2}(32 A_0 B B_0 C_0^2 \eta (A_0 (4 B_0+9 C_0 r)\nonumber \\&\quad +9 C_0 K))]k^{-8}-N, \end{aligned}$$

(23)

where, we set the expressions as follow:

$$\begin{aligned} K&= \nonumber B_0+C_0 r, ~J= \nonumber r \left( A_0+C_0\right) +B_0, ~M= \nonumber 2 B_0+3 C_0 r,\\ B&= \nonumber e^{2 \log (J)-2 ln(K)}, ~N= \nonumber U_0 \left( r^n\right) ^m+\frac{1}{2} n^2 r^{2 n-2}. \nonumber \end{aligned}$$

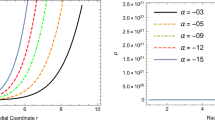
The energy density is positive, while the graphical representation of $p_{r}$ is negative, but the representation of $P_{\phi }$ and $p_{z}$ is initially positive and becomes negative when we move away towards boundary as seen in Fig. 1. The graphical plotting of $\rho +p_r$, $\rho +p_\phi$, and $\rho +p_z$ is negative, which means that NEC is violated as shown in Fig. 2. The graphical behavior in Fig. 3 clearly shows that SEC is violated in a particular regions due to $\rho +3p_r$, $\rho +3p_\phi$ and $\rho +3p_z$. Moreover, It can be seen that DEC is also violated for this case due to the negative nature of $\rho -p_r$ as shown in Fig. 4.

Case (B)

We proceed this case for different metric potentials, which are defined as

$$\begin{aligned} \psi (r)= & {} ln[\zeta (r)+A_{0}r^{2}],\nonumber \\ \chi (r)= & {} ln[\zeta (r)],\nonumber \\ \zeta (r)= & {} B_{0},\quad m=1, \end{aligned}$$

(24)

where, $A_{0}$ and $B_{0}$ are the arbitrary constants. Under the consideration of these metric potentials, we have the following expressions

$$\begin{aligned} \rho&= M\left[ -384 A_0^5 B_0 \eta r^8 e^J-8 A_0^4 B_0^2 r^6 \left( e^J \left( 3 r^2-8 \eta \right) \right. \right. \nonumber \\&\quad \left. -96 \eta e^K\right) -288 A_0^6 \eta r^{10} e^J 2 A_0 B_0^5 r^2\nonumber \\&\quad \times \left( 4 e^K+e^J \left( 2 r^2 U_0 \left( r^n\right) ^m+n^2 r^{2 n}+4\right) \right) \nonumber \\&\quad -8 A_0^3 B_0^3 r^4 \left( e^J \left( 5 r^2-16 \eta \right) -128 \eta e^K\right) +B_0^6 e^J \nonumber \\&\quad \times \left( 2 r^2 U_0 \left( r^n\right) ^m+n^2 r^{2 n}\right) \left. A_0^2 B_0^4 +r^2 \left( e^J \left( 2 r^4 U_0 \left( r^n\right) ^m\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +n^2 r^{2 n+2}-8 \left( 4 \eta +r^2\right) \right) -8 e^K \left( 32 \eta +r^2\right) \right) \right] , \end{aligned}$$

(25)

$$\begin{aligned} p_{r}&= \nonumber M\left[ 288 A_0^6 \eta r^{10} e^J+384 A_0^5 B_0 \eta r^8 e^J\right. \\&\quad \left. +8 A_0^4 B_0^2 r^6 \left( e^J \left( 3 r^2-8 \eta \right) -264 \eta e^K\right) \right. \nonumber \\&\quad +8 A_0^3 B_0^3 r^4 \left( e^J \left( 5 r^2-16 \eta \right) -80 \eta e^K\right) \nonumber \\&\quad +B_0^6 \left( -2 r^2 U_0 e^J \left( r^n\right) ^m-n^2 r^{2 n} \left( 2 e^K+e^J\right) \right) \nonumber \\&\quad +2r^2A_0B_0^5\nonumber \left( -2 e^K \left( n^2 r^{2 n}-2\right) -\right. \left. e^J \left( 2 r^2 U_0 \left( r^n\right) ^m \right. \right. \\&\quad \nonumber \left. \left. +n^2 r^{2 n}+4\right) \right) +A_0^2 B_0^4 r^2(e^J (32 \eta -2 r^4 U_0 \left( r^n\right) ^m\\&\quad \left. -n^2 r^{2 n+2}+8 r^2)-2 e^K \left( 32 \eta +r^2 \left( n^2 r^{2 n}+20\right) \right) \right] , \end{aligned}$$

(26)

$$\begin{aligned} p_{\phi }&= \nonumber M\left[ 384 A_0^5 B_0 \eta r^8 e^J+8 A_0^4 B_0^2 r^6\right. \nonumber \\&\quad \times \left( e^J \left( 3 r^2-8 \eta \right) -48 \eta e^K\right) \nonumber \\&\quad \nonumber +288 A_0^6 \eta r^{10} e^J +8 A_0^3 B_0^3 r^4\\&\quad \nonumber \times \left( 32 \eta e^K+e^J \left( 5 r^2-16 \eta \right) \right) -B_0^6 e^J \left( 2 r^2 U_0 \left( r^n\right) ^m\right. \nonumber \\&\nonumber \quad \left. +n^2 r^{2 n}\right) +2r^2A_0B_0^5\left( 4 e^K-e^J(4\right. \\&\quad \left. \left. +2 r^2 U_0 \left( r^n\right) ^m+n^2 r^{2 n}\right) \right) +A_0^2 B_0^4 r^2 \left( e^J \left( 32 \eta \right. \right. \nonumber \\&\quad \left. \left. \left. -2 r^4 U_0 \left( r^n\right) ^m-n^2 r^{2 n+2}+8 r^2\right) -8 e^K \left( r^2-16 \eta \right) \right) \right] , \end{aligned}$$

(27)

$$\begin{aligned} p_{z}&= \nonumber M\left[ 384 A_0^5 B_0 \eta r^8 e^J+8 A_0^4 B_0^2 r^6 \right. \nonumber \\&\quad \times \left( e^J \left( 3 r^2-8 \eta \right) -48 \eta e^K\right) \nonumber \\&\quad +288 A_0^6 \eta r^{10} e^J +8 A_0^3 B_0^3 r^4\nonumber \\&\quad \nonumber \times \left( 32 \eta e^K+e^J \left( 5 r^2-16 \eta \right) \right) -B_0^6 e^J \left( 2 r^2 U_0 \left( r^n\right) ^m\right. \\&\nonumber \left. +n^2 r^{2 n}\right) +2r^2A_0B_0^5\left( 4 e^K-e^J(4+2 r^2 U_0 \left( r^n\right) ^m\right. \\&\quad \left. \left. +n^2 r^{2 n}\right) \right) +A_0^2 B_0^4 r^2 \left( e^J \left( 32 \eta -2 r^4 U_0 \left( r^n\right) ^m\right. \right. \nonumber \\&\quad \left. \left. \left. -n^2 r^{2 n+2}+8 r^2\right) -8 e^K \left( r^2-16 \eta \right) \right) \right] . \end{aligned}$$

(28)

Here, to reduce the expressions we set the terms as

$$\begin{aligned} K&= 2 \ln \left( A_0 r^2+B_0\right) , \\ J&= 2 \ln \left( B_0\right) ,\\ M&= \frac{e^{-J}}{2 B_0^4 r^2 \left( A_0 r^2+B_0\right) {}^2}. \end{aligned}$$

The graphical behavior of energy density and pressure components and energy conditions for this case is elaborated graphically in Figs. 5, 6, 7 and 8. The graphical analysis of energy density is positive and increasing but the graphical analysis of radial pressure, azimuthal pressure, and axial pressure has the same energy density. All these pressure components are negative with decreasing nature, as shown in Fig. 5. The negative behavior of these components may cause the presence of exotic matter and violation of energy conditions. From Figs. 6, 7 and 8, it can be seen that NEC and SEC are satisfied but DEC is violated for the given region.

Fig. 5

The graphical variation of $\rho$ (MeV/fm$^{3})$, $p_{r}$ (MeV/fm$^{3})$, $p_{\phi }$ (MeV/fm$^{3})$ and $p_{z}$ (MeV/fm$^{3})$ is showed in this figure with respect to the radial co-ordinate r. CASE (B)

Fig. 6

The variation of $(\rho +p_{r})$ (MeV/fm$^{3})$, $(\rho +p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ is shown in this panel. CASE (B)

Fig. 7

This panel shows the behavior of $(\rho +3p_{r})$ (MeV/fm$^{3})$, $(\rho +3p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +3p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) and $A_{0}$. CASE (B)

Fig. 8

These figures shows the behavior of $(\rho -p_{r})$ (MeV/fm$^{3})$, $(\rho -p_{\phi })$ (MeV/fm$^{3})$ and $(\rho -p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. CASE (B)

Case (C)

In this case, we use the following metric potentials

$$\begin{aligned} \chi (r)=ln[\zeta (r)],\quad \zeta (r)=B_{0},\quad m=1. \end{aligned}$$

(29)

The value used for $\chi (r)$ and $\zeta (r)$ is the same as defined in Case B, but here we use a different approach to find out the value of $\psi (r)$. While exploring the cylindrical solutions in the f(G) theory of gravity, Houndjo et al. [35] used an approach to find out the metric potential. The authors developed a relationship between the expression between Gauss-Bonnet and R to find the other parameter. For our current analysis, we are going to investigate the Klein–Gordon equation to develop the other parameter. The Klein–Gordon equation is defined as

$$\begin{aligned} \nabla _{\mu }(F\nabla ^{\mu }\phi )+\epsilon f_{\phi }=0, \end{aligned}$$

(30)

where, $F\equiv \frac{\partial f}{\partial X}$ and $f_{\phi }\equiv \frac{\partial f}{\partial \phi }$. After solving the Eq. (30), we get the expression of the form

Fig. 9

The graphical variation shows the behavior of $\rho$ (MeV/fm$^{3})$, $p_{r}$ (MeV/fm$^{3})$, $p_{\phi }$ (MeV/fm$^{3})$ and $p_{z}$ (MeV/fm$^{3})$. CASE (C)

Fig. 10

This panel shows the variation of $(\rho +p_{r})$ (MeV/fm$^{3})$, $(\rho +p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) and $A_{0}$ parameter with $m=n=1$. CASE (C)

Fig. 11

The graphical variation in this panel shows the behavior of $(\rho +3p_{r})$ (MeV/fm$^{3})$, $(\rho +3p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +3p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) and $A_{0}$ parameter with $m=n=1$ and $\alpha =-0.01$. CASE (C)

Fig. 12

This panel shows the variation of $(\rho -p_{r})$ (MeV/fm$^{3})$, $(\rho -p_{\phi })$ (MeV/fm$^{3})$ and $(\rho -p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $n=m=1$ along with $\alpha =-0.01$. CASE (C)

Fig. 13

This panel illustrate the variation of density (MeV/fm$^{3})$, $p_{r}$ (MeV/fm$^{3})$, $p_{\phi }$ (MeV/fm$^{3})$ and $p_{z}$ (MeV/fm$^{3})$ w.r.t r. CASE (D)

$$\begin{aligned}&-e^{-\chi (r)}\bigg [\phi ''(r)\frac{\partial f}{\partial X}+\phi '(r)\frac{\partial f_{X}}{\partial r}e^{2\chi (r)}\nonumber \\&\quad + \phi '(r) \frac{\partial f}{\partial X}\left( \frac{\psi '(r)}{2}+\frac{\chi '(r)}{2}+\frac{2}{r}\right) \bigg ]\nonumber \\&\quad +\epsilon \frac{\partial f}{\partial \phi }=0. \end{aligned}$$

(31)

To find out the value of $\psi (r)$, we put Eq. (13) and Eq. (29) in Eq. (31) and get

$$\begin{aligned} \psi (r)= & {} c_1+\frac{1}{2} \left[ \frac{2^m m r^2 v_{0} w_{0} \epsilon \left( \frac{d}{r}\right) ^{-2 \sigma _{1}} \left( \left( \frac{d}{r}\right) ^{\sigma _{1}}\right) ^m}{\sigma _{1} ((m-2) \sigma _{1}-2)}\right. \nonumber \\&\left. +4 (\sigma _{1}-1) \log (r) \right] . \end{aligned}$$

(32)

It can be noticed that the metric potential defined in Eq. (29) and the other parameter, which is developed in Eq. (32), are used to observe the graphical analysis. The graphical behavior of energy density is fascinating for this case, as shown in Fig. 9. For this case, it can be observed that the SEC is satisfied, but NEC and DEC are violated due to the negative trends of some pressure components, as shown in Figs. 10, 11 and 12).

Case (D)

In this section, we have done our work by considering the following values

$$\begin{aligned} \chi (r)=ln[\zeta (r)],\quad \zeta (r)=\sqrt{2},\quad m=1. \end{aligned}$$

(33)

As same in the previous case, we used the Klein–Gordon equation to work out the value of a metric potential $\psi (r)$ as

$$\begin{aligned} \psi (r)=c_1-\frac{\sqrt{2} m r^6 V_0 \epsilon \left( \frac{d^2 \phi _0}{r^2}\right) {}^m}{d^4 (6-2 m) \phi _0^2}+2 \log (r). \end{aligned}$$

(34)

The metric potentials mentioned in Eqs. (33) and (34) are utilized to determine the graphical aspects of energy density, pressure components, and energy conditions for this case. The graphical behavior of energy density initially decreases and increases on the radial coordinate, as shown in Fig. 13. The graphical behavior of radial pressure, azimuthal pressure, and axial pressure is negative near the origin but becomes positive when moving away from the center, as represented in Fig. 13. Figure 14 clearly shows the validity of NEC at $r\geqslant 0$ due to the positive nature of all the components. The behavior of SEC and DEC are violated due to the negative nature of pressure components, as shown in Figs. 15 and 16.

Fig. 14

This panel shows the variation of $(\rho +p_{r})$ (MeV/fm$^{3})$ and $(\rho +p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) and $A_{0}$ parameter with $m=n=1$. CASE (D)

Fig. 15

The graphical variation in this panel shows the behavior of $(\rho +3p_{r})$ (MeV/fm$^{3})$, $(\rho +3p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +3p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. CASE (D)

Fig. 16

This panel shows the behavior of $(\rho -p_{r})$ (MeV/fm$^{3})$, $(\rho -p_{\phi })$ (MeV/fm$^{3})$ and $(\rho -p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. CASE (D)

Case (E)

For this case, we consider the different metric potential as follows

$$\begin{aligned} \psi (r)= & {} ln[A_{0}\zeta (r)],\nonumber \\ \chi (r)= & {} ln[\zeta (r)],\nonumber \\ \zeta (r)= & {} B_{0}+C_{0}r,\quad m=1. \end{aligned}$$

(35)

The graphical behavior of energy density, pressure terms, and different energy conditions can be seen through different panels. As shown in Fig. 17, the graphical representation of energy density is positive and has a maximum value near the origin. Whereas the other panels of Fig. 17 shows the negative trends of radial pressure, azimuthal pressure, and axial pressure. The graphical representation of $\rho +p_r$, $\rho +p_\phi$, and $\rho +p_z$ is positive, which means that NEC is satisfied for this case as shown in Fig. 18. Moreover, one can see that the SEC violates throughout the region for $r>0$ as seen in Fig. 19 and DEC is satisfied, as shown in Fig. 20.

Fig. 17

This panel shows the graphical behavior of energy density (MeV/fm$^{3})$, $P_{r}$ (MeV/fm$^{3})$, $P_{\phi }$ (MeV/fm$^{3})$ and $P_{z}$ (MeV/fm$^{3})$ w.r.t r km. CASE (E)

Fig. 18

Here, we shows the variation of $(\rho +p_{r})$ (MeV/fm$^{3})$, $(\rho +p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$. CASE (E)

Fig. 19

This panel shows the behavior of $(\rho +3p_{r})$ (MeV/fm$^{3})$, $(\rho +3p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +3p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. CASE (E)

Fig. 20

These figures shows the behavior of $(\rho -p_{r})$ (MeV/fm$^{3})$, $(\rho -p_{\phi })$ (MeV/fm$^{3})$ and $(\rho -p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. CASE (E)

Case (F)

For this case, the following metric potentials are considered as follows

$$\begin{aligned} \psi (r)= & {} ln[A_{0}r+\zeta (r)],\nonumber \\ \chi (r)= & {} ln[\zeta (r)],\nonumber \\ \zeta (r)= & {} B_{0},\quad m=1. \end{aligned}$$

(36)

Fig. 21

The first graph show the graphical behavior of energy density (MeV/fm$^{3})$ which is positive and increasing w.r.t radial coordinate. Whereas, the graphical behavior of $P_{r}$ (MeV/fm$^{3})$, $P_{\phi }$ (MeV/fm$^{3})$ and $P_{z}$ (MeV/fm$^{3})$ is negative and decreasing w.r.t radial coordinate. CASE (F)

Fig. 22

The graphs shows the variation of $(\rho +p_{r})$ (MeV/fm$^{3})$, $(\rho +p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$. One can clearly sees the validity of NEC through this panel for $r\ge 0$. CASE (F)

Fig. 23

This panel shows the behavior of $(\rho +3p_{r})$ (MeV/fm$^{3})$, $(\rho +3p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +3p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. Here, we can clearly see that the SEC satisfied throughout the region for $r>0$. CASE (F)

Fig. 24

These figures shows the behavior of $(\rho -p_{r})$ (MeV/fm$^{3})$, $(\rho -p_{\phi })$ (MeV/fm$^{3})$ and $(\rho -p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. CASE (F)

The graphical behavior of energy density is positive and increasing w.r.t radial coordinate, as shown in Fig. 21. Whereas, the graphical behavior of $p_{r}$, $p_{\phi }$ and $p_{z}$ has opposite nature like energy density. All these pressure components are negative and have decreasing behavior, as seen in Fig. 21. It can be noticed that NEC, WEC, SEC, and DEC are satisfied due to positive and increasing trends of pressure, as seen in Figs. 22, 23 and 24.

3.2 Comparison

Azadi and his collaborators [32] investigated the cylindrical solutions in f(R) theory of gravity and obtained a new family of solutions with constant Ricci scalar explicitly as a particular case (R=0) and non-zero Ricci scalar. We have investigated the cylindrical solutions in $f(R, \phi , X)$ theory of gravity and observed the graphical behavior of energy density, pressure components, and energy conditions for both zero and non-zero Ricci scalar, which makes our work different from [32, 33]. Houndjo et al. [34] investigated the static cylindrically symmetric vacuum solutions in the framework of f(T) theory of gravity. Now, we have investigated the non-vacuum solutions $f(R, \phi , X)$ theory of gravity. Houndjo et al. [35] discussed the cylindrical solutions for different cases by using potential metrics and investigated only NEC in f(G) gravity. We adopted the same metric potentials for six cases and investigated the graphical analysis of NEC, SEC, and DEC in $f(R, \phi , X)$ theory of gravity. Moreover, the authors assumed the relationship between the Gauss-Bonnet term and Ricci scalar to develop the metric potential. We have developed the metric potentials using the Klein–Gordon equation, making our work different from the previous one.

4 Levi–Civita solution

In this case, we deal with a particular case named Levi–Civita (LC) solution. Therefore, we discussed the solutions by considering $f(R,\phi , X)$ theory of gravity and the following metric parameters as:

$$\begin{aligned} \psi (r)= & {} A_{0}ln[\zeta (r)],\nonumber \\ \chi (r)= & {} B_{0}ln[\zeta (r)],\nonumber \\ \zeta (r)= & {} r,\quad m=1, \end{aligned}$$

(37)

where, $A_{0}$ and $B_{0}$ are any arbitrary constants. The gauge term can be fixed by taking $w(r)=r$ in the LC solutions for making the solutions much charming, which is called harmonic gauge function over the subspace. The harmonic subspace can be defined by choosing two constants sheets, i.e., time and space like sheets constant (r=constant and t=constant). This implies that it satisfies the following equation

$$\begin{aligned} \nabla _{i}\nabla ^{i}\zeta (r)=0. \end{aligned}$$

(38)

The above mentioned Eq. (38) has a linear solution in term of r as $\zeta (r)=D_{0}+D_{1}r$. To find out the value of constants, we used some conditions (i.e.). Using the conical cylinder shift symmetry, we have $D_{0}=0$, and by re-defining r, we set the value of $D_{1}$. Likewise, $\zeta (r)$ we have $\psi (r)$ and $\chi (r)$ in our metric-space defined in Eq. (37). These two metric potentials ${\psi (r), \chi (r)}$ are also harmonic functions satisfies Eq. (38). These three metric potentials are singular when r is near to origin. The interior solution with thickness scale $r_{0}$ for LC metric should be a real comic string, and classical methods do not achieve this thickness for real comic string. Because the core of comic string takes it back to the quantum properties of the singularities. With the choice as defined in Eq. (37), we have the following equations

Fig. 25

This panel shows the graphical behavior of energy density (MeV/fm$^{3})$, $P_{r}$ (MeV/fm$^{3})$, $P_{\phi }$ (MeV/fm$^{3})$ and $P_{z}$ (MeV/fm$^{3})$ w.r.t radial coordinate. CASE (Levi–Civita)

$$\begin{aligned} \rho&=~\frac{1}{2}e^{-M_L}r^{-4 \left( B_0+1\right) }\left[ -8 \eta \left( A_0^2-B_0\right) {}^2 r^{4 A_0} e^{M_L}\right. \nonumber \\&\quad +4r^{2 \left( A_0+B_0\right) }B_0-A_0^2\left( r^2 e^{M_L}+8e^{K_L}\eta \left( B_0+2\right. \right. \nonumber \\&\quad \left. \left. \left. +A_0 \left( -A_0+B_0-1\right) \right) \right) +r^{4 B_0+2} \left( 8 B_0 e^{K_L}\right. \right. \nonumber \\&\quad \left. \left. +e^{M_L} \left( 2 r^2 U_0 \left( r^n\right) ^m+n^2 r^{2 n}\right) \right) \right] , \end{aligned}$$

(39)

$$\begin{aligned} p_{r}&=~ -\frac{1}{2} n^2 r^{2 n-2} \left( 2 e^{2 \left( A_0-B_0\right) ln r}+1\right) +2r^{-4 \left( B_0+1\right) }A_0^2\nonumber \\&\quad -B_0\left( r^{2 \left( A_0+B_0+1\right) }+2 \eta \left( A_0^2-B_0\right) r^{4 A_0} +2 r^{2 B_0}\right. \nonumber \\&\quad \left. \times \left( -4 \eta \left( 3 \left( 1-2 A_0\right) B_0+\left( 1-2 A_0\right) {}^2+3 B_0^2\right) r^{2 A_0}\right. \right. \nonumber \\&\quad \left. \left. -r^{2 B_0+2}\right) e^{2 \left( A_0-B_0\right) ln r}\right) -U_0 \left( r^n\right) ^m, \end{aligned}$$

(40)

$$\begin{aligned} p_{\phi }&= -\frac{1}{2} n^2 r^{2 n-2}+2 \left( A_0^2-B_0\right) r^{2 A_0-2 B_0-4} e^{-M_L} \left( 8 \left( A_0\right. \right. \nonumber \\&\quad \left. \left. -3\right) \eta \left( A_0-B_0-1\right) e^{K_L}+r^2 e^{M_L}\right) \nonumber \\&\quad +4 \eta \left( A_0^2-B_0\right) {}^2 r^{4 A_0-4 B_0-4}-U_0 \left( r^n\right) ^m, \end{aligned}$$

(41)

$$\begin{aligned} p_{z}&=~ \frac{1}{2}e^{-M_L}r^{-4 B_0-5}\left[ 8 \eta \left( A_0^2-B_0\right) {}^2 r^{4 A_0+1} e^{M_L}\right. \nonumber \\&\quad +4r^{2 \left( A_0+B_0\right) }A_0^2-B_0\left( r^3 e^{M_L}+4e^{K_L}\eta \left( 2 A_0^2 r\right. \right. \nonumber \\&\quad \left. \left. \left. +2 r B_0+1\right) B_0+2+A_0 \left( B_0 (1-4 r)-7 r\right) \right) \right) \nonumber \\&\quad +r^{4 B_0+2}\left( -4 A_0 \left( r-B_0\right) e^{K_L}-e^{M_L}r\left( n^2 r^{2 n}\right. \right. \nonumber \\&\quad \left. \left. \left. +2 r^2 U_0 \left( r^n\right) ^m\right) \right) \right] , \end{aligned}$$

(42)

where, $K_{L}=2 A_0 ln r$ and $M_{L}=2 B_0 ln r$. The graphical analysis of energy density is initially decreasing and then becomes increasing, as shown in Fig. 25. On the other panels of Fig. 25 show the graphical depictions of radial pressure, azimuthal pressure, and axial pressure, which are negative. The negative behavior of pressure components indicates the presence of exotic matter and may cause the violation of energy conditions. The graphical depictions of $\rho +p_{\phi }$ and $\rho +p_{z}$ are positive while the remaining component of $\rho +p_r$ is negative, which show that NEC is violated as shown in Fig. 26. We know that WEC is linked with NEC, so we can claim that WEC is also violated for LC solutions. It can also be noticed that SEC is violated due to the negative behavior of $\rho +3p_{r}$, $\rho +3p_{\phi }$ and $\rho +3p_{z}$ as shown in Fig. 27. Moreover, DEC is satisfied for this case due to the positive nature of $\rho -p_{r}$, $\rho -p_{\phi }$ and $\rho -p_{z}$ as shown in Fig. 28.

Fig. 26

The graphs shows the variation of $(\rho +p_{r})$ (MeV/fm$^{3})$, $(\rho +p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$. CASE (Levi–Civita)

Fig. 27

Here, the panel shows the graphical behavior of $(\rho +3p_{r})$ (MeV/fm$^{3})$, $(\rho +3p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +3p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. Here, we can clearly see that the SEC violated throughout the region for $r\ge 0$. CASE (Levi–Civita)

Fig. 28

These graphs shows the behavior of $(\rho -p_{r})$ (MeV/fm$^{3})$, $(\rho -p_{\phi })$ (MeV/fm$^{3})$ and $(\rho -p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $\alpha =-0.01$. CASE (Levi–Civita)

4.1 Comparison

Rodrigues et al. [56] investigated the LC’s Solution in modified Gauss-Bonnet gravity analytically and considered theses solutions as a generalization of the exterior solution of a Cosmic string in the modified Gauss-Bonnet gravity. But, we discuss the physical aspects of LC solutions in this manuscript, which makes our work interesting. This type of special case is also discussed in f(G) gravity for a special model $f(G)=\alpha G^{n}$. Azadi and his collaborators [32] reduced a set of the modified Einstein equations is to a single equation and shown how one can construct exact solutions corresponding to different f(R) models. In this work, we investigated a special case for zero Ricci scalar (i.e $R=0$) with graphical representation, which makes this work charming from Azadi’s work.

5 Cosmic string case

In this section, we discussed a very important sub-case of LC solutions named a Cosmic String Case. We have discussed this case under the application of $f(R, \phi , X)$ theory of gravity for the following metric potentials

$$\begin{aligned} \psi (r)= & {} A_{0}ln[\zeta (r)],\nonumber \\ \chi (r)= & {} B_{0}ln[\zeta (r)],\nonumber \\ \zeta (r)= & {} C_{0}r,\quad m=n=1, \end{aligned}$$

(43)

where, $A_{0}, B_{0}$ and $C_{0}$ are any arbitrary constants. Also, if we put $C_{0}=1$ in Eq. (43) then it becomes LC solutions defined in (40). By taking this, we obtain

$$\begin{aligned} dS^2= & {} (C_0r)^{2A_0}dt^2-(C_0r)^{2-2A_0}d\phi ^2\nonumber \\&-(C_0r)^{2B_0-2A_0}(dr^2+dz^2). \end{aligned}$$

(44)

Now, putting these metric potentials in Eqs. (15)–(18), we have the following equations as

Fig. 29

This panel shows the graphical behavior of energy density (MeV/fm$^{3})$ which is positive w.r.t radial coordinate. Whereas, the graphical behavior of $P_{r}$ (MeV/fm$^{3})$, $P_{\phi }$ (MeV/fm$^{3})$ and $P_{z}$ (MeV/fm$^{3})$ is negative w.r.t radial coordinate

Fig. 30

This panel shows the variation of $(\rho +p_{r})$ (MeV/fm$^{3})$, $(\rho +p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=-3$ and $n=2$. One can clearly sees that NEC is valid at some particular values of the radial coordinate.)

Fig. 31

Here, the graphical behavior of $(\rho +3p_{r})$ (MeV/fm$^{3})$, $(\rho +3p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +3p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=-3$, $n=2$ and $\alpha =-0.01$ shown in this panel. We can clearly see that the SEC violated throughout the region for $r>0$

Fig. 32

These graphs shows the behavior of $(\rho -p_{r})$ (MeV/fm$^{3})$, $(\rho -p_{\phi })$ (MeV/fm$^{3})$ and $(\rho -p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=-3$, $n=2$ and $\alpha =-0.01$. Here, the graphs shows that DEC is satisfied throughout the region

Fig. 33

This panel shows the graphical behavior of energy density (MeV/fm$^{3})$, $p_{r}$ (MeV/fm$^{3})$, $p_{\phi }$ (MeV/fm$^{3})$ and $p_{z}$ (MeV/fm$^{3})$ w.r.t radial coordinate. CASE (Cosmic String)

Fig. 34

This panel shows the variation of $(\rho +p_{r})$ (MeV/fm$^{3})$, $(\rho +p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +p_{z})$ (MeV/fm$^{3})$ w.r.t r (km). CASE (Cosmic String)

Fig. 35

Here, the graphical behavior of $(\rho +3p_{r})$ (MeV/fm$^{3})$, $(\rho +3p_{\phi })$ (MeV/fm$^{3})$ and $(\rho +3p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $C_{0}=0.5$ shown in this panel. CASE (Cosmic String)

Fig. 36

These graphs shows the behavior of $(\rho -p_{r})$ (MeV/fm$^{3})$, $(\rho -p_{\phi })$ (MeV/fm$^{3})$ and $(\rho -p_{z})$ (MeV/fm$^{3})$ w.r.t r (km) with $m=n=1$ and $C_{0}=0.5$. CASE (Cosmic String)

$$\begin{aligned} \rho&= \frac{1}{2r^{4}}(4 \left( B_0-A_0^2\right) e^{-2 B_0 ln \left( C_0 r\right) } \left( 8 \eta \left( A_0 \left( -A_0+B_0-1\right) \right. \right. \nonumber \\&\quad \left. \left. +B_0+2\right) e^{2 A_0 ln \left( C_0 r\right) }+r^2 e^{2 B_0 ln \left( C_0 r\right) }\right) \nonumber \\&\quad \times r^2 \left( 8 B_0 e^{2 \left( A_0-B_0\right) ln \left( C_0 r\right) }+2 r^2 U_0 \left( r^n\right) ^m+n^2 r^{2 n}\right) \nonumber \\&\quad -8 \eta \left( A_0^2-B_0\right) {}^2 \left( C_0 r\right) {}^{4 \left( A_0-B_0\right) }+\left( C_0 r\right) {}^{2 \left( A_0-B_0\right) }), \nonumber \\ \end{aligned}$$

(45)

$$\begin{aligned} p_{r}&= \nonumber -\frac{1}{2 r^4}\left( 2 n^2 r^{2 n+2} e^{2 \left( A_0-B_0\right) ln \left( C_0 r\right) }\right. \nonumber \\&\quad +32 \eta e^{2 \left( A_0-B_0\right) ln \left( C_0 r\right) }\nonumber \\&\quad -4 r^2 \left( A_0^2-B_0\right) \left( C_0 r\right) {}^{2 \left( A_0-B_0\right) }+n^2 r^{2 n+2}\nonumber \\&\quad \times \left( 3 A_0-3 B_0-1\right) \left( A_0-B_0-1\right) \nonumber \\&\quad \times \left( A_0^2-B_0\right) \left( C_0 r\right) {}^{2 \left( A_0-B_0\right) }\nonumber \\&\quad -8 \eta \left( A_0^2-B_0\right) {}^2 \left( C_0 r\right) {}^{4 \left( A_0-B_0\right) }+8 \left( A_0^2-B_0\right) \nonumber \\&\quad \times \left( 4 \eta \left( A_0^2-B_0\right) \left( C_0 r\right) {}^{2 \left( A_0-B_0\right) }+r^2\right) \nonumber \\&\quad \left. e^{2 \left( A_0-B_0\right) ln \left( C_0 r\right) }+2 r^4 U_0 \left( r^n\right) ^m\right) , \end{aligned}$$

(46)

$$\begin{aligned} p_{\phi }&= \nonumber \frac{1}{2 r^4}(-n^2 r^{2 n+2}+4e^{-2 B_0 ln (C_0 r)}(r^2 e^{2 B_0 ln (C_0 r)}\nonumber \\&\quad +8e^{2 A_0 ln (C_0 r)}\eta A_0-3(-1+A_0B_0))A_0^2 \nonumber \\&\quad -B_0(C_0 r){}^{2 (A_0-B_0)}+8 \eta (A_0^2-B_0){}^2 (C_0 ){}^{4 (A_0-B_0)}\nonumber \\&\quad -2 r^4 U_0 (r^n)^m), \end{aligned}$$

(47)

$$\begin{aligned} p_{z}&= \nonumber \frac{1}{2 C_0 r^5}\left( 8 \eta \left( A_0^2-B_0\right) {}^2 \left( C_0 r\right) {}^{4 A_0-4 B_0+1}\right. \nonumber \\&\quad +4e^{-2 B_0 ln \left( C_0 r\right) }A_0^2-B_0\left( C_0 r\right) {}^{2 \left( A_0-B_0\right) }\nonumber \\&\quad \times \left( C_0 r^3 e^{2 B_0 ln \left( C_0 r\right) }\right. \nonumber \\&\quad \left. +4 \eta \left( C_0 r \left( -A_0 \left( 4 B_0+7\right) +2 A_0^2+2 \left( B_0+1\right) \left( B_0+2\right) \right) \right. \right. \nonumber \\&\quad \left. \left. +A_0 B_0\right) e^{2 A_0 ln \left( C_0 r\right) }\right) \nonumber \\&\quad +r^2\left( 4 e^{2 \left( A_0-B_0\right) ln \left( C_0 r\right) }\right. \nonumber \\&\quad \left. \left. A_0 \left( B_0-C_0 r\right) -C_0 r \left( 2 r^2 U_0 \left( r^n\right) ^m+n^2 r^{2 n}\right) \right) \right) . \end{aligned}$$

(48)

These set of Eqs. (45)–(48) involves some constants $A_{0}, B_{0}$ and $C_{0}$. The graphical behavior of energy density and pressure components including energy conditions can be seen through Figs. 29, 30, 31 and 32. If we restrict these constants to some values like $A_{0}=0, B_{0}=0$ and $C_{0}$ only lies between the interval (0, 1) then the space-time is corresponding to the exterior metric of a cosmic string with the following line element [57]

$$\begin{aligned} dS^2=dt^2-(C_0r)^2d\phi ^2-dr^2-dz^2. \end{aligned}$$

(49)

The metric defined in Eq. (49) tells about the exposing the configuration around a straight cosmic string, which is similar is flat space-time. By considering the Ricci flat solutions, we obtained a conical space-time namely zero curvature space-time as a special case, which includes the cosmic string space-time.

Now, after putting the values of $A_{0}=0$ and $B_{0}=0$ in Eqs. (45)–(48), it can be observed that $C_0$ vanish through out the expressions. For our current analysis, we have considered $m=-3$, $n=2$ and observed their three dimensional analysis by varying $V_{0}$ elaborated as shown in Figs. 33, 34, 35 and 36. In Fig. 33, the energy density shows positive behavior under the consideration of $A_{0}=B_{0}=0$ and $C_{0}=0.5$. In Fig. 34, one can clearly sees that NEC is valid for some particular values of the radial coordinate. It can be seen that the SEC violated through out the region for $r>0$ as depicted in Fig. 35. In the last panel of Fig. 36, the graphical analysis show that DEC is satisfied throughout the region.

5.1 Comparison

This type of space-time and Ricci flat solution also discussed in cylindrical solutions in f(R), f(G) and f(T) theories of gravity [32,33,34,35]. Momeni [58] investigated a static cylindrical symmetric solution which describes Cosmic string as a special case and also investigated some possible solutions. In our current analysis, we investigated the Cosmic string solutions by observing the physical features of energy density, radial pressure, azimuthal pressure, and axial pressure. Moreover, we also observed the graphical representation of NEC, WEC, SEC and DEC, which makes our work more interesting.

6 Conclusion

In the current study, we have discussed cylindrically symmetric solutions by using a very compatible model name as $f(R,\phi ,X)$ gravity model. This model is the combination of Ricci Scalar, scalar potential and kinetic term respectively, which make our theory more general and attractive. We have calculated the field equations in term of density and pressure expressions, which are the mathematical expressions for the $\rho$, $p_{r}$, $p_{\phi }$ and $p_{z}$. Firstly, we have discussed six different cases of cylindrically symmetric solutions. Later on, we investigated the Levi–Civita Solutions and a special case named as Cosmic string solutions. Some important outcomes of the study in this paper are itemized as below:

• The graphical behavior of energy density is monotonic and positive, as shown in Fig. 1. On the other hand, graphical representation of $p_{r}$ is negative, but the representation of $P_{\phi }$ and $p_{z}$ is initially positive and becomes negative when we move away towards boundary as seen in Fig. 1. The graphical plotting of $\rho +p_r$, $\rho +p_\phi$, and $\rho +p_z$ is negative, which means that NEC is violated as shown in Fig. 2. The graphical behavior in Fig. 3 clearly shows that SEC is violated in a particular regions due to $\rho +3p_r$, $\rho +3p_\phi$ and $\rho +3p_z$. Moreover, It can be seen that DEC is also violated for this case as shown in Fig. 4. It is worth mentioning that NEC is violated due to exotic matter, which indicates the presence of exotic matter in that particular region.

• The graphical behavior of energy density and pressure components and energy conditions for this case is elaborated graphically in Figs. 5, 6, 7 and 8. The graphical analysis of energy density is positive and all these pressure components are negative with decreasing nature, as shown in Fig. 5. The negative behavior of these components may cause the presence of exotic matter and violation of energy conditions. From Figs. 6, 7 and 8, it can be seen that NEC and SEC are satisfied but DEC is violated for the given region.

• It can be noticed that the metric potential defined in Eq. (29) and the other parameter, which is developed in Eq. (32), are used to observe the graphical nature of energy density and pressure components as well as energy conditions. The graphical behavior of energy density is fascinating for this case, as shown in Fig. 9. For this case, it can be observed that the SEC is satisfied, but NEC and DEC are violated due to the negative trends of some pressure components, as shown in Figs. 10, 11 and 12.

• The metric potentials mentioned in Eq. (33) and Eq. (34) are utilized to determine the graphical aspects of energy density, pressure components, and energy conditions for this case. The graphical behavior of energy density initially decreases and increases on the radial coordinate, as shown in Fig. 13. The graphical behavior of radial pressure, azimuthal pressure, and axial pressure is negative near the origin but becomes positive when moving away from the center, as represented in Fig. 13. Figure 14 clearly shows the validity of NEC at $r\geqslant 0$ due to the positive nature of all the components. The behavior of SEC and DEC are violated due to the negative nature of pressure components, as shown in Figs. 15 and 16.

• The graphical behavior of energy density, pressure terms, and different energy conditions can be seen through different panels. As shown in Fig. 17, the graphical representation of energy density is positive and has a maximum value near the origin. Whereas the other panels of Fig. 17 shows the negative trends of radial pressure, azimuthal pressure, and axial pressure. The graphical representation of $\rho +p_r$, $\rho +p_\phi$, and $\rho +p_z$ is positive, which means that NEC is satisfied for this case as shown in Fig. 18. Moreover, one can see that the SEC violates throughout the region for $r>0$ as seen in Fig. 19 and DEC is satisfied, as shown in Fig. 20.

• The graphical behavior of energy density is positive and increasing w.r.t radial coordinate, as shown in Fig. 21. Whereas, the graphical behavior of $p_{r}$, $p_{\phi }$ and $p_{z}$ has opposite nature like energy density. All these pressure components are negative and have decreasing behavior, as seen in Fig. 21. It can be noticed that NEC, WEC, SEC, and DEC are satisfied due to positive and increasing trends of pressure, as seen in Figs. 22, 23 and 24.

• The graphical analysis of energy density is initially decreasing and then becomes increasing, as shown in Fig. 25. On the other panels of Fig. 25 show the graphical depictions of radial pressure, azimuthal pressure, and axial pressure, which are negative. The negative behavior of pressure components indicates the presence of exotic matter and may cause the violation of energy conditions. The graphical depictions of $\rho +p_{\phi }$ and $\rho +p_{z}$ are positive while the remaining component of $\rho +p_r$ is negative, which show that NEC is violated as shown in Fig. 26. It can also be noticed from Figs. 27 and 28 that SEC is violated but DEC is satisfied for this case.

• The graphical behavior of energy density and pressure components including energy conditions can be seen through Figs. 29, 30, 31 and 32. If we restrict these constants to some values like $A_{0}=0, B_{0}=0$ and $C_{0}$ only lies between the interval (0, 1) then the space-time is corresponding to the exterior metric of a cosmic string. In Fig. 33, the energy density shows positive behavior under the consideration of $A_{0}=B_{0}=0$ and $C_{0}=0.5$. In Fig. 34, one can clearly sees that NEC is valid for some particular values of the radial coordinate. It can be seen that the SEC violated through out the region for $r>0$ as depicted in Fig. 35. In the last panel of Fig. 36, the graphical analysis show that DEC is satisfied throughout the region.