The dark energy star and stability analysis

Abstract

We propose a new model of dark energy star consisting of five zones, namely, the solid core of constant energy density, the thin shell between core and interior, an inhomogeneous interior region with anisotropic pressures, a thin shell, and the exterior vacuum region. We discuss various physical properties. The model satisfies all the physical requirements. The stability condition under a small linear perturbation is also discussed.

1 Introduction

The study of dark energy stars has become a subject of interest due to the fact that the expansion of the universe is accelerating, which was suggested by the High-z supernova Search Team in $1998$ by observing type $1a$ supernovae. Dark energy is the most acceptable hypothesis to explain this accelerating expansion of the universe. According to the work done by the Planck mission team and based on the standard model of cosmology the total mass energy of the universe contains $4.9$ % ordinary matter, $26.8$ % dark matter, and $68.3$ % dark energy. Dark matter is attractive in nature which can not seen by a telescope and it does not absorb or emit light or any gravitational waves. But its existence has been proved by gravitational effects on visible matter and gravitational lensing of background radiation. On the other hand dark energy needs to have a strong negative pressure in order to explain the rate of accelerating expansion of the universe.

To construct a model of a relativistic star we generally assume that the underlying fluid distribution is homogeneous and isotropic. But it is proved by advanced research that highly compact astrophysical objects like the X-ray pulsars, Her-x-1, X-ray buster 4U 1820-30, millisecond pulsar SAXJ1804.4-3658 etc. whose density of core is expected to be beyond the nuclear density ($\sim$ ${10}^{15}$ gm/cc) shows anisotropy. Anisotropy may occur in the existence of solid core, in the presence of a type P superfluid, phase transition, rotation, magnetic field, mixture of two fluid, existence of external field etc. In the case of an anisotropy distribution the pressure inside the fluid sphere is not homogeneous in nature, it can be decomposed into two parts: radial pressure $p_\mathrm{r}$ and transverse pressure $p_\mathrm{t}$. So obviously $p_\mathrm{r}\ne p_\mathrm{t}$. Here $p_\mathrm{t}$ is in the orthogonal direction to $p_\mathrm{r}$. $\Delta =p_\mathrm{t}-p_\mathrm{r}$ is defined as the anisotropic factor whereas $\frac{\Delta }{r}$ is defined as the anisotropic force which is repulsive in nature if $p_\mathrm{t}>p_\mathrm{r}$ and attractive if $p_\mathrm{t}<p_\mathrm{r}$.

In this paper, we are going to model an anisotropic dark energy star characterized by the parameter $\omega =\frac{p_\mathrm{r}}{\rho }$, where $p_\mathrm{r}$ and $\rho$ are, respectively, the radial pressure and energy density. For accelerating expansion the dark energy parameter $\omega <-\frac{1}{3}$ is required. $-1<\omega <-\frac{1}{3}$ is referred to as quintessence. The region where $\omega <-1$ is named the phantom regime and this has a peculiar property, namely an infinitely increasing energy density. $\omega =-1$ corresponds to the Einstein cosmological constant and this value is called the cosmological constant barrier or phantom divide.

A two dimensional Brans–Dicke star model with exotic matter and dark energy was studied in [1]. In that paper, the author has taken the matter state equation as $p=\gamma \rho$, where $\gamma$ is the state parameter of exotic matter which satisfies $-\frac{1}{4}<\gamma <0$ and has shown that the mass of the star decrease if $\gamma$ decrease. An anisotropic dark energy star has been discussed in [2]. A star model with dark energy has been proposed in [3]. In this paper the authors have proposed a model of the dark energy star consisting of four regions and by analyzing the model they conclude that for a static solution at least one of the regions must be constituted by dark energy. An anisotropic dark energy star was studied by Ghezzi et al. [4]. These authors have assumed a variable dark energy which suffers a phase transition at a critical density and the anisotropy. The anisotropy is concentrated on a thin shell where the phase transition takes place, while the rest of the star remains isotropic. The solutions shows several features similar to the gravastar model. Lobo [5] has given a model of a stable dark energy star by assuming two spatial types of mass function: one is of constant energy density and the other mass function is a Tolman–Whitker mass. All the features of the dark energy star have been discussed and the system is stable under a small linear perturbation. The van der Waals quintessence stars have been studied in [6]. In that work, the construction of inhomogeneous compact spheres supported by a van der Waals equation of state is explored. van der Waals gravastars and van der Waals wormholes have also been discussed. A variable equation of state for a generalized dark energy model has been studied in [7]. Yadav et al. have given a dark energy model with a variable equation of state parameter in [8]. Some other works on dark energy stars are [9–16].

The plan of the paper is as follows: In Sect. 2 the basic field equations are given. The model of the dark energy star, exterior spacetime and junction condition, TOV equation, energy condition, and the mass–radius relation are, respectively, discussed in Sects. 3, 4, 5, 6, and 7. The stability analysis under a small radial perturbation is studied in Sect. 8. Finally in Sect. 9 we provide a short discussion and make some concluding remarks.

2 Basic field equations

A static and spherically symmetry spacetime in curvature coordinates is given by the following metric:

$$\begin{aligned} \mathrm{d}s^{2}&= -\mathrm{exp}\left[ {-2\int _r^{\infty }g(\tilde{r})\mathrm{d}\tilde{r}}\right] \mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{1-\frac{2m}{r}}\nonumber \\&+r^{2}(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}), \end{aligned}$$

(1)

where $g(r)$ and $m(r)$ are arbitrary functions of the radial parameters r. The function $m(r)$ is the quasi-local mass and is denoted the mass function. The factor $g(r)$ is termed the ‘gravity profile’, which is used to measure the acceleration due to gravity by the relationship $\mathcal {A}=\sqrt{1-\frac{2m}{r}}g(r)$. For inward gravitational attraction $g(r)>0$, and $g(r)<0$ for outward gravitational repulsion. One can note that $\Phi (r)=-\int _r^{\infty }g(r)\mathrm{d}r$, here $\Phi (r)$ is denoted as the redshift function.

The stress energy momentum tensor is given by the equation

$$\begin{aligned} T_{\mu \nu }=(\rho +p_\mathrm{t})U_{\mu }U_{\mu }+p_t g_{\mu \nu }+(p_\mathrm{r}-p_\mathrm{t})\chi _{\mu }\chi _{\nu } \end{aligned}$$

(2)

where $U^{\mu }$ is the vector $4$-velocity, $\chi ^{\mu }$ is the spacelike vector. $\rho (r)$ is the energy density and $p_\mathrm{r}$ is the radial pressure measured in the direction of the spacelike vector. $p_\mathrm{t}$ is the transverse pressure in the orthogonal direction to $p_\mathrm{r}$ and $\Delta =p_\mathrm{t}-p_\mathrm{r}$ is called the anisotropic factor.

Using the Einstein field equations $G_{\mu \nu }=8\pi T_{\mu \nu }$ we get the following relationship:

$$\begin{aligned} m'=4\pi r^{2}\rho , \end{aligned}$$

(3)

$$\begin{aligned} g=\frac{m+4\pi r^{3}p_\mathrm{r}}{r(r-2m)} ,\end{aligned}$$

(4)

$$\begin{aligned} p_\mathrm{r}'=-\frac{(\rho +p_\mathrm{r})(m+4\pi r^{3}p_\mathrm{r})}{r(r-2m)}+\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r}) \end{aligned}$$

(5)

where $G_{\mu \nu }$ is the Einstein tensor and the prime denotes the derivative with respect to the radial coordinate $r$.

The dark energy equation of state is given by the following equation:

$$\begin{aligned} p_\mathrm{r}=\omega \rho \end{aligned}$$

(6)

where $\omega <0$ is the equation of state parameter.

Now one can note that we have five unknown functions namely $\rho , p_\mathrm{r}, p_\mathrm{t},m(r), g(r)$, and four equations, (3)–(6). To solve the set of equations let us assume a particular choice of the energy density $\rho$. This particular choice of $\rho$ was chosen earlier by Dev and Gleiser [17] to discuss the anisotropic star model. Rahaman et al. have also used this density function in [18]. Using this particular choice of energy density we will find the other parameters in explicit form.

3 Model of the dark energy star

Let us choose the energy density of the star as

$$\begin{aligned} \rho =\frac{1}{8\pi }\left( \frac{a}{r^{2}}+3b\right) \end{aligned}$$

(7)

where both $a$ and $b$ are constants, e.g. $a=\frac{3}{7}$ and $b=0$ corresponds to relativistic Fermi gas which can be seen in the ultradense cores of a neutron star [19]; and for $a=\frac{3}{7}, b \ne 0$ we get a relativistic Fermi gas core in a constant density background.

Using (7) into (3) we obtain the expression of the mass function as

$$\begin{aligned} m=\frac{1}{2}r(a+br^{2}). \end{aligned}$$

(8)

Solving Eqs. (4)–(6) we get

$$\begin{aligned} g(r)=\frac{a(1+\omega )+br^{2}(1+3\omega )}{2r(1-a-br^{2})}, \end{aligned}$$

(9)

From the Buchdahl limit, $\frac{2m(r)}{r}<1$ one can see from Eq. (8) that $1-a-br^{2}>0$. This provides a constraint on the parameters $a,~b$, and radius $r$; thus

$$\begin{aligned} r^{2}<\frac{1-a}{b}. \end{aligned}$$

(9.1)

This yields the restrictions on $a,~b$ of

$$\begin{aligned} a<1 \quad \mathrm{and}\quad b>0. \end{aligned}$$

We have chosen $a=0.5$ and $b=0.00$1, motivated by the choice of Dev and Glaiser [17]. They chose $a=3/7$ and $b=0$ to describe their model. Our chosen values of $a$ and $b$ are very close to their choice. Now using those values for $a$ and $b$ from Eq. (9.1), we get $r^{2}<500$ i.e. $r<22.36$. Now, $g(r)>0$ gives

$$\begin{aligned} \omega >-\frac{a+br^{2}}{a+3br^{2}}. \end{aligned}$$

(9.2)

For large r i.e. in the maximum limit, we get by using (9.1) in (9.2)

$$\begin{aligned} \omega >-\frac{1}{3-2a}. \end{aligned}$$

For small r, from (9.2) we have $\omega >-1$.

Therefore,

$$\begin{aligned} \omega >\mathrm{max}\left( -1,-\frac{1}{3-2a}\right) . \end{aligned}$$

(9.3)

For the above choice, $a=0.5$, $\max \left( -1,-\frac{1}{3-2a}\right) = -0.5$ i.e. $\omega >-0.5$.

Again for $g(r)<0$, we have

$$\begin{aligned} \omega <-\frac{a+br^{2}}{a+3br^{2}}. \end{aligned}$$

(9.4)

For small r, Eq. (9.4) yields

$\omega <-1$ and for large r i.e. in the maximum limit,

$$\begin{aligned} \omega < -\frac{1}{3-2a}. \end{aligned}$$

Thus,

$$\begin{aligned} \omega <\min \left( -1,-\frac{1}{3-2a}\right) . \end{aligned}$$

(9.5)

For our choice of $a$, we get $\omega <-1$. So, we have to choose for $\omega$ either $\omega > -0.5$ or $\omega <-1$ for the plot.

The profiles of $g(r)$ are plotted in Figs. 1 and 2 for $-0.45\le \omega \le -0.1$ and $\omega <-1$ respectively.

From Fig. 1 we see that $g(r)>0$ when $-0.45 \le \omega \le -0.1$ and Fig. 2 shows that for $\omega <-1$, $g(r)<0$ for the above choice of $a$ and $b$.

Fig. 1

Gravity profile, $g(r)$, against $r$ when $-0.45\le \omega \le -0.1$

The radial and transverse pressure can be obtained as

$$\begin{aligned} p_\mathrm{r}=\frac{\omega }{8\pi }\left( \frac{a}{r^{2}}+3b\right) , \end{aligned}$$

(10)

$$\begin{aligned} p_\mathrm{t}=\frac{(1+\omega )(a+3br^{2})}{32\pi r^{2}(1-a-br^{2})}[a(1+\omega )+br^{2}(1+3\omega )]+\frac{3b\omega }{8\pi } .\end{aligned}$$

(11)

The matter density, radial, and transverse pressures are depicted in Fig. 3.

The anisotropy factor $\Delta$ is given by

$$\begin{aligned} \Delta =\frac{(1\!+\omega )(a\!+3br^{2})}{32\pi r^{2}(1\!-a-br^{2})} [a(1\!+\!\omega )\!+br^{2}(1\!+\!3\omega )]-\frac{\omega a}{8\pi r^{2}},\nonumber \\ \end{aligned}$$

(12)

which is shown in Figs. 4 and 5, respectively, for $-0.45 \le \omega \le -0.1$ and $\omega <-1$. Now $\frac{\Delta }{r}$ represents a force due to the pressure anisotropy. The force will be repulsive in nature i.e. in the outward direction if $p_\mathrm{t}>p_\mathrm{r}$ and attractive if $p_\mathrm{t}<p_\mathrm{r}$ or alternatively $\Delta <0$. For our stellar model configuration (see Figs. 4, 5) $\Delta >0$ for both the cases when $-0.5<\omega <-0.1$ and the phantom regime, i.e. for $\omega <-1$.

Fig. 2

Gravity profile, $g(r)$, against $r$ when $\omega \le -1$, $a=0.45$, and $b=0.001$

Fig. 3

Matter density $\rho$, radial pressure $p_\mathrm{r}$, and transverse pressure $p_\mathrm{t}$ of the dark energy model against $r$

Fig. 4

The anisotropy parameter $\Delta =p_\mathrm{t}-p_\mathrm{r}$ against $r$ for $-0.45\le \omega \le -0.1$

Fig. 5

The anisotropy parameter $\Delta =p_\mathrm{t}-p_\mathrm{r}$ against $r$ for $\omega <-1$

Now, one may notice that there is a problem in the model such as the divergence of the physical quantities (energy density and pressures) in the origin. To overcome this problem in order to model a star, we propose that the star contains a core up to radius $r_1$.

3.1 Core solution

To avoid this central singularity we cut the spacetime (1) around its origin and placed an anisotropy fluid of constant density $\rho _0$ (say).

Now, to find the core solution, we assume the radial equation of state to be

$$\begin{aligned} p_\mathrm{r}=k \rho _0,\quad k<0. \end{aligned}$$

(13)

Here, the mass function becomes

$$\begin{aligned} m(r)=Br^{3} \end{aligned}$$

(14)

where $B=\frac{4\pi \rho _0}{3}$.

Using this expression of $m(r)$ from Eq. (4) and using Eq. (14) we get

$$\begin{aligned} g(r)=\frac{Br(1+3k)}{1-2Br^{2}}. \end{aligned}$$

(15)

Therefore the spacetime metric of the core is given by

$$\begin{aligned} \mathrm{d}s^{2}=(1-2Br^{2})^{-\frac{1+3k}{2}}\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{1-2Br^{2}}+r^{2}(\mathrm{d}\theta ^{2} +\sin ^{2}\theta \mathrm{d}\phi ^{2}). \end{aligned}$$

(16)

The transverse pressure can be obtained as

$$\begin{aligned} p_\mathrm{t}=k\rho _0\left[ 1+\frac{(1+k)(1+3k)Br^{2}}{2k(1-2Br^{2})}\right] \end{aligned}$$

(17)

and the anisotropic factor $\Delta$ can be obtained as

$$\begin{aligned} \Delta =\frac{3}{8\pi }(1+k)(1+3k)\frac{B^{2}r^{2}}{1-2Br^{2}}. \end{aligned}$$

(18)

From the expression of $\Delta$ it is clear that $\Delta >0$ if $k<-1$ and $\Delta <0$ if $-1<k<-\frac{1}{3}$. At the center of the star $\Delta =0$, which is expected for a physically reasonable solution. It can also be noted that for $k=-1$ and $k=-\frac{1}{3}$ the anisotropic pressure of the core reduces to the isotropic pressure.

4 Energy conditions

Our particular model of dark energy star consists of five regions:

• 1. Solid core of constant matter density.

• 2. Thin shell between core and interior.

• 3. Interior.

• 4. Thin shell between interior and exterior spacetime.

• 5. Exterior Schwarzschild spacetime.

To check whether our model satisfies all the energy conditions, we have to verify the energy conditions in the first four regions described earlier.

At first check all the energy conditions, for regions 1 and 3, and later we will discuss it for regions 2 and 4. We will consider the following inequalities:

$$\begin{aligned} \mathrm{(i)}~\mathrm{NEC{:}}~\rho +p_\mathrm{r}\ge 0, \end{aligned}$$

(19)

$$\begin{aligned} \mathrm{(ii)}~\mathrm{WEC{:}}~ \rho +p_\mathrm{r}\ge 0,\quad \rho \ge 0, \end{aligned}$$

(20)

$$\begin{aligned} \mathrm{(iii)\, SEC{:}}~ \rho +p_\mathrm{r}\ge 0,\quad \rho +p_\mathrm{r}+2p_\mathrm{t}\ge 0, \end{aligned}$$

(21)

$$\begin{aligned} \mathrm{(iv)\, DEC{:}}~\rho >|p_\mathrm{r}|,\quad \rho >|p_\mathrm{t}|. \end{aligned}$$

(22)

Figure 6 indicates that for our model all the energy conditions are satisfied in the interior region. Figure 7, however, shows the SEC is violated within the core.

Fig. 6

The energy conditions in the interior against $r$

Fig. 7

The energy condition within the core against $r$

5 Exterior spacetime and junction condition

In this section we match our interior spacetime to the exterior Schwarzschild vacuum solution along the junction surface with the junction radius ‘$R$’.The exterior spacetime is given by the metric

$$\begin{aligned} \mathrm{d}s^{2}=-\left( 1-\frac{2M}{r}\right) \mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{1-\frac{2M}{r}}+r^{2}(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}). \end{aligned}$$

(23)

Here, the event horizon lies at $r=2M$. So obviously $R>2M$.

Previously, we have matched our interior spacetime to the exterior Schwarzschild at the boundary $r=R$. Obviously the metric coefficients are continuous at $r=R$, but it does not ensure that their derivatives are also continuous at the junction surface. In other words the affine connections may be discontinuous there. To take care of this let us use the Darmois–Israel [20, 21] formation to determine the surface stresses at the junction boundary. The intrinsic surface stress energy tensor $S_{ij}$ is given by the Lancozs equations in the following form:

$$\begin{aligned} S^{i}_{j}=-\frac{1}{8\pi }(K^{i}_j-\delta ^{i}_j K^{k}_k). \end{aligned}$$

(24)

The discontinuity in the second fundamental form is given by

$$\begin{aligned} K_{ij}=K_{ij}^{+}-K_{ij}^{-} \end{aligned}$$

(25)

where the second fundamental form is given by

$$\begin{aligned} K_{ij}^{\pm }=-n_{\nu }^{\pm }\left[ \frac{\partial ^{2}X_{\nu }}{\partial \xi ^{1}\partial \xi ^{j}}+\Gamma _{\alpha \beta }^{\nu }\frac{\partial X^{\alpha }}{\partial \xi ^{i}}\frac{\partial X^{\beta }}{\partial \xi ^{j}} \right] |_S, \end{aligned}$$

(26)

where $n_{\nu }^{\pm }$ are the unit normal vector defined by

$$\begin{aligned} n_{\nu }^{\pm }=\pm \left| g^{\alpha \beta }\frac{\partial f}{\partial X^{\alpha }} \frac{\partial f}{\partial X^{\beta }} \right| ^{-\frac{1}{2}}\frac{\partial f}{\partial X^{\nu }}, \end{aligned}$$

(27)

with $n^{\nu }n_{\nu }=1$. Here $\xi ^{i}$ is the intrinsic coordinate on the shell. $+$ and $-$ correspond to exterior i.e., Schwarzschild spacetime and interior (our) spacetime, respectively. The model of our dark energy star consists of five zones, namely, the core, the thin shell between core and interior, an inhomogeneous interior region with anisotropic pressures, a thin shell and the exterior vacuum region.

Considering the spherical symmetry of the spacetime the surface stress energy tensor can be written as $S^{i}_j=\mathrm{diag}(-\sigma ,\mathcal {P},\mathcal {P})$, where $\sigma$ and $\mathcal {P}$ are the surface energy density and surface pressure, respectively. We have

$$\begin{aligned} K_{\tau }^{\tau +}=\frac{\frac{M}{R^{2}}+\ddot{R}}{\sqrt{1-\frac{2M}{R}+\dot{R}^{2}}}, \end{aligned}$$

(28)

$$\begin{aligned} K_{\tau }^{\tau -}=\frac{\frac{(1+\omega )a+bR^{2}(1+3\omega )}{2R}+\ddot{R}- \frac{(1+\omega )\dot{R}^{2}(a+3bR^{2})}{2(R-Ra-bR^{3})}}{\sqrt{1-a-bR^{2}+\dot{R}^{2}}}, \end{aligned}$$

(29)

$$\begin{aligned} K_{\theta }^{\theta +}=\frac{1}{R}\sqrt{1-\frac{2M}{R}+\dot{R}^{2}}, \end{aligned}$$

(30)

$$\begin{aligned} K_{\theta }^{\theta -}=\frac{1}{R}\sqrt{1-a-bR^{2}+\dot{R}^{2}}. \end{aligned}$$

(31)

The expressions of $\sigma$ and $\mathcal {P}$ are given by

$$\begin{aligned} \sigma =-\frac{1}{4\pi R}\left[ \sqrt{1-\frac{2M}{R}+\dot{R}^{2}}-\sqrt{1-(a+bR^{2})+\dot{R}^{2}}\right] , \end{aligned}$$

(32)

$$\begin{aligned} \mathcal {P}&= \frac{1}{8\pi R}\left[ \frac{1-\frac{M}{R}+\dot{R}^{2}+R\ddot{R}}{\sqrt{1-\frac{2M}{R}+\dot{R}^{2}}}\right. \nonumber \\&\left. +\frac{1+Rg(R)(1-a-bR^{2}+\dot{R}^{2}) +R\ddot{R}+\frac{bR^{2}}{1-a-bR^{2}}\dot{R}^{2}}{\sqrt{1-a-bR^{2}+\dot{R}^{2}}}\right] .\nonumber \\ \end{aligned}$$

(33)

Using the conservation identity $S_{j,i}^{i}\!=\!-\big [\dot{\sigma }\!+\!2\frac{\dot{R}}{R}(\mathcal {P}\!+\!\sigma )\big ]$, one can obtain

$$\begin{aligned} \sigma '=-\frac{2}{R}(\mathcal {P}+\sigma )+\Xi \end{aligned}$$

(34)

where $\Xi$ is given by

$$\begin{aligned} \Xi =-\frac{1}{4\pi R}\frac{m-m'R}{R-2m}\sqrt{1-a-bR^{2}+\dot{R}^{2}}. \end{aligned}$$

(35)

The surface mass of the thin shell is given by

$$\begin{aligned} m_\mathrm{s}=4\pi R^{2}\sigma . \end{aligned}$$

(36)

Using the expression of $\sigma$ given in Eq. (32) (considering the static case) from Eq. (36) we get

$$\begin{aligned} m_\mathrm{s}=R\left[ \sqrt{1-(a+bR^{2})}-\sqrt{1-\frac{2M}{R}}\right] . \end{aligned}$$

(37)

After a little manipulation of Eq. (37) the total mass of the dark energy star can be obtained as

$$\begin{aligned} M=\frac{1}{2}R(a+bR^{2})-\frac{m_\mathrm{s}^{2}}{2R}+m_\mathrm{s}\sqrt{1-(a+bR^{2})}. \end{aligned}$$

(38)

From Eq. (36) one can obtain

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{2R}\right) ''=\Upsilon -4\pi \sigma '\eta \end{aligned}$$

(39)

(for details of the calculation see the appendix), where

$$\begin{aligned} \eta =\frac{\mathcal {P'}}{\sigma '},\quad \Upsilon =\frac{4\pi }{R}(\sigma +\mathcal {P})+2\pi R\Xi ' \end{aligned}$$

(40)

where the prime denotes the derivative with respect to R.

We will use the parameter $\eta$ to discuss the stability analysis of the system. This $\sqrt{\eta }$ is generally interpreted as the velocity of the sound. So, for physical acceptability one must have $0<\eta \le 1$. The profile of $\eta$ is shown in Figs. 8 and 9.

Fig. 8

The velocity of the sound for different values of mass $M$ against $r$ when the dark energy parameter $\omega$ is fixed

Next we will discuss the evolution identity given by

$$\begin{aligned} \left[ T_{\mu \nu }n^{\mu }n^{\nu }\right] _{-}^{+}=\bar{K}_j^{i}S_i^{j} \end{aligned}$$

(41)

where $\bar{K}_j^{i}=\frac{1}{2}(K_j^{i+}+K_j^{i-})$. From Eq. (41) using Eqs. (28)–(31) one can obtain

$$\begin{aligned}&p_\mathrm{r}+\frac{(\rho +p_\mathrm{r})\dot{R}^{2}}{1-a-bR^{2}}\nonumber \\&\quad =-\frac{1}{2R}\left( \sqrt{1-\frac{2M}{R}+\dot{R}^{2}}+\sqrt{1-a-bR^{2} +\dot{R}^{2}}\right) \mathcal {P}\nonumber \\&\qquad +\frac{1}{2}\left( \frac{\frac{M}{R^{2}}+\ddot{R}}{\sqrt{1-\frac{2M}{R}+\dot{R}^{2}}}\right. \nonumber \\&\qquad \left. +\frac{\frac{(1+\omega )a+bR^{2}(1+3\omega )}{2R}+\ddot{R} -\frac{(1+\omega )\dot{R}^{2}(a+3bR^{2})}{2(R-Ra-bR^{3})}}{\sqrt{1-a-bR^{2}+\dot{R}^{2}}}\right) \sigma . \end{aligned}$$

(42)

Considering static solution at $R=R_0$ with $\dot{R} = \ddot{R}=0$, we get

$$\begin{aligned}&p_\mathrm{r} =-\frac{1}{2R_0}\left( \sqrt{1-\frac{2M}{R_0} }+\sqrt{1-a-bR_0^{2} }\right) \mathcal {P}\nonumber \\&\quad \quad +\frac{1}{2}\left( \frac{\frac{M}{R_0^{2}} }{\sqrt{1-\frac{2M}{R_0} }}+\frac{\frac{(1+\omega )a+bR_0^{2}(1+3\omega )}{2R_0} }{\sqrt{1-a-bR_0^{2} }}\right) \sigma . \end{aligned}$$

(43)

Here, $\sigma <0$, therefore, $p_\mathrm{r}<0,$ i.e. the tension is in the radial direction. Hence a positive tangential surface pressure ${ \mathcal {P}}>0$ is required to keep the shell stable i.e. to hold the shell against collapsing.

Fig. 9

The velocity of the sound for different values of energy parameter $\omega$ against $r$ when the mass of the dark energy star $M$ is fixed

5.1 Junction conditions between core and interior solution

Since the core radius is $r_1$, we match the core solution with interior solution at the junction surface with junction radius $r_1$.

The core extrinsic curvature is given by

$$\begin{aligned}&K_{\tau \tau }^{-}=-Br_1(1+3k)(1-2Br_1^{2})^{-\frac{1}{2}},\\&K_{\theta \theta }^{-}=r_1(1-2Br_1^{2})^{\frac{1}{2}}. \end{aligned}$$

Therefore the surface energy density and surface pressure can be obtained as

$$\begin{aligned} \sigma =-\frac{1}{4\pi r_1}\left[ \sqrt{1-a-br_1^{2}}-\sqrt{1-2Br_1^{2}}\right] , \end{aligned}$$

(44)

$$\begin{aligned} \mathcal {P}\!=\!\frac{1}{8\pi r_1}\left[ \frac{1\!+\!r_1 g(r_1)(1\!-\!a-br_1^{2})}{\sqrt{1\!-\!a-br_1^{2}}}\!-\!\frac{1+(1+3k)Br_1^{2}}{\sqrt{1-2Br_1^{2}}}\right] . \end{aligned}$$

(45)

5.2 Energy conditions for both thin shells i.e. the interior thin shell between core and interior region and the outer thin shell between the interior region and the Schwarzschild spacetime

According to [22] for a thin shell all the energy conditions namely Null Energy conditions (NEC), Weak Energy Conditions (WEC), Dominant Energy conditions (DEC), and Strong Energy Conditions (SEC) will be satisfied if the following inequalities hold.

• 1. NEC: $\sigma +\mathcal {P} \ge 0$;

• 2. WEC: $\sigma \ge 0$ and $\sigma +\mathcal {P} \ge 0$;

• 3. SEC: $\sigma +\mathcal {P}\ge 0$ and $\sigma +2\mathcal {P} \ge 0$;

• 4. DEC: $\sigma +\mathcal {P} \ge 0$ and $\sigma -\mathcal {P} \ge 0$.

Figures 10 and 11 show all energy conditions except DEC are satisfied within both interior and exterior thin shells.

Fig. 10

The energy condition of the thin shell between core and interior region against $r$

Fig. 11

The energy condition of the thin shell between interior region and the exterior Schwarzschild spacetime against $r$

6 TOV equation

The generalized Tolman–Oppenheimer–Volkov (TOV) equation is given by [23]

$$\begin{aligned} -\frac{M_\mathrm{G}(\rho +p_\mathrm{r})}{r^{2}}\mathrm{e}^{\frac{\lambda -\nu }{2}}-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}+\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r})=0. \end{aligned}$$

(46)

Here $M_\mathrm{G}=M_\mathrm{G}(r)$ is the effective gravitational mass inside a sphere of radius $r$ given by the Tolmam–Whittaker formula which can be derived from the equation

$$\begin{aligned} M_\mathrm{G}(r)=\frac{1}{2}r^{2}\mathrm{e}^{\frac{\nu -\lambda }{2}}\nu '. \end{aligned}$$

(47)

The above equations describe the equilibrium conditions of the fluid sphere subject to gravitational, hydrostatics, and anisotropy forces.

Equation (34) can be modified in the form

$$\begin{aligned} F_\mathrm{g}+F_\mathrm{h}+F_\mathrm{a}=0 \end{aligned}$$

(48)

where

$$\begin{aligned} F_\mathrm{g}=-\frac{\nu '}{2}(\rho +p_\mathrm{r}), \end{aligned}$$

(49)

$$\begin{aligned} F_\mathrm{h}=-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}, \end{aligned}$$

(50)

$$\begin{aligned} F_\mathrm{a}=\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r}). \end{aligned}$$

(51)

The profiles of $F_\mathrm{g},F_\mathrm{h},F_\mathrm{a}$ are shown in Fig. 12. The figure shows that our dark energy model is in static equilibrium under gravitational $(F_\mathrm{g})$, hydrostatics $(F_\mathrm{h})$, and anisotropic $(F_\mathrm{a})$ forces.

Fig. 12

The dark energy star is in static equilibrium under gravitational $(F_\mathrm{g})$, hydrostatics $(F_\mathrm{h})$, and anisotropy $(F_\mathrm{a})$ forces

7 Mass radius relation

The mass of the dark energy star is given in Eq. (8).

The compactness of the star is defined as

$$\begin{aligned} u=\frac{m(r)}{r}=\frac{1}{2}(a+br^{2}), \end{aligned}$$

(52)

and the surface redshift is defined by

$$\begin{aligned} Z_\mathrm{s}=(1-2u)^{-\frac{1}{2}}-1=(1-a-br^{2})^{-\frac{1}{2}}-1. \end{aligned}$$

(53)

The profile of mass function, compactness, and surface redshift of the dark energy star are given in Figs. 13, 14, and 15, respectively.

Fig. 13

Mass function $m(r)$ against $r$

Fig. 14

The compactness of the dark energy star against $r$

Fig. 15

The surface redshift $Z_\mathrm{s}$ against $r$

8 Stability analysis

In this section we are going to analyze the stability of our model.

Rearranging Eq. (32) we get

$$\begin{aligned} \dot{R}^{2}+V(R)=0. \end{aligned}$$

(54)

Here $V(R)$ is given by

$$\begin{aligned} V(R)=1-\frac{M-m}{R}-\left( \frac{m_\mathrm{s}}{2R}\right) ^{2}-\left( \frac{M-m}{m_\mathrm{s}}\right) ^{2} \end{aligned}$$

(55)

(for details of the derivation see Appendix 1).

To discuss the linearized stability analysis let us take a linear perturbation around a static radius $R_0$. Expanding $V(R)$ by a Taylor series around the radius of the static solution $R= R_0$ one can obtain

$$\begin{aligned} V(R)=V(R_0)+(R-R_0)V'(R_0)+\frac{(R-R_0)^{2}}{2}V''(R_0) \end{aligned}$$

$$\begin{aligned} \quad \quad \quad \qquad +O[(R-R_0)^{3}] \end{aligned}$$

(56)

where a prime denotes the derivative with respect to $R$.

Since we are linearizing around the static radius $R=R_0$ we must have $V(R_0)=0,V'(R_0)=0$. The configuration will be stable if $V(R)$ has a local minimum at $R_0$ i.e., if $V''(R_0)>0$.

Now from the relation $V'(R_0)=0$ we get

$$\begin{aligned} \left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) ' \!=\!A\left[ F'(R_0)\!-\!2\left( \frac{M-m(R_0)}{m_\mathrm{s}}\right) \left( \frac{M-m(R_0)}{m_\mathrm{s}}\right) '\right] \end{aligned}$$

(57)

where A is defined later

Now the configuration will be stable if $V''(R_0)>0$, i.e., if

$$\begin{aligned} \eta \frac{\mathrm{d}}{\mathrm{d}R}(\sigma ^{2})>\frac{1}{2\pi }\left[ \sigma \Upsilon -\frac{1}{2\pi R_0}(H^{2}-G^{2})\right] . \end{aligned}$$

(58)

For details of the derivation see Appendix 3. We have

$$\begin{aligned} G(R_0)\!=\!A\left[ F'(R_0)\!-\!2\left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) \left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) '\right] , \end{aligned}$$

(59)

$$\begin{aligned} A=\left( \frac{R_0}{m_\mathrm{s}(R_0)}\right) , \end{aligned}$$

$$\begin{aligned} \{H(R_0)\}^{2}=\frac{1}{2}F''(R_0)-\left[ \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right] ^{2}, \end{aligned}$$

$$\begin{aligned} \quad -\left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) \left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) ''. \end{aligned}$$

(60)

Now from Eq. (58) we get

$$\begin{aligned} \eta _0\frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}|_{R_0}>\Omega \end{aligned}$$

(61)

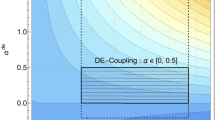
where $\Omega =\frac{1}{2\pi }\left[ \sigma \Upsilon -\frac{1}{2\pi R_0}(H^{2}-G^{2})\right]$. From Eq. (61) the stability regions are dictated by the following inequalities:

$$\begin{aligned} \eta _0>\Omega \left( \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}|_{R_0}\right) ^{-1} \quad \mathrm{if}\,\, \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}|_{R_0} >0, \end{aligned}$$

(62)

$$\begin{aligned} \eta _0<\Omega \left( \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}|_{R_0}\right) ^{-1} \quad \mathrm{if}\,\, \frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}|_{R_0} < 0. \end{aligned}$$

(63)

From the plot of $\frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}$ (see Fig. 16) we see that $\frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}<0$. So the stability region for our model is given by Eq. (63).

Fig. 16

$\frac{\mathrm{d}\sigma ^{2}}{\mathrm{d}R}$ against $R$

9 Discussions and concluding remarks

In this work we have obtained a new class of exact interior solutions by choosing a special form of the energy density which describes a model of the dark energy star parameterized by $\omega =\frac{p_\mathrm{r}}{\rho }<0$. For our choice of $a=0.5$ and $b=0.001$, we have shown that the dark energy parameter $\omega$ lies in either $-0.5<\omega <-0.1$ or $\omega <-1.$ The obtained solutions are well behaved for $r>0$. From Figs. 1 and 2, we see that the gravity profile $g(r)>0$ when $-0.5\le \omega \le -0.1$ and $g(r)<0$ when $\omega$ lies in the phantom regime. The energy density $\rho$, radial pressure $(p_\mathrm{r})$, and transverse pressure $(p_\mathrm{t})$ all are monotonic decreasing function of $r$. The anisotropy factor $\Delta >0$ for $-0.5<\omega <-0.1$ as well as for $\omega <-1$, which implies $p_\mathrm{t}>p_\mathrm{r}$ i.e. the anisotropic force is repulsive in nature. We have matched our interior spacetime to the exterior Schwarzschild spacetime in the presence of a thin shell where we have assumed a positive surface pressure to hold the thin shell against collapse. The mass of the dark energy star in terms of the thin shell mass has been proposed as well as the relationship among $p_\mathrm{r}, \sigma ,\mathcal {P}$ has been given. By keeping $\omega$ fixed and choosing different values of $M$, we have shown that $0<\eta <1$. Similarly by keeping the mass $M$ fixed and for $-0.45\le \omega <-0.1$, we have shown that $0<\eta <1$. All the energy conditions in the interior region are satisfied. However, in the core SEC is violated and both thin shells i.e. for the interior thin shell between the core and interior region and the outer thin shell between the interior region and the Schwarzschild spacetime, DEC is violated.

The mass function is monotonic increasing and regular at the center. For $(3+1)$ dimensional astrophysical object, Buchdahl [24] has shown that $\frac{2M}{R}<\frac{8}{9}$. For our model $\frac{2M}{R}=0.564<\frac{8}{9}$. The stability analysis under a small radial perturbation has also been discussed.

Appendices

Appendix 1

We have

$$\begin{aligned} m_\mathrm{s}=4\pi R^{2}\sigma ; \end{aligned}$$

using the expression of $\sigma$ we get

$$\begin{aligned} \mathrm{or}~~\frac{m_\mathrm{s}}{4\pi R^{2}}=\frac{1}{4\pi R}\left[ \sqrt{1-\frac{2m}{R}+\dot{R}^{2}}-\sqrt{1-\frac{2M}{R}+\dot{R}^{2}}\right] , \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~\frac{m_\mathrm{s}}{a}=\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}-\sqrt{1-\frac{2M}{R}+\dot{R}^{2}}, \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~~\frac{m_\mathrm{s}}{a}-\sqrt{1-\frac{2m}{R}}=-\sqrt{1-\frac{2M}{R}+\dot{R}^{2}}. \end{aligned}$$

Squaring both sides we get

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{R}\right) ^{2}-2\frac{m_\mathrm{s}}{R}\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}=\frac{2}{R}(m-M), \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~~\frac{m_\mathrm{s}}{R}\left[ \frac{m_\mathrm{s}}{R}-2\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}\right] =\frac{2}{R}(m-M), \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~~\frac{m_\mathrm{s}}{R}-2\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}=\frac{2}{m_\mathrm{s}}(m-M), \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~~\frac{m_\mathrm{s}}{R}-\frac{2}{m_\mathrm{s}}(m-M)=2\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}, \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~~~\frac{m_\mathrm{s}}{2R}+\frac{M-m}{m_\mathrm{s}}=\sqrt{1-\frac{2m}{R}+\dot{R}^{2}}; \end{aligned}$$

again squaring both sides we get

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{2R}\right) ^{2}+\left( \frac{M-m}{m_\mathrm{s}}\right) ^{2}+2\frac{M-m}{2R}=1-\frac{2m}{R}+\dot{R}^{2}, \end{aligned}$$

which gives

$$\begin{aligned} \dot{R}^{2}=\left( \frac{m_\mathrm{s}}{2R}\right) ^{2}+\left( \frac{M-m}{m_\mathrm{s}}\right) ^{2}+\frac{M-m}{R}-1. \end{aligned}$$

Now,

$$\begin{aligned} \dot{R}^{2}=-V(R), \end{aligned}$$

which gives

$$\begin{aligned} V(R)=1-\frac{M-m}{R}-\left( \frac{m_\mathrm{s}}{2R}\right) ^{2}-\left( \frac{M-m}{m_\mathrm{s}}\right) ^{2}. \end{aligned}$$

Appendix 2

We have

$$\begin{aligned} m_\mathrm{s}=4\pi R^{2}\sigma , \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~\frac{m_\mathrm{s}}{2R}=2\pi R \sigma . \end{aligned}$$

Differentiating both sides with respect to R we get

$$\begin{aligned} \mathrm{or,}~~\left( \frac{m_\mathrm{s}}{2R}\right) '&= 2\pi (R \sigma '+\sigma )\\&= 2\pi R\left\{ -\frac{2}{R}(\sigma +\mathcal {P})+\Xi \right\} +2\pi \sigma \\&= -4\pi \mathcal {P}+2\pi R \Xi -2\pi \sigma . \end{aligned}$$

Differentiating both sides with respect to R we get

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{2R}\right) ''=-4\pi \mathcal {P}'+2\pi (R \Xi '+\Xi )-2\pi \sigma '. \end{aligned}$$

Using the value of $\sigma '$ we get

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{2R}\right) ''&= -4\pi \mathcal {P}'+2\pi (R \Xi '+\Xi )\nonumber \\&-2\pi \left\{ -\frac{2}{R}(\sigma +\mathcal {P})+\Xi \right\} \end{aligned}$$

$$\begin{aligned} =\frac{4\pi }{R}(\sigma +\mathcal {P})+2\pi R\Xi '-4\pi \eta \sigma '; \end{aligned}$$

therefore,

$$\begin{aligned} \left( \frac{m_\mathrm{s}}{2R}\right) ''=\Upsilon -4\pi \eta \sigma ' \end{aligned}$$

where

$$\begin{aligned} \Upsilon =\frac{4\pi }{R}(\sigma +\mathcal {P})+2\pi R\Xi ' \end{aligned}$$

Appendix 3

We have

$$\begin{aligned} V(R)=F(R)-\left( \frac{m_\mathrm{s}}{2R}\right) ^{2}-\left( \frac{M-m}{m_\mathrm{s}}\right) ^{2}, \end{aligned}$$

$$\begin{aligned} V'(R)=F'(R)-2\left( \frac{m_\mathrm{s}}{2R}\right) \left( \frac{m_\mathrm{s}}{2R}\right) ' \end{aligned}$$

$$\begin{aligned} \qquad \qquad \quad -2\left( \frac{M-m}{m_\mathrm{s}}\right) \left( \frac{M-m}{m_\mathrm{s}}\right) '. \end{aligned}$$

Now, $V'(R_0)=0$ gives

$$\begin{aligned}&\left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) ' =\left( \frac{R_0}{m_\mathrm{s}(R_0)}\right) \nonumber \\&\times \left[ F'(R_0)-2\left( \frac{M-m(R_0)}{m_\mathrm{s}}\right) \left( \frac{M-m(R_0)}{m_\mathrm{s}}\right) '\right] ; \end{aligned}$$

$$\begin{aligned}&\mathrm{let}~~~\left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) '=G(R_0)=\left( \frac{R_0}{m_\mathrm{s}(R_0)}\right) \nonumber \\&\times \left[ F'(R_0)-2\left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) \left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) '\right] ; \end{aligned}$$

now

$$\begin{aligned}&V''(R)=F''(R)-2\left[ \left( \frac{m_\mathrm{s}(R)}{2R}\right) \left( \frac{m_\mathrm{s}(R)}{2R}\right) '' +\left\{ \left( \frac{m_\mathrm{s}(R)}{2R}\right) '\right\} ^{2}\right] \nonumber \\&\quad -2\left[ \left( \frac{M-m(R)}{m_\mathrm{s}(R)}\right) \left( \frac{M-m(R)}{m_\mathrm{s}(R)}\right) ''+\left\{ \left( \frac{M-m(R)}{m_\mathrm{s}(R)}\right) '\right\} ^{2}\right] ,\\&V''(R_0)=F''(R_0)-2\left[ \left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) \left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) '' +G(R_0)^{2}\right] \nonumber \\&\quad -2\left[ \left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) \left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) ''+\left\{ \left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) '\right\} ^{2}\right] . \end{aligned}$$

Now $V''(R_0)>0$ gives

$$\begin{aligned} H(R_0)^{2}> [G(R_0)]^{2}+\left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) \left( \frac{m_\mathrm{s}(R_0)}{2R_0}\right) '' \end{aligned}$$

where

$$\begin{aligned} H(R_0)^{2}=\frac{1}{2}F''(R_0)-\left[ \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right] ^{2} \end{aligned}$$

$$\begin{aligned} \qquad \qquad \qquad -\left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) \left( \frac{M-m(R_0)}{m_\mathrm{s}(R_0)}\right) '', \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~~H^{2}-G^{2}>2\pi R_0\sigma \left[ \frac{4\pi }{R_0}(\sigma \!+\!\mathcal {P})\!+\!2\pi R_0\Xi '-4\pi \eta \sigma '\right] , \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~~H^{2}-G^{2}\! >\!2\pi R_0\sigma (\Upsilon -4\pi \eta \sigma '), \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~~\frac{1}{2\pi R_0}(H^{2}-G^{2})>\sigma \Upsilon -2\pi \eta \frac{\mathrm{d}}{\mathrm{d}a}(\sigma ^{2}), \end{aligned}$$

$$\begin{aligned} \mathrm{or}~~~~\eta \frac{\mathrm{d}}{\mathrm{d}a}(\sigma ^{2})>\frac{1}{2\pi }\left[ \sigma \Upsilon -\frac{1}{2\pi R_0}(H^{2}-G^{2})\right] . \end{aligned}$$