1 Introduction

In the past few decades, complexity science has emerged and developed rapidly. A recent open discussion on the achievements, challenges, and future prospects of the field can be found in Ref. [1]. There has been a growing interest in applying statistical physics concepts and/or methods to study multidisciplinary phenomena in complex social and economic systems, such as social–economic structures and behaviors; see, e.g., Refs. [2, 3], and the most recent thorough review [4] (and references therein). In particular, the emergence of collective order, similar to phase transition, can arise from simple and localized social rules based on expectations or individual decisions, which is a characteristic shared by statistical physics systems. Schelling’s segregation model [5, 6], proposed roughly half a century ago, is a well-known example of this type of model in social and economic sciences, and has obtained significant attention across numerous fields; see, e.g., Refs. [4, 7,8,9,10,11,12,13,14,15,16]. A number of particularly intriguing connections between Schelling’s model and statistical physics have been discussed, e.g., cluster formation [17], connection to the Ising model [18] and to the Blume–Emery–Griffiths (BEG) spin-1 model [19, 20], underlying topological effects [11, 21,22,23,24], and others [25,26,27].

In Schelling’s simple but elegant model, agents are divided into two groups based on attributes such as color (e.g., red and blue) or social–economic mindset (e.g., egoists and altruists), and they move on a grid or blocks according to a tolerance rule. Even a slight preference for similar neighbors can lead to collective segregation, resulting in agents clustering together homogeneously. This phase transition can robustly occur in various model variants, regardless of the underlying topologies, such as regular lattice, random graph or scale-free (SF) network [11]. Notably, Schelling also proposed the prototype metapopulation model in his classic work [5], which replaces the grid with blocks that comprise a large number of agents and still preserves the emergence of segregation phase transition. Unfortunately, the metapopulation version of Schelling’s model was overlooked for a long time until recent years [16, 26, 27]. However, the metapopulation model does not qualitatively change the conclusion of robust segregation phase transition with various underlying topologies. This implies the emergence of segregation phase transition is also robust cross over both the original Schelling’s model on a complex network of grids and that of blocks, in addition to the underlying topologies. On the other hand, considering the importance of eliminating segregation at a social and economic perspective, a natural theoretical question arises whether there exists an underlying topology that could weaken or even eliminate the robust segregation phase transition observed in Schelling’s model.

In a recent study [23], we demonstrated that Schelling’s metapopulation model with a star-shaped underlying topology exhibits novel and counter-intuitive effects, such as collective optimization. Our findings revealed the significant roles played by the star-shaped topology of blocks on both the optimum stationary state and evolutionary dynamics, which were modeled through a triangular-form utility function \(u(\rho )\), where \(\rho \) represents the density of agents living in a block. Surprisingly, we observed that increasing the number of altruistic agents did not help the system approach its optimal state. To explore the possible influences of the evolution of the underlying topology on this phenomenon, we proposed an adding-link mechanism. By adjusting the probability of adding new links between blocks, we discovered that the topology evolves from a star shape to a fully connected network, causing the optimization of the utility function to fade away. This procedure was shown to be influenced by the mono-centric hub of the topology and the connections between peripheral blocks.

However, there is still a lack of sufficient understanding regarding the social–economic significance of this effect. Additionally, one might wonder if this effect is sensitive to the choice of the utility function. These factors have inspired us to revisit the original Schelling metapopulation model with a simple step utility function, in contrast to the one used in Ref. [27], which leads to a diminishment of the global effect of the utility. Thus, we investigate the influences of a star-shaped underlying network on the characteristics of the segregation phase transition and provide a positive answer to the previous question.

In this work, the star topology configuration is composed of a hub block and multiple peripheral blocks. The hub block has the highest degree, while the peripheral blocks have only a single connection. One of the distinctive features of the star topology is its extreme heterogeneity, compared to other network topologies such as the Erdős–Rényi (ER) random graph [28]. We demonstrate that in such a scenario, there is a significant suppression of the segregation phase transition. To gain further insight into how the segregation state evolves, we propose an adding-link mechanism that connects any pair of peripheral blocks, linking the star topology to a fully connected network topology. This allows us to observe the development of segregation over time as it moves from one topology (e.g., star shape) to another, indicating a level of heterogeneity that is independent of size and substantially alters the way in which segregation operates. We report the corresponding scaling law for the order parameter versus the connecting probability.

The rest of the paper is organized as follows: in Sect. 2, we introduce Schelling’s metapopulation model on a star-shaped network of blocks, and major parameters are set up for later use. In Sect. 3, we present our numerical results generated by simulations. We demonstrate the significant suppression of segregation phase in the Schelling’s metapopulation model, and analyze in detail the crucial role played by the underlying star topology of blocks. In Sect. 4, we explore the potential effects of the random adding-link mechanism, and observe the evolution of the interface density S(t). Finally, we sum up our paper with conclusions and final remarks.

2 Schelling’s metapopulation model

In our framework, we adhere to the spirit of the original Schelling’s metapopulation model, with the exception that there are N total agents residing on a star-shaped network of blocks, instead of a two-dimensional lattice city. There are two groups of agents, say, red and blue.

The underlying network consists of Q blocks, with each block having a maximum capacity of M agents. One hub block in the middle is connected to the other \(Q-1\) blocks. The total number of both types of agents can be set to be constant and equal for simplicity. All agents are initially distributed randomly across the network, with an initial average density \(\rho =N/MQ\) set up at the beginning of the simulation.

If there are fewer agents of the unlike type \(n_u\) present at the same block (neighborhood) than the degree of “tolerance” T, which is the maximum tolerable ratio of the sites occupied by unlike agents at the same block, an agent is said to be satisfied with its utility (\(u = 1\)), otherwise unsatisfied (\(u = 0\)). All these can be expressed as

$$\begin{aligned} u_i={\left\{ \begin{array}{ll} 1 &{} \text{ if }\, n_u/M < T\, \text{ in }\, i'\text{ s } \text{ neighborhood }, \\ 0 &{} \text{ otherwise } \,. \end{array}\right. } \end{aligned}$$
(1)

Whether it is satisfied or not, an agent is randomly selected at each time step of the evolution and then attempts to migrate to another unsaturated target block that is connected to the source block. The migration will be accepted if the settlement of the agent on the destination block can make itself satisfied; otherwise, the agent will remain on the source block. Repeat this procedure until a equilibrium, or a steady state that no more agents can move, is reached.

To investigate the segregation phase transition, it is crucial to select an appropriate “order parameter” that accurately represents or identifies the degree of segregation in Schelling’s model. Various measures have been proposed to fulfill this task, such as the ratio of like to unlike neighbors, or the fraction of vacant neighboring sites of an individual agent. Among these, the interface density, denoted as S(t), has been frequently used and serves as a natural observable to measure the state of the system and the emergence of the segregation phase [20, 21, 25]. It is defined as the average fraction of pairs of agents of opposite types to each other on the same node at time step t,

$$\begin{aligned} S(t) = \frac{1}{Q}\sum _{i=1}^Q\frac{2n_{r}(i,t)n_{b}(i,t)}{\left[ n_{r}(i,t)+n_{b}(i,t)\right] \left[ n_{r}(i,t)+n_{b}(i,t)-1\right] } \, , \end{aligned}$$
(2)

where \(n_r(i,t)\) (\(n_b(i,t)\)) is the number of red (blue) agents located in the i-th node at a given time t. That is, the ith node has \(\left[ n_{r}(i,t)+n_{b}(i,t)\right] [n_{r}(i,t)+n_{b}(i,t)-1]/2\) distinct pairs of agents, of which there are \(n_{r}(i,t)n_{b}(i,t)\) opposite type pairs. A high value of S(t) indicates a mixed state, while a low value indicates a segregated state.

Fig. 1
figure 1

The phase structure of Schelling’s metapopulation model with \(Q=20\), \(M=100\). a The stationary interface density S as a function of tolerance T and occupancy density \(\rho \) on a star topology. b The total utility, U, of agents as a function of tolerance T and occupancy density \(\rho \) on star network. c Similar to a but on a fully connected network. d Similar to b but on fully connected network. When compared to the fully connected network scenario (c), the segregation area in the star topology case (a) shrank dramatically. On the other hand, a transition area of total utility U appeared in (b) as opposed to the discontinuous change of total utility U in (d)

Full size image

3 Results of numerical simulations

We now present our results of numerical simulations.

In Fig. 1a, we display the stationary interface density as a function of tolerance (T) and occupancy density (\(\rho \)) for the underlying star topology. In contrast, Fig. 1c shows similar results for a fully connected network. Notably, Fig. 1c exhibits a broad range of segregation areas that are resistant to variations in Schelling’s models and underlying topologies [11, 17, 18, 22]. However, for the star topology in Fig. 1a, the segregation area drastically decreases, particularly at high occupancy density, where the mixed state almost completely fills the tolerance parameter space without interfering with the segregated state.

As a matter of fact, there are two different types of mixed states that are divided by a segregation state, i.e., so-called the “frozen state” and “well-mixed state” [19]. The number of satisfied agents, or alternatively, the total utility of agents, \(U=\sum _{i} u_{i}\), is what distinguishes these mixed states from one another. To further identify these mixed states, the total utility, U, can be used as the second order parameter. We show numerical results in Fig. 1d on fully connected networks. The line separating the dissatisfied state (notice that the “frozen state” is on the left part of the picture) and the satisfied state (i.e., segregated state and “well-mixed state” on the right part) is represented by the discontinuous change of the total utility U. For numerical simulations on star-shape networks, however, a transition area between the unsatisfied and satisfied states can be seen, as shown in Fig. 1b.

The results in Fig. 1 can be further understood by examining the dynamic distribution of the agents in the network. This is illustrated in the upper panel of Fig. 2, which shows snapshots of the distribution of both types of agents at various points in their evolutionary history. In this parameter regime where segregation would have emerged in the original Schelling’s metapopulation model, one type of agents gathers at the central node, while the other type of agents tends to flee from it, even though they were initially randomly distributed throughout the entire system.

We emphasize that the main reason for the suppression of degree of segregation is the saturation of agents on the central node. Specifically, since there are no other destinations available for these agents to migrate to, the dominance of red- (blue-) colored agents on the central node can prevent blue- (red-) colored agents from leaving their unsatisfied peripheral nodes. On the other hand, the dominant type of agents on the central node can continue to relocate using it as a bridge until all their prevailing nodes, including the central one, are saturated. As a result, the other agents, whether satisfied or not, are also unable to migrate. The saturation of nodes is the primary reason why segregation is more easily suppressed at high occupancy density. Based on these two mechanisms, when the stationary state is reached, some agents of the central dominant type and all agents of the other type are forced to remain in an unsatisfied mixed state. The transition zone between the unsatisfied and satisfied states, as seen in Fig. 1b, can also be explained by these mechanisms. For comparison, simulations using the same parameter set but on a fully connected network are displayed in the lower panel of Fig. 2. These simulations demonstrate an evolutionary process that leads to an apparent segregation state where each node is entirely occupied by a single type of agent and all agents are satisfied.

Fig. 2
figure 2

Distribution of the two types of agents across nodes. Upper panel: the distribution at time steps \(t=0\), \(t=80\), and stationary state on star-shape network, respectively. Note that the leftmost bar in each subplots represents the agents’ distribution on central node. Lower panel: similar to the upper one, the distribution at \(t=0\), \(t=800\), and equilibrium state on fully connected network, respectively. The city size \(Q=20\), each node’s capacity \(M=100\), the occupancy density \(\rho =0.8\), and the tolerance \(T=0.4\) are set throughout simulations. As can be seen, only one type of agent eventually occupies the star-shape network’s central node, while the other nodes continue to be mixed. In contrast, the fully connected network achieves an segregation state with the same parameter set, where each node has just one type of agent

Full size image

It may be confusing to reconcile the seeming contradiction between our simulation results and the claim that “segregation is topology independent” [11, 22]. However, careful examination reveals that these two claims are based on different mechanisms. When the topological effect only affects neighborhood structures and does not impact the agents’ migratory paths, the result is topology independent segregation. In contrast, the topological effect we focus on in this study limits the agents’ migratory paths to those between the central node and the periphery. Essentially, the segregation process cannot be affected by the heterogeneity of neighborhood architecture. However, the extreme heterogeneity in migration path topologies can severely inhibit the trend toward collective segregation. This is critical in understanding why the emergence of segregation is significantly suppressed in Schelling’s model of star topology, comparing to that of a fully connected network with the same parameters.

4 The random adding-link mechanism

Another important issue to consider is the impact of changes in the heterogeneity of the underlying network structure on the degree of agent mixing. As we have analyzed before, the limited migratory paths of agents on peripheral nodes to the central node are the main reason for the suppression of segregation. Therefore, it is reasonable to conclude that the robustness of segregation may be reestablished at a suitable limit of topological heterogeneity. We have addressed this issue by adding links with probability \(\Pi _{i}\) between peripheral nodes, which is similar to constructing a random graph as peripheral nodes are initially not interconnected with each other [28].

The phase structure of interface density S(t) as a function of tolerance T and the adding-link probability \(\Pi \), with \(\rho =0.9\), \(Q=50\), and \(M=100\), respectively, is shown in Fig. 3. As the number of added links increases, the emergence of segregation becomes more and more obvious, and the parameter region where segregation occurs becomes wider. When \(\Pi \rightarrow 1\), the equilibrium phase diagram converges to that of a fully connected network.

Fig. 3
figure 3

The phase structure of interface density as a function of tolerance T and adding-link probability \(\Pi \), with \(\rho =0.9\), \(Q=50\), and \(M=100\), respectively. The segregation region that had disappeared gradually starts to reappear as the adding-link probability \(\Pi _{i}\) increasingly rises

Full size image

Consider that the increase of links between peripheral nodes actually breaks the constraint on the migration path of agents on peripheral nodes, in other words, it mitigates the extreme heterogeneity of the star network. Therefore, when a new link is added to each peripheral node on average, the inhibitory effect of the extreme heterogeneity on the segregation regions in the parameter space accordingly fades away to some extent. This is actually equivalent to the condition for the emergence of a giant connected cluster in ER random graph, i.e., for an ER random graph with \(Q-1\) nodes, there exists a critical probability \(\Pi _{c} \propto 1/(Q-1)\) for the emergence of a giant connected cluster [28], and the latter is close to a fully connected network in topological structure. The important enlightenment is the change of pivot role of the hub.

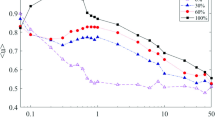
To verify this theoretical expectation, we conducted numerical simulations and compared results of the stationary state for systems with different block sizes Q, where \(Q\gg 1\), as we increased \(\Pi \) for a given density and tolerance, as shown in Fig. 4a. It is worth noting that a scaling of the averaged stationary interface density \(\langle S\rangle \) versus the re-scaled size, i.e., \(\Pi _{r}=(\Pi -\Pi _{c})Q\) can be observed. The collapsed data points shown in Fig. 4b confirm this scaling. This observation suggests that there is a size-independent degree of heterogeneity that can significantly impact the nature of segregation.

Fig. 4
figure 4

a Average interface density \(\langle S\rangle \) as a function of the adding-link probability \(\Pi \) in linear-log scale for different sizes of systems \(Q = 20\) (black open square), 50 (red open circles), and 100 (blue open triangles), respectively, with occupancy density \(\rho =0.9\), tolerance \(T=0.5\). Three vertical dashed lines (in the upper panel) correspond to the critical probability \(\Pi _c\) (from right to left) for \(Q = 20\), 50, and 100, respectively; b Collapse of datum after re-scaling with respect to \(\Pi _{r}=(\Pi -\Pi _{c})Q\) in a linear scale, using the same data as in (a). The re-scaled critical probability \(\Pi _{c}\) is labeled with dashed line. The scaling of \(\langle S\rangle \) versus \(\Pi _r=(\Pi -\Pi _{c})Q\) is obvious

Full size image

5 Conclusions and remarks

To sum up, although Schelling’s segregation model has long been considered as a simple prototype for illustrating the segregation phenomenon, our present study demonstrates a considerable inhibition of segregation phase in a metapopulation version of Schelling’s model with a star-shaped underlying topology. The degree of suppression is dependent on occupancy density, and it is even more significant at higher densities. We distinguish between two types of topological effects in Schelling’s segregation model and identify their influences on agents’ migration paths. Based on the constraints imposed by the heterogeneity of the underlying star-shaped network on agents’ migration routes, we propose a scheme that significantly suppresses the emergence of segregation phase. Our numerical simulations confirm the effectiveness of this scheme.

In addition, we also investigated the impact of a randomly adding-link mechanism and discovered a scaling law that relates the average stationary interface density to the re-scaled probability of adding links. This scaling law helped us understand to what extent the extreme heterogeneity of the underlying network structure suppresses the emergence of segregation. Interestingly, we found that the scaling law in the present model is quite similar to the one discovered in Ref. [23]. However, we have to point out that the mechanisms behind the scaling laws in the two Schelling models (with different utility functions) are not the same. In our current study, we used a simple step function for our utility function, while in Ref. [23], the utility function was a non-monotonic, \(\rho \)-dependent function. It remains unclear if there exists a deeper connection between these apparent similarities, and further studies along this line are currently ongoing.

Finally, we want to acknowledge an important issue that we did not consider in our study, which is the influence of temperature (or noise) on the segregation phase transition in Schelling’s metapopulation model. Introducing environmental noise to an agent’s decision can affect their behavior and preferences. A possible way to incorporate this is using a Fermi–Dirac-like function for the dynamical rule allowing agents to move between blocks, to be specific, \(P \sim 1/\left( 1+e^{-\beta \bigtriangleup G}\right) \), where G represents the “free energy” and \(\beta \) is the inverse environmental temperature. While a naive expectation may seem that this modification will not fundamentally alter the overall physics picture, a detailed numerical investigation is necessary to explore the phase structure and segregation dynamics that could emerge. Currently, we are actively investigating this issue, and plan to report our findings in the near future.