Analysis of macroscopic traffic flow model considering throttle dynamics

Abstract

Due to the continuous development of economy and society, the pace of life is also accelerated, so people pay more and more attention to the time cost, and the transportation time cost is also a very important part of it. The traffic system is an important carrier to realize the traffic operation. The increase of automobile ownership requires the traffic system to be higher and higher. Moreover, vehicles in congested traffic flow inevitably start and stop operations with high frequency, which undoubtedly increases vehicle exhaust emissions, environmental pollution, noise pollution and other problems. For today’s traffic system, vehicle dynamics information is also an important factor which affects the traffic system. Therefore, adding throttle, vehicle dynamics information, to the macro-traffic flow modeling research in this paper is a supplement and improvement to the current traffic flow theory research. By analyzing the equilibrium point, this paper proves the conditions for the existence of Hopf branch and saddle junction branch. Finally, numerical simulation is carried out, and the space–time diagram of density and phase plane are obtained through simulation, which can be used to describe the actual traffic phenomenon. Through numerical simulation, it is found that this model can better describe the congestion phenomenon of the actual traffic system, and provide scientific theoretical support for macroscopic traffic flow state analysis.

Graphical abstract

1 Introduction

With the acceleration of urbanization, daily travel has caused great pressure on the urban road traffic system, which eventually leads to more complex and crowded traffic flow. Traffic congestion will not only lead to accidents, but also aggravate environmental pollution, which is bound to have a negative impact on people’s lives. To explore the intrinsic characteristics of traffic flow and the causes of traffic congestion, and take effective measures to curb it. It is necessary to develop more realistic traffic flow models, such as micro model [1,2,3,4,5,6,7,8,9,10,11,12] and macro model [13,14,15,16,17,18,19]. In addition, to reduce fuel costs and carbon emissions, researchers have developed fuel consumption models and emission models [20,21,22].

At present, complex nonlinear traffic phenomena have been the focus of research in recent years. Many traffic engineers, physicists and mathematicians have conducted in-depth nonlinear research on macroscopic traffic flow models. For traffic, a complex nonlinear system, the problem of traffic congestion can be essentially solved only by starting from its nonlinear nature. Branch Analysis Method can describe and predict nonlinear traffic phenomena from the perspective of the global stability of the system, which will provide theoretical basis for fundamentally helping to solve traffic problems. In 1999, Yuji Igarashi et al. [23] studied the branch phenomenon of traffic flow based on the optimal velocity model proposed by Bando et al. [24]. Yuji Igarashi et al. proved the existence of Hopf branch in the model and described the traffic phenomenon. In 2010, Jin et al. [25] used the full-speed difference model to study the divergence problem, and carried out Hopf divergence analytic calculation on the model with Hopf theorem. In 2015, Ai et al. [26] proposed a branch analysis method based on macro-traffic flow model to describe and predict nonlinear traffic phenomena on highways from the perspective of global stability of the system, and obtained Hopf branch and saddle node branch of the model using this method. Then in 2018, Ge et al. carried out Hopf branch analysis and obtained Hopf branch points. The effects of delay time and velocity difference sensitivity in the model are discussed from Hopf branch. In 2021, Ge et al. [27, 28], based on the analysis of a micro traffic flow model, carried out Taylor expansion on the micro model to obtain the branch analysis of the macro model, and obtained the existence conditions and stability of the model Hopf branch.

Macro traffic flow modeling is also a method to describe traffic phenomena. Generally, macro-traffic flow modeling describes the behavioral evolution of traffic flow according to the relationship among traffic flow, average speed and average density in traffic flow. The research on macroscopic traffic flow model has been carried out for several decades, and many models have been proposed successively. The Fluid Dynamics Theory in the macroscopic model was proposed by Lighthill, Whitham and Richards [29, 30]. Therefore, in terms of macroscopic traffic flow modeling, current studies focus more on the mechanism of action and evolution characteristics of traffic flow, etc. Traditional macro-traffic flow models pay more attention to the average density, average speed, traffic flow and other vehicle state information and road structure information, etc. The impact factors are relatively simple, and the impact of throttle dynamics information on traffic flow evolution has not been considered at the macro level. Centering on the idea of macroscopic traffic flow modeling, this paper takes the influence of electronic throttle dynamics information [31, 32] on traffic flow evolution into consideration in macroscopic traffic flow modeling research.

In the field of macro-traffic flow modeling, most studies mainly consider the influence of factors such as vehicle state information and road structure information [33,34,35]. In the actual traffic system, vehicle dynamics information is also an important factor affecting the traffic system. Therefore, adding the vehicle dynamics information of throttle valve into the research of macroscopic traffic flow modeling is a supplement and perfection to the current research of traffic flow theory. The throttle dynamics information is added to the macroscopic traffic flow modeling. By considering the vehicle state information and throttle dynamics information at the same time, the evolution behavior of traffic flow is analyzed, and then the influence of throttle dynamics information on the evolution of traffic prevalence is analyzed. It has important research significance to provide scientific theoretical support for the macroscopic traffic flow state analysis.

2 Establishment of model

Electronic throttle is an important control component of vehicle engine, and electronic throttle system in the throttle opening accurate control is conducive to reducing vehicle exhaust emissions. It is worth mentioning that the more accurate throttle opening control, the more responsive the vehicle can meet the requirements of the public. Therefore, it is very necessary to add the dynamic information of electronic throttle into traffic flow modeling [36, 37].

We added throttle dynamics information into the research of macro-traffic flow modeling, and then carried out the design from the relationship model ET model of vehicle state information and vehicle dynamics information. ET model [38] was studied and proposed by Ioannou et al. which mainly described the relationship between the dynamic information of electronic throttle and vehicle speed and acceleration. The driver can control the speed of the vehicle by controlling the opening of the electronic throttle valve. According to the ET model, at time t, the acceleration of car i can be expressed as:

$$\begin{array}{c}{a}_{i}\left(t\right)=-b\left[{v }_{i}\left(t\right)-{v }_{0} \right]+c\overline{{\theta }_{i}}+{d}_{i}\end{array}$$

(1)

Among it, ${a}_{i}\left(t\right)$ and ${v}_{i}\left(t\right)$ respectively represent the acceleration and speed of the number i car at time t, $\overline{{\theta }_{i}}$ is the deviation for throttle, $\overline{{\theta }_{i}}={\theta }_{i}-{\theta }_{0}$, ${\theta }_{0}$ is constant, ${v}_{0}$ is the vehicle speed in stable state, $b$ and $c$ changes over time, and ${d}_{i}$ is the other perturbation not considered.

By analyzing the above ET model, the expression of electronic throttle deviation can be obtained, and then the expression of electronic throttle difference regarding vehicle speed and acceleration can be obtained:

$$\begin{array}{c}\overline{{\theta }_{i}}=\left\{\left[{a}_{i}\left(t\right)+b\left({v}_{i}\left(t\right)-{v}_{0}\right)\right]-{d}_{i}\right\}/c+{\theta }_{0}\end{array}$$

(2)

It follows that:

$$\begin{array}{c}\Delta {\theta }_{i}={\theta }_{i+1}-{\theta }_{i}=\left[{a}_{i+1}\left(t\right)-{a}_{i}\left(t\right)+b\Delta {v}_{i}\left(t\right)\right]/c\end{array}$$

(3)

where the velocity difference $\Delta {v}_{i}\left(t\right)={v}_{i+1}\left(t\right)-{v}_{i}(t)$. In addition, we know that the expression of T-FVD microscopic model [39,40,41,42,43] is:

$$\begin{array}{c}{a}_{i}\left(t\right)=k[V\left(\Delta {x}_{i}\left(t\right))-{v}_{i}\left(t\right)\right]+\lambda \Delta {v}_{i}\left(t\right)+\beta \Delta {\theta }_{i}\end{array}$$

(4)

As the $V(\Delta {x}_{i}\left(t\right))$ is the best velocity function and position difference $\Delta {x}_{i}\left(t\right)={x}_{i+1}\left(t\right)-{x}_{i}(t)$, $\beta >0$, $k>0$, $\lambda >0$ is for sensitive coefficient.

Substituting Eq. (3) into Eq. (4) we can get a microscopic model that takes into account the throttle dynamics:

$$\frac{\mathrm{d}{v}_{n}\left(t\right)}{\mathrm{d}t}=k[V\left(\Delta {x}_{i}\left(t\right))-{v}_{i}\left(t\right)\right]+\lambda \Delta {v}_{i}\left(t\right)+k\{[{a}_{i+1}\left(t\right)-{a}_{i}\left(t\right)+b\Delta {v}_{i}\left(t\right)]/c\}$$

(5)

Starting from the improved model, to obtain the corresponding macro-traffic flow model, a single discrete variable needs to be converted into a continuous variable. Specifically, first assume that the instantaneous speed of the $i+1$ vehicle at the position x is equal to the average speed on the $\left[x-\frac{\Delta }{2},x+\frac{\Delta }{2}\right]$ section, and the speed of the $\left[x-\frac{\Delta }{2},x+\frac{\Delta }{2}\right]$ section depends on the average speed of the $\left[x+\frac{\Delta }{2},x+\frac{3\Delta }{2}\right]$ section, where $\Delta$ corresponds to $\Delta x$ in the microscopic traffic flow model, and changes with the spacing between different continuous vehicles.

From the connection between micro and macro, acceleration can be expressed as:

$${a}_{i}\left(t\right)=\frac{\mathrm{d}u\left(x,t\right)}{\mathrm{d}t}=\frac{\partial u\left(x,t\right)}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial u\left(x,t\right)}{\partial t}=\frac{\partial u\left(x,t\right)}{\partial x}u\left(x,t\right)+\frac{\partial u\left(x,t\right)}{\partial t}$$

(6)

$${a}_{i+1}\left(t\right)=\frac{\mathrm{d}u\left(x+\Delta ,t\right)}{\mathrm{d}t}=\frac{\partial u\left(x+\Delta ,t\right)}{\partial x\left(x+\Delta \right)}\frac{\partial \left(x+\Delta \right)}{\partial t}+\frac{\partial u\left(x+\Delta ,t\right)}{\partial t}=\frac{\partial u\left(x,t\right)}{\partial x}u\left(x+\Delta ,t\right)+\frac{\partial u\left(x+\Delta ,t\right)}{\partial t}$$

(7)

And there is

$$\begin{array}{c}{v}_{i}\left(t\right)\to v\left(x,t\right),{v}_{i+1}\left(t\right)\to v\left(x+\Delta ,t\right)\end{array}$$

(8)

$$ v(x + \Delta ,t) = v(x,t) + \Delta v^{\prime}_{x} (x,t) + \frac{1}{2}\Delta^{2} v^{\prime\prime}_{x} $$

(9)

We bring this into the formula and ignore the nonlinear term to get:

$$ \frac{{{\text{d}}v(x,t)}}{{{\text{d}}t}} = \frac{1}{T}(v_{{\text{e}}} - v) + \left( {\lambda + \frac{bk}{c}} \right)\left( {\Delta v^{\prime}_{x} + \frac{1}{2}\Delta^{2} v^{\prime\prime}_{x} } \right) + kv^{\prime\prime}_{x} \Delta v $$

(10)

Organize the above equation as follows:

$$\begin{aligned} \frac{{{\text{d}}v(x,t)}}{{{\text{d}}t}} &= \frac{1}{T}(v_{{\text{e}}} - v) + \left( {\lambda \Delta + \frac{bk}{c}\Delta } \right)v^{\prime}_{x} \nonumber \\ &\quad + \left( {\frac{\lambda }{2}\Delta^{2} + \frac{bk}{{2c}}\Delta^{2} + k\Delta v} \right)v^{\prime\prime}_{x}\end{aligned} $$

(11)

Expand the left side of the above equation as follows:

$$\begin{array}{c}\frac{\mathrm{d}v\left(x,t\right)}{\mathrm{d}t}=\frac{\partial v\left(x,t\right)}{\partial t}+v\frac{\partial v}{\partial x}\end{array}$$

(12)

Among them: $k=\lambda =\frac{1}{T}$, $\frac{\Delta }{T}=c0$, $\frac{{\Delta }^{2}}{2T}=\mu$

Combined with conservation equations, we can get new macroscopic traffic flow models

$$\begin{array}{c}\left\{\begin{array}{c}\frac{\partial \rho }{\partial t}+\frac{\partial \left(\rho v\right)}{\partial x}=0\\ \frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}=\frac{1}{T}\left({v}_{e}-v\right)+\left(\frac{b}{c}{c}_{0}+{c}_{0}\right)\frac{\partial v}{\partial x}+\left(\mu +\frac{b}{c}\mu +{c}_{0}v\right)\frac{{\partial }^{2}v}{\partial {x}^{2}}\end{array}\right.\end{array}$$

(13)

This model uses the periodic boundary condition, and the traffic phenomenon generated by the fulcrum is actually more obvious on the open loop section than the closed loop section, so this paper assumes that the main road section is an open boundary condition, that is:

$$\rho \left(1,t\right)=\rho \left(2,t\right),\rho \left(L,t\right)=\rho \left(L-1,t\right),v\left(1,t\right)=v\left(2,t\right),v\left(L,t\right)=v\left(L-1,t\right)$$

Assume that model (13) has traveling-wave solution $\rho (z)$ and $v(z)$, in which $z=x-ct$ and traveling-wave velocity $c<0$. Using the above results and substituting them into Eq. (13), we can obtain:

$$\begin{array}{c}-c{\rho }_{z}+{q}_{z}=0\end{array}$$

(14)

$$-c\frac{\partial v}{\partial z}+\left(v-\frac{b}{c}{c}_{0}-{c}_{0}\right)\frac{\partial v}{\partial z}=\frac{1}{T}\left({V}_{\mathrm{e}}\left(\rho \right)-v\right)+\left(\mu +\frac{b}{c}\mu +{c}_{0}v\right)\frac{{\partial }^{2}v}{\partial {z}^{2}}$$

(15)

From the formula, we get:

$$\begin{array}{c}{q}_{z}=c{\rho }_{z}\end{array}$$

(16)

The derivative of $\uprho v=q$ with respect to $z$ at both ends of the equation yields:

$$\begin{array}{c}{q}_{z}=\rho {v}_{z}+v{\rho }_{z}\end{array}$$

(17)

Available from:

$$\begin{array}{c}{V}_{z}=\frac{c{\rho }_{z}}{\rho }-\frac{q{\rho }_{z}}{{\rho }^{2}}\end{array}$$

(18)

$$\begin{array}{c}{V}_{zz}=\frac{c\rho -q}{{\rho }^{2}}{\rho }_{zz}\end{array}$$

(19)

Meanwhile, in the formula, $\mathrm{z}$ is integrated, then:

$$\begin{array}{c}-c\rho +q=const={q}_{*}\end{array}$$

(20)

At the same time, it obtains:

$$\begin{array}{c}q={q}_{*}+c\rho \end{array}$$

(21)

So, bring it in, and after rewriting, you get:

$$\left(v-{c}_{1}-\frac{b}{c}{c}_{0}+{c}_{0}\right)\left(\frac{{c}_{1}}{\rho }-\frac{q}{{\rho }^{2}}\right){\rho }_{z}=\frac{1}{T}\left({V}_{\mathrm{e}}\left(\rho \right)-v\right)+\frac{{c}_{1}\rho -q}{{\rho }^{2}}\left(\mu +\frac{b}{c}\mu +{c}_{0}v\right){\rho }_{zz}$$

(22)

Simplification yields about second-order ordinary differential equations:

$$\begin{array}{c}{\rho }_{zz}-G\left(\rho ,{q}_{*}\right){\rho }_{z}-F\left(\rho ,c,{q}_{*}\right)=0\end{array}$$

(23)

Among it:

$$\begin{array}{c}G\left(\rho ,{q}_{*}\right)=\frac{{cq}_{*}+2{c}_{1}c\rho +{c}_{0}\rho \left(b+c\right)}{\rho \mu \left(c-b\right)+c{c}_{0}\left({q}_{*}+{c}_{1}\rho \right)}\end{array}$$

(24)

$$\begin{array}{c}F\left(\rho ,c,{q}_{*}\right)=\frac{\rho {V}_{\mathrm{e}}\left(\rho \right)-{q}_{*}-{c}_{1}\rho }{T{q}_{*}}*\frac{{\rho }^{2}c}{\left(\rho \mu \left(c-b\right)+c{c}_{0}\left({q}_{*}+{c}_{1}\rho \right)\right)}\end{array}$$

(25)

Let $y=\frac{\mathrm{d}\rho }{\mathrm{d}z}$, Eq. (1) can be converted to a system of first-order ordinary differential equations:

$$\begin{array}{c}\left\{\begin{array}{c}\frac{\mathrm{d}\rho }{\mathrm{d}z}=y\\ \frac{\mathrm{d}y}{\mathrm{d}z}=G(\rho ,{q}_{*})y+F(\rho ,c,{q}_{*})\end{array}\right.\end{array}$$

(26)

Then, for the type of equilibrium point and its stability, it is mainly determined from the equations formed by Eq. (26), let the right end of Eq. (26) is 0, it is known that $y=0$ and $F=0$, the equilibrium point coordinate $({\rho }_{i},0)$ can be obtained. Then, according to the equilibrium point coordinates, the Eq. (26) is expanded by Taylor, and the linear representation of the system can be obtained:

$$\begin{array}{c}\left\{\begin{array}{c}{\rho }^{{\prime}}=y\\ {y}^{{\prime}}=G\left({\rho }_{i},{q}_{*}\right)y+{F}^{{\prime}}\left({\rho }_{i},c,{q}_{*}\right)\left(\rho -{\rho }_{i}\right)\end{array}\right.\end{array}$$

(27)

Thus, the Jacobian matrix of the system at the equilibrium point can be written:

$$\begin{array}{c}L=\left[\begin{array}{cc}0& 1\\ {F}_{i}^{{\prime}}& {G}_{i}\end{array}\right]\end{array}$$

(28)

The corresponding characteristic equation is:

$$\begin{array}{c}{\lambda }^{2}-{G}_{i}\lambda -{F}_{i}^{{\prime}}=0\end{array}$$

(29)

where ${G}_{i}({\rho }_{i},c,{q}_{*})=G(\rho ,c,{q}_{*})$, ${F}^{\mathrm{^{\prime}}}=F(\rho ,c,{q}_{*})$ is obtained:

$$\begin{array}{c}{G}_{i}=\frac{{cq}_{*}+2{c}_{1}c{\rho }_{i}+{c}_{0}{\rho }_{i}\left(b+c\right)}{{\rho }_{i}\mu \left(c-b\right)+c{c}_{0}\left({q}_{*}+{c}_{1}{\rho }_{i}\right)}\end{array}$$

(30)

$$\begin{array}{c}{{F}_{i}}^{{\prime}}=\frac{1}{T{q}_{*}}\frac{\begin{array}{c}(3{\rho }_{i}^{2}c{V}_{\mathrm{e}}({\rho }_{i})+c{V}_{\mathrm{e}}^{{\prime}}({\rho }_{i})-2{\rho }_{i}c{q}_{*}\\ -2{\rho }_{i}c{c}_{1})({\rho }_{i}\mu (c-b) +c{c}_{0}({q}_{*}+{c}_{1}{\rho }_{i})\\ -({\rho }_{i}^{3}c{V}_{\mathrm{e}}({\rho }_{i})-{\rho }_{i}^{2}c{q}_{*}-c{c}_{1}{\rho }_{i}^{2})(\mu (c-b)+c{c}_{0}{c}_{1}\end{array}}{{\left({\rho }_{i}\mu \left(c-b\right)+c{c}_{0}\left({q}_{*}+{c}_{1}{\rho }_{i}\right)\right)}^{2}}\end{array}$$

(31)

Because at the equilibrium point $({\rho }_{i},0)$, $F=0$, then ${\rho }_{i}{V}_{\mathrm{e}}(\rho )-{\mathrm{q}}_{*}-{c}_{1}{\rho }_{i}=0$, according to the qualitative theory of differential equation, it can determine the linear system (26) the type of equilibrium point is as follows: (a) when ${F}_{i}^{\mathrm{^{\prime}}}>0$, the equilibrium point is the saddle point; (b) When ${G}_{i}^{2}+4{F}_{i}^{\mathrm{^{\prime}}}>0$ and ${F}_{i}^{\mathrm{^{\prime}}}<0$, the equilibrium is the node; (c) When ${G}_{i}^{2}+4{F}_{i}^{\mathrm{^{\prime}}}<0$ and ${G}_{i}\ne 0$, the equilibrium point is the focus; (d) When ${F}_{i}^{\mathrm{^{\prime}}}<0$ and ${G}_{i}=0$, the equilibrium is centered. When $z\to \pm \infty$, the stability of linear systems at saddle points is unstable. When ${G}_{i}<0$ (or ${G}_{i}>0$)), the stability at nodes and focal points is stable for $z\to +\infty$ (or $z\to -\infty$).

According to Hartman-Grossman linearization theory, nonlinear system (26) and linear system (27) have the same equilibrium point. For the equilibrium point that is not the center, the stability case at the equilibrium point, the nonlinear system (26) and the linear system (27) are consistent. Given the values of any set of traveling-wave velocity c and traveling-wave parameter ${q}_{*}$, the equilibrium ${\rho }_{1},{\rho }_{2},{\rho }_{3}$ of the linear system (26) can be solved. The equilibrium velocity function proposed in literature [44] is selected as follows:

$$\begin{array}{c}{V}_{\mathrm{e}}\left[\rho \right]={v}_{\mathrm{f}}\left\{{\left[1+\mathrm{exp}\left(\frac{\frac{\rho }{{\rho }_{\mathrm{m}}}-0.25}{0.06}\right)\right]}^{-1}-3.72\times 1{0}^{-6}\right\}\end{array}$$

(32)

Here, ${v}_{f}$ represents the free flow velocity and ${\rho }_{\mathrm{m}}$ represents the maximum or congestion density.

The values of parameters in the model in this chapter are as follows: ${v}_{\mathrm{f}}=$ 30 m/s, ${\rho }_{\mathrm{m}}=0.2$ $\mathrm{veh}/\mathrm{m}$, $T=10$ s, ${c}_{0}=11$ m/s, $\mu =550$. When $\rho$ equals 0, this is a trivial equilibrium point, and it has no practical significance, so this paper only needs to discuss other equilibrium points. Based on the above discussion and Eq. (31), the type and stability of the equilibrium point can be determined, as shown in Table 1, where the equilibrium point is indicated by ${\rho }_{i}(i=\mathrm{1,2},3)$.

Table 1 Types of equilibrium points and their stability when it gives model parameters ${\Delta }_{i}={{G}_{i}}^{2}+4{{F}_{i}}^{\mathrm{^{\prime}}}$, $i=\mathrm{1,2},3$

The two sets of parameters in Table 1 were selected to numerically simulate the stability at the equilibrium point of the nonlinear system (26).

Figure 1 corresponds to the first scenario in Table 1. It can be seen from Table 1 that when $z\to \pm \infty$, the system is unstable at the equilibrium point $({\rho }_{1},0)$ and $({\rho }_{3},0)$, and the nearby rails are far away from the point. As $z\to +\infty$, there are several helical rails close to the saddle point $({\rho }_{1},0)$ tend to focus $({\rho }_{2},0)$, and because of the influence of the nearby saddle point $({\rho }_{3},0)$, the helical state of the rails tend to focus is not obvious. As z goes to $z\to -\infty$, the orbitals move away from the focus and eventually approach infinity. It is shown that the system is stable at $({\rho }_{2},0)$ when $z\to +\infty$. As z goes to $z\to -\infty$, these orbitals move away from the focus and eventually approach infinity. These orbitals can be regarded as the saddle-focal-saddle point solution of the system. It is shown that the system is stable at the equilibrium point $({\rho }_{2},0)$ when $z\to +\infty$ and unstable at the equilibrium point $({\rho }_{2},0)$ when $z\to -\infty$.

Fig. 1

Phase $\rho -{\text{y}}$ planar track diagram with traveling-wave velocity $c=-1.371$, traveling-wave parameters ${q}_{*}=0.2$

Figure 2 corresponds to the second scenario in Table 1. Figure 2 also shows that the system is unstable at the equilibrium point $({\rho }_{1},0)$. The spiral triggered near (0.05,0) tends to focus $({\rho }_{2},0)$ when $z\to +\infty$, and the system is stable at this point; As $z\to -\infty$, away from the focus $({\rho }_{2},0)$, the system is unstable.

Fig. 2

Phase $\rho -{\text{y}}$ planar track diagram with traveling-wave velocity $c=-1.38$ traveling-wave parameters ${q}_{*}=0.64$

The overall structure of multiple equilibrium points interacting with each other can be clearly seen from the two-phase planar graph, and the influence of the equilibrium point on the curve trajectories around the equilibrium point can be seen from the changes of the curve trajectories around the equilibrium point, which is consistent with the analysis results.

3 Hopf branching conditions for the model

Lemma 1

[45] Consider the system $\stackrel{.}{x}=f(x,\lambda ),x\in {R}^{n},\lambda \in R,\lambda$ as a variadic parameter. If $({x}_{0},\lambda )$ the equilibrium condition is satisfied, $f(x,\lambda {)}_{\left|({x}_{0},{\lambda }_{0})\right.}={0}_{n\times 1}$, it is noted $L={D}_{x}f(x,\lambda )\left|({x}_{0},{\lambda }_{0})\right.$ that its eigenvalue is, $\alpha (\lambda )\pm i\beta (\lambda )$ and if $\alpha ({\lambda }_{0})=0$ and $\beta ({\lambda }_{0})=\omega >0$, then the system has $c=\stackrel{.}{a}(\lambda )\left|{\lambda }_{0}\right.\ne 0$ Hopf branch $\lambda ={\lambda }_{0}$ at the place.

For the system (26) let ${q}_{*}$ be a variable parameter, it for all ${q}_{*}$ equilibrium point $({\rho }_{0},0)$, the derivative matrix $L\left({q}_{*}\right)$ out of the equilibrium point is also the Jacobian matrix of the system at the equilibrium point, as shown below:

$$\begin{array}{c}L\left({q}_{*}\right)={\left(\begin{array}{cc}0& 1\\ F\left(\rho ,c,{q}_{*}\right)& G\left(\rho ,{q}_{*}\right)\end{array}\right)\left| \right.}_{{\begin{array}{c}\rho ={\rho }_{0}\\ {q}_{*}={q}_{*}\end{array}}_{0}}\triangleq \left(\begin{array}{cc}{A}_{1}& {A}_{2}\\ {A}_{3}& {A}_{4}\end{array}\right)\end{array}$$

(33)

Among it:

$$\begin{array}{c}G\left(\rho ,{q}_{*}\right)=\frac{{cq}_{*}+2{c}_{1}c\rho +{c}_{0}\rho \left(b+c\right)}{\rho \mu \left(c-b\right)+c{c}_{0}\left({q}_{*}+{c}_{1}\rho \right)}\end{array}$$

(34)

$$\begin{array}{c}F\left(\rho ,c,{q}_{*}\right)=\frac{\rho {V}_{e}^{{\prime}}\left(\rho \right)-{q}_{*}-{c}_{1}\rho }{T}*\frac{{\rho }^{2}c}{\left(\rho \mu \left(c-b\right)+c{c}_{0}\left({q}_{*}+{c}_{1}\rho \right)\right){q}_{*}}\end{array}$$

(35)

Let its eigenvalue be $\lambda$, $\lambda =\alpha ({q}_{*})\pm j\beta ({q}_{*})$ then its eigenequation is:

$$\begin{array}{c}{\lambda }^{2}-\left({A}_{1}+{A}_{4}\right)\lambda +\left({A}_{1}{A}_{4}-{A}_{2}{A}_{3}\right)=0\end{array}$$

(36)

The equation has a pair of complex eigenvalues $\alpha ({q}_{*})\pm j\beta \left({q}_{*}\right)$ then:

$$ \begin{array}{*{20}c} {\alpha \left( {q_{*} } \right) = \frac{{A_{1} + A_{4} }}{2} = \frac{1}{2}\left( {\frac{{cq_{*} + 2c_{1} c\rho + c_{0} \rho \left( {b + c} \right)}}{{\rho \mu \left( {c - b} \right) + cc_{0} \left( {q_{*} + c_{1} \rho } \right)}}} \right)} \\ \end{array} $$

(37)

$$ \begin{aligned} \beta \left( {q_{*} } \right) = & \sqrt {\left( {A_{1} A_{4} - A_{2} A_{3} } \right) - \frac{{(A_{1} + A_{4} )^{2} }}{4}} \\ = & \sqrt { - \frac{{\rho V_{e}^{{\prime}} \left( \rho \right) - q_{*} - c_{1} \rho }}{T}*\frac{{\rho^{2} c}}{{\left( {\rho \mu c - b\rho \mu + cc_{0} \left( {q_{*} + c_{1} \rho } \right)} \right)q_{*} }} - \frac{1}{4}\left( {\frac{{cq_{*} + 2c_{1} c\rho + c_{0} \rho \left( {b + c} \right)}}{{\rho \mu \left( {c - b} \right) + cc_{0} \left( {q_{*} + c_{1} \rho } \right)}}} \right)^{2} } \\ \end{aligned} $$

(38)

$$\begin{array}{c}c=\stackrel{.}{\alpha }({q}_{*}{)}_{{{q}_{*}}_{0}}= \frac{1}{2}\frac{\left(\rho \mu c-b\rho \mu \right)c-{(c}_{1}c\rho +{c}_{0}b\rho +{c}_{0}c\rho )c{c}_{0}}{{\left(\rho \mu \left(c-b\right)+c{c}_{0}\left({q}_{*}+{c}_{1}\rho \right)\right)}^{2}}\ne 0\end{array}$$

(39)

Cause $\alpha ({\rho }_{0},{q}_{*0})=0$, namely:

$$\begin{array}{c}\alpha \left({\rho }_{0},{q}_{*}\right)=\frac{1}{2}\left(\frac{{q}_{*}c+2{c}_{1}c{\rho }_{0}+{c}_{0}{\rho }_{0}\left(b+c\right)}{{\rho }_{0}\mu c-b{\rho }_{0}\mu +c{c}_{0}\left({q}_{*}+{c}_{1}{\rho }_{0}\right)}\right)\left|{q}_{*}={q}_{{*}_{0}}\right.\approx 0\end{array}$$

(40)

From this, we get:

$$\begin{array}{c}{q}_{{*}_{0}}=-\frac{2{c}_{1}c{\rho }_{0}+{c}_{0}{\rho }_{0}\left(b+c\right)}{c}\end{array}$$

(41)

At the same time,

$$\begin{aligned} &\beta \left({\rho }_{0},{q}_{{*}_{0}}\right)\nonumber \\ &\quad =\sqrt{-\frac{\rho {V}_{\mathrm{e}}^{{\prime}}\left(\rho \right)-{q}_{*}-{c}_{1}\rho }{T}*\frac{{\rho }^{2}c}{\left(\rho \mu c-b\rho \mu +c{c}_{0}\left({q}_{*}+{c}_{1}\rho \right)\right){q}_{*}}}\nonumber \\ &\qquad \left|\begin{array}{c}\rho ={\rho }_{0}\\ {q}_{*}={q}_{{*}_{0}}\end{array}\right.\end{aligned}$$

(42)

Because the ${V}_{\mathrm{e}}^{\mathrm{^{\prime}}}(\rho )<0$, so when $-{\rho }^{2}{{V}_{\mathrm{e}}}^{\mathrm{^{\prime}}}({\rho }_{0})>{q}_{*0}>0\beta ({\rho }_{0},{q}_{*0})>0$. In this case, the system has Hopf branch at ${q}_{*}={q}_{*0}$.

4 Hopf branch types for models

For Hopf branch problem, since N-dimensional systems can be restricted to two-dimensional central manifolds by the central manifold method, only Hopf branch of two-dimensional systems is considered.

Lemma 2

[45]: Set up a two-dimensional system with parameters

$$\begin{array}{c}{x}^{{\prime}}=f(x,\gamma ),x=({x}_{1},{x}_{2}{)}^{T}\in {R}^{2},\gamma \in R\end{array}$$

(43)

The equilibrium point of is the origin $O(\mathrm{0,0})$, and the eigenvalues at the origin are $\alpha (\gamma )\pm i\omega (\gamma )$. At that time, $\gamma =0$ the partial derivative matrix of the system has a pure virtual eigenvalue, $i{\omega }_{0}$ that is $\alpha (0)=0,\omega (0)={\omega }_{0}>0.$ By means of coordinating transformation, the system (43) can be written as

$$\begin{array}{c}\left\{\begin{array}{c}{{x}^{{\prime}}}_{1}=\alpha \left(\gamma \right){x}_{1}-\omega \left(\gamma \right){x}_{2}+{\widetilde{f}}_{1}\left({x}_{1},{x}_{2},\gamma \right)\\ {{x}^{{\prime}}}_{2}=\omega \left(\gamma \right){x}_{1}+\alpha \left(\gamma \right){x}_{2}+{\widetilde{f}}_{2}\left({x}_{1},{x}_{2},\gamma \right)\end{array}\right.\end{array}$$

(44)

where $\widetilde{{f}_{1}},\widetilde{{f}_{2}}=O({{x}_{1}}^{2}+{{x}_{2}}^{2})$.

Theorem 1

(ODE’s Hopf branching theorem) Let the partial matrix at the re-origin of the system (Eq 43) have eigenvalues $D(\gamma )$ and satisfy $\alpha (\gamma )\pm i\omega (\gamma )$ the sum $\alpha (0)=0,\omega (0)={\omega }_{0}>0$, then there is an analytic function $c={\alpha }^{\mathrm{^{\prime}}}(0)\ne 0$

$$\begin{array}{c}\gamma \left(\varepsilon \right)=\mathop{\sum }\limits_{k=0}^{\infty }{\gamma }_{k}{\varepsilon }^{k}\end{array}$$

(45)

Such that $\gamma =\gamma (\varepsilon )\ne 0$ for the pair, the system (42) has a unique closed orbit within the sufficiently small neighborhood of the origin of ${\Gamma }_{\varepsilon }$ its period

$$\begin{array}{c}T\left(\varepsilon \right)=\frac{2\pi }{{\omega }_{0}}\left(1+\mathop{\sum }\limits_{k=0}^{\infty }{\gamma }_{k}{\varepsilon }^{k}\right)\end{array}$$

(46)

When $\varepsilon \to 0$,$\gamma (\varepsilon )\to 0$ comes, ${\Gamma }_{\varepsilon }$ tends to the origin. ${\gamma }_{k1}$ is denoted as the first coefficient in expansion Eq. (45) that is not equal to zero.${\Gamma }_{\varepsilon }$ is a stable limit ring when ${\gamma }_{k1}$ is the same sign with $c$, ${\Gamma }_{\varepsilon }$ is an unstable limit when ${\gamma }_{k1}$ is different with sign$c$.

Literature [46] gives a proof of theorem one and the equations for calculating the coefficients ${\gamma }_{k1}$, ${\tau }_{k}$, especially when $k=2$,

$$\begin{array}{c}{\gamma }_{2}=-\frac{a}{c},{\tau }_{2}=-\frac{b+{\gamma }_{2}{\omega }^{{\prime}}\left(0\right)}{{\omega }_{0}}\end{array}$$

(47)

Among them, the first Lyapunov index of the system can be calculated as follows:

$$\begin{aligned} a = & \left( \frac{1}{16} \right)\left[ {\tilde{f}_{1xxx} + \tilde{f}_{1xyy} + \tilde{f}_{2xxy} + \tilde{f}_{2yyy} } \right]\nonumber \\ &+ \left( {\frac{1}{{16\omega_{0} }}} \right)\Big[\tilde{f}_{1xy} \left( {\tilde{f}_{1xx} + \tilde{f}_{1yy} } \right)\nonumber \\ & - \tilde{f}_{2xy} \left( {\tilde{f}_{2xx} + \tilde{f}_{2yy} } \right) - \tilde{f}_{1xx} \tilde{f}_{2yy} + \tilde{f}_{1yy} \tilde{f}_{2yy} \Big] \\ \end{aligned} $$

(48)

where $\tilde{f}_{1xxx} ,\tilde{f}_{2xxx}$ etc. are the partial derivative at $\tilde{f}_{1} ,\tilde{f}_{2} \;(0,0,0)$. Here, $a$ is an important parameter for judging the stability of the limit ring, assuming that the theorem condition is true, according to the Hopf branch, there are the following stability conclusions:

• If $a<0(>0)$. then the limit ring ${\Gamma }_{\varepsilon }$ is stable (unstable).

• If $a$ is different (same) sigh with the $c$, the Hopf branch is supercritical (subcritical);

• If $a=0$ so, the Hopf branch is degenerate.

For system (26), set ${q}_{*}$ as variable parameter, It has an equilibrium $({\rho }_{0},0)$ for everything ${q}_{*}$, make $\widetilde{\rho }=\rho -{\rho }_{0}$ coordinate translation, the equilibrium point moves to the origin, then the system can be expressed as follows:

$$\begin{array}{c}\left\{\begin{array}{c}{\widetilde{\rho }}^{{\prime}}=y,\\ {y}^{{\prime}}=\widetilde{G}(\widetilde{\rho },{q}_{*})y+\widetilde{F}(\widetilde{\rho },c,{q}_{*}).\end{array}\right.\end{array}$$

(49)

By $(\widetilde{\rho },y)=(\mathrm{0,0})$ performing a Taylor unfolding at the equilibrium point, the system can be linearized to:

$$\begin{array}{c}{\widetilde{x}}^{{\prime}}=L\left({q}_{*}\right)\widetilde{x}+f\end{array}$$

(50)

where $f$ is a smooth vector function whose constituent elements ${f}_{\mathrm{1,2}}$ are the Taylor expansion of the least quadratic term with respect to $\widetilde{x}$, which can be expressed as follows:

$$f=\left[\begin{array}{c}0\\ {k}_{11}{\widetilde{\rho }}^{2}+{k}_{22}{y}^{2}+{k}_{12}\widetilde{\rho }y+{k}_{111}{y}^{3}+{k}_{112}{\widetilde{\rho }}^{2}y\\ +{k}_{122}\widetilde{\rho }{y}^{2}+O(\widetilde{\rho },y{)}^{4}\end{array}\right]$$

(51)

The Jacobi matrix $L({q}_{*})$ can be expressed as follows:

$$ \begin{aligned} L(q_{*} ) = &\left( {\begin{array}{*{20}c} 0 & 1 \\ \frac{{\rho V_{{\text{e}}}^{\prime } (\rho ) - q_{*} - c_{1} \rho }}{T} & \\ *\frac{{\rho^{2} c}}{{(\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho ))q_{*} }} & {\frac{{cq_{*} + 2c_{1} c\rho + c_{0} \rho (b + c)}}{{\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho )}}} \\ \end{array} } \right) \\ = & \left( {\begin{array}{*{20}c} 0 & 1 \\ {b(q_{*} )} & {d(q_{*} )} \\ \end{array} } \right) \\ \end{aligned} $$

(52)

Its eigenvalues are the root of the following characteristic equation:

$$\begin{array}{c}{\lambda }^{2}-\sigma \lambda +\Delta =0\end{array}$$

(53)

thereinto, $\sigma =\sigma ({q}_{*})=d({q}_{*})=trL({q}_{*})$, $\Delta =\Delta ({q}_{*})=-b({q}_{*})=\mathit{det}L({q}_{*})$,

$$\begin{array}{c}{\lambda }_{\mathrm{1,2}}\left({q}_{*}\right)=\frac{1}{2}\left(\sigma \left({q}_{*}\right)\pm \sqrt{{\sigma }^{2}\left({q}_{*}\right)-4\Delta \left({q}_{*}\right)}\right)\end{array}$$

(54)

Obtained by the Hopf branching condition:

$$\begin{array}{c}\sigma \left(0\right)=0,\Delta \left(0\right)={{\omega }_{0}}^{2}>0\end{array}$$

(55)

For smaller $\left|{q}_{*}\right|$ ingestible variables:

$$\begin{array}{c}\alpha \left({q}_{*}\right)=\frac{1}{2}\sigma \left({q}_{*}\right),\omega \left({q}_{*}\right)=\frac{1}{2}\sqrt{4\Delta \left({q}_{*}\right)-{\sigma }^{2}\left({q}_{*}\right)}\end{array}$$

(56)

This results in the following eigenvalue expression:

$$\begin{array}{c}{\lambda }_{1}\left({q}_{*}\right)=\lambda \left({q}_{*}\right),{\lambda }_{2}\left({q}_{*}\right)=\overline{\lambda }\left({q}_{*}\right)\end{array}$$

(57)

Thereinto:

$$\begin{array}{c}\lambda \left({q}_{*}\right)=\alpha \left({q}_{*}\right)+i\omega \left({q}_{*}\right),\alpha \left(0\right)=0,\omega \left(0\right)={\omega }_{0}>0\end{array}$$

(58)

Let ${\omega }_{\text{re}}+i{\omega }_{\text{im}}$ be the eigenvector of $L({q}_{*})$ corresponding to the eigenvalue $\lambda ({q}_{*})$, and have:

$$\begin{array}{c}L\left({\omega }_{\text{re}}+i{\omega }_{\text{im}}\right)=i{\omega }_{0}\left({\omega }_{\text{re}}+i{\omega }_{\text{im}}\right)\end{array}$$

(59)

Considering that the real and imaginary parts on both sides of the above equation equal sign are equal, we get:

$$\begin{array}{c}\left\{\begin{array}{c}L{\omega }_{im}={\omega }_{0}{\omega }_{re}\\ L{\omega }_{re}=-{\omega }_{0}{\omega }_{im}\end{array}\right.\end{array}$$

(60)

The collation Eq. (60) is as follows:

$$\begin{array}{c}L\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]=\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]\left[\begin{array}{cc}0& -{\omega }_{0}\\ {\omega }_{0}& 0\end{array}\right]\end{array}$$

(61)

From this:

$$\begin{array}{c}{\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]}^{-1}L\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]=\left[\begin{array}{cc}0& -{\omega }_{0}\\ {\omega }_{0}& 0\end{array}\right]\end{array}$$

(62)

Cause:

$$\begin{array}{c}\widetilde{y}={\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]}^{-1}\widetilde{x}\end{array}$$

(63)

Namely:

$$\begin{array}{c}{\widetilde{y}}^{{\prime}}={\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]}^{-1}{\widetilde{x}}^{{\prime}}\end{array}$$

(64)

Bringing Eq. (50) into Eq. (64) yields:

$${\widetilde{y}}^{{\prime}}={\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]}^{-1}L\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]\widetilde{y}+{\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]}^{-1}f=\left[\begin{array}{cc}0& -{\omega }_{0}\\ {\omega }_{0}& 0\end{array}\right]\widetilde{y}+{\left[{\begin{array}{cc}{\omega }_{\text{im}}& \omega \end{array}}_{re}\right]}^{-1}f$$

(65)

In addition, $L({q}_{*})$ the eigenvectors can be calculated as follows:

$$\begin{array}{c}{\omega }_{\text{re}}+i{\omega }_{\text{im}}=\left[\begin{array}{c}0\\ 1\end{array}\right]+i\left[\begin{array}{c}-\frac{1}{\sqrt{-b\left({q}_{*}\right)}}\\ 0\end{array}\right]\end{array}$$

(66)

Bringing the values of Eq. (51) and sum into equation ${\omega }_{im}({\omega }_{re}$65) yields:

$${\widetilde{y}}^{{\prime}}=\left[\begin{array}{cc}0& -{\omega }_{0}\\ {\omega }_{0}& 0\end{array}\right]\widetilde{y}+\left[\begin{array}{c}0\\ {k}_{11}{\widetilde{\rho }}^{2}+{k}_{22}{y}^{2}+{k}_{12}\widetilde{\rho }y+{k}_{111}{y}^{3}\\ +{k}_{112}{\widetilde{\rho }}^{2}y +{k}_{122}\widetilde{\rho }{y}^{2}+O(\widetilde{\rho },y{)}^{4}\end{array}\right]$$

(67)

Equation (67) is in the same form as Eq. (44), so according to Eq. (48), the system (26) can $a$ be calculated as follows:

$$a=\left(\frac{1}{16}\right)\left[{\widetilde{f}}_{2\widetilde{{y}_{1}}\widetilde{{y}_{1}}\widetilde{{y}_{2}}}+{\widetilde{f}}_{2\widetilde{{y}_{2}}\widetilde{{y}_{2}}\widetilde{{y}_{2}}}\right]+\left(\frac{1}{16{\omega }_{0}}\right)\left[-{\widetilde{f}}_{2\widetilde{{y}_{1}}\widetilde{{y}_{2}}}\left({\widetilde{f}}_{2\widetilde{{y}_{1}}\widetilde{{y}_{1}}}+{\widetilde{f}}_{2\widetilde{{y}_{2}}\widetilde{{y}_{2}}}\right)\right]$$

(68)

Further, the value of c can be calculated as follows:

$$\begin{array}{c}c={\alpha }^{{\prime}}\left({q}_{*}\right)=\frac{1}{2}\left(\frac{{cq}_{*}+2{c}_{1}c\rho +{c}_{0}\rho \left(b+c\right)}{\rho \mu \left(c-b\right)+c{c}_{0}\left({q}_{*}+{c}_{1}\rho \right)}\right)\left|{q}_{*}=0\right.>0\end{array}$$

(69)

Therefore, for the system (26), the Hopf branch is supercritical when $a<0$ and subcritical when $a>0$.

5 Saddle branching conditions for the model

Lemma 3

[45]: Consider the system ${x}^{\mathrm{^{\prime}}}=f(x,\lambda ),x\in {R}^{n},\lambda \in R,\lambda$ is a variable parameter. If $({x}_{0},\lambda )$ satisfies the equilibrium condition $f(x,\lambda )\left|({x}_{0},{\lambda }_{0})={0}_{n\times 1}\right.$, note $L={D}_{x}f(x,\lambda )\left|({x}_{0},{\lambda }_{0})\right.$, make $\Psi$ and $\Phi$ L about unit characteristic vectors, respectively, namely $\Psi L=0$ and $L\Phi =0$, is when the following conditions to satisfy, $\lambda ={\lambda }_{0}$ is saddle section branch of the system.

$$\begin{array}{c}(i) a=\Psi \frac{\partial }{\partial {q}_{*}}f(x,\lambda {)}_{\left|\left({x}_{0},{\lambda }_{0}\right)\right.}\ne 0\end{array}$$

(70)

$$\begin{array}{c}(ii) b=\Psi \cdot \mathop{\sum }\limits_{i=1}^{n}{e}_{i}\left[{\Phi }^{T}\frac{{\partial }^{2}}{\partial {x}^{2}}{f}_{i}\left(x,\lambda \right)\left|\left({x}_{0},{\lambda }_{0}\right)\Phi \right.\right]\ne 0\end{array}$$

(71)

Is for any small $\varepsilon >0$, the solution of curve near $({x}_{0},{\lambda }_{0})$, approximate expression for:

$$\begin{array}{c}x=\varepsilon \Phi +o\left({\varepsilon }^{2}\right),\lambda =\frac{{\varepsilon }^{2}b}{2a}+o\left({\varepsilon }^{3}\right).\end{array}$$

(72)

For system (26), set ${q}_{*}$ to variable parameters, the matrix of derivatives at the equilibrium point is shown in Eq. (33). When ${q}_{*}=-{\rho }^{2}{{V}_{e}}^{\mathrm{^{\prime}}}(\rho )$ there is $\Phi =\left(\begin{array}{c}1\\ 0\end{array}\right)$ satisfaction $L\Phi =0$.

At this point,

$$\begin{array}{c}\Psi L=0\Rightarrow \Psi =\left(\begin{array}{cc}\frac{{cq}_{*}+2{c}_{1}c\rho +{c}_{0}\rho \left(b+c\right)}{\rho \mu \left(c-b\right)+c{c}_{0}\left({q}_{*}+{c}_{1}\rho \right)}& 1\end{array}\right)\end{array}$$

(73)

Substituting the variables $\Psi$ and $\Phi$ into Eqs. (70) and (71) gives:

$$ \begin{aligned} a = &\Psi \frac{\partial }{{\partial q_{*} }}f(x,q_{*} )_{{\left| {(x_{0} ,q_{*0} )} \right.}} & & & & & & & & & & & & & & & & & & & & & & & & & \\ = & \left(\begin{array}{*{20}c} {\frac{{cq_{*} + 2c_{1} c\rho { + }c_{0} \rho (b + c)}}{{\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho )}}} & 1 \\ \end{array} \right)\left(\begin{array}{*{20}c} 0 \\ { - \frac{{\rho^{2} c}}{{T(\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho ))}}} \\ \end{array} \right) & & & \\ = & - \frac{{\rho^{2} c}}{{T(\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho ))}} \ne 0 \\ \end{aligned} $$

(74)

$$ \begin{aligned} b = &\uppsi \sum\limits_{i = 1}^{n} e_{i} [\Phi^{T} \frac{{\partial^{2} }}{{\partial x^{2} }}f_{1} \left( {x,\lambda } \right)|\left( {x_{0} ,\lambda_{0} } \right)\Phi ] \\ = & \left( {\begin{array}{*{20}c} {\frac{{cq_{*} + 2c_{1} c\rho_{0} + c_{0} \rho_{0} (b + c)}}{{\rho_{0}\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho_{0} )}}} & 1 \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]} & {\left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \right]} & {\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]} \\ \\ {\left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]} & {\left[ {\begin{array}{*{20}c} Z & L \\ L & 0 \\ \end{array} } \right]} & {\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right]} \\ \end{array} } \right) \\ = & \frac{\begin{gathered} cc_{0} (q_{*} + c_{1} \rho_{0} ))^{2} + cV_{e}^{\prime } (\rho_{0} ) - 2\rho_{0} cq_{*} - 2c_{1} c\rho_{0} )(\rho_{0}\upmu (c - b)) \hfill \\ + (3\rho_{0}^{2} cV_{e} (\rho_{0} ) + cV_{e}^{\prime } (\rho_{0} ) - 2\rho_{0} cq_{*} - 2c_{1} c\rho_{0} )(\upmu (c - b) + cc_{0} c_{1} ) \hfill \\ + cc_{0} (q_{*} + c_{1} \rho_{0} ) - (\rho_{0}^{3} cV_{e} (\rho_{0} ) - \rho_{0}^{2} cq_{*} - c_{1} c\rho_{0}^{2} ) \hfill \\ (\upmu (c - b) + cc_{0} c_{1} ) - 2(\rho_{0}\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho_{0} ))(\upmu (c - b) \hfill \\ + cc_{0} c_{1} ) (3\rho_{0}^{2} cV_{e} (\rho_{0} )+ ((3\rho_{0}^{2} cV_{e}^{\prime } (\rho_{0} ) + 6\rho_{0} cV_{e} (\rho_{0} ) + cV_{e}^{\prime \prime }\hfill \\ (\rho_{0} ) - 2cq_{*} - 2cc_{1} )\rho_{0}\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho_{0} )) \hfill \\ - (3\rho_{0}^{2} cV_{e} (\rho_{0} ) + \rho_{0}^{3} cV_{e}^{\prime } (\rho_{0} ) - 2\rho_{0} cq_{*} - 2c_{1} c\rho_{0})\hfill \\ (\upmu (c - b) + cc_{0} c_{1} )(\rho_{0}\upmu (c - b) \hfill \\ \end{gathered} }{{(\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho ))^{4} }} \\ \ne & 0 \\ \end{aligned} $$

(75)

Thereinto

$$\begin{aligned} &Z(\rho_{i} ,c,q_{*} ) \\ &\quad = \frac{\begin{gathered} cc_{0} (q_{*} + c_{1} \rho )) + cc_{0} (q_{*} + c_{1} \rho ))^{2} \hfill \\ - (\rho_{0}^{3} cV_{e} (\rho_{0} ) - \rho_{0}^{2} cq_{*} - c_{1} c\rho_{0}^{2} )(\upmu (c - b) + cc_{0} c_{1} ) \hfill \\ - 2(\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho ))(\upmu (c - b) + cc_{0} c_{1} )\hfill \\ (3\rho_{0}^{2} cV_{e} (\rho_{0} ) + (3\rho_{0}^{2} cV_{e} (\rho_{0} ) + cV_{e}^{\prime } (\rho_{0} ) \hfill \\ - 2\rho cq_{*} - 2c_{1} c\rho )(\upmu (c - b) + cc_{0} c_{1} ) \hfill \\ + ((3\rho_{0}^{2} cV_{e}^{\prime } (\rho_{0} ) + 6\rho_{0} cV_{e} (\rho_{0} ) + cV_{e}^{\prime \prime } (\rho_{0} ) - 2cq_{*} - 2cc_{1} ) \hfill \\ \rho\upmu (c - b) + cc_{0} (q_{*} + c_{1}\uprho _{0} ))^{2} + cV_{e}^{\prime } (\rho_{0} ) \hfill \\ - 2\rho cq_{*} - 2c_{1} c\rho )(\rho_{0}\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho )) \hfill \\ - (3\rho_{0}^{2} cV_{e} (\rho_{0} ) + \rho_{0}^{3} cV_{e}^{\prime } \hfill \\ (\rho_{0} ) - 2\rho cq_{*} - 2c_{1} c\rho )(\upmu (c - b) + cc_{0} c_{1} )(\rho\upmu (c - b) \hfill \\ \end{gathered} }{{(\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho ))^{4} }}\end{aligned} $$

(76)

And

$$ L(\rho_{i} ,c,q_{*} ) = \frac{\begin{gathered} (2c_{1} c + c_{0} (b + c))(\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho )) \hfill \\ - (cq_{*} + 2c_{1} c\uprho + c_{0} \rho (b + c))(\upmu (c - b) + cc_{0} c_{1} ) \hfill \\ \end{gathered} }{{(\rho\upmu (c - b) + cc_{0} (q_{*} + c_{1} \rho ))^{4} }} $$

(77)

So when the ${{q}_{*}}_{0}=-{{\rho }_{0}}^{2}{{V}_{e}}^{\mathrm{^{\prime}}}({\rho }_{0})$ system (26) exists in ${q}^{*}={q}_{0}^{*}$ the saddle branch.

6 Numerical simulation

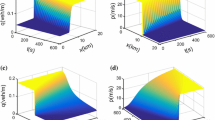
First, to verify that our newly proposed model can reproduce the stop-and-go phenomenon of real traffic flow under different initial densities, we choose different initial densities to simulate the density space–time diagram. The figure shows the spatio-temporal plot of density when the initial density is $0.01\mathrm{ veh}/\mathrm{m}<{\rho }_{0}<0.09\mathrm{ veh}/\mathrm{m}$.

The numerical results under different initial densities are shown in the figure. According to the figure, we find that the traffic condition will be unstable when the initial density is $0.01\frac{\mathrm{veh}}{\mathrm{m}}<{\rho }_{0}<0.09\mathrm{ veh}/\mathrm{m}$.

Under the given initial boundary conditions mentioned above, the following conclusions can be drawn according to the simulation diagram of the density waveform of the new model shown in Fig. 3a–f:

• (1) As can be seen from Fig. 3a–f, when the initial density value is small, the new model can eliminate the external disturbance well, as shown in Fig. 3a, b. However, with the increase of the initial density, the traffic flow gradually becomes less stable, and the disturbance does not decrease with the passage of time, but produces greater fluctuations, as shown in Fig. 3c–e. When the initial density continues to increase, the initial density value reaches the stable interval of the macroscopic traffic flow model. The disturbance wave of the density space–time diagram gradually disappears, eliminating external interference, and the traffic flow gradually returns to a stable state, as shown in Fig. 3f.

• (2) As shown in Fig. 3c–e, within a certain range, with the increase of the initial density, the disturbance does not decrease, but instead as time goes on, multiple aggregation waves as shown in Fig. 3c, multiple disturbance waves as shown in Fig. 3d, and an increase in disturbance as shown in Fig. 3e are generated. When the traffic flow density is lower than the critical density, the small disturbance will dissipate quickly and evolve into a uniform flow. When the initial density increases to ${\rho }_{0}=0.04586\mathrm{ veh}/\mathrm{m}$, a complex local structure consisting of two or more clusters is formed. Therefore, the local clustering phenomenon of traffic flow is reproduced in Fig. 3c, and the actual traffic state will eventually appear congestion. However, when the initial density continues to increase, as shown in Fig. 3f, the disturbance gradually disappears and the traffic flow gradually returns to a stable state as time goes by. In summary, through numerical simulation, the stable state of traffic flow described by the macro model proposed in this paper is observed, and its boundary stability conditions are obtained. When the initial density ${\rho }_{0}>0.09\mathrm{ veh}/\mathrm{m}$, or ${\rho }_{0}<0.01\mathrm{ veh}/\mathrm{m}$, the disturbance in the traffic flow will not be amplified; When ${\rho }_{0}$ is not in the stable condition area, the disturbance will be amplified, and even appear local cluster effect, stop-and-go vehicle phenomenon.

• (3) As shown in the Fig. 3g–j, 3g, i are the density space–time diagram of macro model considering throttle information, Fig. 3h, j are the density space–time diagram of FVD macro model. We find that under the same parameter conditions, as the density decreases or increases, the small perturbations develop into single clusters and multiple clusters; under the same initial density $\rho$, the influence of throttle opening angle can effectively suppress traffic congestion.

Fig. 3

a–f Spatio-temporal graph of density under different initial densities. g–j Under the same density, the FVD model is compared with the space–time diagram considering the density of the throttle model

According to the simulation results of the FVD macro model and the throttle macro model, the following conclusions can be drawn: whether the traffic flow is in a stable state (Fig. 3i, j) or an unstable state (Fig. 3g, h), under the same initial density conditions, the fluctuation of the density waveform of the macro model considering the throttle is smaller than that of the FVD macro model when the disturbance diverges or the disturbance disappears. Therefore, it can be concluded that the macroscopic traffic flow model considering the influence of electronic throttle dynamics can effectively curb traffic congestion. The stability, anti-interference ability and ability to eliminate external disturbances of the new macro model are stronger than those of the FVD macro model without considering the throttle dynamics information, which further verifies the effectiveness of the new model.

Next, we choose different equilibrium points as starting points to study various branch of nonlinear systems (26). In the beginning, we use the above equilibrium point as an example to plot the following figure, where the parameters are selected as variable parameters with an initial value of 0.2. You can find three special points in this range which respectively are a Hopf branch point (H) and two limiting branch points (LP), as shown in Fig. 4.

Fig. 4

a The branch diagram where ${q}_{*}$ takes the state variable of a large range of parameters as; b Branch graphs with appropriate parameter interval ${q}_{*}$

When ${q}_{*}$ is 0.817848, the state variables for Hopf branch point is (0.050047,0), at this time, the vehicle density is ${\rho }_{0}=0.050047\mathrm{eh}/\mathrm{m}$, and two eigenvalues were 4.4729e−08 + 0.019825i and 4.4729e−08−0.019825i. The real part of a pair of conjugate eigenvalues is considered to be 0, which is the sign of judging it as a Hopf branch, and its maximum lyapunov exponent is 5.555356e + 01.

The first limit branch occurs when the variable parameter is 0.891695. The state variables is (0.040665,0), the corresponding vehicle density is ${\rho }_{0}=0.040665\mathrm{eh}/\mathrm{m}$. The eigenvalues were − 1.8044e−05 and 0.018863, respectively. Obviously the previous eigenvalue is 0, which is the sign for the branch of the limit point. In addition, the second normalization coefficient is a = −7.303210e−01.

A second limit branch occurs when the variable parameter is 0.172588. The state variables is (0.112377,0), and the corresponding vehicle density is ${\rho }_{0}=0.112377\mathrm{eh}/\mathrm{m}$. The eigenvalues are −6.0878e−05 and 0.038439, respectively. It is also clear that the first eigenvalue is 0, which is a sign that it is a branch of the limit point. The second normalization coefficient is a = 3.502079e−01.

Below, this paper analyzes the stability changes of the traffic system when the parameters pass some branch critical points calculated above. First, to study the effect of Hopf branch on traffic flow, the stability of the system on the phase plane is investigated in this paper when parameter ${q}_{*}$ passes 0.817848.

Figure 5a shows that when the parameter is ${q}_{*}<0.817848$, point $(\mathrm{0.036995,0})$ is an equilibrium node. Meanwhile, the equilibrium point $(\mathrm{0.044323,0})$ is a spiral point, and all curves approach the point $(\mathrm{0.044323,0})$ within the red line. Therefore, the system inside the red line is stable, and the system outside the red line is unstable.

Fig. 5

Phase planar graph of Hopf branch with parameter ${q}_{*}<0.817848$ and parameter ${q}_{*}>0.817848$ a phase planar graph with variable parameter ${q}_{*}=0.80$; b phase plan for variable parameter ${q}_{*}=0.88$

As can be seen from Fig. 5b, when parameter ${q}_{*}>0.817848$, no new equilibrium point appears at Hopf branch point, but periodic solution exists (black region in Figure). This is because in Fig. 5b, when $z\to +\infty$, one spiral trajectory starts from the point $\left(\mathrm{0.030112,0}\right)$ and approaches the focus $\left(\mathrm{0.051189,0}\right)$, and eventually evolves into constant amplitude oscillation as $z\to -\infty$, while the other spiral trajectory approaches the periphery of the constant amplitude oscillation region as $z\to -\infty$ and approaches infinity as $z\to +\infty$. So there’s a limit cycle between the blue and black lines. These theoretical analyses are also consistent with the above numerical results.

By selecting some branch points as the initial average density of density time evolution, it is helpful for us to better understand the complex phenomena in congested traffic. We analyze the application of local perturbation under the condition of initial uniform density. The initial density is shown below [47].

$$\begin{aligned} \rho (x,0)& ={\rho }_{0}+\Delta {\rho }_{0}\left\{{\mathrm{cosh}}^{-2}\left[\frac{160}{L}\left(x-\frac{5L}{16}\right)\right]\right.\\ & \quad \left.-\frac{1}{4}{\mathrm{cosh}}^{-2}\left[\frac{40}{L}\left(x-\frac{11L}{32}\right)\right]\right\}\end{aligned}$$

(78)

$$\begin{array}{c}v(x,0)=V(\rho (x,0))x\in [0,L]\end{array}$$

(79)

where ${\rho }_{0}$ is the initial density, $\Delta {\rho }_{0}=0.01\mathrm{veh}/\mathrm{m}$ is the disturbance density, $L=32.2\mathrm{km}$ is the section length, and the dynamic near boundary condition is given by the following formula:

$$\rho \left(1,t\right)=\rho \left(2,t\right),\rho \left(L,t\right)=\rho \left(L-1,t\right),v\left(1,t\right)=v\left(2,t\right),v\left(L,t\right)=v\left(L-1,t\right)$$

(80)

To facilitate simulation implementation, the space spacing is equal to 100 m, and the time interval is 1 s. The values of other parameters in the model are as follows: $T=10\mathrm{ s},{c}_{0}=11\frac{\mathrm{m}}{\mathrm{s}}, \mu =550,{v}_{\mathrm{f}}=\frac{30\mathrm{m}}{\mathrm{s}},{\rho }_{\mathrm{m}}=0.2\mathrm{veh}/\mathrm{m}.$

The state variable ${\rho }_{0}=0.050047\mathrm{veh}/\mathrm{m}$ corresponding to Hopf branch point is selected as the initial uniform density value, and a local small disturbance with amplitude $\Delta {\rho }_{0}=0.01\mathrm{ veh}/\mathrm{m}$ is applied to draw the density space–time diagram of the system, as shown in Fig. 6:

Fig. 6

The space–time diagram of density with Hopf branch as the initial value

We know from the property of Hopf branching that the system generates a periodic solution from the equilibrium point when the parameter passes through the branching point. Since the initial density value at this time is within the unstable range of the model, the small disturbance on the initial uniform density is amplified, as shown in Fig. 6, and then evolves into periodic oscillation of constant amplitude, which is consistent with the characteristics of the limit cycle solution, indicating that under the initial uniform traffic condition, when the parameter passes Hopf branch point, the small disturbance will change into walking and stopping wave. It is also shown that the results are in agreement with the actual phenomenon and the numerical results, which verifies the correctness of the theoretical analysis.

Next, this paper studies the effect of limit cycle branch on traffic flow when parameter ${q}_{*}$ passes 0.891695. When the traffic system passes through the first LP bifurcating point with parameter 0.891695, the stability of the traffic flow will change significantly. First, consider ${q}_{*}<0.891695$. At this point, we set ${q}_{*}=0.79,$ the system has two point, one is a saddle point (0.029518,0), the other is a spiral point (0.051791,0), as shown in Fig. 7a. All curve within the red line point to point (0.051791,0). Therefore, the traffic system inside the Red Line is stable, while the traffic system outside the Red line is unstable. With the increase of the parameter, the two equilibrium points gradually move towards the middle. When the parameter is ${q}_{*}=0.891695$, the two equilibrium points shown in Fig. 7a merge into one equilibrium point and a saddle knot branch occurs, as shown in Fig. 7b. Again, the traffic system inside the Red Line is stable, while the traffic system outside the Red line is unstable. With the continuous increase of parameter value, when parameter ${q}_{*}>0.891695$, the equilibrium point disappears, as shown in Fig. 7c, and the whole traffic system becomes unstable.

Fig. 7

Phase plan of saddle junction branch when variable parameters ${q}_{*}>0.891695$, ${q}_{*}=0.891695$ and ${q}_{*}<0.891695$ change from small to large

According to the Hartman-Grossman linearization theorem, when the real part (29) of the eigenvalue of the equation is non-zero, the stability of the equilibrium point of the nonlinear system (26) can be approximated by the saturation of the corresponding linearized system (27). When the equilibrium point is not the central point, the two systems are uniformly stable or uniformly unstable at these equilibrium points. We can solve the equilibrium point of Eq. (26). The optimal speed function in the model is specified as follows:

$$\begin{array}{c}{V}_{\mathrm{e}}\left(\rho \right)={v}_{\mathrm{f}}\left\{{\left[1+\mathrm{exp}\left(\frac{\rho /{\rho }_{\mathrm{m}}-0.25}{0.06}\right)\right]}^{-1}-3.72\times 1{0}^{-6}\right\}\end{array}$$

(81)

In the original model:

$$\begin{aligned} &{V}_{\mathrm{e}}\left(\frac{\rho \left(x,t\right)}{1+\delta }\right)\nonumber \\ &\quad ={v}_{\mathrm{f}}\left\{{\left[1+\mathrm{exp}\left(\frac{\rho /\left(1+\delta \right){\rho }_{\mathrm{m}}-0.25}{0.06}\right)\right]}^{-1}-3.72\times 1{0}^{-6}\right\}\end{aligned}$$

(82)

${v}_{\mathrm{f}}$ represents the free flow velocity and ${\rho }_{\mathrm{m}}$ represents the maximum crowding density.

This may help improve our understanding of complex phenomena in heavy traffic by selecting some branch points as the initial average density of the time evolution of density. We analyze the application of local perturbation under the condition of initial uniform density. The initial density is used as follows [47]:

$$\begin{aligned} \rho \left(x,0\right)&={\rho }_{0}+\Delta {\rho }_{0}\left\{{\mathrm{cosh}}^{-2}\left[\frac{160}{L}\left(x-\frac{5L}{16}\right)\right]-\frac{1}{4}{\mathrm{cosh}}^{-2}\right. \nonumber \\ &\quad \left.\left[\frac{40}{L}\left(x-\frac{11L}{32}\right)\right]\right\}x\in \left[0,L\right]\end{aligned} $$

(83)

$$\begin{array}{c}v\left(x,0\right)=V\left(\rho \left(x,0\right)\right),x\in \left[0,L\right]\end{array}$$

(84)

where ${\rho }_{0}$ is the initial mean density, $\Delta {\rho }_{0}$ is the amplitude of the local disturbance, and $L=32.2\mathrm{km}$ is the length of the considered section. The dynamic approximate boundary conditions are given by Eq. (84).

For calculation purposes, the space domain is divided into equal intervals of 100 m in length, and the time interval is selected as 1 s. Relevant parameters of this model are as follows:

$$\Delta =5 \mathrm{m},{c}_{0}=11\mathrm{m}/\mathrm{s},p=0.2,{v}_{\mathrm{f}}=30\mathrm{m}/\mathrm{s},{\rho }_{\mathrm{m}}=0.2\mathrm{veh}/\mathrm{m},\delta =0.5$$

When parameter ${q}_{*}$ passes LP bifurcating point $0.891695$, Vehicle density ${\rho }_{0}=0.040668$, saddle junction bifurcating occurs. From the above data, it can be seen that before and after the vehicle density passes the saddle junction branch, the fluctuation range of traffic flow density becomes significantly larger, which indicates that when the system passes the saddle junction branch, the traffic flow system changes from a stable state to an unstable state, as shown in Fig. 8.

Fig. 8

Density fluctuation state near saddle junction branch under different initial densities. a ${\uprho }_{0}=0.040225\mathrm{veh}/\mathrm{m}$, b ${\uprho }_{0}=0.041231\mathrm{veh}/\mathrm{m}$

Secondly, when parameter ${\mathrm{q}}_{*}$ passes through another LP branch point 0.172588, the stability of traffic flow will also change obviously. Firstly, ${\mathrm{q}}_{*}>0.172588$, set ${\mathrm{q}}_{*}=0.20$, the system has three balance point, a saddle point (0.0065382,0), a focus (0.093766,0) and a saddle point (0.14471,0), as shown in Fig. 9a. Due to the monotonically increasing relationship between variable ${\mathrm{q}}_{*}$ and vehicle density, the traffic system on the left of the first red line gradually changes from unstable to stable, the traffic system between the two red lines changes from stable to unstable, and the traffic system on the right of the second red line is unstable. With the decrease of the parameter ${\mathrm{q}}_{*}$, the first red line moves to the right, the second red line moves to the left, and the two lines gradually move closer to the center. When the parameter ${\mathrm{q}}_{*}=0.172588$, As shown in Fig. 9a of the two balance (0.093766,0) and point (0.14471,0) in point (0.11229,0) fuse for a balance, a saddle node branch, as shown in Fig. 9b. If the value of parameter ${\mathrm{q}}_{*}$ continues to decrease, that is, when ${\mathrm{q}}_{*}<0.172588$, the equilibrium point disappears and all the solutions move to the right, as shown in Fig. 9c, the traffic system becomes unstable.

Fig. 9

Phase plane plan of saddle junction branching when variable parameters ${\mathrm{q}}_{*}>0.172588$, ${\mathrm{q}}_{*}=0.172588$ and ${\mathrm{q}}_{*}<0.172588$ change from large to small

When parameter ${\mathrm{q}}_{*}$ passes LP bifurcating point 0.891695, namely vehicle density ${\uprho }_{0}=0.112290$, the second saddle junction bifurcating point appears. As can be seen from Fig. 10, before the vehicle density passes through the saddle junction branch, the traffic system is in a stable state; after the vehicle density passes through the saddle junction branch, the fluctuation range of the traffic flow density becomes significantly larger, which indicates that when the system passes through the saddle junction branch, the traffic flow system changes from a stable state to an unstable state, as shown in Fig. 10a, b.

Fig. 10

Density fluctuation state near saddle junction branch under different initial densities. a ${\uprho }_{0}=0.104885\mathrm{veh}/\mathrm{m}$ b ${\uprho }_{0}=0.12448531\mathrm{veh}/\mathrm{m}$

7 Conclusion

Macro traffic flow theory studies the overall behavior of vehicles in the traffic system, which mainly observes the behavior evolution characteristics of traffic flow formed by a large number of vehicles in road traffic. In this paper, the throttle dynamics information of automobile dynamics is studied at the macroscopic traffic level. Firstly, a macro-traffic flow model considering throttle dynamics information is proposed, and the effectiveness of the model is analyzed. Secondly, in view of the proposed macro model, the stability analysis of the proposed macro-traffic flow model is carried out using the small perturbation method, and the branch analysis method is used to discuss the type and stability of the equilibrium solution, and prove the existence conditions of hopf branch and saddle node branch, and the stability changes of the system when it passes through the branch point are analyzed by numerical simulation. Finally, it is concluded from the spatio-temporal diagram of the system density that the new model has a good effect on stability, elimination of external disturbance and anti-interference ability, which further verifies the validity of the proposed continuous model and it is consistent with the theoretical analysis results. However, vehicles in the actual complex traffic system are affected by a variety of dynamic information, such as wind resistance, tire side longitudinal force and other dynamic information, which also are some directions that need to be further understood in the future.