Role of spin-orbit coupling effects in rare-earth metallic tetra-borides: a first principle study

Abstract

Recent observation of magnetization plateau in rare-earth metallic tetra-borides, $\text {RB}_{4}$, have drawn lot of attention to this class of materials. In this article, using first principle electronic structure methods (DFT) implemented in Quantum Espresso (QE), we have studied hither-to neglected strong spin-orbit coupling (SOC) effects present in these systems on the electronic structure of these system in the non-magnetic ground state. The calculations were done under GGA and GGA+SO approximations. In the electronic band structure, strong SOC effect lifts degeneracy at various symmetry points. The projected density of states consists of 3 distinct spectral peaks well below the Fermi energy and separated from the continuum density of states around the Fermi energy. The discrete peaks arise due to rare-earth ${\varvec{s}}$, rare-earth ${\varvec{p}}$ + B ${\varvec{p}}$ and B ${\varvec{p}}$ while the continuum states around the Fermi level arises due to hybridized B ${\varvec{p}}$, rare-earth ${\varvec{p}}$ and ${\varvec{d}}$ orbitals. Upon inclusion of SOC the peak arising due to rare-earth p gets split into two peaks corresponding to ${\varvec{j}}={\textbf {0.5}}$ and ${\varvec{j}}={\textbf {1.5}}$ configurations. The splitting gap (${\varvec{\Delta }} {\varvec{E}}_{\text {gap}}$) between ${\varvec{j}}={\textbf {0.5}}$ and ${\varvec{j}}={\textbf {1.5}}$ manifold shows power law (${\varvec{\Delta }} {\varvec{E}}_{\text {gap}}\varvec{\propto } {\varvec{Z}}^{{\varvec{n}}}$, ${\varvec{Z}}$ is the atomic number of the rare-earth atom involved) behaviour with n =4.82. In case of $\text {LaB}_{4}$, in the presence of SOC, spin-split ${\textbf {4}}{\varvec{f}}$ orbitals contributes to density of states at the Fermi level while the density of states at the Fermi level largely remains unaffected for all other materials under consideration.

Graphic abstract

1 Introduction

Compounds involving boron like boron carbide, $\text {MgB}_{2}$ [1], hexagonal boron nitride [2], $\text {SmB}_{6}$ and various tetra-borides show exotic properties like high $\text {T}_{c}$ superconductivity, semi-metals with topological properties, Kondo insulator, magnetization plateau. Recently Pan et. al. have studied mechanical, thermodynamic and electronic properties of wide class of transition metal borides like $\text {MoSiB}_{2}$ [3], $\text {CrB}_{4}$ [4, 5], vanadium borides [6], ruthenium borides [7, 8]. These materials show exceptional hardness and have promising applications in the area of high pressure systems, design of new class of functional materials etc. In the present study we consider another class of borides namely rare-earth metallic tetra-borides, $RB_{4}$ (R = rare-earth atom). These materials have drawn lot of attention due to their exotic phase diagram.

The strong Coulomb correlations present in 3d and 4d transition metal compounds as well as in 4f lanthanides and 5f actinides are key to understanding novel and exotic properties. The rare earth lanthanides except Pm are good conductors of heat and electricity. Pm is radioactive with very short life and its occurrence in nature is extremely rare. The rare-earth metallic tetra-borides exhibit various valency such as di, tri and tetravalent state [9]. Cerium (Ce) and terbium (Tb) primarily show tetravalent state where as the other metallic tetraborides mostly show trivalent state [9]. Recently, in $YbB_{4}$, intermediated valance state of Yb between $\text {Yb}^{2+}$ and $\text {Y}b^{3+}$ is experimentally observed [10]. Also the Kondo interaction is found to be significantly large in this system.

Recent observation of fractional magnetic plateau in $\text {TmB}_{4}$ [11] and $\text {NdB}_{4}$, $\text {HoB}_{4}$ [12] have created a lot of interest in these class of materials. Stable magnetization plateau occurring at 1/2 fraction (of saturation magnetization) and fractional plateaus at $1/7, 1/8, \cdots$ etc. [11, 12] fractions are similar to the plateaus observed in the Hall resistivity of two dimensional degenerate electron gases subject to a perpendicular magnetic field.

It is interesting to mention that the position of the rare-earth atoms as shown in Fig. 1 forms a two dimensional Archimedian Shastry-Sutherland lattice (SSL) [13]. Nearest neighbour spin-1/2 SSL is an example of geometrically frustrated system with huge spin degeneracy and the observation of magnetization plateaus is often attributed to this degeneracy. Insulating $\text {SrCu}_{2}(\text {BO}_{3})$ [14] is a well studied system which can be effectively mapped onto a nearest-neighbour SSL. However in metallic rare-earth tetraborides “localized” spins interacts only through long range RKKY [15] type of interactions. Hence the mapping of interacting fermionic model onto an effective spin-1/2 models on SSL with nearest neighbour interaction is highly non-trivial [16]. Correlated and frustrated systems are of great academic interest as well as they have many potential technological applications like memory devices, spintronics, quantum computation etc.

The very first step towards understanding the intriguing thermodynamic and transport properties in these complex systems is to study their electronic band structure. It is important to mention that the study of thermodynamic, electronic and other properties requires structural stability of a given system as has been shown by Pan et. al. in wide class of materials involving boron and various transition metal elements [17,18,19,20,21]. However, the rare-earth tetra-borides have been synthesized and studied experimentally over the last couple of decades. They are found to be both structurally and thermodynamically stable. In an earlier work [22] electronic structure of $\text {RB}_{4}$ (except $\text {TmB}_{4}$) have been studied using first principle methods. Electronic band structure of $\text {TmB}_{4}$ has also been reported [23, 24]. However strong atomic spin-orbit coupling effects present in rare-earth atoms have been neglected [22]. Inclusion of SOC for certain systems [R= Yb, Pr, Gd, Tb, Dy] in the magnetic state have been considered [25]. But there is no systematic study of such effects in the non-magnetic (paramagnetic) state of such systems. In the present work we report a detailed study of SOC effects on the electronic structure of rare earth tetra-borides in the non-magnetic ground state. In particular we have chosen systems (R=La, Ce, Nd, Sm) with relatively low SOC effects as well as systems (R=Ho,Er,Tm,Lu) with relatively high SOC effects. The present study is relevant for the paramagnetic state of these systems.

The organization of the rest of the paper is as follows. In Sect. 2 we discuss the crystal structure of the system. In Sect. 3 we elaborate the computational details for electronic band structure. In Sect. 4 we discuss the results for systems characterised by varying strength of SOC effects and finally in Sect. 5 we conclude.

2 Crystal structure

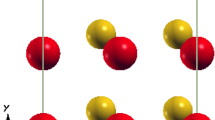
$\text {RB}_{4}$ crystallizes in the tetragonal symmetry with space group P4/mbm [26, 27]. Figure 1 summarizes crystal structure of $\text {RB}_{4}$ from different perspectives. Figure 1a displays the full tetragonal structure which consists of alternate layers of rare-earth (R) and B ions stacked along c-axis. Figure 1b shows the top view of the crystal structure. There are two distinct types of B atoms - (i) planar and (ii) octahedral. Boron atoms form octahedra as well as 7-atom rings in the $a-b$ plane [28]. Ring forming planar B atoms (shown in blue) which are not part of octahedra also forms dimers and these dimers are arranged in a regular pattern. In Fig. 1c we show one unit cell formed by four such B octahedra. In Fig. 1d we show SSL formed by the B atoms. From Fig. 1b it is clear that out of the 4 B atoms two are nearer than other two. The exchange interaction between the two near R atoms mimics the nearest neighbour interaction (J) and the interaction between the distant R atoms mimics interaction along alternate diagonals. It is important to mention that B atoms play a crucial role in the electronic structure of these systems as they are in the sp-hybridized state.

Fig. 1

Tetragonal crystal structure of $RB_{4}$. Panel (a) represents the full structure consisting of different layers of rare-earth, R, ions (red) and B (green) stacked along c-axis. Panel (b) Top view of the B sub lattice (in the $a-b$ plane) comprising of 7 atom ring and a square formed by the position of the R atoms. Panel (c) Side view of the B sub lattice (along c-axis) showing two different types of B; one forming dimer (shown in blue) and the other part of the B octahedra (shown in green). Panel (d) Shastry–Sutherland lattice in two dimension

3 Computational details

First-principle calculations were performed using density functional theory (DFT) [29, 30] as implemented in the open source package Quantum Espresso [31] and also under the BURAI [32] framework. The calculations are done within GGA and GGA+SO approximation. We have used Ultra soft pseudo-potentials [33], Marzari–Vanderbit smaering [34] for structural optimization and total energy calculation of the system. Further, Perdew-Burke-Ernzerhof Generalized Gradient Approximation (PBE-GGA) exchange- correlation functional within the linearized augmented plane wave (LAPW) method is employed [35, 36]. For the case with SOC effect full relativistic Ultra soft pseudo-potentials were used. It is important to mention that the choice of the pseudopotential does not involve 4f orbital and hence the projected density of states (PDOS), except for $LaB_{4}$, does not involve any 4f state. This choice of pseudopotential is suitable for non-magnetic calculations. The total Hamiltonian for the Kohn-Sham DFT calculations with spin-orbit coupling can be written as [36, 37]

$$\begin{aligned} \hat{H} = \hat{T} + \hat{V}_{ext} + \hat{V}_{es} + \hat{V}_{xc} + \hat{H}^{SOC} = \hat{T} + \hat{V}_{a} + \hat{H}^{SOC},\nonumber \\ \end{aligned}$$

(1)

where, $\hat{T}$,$\hat{V}_{ext}$,$\hat{V}_{es}$,$\hat{V}_{xc}$ and $\hat{H}^{SOC}$ are the kinetic energy operator, external potential operator, electrostatic or Hartree potential operator, exchange-correlation potential operator and spin-orbit coupling operator respectively. $\hat{V}_{a}$ is the applied field or Kohn-Sham potential operator. The Hamiltonian, $\hat{H}^{SOC}$, in the relativistic limit can be expressed in terms of momentum and spin operators as [36, 37]

$$\begin{aligned} \hat{H}^{SOC}= \frac{i}{4c^2}({\nabla }\hat{V}_{a} \times \hat{p}).\hat{s} \end{aligned}$$

(2)

Under central field approximation the Hamiltonian, $\hat{H}^{SOC}$, [36] can be written as

$$\begin{aligned} \hat{H}^{SOC} = \zeta \hat{l}.\hat{s} \end{aligned}$$

(3)

where $\hat{l}$ is the angular momentum and $\zeta = \frac{1}{2\,m^2c^2r}\frac{d\hat{V}_{a}}{dr}$, where c is the speed of light.

Table 1 Comparison between experimental and calculated lattice constants used for various systems under consideration. Experimental data is taken from Ref. [38]

The lattice information were taken from the materials research project site [38]. The experimentally determined lattice constants (as obtained from x-ray crystallography) as well as those obtained from relaxation of input structures for various $\text {RB}_{4}$ are summarised in Table 1. Interestingly, they are nearly same. All the calculations were performed on three dimensional crystals consisting of primitive tetragonal lattice with 20 atoms. The energy conservation was achieved using $8^{3}$-points in the full Brillouin zone for sampling. Energy convergence criteria of $10^{-6}$ Ry were used for self-consistent calculations. The band structure is plotted along the path involving high symmetry points. The high symmetry points for tetragonal lattice system in the first Brillouin zone are $\Gamma$=(0, 0, 0), X= ($\frac{\pi }{a}$,0,0), M=($\frac{\pi }{a}$,$\frac{\pi }{a}$,0), Z=(0,0,$\frac{\pi }{c}$), R=($\frac{\pi }{a}$,0,$\frac{\pi }{c}$), A=($\frac{\pi }{a}$,$\frac{\pi }{a}$,$\frac{\pi }{c}$). Calculated band structures were plotted along the high symmetry directions $\Gamma -X-M-\Gamma$, $Z-R-A-Z$, $X-R$, $M-A$.

Table 2 Spin-orbit coupling energy of rare-earth atoms in various systems under consideration. Data is taken from Ref. [39]

Fig. 2

Total Energy as a function of kinetic energy cut-off and number of k-points along irreducible edges. Panel (a) and (b): Results for $\text {LaB}_{4}$. Panel (c) and (d): Results for $\text {LuB}_{4}$

Table 3 Total energy cutoff (Ecutwfc) and Coulomb energy cutoff (Ecutrho) used for various systems under consideration

4 Results and discussion

In this study we have considered 4 canonical systems, $\text {LaB}_{4}$, $\text {CeB}_{4}$, $\text {NdB}_{4}$ and $\text {SmB}_{4}$, with relatively small spin-orbit coupling strength and 4 canonical systems, $\text {HoB}_{4}$, $\text {ErB}_{4}$, $\text {TmB}_{4}$ and $\text {LuB}_{4}$, with much larger spin-orbit coupling effect. In Table 1. we have compared the lattice constants with experimental values for systems under consideration. In Table 2. we have summarized the atomic spin-orbit coupling energy [39](in units of $\text {cm}^{-1})$ of rare-earth atoms in various systems under consideration. It is important to mention that the choice of kinetic energy cut-off and the number of k-points chosen over the irreducible Brillouin zone are extremely crucial in band structure calculations. To be more precise for electronic band structure calculation we need to first obtain converged self consistent field (SCF). The convergence of SCF critically depends on energy cut-off, charge density cut-off and number of k-points over the irreducible Brillouin zone. Our choice of various cut-off parameters and number of k-points are sufficient for converged SCF calculation as evident from Fig. 2. In particular, we have calculated the total energy as a function of the plane wave kinetic energy cut-off as well as the number of k-points over irreducible Brillouin zone. In Fig. 2a, b we show the convergence of the total energy as a function of kinetic energy cutoff and number of k-points for one canonical system $\text {LaB}_{4}$ with low spin-orbit coupling strength. In Fig. 2c, d we have shown the same for $\text {LuB}_{4}$, a material with much larger SOC strength. It is clear that the kinetic energy cut-off in the range of 20–50 Ry and 30–50 Ry are sufficient for convergence of total energy in these two systems, respectively. The charge density cut-off (Ecutrho) values have been taken eight times more than the kinetic energy cut-off (Ecutwfc) values because of the ultrasoft pseudo-potential used in our calculations. In Table 3, we have summarized kinetic energy cut-off and charge density cut-off of various $RB_{4}$ systems under consideration. Also, we have found that $4\times 4\times 4$ k-mesh (defined over irreducible Brillouin zone) is sufficient for relative stability of tetragonal structure. For the entire calculation we have chosen a k-mesh of size $8\times 8\times 8$.

Table 4 Effect of spin-orbit coupling on the Fermi energy of systems with relatively low SOC strength

Fig. 3

Panel: (a) Electronic band structure for $\text {LaB}_{4}$ with SOC (red) and with out SOC (black). Panel: (b) Same band structure in the narrower energy window about the Fermi level (set to zero)

4.1 Systems with low SOC effect

Taking the optimized crystal structure, we have calculated the electronic band structures and projected density of states (PDOS) with and without spin-orbit coupling effects under generalized gradient approximations (GGA) and GGA+SO, respectively. In Table 4. we have compared Fermi energy for systems with and with out SOC. The Fermi energy for $\text {LaB}_{4}$ changes significantly but for other systems change is only at the second decimal place. The main reason is that except for $\text {LaB}_{4}$ (with SOC) the pseudo-potentials in the non-magnetic state does not involve highly localised 4f orbitals and SOC strongly affects 4f orbitals and its effect on other orbitals are only secondary through hybridization with 4f orbitals. In Fig. 3a we have shown the band structure for $\text {LaB}_{4}$ with and without SOC effect. The Fermi level is set to zero for both the cases. As can be clearly observed from Fig. 3a, b except at discrete symmetry points $\Gamma$, Z and R there is no significant SOC effect, especially near the Fermi energy. However SOC lifts degeneracy at special symmetry points. Also, it can be observed that along the path $R-A$ bands are very flat and there is wide gap (of about 4 eV) between the top and bottom bands in this region. Flat bands correspond to non-dispersive localized bands arising mainly from deep core level states. In Fig. 4a, b we have shown projected DOS from various orbitals at a given site in the absence of SOC. At the Fermi level the contribution is predominantly from hybridized B p and La d orbitals. Discrete spectral peaks at $-$32 eV, $-$15 eV etc. arises due to deep core level states like B s, La s and p. In Fig. 4 top panels we show combined PDOS from all atoms as well as the total DOS. When we switch on SOC the B p state gets split into two peaks corresponding to $j=0.5$ and $j=1.5$ configurations. Also La p state gets split into two peaks corresponding to $j=0.5$ and $j=1.5$ configuration. In the presence of SOC there is contribution of 4f state (split into $j=2.5$ and $j=3.5$) at the Fermi energy. This is an unique feature in the case of $\text {LaB}_{4}$ and is absent in all other systems we have considered in this study. PDOS corresponding to 4f is spread over wide range of energy, from $-$10 eV to 7 eV but the total spectral weight is much smaller than the hybridized B p and La d orbitals. Just above the Fermi level, in the range 0 to 7.5 eV, PDOS arises due to strong hybridization between La d orbitals and B s, p orbitals.

Fig. 4

Panel (a) and (b): PDOS of $\text {LaB}_{4}$ in the absence of SOC. Contributions from different orbitals of B and La are shown. Top left panel shows combined contribution from all orbitals. Discrete peaks at $-$32 eV, $-$16.5 eV arises mainly due to La s and La p orbitals while the peak at $-$15 eV due to B p. Panel (c) and (d): PDOS in the presence of spin-orbit coupling effect. The peak at $-$16.5 eV gets split into two peaks with $j=0.5$ and $j=1.5$. Inset of panel (d) shows contribution of spin-split f orbitals about Fermi level. Top right panel shows the combined contribution from all orbitals

In Fig. 5 we summarize the band structure and projected density of states of $\text {CeB}_{4}$ with and without SOC effects. Ce is the first atom in the lanthanides series which contains 4f orbital. In the presence of SOC effect, as can be clearly seen from Fig. 5a, b, otherwise degenerate bands split at $\Gamma$ and R points but the bands remain degenerate at Z point. As in the case of $\text {LaB}_{4}$ there exists non-dispersive flat bands along $R-A-Z$ directions and there is a gap of around 4.5 eV between the top and the bottom bands. In Fig. 5c we show the PDOS arising from various atomic orbitals in the absence of SOC effects. The distinct spectral peaks appearing at $-$14 eV and at $-$17 eV are due to B p and Ce p orbitals, respectively. The extremely narrow spectral peak at $-$34 eV arises due to deep core level Ce s state and B p state. The continuum density of states in the energy window $-$10 eV to 8 eV arises due to hybridized B p, Ce p and d orbitals. In Fig. 5d we show the effect of SOC on PDOS. As in the case of $\text {LaB}_{4}$ there is appearance of extremely narrow peak at $-$19 eV due to splitting of spin-degenerate B p and Ce p orbitals into $j=0.5$ and $j=1.5$ manifolds. The DOS in the energy window $-$10 eV to 8 eV remains largely unaffected as in the case of $\text {LaB}_{4}$ and there is no additional contribution due to spin split Ce 4f orbitals.

Fig. 5

Panel (a): Combined electronic band structure of $\text {CeB}_{4}$ with (red) and with out SOC (black) effects. Panel (b): Same band structure in the narrower energy window about the Fermi level (set to zero). Degenerate bands split at $\Gamma$ and R points. Panel (c) and (d): Partial density of states for $\text {CeB}_{4}$ in the absence and presence of SOC effect, respectively. Distinct spectral peaks appearing at $-$14 eV and at $-$17 eV are due to B p and Ce p orbitals, respectively. The continuum density of states in the energy window $-$10 eV to 8 eV, is due to hybridized B p and Ce p and d orbitals

The band structure and projected density of states of $\text {NdB}_{4}$ with and without SOC effects have been summarised in Fig. 6. As shown in Fig. 6a, b, the spin degenerate bands splits in various regions due to SOC effects present in these systems. Band splitting is more explicit along the direction $\Gamma - Z - R$ and $A-Z$. Very few bands cross the Fermi level and far from Fermi level most of the bands are much less dispersed and nearly flat. In Fig. 6c we show the PDOS from various atoms without SOC effects. As in the earlier cases the distinct spectral peak at $-$15 eV arises due to B p orbitals and the spectral peak at $-$19 eV arises due to B p and Nd p orbitals, respectively. The extremely narrow spectral peak at $-$38 eV arises mainly due to non-dispersive deep core-level Nd s state. However B p orbitals have also contribution towards the peak at $-$38 eV. The continuum density of states in the energy range between $-$10.5 eV to 7.5 eV arises due to hybridized B p and Nd p and d orbitals. Finally, in Fig. 6d we show the PDOS in the presence of SOC effect. The continuum DOS in the range $-$10.5 eV to 7.5 eV remains largely unaffected. However, the peak at $-$19 eV gets split into two peaks at $-$18 eV and $-$21 eV. This arises due to otherwise degenerate B p and Nd p orbitals splitting into $j=0.5$ and $j=1.5$ manifolds due to SOC effects.

Fig. 6

Panel (a): Combined band structure of $\text {NdB}_{4}$ with out (black) and with (red) SOC effect. Panel (b): Same band structure in the narrower energy window about the Fermi level (set to zero). Panel (c) and (d): Partial density of states for $\text {NdB}_{4}$ with out and with SOC effects, respectively. Narrow spectral peak at $-$38 eV arises due to non-dispersive deep core-level Nd s (predominantly) and B p orbitals, respectively. The continuum density of states in the energy range $-$10.5 eV to 7.5 eV arises due to hybridized B p, Nd p and d orbitals

Figure 7 represents the band structure and density of states of $\text {SmB}_{4}$ with and without SOC effects. It is interesting to mention that $\text {SmB}_{4}$ is metallic whereas $\text {SmB}_{6}$ is a Kondo insulator where Sm shows mixed valency $\text {Sm}^{+2}$ and $\text {Sm}^{+3}$ at the ratio 3:7. In Fig. 7a, b we show electronic band structure. Splitting of energy bands in the $\Gamma -Z-R$ direction is much more prominent due to much larger SOC effects. Energy bands along $R-A-Z$ continues to remain flat. In Fig. 7c we show PDOS. The discrete peak arising due to Sm s shifts further down to $-$41 eV. The spectral peak at $-$20.5 eV and $-$14.5 eV arises due to B p, Sm p respectively. The origin of continuum states in the range $-$10.5 eV to 8 eV is same as earlier. When we switch on the SOC effect the spectral peak arising due to p-orbitals of B and Sm gets split into $j=0.5$ and $j=1.5$ states (Fig. 7d) and the corresponding spectral peaks appears at $-$22.75 eV and $-$19 eV, respectively.

Fig. 7

Panel (a): Combined band structure of $\text {SmB}_{4}$ in the absence (black) and presence (red) of SOC effect, respectively. Panel (b): Same band structure in the narrower energy window about the Fermi level (set to zero). Panel (c) and (d): The partial density of states of $\text {SmB}_{4}$ with out and with SOC effect, respectively. The isolated spectral peaks at $-$20.5 eV and $-$14.5 eV arises due to B p, Sm p respectively. The origin of deep core level state at $-$41 eV and the continuum density of states around the Fermi level is same as earlier

4.2 Systems with large SOC effect

In the previous section we have considered SOC effects on 4 canonical systems with relatively low SOC effect. In this section we consider SOC effects on the electronic band structure of 4 canonical systems with relatively large SOC strength. In Table. 5 we have summarized the Fermi energy in the absence and presence of SOC effects. The change in the Fermi energy is only at the third decimal place which is consistent with the size of the SOC strength. In $\text {LuB}_{4}$ there is no change in the Fermi energy in the presence of SOC effect. This is mainly due to significant change in the lattice parameters under structural relaxation in SCF calculation.

Table 5 Effect of spin-orbit coupling on Fermi energy of systems with relatively large SOC strength

In Fig. 8a, b we have shown the band structure and partial density of states for $\text {HoB}_{4}$ with and without SOC effects. The SOC effects on the splitting of degenerate energy bands are prominent for wider range of energies. The energy bands far away from the Fermi energy are also affected due to much stronger SOC effects. Degeneracy lifting effect along the $\Gamma -Z-R$ direction is now quite explicit. Fermi level crossing bands along the $Z-R$ direction are also affected. However, flat bands along the $R-A-Z$ path are not affected by the SOC effect as earlier. In Fig. 8c we show partial DOS due to various atoms in the absence of SOC effects as earlier. The continuum DOS in the range $-$10.5 eV to 7.5 eV arises due to strong hybridization between d orbitals of Ho and p orbitals of B atoms. The spectral peak at $-$14 eV arises due to p orbitals of B atoms while the peak at $-$24 eV arises due to Ho p orbital. Extremely narrow and isolated peak at $-$48 eV arises due to deep core level s orbital of Ho atom. In Fig. 8d, we show the effect of SOC on PDOS. There is enhancement of PDOS around the Fermi level. The spectral peak at $-$24 eV gets split into two peaks at $-$27.5 eV and $-$22.5 eV with $j=0.5$ and $j=1.5$ configuration.

Fig. 8

Panel (a): Electronic band structure of $\text {HoB}_{4}$ without (black) and with (red) SOC effect. Panel (b): Same band structure in the narrower energy window about the Fermi level (set to zero). Panel (c) and (d): Projected DOS of $\text {HoB}_{4}$ in the absence and presence of SOC effect. The isolated narrow peak at $-$48 eV arises due to deep core level Ho s states while the peak at $-$14 eV and $-$24 eV arises due to p orbital of B and Ho atoms, respectively

Figure 9 indicates the band structure and projected density of states of $\text {ErB}_{4}$ in the presence and absence of SOC effects. As seen in Fig. 9a, b, spin-split bands are quite visible in the energy range $-$4 eV to $-$6 eV along the $\Gamma -Z-R$ direction. Band splitting effects near the Fermi level also starts showing up. Projected density of states as shown in Fig. 9c follows similar trend as in the case of other tetra-borides. The continuum density of states in the range $-$10 eV to 7 eV arises from the hybridized B p and Er d orbitals. The spectral peak due to Er s is now at $-$51 eV. The spectral peak at $-$24.5 eV is due to B p and Er p core level states. The smaller peak arising due to B p is now at $-$15 eV. As shown in Fig. 9d, inclusion of SOC effect causes splitting of the $-$24.5 eV peak into $j=0.5$ and $j=1.5$ states situated at $-$28.5 eV and $-$23 eV, respectively.

Fig. 9

Panel (a): Combined band structure of $\text {ErB}_{4}$ with (red) and without SOC (black) effect. Panel (b): Same plot in a narrower energy window about the Fermi level (set to zero). The spin-split bands appearing in the energy range $-$4 eV to $-$6 eV along the $\Gamma -Z-R$ direction. Panel (c) and (d): Projected DOS of $\text {ErB}_{4}$ in the absence and presence of SOC effect. The spectral peak due to core level Er s is now at $-$51 eV. The peak at $-$24.5 eV is due to Er p (predominantly) and B p orbitals. The distinct peak at $-$15 eV is solely due to B p orbital. Inclusion of SOC effect causes splitting of the $-$24.5 eV peak into $j=0.5$ and $j=1.5$ states situated at $-$28.5 eV and $-$23 eV, respectively

Fig. 10

Panel (a): Combined electronic band structure of $\text {TmB}_{4}$ without (black) and with (red) SOC effect. Panel (b): Same band structure in the narrower energy window about the Fermi level (set to zero). Panel (c) and (d): Projected DOS of $\text {TmB}_{4}$ in the absence and presence of SOC effect, respectively. The isolated peak due to Tm s is now at $-$52.5 eV. In the presence of SOC effect the $-$25.5 eV peak split into peaks at $-$29.5 eV and $-$23.5 eV, corresponding to $j=0.5$ and $j=1.5$ configurations, respectively

Fig. 11

Panel (a): Combined electronic band structure of $\text {LuB}_{4}$ without (black) and with (red) SOC effect. Panel (b): Same band structure in the narrower energy window about Fermi level (set to zero). Panel (c) and (d): Projected DOS of $\text {LuB}_{4}$ in the absence and presence of SOC effect, respectively. The isolated Lu s spectral peak is pushed further down to $-$56 eV. The peak due to B p and Lu p is now at $-$27 eV. In the presence of SOC effect the peak at $-$27 eV gets split onto two peaks at $-$32 eV and $-$25 eV with $j=0.5$ and $j=1.5$, respectively

In Fig. 10 we summarize the electronic band structure and projected density of states of $\text {TmB}_{4}$. In an earlier study band structure for $\text {TmB}_{4}$ in the anti-ferromagnetic state was reported. So the present study is relevant in the paramagnetic state of this system. As shown in Fig. 10a, b energy bands far from the Fermi level are strongly affected due to SOC effect. Energy bands in the energy range $-$4 eV to $-$6 eV show significant splitting especially along the $\Gamma -Z-R$ direction. Similar features can also be observed in the window 1 eV to 2 eV. Some of the Fermi level crossing bands show degeneracy lifting effects near Fermi level. The spectral features are similar to the other tetraborides. The peaks arising due to Tm s, p and B p are at $-$52.5 eV and $-$25.5 eV respectively. The continuum DOS in the energy range $-$11 eV to 7 eV arises due to hybridization between Tm p, d orbitals and B p orbitals. Inclusion of SOC, as shown in Fig. 10d, causes splitting of the $-$25.5 eV spectral peaks into a $j=0.5$ peak at $-$29.5 eV and a $j=1.5$ peak at $-$23.5 eV.

Finally, in Fig. 11 we show our results for $\text {LuB}_{4}$. Incidentally Lu is the last member of the lanthanide series with completely filled 4f orbitals. As in the case of $\text {TmB}_{4}$ there is strong SOC effects on the energy bands in the energy window $-$6 eV to $-$4 eV as well as in the window 1 eV to 2 eV. SOC effects on the Fermi level crossing bands near the Fermi energy are less compared to $\text {TmB}_{4}$. These features are well summarised in Fig. 11a, b. In Fig. 11c, d we show the projected DOS in the absence and presence of SOC effects, respectively. The spectral peak at $-$56 eV is due to Lu s orbital while the peak at $-$15 eV is due to B s and p. There is a strong peak at $-$27 eV arising due to Lu p orbital. The height of this peak is much more than the other two discrete peaks. The continuum of density of states around the Fermi level arises due to hybridized B p and Lu d orbitals. In the presence of SOC the peak at $-$27 eV gets split onto two peaks at $-$32 eV and $-$25 eV characterized by $j=0.5$ and $j=1.5$, respectively.

To summarize, we have systematically studied electronic band structure and partial DOS for 4 canonical systems $\text {LaB}_{4}$, $\text {CeB}_{4}$, $\text {NdB}_{4}$ and $\text {SmB}_{4}$ with relatively weak spin-orbit coupling strength and 4 canonical systems $\text {HoB}_{4}$, $\text {ErB}_{4}$, $\text {TmB}_{4}$ and $\text {LuB}_{4}$ with relatively large spin-orbit coupling strength. In the absence of SOC effect 3 discrete low energy spectral peaks, well separated from the continuum of states around the Fermi level, are common features. The discrete peaks, with increasing order of energy, arises due to rare-earth s states, rare-earth p+ B p and B p states whereas the continuum DOS arises due to hybridized B p and rare-earth d orbitals. In the presence of SOC effect the discrete middle peak splits into two peaks with $j=1.5$ and $j=0.5$ configurations. Except for $\text {LaB}_{4}$ the continuum DOS around the Fermi level remains largely unaffected. For $\text {LaB}_{4}$ additional states due to 4f orbitals appears around the Fermi level. In Fig. 12 we have plotted energy splitting, $\Delta E_{\text {gap}}$, between the $j=1.5$ and $j=0.5$ peaks as a function of atomic number, Z, of the rare-earth atom. The splitting gap is found to be proportional to $Z^{n}$ with $n=4.82$. It is interesting to mention that the SOC strength is proportional to $Z^4$ (in hydrogen atom model) and the energy splitting of the discrete middle peak is roughly proportional to the strength of the spin-orbit coupling. So, the behaviour of $\Delta E_{\text {gap}}$ is consistent with atomic level splitting due to SOC effect.

Fig. 12

Energy splitting of the discrete peak arising from rare-earth p (predominantly) and boron p orbital due to spin-orbit coupling effect. The splitting gap, $\Delta E_{\text {gap}}$ shows power law behaviour, $\Delta E_{\text {gap}}\propto Z^{n}$, (solid green line) with $n=4.82$ and Z is the atomic number of the rare-earth atom involved

5 Conclusion

We have investigated the electronic structure of $\text {RB}_{4}$ with non-magnetic ground state. The electronic band structure shows splitting due to interaction between spin and angular momentum. The bands splitting has been interpreted with the help of PDOS. It has been observed that the two new branches for p-orbital appearing due to SOC effect. In case of $\text {LaB}_{4}$ with SOC, the contribution of 4f orbitals to the DOS about the Fermi level has been observed. It has also been observed that the splitting gap ($\Delta E_{\text {gap}}$) is proportional to $Z^{n}$ with n =4.82.

The role of magnetic ordering and strong correlation effects present in these narrow orbital systems will be considered in a future work. Also, secondary effects of spin-orbit coupling effects (through electron-lattice coupling) on the mechanical and thermodynamic properties will be investigated in a subsequent work.