Insights of $\hbox {XPt}_2$ ($\hbox {X}=\hbox {Eu}$ and Gd) intermetallic systems: An ab-initio approach

Abstract

Rare earth (RE)-based $\hbox {MgCu}_2$-type intermetallic compounds are studied by first-principles calculations to search their spintronic applications and thermodynamic stability. We found in our observations that both $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ have half-metallic properties. The band gap arises in spin-down channel which is found to be enhanced when we move from $\hbox {EuPt}_2$ (0.91 eV) to $\hbox {GdPt}_2$ (1.04 eV). From magnetic properties we got to know that the magnetic moments of RE and Pt are opposite in direction and total magnetic moment is found to be $7.01\,\mu _{\mathrm {B}}$ and 4.1 $\mu _{\mathrm {B}}$ for $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ respectively. Presence of 5$d^1$ electron in Gd valance shell is the reason for this difference in magnetic moments. No negative frequency has been observed in the phonon dispersion curve of both systems indicating the dynamic stability of $\hbox {MgCu}_2$-type structure. Several thermodynamical potentials are also explored in the present study using quasiharmonic approximation. The half-metallicity of dynamically stable $\hbox {REPt}_2$ systems is appropriate for spintronic applications.

1 Introduction

Intermetallic compounds have specific crystallographic and electronic structures that generally result in different physical and chemical properties from the ones observed in substitutional alloys. From the point of view of their chemical reactivity, the surfaces of intermetallic compounds can show good resistance towards oxidation [1]. In systems containing transition metals (TM), the electron localisability approach has proven to be a powerful tool to explore chemical bonding [2,3,4,5,6,7,8]. Our paper in particular focusses on Laves phases of intermetallic compounds which consist of nearly 1400 representative compounds with the ideal composition $\hbox {AB}_2$. An intermetallic compound is classified as a Laves phase purely on the basis of the geometry of the crystal structure. Possible structures of Laves phase are of several types: cubic $\hbox {MgCu}_2$ (C15), hexagonal $\hbox {MgZn}_2$ (C14), hexagonal $\hbox {MgNi}_2$ (C36) and orthorhomic $\hbox {CeCu}_2$-type structures [9,10,11,12,13]. These compounds were discovered in 1927 by James Friauf [14, 15]. Fritz Laves structures were studied exhaustively in the 1930’s [16]. The name Fritz Laves structure or generally Laves phases, was derived from the names of the two researchers, Friauf and Laves. These phases are characterised by a mixture ratio of two specific metal elements, which distinguishes them from conventional metal intermetallics. They are compact ordered structures with the chemical formula $\hbox {AB}_2$ for the stoichiometric compound and an ideal ratio of radii $r_{\mathrm {A}}/r_{\mathrm {B}}$ around $(3/2)^{1/2}$ [17]. The study of Laves phase has disclosed several issues in our understanding of intermetallic compounds. Better chemical bonding and stability than steel alloys can be expected from these materials [18]. Density functional theory (DFT)-based studies have been performed to study various properties such as electronic and mechanical features of Laves phase materials. Using linear muffin-tin orbital (LMTO-NFP), two groups have studied these materials. Mayer et al [19] studied $\hbox {MAl}_2$ (M$=$Ca, Y, Sc and La) and $\hbox {MCr}_2$ (M$=$Ti, Zr, Nb and Ta), Kumar et al [20, 21] studied $\hbox {MCr}_2$ (M$=$Ti, Zr, Ta, Nb, Sc, Y, La). Similarily, Vienna ab-initio simulation package (VASP) has been employed by several groups to study Laves phase intermetallic materials. Tao et al [22] studied $\hbox {MAl}_2$ (M $=$ Sc, Y, La, Ce-Lu), Ouyang et al [23] studied $\hbox {MMg}_2$ (M$=$La, Ce, Pr, Nd, Pm, Sm, Gd), Kal et al [24] studied $\hbox {MZn}_2$ (M$=$Ca and Sr) and $\hbox {MAl}_2$ (M$=$Sr and Ba). The results indicate that DFT calculations provide realistic results which are difficult to obtain experimentally [13]. New niobium beryllide ($\hbox {Nb}_3$Be) with the A15-type structure has been synthesised by Tuleushev et al by thermal treatment of the amorphous film system [25]. He reported that the superconductivity in $\hbox {Nb}_3$Be is 10 K which is quite large [26]. Phases that include ferromagnetic transition metals Fe, Co and Ni are of particular importance due to their interesting magnetic behaviour. Moreover, RE-based compounds, e.g. $\hbox {TbFe}_2$ and $\hbox {SmFe}_2$, have been studied widely because of their excellent magnetostrictive properties [27]. As a result, their dimensions change during the magnetisation process allowing their application in sensors, actuators and transducers. The solid solution of $\hbox {TbFe}_2$ and $\hbox {DyFe}_2$ (Terfenol-D) is a prominent example of a magnetostrictive material that was developed by the Naval Ordnance Laboratory in the 1970s [28, 29]. All the aforementioned materials that are of interest for their use in devices comprise RE elements. Taking inspiration from the above findings, we are presenting our study of RE-based intermetallic compounds $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ to explore their electronic, magnetic, phonon and thermodynamic features using DFT calculations.

2 Computational details

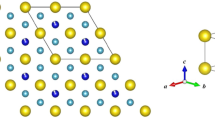
The general structure of $\hbox {MgCu}_2$-type cubic compound is given in figure 1 where X (Eu, Gd) occupies (0,0,0) site and Pt occupies (0.625, 0.625, 0.625) position. Quantum Espresso code [30] based on DFT [31] was employed to study the spin-dependent calculations. The generalised gradient approximation (GGA) of Perdew et al (PBE) [32] has been used to obtain accurate information of electronic and magnetic structures of the material. Projector augmented wave (PAW) [33] pseudopotentials with PBE were used for each calculation. A kinetic energy cut-off of 780 eV is used for plane-wave basis set for each calculation. The Monkhorst–Pack [34] meshes of $11\times 11\times 11$ was used for the Brillouin zone (BZ) sampling of conventional unit cell. Structural optimisation was performed with convergence better than 1.0 meV for total forces and ground-state energy. Phonon calculation was performed at $4\times 4\times 4$ irreducible  q-point grid, centred at $q = (0, 0, 0)$ to study the dynamic stability of the system. Quasiharmonic approximation has been used to study the thermodynamic properties.

Fig. 1

Crystal structure of $\hbox {XPt}_2$; red balls indicate RE atoms (Eu, Gd) and yellow balls indicate Pt atoms.

Fig. 2

Electronic band structures of $\hbox {EuPt}_2$ in spin-up and spin-down states. Fermi level is set to zero energy on the y-axis.

Fig. 3

Partial density of states of $\hbox {EuPt}_2$ in spin-up and spin-down states. Fermi level is set to zero energy on the x-axis.

3 Results and discussion

3.1 Electronic structure

The electronic properties are calculated along high symmetry directions with partial density of states (PDoS) of each atom. Electronic band structure of $\hbox {EuPt}_2$ is shown in figure 2 with spin-up and spin-down states. We find here that in spin-up channel, $\hbox {EuPt}_2$ is having a band crossing the Fermi level $E_f$ while a clear semiconducting band gap of 0.91 eV is present in spin-down channel. From these observations, it can also be concluded that electrons are more localised in spin-down state than in spin-up state. This finding brings this RE intermetallic compound in the group of half-metallics. To check the atom responsible for the metallicity in spin-up state we shall now analyse its PDoS given in figure 3. Here we can find that 5d states of Eu are causing metallicity in spin-up state while the band gap in spin-down state is coming between Eu 5d and Pt 5d states. Eu 4f states are observed after $-0.8$ eV which are far enough from $E_f$. The electronic band structure of $\hbox {GdPt}_2$ is shown in figure 4. Here we can clearly see that it is also following a similar trend as $\hbox {EuPt}_2$, i.e. there is a band crossing $E_f$ in spin-up state while a band gap of 1.04 eV in spin-down state. This indicates the half-metallic character of the material with localised electrons in spin-down state. It is generally considered that PBE functional underestimates the band gap of the systems. Thus, to confirm the half-metallic character of our systems, we have performed HSE calculations as well. The obtained band structures are given in figure S1 (Supplemetary Information). To find the atom due to which the metallic nature is exhibited in spin-up state, we shall now study the PDoS of $\hbox {GdPt}_2$ as given in figure 5. On observing the PDoS, we can say that 5d states of Gd are responsible for the metallic nature in spin-up channel while 6p and 5d states of Pt are responsible for the band gap in spin-down state. The electronic configuration of Eu is 4$\hbox {f}^7$ 6$\hbox {s}^2$, of Gd is 4$\hbox {f}^7$ 5$\hbox {d}^1$ 6$\hbox {s}^2$ and of Pt is 4$\hbox {f}^{14}$ 5$\hbox {d}^9$ 6$\hbox {s}^1$. As we move from Eu to Gd 1 electron of 5d states is contributing in the electronic state of the material. The ionic radii of Gd is smaller than Eu, and due to its relatively large size, the bond length between Gd and Pt got reduced and charge transfer between the atoms becomes easy. As the electronegativity of Pt is greater than Gd, the flow of charges will take place from Gd to Pt. The 5d electron of Gd will flow to the valance band of Pt and hence we get relatively high peaks in the valence band region of 5d Pt states compared to the 5d states of Gd in figure 4. This charge transfer is the reason of increased band gap in $\hbox {GdPt}_2$.

Fig. 4

Electronic band structure of $\hbox {GdPt}_2$ in spin-up and spin-down states. Fermi level is set to zero energy on the y-axis.

Fig. 5

Partial density of states of $\hbox {GdPt}_2$ in spin-up and spin-down states. Fermi level is set to zero energy on the x-axis.

3.2 Magnetic properties

In the present work, we have studied the magnetic properties of$\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ where GGA approximation is used to analyse the local magnetic moment of atoms and to find the possible exhibition of magnetism. The local magnetic moment observed in Eu is 7.01 $\mu _{\mathrm {B}}$ and in Pt is $-0.1991$ $\mu _{\mathrm {B}}$. The negative sign of the magnetic moment in Pt shows that it is trying to reduce total magnetic moment of the system which is found to be 7.44 $\mu _{\mathrm {B}}$. This can be seen in the spin direction of both atoms and their alignment with respect to the z-axis in figure 6. Here we can clearly see that Pt has antiparallel spin similar to Eu. Similarly, in $\hbox {GdPt}_2$, local magnetic moment of Gd is recorded as $4.1\,\mu _{\mathrm {B}}$ while for Pt it is $-0.0995$ $\mu _{\mathrm {B}}$. We find a large difference between the local magnetic moment of Eu and Gd. This may be due to the presence of 5$\hbox {d}^1$ electron in the valance shell of Gd which is the main bearer of magnetic moment in $\hbox {GdPt}_2$ while in $\hbox {EuPt}_2$ the magnetic moment is mainly due to 4$\hbox {f}^7$ electron. The total magnetic moment of $\hbox {GdPt}_2$ is found to be 4.34 $\mu _{\mathrm {B}}$. The variation of local and total magnetic moment of each atom in both compounds with respect to lattice constant is shown in figure 7. We can see here that, in $\hbox {EuPt}_2$ the magnetic moment of Eu is increasing linearly with increasing lattice constant while a decreasing trend is noticed for Pt and an increment is seen in the total magnetic moment of the system. For $\hbox {GdPt}_2$ also we can see similar pattern for local and total magnetic moments.

Fig. 6

Direction of magnetic moment along the z-axis.

Fig. 7

Variation of magnetic moment with respect to lattice constant.

3.3 Phonon properties

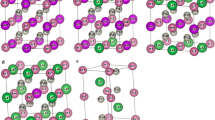
It is important to know the dynamic stability of the material. To do so, phonon dispersion calculation plays an important role. With the help of phonon dispersion curves, we have easily analysed several properties like acoustic, thermodynamic, dynamical etc. In particular, a dynamically stable system will have positive frequency along high-symmetry directions, otherwise, it will be dynamically unstable. In figure 8, we can see the phonon dispersion curves of $\hbox {EuPt}_2$ (left) and $\hbox {GdPt}_2$ (right). In both the curves, negative frequency bands are not found, revealing the dynamic stability of the structure. The high-frequency bands, i.e. optical modes, come from the atoms having lighter mass, i.e. RE atoms Eu and Gd while the heavy atom Pt mainly contributes in the acoustic modes. The mode symmetry point group found in $\hbox {EuPt}_2$ is $C3_v$ with irreducible representation $A_1+ E$ having $A_1$ at 15.8 $\hbox {cm}^{-1}$ and E at 58.3 $\hbox {cm}^{-1}$. The direction of atomic displacement at $A_1$ and E are shown in figure 9a. The displacements of Eu atoms are found to be in the X–Z plane whereas Pt atom has the displacement in opposite direction. Similar point group is found in $\hbox {GdPt}_2$ as well with $A_1$ at 46.2 $\hbox {cm}^{-1}$ and E at 37.9 $\hbox {cm}^{-1}$. The directions of atomic displacements are given in figure 9b where the Gd atoms show displacement along the X–Y plane with Pt in opposite direction in $A_1$ and X–Z plane displacement is shown by Gd and Pt as well in E.

Fig. 8

Phonon dispersion curve of $\hbox {EuPt}_2$ (left) and $\hbox {GdPt}_2$ (right).

Fig. 9

Direction of atomic displacement of (a) $\hbox {EuPt}_2$ and (b) $\hbox {GdPt}_2$ in mode symmetry point group $C3_v$.

3.4 Thermodynamic properties

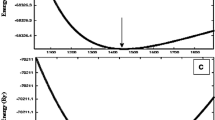
Thermodynamic potentials provide a complete description of the system’s equilibrium. Here we have obtained thermodynamical potentials such as Helmholtz free energy (vibrational energy) (F), internal energy (E) and specific heat $C_v$ at zero pressure via phonon vibrations employing quasiharmonic approximation (QHA) [35]. The mathematical expressions for these potentials are given in [36] which are dependent on phonon frequency. The calculated thermodynamic potentials of $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ are given in figure 10 in the temperature range of 0–500 K. It is evident from figure 10 that internal energy and specific heat increase while vibrational energy decreases with temperature. The increment in specific heat at low temperature is quite higher than internal energy which indicates that the specific heat is more sensitive towards variation in temperature than internal energy. In general, both phonon (lattice) and electron give their contributions in specific heat where phonon contribution is more dominant at low temperatures while electronic contribution is dominant at relatively higher temperatures. From figure 10, it is clear that at low temperature specific heat at constant volume $C_v$ obeys $T^3$ law and becomes temperature-independent at high temperatures and finally reaches a constant value 6.83 and 5.79 J/K for $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ respectively which is known as Dulong–Petit limit [37]. At low temperature, vibration of atoms is maximum which decreases with increasing temperature. Values of thermodynamical potentials for $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ at room temperature are listed in table 1. The Debye temperature ($\theta _{\mathrm {D}}$) is a very crucial thermodynamic parameter for measuring physical properties of crystals such as specific heat, thermal expansion, melting point etc. [38]. Hence, it is necessary to determine the Debye temperature of our compounds. In Debye theory, the Debye temperature is the temperature at which a crystal shows highest normal mode of vibration. Hence, Debye temperature $\theta _{\mathrm {D}}$ is the highest temperature that can be achieved due to a single normal lattice vibration. The calculated Debye temperature of $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ are listed in table 1.

Fig. 10

Thermodynamic potentials of $\hbox {EuPt}_2$ (top) and $\hbox {GdPt}_2$ (bottom) in the temperature range 0–500 K.

Table 1 Thermodynamical potentials of $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ at room temperature (300 K).

4 Conclusions

In summary, in the present work, we have extensively investigated the electronic, magnetic, phonon and thermodynamic properties of RE-based $\hbox {MgCu}_2$-type Laves phase. We have found that both compounds ($\hbox {EuPt}_2$ and $\hbox {GdPt}_2$) exhibit half-metallic character. There exist a band gap in the spin-down state which increases when we move from $\hbox {EuPt}_2$ (0.91 eV) to $\hbox {GdPt}_2$ (1.04 eV). Magnetic properties showed that the magnetic moments of RE and Pt are aligned in antiparallel fashion. Total magnetic moments of $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ are observed to be 7.44 $\mu _{\mathrm {B}}$ and 4.34 $\mu _{\mathrm {B}}$ respectively. Both structures are found dynamically stable with no negative frequency in the phonon dispersion curve. Debye temperatures of $\hbox {EuPt}_2$ and $\hbox {GdPt}_2$ are found to be 67.09 K and 52.98 K respectively.