Elastic and thermodynamic properties of cubic perovskite type $\hbox {NdXO}_{3}$ (X=Ga, In)

Abstract

The elastic and thermodynamic properties of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ with the space group Pm$\bar{3}$m (no. 221) are studied for the first-time using density functional theory. The computed equilibrium lattice constants at stable phase are found to be 3.89 and 4.14 Å which are in a good agreement with literature. Elastic constants are computed to evaluate mechanical behaviours of materials. By applying Born stability criteria for elastic constants, it is found that both materials are mechanically stable. Moreover, bulk and shear modulus, Poisson’ ratio, Cauchy pressures, and Young modulus are examined. Ductile and brittle behaviour analysis indicates that both materials are ductile in nature. The thermodynamic properties such as thermal expansion coefficient, Grüneisen parameter, bulk modulus, specific heat capacities, and entropy are computed at a temperature range of 0–1000 K. The calculated elastic and thermodynamic properties can serve as a reference for future investigations as some of these physical properties can be difficult to determine experimentally.

Graphic abstract

1 Introduction

Perovskite family shown as $\hbox {ABO}_{3}$ is one of the important representative of inorganic compounds owing to their large variety of properties such as piezoelectricity, ferroelectricity, and thermal and chemical stability [1]. These types of materials are used in many areas; capacitors, ultrasonic transducers, pyroelectric surveillance systems, high-temperature superconductors, interconnect material for solid oxide fuel cells, etc. [1, 2]. In addition, $\hbox {NdGaO}_{3}$ is reported to be a good substrate for high-temperature super-conducting thin films [3]. Electronic structure and magnetic properties of $\hbox {NdGaO}_{3}$ were investigated using density functional theory by several researchers [1, 4]. Half-metallic ferromagnetic properties of cubic perovskite $\hbox {NdInO}_{3}$ were studied recently by Monir [5] and reported that the biggest contribution to the total magnetic moment comes from Nd atoms. In another study carried out by Monir et al. [4], it was found that for $\hbox {NdGaO}_{3}$, half-metallic ferromagnetism is caused by hybridisation between O-2p and Nd-4f orbitals. The electronic and magnetic behaviour of $\hbox {NdInO}_{3}$ was also investigated by Butt et al. [6]. A half-metallic nature due to a crossover of valence and conduction band in spin up states and a band gap in spin down states was reported. Since these materials are good candidates for spintronics, optoelectronic devices, substrate materials, and high-temperature applications. It is worthwhile to investigate their elastic properties, anisotropy, and thermodynamic properties such as specific heat capacity thoroughly. Thus, this study aims to reveal elastic and thermodynamic properties of perovskite type cubic $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ using first-principles calculations. Many critical parameters such as bulk, Shear modulus, Young’s modulus, and Poisson’s ratio are computed along with directional anisotropy. To accomplish this aim, density functional theory (DFT) was adopted. Density functional theory can offer great deal of information about materials. For example, calculation of total energy or energy difference between perfect and distorted crystals can reveal thermodynamic properties. Moreover, elastic and bonding properties such as ductility and brittleness can be obtained from the response of materials against deformation under stress. Therefore, density functional theory was adopted in this study to reveal elastic and thermodynamic properties of cubic perovskite type $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$.

2 Method

The calculations were conducted using density functional theory and pseudopotential plane wave’s method within Quantum-Espresso software package [7]. The harmonic and quasi-harmonic computations were done by adopting thermo pw package. All the computations were carried out using Projector augmented-wave (PAW) pseudopotentials with PBE functional which were obtained from the pslibrary [8]. Brillouin zone integration was done using a 8 $\times$ 8 $\times$ 8 k-point mesh. The cut-off energy was taken as 60 Ry for the expansion of electronic wave functions. The kinetic energy was set to 600 Ry for evaluation of electronic charge density. Methfessel–Paxton smearing method was adopted to carry out integration up to Fermi level with a smearing parameter of 0.02 Ry [9]. The materials’ elastic constants were obtained from energy difference between distorted and undistorted lattice cell using the technique of stress-finite strain as implemented in thermo pw package within a strain range of − 0.0075 to $+$ 0.0075 at a step of 0.005. The details of this implementation were given in ref [10]. The equations that were used to obtain elastic constants are given in [11, 12]. Using elastic constants, several parameters were obtained.

The Bulk modulus of materials are obtained as follows:

$$\begin{aligned} B=\frac{C_{11}+{2C}_{12}}{3}. \end{aligned}$$

(1)

The shear modulus (G) is the ratio of shear stress to shear strain and given by

$$\begin{aligned} G=\frac{G_\mathrm{v}+G_\mathrm{R}}{2}, \end{aligned}$$

(2)

where $G_\mathrm{v}$ is Voigt’s shear modulus and $G_\mathrm{R}$ is Reuss’s shear modulus. $G_\mathrm{v}$ and $G_\mathrm{R}$ correspond to upper and lower bounds of G, respectively, and are expressed as

$$\begin{aligned} G_\mathrm{v}= & {} \frac{C_{11}-C_{12}+3C_{44}}{5} \end{aligned}$$

(3)

$$\begin{aligned} G_\mathrm{R}= & {} \frac{5(C_{11}-C_{12})C_{44}}{3\left( C_{11}-C_{12}. \right) +4C_{44}} \end{aligned}$$

(4)

The anisotropy factor (A) is given as

$$\begin{aligned} A=\frac{2C_{44}}{(C_{11}-C_{12})}. \end{aligned}$$

(5)

As the value of A becomes closer to unity (1), the material becomes isotropic. For an isotropic material, Young’s modulus can be calculated using bulk modulus (B) and shear modules (G) as follows:

$$\begin{aligned} E=\frac{9BG}{3B+G}. \end{aligned}$$

(6)

In addition, the Poisson’s ratio can be computed using Young’s and bulk modulus as follows:

$$\begin{aligned} \sigma =\frac{1}{3}\left( 1-\frac{E}{3B}\right) . \end{aligned}$$

(7)

2D directional change of compressibility, Poisson’s ratio, and Shear and Young Modulus of materials are computed using ELATE code [13]. Also, thermodynamic computations to get variables such as heat capacity and thermal expansion coefficient were done using the Debye Model within Gibbs2 code described in [14].

3 Results and discussion

3.1 Structural and elastic properties

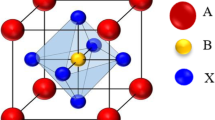
The schematic representations of crystal structures of ideal perovskite type $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ materials with the space group $Pm\bar{3}m$ (no.221) are demonstrated in Fig. 1. The structure has one formula per unit cell with the Wyckoff positions; gallium (Ga)/Indium (In) atoms are in the middle (1/2, 1/2, 1/2), and neodymium (Nd) atoms are at corners (0, 0, 0) and oxygen (O) atoms are at (0, 1/2, 1/2), (1/2, 0,1/2), (1/2, 1/2, 0) positions. Total energies are calculated for different volumes close to the equilibrium positions, and then, these data are fitted to well-known Murnaghan’s equation of state [15] to reveal ground state properties of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$. Also, the equilibrium lattice constants of materials are obtained by optimisation and presented in Table 1. The obtained equilibrium lattice constants are then compared to available data in the literature. The computed lattice constants of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ are in well accordance with the given references [4, 6, 16] in Table 1.

Fig. 1

Crystal structure representative of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$

Table 1 The calculated lattice constants ($a, {\AA }$), bulk modulus ($B, \hbox {GPa}$), elastic constants ($C_{\mathrm {11}}$,$C_{\mathrm {12}}$, $C_{\mathrm {44,}} \hbox {GPa}$), and Cauchy Pressures ($C_{\mathrm {P}})$ of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$

Table 2 The calculated bulk modulus ($B, \hbox {GPa})$, shear modulus (G, GPa), B/G ratios, anisotropy factor (A), Poisson’s ratios ($\sigma )$and Young’s modulus ($E, \hbox {GPa}$), Vickers hardness (GPa), and Debye Temperatures ($\varTheta _\mathrm{D}$, K) of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$

Table 3 The calculated maximum and minimum values of Young’s modulus (E), linear compressibility ($\beta$, $\hbox {TPa}^{\mathrm {-1}})$, shear modulus (G), and Poisson’s ratios ($\sigma )$ of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$

Fig. 2

2D curves of Lineer compressibility of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$

Fig. 3

2D curves of Young Modulus of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$

By knowing the elastic constants, several critical parameters can be derived and extensive information such as mechanical stability, ductility, and anisotropic behaviour can be extracted [17]. There are three elastic constants defined for a cubic symmetry. These independent elastic constants are, $C_{11}, C_{12}$, and $C_{44}$ and given in Table 1 for $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$. The well-known Born mechanical stability criteria is given as [18]

$$\begin{aligned} {(C}_{11}\!-\!C_{12}) \!>\!0,\quad C_{11}\!>\!0,C_{44}>0,\quad (C_{11}\!+\!2C_{12})>0.\nonumber \\ \end{aligned}$$

(8)

Equation 1 is also deducted as

$$\begin{aligned} C_{12}<B<C_{11}. \end{aligned}$$

(9)

The calculated elastic constants of materials are all positive and follow the rules given in Eqs. 8 and 9, indicating that both $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ fulfil the well-known Born mechanical stability criteria. Thus, these materials can be classified as mechanically stable materials. Further examination has been carried out on elastic constants by evaluation of unidirectional compression along x-axis using $C_{11}$ [19]. Table 1 indicates that both materials have much higher $C_{11}$ value than $C_{44}$ value. This implies that both materials will show higher resistance towards unidirectional compression than resistance against shear deformation compression. By comparing $\hbox {NdGaO}_{3}$ with $\hbox {NdInO}_{3}$, it can be said that $\hbox {NdInO}_{3}$ will show less resistance against unidirectional compression compared to $\hbox {NdGaO}_{3}$ due to having lower value of $C_{11}$ [20].

Fig. 4

2D curves of shear modulus of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ (The green and blue surfaces are the minimal and maximal positive values the elastic property takes)

The response of material’s towards external stress is determined by its elastic constants which are related to the material’s mechanical failure. Based on elastic constants of materials, several polycrystalline elastic properties are computed and given in Table 2. The details of derivations are presented in [20]. Bulk modulus of a material is considered to be the resistance towards shape change under applied pressure. Therefore, it can be used to evaluate bond strength, since it is related to cohesive and binding energies of atoms. The resistance towards shape change becomes stronger as bulk modulus of material increases [21]. The bulk modulus of $\hbox {NdGaO}_{3}$ is higher than that of $\hbox {NdInO}_{3}$, indicating that $\hbox {NdGaO}_{3}$ displays higher resistance to shape change under pressure compared to $\hbox {NdInO}_{3}$ which is also an indication of mechanical hardness. Additionally, shear moduli (G) of materials are computed and compared. Shear modulus is also a degree of resistance towards shear stress and the higher value represents more directional bonding between atoms. By comparing $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$, it is clear that $\hbox {NdGaO}_{3}$ has the strongest capacity to resist deformation and volume change under pressure, indicating the existence of covalent bonding cohesion between atoms and a rigid structure [22].

The ductility and brittleness of the materials are investigated via Cauchy Pressures and the ratio of bulk modulus to shear modulus (B/G). The angular characteristics of materials can be estimated by using Cauchy pressures [23]. A negative Cauchy pressure suggests directional bonding, angular character, and brittleness, whereas a positive Cauchy pressure describes ductility and metallic nature. Additionally, the ratio of B/G is considered to evaluate ductility and brittleness of materials according to Pugh‘s criteria [24]. As Pugh suggested that if ratio of B/G is higher than 1.75, the material is ductile, in the opposite case, it is brittle. As seen in Table 2 that both materials have a higher value of B/G ratios, indicating that both perovskite materials are ductile in nature. Ductility of materials are critical in terms of portable usage of these materials since handing of storage material is also another issue for hydrogen technology.

Fig. 5

2D curves of Poisson’s ratios of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ (The green and blue surfaces are the minimal and maximal positive values the elastic property takes)

Additionally, $C_{\mathrm {P}}$ (Cauchy Pressure) is computed. Cauchy pressures of both materials are positive which supports metallic and ductile properties of materials that is indicated by B/G ratios. Another parameter that is examined is that Poisson’s ratio ($\sigma )$ which also provides information about bonding characteristics of materials. If Poisson’s ratio is around 0.1, the material has mostly covalent bonding; if Poisson’s ratio is around 0.25, it mostly has ionic bonding [25]. As this ratio gets higher, the plasticity of material increases [26]. Moreover, it was said that the ratio between 0.5 and 0.25 represents upper and lower limits for central force of a solid [19]. The Poisson’s ratios of both perovskite materials are in the range of these limits, indicating that both materials show dominant ionic nature and have central forces.

Young Modulus (E) of materials is also calculated. It is given as the ratio of tensile stress to tensile strain. Higher Young modulus represents stiffness of materials [27]. As can be seen from Table 2 that $\hbox {NdGaO}_{3}$ is the stiffest material compared to $\hbox {NdInO}_{3}$.

Debye temperature of materials is a solid-state physics quantity which is related to lattice vibrations, elastic constants, specific heat, thermal conductivity, and melting points [28]. The higher value of $\varTheta _\mathrm{D}$ of $\hbox {NdGaO}_{3}$ implies higher thermal conductivity compared to $\hbox {NdInO}_{3}$. The hardness of materials is also examined using Vickers hardness given in Table 2. By comparing two materials, it is seen that $\hbox {NdGaO}_{3}$ is the hardest.

Elastic anisotropy of materials reflect different bonding characteristics in different directions and correlate with micro-cracks, precipitation, anisotropic plastic deformation, elastic instability, and internal friction [29, 30]. For a complete isotropic material, the anisotropy factor equals to 1, and any value smaller or greater than 1 implies anisotropy. The three independent constants can be used to compute anisotropy factor ($A=2C_{44}/( C_{11}{-}C_{12}).$ The obtained anisotropy factors for both $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ is lower than 1, indicating anisotropy in both materials given in Table 2. Since both materials are anisotropic, 2D directional change of compressibility, Poisson’s ratio, and Shear and Young Modulus of $\hbox {MgNiH}_{3}$ and $\hbox {MgCuH}_{3}$ are calculated using ELATE program code [13]. The results are presented in Table 3. As Fig. 2 demonstrates that the compressibility at all directions is spherical and isotropic. However, Poisson’s ratio, and Shear and Young Modulus of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ depict a divergence from isotropy and show an anisotropic behaviour at all directions, as shown in Figs. 3, 4 and 5.

Fig. 6

Bulk modulus variations of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ with temperature

Fig. 7

Temperature dependence of entropy of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$

3.2 Thermodynamic properties

The thermodynamic properties of materials are obtained in the temperature range of 0–1000 K using Debye model implemented in Gibbs2 code [14]. As a first step, variations in bulk modulus with temperature are investigated for both materials. Figure 6 illustrates that bulk modulus of both materials decreases gradually with temperature. The decrease is very slow around the ground state temperature, and at about 100 K, it starts to be steeper and continues linearly. This implies that a decline in temperature can improve both materials‘ hardness.

The variations of vibrational entropy with temperature are obtained using quasi-harmonic Debye model and presented in Fig. 7. As can be seen from the figure that entropy of materials increases monotonically with temperature. The entropy of $\hbox {NdGaO}_{3}$ is lower than that of $\hbox {NdInO}_{3}$, probably owing to the different bonding characteristics and/or strength [31].

The specific heat is an important parameter in solid-state physics, since it provides information about phase transitions, heat loss, and energy bands. The specific heat capacities at constant volume and pressure are computed and presented in Fig. 8. From Fig. 8, it is obvious that specific heat capacities increase fast until 400 K, and then, a slow increase is seen up until 900 K. After that, it approaches a constant value which is defined as Dulong–Petit limit [32] where a saturation limit occurs.

The linear thermal expansion coefficient ($\alpha )$ defines thermal expansion capacity of a material under heat owing to vibrations of atoms. Figure 9a depicts thermal expansion coefficients of both materials. From Fig. 9, it is seen that there is quick increase in $\alpha$ up to 400 K, and then, a slow rise is observed with temperature. This increase in $\alpha$ at low temperature follows the $\hbox {T}^{3}$ rule [33].

Materials’ Grüneisen parameters ($\gamma )$ are also computed using the quasi-harmonic approximation. $\gamma$ can be used for predicting anharmonic properties of materials which are presented in Fig. 9b. A small change in $\gamma$ is seen with temperature. Generally, $\gamma$ at 0 K is proportional to the logarithmic derivative of $\hbox {T}^{3}$ coefficient in the heat capacity with respect to volume [34].

Fig. 8

The obtained specific heat capacities at constant volume ($C_{\mathrm {v}})$ (a) and pressure ($C_{\mathrm {p}})$ (b) of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$

Fig. 9

Thermal expansion coefficient (a) and Grüneisen parameter (b) against temperature for $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$

4 Conclusions

Elastic and thermodynamic properties of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ are calculated by means of density functional theory for the first time. The calculated elastic constants of materials satisfy Born stability condition, suggesting that both materials are mechanically stable. By comparing elastic constants of both materials, it can be said that $\hbox {NdInO}_{3}$ will show less resistance against unidirectional compression in comparison with $\hbox {NdGaO}_{3}$, since it has lower $C_{11}$ value. This is also confirmed using bulk modulus. $\hbox {NdGaO}_{3}$ has higher bulk modulus than that of $\hbox {NdInO}_{3}$, meaning that $\hbox {NdGaO}_{3}$ will depict higher resistance to shape change under pressure in comparison with $\hbox {NdInO}_{3}$ which is also an indication of mechanical hardness. Ductile and brittle behaviour and bonding characteristics are examined via B/G ratios, Poisson’s ratio, and Cauchy pressures. From the knowledge of B/G ratios, it is seen that both materials are ductile in nature, since both have higher B/G ratio higher than Pugh’s criteria (1.75). Cauchy pressures and Poisson’s ratio of materials indicate metallic, dominant ionic nature, and central forces. Anisotropy calculations demonstrate that Poisson’s ratio, and Shear and Young modulus of $\hbox {NdGaO}_{3}$ and $\hbox {NdInO}_{3}$ depict a divergence from isotropy and show an anisotropic behaviour at all directions. Several thermodynamic properties such as Debye temperature, entropy, specific heat capacities, thermal expansion coefficients, and Grüneisen parameter are computed. Debye temperature and Vickers hardness of $\hbox {NdGaO}_{3}$ are found to be higher than $\hbox {NdInO}_{3}$, showing higher thermal conductivity and hardness. The presented data in this study can serve as a reference for future investigations and applications, since there are no data found in the literature for these perovskite materials.