Resonances in low-energy nuclear processes and nuclear astrophysics and asymptotic normalization coefficients: a review

Abstract

This paper is continuation of the previous review [Mukhamedzhanov and Blokhintsev, Eur. Phys. J. A 58, 29 (2022)] in which the ANC of a bound state was addressed. However, the ANC is important characteristics not only of bound states but also resonances. In this paper, the role of the ANCs in resonance processes is addressed. Among various topics considered here are Gamow–Siegert resonance wave functions for charged particles and their normalization, relationship between ANCs and resonance widths. Significant part is devoted to the R-matrix approach for resonance processes. The resonance wave functions, internal and external and their projections on the two-body channel are given. Important ingredients of the R-matrix method for resonance states are also discussed. Elastic resonance scatterings are analyzed and extended for subthreshold resonances. It is shown how the notion of the subthreshold resonance works in practical analysis. To this end, the $^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}$ reaction, which is considered to be the main neutron supply to build up heavy elements from iron-peak seed nuclei in AGB stars, is analyzed. Important part of the review is analysis of the relationship between resonance width and ANC of mirror resonance and bound states using the Pinkston–Satchler equation and the Wronskian method. Practical examples are given. Among important parts of the theoretical research is the theory of transfer reactions populating resonance states. Comparative analysis of prior and post-form DWBA amplitudes shows that the prior form is preferable over the post form due to faster convergence over $r_{nA}$. Calculations of the stripping to resonance reaction ${}^{16}\textrm{O}(d,\,p){}^{17}\textrm{O}(1d_{3/2})$ performed using the prior form of the CDCC method. A special attention is given to resonance astrophysical processes. Useful equations for internal and external radiative widths are given. Radiative capture through subthreshold resonance is considered. In particular, radiative capture reactions ${}^{11}\textrm{C}(p,\gamma ){}^{12}\textrm{N}\,$ and $\,{}^{15}\textrm{N}(p,\gamma ){}^{16}\textrm{O}\,$ and the role of the ANC is addressed in detail.

1 Introduction

Resonances are one of the general and dominating aspects of different branches of physics and, undoubtedly, one of the essential phenomena in low-energy nuclear physics and nuclear astrophysics. In one paper, covering even the main aspects of the resonances in low-energy nuclear physics is unrealistic. This review is a continuation of the review paper by Mukhamedzhanov and Blokhintsev [1]¹ in which addressed the bound state asymptotic normalization coefficients (ANCs) in scattering and direct reactions. I, therefore, put constraints on the topics covered in this review, addressing some selected topics of low-energy nuclear resonances in nuclear reactions and astrophysical resonance processes in which special attention is given to the role of the ANCs in treating resonance processes.

This theoretical paper contains basic and advanced concepts of treating nuclear resonances, resonance wave functions, and resonance reactions. It serves the interests of researchers of different levels, with the main aim of this paper to assess the attitude of graduate students, Ph. D students, and postdocs.

The paper consists of thirteen sections and three Appendices. Section 2 considers the Gamow–Siegert resonance wave functions, which are regular solutions at the origin ($r=0$) with the outgoing wave in the asymptotic region. An important part of this section is the proof that the Gamow–Siegert wave functions, which have exponentially diverging asymptotic behavior, can be normalized in the entire coordinate space for potentials having the Coulomb tail. The normalizable Gamow–Siegert wave functions is used to generalize the Berggren completeness relationship, which includes bound states, resonances, and continuum, for the potentials with the Coulomb tail.

Section 3 addresses important proof of the relationship between the resonance widths, residues of the elastic scattering S-matrix in the resonance pole, and the ANCs of the resonance states, which are the amplitudes of the tail of the Gamow–Siegert wave functions. After that, the tails of the resonant overlap functions are presented.

One of the most effective and powerful methods to treat resonance processes is the R-matrix method. This paper will employ the R-matrix approach in many sections below. Section 4 addresses the first application of the R-matrix method. We consider the R-matrix multichannel scattering wave functions. The R-matrix approach is based on splitting the configuration space into internal and external subspaces. That is why the internal and external scattering wave functions and their projections on two-body channels are considered separately.

In Sect. 5 are considered the different ingredients of the R-matrix approach: the reduced width amplitude, the logarithmic derivative of the outgoing Coulomb solution, and the ANC. Important relationships between these quantities both for bound and resonance states are derived. We define the formal and observable single-particle reduced widths used in the R-matrix formalism and their connections to the single-particle ANC and full ANC via the Whittaker function describing the external part of the bound-state wave function. After that, we generalize the obtained equations for the resonance state using the normalizable Gamow–Siegert wave functions.

In Sect. 6 we consider the simplest single-channel, single-level resonance elastic scattering S-matrix and elastic scattering amplitude. We obtain the near-resonance behavior of the elastic scattering amplitude in terms of the observable resonance width. Another interesting case to address is the elastic scattering in the presence of the subthreshold bound state (aka subthreshold resonance). We derive the expression for the residue of the elastic scattering amplitude in the subthreshold pole in the energy plane and express the ANC of the subthreshold bound state in terms of the reduced width of the subthreshold bound state and the observable partial resonance width of the subthreshold resonance at positive energies.

To further discuss the resonance processes within the R-matrix approach, in Sect. 7 we consider the two-channel, single- and multi-level resonance elastic scattering and reaction generalizing results obtained in Sect. 6. The expressions for the resonance pole of the scattering amplitude and the observable resonance width are presented. We also take into account the presence of the subthreshold resonance.

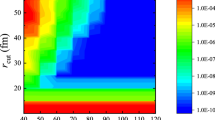
In Sect. 8 is demonstrated how the equations presented in Sect. 7 for the reaction amplitude proceeding through the subthreshold resonance can be used for the analysis of the important astrophysical reaction $^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}$ reaction, which is considered to be the main neutron supply to build up heavy elements from iron-peak seed nuclei in AGB stars. The level of $\,{}^{17}\textrm{O}\,$ at $\,E_{x}= 6.356\,$ MeV gives the dominant contribution to the reaction under consideration in the Gamow window. The location of this level is under discussion and the currently accepted value is 4.7 keV above the threshold. To find the reduced width of this level we use the reduced widths of the subthreshold bound states and extrapolate them to the resonance state. Using the determined reduced width of the resonance state 4.7 keV we calculated the S(0)-factor of the reaction $\,^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}.\,$

The width of a narrow resonance can be expressed in terms of the ANC of the Gamow–Siegert wave function (Sect. 3.1). That is why we can extend the relationship between the ANCs of mirror bound states to the relationship between resonance widths and ANCs of the mirror nuclei. Section 9 discusses the connection between the resonance widths and the ANCs of the mirror states using the Pinkston–Satchler equation. The obtained ratio of the resonance width and the ANC of the mirror states is expressed in terms of the ratio of the Wronskians containing the overlap functions of the mirror resonance and bound states in the internal region. In the Wronskian method, which is used here, one needs the wave functions only in the internal region, in which it is very convenient to use the R-matrix method. The connection between the ANC and the resonance width of the mirror resonance state provides a powerful indirect method to obtain information that is unavailable directly. If, for instance, the resonance width is unknown, one can find it through the known ANC of the mirror state and vice versa. The relationship between the mirror resonance width and the ANC allows us to find the resonance width from the ANC of the mirror bound state. Also loosely bound states $\alpha + A$ become resonances in the mirror nucleus $\alpha + B$, where charge $Z_{B}e > Z_{A}e$. Using the method developed in Sect. 9, one can find missing quantities, the resonance width of the narrow resonance state, or the mirror ANC.

In Sect. 10, the Wronskian method is applied for the ratio ${\Gamma _{{p\,^{12}}{\textrm{C}}}}/C_{{n\,^{12}}{\textrm{C}}}^2$ of the resonance state ${}^{13}\textrm{N}(1d_{5/2})$ and the ANC of the mirror bound state ${}^{13}\textrm{C}(1d_{5/2})\,$ and the ratio ${\Gamma _{{\alpha \,^{14}}{\textrm{O}}}}/C_{{\alpha \,^{14}}{\textrm{C}}}^2$ of the mirror states ${}^{18}\textrm{Ne}(1^{-})$ and ${}^{18}\textrm{O}(1^{-})$.

Analysis of the S-matrix pole structure is a powerful method in quantum physics. The S-matrix in the complex momentum (or energy) plane has poles corresponding to bound, virtual, and resonance states. The resonance states are described by the wave functions containing asymptotically only the outgoing waves, which exponentially increase due to the complex momenta. In Sect. 11 we employ the Gamow–Siegert resonance wave functions to describe resonance states.

A few different techniques to determine the resonance energy, width and resonance wave function based on the solution of the Schrödinger equation are described. One of them is Zel’dovich’s normalization procedure, which we discussed in Sect. 2.3. Another method is the complex scaling method CSM (see Appendix C). In this method the normalization of the resonant wave function is achieved using the rotation of the integration countour over r from $R_{max}$ to the complex plane, where the nuclear potential is cut to zero. In this method, the complex eigenvalue and the Gamow wave function can be found by integration of the Schrödinger equation imposing the boundary conditions in the origin and the asymptotic region. Finally, we mention a pole search by the solution of the Schrödinger equation with the short-range interaction for the scattering wave function. The method allows one to find resonances and even subthreshold resonances. We illustrate how different theoretical approaches can be used to determine the parameters of the resonances ${}^{15}\textrm{F}(1/2^{+},\,5/2^{+})$ testing the predictive power of the used methods. We address two approaches based on the definition of the resonance energy and width: the potential model based on the solution of the Schrödinger equation and the analytical expression for the S-matrix. We compare the results of these two approaches with the R-matrix method.

Section 12 is devoted to the theory of the (d, p) stripping reactions populating resonance states. The standard method of analyzing the nucleon transfer reactions populating bound states for a long time was the distorted-wave-Born approximation (DWBA). However, an adequate theory for transfer reactions to resonance states has yet to be developed because the resonance wave function is large in the nuclear interior, where different channels are coupled. In the outer region, the resonance wave function is the Gamow–Siegert wave function, whose asymptotic is given by the outgoing Coulomb scattered wave. The stripping pattern to resonances can differ from stripping to bound states. For regularization of the reaction matrix elements, one can use the Zel’dovich regularization procedure (see Sect. 2) or CSM (see Appendix C). Nowadays, the standard DWBA is being replaced by more advanced approaches such as continuum discretized coupled channels (CDCC), adiabatic distorted wave (ADWA), coupled reaction channels (CRC), and the coupled channels in Born approximation (CCBA) available in FRESCO code.

Below we describe a theory of deuteron stripping that will solve the problems mentioned above for the deuteron stripping to resonant states. We start with considering the conventional DWBA amplitude and then consider the CDCC one. By splitting the post and prior forms into the internal post, surface, and prior external form, we can analyze the convergence of the resonant DWBA amplitude. We compare post and prior forms and show that for the stripping to resonance, the prior form has an advantage over the post form due to the faster convergence. To demonstrate the theoretical conclusions, the calculations of the stripping to resonance ${}^{16}\textrm{O}(d,p){}^{17}\textrm{O}(1d_{3/2})$ at $\,E_{d}=36\,$ MeV using the CDCC final-state wave functions are presented. We showed that the prior form convergence was much faster than the post form. By normalizing the calculated prior differential cross-section to the experimental one, we determined the resonance width and its uncertainty caused by the uncertainty of the radial parameter of the Woods–Saxon potential used to calculate the resonance state. A strong dependence of the SF on the radial parameter of this potential confirms that the surface amplitude provides a significant contribution.

Section 13 addresses the radiative capture reactions in which a nucleus fuses with another, accompanied by the emission of electromagnetic radiation, which plays a crucial role in nuclear astrophysics. The radiative capture reactions caused by the electromagnetic interaction are significantly slower than reactions induced by the strong interactions. Hence these slow reactions control the rate and time of cycles of nucleosynthesis.

In nuclear astrophysics, many important nucleon capture reactions occur through resonance states which then decay to bound states. The interference of resonant and non-resonant contributions gives the total capture cross-section for such reactions. Many theoretical models for resonant and non-resonant cross-sections require proper knowledge of the initial and final state, the nature and multipolarity of the transition, and the radiative width. For many nuclei, radiative capture reactions are the only p- or $\alpha$-capture processes with positive Q-values. Hence the reaction rates of these reactions are crucial for determining stellar energy production. The radiative capture reactions represent the most practical application of the indirect ANC method in nuclear astrophysics. One of the main input parts of the radiative capture amplitude is the radiative width, one of the important observables whose precise value is required to accurately determine the resonance capture cross-sections and which is often the main source of uncertainty. That is why we start our discussion from the radiative width amplitudes splitting them into the internal and external (channel) parts. To calculate the channel radiative width amplitude, one needs to know two observables: the ANC of the final bound state and partial resonance width. Therefore, with precise knowledge of these quantities, the channel radiative width amplitude can be calculated quite accurately. The internal radiative width amplitude is usually a fitting parameter in the R-matrix method.

The combination of the peripheral transfer reactions allowing one to determine the ANCs and the radiative capture reactions whose amplitudes are parameterized in terms of the ANCs extracted from the transfer reactions is the essence of the indirect ANC method in nuclear astrophysics. In what follows, we present useful R-matrix equations for radiative capture amplitudes and then present two examples of using the indirect ANC method to determine the astrophysical factors. These are astrophysical radiative capture processes, $\,{}^{11}\textrm{C}(p,\,\gamma ){}^{12}\textrm{N}\,$ and ${}^{15}\textrm{N}(p,\,\gamma ){}^{16}\textrm{O},\,$ in which the role of the ANC is elucidated. The paper uses the system of units in which $\hbar =c=1$.

2 Gamow–Siegert resonance wave functions

2.1 Introduction

In 1928, Gamow [2] introduced the energy eigenfunction with complex eigenvalue in the paper on the $\alpha$ decay of nuclei. Gamow eigenfunctions are called Gamow vectors. The complex energy eigenvalue consists of the real part, the observable resonance energy, and the imaginary part, the resonance width. Gamow eigenfunctions are exponentially decreasing with time. Gamow developed a phenomenological approach because, in the conventional quantum mechanical approach, the eigenvalues of self-adjoint operators are real. In 1939, Siegert [3] defined resonant states as solutions of the stationary Schrödinger equation regular at the origin and satisfying asymptotic outgoing boundary condition. Owing to the complex eigenvalue, the asymptotic term of the Siegert wave function has an exponentially diverging term. In what follows, using the standard potential scattering theory we show how to derive the resonant Gamow–Siegert wave functions corresponding to the complex eigenvalues from the scattering eigenfunctions. They play an important role in the following up discussions. In particular, I will discuss the normalization of the Gamow–Siegert wave functions for Coulomb plus nuclear potentials and the generalized completeness relationship, which includes bound states, resonances, and continuum states at complex energies. The normalizable Gamow–Siegert resonance wave functions allow us to establish a relationship between the ANC and the resonance width. That is why it is clear why the notion of the ANC is so essential in the analysis of resonance processes.

In papers Michel et al. [4] and [5], a new application of the Gamow–Siegert wave functions emerged: the nuclear shell model, which is based on the Berggren’s generalized completeness condition (Berggren [6]). The Berggren’s complete set includes bound states, resonances, and continuum states. Full review of the Gamow Shell Model is available in Michel et al. [7], Michel and Płoszajczak [8]. Recently, the Gamow Shell Model was extended for studying of proton and neutron radiative capture reactions using the coupled channel representation (Fossez et al. [9], Michel et al. [10]). However, Berggren considered only short-range (nuclear) interaction, which was also employed in earlier Gamow Shell Model papers. In 2008, Michel proved completeness of the eigenfunctions of the Schrödinger equation with potentials possessing Coulomb tail. To prove it, he introduced the cut-off radius R, which was eventually taken to infinity. However, the subtle point is the behavior of the wave functions at $k=0$ in the limit $R \rightarrow \infty$. The proof is quite intricate. Earlier, in 2008, Mukhamedzhanov and Akin proved that the Coulomb scattering wave functions form a complete basis (Mukhamedzhanov and Akin [11]). It allows one to extend the Berggren’s generelazied completeness relationship for the eigenfunction of the Schrödinger equation with nuclear plus Coulomb potentials. The Berggren’s generalized complete set is the foundation of Gamow Shell Model method (Michel and Płoszajczak [8]).

2.2 From scattering to resonance wave functions

In this section we derive the Gamow–Siegert resonance wave functions for the sum of the Coulomb plus nuclear potentials taking into account that in the previous publications (Siegert [3] and Berggren [6]) these wave functions were considered only for short-range potentials. We start from the regular non-resonant scattering wave functions, which are solutions of the radial Schrödinger equation

$$\begin{aligned}&\frac{ \textrm{d}^{2}\varphi _{l}(k,r)}{\textrm{d} r^{2}} - V(r)\,\varphi _{l}(k,r) - \frac{ l(l+1) }{r^{2}}\,\varphi _{l}(k,r) \nonumber \\&\quad = -k^{2}\,\varphi _{l}(k,r). \end{aligned}$$

(1)

Here V(r) is given by the sum of the Coulomb and short-range nuclear potentials. The regular solutions are defined up to a normalization factor. We seek a solution of Eq. (1) in the following form:

$$\begin{aligned} \varphi _{l}(k,r)&= \frac{1}{2\,i\,k}\,\Big [ f_{l}^{(+)}(k)\,f_{l}^{(-)}(k,r) \nonumber \\&\quad - (-1)^{l}\,f_{l}^{(-)}(k)\,f_{l}^{(+)}(k,r)\Big ] \end{aligned}$$

(2)

with the boundary condition

$$\begin{aligned} \lim \limits _{r \rightarrow 0}\,\varphi _{l}(k,r) \sim r^{l+1}. \end{aligned}$$

(3)

$f_{l}^{(\pm )}(k,\,r)$ are the singular at the origin Jost solutions satisfying the boundary condition:

$$\begin{aligned} \lim \limits _{r \rightarrow \infty } f_{l}^{(\pm )}(k,r) = \lim \limits _{r \rightarrow \infty } f_{l}^{C(\pm )}(k,r) = e^{\pm i[k\,r - \eta \,\ln (2\,k\,r)]}, \end{aligned}$$

(4)

where the Coulomb Jost functions $f_{l}^{C(\pm )}(k,r)$ are defined in Eq. (A.17) and (A19) from review [1].

The Jost functions are defined as

$$\begin{aligned} f_{l}^{(\pm )}(k) = \lim \limits _{r \rightarrow 0} ({\mp } 2\,i\,k\,r)^{l}\,f_{l}^{(\pm )}(k,\,r). \end{aligned}$$

(5)

At real k

$$\begin{aligned} f_{l}^{(-)}(k) =f_{l}^{(+)*}(k). \end{aligned}$$

(6)

From Eq. (2) follows that

$$\begin{aligned} f_{l}^{(+)}(k) =-\mathcal{W}[ f_{l}^{(+)}(k,r),\,\varphi _{l}(k,r) ], \end{aligned}$$

(7)

where $\mathcal{W}[ f_{l}^{(+)}(k,r),\,\varphi _{l}(k,r) ]$ is the Wronskian of $f_{l}^{(+)}(k,r)$ and $\varphi _{l}(k,r)$, and $\mathcal{W}[ f_{l}^{(+)}(k,r),\, f_{l}^{(-)}(k,r)]= -2\,i\,k.$

Jost solution $f_{l}^{+}(k,\,r)$ and Jost function $f_{l}^{+}(k)$ ($f_{l}^{-}(k,\,r)$ and $f_{l}^{-}(k)$) have a cut along the negative (positive) imaginary axis in the complex k plane. Hence the wave function $\varphi _{l}(k,r)$ is not analytical in the complex k plane where it has a cut along the entire imaginary axis (Mentkovsky [12] and review [1]). We consider this wave function only for $\textrm{Re}k >0$.

The elastic scattering S-matrix element is given by

$$\begin{aligned} {{\mathbb {S}}}_{l}(k)= \frac{ f_{l}^{(-)}(k) }{ f_{l}^{(+)}(k) }. \end{aligned}$$

(8)

Let $k=k_{n}$ be the zero point of the Jost function $f_{l}^{(+)}(k)$. This point is a pole of the S-matrix corresponding to bound state or resonance. From

$$\begin{aligned} f_{l}^{(+)}(k) {\mathop {\approx }\limits ^{k \rightarrow k_{n}}} {\dot{f}}_{l}^{(+)}(k_{n})\,(k- k_{n}) \end{aligned}$$

(9)

follows

$$\begin{aligned} {{\mathbb {S}}}_{l}(k){\mathop {\approx }\limits ^{k \rightarrow k_{n}}} \frac{ f_{l}^{(-)}(k) }{ \dot{f_{l}}^{(+)}(k_{n})\,(k-k_{n}) } = \frac{A_{l}}{k-k_{n}}. \end{aligned}$$

(10)

Here $\dot{f_{l}}^{(+)}(k_{n}) = \frac{\textrm{d}f_{l}^{(+)}(k)}{\textrm{d}k}\Big |_{k=k_{n}}$ and $A_{l}$ is the residue of the S-matrix at the pole $k=k_{n}$.

From Eq. (2) we get the wave function corresponding to $k_{n}$:

$$\begin{aligned} \varphi _{l}(k_{n},r)&= c^{-1}\,f_{l}^{(+)}(k_{n},r), \end{aligned}$$

(11)

$$\begin{aligned} c&= \,\frac{2\,i\,k_{n}}{f_{l}^{(-)}(k_{n})}. \end{aligned}$$

(12)

It is important to emphasize that left and right-hand sides of Eq. (11) are regular at $r=0$. For $k_{n}=k_{R}$ the resonance wave function $\varphi _{l}(k_{R},r)$ is the Gamow–Siegert wave function $\varphi _{l}^{GS}(k_{R},r).$ $\,k_{R}= k_{0} - i\,k_{I}$ is the momentum of the resonance, $k_{0}=\textrm{Re}k >0$ and $k_{I} = \textrm{Im} k_{R} >0$.

According to Newton [13],

$$\begin{aligned} \dot{f_{l}}^{(+)}(k_{n})&= (-1)^{l+1}\,2\,c\,k_{n}\,N^{2}, \end{aligned}$$

(13)

$$\begin{aligned} N^{2}&= \int \textrm{d }r\,\varphi _{l}^{2}(k_{n},r). \end{aligned}$$

(14)

We now derive the coefficient c in terms of the ANC for resonance state ($n=R$). In the next subsection, we prove that the Gamow–Siegert wave functions are normalizable. From now on, we assume that $N=1$.

The behavior of the elastic scattering S-matrix at $k \rightarrow k_{R}$ is defined by Eq. (10) with the residue in the pole $A_{l}$ expressed in terms of the ANC of resonance state, see Eq. (40) below. Equations (10), (12), (13) and (40) are all that are needed to write

$$\begin{aligned} A_{l}= \frac{f_{l}^{(-)}(k_{R})}{{\dot{f}}_{l}^{(+)}(k_{R}) } = i\,\frac{[f_{l}^{(-)}(k_{R})]^{2}}{4\,(-1)^{l}\,k_{R}^{2}} = -i^{2\,l +1}\,e^{-\pi \,\eta _{R}}\,C_{l}^{2}, \end{aligned}$$

(15)

and

$$\begin{aligned} c^{-1}= e^{-\pi \,\eta _{R}/2}\,C_{l}. \end{aligned}$$

(16)

We introduced the ANC in Eq. (15) using the results of subsection 3.1. In view of Eq. (11), we have

$$\begin{aligned} \varphi _{l}^{GS}(k_{R},r) = e^{-\pi \,\eta _{R}/2}\,C_{l}\,f_{l}^{(+)}(k_{R},r). \end{aligned}$$

(17)

In the nuclear interior the wave function $\varphi _{l}(k_{R},r)$ can be found as a regular solution of the Schrödinger equation with the complex eigenvalue $E_{R}$. However, in the external region where the nuclear interaction can be neglected,

$$\begin{aligned} \varphi _{l}^{GS}(k_{R},r)&= e^{-\pi \,\eta _{R}/2}\,C_{l}\,f_{l}^{C(+)}(k_{R},r) \nonumber \\&{\mathop {=}\limits ^{r> R_{ch}}} C_{l}\,W_{-i\,\eta _{R},\,l+ 1/2}(-2\,i\,k_{R}\,r) \nonumber \\&{\mathop {\approx }\limits ^{r \rightarrow \infty }} e^{-\pi \,\eta _{R}/2}\, C_{l} e^{i\,\rho (k_{R},r)}. \end{aligned}$$

(18)

The channel radius $R_{c h} > R_{N},\,$ where $R_{N}$ is the $a-A$ nuclear interaction radius. $\,\eta _{R}= Z_{a}\,Z_{A}\,e^{2}\,\mu /k_{R}$ is the Coulomb parameter for the resonant state, $Z_{a}e$ and $Z_{A}e$ are charges of particles forming resonance state and $\mu =\mu _{aA}$ is their reduced mass. Also

$$\begin{aligned} \rho (k_{R},r)= k_{R}\,r - \eta _{R}\,\ln (2\,k_{R}\,r). \end{aligned}$$

(19)

Because both bound states and resonances are the poles of the scattering S-matrix, the resonance wave function $\varphi _{l}^{GS}(k_{R},r)$ can be obtained from the bound state one by replacing the bound-state wave number $\kappa$ in Eq. (98) review [1] with $-i\,k_{R}$.

We introduced the ANC $C_{l}$ for the resonance state as the amplitude of the tail of the Gamow–Siegert wave function. In Sect. 3.1 we prove that the residue of the elastic scattering S-matrix in the resonance pole is expressed in terms of the ANC $C_{l}$. Being completely accurate, we should use the single-particle normalization coefficient here rather than the ANC $C_{l}$, which is the normalization constant for the overlap function. The ANC is related to the single-particle ANC by Eq. (111) from review [1]. We assume here that the SF of the resonance state is unity. That is why the usage of $C_{l}$ as the normalization constant of the wave function $\varphi _{l}^{GS}(k_R,\,r)$ in the outer region is justified.

2.3 Normalization of resonance Gamow–Siegert wave functions for charged particles

We continue to consider Gamow–Siegert solutions of the Schrödinger equation with complex eigenvalues, which are regular at the origin and satisfy the purely outgoing asymptotic condition. These wave functions alike the continuum wave functions are not $L^{2}$ integrable, and a particular procedure (Zel’dovich’s exponential regulator (Baz et al. [14]))² ought to be introduced to normalize Gamow–Siegert wave functions.

To normalize resonant wave functions, we need to introduce the dual wave functions ${{{\tilde{\varphi }}}}_{l}({k},r)$, which are also solutions of Eq. (1)³:

$$\begin{aligned} {{{\tilde{\varphi }}}}_{l}^{GS}(k,r)= [\varphi _{l}^{GS}(k,r)]^{*}= \varphi _{l}^{GS*}(k^{*},r). \end{aligned}$$

(21)

To include not square integrable vectors, one can use the so-called equipped Hilbert space, also called the rigged Hilbert space, introduced by Gelfand and Vilenkin [15], Maurin [16], see Appendix A. The rigged Hilbert space allows one to work both with the continuum wave functions and eigenfunctions with complex eigenvalues. Even generalized functions (distributions), for example, Dirac delta-functions, belong to the rigged Hilbert space. Then resonances are connected with the point spectrum of complex-scaled Hamiltonians, see Appendix C.

In Appendix B we show that Zel’dovich regularization procedure permits us to normalize the Gamow–Siegert resonance wave functions for Coulomb plus nuclear potentials:

$$\begin{aligned} \mathcal{I}_{0}^{\infty }=\lim \limits _{\beta \rightarrow +0}\int _{0}^{\infty }\,\textrm{d}r\,e^{-\beta \,r^{2} }\, [{{{\tilde{\varphi }}}}_{l}^{GS}(k,r)]^{*}\,\varphi _{l}^{GS}(k,\,r) =1. \end{aligned}$$

(22)

Here the factor $\,e^{-\beta \,r^{2} }\,$ is a regulator of the integral.

Zel’dovich’s regularization method is not unique, and other regularization techniques can be used. In particular, more general exponential regulator $exp(-\beta \,r^{n}),\;n>2,$ can be used. It will allow one to include more distant resonances. Another interesting regularization technique is the so-called complex scaling method (CSM), see Appendix C.

The existence of the norm of the Gamow–Siegert wave functions is all that is needed to write

$$\begin{aligned} \mathcal{I}_{0}^{\infty }&=\int \limits _{0}^{R} \textrm{d}r\,[\varphi _{l}^{GS}(r)]^{2}+ C_{l}^{2}\,\frac{e^{- \pi \,\eta _{R}}}{(2\,k_{R})^{i\,2\,\eta _{R}}} \nonumber \\&\quad \times \mathop {\lim }\limits _{\beta \rightarrow +0}\, \int \limits _{R}^{\infty } \textrm{d}r\,\frac{e^{i\,2\,k_{R}\,r}}{r^{i\,2\,\eta _{R}}}\,e^{-\beta \,r^{2}} =1, \end{aligned}$$

(23)

where $\varphi _{l}^{GS}(r)\,[{{{\tilde{\varphi }}}}_{l}^{GS}(r)]^{*}= [\varphi _{l}^{GS}(r)]^{2},\,$ and

$$\begin{aligned}&\mathop {\lim }\limits _{\beta \rightarrow +0}\, \int \limits _{R}^{\infty } \textrm{d}r\,e^{i\,2\,k_{R}\,r}\,r^{-2\,i\,\eta _{R}}\,e^{-\beta \,r^{2}} \end{aligned}$$

(24)

$$\begin{aligned}&=-\frac{R^{-2\,i\,\eta _{R}}}{i\,2\,k_{R}}\,e^{i\,2\,k_{R}\,R}\,\Big [1+ \frac{\eta _{R}}{k_{R}\,R} - O\big (\frac{1}{(2\,k_{R}\,R)^{2}}\big ) \Big ]. \end{aligned}$$

(25)

The asymptotic expansion in power of $2\,i\,k_{R}\,R$ in Eq. (25) is obtained by integrating by parts of the integral in Eq. (24).

Then from Eq. (23) for $R \rightarrow \infty$ one gets

$$\begin{aligned} \int \limits _{0}^{R} \textrm{d}r\,[\varphi _{l}^{GS}(r)]^{2}&= 1 - i\,C_{l}^{2}\,\frac{e^{- \pi \,\eta _{R}}}{(2\,k_{R}R)^{i\,2\,\eta _{R}}} \,\frac{e^{i\,2\,k_{R}\,R}}{2\,k_{R}} \nonumber \\&=1 - C_{l}^{2}\,e^{- \pi \,\eta _{R}}\,\frac{i}{2\,k_{R}}\,e^{2\,i\,\rho (k_{R},\,R) }. \end{aligned}$$

(26)

The fact that the Gamow–Siegert wave functions for charged particles can be normalized has significant consequences in a few important derivations.

2.4 Berggren’s contour and generalized completeness relationship

Berggren [6] generalized the completeness relationship for short-range potentials by including discrete resonance Gamow–Siegert states. It is achieved by deforming the integration contour over the continuum to the fourth quadrant. Using Cauchy’s integral theorem, one can single out resonances (see subsection  3.2 and Mukhamedzhanov and Kadyrov [17]) and add them to the sum over the bound states. The price one pays for including the resonant states is the deformation of the integration contour into the complex plane. Considering that the Gamow–Siegert wave functions are normalizable, see previous Sect. 2.3, we can generalize Berggren’s method for the Coulomb plus short-range potential. The deformed integration contour C is shown in Fig. 1.

Fig. 1

The deformed integration contour C allowing one to include resonance states in the completeness relationship

Including the resonance states leads to the generalized completeness relationship

$$\begin{aligned} \delta (r'-r)&= \sum \limits _n\,\varphi _{nl} (r')\, \varphi _{nl} (r)\, + \sum \limits _{n'}\, [ {{{\tilde{\varphi }}}}_{n'l}^{GS} (r')]^{*}\,\varphi _{n'l}^{GS} (r)\, \nonumber \\&\quad +\frac{1}{2\,\pi }\, \int \limits _C \textrm{d}k\,e^{-\pi \,\eta }[{{{\tilde{\varphi }}}}_{l}(k,r')]^{*}\,\varphi _{l}(k,r), \end{aligned}$$

(27)

validating Berggren’s relationship for the Coulomb plus nuclear potentials. Note that only resonances with $k_{0}> k_{I}$, where $k_{R}= k_{0}-i\,k_{I}$, are included into sum (27).

3 Residue in resonance pole of S-matrix and ANC for resonance state

In review [1]), the ANCs for bound states were considered. In this section, we extend the notion of the ANC for resonance states (we have already done it, without proof, in Sect. 2.2) and will establish the fundamental connection between the ANC and the resonance width for resonance states. Engaging the normalizable Gamow–Siegert resonance wave functions is an essential part of the proof.

To establish the connection between the ANC and the resonance width, we employ the behavior of the Coulomb-modified nuclear scattering amplitude $\mathcal{T}^{CN}(k)$ near the resonance pole. I refer now the reader to (Eq. (31) review [1]) from which follows that this amplitude has a cut along the entire imaginary axis in the k-plane, which cuts the scattering amplitude into two parts. To consider the resonances, we can use the amplitude at $\textrm{Re}k >0.$ The behavior of $\mathcal{T}^{CN}(k)$ near the resonance pole is considered.

It is also shown how we can single out the resonance term from the two-body Green function using the Gamow–Siegert wave functions. Finally, we consider the asymptotic of the resonance overlap functions whose amplitudes are expressed in terms of the resonance state ANC.

3.1 ANC and resonance width

Let us consider the elastic scattering S-matrix of two spinless particles a and $A.\,$ We assume now that at the orbital angular momentum l, the system $a+A$ has a resonance. From the fundamental principles of the analyticity, unitarity, and symmetry of the S-matrix follows locations of its poles in the complex k plane, see Fig. (2). It has poles corresponding to bound states located along the positive imaginary axis and the poles corresponding to resonances situated in the fourth and third quadrants. Note that the poles in the low half-plane should be symmetric relative to the negative imaginary axis.

Fig. 2

S-matrix poles: (a) complex energy plane; the resonance and the virtual state are shown on the second energy sheet; (b) complex momentum plane

The elastic scattering S-matrix may be written as (see review [1], subsection 2.4)

(28)

where

(29)

is the Coulomb-modified nuclear elastic scattering amplitude, ${{\mathbb {S}}}_{l}^{CN}(k)= e^{2\,i\,\delta _{l}^{CN}}$ is the Coulomb-modified nuclear elastic scattering S-matrix and ${{\mathbb {S}}}_{l}^{C}(k)= e^{2\,i\,\sigma _{l}^{C}}$ is the Coulomb scattering S-matrix.

is defined as (see review [1]), Eq. (31))

(30)

Owing to the presence of the factor $e^{-\,\pi \,\eta \,\mathrm{sign~Re}k}$ we conclude that ${{\mathcal {T}}}_{l}^{CN}(k)$ has a discontinuity along the entire imaginary axis in the k plane dividing it into different analytical functions. One is in the left half-plane ($\textrm{Re}k <0$), and the other is in the right half-plane ($\textrm{Re}k >0$). The renormalized scattering amplitude ${\tilde{\mathcal{T}}}_{l}^{CN}(k)$ is an analytic function on the physical sheet of the Riemann surface ($\textrm{Im}k >0$) where its analytic structure is similar to the pure nuclear scattering amplitude. However, in the low half-plane ($\textrm{Im} k <0$) the scattering amplitude $\,{\tilde{\mathcal{T}}}_{l}^{CN}(k)$ has a discontinuity along the negative imaginary axis. Similar to the nuclear scattering amplitude, it may have resonance poles in the 3rd and 4th quadrants of the k plane. Hence we can find the residue of the amplitude $\,{\tilde{\mathcal{T}}}_{l}^{CN}(k)$ in these poles. Since these poles are located away from the cut imposed by the factor $e^{-\pi \,\eta \,\textrm{sign Re}k}$, we can also find the residues in the resonance poles of the amplitude ${{\mathcal {T}}}_{l}^{CN}(k).$ The same is true for elastic scattering S-matrix ${{\mathbb {S}}}_{l}^{CN}(k)$.

The most general expression for the elastic scattering S-matrix is (Baz et al. [14])

$$\begin{aligned} {{\mathbb {S}}}_{l}^{CN}(k)= e^{2\,i\,\delta _{l}^{p}(k)}\,\frac{(k- k_{R}^{*})(k+k_{R})}{(k- k_{R})(k+ k_{R}^{*})}. \end{aligned}$$

(31)

Here $\delta _{l}^{p}(k)$ is the Coulomb-modified nuclear potential (nonresonant) scattering phase shift. Resonance momentum $k_{R}$ is related to the resonance energy as $\,E_{R} = E_{0} - i\,\Gamma _{l}/2= k_{R}^{2}/(2\,\mu )$. $\,E_{0}\,$ is the real part of the resonance energy, $\,\Gamma _{l}\,$ is the resonance width in the partial wave l.

From Eq. (31) follows that

$$\begin{aligned} {{\mathbb {S}}}_{l}^{CN}(k) {\mathop {=}\limits ^{ k \rightarrow k_{R}}}\,\frac{A_{l}}{k- k_{R}} + g_{l}(k), \end{aligned}$$

(32)

where $g_{l}(k)$ is a regular function at $k=k_{R}.$ The residues of the S-matrix and the scattering amplitude in the resonance pole for the Breit–Wigner resonance ($\Gamma _{l}<< E_{0}$) are

$$\begin{aligned} \textrm{Res}\,S_{l}^{CN}=A_{l}= -\,ie^{2\,i\,\delta _{l}^{p}(k_0)}\,\frac{\mu }{k_{0}}\,\Gamma _{l} \end{aligned}$$

(33)

and

$$\begin{aligned} \textrm{Res}\,{{\mathcal {T}}}_{l}^{CN}=\frac{1}{2\,i\,k_{0}}\,A_{l}= -\,e^{2\,i\,\delta _{l}^{p}(k_0)}\,\frac{\mu }{2k_{0}^{2}}\,\Gamma _{l}. \end{aligned}$$

(34)

Now we derive the relationship between the ANC and the partial resonance width. To this end, we can use the method presented in review [1], which is quite general, and the information about the bound state was introduced only beginning from Eq. (92) [1]. Since this equation is essential for our derivation, we write it down again:

$$\begin{aligned} \int \limits _0^{R} dr\,{{\hat{\varphi }}}_{l}^2(k,r)&= \, \frac{1}{{2k}}\left[ \frac{{\partial {{{\hat{\varphi }}}_{l}}({k,R})}}{{\partial k}}\frac{{\partial {{{\hat{\varphi }}}_{l}}({k,R})}}{{\partial {R}}} \right. \nonumber \\&\left. \quad - {{{\hat{\varphi }}}_{l}}({k,R})\frac{{{\partial ^2}{{{\hat{\varphi }}}_{l}}({k,R})}}{{\partial k\,\partial {R}}} \right] . \end{aligned}$$

(35)

To further simplify this equation, we need to present a few additional equations. At large real k the elastic scattering wave function ${{\hat{\varphi }}}_{l}(k,r)$ (Eq. (2.90), review [1]) can be replaced by its leading asymptotic term which contains the ingoing and outgoing waves:

$$\begin{aligned} {{{\hat{\varphi }}}_{l}}({k,r}) \approx {{{\mathbb {C}}}}_{l}(k)\,\left[ {{e^{i\rho (k,r) }} - ( - 1)^{l}\,{{\mathbb {S}}}_{l}^{ - 1}(k){e^{ - i\rho (k,r) }}} \right] , \end{aligned}$$

(36)

where $\; \eta$ is the Coulomb parameter of the interacting nuclei, ${{\mathbb {C}}}_{l}(k)$ is some normalization constant whose meaning is determined below. To adapt the derivation for the resonance state we consider Eq. (36) for $k \rightarrow k_{R}$. In view of Eqs. (28) and (33), we get the radiation condition

$$\begin{aligned} {{\hat{\varphi }}}_{l}(k_R,\,r) {\mathop {=}\limits ^{r \rightarrow \infty }} {{{\mathbb {C}}}_{l}}(k_{R})\,e^{i\rho (k_{R},\,r) }. \end{aligned}$$

(37)

Comparing this equation with Eq. (18) one can easily verify that

$$\begin{aligned} {{\mathbb {C}}}_{l}= C_{l}\,e^{-\pi \,\eta _{R}/2}. \end{aligned}$$

(38)

Note that the scattering wave function $\,{{\hat{\varphi }}}_{l}(k,\,r)\,$ at large r at real momentum k contains ingoing and outgoing waves and is not normalizable in the entire space while ${{\hat{\varphi }}}_{l}(k_R,\,r)$ asymptotically contains only the outgoing wave and regular at $r=0$. Hence this wave function is the Gamow–Siegert resonance wave function.

Substituting Eqs. (36) and (32) into the right-hand-side of Eq. (35) and performing the differentiation over k and R and taking $k=k_R$ one gets

$$\begin{aligned} \int \limits _{0}^{{R}} \textrm{d}r\,[ \varphi _{l}^{GS}(k_R,\,r)]^{2} =&i\,(-1)^{l+1}{{\mathbb {C}}}_{l}^{2}(k_{R})/A_{l} \nonumber \\&- {{\mathbb {C}}}_{l}^{2}\,\frac{i}{2\,k_R}\,e^{2\,i\,\rho (k_{R},\,R)}. \end{aligned}$$

(39)

Comparing Eqs. (26), (38) and (39) we find that the residue in the resonance pole is expressed in terms of the standard ANC $C_{l}$:

$$\begin{aligned} \textrm{Res}\,S_{l}^{CN} = A_{l}= -i^{2\,l +1}\,e^{-\pi \,\eta _{R}}\,C_{l}^{2}. \end{aligned}$$

(40)

This relationship is universal and valid for bound state poles and resonances.

Equations Eqs. (33) and (40) are all that are needed to write the relationship between the ANC and the resonance width for the Breit–Wigner resonance:

$$\begin{aligned} C_{l}^{2}= i^{-2\,l}\, e^{\pi \,\eta _{R}}\,e^{2\,i\,\delta _{l}^{p}(k_R)}\,\frac{\mu }{k_{R}}\,\Gamma _{l}. \end{aligned}$$

(41)

This equation is valid for the Breit–Wigner resonance. Then in the external region Eq. (18) takes the form:

$$\begin{aligned} \varphi _{l}^{GS}(k_{R},\,r)&{\mathop {=}\limits ^{r >{ R}_{ch}}} i^{-l}\,e^{\pi \,\eta _{R}/2}\,e^{i\,\delta _{l}^{p}(k_R)}\,\sqrt{\frac{\mu }{k_{R}}\,\Gamma _{l}} \nonumber \\&\quad \times W_{-i\,\eta _{R},\,l+ 1/2}(-2\,i\,k_{R}\,r) \nonumber \\&= i^{-l}\,e^{i\,\delta _{l}^{p}(k_R)}\,\sqrt{\frac{\mu }{k_{R}}\,\Gamma _{l}}\,f_{l}^{C(+)}(k_{R},r) \nonumber \\&=e^{i\,\delta _{l}^{p}(k_R)}\,\sqrt{\frac{\mu }{k_{R}}\,\Gamma _{l}}\,O_{l}(k_{R},r), \end{aligned}$$

(42)

where we took into account that

$$\begin{aligned} O_{l}(k,r)&= e^{-i\,\pi \,l/2}\,f_{l}^{C(+)}(k,r) \nonumber \\&= e^{-i\,\pi \,l/2}\,e^{\frac{1}{2}\,\pi \,\eta \,\mathrm{sign~Re}k}\,W_{-\,i\,\eta , l+1/2}(-2\,i\,k\,r). \end{aligned}$$

(43)

We can replace $k_{R} \rightarrow k_{0},\,$ especially in the nonresonant scattering phase shift $\delta _{l}^{p},$ for the Breit–Wigner resonance under consideration.

Now we show how to relate the ANC $C_{l}$ to the resonance width $\Gamma _{l}$ for general case. We use the following definitions:

$$\begin{aligned} E_{0}&= \big [k_{0}^{2}- (k_{I})^{2}\big ]/(2\,\mu ), \nonumber \\ \Gamma _{l}&= 2\,k_{0}\,k_{I}/\mu . \end{aligned}$$

(44)

From Eq. (31) at $k \rightarrow k_{R}$ we get the residue in the resonance pole:

$$\begin{aligned} A_{l}&= -2\,i\,k_{R}\,\tau _{R}\,\big [(1+ \tau _{R}^{2})^{1/4} +\,(1+ \tau _{R}^{2})^{-1/4} ]^{-1}\, \nonumber \\&\quad \times e^{i[2\,\delta _{l}^{pot}(k_{R}) - \frac{1}{2}\,\arctan (\tau _{R}) ]}, \end{aligned}$$

(45)

$\tau _{R}= \frac{\Gamma _{l}}{2\,E_{0}}$. Equation (45) expresses the residue of the elastic scattering S-matrix in terms of the resonance energy and the resonance width for broad resonances.

Recovering now all the quantum numbers one gets for a narrow resonance ($\tau _{R}<<1$) the residue of the elastic scattering S-matrix element in the resonance pole (up to terms of order $\sim \tau _{R}$ )

$$\begin{aligned} A_{l_{B}j_{B}}^{J_{B}}&= -\,ie^{2\,i\,\delta _{l_{B}}^{p}(k_{aA}^{0})}\,\frac{\mu _{aA}}{k_{aA\,(0)}}\,\Gamma _{aA\,l_{B}j_{B}J_{B}} \nonumber \\&= -i^{2\,l_{B} + 1}\,e^{-\pi \,\eta _{aA(0)}}(C_{aA\,l_{B}\,j_{B}\,J_{B}}^{B})^{2} \end{aligned}$$

(46)

and

$$\begin{aligned} \big (C^{B}_{aA\,l_{B}\,j_{B}\,J_{B}}\big )^{2}&= i^{-2\,l_{B}}\,e^{\pi \,\eta _{aA(0)} }e^{i\,2\,\delta _{l_{B}}^{p}(k_{aA(0)})}\, \nonumber \\&\quad \times \frac{\mu _{aA}\,\Gamma _{aA\,l_{B}\,j_{B}\,J_{B}}}{k_{aA(0)}}, \end{aligned}$$

(47)

where $l_{B},\,j_{B}$ and $J_{B}$ are the quantum numbers of the resonance $B=(aA)$: orbital angular momentum, total angular momentum of particle a and total spin of the resonance, respectively. $\Gamma _{aA\,l_{B}\,j_{B}\,J_{B}}$ is the resonance width for the resonance decay $B \rightarrow a+A$, $\,\delta _{l_{B}}^{p}(k_{aA\,(0)})$ is the potential (nonresonant) scattering phase shift at the real resonance relative momentum $\,k_{aA\,(0)}$, $\,\eta _{aA(0)}= Z_{a}\,Z_{A}\,e^{2}\,\mu _{aA}/k_{aA\,(0)}$. Equation (47) is general and valid for arbitrary SF.

3.2 Resonance part of Green function in terms of Gamow–Siegert wave functions

We now take up another interesting application of the Gamow–Siegert wave functions. We consider the Green function describing the propagation of two spinless particles and show how to single out the Green function resonance part, modifying the spectral decomposition of the Green function. The resonance part will be expressed in terms of the Gamow–Siegert wave functions.

The starting point is a formula for the two-body Green’s function resolvent:

$$\begin{aligned} G(z)= \frac{1}{z - {{\hat{T}}} -V}, \end{aligned}$$

(48)

where $\,{{\hat{T}}}$ is the kinetic energy operator of the relative motion of the interactiing particles, $\,V= V^{C}+V^{N}$ is their interaction potential given by the sum of the Coulomb and nuclear potentials. The spectral decomposition of the two-body Green function taken in the coordinate representation is

$$\begin{aligned} G({{\textbf {r}}}',\,{{\textbf {r}}};E) = 2\,\mu \,\int \,\frac{\textrm{d} {{\textbf {k}}}}{(2\,\pi )^{3}}\,\frac{ \big | \Psi _{ {{\textbf { k}}}}^{(-)}({{\textbf {r}}}')> <\Psi _{ {{\textbf {k}}}}^{(-)}({{\textbf {r}}})\big | }{ E - k^{2}/(2\,\mu ) + i0 }. \end{aligned}$$

(49)

The scattering wave function $\Psi _{ {{\textbf {k}}}}^{(-)}({{\textbf {r}}})$ is a solution of the Schrödinger equation

$$\begin{aligned} \Psi _{ {{\textbf {k}}}}^{(-)}({{\textbf {r}}})\Big ( k^{2}/(2\,\mu ) - {\overleftarrow{{\hat{T}}}} -V \Big )=0 \end{aligned}$$

(50)

corresponding to the relative kinetic energy $k^{2}/(2\,\mu )$, $\mu$ is the reduced mass of the interacting particles. Note that in the spectral decomposition (49) we can use $\Psi _{ {{\textbf {k}}}}^{(+)}({{\textbf {r}}})$ wave functions rather than $\Psi _{ {{\textbf {k}}}}^{(-)}({{\textbf {r}}})$. As a reminder, the partial-wave expansion of $\Psi _{ {{\textbf {k}}}}^{(-)}({{\textbf {r}}})$ is given by

$$\begin{aligned} \Psi _{ {{\textbf {k}}}}^{(-)}({{\textbf {r}}})&= \Psi _{- {{\textbf {k}}}}^{(+)*}({{\textbf {r}}}) = 4\,\pi \,\sum \limits _{l\,m_{l}}\,i^{-l}\,Y_{l\,m_{l}}(-{\hat{{{\textbf {k}}}}})\,Y_{l\,m_{l}}^{*}({{\hat{{{\textbf {r}}}}}})\, \nonumber \\&\quad \times \frac{1}{k\,r}\,\Psi _{k\,l}^{(+)*}(r) \end{aligned}$$

(51)

with the partial-wave scattering wave function

$$\begin{aligned}&\Psi _{k\,l}^{(-)}(r) = -\frac{i}{2\,k\,r}\,\Big [f_{l}^{(-)*}(k,\,r) - {{\mathbb {S}}}_{l}^{*}\,f_{l}^{(+)*}(k,\,r)\Big ]. \end{aligned}$$

(52)

Also $\Psi _{ {{\textbf {k}}}}^{(-)*}({{\textbf {r}}})= \Psi _{ -{{\textbf {k}}}}^{(+)}({{\textbf {r}}}).$ The elastic scattering S-matrix element ${{\mathbb {S}}}_{l}^{*}$ does not have a resonance pole on the second energy sheet at $E=E_{R}$. It also follows from the unitarity condition $\,{{\mathbb {S}}}_{l}\,{{\mathbb {S}}}_{l}^{*}=1\,$ from which it is clear that at the resonance pole of ${{\mathbb {S}}}_{l}$ the conjugated ${{\mathbb {S}}}_{l}^{*}$ has zero. Hence in the product

$$\begin{aligned} \Psi _{k\,l}^{(-)}(r')\,\Psi _{k\,l}^{(+)}(r)&= \frac{1}{4\,k^{2}\,r'\,r}\,\Big [f_{l}^{(-)*}(k,\,r') - {{\mathbb {S}}}_{l}^{*}\,f_{l}^{(+)*}(k,\,r')\Big ] \nonumber \\&\quad \times \Big [f_{l}^{(-)}(k,\,r) - {{\mathbb {S}}}_{l}\,f_{l}^{(+)}(k,\,r)\Big ] \end{aligned}$$

(53)

only the term $-\frac{1}{4\,k^{2}\,r'\,r}\,f_{l}^{(-)*}(k,\,r')\,{{\mathbb {S}}}_{l}\,f_{l}^{(+)}(k,\,r)$ contains the resonance in the fourth quadrant in the complex k-plane (fourth quadrant of the second energy sheet).

We need to do the following steps to single out the resonance term from the spectral decomposition (49) of the Green function.

• 1. First we perform the integration over the solid angle $\Omega _{{{\textbf {{ k}}}}}$.

• 2. Then, we select the term containing the S-matrix element ${{\mathbb {S}}}_{l}$ which has a resonance pole on the second Riemann sheet at the relative energy $E =E_{R}=E_{0} - i\Gamma /2$, where $\Gamma$ is the total resonance width. In the momentum plane this resonance pole occurs at the relative momentum $k_{\textrm{R}}= k_{0} - i\,k_{I}$.

• 3. When $k \rightarrow k_{\textrm{R}}$ the integration contour over k moves down to the fourth quadrant pinching the contour to the pole at $k_{\textrm{R}}$. Taking the residue at the pole $\,E= E_{\textrm{R}}\,$ one can single out the resonance contribution to $\,G({{\textbf {r}}}',\,{{\textbf {r}}};E)\,$.

Now we can proceed to the practical realization of the outlined scheme.

After integration over $\Omega _{{{\textbf {{ k}}}}}$ Eq. (49) reduces to

$$\begin{aligned}&G({{\textbf {r}}}',\,{{\textbf {r}}};E) = \frac{1}{2\,\pi \,r'\,r}\,\sum \limits _{l\,m_{l}}\,Y_{l\,m_{l}}^{*}({\hat{{{\textbf {r}}}}}')\,Y_{l\,m_{l}}({\hat{{{\textbf {r}}}}})\nonumber \\&\quad \int \limits _{0}^{\infty }\,\textrm{d}k \,\frac{ \Big [f_{l}^{(-)*}(k,\,r') - {{\mathbb {S}}}_{l}^{*}(k)\,f_{l}^{(+)*}(k,\,r')\Big ] \Big [f_{l}^{(-)}(k,\,r) - {{\mathbb {S}}}_{l}(k)\,f_{l}^{(+)}(k,\,r)\Big ] }{ E - k^{2}/(2\,\mu ) + i0 }. \end{aligned}$$

(54)

To be definite, assume that a resonance occurs at $l=l_{0}$. Then the resonance contribution to $G({{\textbf {r}}},\,{{\textbf {r}}};E)$ comes from the partial Green function

$$\begin{aligned} G_{l_{0}}(r',\,r;E) = \frac{1}{2\,\pi \,r'\,r}\,\int \,\textrm{d}k \,\frac{f_{l_{0}}^{(+)}(k,\,r'){{\mathbb {S}}}_{l_{0}}(k)\,f_{l_{0}}^{(+)}(k,\,r)}{ E - k^{2}/(2\,\mu ) + i0 }, \end{aligned}$$

(55)

where we took into account that at real k $\;f_{l}^{(-)*}(k,\,r) = f_{l}^{(+)}(k,\,r).$ The S-matrix elastic scattering element ${{\mathbb {S}}}_{l_{0}}(k)$ for the single-channel, single-level case is given by Eq. (87), see below.

At $k \rightarrow k_{R}$ the integration contour over k moves down to the fourth quadrant pinching the contour to the resonance pole $k=k_{R}$. Note that this pole corresponds to the pole in the energy plane at $E=E_{R}$ located in the fourth quadrant of the second energy sheet. Substituting Eq. (87) for ${{\mathbb {S}}}_{l_{0}}(k)$ and taking the residue in the resonance pole we get what we sought:

$$\begin{aligned} G_{l_{0}}(r',\,r;E) = G_{l_{0}}^{R}(r',\,r;E) + G_{l_{0}}^{NR}(r',\,r;E), \end{aligned}$$

(56)

where

$$\begin{aligned}&G_{l_{0}}(r',\,r;E) =- \frac{ {\, \big | \phi _{\textrm{R}}(r')> < {{{\tilde{\phi }}}}_{\textrm{R}}(r)} {\big |}}{ E - k_{R}^{2}/(2\,\mu ) }, \end{aligned}$$

(57)

$\,\phi ^{GS}_{l}(r)= \varphi _{l}^{GS}(r)/r\,$ and

$$\begin{aligned} \varphi _{l_{0}}^{GS}(r)&= e^{i\,\delta ^{p}(k_{0})} \,\sqrt{ \frac{\mu }{k_{\textrm{R}}}\,\Gamma }\,f_{l_{0}}^{(+)}({k_{\textrm{R}}},{r}), \end{aligned}$$

(58)

$$\begin{aligned} {{{\tilde{\varphi }}}}_{l_{0}}^{GS}(r)&= e^{-i\,\delta ^{p}(k_{0})} \,\sqrt{ \frac{\mu }{k_{\textrm{R}}^{*}}\,\Gamma }\,\big [f_{l_{0}}^{(+)}({k_{\textrm{R}}},{r})\big ]^{*} \end{aligned}$$

(59)

are the Gamow–Siegert resonant wave functions. Note that $\, {{{\tilde{\phi }}}}_{\textrm{R}}(r)\,$ is the Gamow–Siegert wave function from the dual basis. The Jost solution $f_{l_{0}}^{(+)}({k_{\textrm{R}}},{r})$ is regular in the origin ($r=0$). For narrow resonances $k_{R}$ can be replaced by $k_{0}$.

3.3 ANCs and overlap functions for resonance states

Equations obtained in Sect. 3.1, which express the residues of the S-matrix elastic element in terms of the ANCs of the bound states and resonances, provide the most general and model-independent definition of the ANCs. From other side, we introduced the ANC as the amplitude of the tail of the two-body Gamow–Siegert resonance functions.

To introduce the ANC for composite particles we need to engage the overlap functions (see review [1]). Formally the radial resonance overlap function for the Breit–Wigner resonance in the external region ($r_{aA} > R_{ch(aA)}$, where $R_{ch(aA)}$ is the channel radius in the channel $a+A$) can be obtained from Eq. (107), review [1] by the substitution $\kappa _{{aA} }=-i\,k_{aA\,(R) }$:

$$\begin{aligned}&I_{aA\,\,{l_B}\,{j_B}\,J_{B}}(k_{aA(R)},\,{r_{aA}}) \nonumber \\&\quad =\,\,{C^{B}_{aA\,{l_B}\,{j_B}\,J_{B}}}\frac{{{W_{ - i\,{\eta _{aA( R)}},\,\,{l_B} + 1/2}}(-2\,i\,k_{aA\,( R)}{r_{aA}})}}{{{r_{aA}}}} \end{aligned}$$

(60)

$$\begin{aligned}&\xrightarrow {{{r_{aA}} \rightarrow \infty }}{C^{B}_{aA\,{l_B}{j_B} J_{B}}}\,e^{-\pi \,\eta _{aA( R)}/2} \frac{{{e^{ i\,k_{aA\,( R)}\,{r_{aA}} - \,i\,\eta _{aA( R)}\ln (2\,i\,k_{aA\,(R)}\,{r_{aA}})}}}}{{{r_{aA}}}}. \end{aligned}$$

(61)

This asymptotic behavior agrees with the asymptotic behavior of the resonant Gamow wave function given by Eq. (18).

4 Resonance wave functions and S-matrix in R-matrix approach

One of the most effective and powerful methods to treat resonance processes is the R-matrix method. In a number of cases, in this section and the sections below, we will employ the R-matrix approach. There have been few systematic and excellent reviews on the R-matrix method. First and foremost of them is a “bible” of the R-matrix method by Lane and Thomas [18]. It is also worth mentioning the reviews by Vogt [19], Descouvemont and Baye [20]. One of the significant practical contributions of the R-matrix method has been made by Barker ( see Barker [21], Barker and Kajino [22] and references therein). Azuma et al. [23] developed the most advanced R-matrix code AZURE. It is necessary to single out an excellent work by Brune [24] in which the ANC in the R-matrix formalism was considered. Finally, I need to refer the reader to another very important work by Maxaux and Weidenmüller [25]. In some derivations below we followed these works.

The first application of the R-matrix method are the multichannel scattering wave functions. The R-matrix approach is based on splitting the configuration space into the internal and external subspaces. That is why it makes sense to consider separately internal and the external scattering wave functions and then their matching at the channel radius.

4.1 Internal scattering wave function

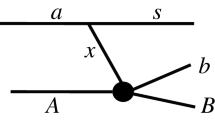
A general equation for the internal wave function contains the sum over total angular momentum $J_{F}$ and its projection $M_{F}$. Since we are interested in a wave function $\Psi _{bB}^{(-)}$ describing a resonance in the system $F=b+B$, we consider only the internal wave function at given $J_{F}$, at which resonance occurs in the presence of a few levels and two channels. We also use the LS-coupling scheme, that is, the channel spin representation, which is customary in the R-matrix approach. In the internal region in the state with the total momentum $J_{F}$, channel spin s (its projection $m_{s}$) in the initial channel $c=b+B$ the wave function $\Psi _{bB}^{(-)}$ can be written as

$$\begin{aligned} \Psi _{c\,s\,m_{s}}^{J_{F}(int)}&= \,\frac{2\,\pi }{k_{c}}\,\sqrt{\frac{k_{c}}{\mu _{c}}} \,\sum \limits _{M_{F}\,l\,m_{l}}\, e^{-i\,(\delta _{c\,l}^{hs}- \sigma _{cl}^{C})}\,i^{l}\,<s\,m_{s}\,\,l\,m_{l}|J_{F}\,M_{F}> \nonumber \\&\quad \times Y_{l\,m_{l}}^{*}({{\hat{{{\textbf {k}}}}}}_{c})\,\sum \limits _{\nu ,\tau = 1}^N [\Gamma _{\nu \,c\,s\,l\,J_{F}}(E_{c})]^{1/2}\,\big [\mathbf{\mathcal{A}}(E)\big ]_{\nu \tau }\,X_{\tau \,}^{J_{F}M_{F}}. \end{aligned}$$

(62)

Here $\,X_{\tau }^{J_{F}\,M_{F}}$ is an eigenfunction of the Hamiltonian in the internal region describing the compound system $F=b+B$ coupled with open channels and excited to the discrete level $\tau$ with the total angular momentum $J_{F}$ and its projection $M_{F}$,⁴$\,N$ is the number of the levels included, $\sigma _{cl}^{C}$ is the Coulomb scattering phase shift in channel $c,\,$ $\,\mathbf{\mathcal{A}}$ is the R-matrix level matrix:

$$\begin{aligned}{}[\mathbf{\mathcal{A}^{-1}}(E)]_{\nu \,\tau }&= (E_{\nu }- E_{c}) \delta _{\nu ,\tau } - \sum \limits _{{{\tilde{c}}}}\,\gamma _{\nu \,{{\tilde{c}}}}\,\gamma _{\tau \,{{\tilde{c}}}}\,\Big [{{\hat{S}}}_{{{\tilde{c}}}}(E_{{{\tilde{c}}}}) - B_{{{\tilde{c}}}} \nonumber \\&\quad +i\,P_{{{\tilde{c}}}}(E_{c},\,R_{ch({{\tilde{c}}})})\Big ]. \end{aligned}$$

(63)

Here $\sum \limits _{{{\tilde{c}}}}$ is the sum over all the open coupled channels, $E_{\nu }$ is the R-matrix energy of the level $\nu$, $\gamma _{\nu \,c}$ is the formal reduced width amplitude of the level $\nu$ in channel c, ${{\hat{S}}}_{c}(E_{c})$ is the level shift, $B_{c}$ is the level-independent boundary condition, $\,P_{c}(E_{c},\,R_{ch(c)})$ is the R-matrix penetrability factor in channel c. Also s is the channel spin, $l\, (m_{l})$ is the resonance orbital angular momentum (its projection), $\,E_{c}=E_{bB}$ and ${{\textbf {k}}}_{c}={{\textbf {k}}}_{bB}$ are the relative energy and momentum of particles b and B, $\,\mu _{c}= \mu _{bB}$, $\, \Gamma _{\nu \,c}(E_{c})$ is the formal (R-matrix) partial resonance width of the level $\nu$ in the channel $\,c=b+B$, $\,\delta _{c\,l}^{hs}$ is the hard-sphere scattering phase shift in the channel c given by

$$\begin{aligned} e^{-2\,i\,(\delta _{c\,l}^{hs} - \sigma _{cl}^{C} ) }&=\frac{I_{l}(k_{c},\,R_{ch(c)})}{O_{l}(k_{c},\,R_{ch(c)})}\nonumber \\&= \frac{G_{l}(k_{c},\,R_{ch(c)}) - i\,F_{l}(k_{c},\,R_{ch(c)})}{G_{l}(k_{c},\,R_{ch(c)}) + i\,F_{l}(k_{c},\,R_{ch(c)})}\,e^{i\,2\,\sigma _{c\,l}^{C}}, \end{aligned}$$

(64)

where $\sigma _{cl}^{C}$ is the Coulomb scattering phase shift in the channel c, $I_{l}(k_{c},r_{c})$ and $O_{l}(k_{c},r_{c})$ are the Coulomb ingoing and outgoing Jost singular solutions, $\,F_{l}(k_{c},\,r_{c})$ and $G_{l}(k_{c},\,r_{c})$ are regular and singular Coulomb solutions, $\,R_{ch(c)}$ is the channel radius in the channel c.

A separable form for $\Psi _{c\,s\,m_{s}}^{J_{F}(int)}$ reflects the fact that we consider the $b+B$ interaction proceeding through resonance states. The entry channel of this scattering is the channel $c=b+B$. The inverse level matrix contains contribution from all N resonance levels. In a simple one-level case it reduces to the well-known Breit–Wigner type resonance propagator. All the open channels coupled to c contribute to $X_{\tau }^{J_{F}\,M_{F}}$ and determine possible exit channel contributions into resonance scattering. We assume that the initial channel $b+B$ is coupled via the resonance scattering to two channels, $c=b+B$ and $c'=n+A$. Hence in the internal region, where these open channels are coupled, $X_{\tau }^{J_{F}\,M_{F}}$ can be written as a nonorthogonal sum:

$$\begin{aligned} X_{\tau }^{J_{F}\,M_{F}} = \sum \limits _{ {{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{\tilde{s}}}}\,\frac{1}{r_{{\tilde{c}}}}\,{{\hat{A}}}_{c}\left\{ \xi _{{{\tilde{c}}}}\,\phi _{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{\tilde{s}}}}^{J_{F}\,M_{F}}\,u_{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}}\right\} , \end{aligned}$$

(65)

Here ${{\hat{A}}}_{{\tilde{c}}}$ is the antisymmetrization operator between the nucleons of the fragments in the channel ${{\tilde{c}}}$. For example, for the channel $c=b+B$

$$\begin{aligned} {{\hat{A}}}_{{\tilde{c}}} = {{\hat{A}}}_{bB} = \left( \begin{aligned} b+B \\ \;\;\;b \\ \end{aligned} \right) ^{-\frac{1}{2}}\,\sum \limits _{p}\,(-1)^{p}\,{{\hat{P}}}, \end{aligned}$$

(66)

${{\hat{P}}}$ is the operator of the permutations of the nucleons of b and B. Sum p stands for all the possible permutations of one, two,... b nucleons from each nucleus. Then $(-1)^{p}$ determines the parity of the permutaion ($p=-1$ for odd and $p=1$ for even permutaions). Also $\xi _{{\tilde{c}}}$ is the product of the antisymmetrized bound-state wave functions of the fragments in the channel ${{\tilde{c}}}$, $\,{{\tilde{c}}}=c,\,c'$, $\,\,u_{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}}$ is the wave function of the relative motion of the fragments in the state $\{ {{\tilde{s}}}\,{{\tilde{l}}}\,J_{F} \}$ in some adopted potential with the same boundary condition as $X_{\tau }^{J_{F}\,M_{F}}.\,$ $\,{{\tilde{s}}},\,{{\tilde{l}}},\,J_{F}$ are the channel spin, orbital angular momentum and the total angular momentum of the fragments in channel ${{\tilde{c}}}$.

The channel spin-angular wave function (in LS-coupling) $\,\phi _{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{\tilde{s}}}}^{J_{F}\,M_{F}}\,$ in the channel $\{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{\tilde{s}}}\}$ is given by

$$\begin{aligned} \phi _{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{\tilde{s}}}}^{J_{F}\,M_{F}}&= \,\sum \limits _{m_{{\tilde{l}}}}\,< {{\tilde{s}}}\,m_{{{\tilde{s}}}}\,\,{{\tilde{l}}}\, m_{{\tilde{l}}}|\,J_{F}\,M_{F} >\,Y_{{{\tilde{l}}}\,m_{{\tilde{l}}}}({\widehat{{{\textbf {r}}}}}_{{{\tilde{c}}}}) \nonumber \\&\quad \times \psi _{{{\tilde{c}}}\,{{\tilde{s}}}\,m_{{\tilde{s}}}}. \end{aligned}$$

(67)

$\psi _{{{\tilde{c}}}\,{{\tilde{s}}}\,m_{{\tilde{s}}}}$ is the channel-spin wave function in the channel $\{{{\tilde{c}}}\,{{\tilde{s}}}\,m_{{\tilde{s}}}\}$. For example, in channel $\{c\,s\,m_{s}\}$

$$\begin{aligned} \psi _{c\,s\,m_{s} }&= \sum \limits _{M_{b}\,M_{B}}\,<J_{b}\,M_{b}\,\,J_{B}\,M_{B}|{s}\,m_{s}> \nonumber \\&\quad \times \psi _{J_{b}\, M_{b}}\,\psi _{J_{B}\, M_{B}}. \end{aligned}$$

(68)

Here $\,\,\psi _{J_{i}\, M_{i}}$ is the spin wave function of particle i, $s\,(m_{s})$ is the channel spin (its projection) of channel c, $\,{{\textbf {r}}}_{c}= {{\textbf {r}}}_{bB}$ is the radius-vector connecting c.m.(s) of particles b and B. The sum over $m_{{\tilde{l}}}$ in Eq. (67) is formal because $m_{{\tilde{s}}}$ and $M_{F}$ are fixed in this equation.

We introduce now the projection of the wave function $\,\Psi _{c}^{(int)}\,$ with the incident channel c on the two-cluster channel ${{\tilde{c}}}$: $\Upsilon _{c;{{\tilde{c}}}}= <{{\hat{A}}}_{{\tilde{c}}}\,\xi _{{{\tilde{c}}}}|\Psi _{c}^{(int)}>.$ Then

$$\begin{aligned} \Upsilon _{c\,s\,m_{s}; {{\tilde{c}}}}^{J_{F}\,(int)}&=\,<{{\hat{A}}}_{{{\tilde{c}}}}\,\xi _{{{\tilde{c}}}}|\Psi _{c\,s\,m_{s}}^{J_{F}(int)}> \nonumber \\&= \,\frac{2\,\pi }{k_{c}}\,\sqrt{\frac{k_{c}}{\mu _{c}}} \,\sum \limits _{M_{F}\,l\,m_{l}}\, e^{-i\,(\delta _{c\,l}^{hs}- \sigma _{cl}^{C})}\,i^{l}\,<s\,m_{s}\,\,l\,m_{l}|J_{F}\,M_{F}> \nonumber \\&\quad \times Y_{l\,m_{l}}^{*}({{\hat{{{\textbf {k}}}}}}_{c})\,\sum \limits _{\nu ,\tau = 1}^N [\Gamma _{\nu \,c\,s\,l\,J_{F}}(E_{c})]^{1/2}\,\big [\mathbf{\mathcal{A}}^{ - 1}\big ]_{\nu \tau }\, \Xi _{\tau \,{{\tilde{c}}}}^{J_{F}M_{F}}, \end{aligned}$$

(69)

where

$$\begin{aligned} \Xi _{\tau \,{{\tilde{c}}}}^{J_{F}M_{F}}&=\,<{{\hat{A}}}_{{{\tilde{c}}}}\,\xi _{{{\tilde{c}}}}|X_{\tau }^{J_{F}M_{F}}> \nonumber \\&= N_{{\tilde{c}}}\,<\xi _{{{\tilde{c}}}}|X_{\tau }^{J_{F}M_{F}}>. \end{aligned}$$

(70)

Here the orbital angular momenta l in the incident channel and ${{\tilde{l}}}$ in the exit channel are fixed. $N_{{\tilde{c}}} = \big [\frac{(A_{1}+A_{2})!}{A_{1}!\,A_{2}!}\big ]^{1/2},$ $A_{1}$ and $A_{2}$ are the number of nucleons of the fragments of the channel ${{\tilde{c}}}$. Here we used the fact that ${{\hat{A}}}$ is the Hermitian (self-adjoint) operator. That is why it can be moved from the bra to ket state acting on $X_{\tau }^{J_{F}\,M_{F}}$. Since $X_{\tau }^{J_{F}\,M_{F}}$ is fully antisymmetrized, ${{\hat{A}}}_{{\tilde{c}}}\,X_{\tau }^{J_{F}\,M_{F}}=N_{{\tilde{c}}}\,X_{\tau }^{J_{F}\,M_{F}}.$

4.2 Reduced width amplitudes

We adopt the channel radius $R_{ch({{\tilde{c}}})}$ large enough to neglect antisymmetrization between the nucleons of the fragments of channel ${{\tilde{c}}}$ at $r_{{\tilde{c}}}= R_{ch({{\tilde{c}}})}$, that is,

$$\begin{aligned}&{{\hat{A}}}\{\xi _{{{\tilde{c}}}}\,\phi _{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{\tilde{s}}}}^{J_{F}\,M_{F}}\,u_{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}\,}\}\Big |_{r_{{{\tilde{c}}}}= R_{ch({{\tilde{c}}})}} \nonumber \\&\quad \approx N_{{{\tilde{c}}}}^{-1}\,\xi _{{\tilde{c}}}\,\phi _{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{{\tilde{s}}}}}^{J_{F}\,M_{F}}\,u_{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}\,}\Big |_{r_{{{\tilde{c}}}} = R_{ch({{\tilde{c}}})}}. \end{aligned}$$

(71)

Assuming that the overlap of channels c and ${c'}$ at the channel radius is negligible, we get the projection of $X_{\tau }^{J_{F}\,M_{F}}$ on channel ${{\tilde{c}}}$ at $r_{{{\tilde{c}}}}= R_{ch({{\tilde{c}}})}$:

$$\begin{aligned} \Xi _{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,m_{{\tilde{s}}}}^{J_{F}\,M_{F}}(R_{{{\tilde{c}}}}{{\hat{{{\textbf {r}}}}}}_{{{\tilde{c}}}})&= N_{{\tilde{c}}}\,<\xi _{{{\tilde{c}}}}|X_{\tau }^{J_{F}\,M_{F}}>\Big |_{r_{{{\tilde{c}}}}= R_{{{\tilde{c}}}} } \nonumber \\&= \frac{1}{R_{ch({{\tilde{c}}})}}\,\sum \limits _{{{\tilde{l}}}}\,\phi _{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{{\tilde{s}}}}}^{J_{F}\,M_{F}}\,u_{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}}(R_{ch({{\tilde{c}}})}), \end{aligned}$$

(72)

where we used Eq. (71). Here $u_{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}}(R_{ch({{\tilde{c}}})})$ is the R-matrix level $\tau$ wave function, which the closest to resonance level under consideration.

At $r_{{{\tilde{c}}}}= R_{ch({{\tilde{c}}})}$, by definition,

$$\begin{aligned} u_{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}}(R_{ch({{\tilde{c}}})}) = \sqrt{2\,\mu _{{{\tilde{c}}}}\,R_{ch({{\tilde{c}}})}}\,\gamma _{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}}, \end{aligned}$$

(73)

where $\,\gamma _{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}}$ is the formal reduced width amplitude of the level $\tau$ in the channel ${{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}$. Thus in the R-matrix approach the reduced width amplitude is introduced as the boundary value (at $R_{ch({{\tilde{c}}})}$) of the internal radial wave function. It is useful to remind that the system of units ${\hbar }=c=1$ is being used throughout the paper if not specified otherwise. Then

$$\begin{aligned} \Xi _{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,m_{{\tilde{s}}}}^{J_{F}\,M_{F}}(R_{{{\tilde{c}}}}{{\hat{{{\textbf {r}}}}}}_{{{\tilde{c}}}})= & {} N_{{\tilde{c}}}\,<\xi _{{{\tilde{c}}}}|X_{\tau }^{J_{F}\,M_{F}}>\Big |_{r_{{{\tilde{c}}}}= R_{{{\tilde{c}}}} } \nonumber \\= & {} \frac{1}{R_{ch({{\tilde{c}}})}}\,\sum \limits _{{{\tilde{l}}}}\,\phi _{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{{\tilde{s}}}}}^{J_{F}\,M_{F}}\,\sqrt{2\,\mu _{{{\tilde{c}}}}\,R_{ch({{\tilde{c}}})}}\,\gamma _{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}}. \nonumber \\ \end{aligned}$$

(74)

Thus we can express the component $\Xi _{\tau \,{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,m_{{\tilde{s}}}}^{J_{F}\,M_{F}}(R_{{\tilde{c}}})$ taken at the channel radius $r_{{{\tilde{c}}}}= R_{ch({{\tilde{c}}})}$ in terms of the sum of the reduced widths amplitudes in all allowed partial waves ${{\tilde{l}}}$ in the channel ${{\tilde{c}}}$ at given $J_{F}$ and ${{\tilde{s}}}$.

4.3 External scattering wave function

Now we proceed to the expression for the $\Psi _{c}^{(+)}$ in the external region, where $r_{c} > R_{ch(c)}$ or $r_{c'} > R_{ch(c')}$. In the external region the wave function $\Psi _{c\,s\,m_{s}}^{(ext)(+)}$ with fixed channel spin and its projection in the incident channel c can be written as

$$\begin{aligned} \Psi _{c\,s\,m_{s}}^{(ext)(+)} = \Psi _{c\,s\,m_{s}}^{(0)} + \Psi _{c\,s\,m_{s};r}^{(ext)(+)}, \end{aligned}$$

(75)

where the first term is the incident wave and the second term is the sum of the outgoing waves in all the open channels. The incident term is

$$\begin{aligned} \Psi _{c\,s\,m_{s}}^{(ext)(0)}&= \,4\,\pi \,\xi _{c}\,\sum \limits _{J_{F}\,M_{F}}\,\sum \limits _{l\,m_{l}\,m_{s''}}\,i^{l}\,<s\,m_{s}\,\,l\,m_{l}\,|J_{F}\,M_{F}>\, \nonumber \\&\quad \times <s\,m_{s''}\,\,l\,m_{l}|J_{F}\,M_{F}\nonumber \\&>\,Y_{l\,m_{l}}^{*}({{\hat{{{\textbf {k}}}}}}_{c})\,\frac{e^{2\,i\,\sigma _{cl}^{C}}\, F_{l}(k_{c},\,r_{c}) }{k_{c}\,r_{c}} \nonumber \\&\quad \times Y_{l\,m_{l}}({\hat{{\textbf {r}}}}_{c})\,\phi _{c\,s\,m_{s''}}, \end{aligned}$$

(76)

where $F_{l}$ is the regular Coulomb solution. The subscript c means that the incident wave is in channel c. The sum over $m_{s''}$ is a formal because

$$\begin{aligned} \sum \limits _{J_{F}\,M_{F}}&<s\,m_{s}\,\,l\,m_{l}\,|J_{F}\,M_{F}>\,<s\,m_{s''}\,\,l\,m_{l}|J_{F}\,M_{F}> \nonumber \\&= \delta _{m_{s}\,m_{s''}}. \end{aligned}$$

(77)

Note that here we use the incident wave with the unit amplitude rather than with the unit flux density. The component $\Psi _{c\,s\,l\,m_{s};c\,s\,l\,m_{s''}}^{J_{F}(ext)(0)}$, which corresponds to the exit channel $\{c\,s\,l\,m_{s''}\}$ and fixed $J_{F}$, projected on $\xi _{c}$ reduces to

$$\begin{aligned} \Upsilon _{c\,s\,l\,m_{s};c\,s\,l\,m_{s''}}^{J_{F}(ext)(0)}&= \,4\,\pi \,\sum \limits _{M_{F}\,m_{l}}\,i^{l}\,<s\,m_{s}\,\,l\,m_{l}\,|J_{F}\,M_{F}> \nonumber \\&\quad \times <s\,m_{s''}\,\,l\,m_{l}|J_{F}\,M_{F}> \,Y_{l\,m_{l}}^{*}({{\hat{{{\textbf {k}}}}}}_{c})\,\frac{e^{2\,i\,\sigma _{cl}^{C}}\,F_{l}(k_{c},\,r_{c}) }{k_{c}\,r_{c}} \nonumber \\&\quad \times Y_{l\,m_{l}}({\hat{{\textbf {r}}}}_{c})\,\phi _{c\,s\,m_{s''}}. \end{aligned}$$

(78)

Thus the incident wave is the pure Coulomb scattering wave function in the incident channel c. Taking into account that

$$\begin{aligned} F_{l}(k_{c},r_{c}) = \frac{e^{i\,\sigma _{c\,l}^{C}}\,O_{l}(k_{c},r_{c}) - e^{-\sigma _{c\,l}^{C}}\,I_{l}(k_{c},r_{c})}{2\,i}, \end{aligned}$$

(79)

one can rewrite $\Upsilon _{c\,s\,l\,m_{s};c\,s\,l\,m_{s''}}^{J_{F}\,(ext)(0)}$ in the form

$$\begin{aligned} \Upsilon _{c\,s\,l\,m_{s};c\,s\,l\,m_{s''}}^{J_{F}(ext)(0)}&= \frac{2\,\pi }{k_{c}\,r_{c} }\,i^{l+1} \sum \limits _{M_{F}\,m_{l}}\,<s\,m_{s}\,\,l\,m_{l}\,|J_{F}\,M_{F}>\, \nonumber \\&<s\,m_{s''}\,\,l\,m_{l}|J_{F}\,M_{F}> \nonumber \\&\quad \times \,Y_{l\,m_{l}}^{*}({{\hat{{{\textbf {k}}}}}}_{c})\,\Big [I_{l}(k_{c},\,r_{c}) - e^{i\,2\,\sigma _{c\,l}^{C}}\,O_{l}(k_{c},\,r_{c})\Big ]\nonumber \\&\quad \,Y_{l\,m_{l}}({\widehat{{\textbf {r}}}}_{c})\,\phi _{c\,s\,m_{s''}}. \end{aligned}$$

(80)

The second term in Eq. (75) is given by the sum of the outgoing waves in the open channels:

$$\begin{aligned} \Psi _{c\,s\,m_{s}}^{(ext)( + )}&= \,i\,\frac{2\,\pi }{k_{c}}\,\sum \limits _{{\tilde{c}}}\,\sqrt{\frac{v_{c}}{v_{{\tilde{c}}}}}\,\frac{1}{r_{{\tilde{c}}}}\,\xi _{{\tilde{c}}}\, \sum \limits _{J_{F}\,M_{F}\,{{\tilde{s}}}\,l\,{{\tilde{l}}}\,m_{{\tilde{s}}}\,m_{l}\,m_{{\tilde{l}}}}\,\,\nonumber \\ i^{l}\,&<s\,{m_s}\,\,l\,m_{l}|J_{F}\,M_{F}>\,Y_{l\,m_{l}}^{*}({{\hat{{{\textbf {k}}}}}}_{c}) \nonumber \\&\quad \times \, \Big [ e^{i\,2\,\sigma _{c\,l}^{C}}\,\delta _{{{\tilde{c}}}\,c}\,\delta _{{{\tilde{s}}}\,s}\,\delta _{{{\tilde{l}}}\,l} - {{\mathbb {S}}}_{ {{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}};c\,s\,l}^{J_{F}}(k_{c}) \Big ]\,O_{l}(k_{c},\,r_{c}) \, \nonumber \\&< {{\tilde{s}}}\,m_{{\tilde{s}}}\,\,{{\tilde{l}}}\,m_{{\tilde{l}}}|J_{F}\,M_{F} >\, Y_{ {{\tilde{l}}}\,m_{{\tilde{l}}} }({{\hat{{{\textbf {r}}}}}}_{{\tilde{c}}})\,\phi _{{{\tilde{c}}}\,{{\tilde{s}}}\,m_{{\tilde{s}}}}. \end{aligned}$$

(81)

Here $\,{{\mathbb {S}}}_{ {{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}};c\,s\,l}^{J_{F}}(k_{c})$ is the S-matrix element for transition $\{c\,s\,l\,J_{F}\} \rightarrow \{{{\tilde{c}}}\,{{\tilde{s}}}\,{{\tilde{l}}}\,J_{F}\}$. Note that we consider the outgoing waves in the channel with given total angular momentum $J_{F}$, initial channel spin s (its projection $m_{s}$) and final channel spin ${{\tilde{s}}}$ (its projection $m_{{\tilde{s}}}$). Since only two open channels are taken into account here, we will write explicitly the outgoing waves in both channels.

4.4 ${\textbf{S}}$-matrix in R-matrix approach

Now we have everything to derive the expression for the matrix elements of the S-matrix in the R-matrix approach. Since the wave function $\Psi _{c}^{(+)}$ is continuous we can equate the projections of the internal and external wave functions at the channel radius $R_{ch}$:

$$\begin{aligned} \Upsilon _{c\,s\,l\,\,m_{s}; c\,s\,l\,m_{s''}}^{J_{F}(int)}(R_{ch(c)})&= \Upsilon _{c\,s\,l\,m_{s};c\,s\,l\,m_{s''}}^{J_{F}(ext)(0)}(R_{ch(c)}) \nonumber \\&\quad + \Upsilon _{c\,s\,l\,m_{s};c\,s\,l\,m_{s''}}^{(ext)( + )}(R_{ch(c)}), \end{aligned}$$

(82)

This equation boils down to

$$\begin{aligned}&e^{-i\,(\delta ^{hs}_{c\,l} - \sigma _{cl}^{C})}\,\sum \limits _{\nu ,\tau = 1}^N [\Gamma _{\nu \,c\,s\,l\,J_{F}}(E_{c})]^{1/2}\,\big [\mathbf{\mathcal{A}}^{-1}\big ]_{\nu \tau }\,\sqrt{2\,k_{c}\,R_{ch(c)}}\, \nonumber \\&\quad \times \gamma _{\tau \,c\,s\,l\,J_{F}}= i\,\big [ I_{l}(k_{c},\,R_{ch(c)}) \nonumber \\&\quad - {{\mathbb {S}}}_{c\,s\,l;c\,s\,l}^{J_{F}}(k_{c})\,O_{l}(k_{c},\,R_{ch(c)}) \big ]. \end{aligned}$$

(83)

Assembling Eq. (64),

$$\begin{aligned} \Gamma _{\tau \,c\,s\,l\,J_{F}}(E_{c})= 2\,P_{c\,l}(E_{c},\,R_{ch(c)})\,\gamma _{\tau \,c\,s\,l\,J_{F}}^{2} \end{aligned}$$

(84)

and the Coulomb-centrifugal barrier penetrability

$$\begin{aligned} P_{c\,l}(E_{c},\,R_{ch(c)}) = \frac{k_{c}\,R_{ch(c)}}{F_{l}^{2}(k_{c},\,R_{ch(c)}) + G_{l}^{2}(k_{c},\,R_{ch(c)})} \end{aligned}$$

(85)

into Eq. (83) we get the elastic scattering S-matrix element:

$$\begin{aligned}&{{\mathbb {S}}}_{c\,s\,l;\,c\,s\,l}^{J_{F}}(k_{c})= e^{-2\,i\,(\delta _{c\,l}^{hs} - \sigma _{cl}^{C})}\, \nonumber \\&\quad \Bigg (1+ i\,\sum \limits _{\nu ,\tau = 1}^N [\Gamma _{\nu \,c\,s\,l\,J_{F}}(E_{c})]^{1/2}\,\big [\mathbf{\mathcal{A}}^{-1} \big ]_{\nu \tau }\,[\Gamma _{\tau \,c\,s\,l\,J_{F}}(E_{c})]^{1/2} \Bigg ). \end{aligned}$$

(86)

For simpler single-channel, single-level case Eq. (86) turns into familiar resonant S-matrix expression:

$$\begin{aligned} {{\mathbb {S}}}_{c\,s\,l;\,c\,s\,l}^{J_{F}}(k_{c})= e^{-2\,i\,(\delta _{c\,l}^{hs} - \sigma _{cl}^{C})}\,\frac{E_{0(c)} - E_{c} + i\,\Gamma _{c\,s\,l}(E_{c})/2}{E_{0(c)} - E_{c} - i\,\Gamma _{c\,s\,l}(E_{c})/2}, \end{aligned}$$

(87)

where $E_{0(c)}$ is the real part of the complex resonance energy in the channel c. This equation is different from the Breit -Wigner S-matrix formula for a single resonance because it contains the energy-dependent resonance width $\Gamma _{c\,s\,l}(E_{c})$ rather than $\Gamma _{c\,s\,l}$, which appears in the Breit–Wigner expression. The presence of $\Gamma _{c\,s\,l}(E_{c})$ reflects a simple fact that the resonance S-matrix in the R-matrix approach takes effectively into account a background absent in the Breit–Wigner approximation.

From Eq. (87) follows the unitarity of the S-matrix:

$$\begin{aligned}{}[{{\mathbb {S}}}_{c\,s\,l;\,c\,s\,l}^{J_{F}}(k_{c})]^{*}\,{{\mathbb {S}}}_{c\,s\,l;\,c\,s\,l}^{J_{F}}(k_{c})=1. \end{aligned}$$

(88)

Note that $[{{\mathbb {S}}}_{c\,s\,l;\,c\,s\,l}^{J_{F}}(k_{c})]^{*}$ does not posses a resonance pole in the fourth quadrant of the energy plane.

From equality

$$\begin{aligned} \Upsilon _{c\,s\,m_{s};c'\,s'\,m_{s'}}^{J_{F}(int)}(R_{ch(c')}) = \Upsilon _{c\,s\,l\,m_{s};c'\,s'\,l'\,m_{s'}}^{(ext)( + )}(R_{ch(c')}) \end{aligned}$$

(89)

we obtain the reaction matrix element:

$$\begin{aligned}&{{\mathbb {S}}}_{c\,s\,l;\,c'\,s'\,l'}^{J_{F}}(k_{c})= i\,e^{-\,i\,(\delta _{c\,l}^{hs} - \sigma _{cl}^{C})}\,e^{-\,i\,(\delta _{c'\,l'}^{hs} - \sigma _{c'l}^{C})}\,\sum \limits _{\nu ,\tau = 1}^N \nonumber \\&\quad \times [\Gamma _{\nu \,c\,s\,l\,J_{F}}(E_{c})]^{1/2} \big [\mathbf{\mathcal{A}}^{-1} \big ]_{\nu \tau }\,[\Gamma _{\tau \,c'\,s'\,l'\,J_{F}}(E_{c'})]^{1/2}. \end{aligned}$$

(90)

To derive this equation we took into account that

$$\begin{aligned} O_{l'}(k_{c'},R_{ch(c')})&= e^{\,i\,(\delta _{c'\,l'}^{hs} - \sigma _{c'l'}^{C})}\nonumber \\&\quad \sqrt{[F_{l'}(k_{c'},R_{ch(c')})]^{2} + [G_{l'}(k_{c'},R_{ch(c')})]^{2}} \nonumber \\&= e^{\,i\,(\delta _{c'\,l'}^{hs} - \sigma _{c'l}^{C})}\,\sqrt{\frac{ k_{c'}\,R_{ch(c')} }{P_{c'\,l'}(E_{c'},\,R_{ch(c')})} }. \end{aligned}$$

(91)

The obtained matrix elements of the S-matrix confirm that the relative normalization of the internal and external wave parts of $\Psi _{bB}^{(+)}$ are correct and one can use them to calculate the reaction amplitude proceeding through resonance states.

5 ANC and reduced widths in the R-matrix approach

Now we can consider the important ingredients of the R-matrix approach: the reduced width amplitude, the logarithmic derivative of the outgoing Coulomb solution, and the ANC. We derive an important relationship between these quantities both for bound and resonance states. We define the formal and observable single-particle reduced widths used in the R-matrix formalism and their connections to the single-particle ANC and full ANC via the Whittaker function describing the external part of the bound-state wave function. While the derivation is standard for the bound state, it is not the case for the resonance state and requires employing the normalizable Gamow–Siegert resonance wave functions. To avoid complications, we consider only narrow resonances. Again, as in Sect. 3, but using a different approach, we obtain the relationship between the ANC and the resonance width.

5.1 Reduced width and ANC for bound state

One of the main ingredients of the R-matrix is the reduced width amplitude, which has been introduced in Sect. 4.2. We start our consideration from the single-particle reduced width amplitude

$$\begin{aligned} {{{\tilde{\gamma }}}}_{l}^{sp} = \frac{ u_{l}(k,r)}{\sqrt{ 2\,\mu \,R_{ch}\,\displaystyle \int \nolimits _{0}^{R_{ch}}\textrm{d}r\,u_{l}^{2}(k,r)}}, \end{aligned}$$

(92)

which is the amplitude of the resonant or bound-state wave functions at the channel radius $R_{ch}$ assuming that the wave function is normalized to unity in the internal region $0 \le r \le R_{ch}$. $({{{\tilde{\gamma }}}}_{l}^{sp})^{2}$ is the reduced width. The single-particle wave function $u_{l}(k,\,r)$ is given by

$$\begin{aligned} u_{l}(k,r)&= 2\,i\,k\,\varphi _{l}(k,\,r)\nonumber \\&= \Big [f_{l}^{(-)}(k,r) + (-1)^{l+1}\,{{\mathbb {S}}}_{l}(k)\,f_{l}^{(+)}(k,r) \Big ], \end{aligned}$$

(93)

where $f_{l}^{(\pm )}(k,r)$ are the Jost (singular at the origin $r=0$) solutions. The wave function $\varphi _{l}(k,\,r)$ has been introduced in Eq. (2).

In the R-matrix method in which the coordinate space is split into the internal and external regions, it is customary to normalize the wave function in the internal region, although the bound-state and the resonant wave functions (see Sect. 2.3) can be normalized to unity in the whole coordinate space.

Often is used the dimensionless formal single-particle reduced width

$$\begin{aligned} ({{{\tilde{\theta }}}}_{l}^{sp})^{2}= \mu \,R_{ch}^{2}\,({{{\tilde{\gamma }}}}_{l}^{sp})^{2}=\frac{R_{ch}\,u_{l}^{2}(k,r)}{2\,\displaystyle \int \nolimits _{0}^{R_{ch}}\textrm{d}r\,u_{l}^{2}(k,r) }. \end{aligned}$$

(94)

Another important equation is the logarithmic derivative of $u_{l}(k,r)$ taken at $r>R_{ch}$. In this region $f_{l}^{\pm }(k,r)=f_{l}^{C(\pm \,)}(k,r)$ and

$$\begin{aligned} I_{l}(k,\,r)&= e^{i\,\pi \,l/2}\,f_{l}^{C(-)}(k,r), \end{aligned}$$

(95)

$$\begin{aligned} O_{l}(k,\,r)&= e^{-i\,\pi \,l/2}\,f_{l}^{C(+)}(k,r). \end{aligned}$$

(96)

Then Eq. (93) yields

$$\begin{aligned} \frac{\textrm{d} \ln u_{l}(k,r)}{\textrm{d}r} = \frac{{{\mathbb {S}}}_{l}^{-1}(E)\,\frac{\textrm{d}I_{l}(k,r)}{\textrm{d}r} - \frac{\textrm{d}O_{l}(k,r)}{\textrm{d}r}}{{{\mathbb {S}}}_{l}^{-1}(E)\,I_{l}(k,r) - O_{l}(k,r)}. \end{aligned}$$

(97)

Below, we will show how to introduce the ANC for bound states and resonances in the R-matrix approach. First, we consider the radial Schrödinger equation

$$\begin{aligned}&\Big (E + \frac{1}{2\,\mu }\,\frac{\textrm{d}^{2}}{\textrm{d}r^{2}}- V^{centr}_{l}(r) - V^{C}(r) \Big )\,u_{l}(k,r) \nonumber \\&\quad = V^{N}(r)\,u_{l}(k,r), \end{aligned}$$

(98)

where E is the relative kinetic energy of the interacting particles, $V^{N}(r),\,V^{C}(r)$ and $\,V^{centr}_{l}(r)\,$ are the nuclear, Coulomb and the centrifugal potentials.

Now we write down the Schrödinger equation (98) for two different energies $E_{i},\;i=1,2$, and two corresponding wave functions $u_{l (i)}(k,r),\;i=1,2$, multiply from the left the Schrödinger equation for $u_{l (1)}(k,r)$ ( $u_{l (2)}(k,r)$) by $u_{l (2)}(k,r)$ ($u_{l (1)}(k,r)$) and subtract the second equation from the first one:

$$\begin{aligned}&\frac{1}{2\,\mu }\,\frac{\textrm{d}}{\textrm{d}r}\Big [u_{l(1)}(k,r)\,\frac{ \textrm{d}u_{l (2)}(k,r)}{\textrm{d}r} - u_{l(2)}(k,r)\,\frac{\textrm{d}u_{l (1)}(k,r)}{\textrm{d}r}\Big ] \nonumber \\&\quad = (E_{1}-E_{2})\,u_{l(1)}(k,r)\,u_{l (2)}(k,r). \end{aligned}$$

(99)

Integrating both sides of Eq. (99) over r from $r_{1}$ to $r_{2}$ we obtain

$$\begin{aligned}&\frac{1}{2\,\mu }\,u_{l(1)}(k,r)\,u_{l(2)}(k,r)\,\Big [\frac{ \textrm{d}\ln \big (u_{l (2)}(k,r)\big )}{\textrm{d}r} - \frac{\textrm{d}\ln \big (u_{l (1)}(k,r) \big )}{\textrm{d}r}\Big ]\Big |_{r_{1}}^{r_{2}}\nonumber \\&\quad =(E_{1}-E_{2})\,\int \limits _{r_{1}}^{r_{2}}\textrm{d}r\,u_{l(1)}(k,r)\,u_{l (2)}(k,r). \end{aligned}$$

(100)

Taking the limit $E_{1} \rightarrow E_{2}$ (that is, $u_{l(1)}(k,r) \rightarrow u_{l(2)}(k,r)$) leads to

$$\begin{aligned} - \frac{1}{2\,\mu }\,\Big [u_{l}^{2}(k,r)\, \frac{\partial }{\partial E}\,\Big (\frac{ \textrm{d}\ln \big (u_{l }(k,r)\big )}{\textrm{d}r}\Big )\Big ]\Big |_{r_{1}}^{r_{2}} = \int \limits _{r_{1}}^{r_{2}}\,\textrm{d}r\,u_{l}^{2}(k,r). \end{aligned}$$

(101)

Taking $r_{1}=0$ and $r_{2}=R_{ch}$, and recalling that $u_{l}(k,0)=0$ we get

$$\begin{aligned}&- \frac{1}{2\,\mu }\,\Big [u_{l}^{2}(k,r)\, \frac{\partial }{\partial E}\,\Big (\frac{ \textrm{d}\ln \big (u_{l }(k,r)\big )}{\textrm{d}r}\Big )\Big ]\Big |_{r=R_{ch}} \!=\! \int \limits _{0}^{R_{ch}}\,\textrm{d}r\,u_{l}^{2}(k,r). \nonumber \\ \end{aligned}$$

(102)

The R-matrix formalism developed for resonance states can be extended for bound states for which $k=i\,\kappa ,\;E = - \kappa ^{2}/{2\,\mu } = - \varepsilon .$ In this case the bound-state wave function can be normalized to unity over the whole coordinate space:

$$\begin{aligned} \int \limits _{0}^{R_{ch}}\,\textrm{d}r\,u_{l}^{2}(i\,\kappa ,r) + \int \limits _{R_{ch}}^{\infty }\,\textrm{d}r\,u_{l}^{2}(i\,\kappa ,r) =1. \end{aligned}$$

(103)

Taking $r_{1}=R_{ch}$ and $r_{2}=\infty$ in Eq. (101), and recalling that $u_{l}(i\,\kappa ,r) {\mathop {=}\limits ^{r \rightarrow \infty }}0$ we get

$$\begin{aligned} \int \limits _{R_{ch}}^{\infty }\,\textrm{d}r\,u_{l}^{2}(i\,\kappa ,r)= \frac{1}{2\,\mu \,R_{ch}}\,u_{l}^{2}(i\,\kappa ,R_{ch})\, \frac{\partial {{\hat{S}}}_{l}(E)}{\partial E}\,\Big |_{E=-\varepsilon }, \end{aligned}$$

(104)

where

$$\begin{aligned}&\frac{ \textrm{d}\ln \big (u_{l }(i\,\kappa ,r)\big )}{\textrm{d}r}\Big |_{r=R_{ch}} = \frac{ \textrm{d}\ln \big (O_{l }(i\,\kappa ,r)\big )}{\textrm{d}r}\Big |_{r=R_{ch}} \nonumber \\&\quad = {{\hat{S}}}_{l}(E)\Big |_{E=-\kappa ^{2}/(2\,\mu )}. \end{aligned}$$

(105)

Introducing the wave function normalized over the internal region

$$\begin{aligned} {{\tilde{u}}}_{l}(k,r) = \frac{u_{l}(k,r)}{ \int \limits _{0}^{R_{ch}}\,\textrm{d}r\,u_{l}^{2}(k,r)} \end{aligned}$$

(106)

we can rewrite Eq. (104) as

$$\begin{aligned} \int \limits _{R_{ch}}^{\infty }\,\textrm{d}r\,{{\tilde{u}}}_{l}^{2}(i\,\kappa ,r)= ({{{\tilde{\gamma }}}}_{l}^{sp})^{2}\, \frac{\partial {{\hat{S}}}_{l}(E)}{\partial E}\Big |_{E=-\varepsilon }. \end{aligned}$$

(107)

Here ${{{\tilde{\gamma }}}}_{l}^{sp}$ is defined in Eq. (92).

Since in the R-matrix approach the bound-state wave function $u_{l}(i\,\kappa ,r)$ should be normalized over the internal space rather than over the entire coordinate space, we can express the normalization integral over the entire region in terms of the normalization integral over the internal region:

$$\begin{aligned} I_{0}^{\infty }&=\int \limits _{0}^{\infty }\,\textrm{d}r u_{l}^{2}(i\,\kappa ,r)= \Bigg [ 1 + {\int \limits _{R_{ch}}^{\infty }\,\textrm{d}r {{\tilde{u}}}_{l}^{2}(i\,\kappa ,r)}\Bigg ]\,\int \limits _{0}^{R_{ch}}\,\textrm{d}r u_{l}^{2}(i\,\kappa ,r) \nonumber \\&=\Big [ 1+ ({{{\tilde{\gamma }}}}_{l}^{sp})^{2}\, \frac{\partial {{\hat{S}}}_{l}(E)}{\partial E}\Big |_{E=-\varepsilon }\Big ]\,\int \limits _{0}^{R_{ch}}\,\textrm{d}r u_{l}^{2}(i\,\kappa ,r). \end{aligned}$$

(108)

To satisfy normalization condition (103) one can introduce $\frac{u_{l}^{2}(i\,\kappa ,R_{ch})}{I_{0}^{\infty }}$. Asymptotic of this single-particle wave function is expressed in terms of the single-particle ANC $\,b_{l}$. To show it we write

$$\begin{aligned} \frac{u_{l}^{2}(i\,\kappa ,R_{ch})}{I_{0}^{\infty }}&= 2\,\mu \,R_{ch}\,\frac{ ({{{\tilde{\gamma }}}}_{l}^{sp})^{2} }{1 + ({{{\tilde{\gamma }}}}_{l}^{sp})^{2}\,\frac{\partial {{\hat{S}}}}{\partial E}\Big |_{ E= -\varepsilon }} \nonumber \\&= b_{l}^{2}\,W_{-\eta ^{bs},\,l+1/2}^{2}(2\,\kappa \,R_{ch}), \end{aligned}$$

(109)

$\eta ^{bs}$ is the Coulomb parameter of the bound state.

The formal single-particle reduced width $({{{\tilde{\gamma }}}}_{l}^{sp})^{2}$ is related to the single-particle observable width $({\gamma }_{l}^{sp})^{2}$:

$$\begin{aligned} ({\gamma }_{l}^{sp})^{2}= \frac{({{{\tilde{\gamma }}}}_{l}^{sp})^{2}}{1 + ({{{\tilde{\gamma }}}}_{l}^{sp})^{2}\, \frac{\partial {{\hat{S}}}}{\partial E}\Big |_{E=-\varepsilon }}. \end{aligned}$$

(110)

Then the single-particle ANC is

$$\begin{aligned} b_{l}^{2}= \frac{2\,\mu \,R_{ch}}{W_{-\eta ^{bs},l+1/2}^{2}(2\,\kappa \,R_{ch})}\, ({\gamma }_{l}^{sp})^{2}. \end{aligned}$$

(111)

Recalling the SF ${\mathtt S}$ introduced in review [1], we get the relationship between the ANC and the observable width:

$$\begin{aligned} C_{l}^{2}= \frac{2\,\mu \,R_{ch}}{W_{-\eta ^{bs},l+1/2}^{2}(2\,\kappa \,R_{ch})}\,\gamma _{l}^{2}, \end{aligned}$$

(112)

where the observable reduced width $\gamma _{l}^{2}$ is related to the observable single-particle reduced width via the SF ${\mathtt S}$:

$$\begin{aligned} {\gamma _{l}}^{2} = {\mathtt S}\,({\gamma }_{l}^{sp})^{2} \end{aligned}$$

(113)

and

$$\begin{aligned} C_{l}^{2}= {\mathtt S}\,b_{l}^{2}. \end{aligned}$$

(114)

Finally, for $r > R_{ch}$

$$\begin{aligned} {\mathtt S}^{1/2}\,\frac{u_{l}(i\,\kappa ,r)}{\sqrt{I_{0}^{\infty }}}= \sqrt{ 2\,\mu \,R_{ch} }\,{\gamma }_{l}\, \frac{W_{-\eta ^{bs},l+1/2}(2\,\kappa \,r)}{W_{-\eta ^{bs},l+1/2}(2\,\kappa \,R_{ch})}. \end{aligned}$$

(115)

5.2 Reduced width, ANC and resonance width for resonance state

The derivation of Eqs. (111) and (112) can be generalized for resonance states. To this end, we replace the bound-state wave function $u_{l}(i\,\kappa ,r)$ with the normalizable Gamow–Siegert one. There is some point that should be discussed about the extension of the results of Sect. 5.1 for resonance states. The standard R-matrix approach deals with real energies while applying the Gamow–Siegert wave functions requires some opportunistic step in the R-matrix formalism: operating with complex resonance energy $E_{R}$. To avoid the complication of using complex energy, we consider only the Breit–Wigner resonances ($\Gamma /E_{0}<<1$). Then we can treat the imaginary part $\Gamma$ as an infinitesimal parameter.

Let us consider, for example, an important relationship (105) introduced for bound states. A specific of the bound states is that the asymptotic of the bound-state wave function has only the real outgoing wave $\,O_{l}(i\,\kappa \,r)\,$ in contrast to scattering wave functions. The Gamow–Siegert wave function in the external region also has only the outgoing wave $O_{l}(i\,k_{R})$ and for the resonance state

$$\begin{aligned} R_{ch}\,\Big (\frac{ \textrm{d}\ln \big (u^{GS}_{l }(i\,k_{R},r)\big )}{\textrm{d}r}\Big )\Big |_{r=R_{ch}}&= R_{ch}\,\Big (\frac{ \textrm{d}\ln \big (O_{l }(k_{0},r)\big )}{\textrm{d}r}\Big )\Big |_{r=R_{ch}} \nonumber \\&= {{\hat{S}}}_{l}(E)\Big |_{E=E_{0}}. \end{aligned}$$

(116)

Correspondingly, Eq. (112) generalized for the narrow resonance states takes the form

$$\begin{aligned} C_{l}^{2}= \frac{2\,\mu \,R_{ch}}{ W_{-i\eta _{0},l+1/2}^{2}(-2\,i\,k_{0}\,R_{ch}) }\,\gamma _{l}^{2}. \end{aligned}$$

(117)

This equation obtained in the R-matrix approach also follows from Eq. (41) derived in the potential approach. To this end, we need to recall Eqs. (85) and (43).

Let us now assemble these equations into Eq. (117) to obtain

$$\begin{aligned} C_{l}^{2}= i^{-2\,l}\, e^{\pi \,\eta _{0}}\,e^{-2\,i\,[\delta _{l}^{hs}(k_0) - \sigma _{l}^{C}(k_{0})]}\,\frac{\mu }{k_{0}}\,\Gamma _{l}, \end{aligned}$$

(118)

which is valid for Breit–Wigner resonances ($\Gamma<< E_{0}$). Equation (118) is the same as Eq. (41) in which the substitution $k_{R} \rightarrow k_{0}$ has been done. Note that the potential phase shift $\delta _{l}^{p}(k_{R})$ is replaced by the potential scattering phase shift in the R-matrix formalism $-\delta _{l}^{hs}(k_0) + \sigma _{l}^{C}(k_{0})$, where $-\delta _{l}^{hs}(k_0)$ is the hard-sphere scattering phase shift. Thus the relationship, which has been derived in Sect. 3.1 using the analytical expression for the S-matrix and potential approach, can be obtained using the R-matrix formalism employing the Gamow–Siegert wave functions.

6 Single-channel, single-level elastic resonance scattering

Having discussed reduced widths and elastic scattering S-matrix, we are now in a position to discuss the simplest single-channel, single-level resonance elastic scattering S-matrix and elastic scattering amplitude. We obtain the near-resonance behavior of the elastic scattering amplitude in terms of the observable resonance width. Another interesting case to address is the elastic scattering in the presence of the subthreshold bound state (aka subthreshold resonance). We derive the expression for the elastic scattering amplitude at energy $E \rightarrow 0$ and explain why the low-energy elastic scattering amplitude behaves as there is a resonance at negative energy in the presence of the subthreshold bound state. Also, we derive the expression for the residue of the elastic scattering amplitude in the subthreshold pole in the energy plane. It allows us to express the ANC of the subthreshold bound state in terms of the reduced width of the subthreshold bound state and the observable partial resonance width of the subthreshold resonance at positive energies. Finally, the expression for the radiative capture cross-section and astrophysical factor to subthreshold resonance expressed in terms of the ANC is derived. These equations underscore the role of the ANC in the analysis of the resonance elastic scattering in the presence of the subthreshold resonance.

6.1 Single-level, single-channel elastic scattering S-matrix and amplitude

Let us consider a single-level, single-channel case. The elastic scattering S-matrix can be written as

$$\begin{aligned} {{\mathbb {S}}}_{l}(E)= S_{l}^{RP}(E)\,S_{l}^{R}(E), \end{aligned}$$

(119)

where

$$\begin{aligned} {{\mathbb {S}}}_{l}^{RP}(E) = e^{-2\,i\,[\delta ^{hs}_{l}(E) - \sigma _{l}^{C}(E)]} \end{aligned}$$

(120)

is the potential elastic scattering S-matrix in the R-matrix formalism and

$$\begin{aligned}&{{\mathbb {S}}}_{l}^{R}(E) = e^{2\,i\,\delta _{l}^{N}(E)} =\frac{E_{1}-E - ({{{\tilde{\gamma }}}}_{1}^{sp})^{2}[{{\hat{S}}}_{l}^{0}(E) -i\,P_{l}(E,R_{ch})]}{E_{1}-E - ({{{\tilde{\gamma }}}}_{1}^{sp})^{2}[{{\hat{S}}}_{l}^{0}(E) + i\,P_{l}(E,R_{ch}]} \end{aligned}$$

(121)

is the resonance part of the R-matrix elastic scattering S-matrix. Here ${{\hat{S}}}_{l}^{0}(E)= {{\hat{S}}}_{l}(E) - B$, B is the boundary condition, $\,{{{\tilde{\gamma }}}}_{1}^{sp} = {{{\tilde{\gamma }}}}_{1}^{sp}(E_{1})\,$ is the single-particle reduced width amplitude corresponding to the level energy $E_{1}$, $\delta _{l}(E)= \delta _{l}^{N}(E) - \delta _{l}^{hs}(E) + \sigma _{l}^{C}(E)\,$ is the total partial scattering phase shift, $\,\delta _{l}^{N}(E)\,$ is the partial nuclear scattering phase shift. In what follows, to simplify notations, we omit an explicit indication of the energy dependence of $\delta _{l}^{hs}(E)$ and $\sigma _{l}^{C}(E).$ Note that in the R-matrix approach, the adopted the channel radius $R_{ch}$ is assumed to be so large that the nuclear interaction between the interacting particles can be neglected. To calculate the barrier penetrability $P_{l}(E,R_{ch})(E)$ at smaller $R_{ch}$, one needs to take into account the nuclear interaction. Since the nuclear potential is negative, the height of the barrier decreases. However, it is not easy to calculate the effect of the nuclear interaction because it depends on the energy, parameters of the nuclear potential, and the orbital angular momentum.

From Eq. (121) follows that the partial nuclear scattering phase shift is

$$\begin{aligned} \delta _{l}^{N}(E)= \arctan \left[ \frac{ ({{{\tilde{\gamma }}}}_{1}^{sp})^{2}\,P_{l}(E,R_{ch})}{E_{1}-E- ({{{\tilde{\gamma }}}}_{1}^{sp})^{2}[{{\hat{S}}}_{l}(E) - B]}\right] . \end{aligned}$$

(122)

The formal single-particle resonance widths is

$$\begin{aligned} {{{\tilde{\Gamma }}}}_{l}^{sp}(E)= 2\,P_{l}(E,R_{ch})\,[{{{\tilde{\gamma }}}}_{1}^{sp}(E)]^{2}. \end{aligned}$$

(123)

We remind that in the R-matrix method, the dependence of the resonance width on E appears because the background is included in the resonance S-matrix.

The phase shift $\,\delta _{l}^{N}(E_{0}) =\pi /2\,$ defines the real part of the resonance energy

$$\begin{aligned} E_{0}= E_{1} - ({{{\tilde{\gamma }}}}_{1}^{sp})^{2}[{{\hat{S}}}_{l}(E_{0}) - B], \end{aligned}$$

(124)

where $({{{\tilde{\gamma }}}}_{1}^{sp})^{2}[{{\hat{S}}}_{l}(E_{0}) - B]$ is the energy shift determining the difference between the level energy $E_{1}$ and the real part of the resonance energy $E_{0}$.

Assume now that the level energy $E_{1}=E_{0}$. Then the formal single-particle resonance widths is ${{{\tilde{\Gamma }}}}_{l}^{sp} = {{{\tilde{\Gamma }}}}_{l}^{sp}(E_{1}).$

Now we can introduce the observable reduced width and observable resonance width. Since $E_{1}=E_{0}$, the energy shift is zero at $E=E_{1}$. Hence $B= {{\hat{S}}}_{l}(E_{1})$. Then for $\,E \rightarrow E_{1}$

$$\begin{aligned}&E_{1} - E - ({{{\tilde{\gamma }}}}_{1}^{sp})^{2}\big [{{\hat{S}}}_{l}(E) - {{\hat{S}}}_{l}(E_{1})\big ] \nonumber \\&\quad \approx (E_{1} - E)\,\Big [1 + ({{{\tilde{\gamma }}}}_{1}^{sp})^{2}\,\frac{\textrm{d}{{\hat{S}}}_{l}(E)}{ \textrm{d}E}\Big |_{E=E_{1}}\Big ]. \end{aligned}$$

(125)

Substitute it into Eq. (122) we get

$$\begin{aligned} \delta _{1}^{N}(E)= \arctan \Big [\frac{ (\gamma _{1}^{sp})^{2}\,P_{l}(E,R_{ch})}{E_{1}-E} \Big ], \end{aligned}$$

(126)

where

$$\begin{aligned} (\gamma _{1}^{sp})^{2}= \frac{({{{\tilde{\gamma }}}}_{1}^{sp})^{2}}{1 + ({{{\tilde{\gamma }}}}_{1}^{sp})^{2}\,\frac{\textrm{d}{{\hat{S}}}_{l}(E)}{\textrm{d}E}\Big |_{E=E_{1}} } \end{aligned}$$

(127)

is the observable single-particle reduced width. Introducing the observable reduced width

$$\begin{aligned} \gamma _{l}^{2}= {\mathtt S}\,(\gamma _{l}^{sp})^{2} \end{aligned}$$

(128)

we get the observable resonance width:

$$\begin{aligned} \Gamma _{l}= \Gamma _{l}(E_{1}) = 2\,\gamma _{l}^{2}\,P_{l}(E_{1},R_{ch}). \end{aligned}$$

(129)

It is also called the experimental width and is equal to the full width at half maximum of a resonance peak. For Breit–Wigner resonances this observable resonance width and the ANC are related by Eq. (118).

Introduction of the SF $\,{\mathtt S}\,$ in Eq. (128) requires additional comments. From the beginning we worked in the single-particle approach. It means that the SF is assumed to be equal to unity. However, the observable reduced width and the resonance width should be compared to the corresponding experimental quantities. That is why we need to correct the single-particle approach by adding the SF of the resonance state. It makes sense to call this SF phenomenological one because it can be obtained by comparing the single-particle observable quantities with the experimental counterparts.

Now we introduce the elastic scattering amplitude in the R-matrix method. To this end we consider

$$\begin{aligned} {{\mathcal {T}}}_{l}(E)= \frac{{{\mathbb {S}}}_{l}-1}{2\,i\,k} = {{\mathcal {T}}}_{l}^{R}(E) + {{\mathcal {T}}}_{l}^{RP}(E), \end{aligned}$$

(130)

where

$$\begin{aligned} {{\mathcal {T}}}_{l}^{RP}(E) = \frac{ e^{-2\,i\,[\delta ^{hs}_{l} - \sigma _{l}^{C}]} -1}{2\,i\,k} \end{aligned}$$

(131)

is the potential scattering amplitude. The single-channel elastic scattering amplitude $\mathcal{T}_{l}^{R}(E)$ in the standard R-matrix form reduces to

$$\begin{aligned} \mathcal{T}_{l}^{R (sp)}(E)&= e^{-2\,i\,[\delta ^{hs}_{l} - \sigma _{l}^{C}]}\,\frac{{{\mathbb {S}}}_{l}^{R}(E) -1}{2\,i\,k} \nonumber \\&= \frac{1}{2\,k}\,e^{-2\,i\,(\delta ^{hs}_{l} -\sigma _{l}^{C})}\,\nonumber \\&\quad \frac{ 2\,({{{\tilde{\gamma }}}}_{l}^{sp})^{2} \,P_{l}(E,R_{ch})}{E_{1} - E - ({{{\tilde{\gamma }}}}_{l}^{sp})^{2}\, [{{\hat{S}}}_{l}(E) - B + i\,P_{l}(E,R_{ch})]}. \end{aligned}$$

(132)

To underscore that this equation is obtained in the single-particle approximation, we added the superscript “(sp)” in $\mathcal{T}_{l}^{R(sp)}(E)$.

Assume that the level energy $E_{1}$ is the resonance energy and $B={{\hat{S}}}(E_{1})$. Then for $E \rightarrow E_{1}$ using approximation (125) we can rewrite

$$\begin{aligned} \mathcal{T}_{l}^{R(sp)}(E)&= \frac{1}{2\,k}\,e^{-2\,i\,(\delta ^{hs}_{l} - \sigma _{l}^{C})}\,\frac{ 2\,({\gamma }_{l}^{sp})^{2} \,P_{l}(E,R_{ch})}{E_{1} - E - i\,({\gamma }_{l}^{sp})^{2}\,P_{l}(E,R_{ch})} \nonumber \\&= \frac{1}{2\,k}\,e^{-2\,i\,(\delta ^{hs}_{l} - \sigma _{l}^{C})}\,\frac{ \Gamma _{l}^{sp}(E)}{E_{1} - E - i\,\Gamma _{l}^{sp}(E)/2}. \end{aligned}$$

(133)

6.2 Subthreshold resonance

Now we consider a very interesting and important case when elastic scattering occurs in the presence of a loosely bound state, which reveals itself at low energies as a resonance. Nuclear excited states below the particle emission threshold typically undergo decay to lower lying states. These decays result in the initial excited states having their natural width. In the case when $\gamma$ emission is the only open decay channel, the natural radiative width $\Gamma _{\gamma }$ is typically $\sim$ eV. If a particle-bound excited state lies very close to the particle threshold, the natural width can result in the tail of the wave function extending above the particle threshold. As a result of this tail, the subthreshold bound state can behave like a resonance state in a capture reaction. Such states are often referred to as subthreshold resonance states and can play an essential role in determining reaction rates of interest in nuclear astrophysics. Consider the capture of particle a by particle A at very low relative kinetic energy $E_{aA}$ and assume that there is a subthreshold bound state $B_{s}$ in the system (aA). There are three possible mechanisms by which the capture can occur:

• (i) direct radiative capture to the ground state B,

• (ii) radiative capture to the ground state through the subthreshold resonance,

• (iii) direct radiative capture into the subthreshold bound state with $\gamma$ emission.

Process (i) corresponds to the emission of a photon with the energy equal to the difference between the initial energy $E_{aA}$ and the final energy $-\varepsilon _{aA}$ where $\varepsilon _{aA}$ is the binding energy of the ground state $B=(aA)$:

$$\begin{aligned} E_{\gamma }= E_{aA} + \varepsilon _{aA}. \end{aligned}$$

(134)

Process (ii) is the two-step process. In the first step, the non-radiative capture of particle a occurs at positive energies to the tail of the subthreshold bound state $B_{s}=(aA)_{s}$, which reveals itself as the subthreshold resonance. In the second step, the subthreshold resonance undergoes $\gamma$ decay into the ground state $B=(aA)$. Note that only one gamma is emitted in the process (ii), and it occurs after capture into the subthreshold $B_{s}$ state. The energy of the emitted photon is given by the same Eq. (134) since the initial and final states of the process (ii) are the same as in the process (i).

Process (iii) is a two-step process resulting initially in a photon with energy

$$\begin{aligned} E_{\gamma }= E_{aA}+ \varepsilon _{s}, \end{aligned}$$

(135)

where $\varepsilon _{s}$ is the binding energy of the subthreshold bound state $B_{s}$. This subthreshold bound state $B_{s}$ is then deexcited to the ground state c by emitting a photon with energy $\varepsilon _{aA} - \varepsilon _{s}$. Again, the total energy of the emitted protons is the same as in the two previous processes.

Note that in mechanisms (ii) and (iii), the capture occurs in the same state, but in the (ii) process, this state reveals itself as a resonance, while in (iii), it acts as an actual bound state. All three of these capture processes occur in nature and are important in determining reaction rates for nuclear astrophysics.

Below we derive the equation relating the ANC of the subthreshold bound state to the resonance width, which is an extension of the relationship (47) between the ANC and the width of the Breit–Wigner resonance above the threshold. The equations presented below are valid for elastic scattering amplitudes in K- and R-matrix theory at negative energies, and they can be used to find the ANC by extrapolating elastic scattering phase shifts to the pole corresponding to the subthreshold bound state.

The subscript/superscript s stands for the subthreshold bound state. The low-energy elastic scattering amplitude in the presence of the subthreshold bound state is given by Eq. (132) in which $({{{\tilde{\gamma }}}}_{l}^{sp})^{2}$ is the single-particle formal reduced width of the subthreshold bound state with the binding energy $\,\varepsilon _{s}$. If we choose $E_{1}=-\varepsilon _{s}$ and the boundary condition parameter $\,B= {{\hat{S}}}_{l}(- \varepsilon _{s } )$, in the low-energy region where the linear approximation is valid

$$\begin{aligned} {{\hat{S}}}_{l}(E) - {{\hat{S}}}_{l}(-\varepsilon _{s}) \approx \frac{ \textrm{d}\,{{\hat{S}}}_{l}(E) }{\textrm{d}E}\,\Big |_{E=-\varepsilon _{s}}\, (E +\varepsilon _{s}). \end{aligned}$$

(136)

Then at small E the R-matrix elastic scattering amplitude

$$\begin{aligned} \mathcal{T}_{l}^{s(sp)}(E) = - \frac{e^{-2\,i\,(\delta ^{hs}_{l} - \sigma _{l}^{C})}}{2\,k}\,\frac{2\, P_{l}(E,R_{ch})(\gamma _{l}^{sp})^{2} }{\varepsilon _{s} + E + i\,(\gamma _{l}^{sp})^{2}\,P_{l}(E,R_{ch}) }. \end{aligned}$$

(137)

6.3 Residue of elastic scattering amplitude in subthreshold pole

To further discuss the properties of the elastic scattering amplitude we note that it has a pole at $\,E= -\varepsilon _{s}$ because $P_{l}(E,R_{ch} )$ vanishes for $E \le 0$. Hence we can find a residue of the elastic scattering amplitude in this pole. To this end, one should extrapolate Eq. (137) down to the bound state pole at $E= - \varepsilon _{s}$. The penetrability factor $\,P_{l}(E,R_{ch})\,$, which contains $|Q_{l}(E,R_{ch})|^{2}=[F_{l}(E,R_{ch})]^{2} + [G_{l}(E,R_{ch})]^{2}$, is not an analytic function. We take in the denominator $P_{l}(E, R_{ch})=0$ at $E<0,\,$ since in the denominator the imaginary part contains the penetrability factor, and then we recall that $\,P_{l}(E,R_{ch})\,$ is the imaginary part of the logarithmic derivative of $O_{l}(k,r)$ taken at $r=R_{ch}$, which is real at negative energies.

However, in the numerator we have

$$\begin{aligned} e^{-2\,i\,(\delta ^{hs}_{l} - \sigma _{l}^{C})}\, P_{l}(E,R_{ch})&= \frac{k\,R_{ch}}{e^{-2\,i\,\sigma _{l}^{C}}\,[G_{l} (k,R_{ch}) + i\,F_{l}(k,R_{ch})]^{2}} \nonumber \\&= \frac{k\,R_{ch}}{[O_{l}(k,R_{ch})]^{2}}, \end{aligned}$$

(138)

where $O_{l}(k,R_{ch})$ defined by Eq. (96) is an analytic function in the entire complex plane, $|k| < \infty$, except for the cut along the imaginary negative axis $\textrm{Im}k <0$ and the point $k=0$. Hence we can extrapolate Eq. (138) to the subthreshold bound state pole $\,k=i\,\kappa _{s}\,$ located in the upper half k plane, bypassing the singular point at $\,k=0$.

From Eq. (96) follows that at $k=i\,\kappa _{s}$, where $\kappa _{s} = \sqrt{2\,\mu \varepsilon _{s}}$ is the subthreshold bound-state wave number,

$$\begin{aligned} O_{l}(i\,\kappa _{s},\,r)= e^{-i\,\pi \,l/2}\,e^{-\frac{1}{2}\,i\pi \,\eta ^{s}}\,W_{-\,\eta ^{s}, l+1/2}(2\,\kappa _{s}\,r). \end{aligned}$$

(139)

Here $W_{-\eta ^{s},\,l+1/2}(\,2\,\kappa _{s}R_{ch})$ is the Whittaker function, $\eta ^{s}= (Z_{a}\,Z_{A}/137)\mu /\kappa _{s}$ and $\kappa _{s}$ are the $a-A$ Coulomb parameter of the subthreshold state $(aA)_{s}$, $\,\mu$ is the reduced mass of a and A, $\,Z_{j}\,e$ is the charge of nucleus j.

At negative energies near this pole, we get

$$\begin{aligned}&\mathcal{T}_{l}^{s(sp)}(E) {\mathop {\approx }\limits ^{k \rightarrow i\,\kappa _{s}}} \nonumber \\&\quad - e^{i\,\pi \,l}\,e^{i\,\pi \,\eta ^{s}}\frac{R_{ch}\,(\gamma _{l}^{sp})^{2}}{[W_{\,-\eta ^{s}, l+1/2}(2\,\kappa _{s}\,R_{ch})]^{2}}\, \frac{1}{E+ \varepsilon _{s}} \end{aligned}$$

(140)

$$\begin{aligned}&= i\,e^{i\,\pi \,l}\,e^{i\,\pi \,\eta ^{s}}\,\frac{\mu }{\kappa _{s}}\frac{R_{ch}\,(\gamma _{l}^{sp})^{2}}{[W_{\,-\eta ^{s}, l+1/2}(2\,\kappa _{s}\,R_{ch})]^{2}}\, \frac{1}{k - i \kappa _{s}} \end{aligned}$$

(141)

$$\begin{aligned}&= i\,e^{i\,\pi \,l}\,e^{i\,\pi \,\eta ^{s}}\,\frac{1}{2\,\kappa _{s}}\,\frac{b_{l}^{2}}{k- i\,\kappa _{s}}, \end{aligned}$$

(142)

where

$$\begin{aligned} ( \gamma _{l}^{sp})^{2}= \frac{ ({{{\tilde{\gamma }}}}_{l}^{sp})^{2} }{ 1+({{{\tilde{\gamma }}}}_{l}^{sp})^{2} [\textrm{d}{{\hat{S}}}_{l}(E)/\textrm{d}E]\big |_{E=-\varepsilon _{s}}} \end{aligned}$$

(143)

is the observed single-particle reduced width of the subthreshold resonance and

$$\begin{aligned} b_{l}^{2} = 2\,\mu \,R_{ch}\,\frac{(\gamma _{l}^{sp})^{2}}{[W_{-\,\eta ^{s}, l+1/2}(2\,\kappa _{s}\,R_{ch})]^{2}} \end{aligned}$$

(144)

is the single-particle ANC of the subthreshold bound state.

Equation (144) is obtained by comparing Eqs. (142), (141) and Eq. (36) from review [1]. Since we use the single-particle approximation, the single-particle ANC $b_{l}$ rather than the ANC $C_{l}$ appears in Eq. (142).

Then the ANC is

$$\begin{aligned} C_{l}^{2}&={\mathtt S}\,b_{l}^{2} = 2\,\mu \,R_{ch}\,\frac{\gamma _{l}^{2}}{[W_{-\,\eta ^{s}, l+1/2}(2\,\kappa _{s}\,R_{ch})]^{2}} \nonumber \\&= \frac{2}{R_{ch}}\frac{\gamma _{l}^{2}}{[W_{-\,\eta ^{s}, l+1/2}(2\,\kappa _{s}\,R_{ch})]^{2} }\theta _{l}^{2}, \end{aligned}$$

(145)

where $\gamma _{l}^{2}$ is related to $(\gamma _{l}^{sp})^{2}$ via Eq. (128) and

$$\begin{aligned} \theta _{l}^{2}= \mu \,R_{ch}^{2}\,\gamma _{l}^{2}. \end{aligned}$$

(146)

Thus, introducing the SF ${\mathtt S}$ of the subthreshold bound state, we derived the relationship between the ANC and the observable reduced width.

The full elastic scattering amplitude at $k \rightarrow i\,\kappa _{s}$ takes the form:

$$\begin{aligned} \mathcal{T}_{l}^{s}(E)&= {\mathtt S}\,\mathcal{T}_{l}^{s(sp)}(E)\nonumber \\&{\mathop {\approx }\limits ^{k \rightarrow i\,\kappa _{s}}} i\,e^{i\,\pi \,l}\,e^{i\,\pi \,\eta ^{s}}\,\frac{\mu }{\kappa _{s}}\frac{R_{ch}\,(\gamma _{l}^{2})}{[W_{\,-\eta ^{s}, l+1/2}(2\,\kappa _{s}\,R_{ch})]^{2}}\, \frac{1}{k - i \kappa _{s}} \end{aligned}$$

(147)

$$\begin{aligned}&= i\,e^{i\,\pi \,l}\,e^{i\,\pi \,\eta ^{s}}\,\frac{1}{2\,\kappa _{s}}\,\frac{C_{l}^{2}}{k- i\,\kappa _{s}}. \end{aligned}$$

(148)

The observable partial resonance width of the subthreshold resonance is given by

$$\begin{aligned} \Gamma _{l}^{(s)}(E)&= 2\,P_{l}(E,R_{ch})\,\gamma _{l}^{2}= P_{l}(E,R_{ch})\,\frac{R_{ch}}{\mu }\Big ({I^{s}(R_{ch}) \Big )^{2} } \nonumber \\&= P_{l}(E,R_{ch})\,\frac{1}{\mu \,R_{ch}} C_{l}^{2}\,W_{-\,\eta ^{s}\,l+1/2}^{2}(2\,\kappa _{s},\,R_{ch}), \end{aligned}$$

(149)

where we took into account that the external part of the radial overlap function of the bound-state wave function of $(a\,A)_{s}$, $a\,$ and $\,A$ takes the form

$$\begin{aligned} I^{(s)}(r) = C_{l}\,\frac{W_{-\,\eta ^{s}\,l+1/2}(2\,\kappa _{s}\,r)}{r}. \end{aligned}$$

(150)

Equation (149) has a fundamental importance. It shows that the subthreshold bound state at $E>0$ behaves as a resonance with the resonance width expressed in terms of the radial overlap function of this bound state at $r=R_{ch}$. Note that $\,\Gamma _{l}(E)>0\,$ for $E>0$ and vanishes at $E \le 0.$ The physical importance of $\Gamma _{l}(E)$ will be clear when we consider the radioactive capture reactions.

6.4 Radiative capture cross-section and astrophysical factor to subthreshold resonance

We can find now the behavior of the cross-section for the radiative capture from the continuum channel i to the subthreshold resonance at $E \rightarrow 0$. The cross-section for this capture is given by

$$\begin{aligned} \sigma _{\gamma \,i}(E)&= {{\hat{l}}}\,8\,\pi \,\mu \,|\mathcal{T}_{i\,\gamma }|^{2} = {{\hat{l}}}\,\frac{\pi }{k^{2}}\,\frac{\Gamma _{\gamma }\,\Gamma _{s}}{(E+\varepsilon _{s})^{2}+ \Gamma _{s}^{2}/4} \nonumber \\&= {{\hat{l}}}\,\frac{\pi }{\mu \,k}\,\left( \frac{k}{\kappa _{s}}\right) ^{2\,l}\,e^{-\pi \,\eta }\,\Big (\frac{|\Gamma (l+i\,\eta +1|}{\Gamma (l+1+ \eta ^{s}}\Big )^{2}\, \frac{\Gamma _{\gamma }\,C_{l}^{2}}{(E+\varepsilon _{s})^{2} + \Gamma _{s}^{2}/4} \nonumber \\&{\mathop {\approx }\limits ^{E \rightarrow 0}} {{\hat{l}}}\,\frac{\pi ^{2}\,\kappa _{s}}{\mu ^{2}}\,\frac{e^{-2\,\pi \,\eta }}{E}\, \frac{ (\eta ^{s})^{{\hat{l}}}}{[\Gamma (l+1+\eta ^{s})]^{2}}\,\frac{\Gamma _{\gamma }\,C_{l}^{2}}{(E+\varepsilon _{s})^{2}}, \end{aligned}$$

(151)

where ${{\hat{l}}}= 2l+1$.

The astrophysical S-factor used in nuclear astrophysics for the radiative capture to the subthreshold resonance takes the form⁵

$$\begin{aligned} S(E)&= E\,e^{2\,\pi \,\eta }\,\sigma _{\gamma \,i}(E) \nonumber \\&{\mathop {\approx }\limits ^{E \rightarrow 0}} {{\hat{l}}}\,\frac{\pi ^{2}\,\kappa _{s}}{\mu _{aA}^{2}}\, \frac{ (\eta ^{s})^{{\hat{l}}}}{[\Gamma (l+1+\eta ^{s})]^{2}}\,\frac{\Gamma _{\gamma }\,C_{l}^{2}}{(E+\varepsilon _{s})^{2}}. \end{aligned}$$

(152)

One can see that the S-factor for the radiative capture to the subthreshold bound state increases toward low E with a peak at $E=0$. This behavior is similar to the behavior of a resonance at $E \approx 0$. That is why the subthreshold bound state can be considered as a subthreshold resonance.

7 Two-channel resonance scattering and reactions

To discuss further the resonance processes within the R-matrix approach, we now consider the two-channel, single-level resonance elastic scattering and reaction generalizing results obtained in Sect. 6. The expressions for the resonance pole of the scattering amplitude and the observable resonance width are presented. We also take into account the presence of the subthreshold resonance. The two-channel, multi-level resonant reaction is also included.

7.1 Resonance scattering

Now we consider the elastic scattering $a+ A \rightarrow a+A$ in the presence of the subthreshold bound state $F^{s}$ in the channel $i =a+ A$ which is coupled to the second channel $f=b+B$. The relative kinetic energies in the channels i and f are related by $E_{f} \equiv E_{bB} = E_{i} + Q,$ where $\,Q= m_{x} + m_{A} - m_{b} - m_{B} > 0$, $E_{j}\; (j=i,f)\,$ is the relative kinetic energy of particles in the channel j. We assume that $\,Q>0$, that is, the channel f is open for $\,E_{i} \ge 0$. For the sake of simplicity, we assume that the channel radius is the same in channels i and f.

The resonance part of the elastic scattering amplitude in the channel $i=a+A$ in the single-level, two-channel R-matrix approach, is

$$\begin{aligned} \mathcal{T}_{ii}&= \frac{1}{2\,k}\,e^{-2\,i\,(\delta _{l}^{hs} - \sigma _{l}^{C} )}\,\nonumber \\&\quad \frac{2\, P_{i}\,({{{\tilde{\gamma }}}}_{i}^{sp})^{2} }{ E_{1} - E_{i} - \sum \limits _{c=i,f}\,({{{\tilde{\gamma }}}}_{c}^{sp})^{2}\,[{{\hat{S}}}_{c}(E_{c}) - B_{c} + i\,P_{c}]}, \end{aligned}$$

(153)

where ${{{\tilde{\gamma }}}}_{c}^{sp}$ is the formal single-particle reduced width in the channel $c=i,\,f$. $\,P_{c} \equiv P_{l_{c}} (E_{c},\,R_{ch})$ is the penetrability factor in the channel c, $l_{c}$ is the orbital angular momentum in channel c. There are two fitting parameters in the single-level, two-channel R-matrix fit: $\gamma _{i}^{sp}$ and $\gamma _{f}^{sp}$ at fixed channel radius $R_{ch}$.

Again, we assume that $E_{1}$ is the resonance energy and use the boundary condition $B_{c}= {{\hat{S}}}_{c}(E_{1})$. The energy $E_{i}=E_{1}$ in the channel i corresponds to $E_{f}= Q + E_{1}$ in the channel f. Assuming a linear energy dependence of ${{\hat{S}}}_{c}(E_{c})$ at small $E_{i}$ close to $E_{1}$, we get

$$\begin{aligned} T_{ii} \approx \frac{1}{2\,k}\,e^{-2\,i\,(\delta _{l}^{hs} - \sigma _{l}^{C} )}\,\frac{2\,P_{i}\,\big (\gamma _{i}^{sp}\big )^{2} }{E_{1} - E_{i} - i\,\sum \limits _{c=i,f}\,(\gamma _{c}^{sp})^{2}\,P_{c}}, \end{aligned}$$

(154)

where

$$\begin{aligned} (\gamma _{c }^{sp})^{2}= \frac{ ({{{\tilde{\gamma }}}}_{c}^{sp})^{2} }{ 1+\sum \limits _{t=i,f}\, ({{{\tilde{\gamma }}}}_{t}^{sp})^{2}\,[\textrm{d}{{\hat{S}}}_{t}(E_{t})/\textrm{d}E_{t}]\big |_{E_{i}=E_{1} }} \end{aligned}$$

(155)

is the observable single-particle reduced width in the channel c. Then the observable resonance width in the channel c is

$$\begin{aligned} \Gamma _{c}= \Gamma _{c}(E_{1})= 2\,P_{c}\,{\mathtt S}_{c}\,(\gamma _{c }^{sp})^{2}. \end{aligned}$$

(156)

${\mathtt S}_{c}$ is the SF in the channel c, and the total observable width is

$$\begin{aligned} \Gamma = \Gamma (E_{1}) = \Gamma _{i} + \Gamma _{f}. \end{aligned}$$

(157)

One can find from Eq. (154) the pole of the elastic scattering amplitude for the two-channel, one-level case:

$$\begin{aligned} E_{R}= E_{1} - i\,\sum \limits _{c=i,f}\,(\gamma _{c}^{sp})^{2}\,P_{c}. \end{aligned}$$

(158)

This pole is shifted further from the real axis due to the presence of the additional imaginary term, $- i\,P_{f}\,(\gamma _{f}^{sp})^{2}.\,$ We recall that in Eq. (158) $P_{c}$ and $(\gamma _{c}^{sp})^{2}$ are calculated at $E_{i}=E_{1}$.

7.2 Subthreshold resonance

The elastic scattering amplitude for two-channel and single-level case, when one of the channels is contributed by the subthreshold resonance in channel i takes the form

$$\begin{aligned} \mathcal{T}_{ii}&= \frac{1}{2\,k}\,e^{-2\,i\,(\delta _{l}^{hs} - \sigma _{l}^{C} )}\,\nonumber \\&\quad \frac{2\, P_{i}\,({{{\tilde{\gamma }}}}_{i}^{sp})^{2} }{ -\varepsilon _{i(s)} - E_{i} - \sum \limits _{c=i,f}\,({{{\tilde{\gamma }}}}_{c}^{sp})^{2}\,[{{\hat{S}}}_{c}(E_{c}) - B_{c} + i\,P_{c}]}. \end{aligned}$$

(159)

Again, here we use the boundary condition $B_{c}= {{\hat{S}}}_{c}(-\varepsilon _{i(s)})$ and $E_{1}=-\varepsilon _{i(s)}, {\epsilon _{i(s)}}$ is the binding energy of the subthreshold state in the channel i, $({{{\tilde{\gamma }}}}_{c}^{sp})^{2}$ is the formal single-particle reduced width in the channel c. Note that we use this choice for the energy level $E_{1}$ in all the cases considered below. The energy $E_{i}=-\varepsilon _{i(s)}$ in the channel i corresponds to $E_{f}= Q-\varepsilon _{i(s)}$ in the channel f. It is assumed that in the channel f $\,E_{f}= Q -\varepsilon _{i(s)} >0$, that is, the subthreshold bound state in the channel i corresponds to a resonance in the channel f. Assuming a linear energy dependence of ${{\hat{S}}}_{c}(E_{c})$ at small $E_{i}$, we get

$$\begin{aligned} \mathcal{T}_{ii} \approx -\frac{1}{2\,k}\,e^{-2\,i\,(\delta _{l}^{hs} - \sigma _{l}^{C} )}\,\frac{P_{i}\,\big (\gamma _{i}^{sp}\big )^{2} }{\varepsilon _{i(s)} + E_{i} + i\sum \limits _{c=i,f}\,P_{c}\,(\gamma _{c}^{sp})^{2}}, \end{aligned}$$

(160)

where the observed single-particle reduced width in the channel c is

$$\begin{aligned} ({\gamma }_{c }^{sp})^{2}= \frac{({{{\tilde{\gamma }}}}_{c}^{sp})^{2} }{ 1+\sum \limits _{t=i,f}\,({{{\tilde{\gamma }}}}_{t }^{sp})^{2}[\textrm{d}{{\hat{S}}}_{t}(E_{t})/\textrm{d}E_{t}]\big |_{E_{t}=E_{t(s)} }}, \end{aligned}$$

(161)

$E_{i(s)}= -\varepsilon _{i(s)}$ and $E_{f(s)}=Q - \varepsilon _{i(s)}$. Correspondingly, the observed partial resonance width in the channel c

$$\begin{aligned} \Gamma _{c}(E_{c}) = 2\,P_{c}\,{\mathtt S}_{c}(\gamma _{c}^{sp})^{2}, \end{aligned}$$

(162)

with the total width

$$\begin{aligned} \Gamma (E_{i}) = \Gamma _{i(s)}(E_{i}) + \Gamma _{f}(E_{f}). \end{aligned}$$

(163)

This equation requires additional comments. At energy $\,E_{i}= - \varepsilon _{i(s)}<0\,$ $\, \Gamma _{i(s)}(E_{i})=0$ and $\,\Gamma (E_{i}) = \Gamma _{f}(E_{f}).$ Only for $\,E_{i} >0\,$ $\, \Gamma _{i(s)}(E_{i}) >0\,$ and $\,\Gamma (E_{i}) = \Gamma _{i(s)}(E_{i}) + \Gamma _{f}(E_{f}).$

The presence of the open channel coupled to the elastic scattering channel generates an additional term $\,c=f$ in the denominators of Eqs. (153), (160) and (155). It results in shifting of the pole of the elastic scattering amplitude from $E_{i}= - \varepsilon _{i(s)}<0$ to the complex plane $E_{i(R)} = - \varepsilon _{i(s)} - i\,P_{f}\,(\gamma _{f}^{sp})^{2},$ where $P_{f}= P_{f}(Q-\varepsilon _{i(s)},R_{ch})$. Extrapolating $\mathcal{T}_{ii}$ to this pole and assuming that $\,P_{f}\,(\gamma _{f}^{sp})^{2}\,$ is small and can be neglected in all the factors except the resonance denominator we get from Eq. (140)

$$\begin{aligned} \mathcal{T}_{ii}&\approx \,- e^{i\,\pi \,l}\,e^{i\,\pi \,\eta ^{s}}\,\frac{R_{ch}\,(\gamma _{l(s)}^{sp})^{2}}{[W_{\,-\eta ^{s}, l+1/2}(2\,\kappa _{i(s)}\,R_{ch})]^{2}}\, \nonumber \\&\quad \frac{1}{ \varepsilon _{i(s)} + E_{i} + i\,P_{f}\,(\gamma _{f}^{sp})^{2} }. \end{aligned}$$

(164)

Again, the ANC, as a residue in the pole of the scattering amplitude is given by Eq. (145) in which $(\gamma _{l(s)})^{2}$ should be replaced by $(\gamma _{i (s)})^{2}$:

$$\begin{aligned} (\gamma _{i (s)})^{2} = {\mathtt S}_{i}\,(\gamma _{i (s)}^{sp})^{2}. \end{aligned}$$

(165)

7.3 Resonant reactions

Presented in this subsection equations for the reaction amplitudes proceeding through the intermediate resonance $F^{*}$ are the standard R-matrix equations. Let us consider now the resonant reaction

$$\begin{aligned} a + A \rightarrow F^{*} \rightarrow b +B. \end{aligned}$$

(166)

The two-channel, single-level R-matrix amplitude describing the resonant reaction in which in the initial state the colliding particles a and A can be obtained by generalizing Eq. (153):

$$\begin{aligned} \mathcal{T}_{f\,i}&= \frac{1}{2\,k_{i}}\,e^{-\,i(\delta _{i}^{hs} - \sigma _{i}^{C}+ \delta _{f}^{hs} - \sigma _{f}^{C}) }\nonumber \\&\quad \frac{ \sqrt{ P_{f} }\,{{{\tilde{\gamma }}}}_{f}^{sp}\, \sqrt{ P_{i} }\,{{{\tilde{\gamma }}}}_{i}^{sp} }{E_{1} - E_{i} -\sum \limits _{c=i,f}\,({{{\tilde{\gamma }}}}_{c}^{sp})^{2}\,[{{\hat{S}}}_{c}(E_{c}) - B_{c} + i\,P_{c}]}. \end{aligned}$$

(167)

Again we assume that level energy $E_{1}$ is the real part of the resonance energy in the channel $i=a+A$. Then the behavior of $\mathcal{T}_{f\,i}$ at $E_{i} \rightarrow E_{1}$ can be handled in much the same way as it was done for the elastic scattering:

$$\begin{aligned} \mathcal{T}_{f\,i}&= \frac{1}{2\,k_{i}}\,e^{-\,i(\delta _{i}^{hs} - \sigma _{i}^{C}+ \delta _{f}^{hs} - \sigma _{f}^{C}) }\, \frac{\sqrt{P_{f}}\,\gamma _{f}^{sp}\, \sqrt{ P_{i} }\,\gamma _{i}^{sp} }{E_{1} - E_{i} -i\,\sum _{c=i,f}\,(\gamma _{c}^{sp})^{2}\,P_{c}}, \end{aligned}$$

(168)

where $(\gamma _{c}^{sp})^{2}$ is given by Eq. (161).

The astrophysical S-factor is

$$\begin{aligned} S(E) (keVb)&= E\,e^{2\,\pi \,\eta _{i}}\,\sigma _{fi}(E_{i}) \nonumber \\&= \frac{{{\hat{J}}}_{R}}{{{\hat{J}}}_{a}\,{{\hat{J}}}_{A}}\,\lambda _{N}^{2}\,\,m_{au}^{2}\,e^{2\,\pi \,\eta _{i}}\,\frac{20\,\pi }{\mu _{i}} \nonumber \\&\quad \frac{ P_{f}\,P_{i}\,(\gamma _{f}^{sp})^{2}\,(\gamma _{i}^{sp})^{2} }{\Big (E_{1}\! - \!E_{i} \!-\! \sum _{c=i,f}\,({\gamma }_{c}^{sp})^{2}\,[{{\hat{S}}}_{c}(E_{c}) - {{\hat{S}}}_{c}(E_{1})]\Big )^{2}\! +\! \Big [\sum _{c=i,f}\,({\gamma }_{c}^{sp})^{2}\,P_{c}\,\Big ] ^{2}} , \end{aligned}$$

(169)

where $\sigma _{fi}(E_{i})$ is the cross-section for the reaction (166), $J_{R}$ is the spin of the resonance at $E_{i}=E_{1}$, $J_{i}$ is the spin of particle i, $\,{{\hat{J}}}= 2\,J+1$, $\,\mu _{i}=\mu _{aA},\,\,m_{au}=931.5$ MeV is the atomic mass unit, $\lambda _{N}=0.2118$ fm is the nucleon Compton wavelength, $\eta _{i}= \eta _{aA}$ is the Coulomb parameter of the $a+A$ in the continuum. All the reduced width amplitudes are expressed in MeV$^{1/2}$.

Now we consider 2 interfering levels and two channels in each level. All the quantities related to the levels $\nu$ and $\tau$ have additional subscripts $\nu$ or $\tau$, correspondingly. We assume that the level $\tau =1$ corresponds to the subthreshold state in the channel $i=a+A$, which decays to a resonant state corresponding to the level $\tau =1$ in the channel $f=b+B$. The level 2 describes the resonance in the channel $a+A$, which decays into the resonant state in the channel $f= b+ B$. The level $\tau =2$ lies higher than the level $\tau =1$ but both levels do interfere. The reaction amplitude is given by

$$\begin{aligned} \mathcal{T}_{f\,i}&=\frac{1}{2\,k_{i}}\,e^{-\,i(\delta _{i}^{hs} - \sigma _{i}^{C}+ \delta _{f}^{hs} - \sigma _{f}^{C}) }\, \sqrt{P_{f}}\,\sqrt{ P_{i} }\nonumber \\&\quad \times \sum \limits _{\nu \,\tau }\,{{{\tilde{\gamma }}}}_{f\,\nu }^{sp}\,\big [{{\mathcal{A}}}^{-1}\big ]_{\nu \,\tau }\,{{{\tilde{\gamma }}}}_{i\,\tau }^{sp}, \end{aligned}$$

(170)

where

$$\begin{aligned} \big [{{\mathcal{A}}}\big ]_{\nu \,\tau }&= (E_{1} - E_{i} )\,\delta _{\nu \,\tau } \nonumber \\&\quad - \sum \limits _{c=i,f}\,{{{\tilde{\gamma }}}}_{c\,\nu }^{sp}\, {{{\tilde{\gamma }}}}_{c\,\tau }^{sp}\,\big [{{\hat{S}}}_{c}(E_{c}) -B_{c}+ i\,P_{c} \big ]. \end{aligned}$$

(171)

The corresponding astrophysical $S(E_{i})$ factor is

$$\begin{aligned} S(E_{i})(keVb)&= \frac{{{\hat{J}}}_{R}}{{{\hat{J}}}_{a}\,{{\hat{J}}}_{A}}\,\lambda _{N}^{2}\,\,m_{au}^{2}\,e^{2\,\pi \,\eta _{i}}\,\frac{20\,\pi }{\mu _{i}} \,P_{f}\,P_{i}\,\nonumber \\&\quad \Big |\sum \limits _{\nu \,\tau }\,{{{\tilde{\gamma }}}}_{f\,\nu }^{sp}\,\big [{{\mathcal{A}}}^{-1}\big ]_{\nu \,\tau }\,{{{\tilde{\gamma }}}}_{i\,\tau }^{sp}\,\Big |^{2}. \end{aligned}$$

(172)

7.4 Reactions proceeding through subthreshold resonance

Based on the previously obtained equations we obtain the corresponding astrophysical factors which will be used in the next section to analyze the experimental data obtained from direct and indirect measurements of the important astrophysical reaction $\alpha + {}^{13}\textrm{C} \rightarrow {}^{17}\textrm{O}(1/2^{+},\,E=6.356 \textrm{MeV}) \rightarrow n + {}^{16}\textrm{O}$. Note that presented here expressions for the astrophysical factors are written in the convenient R-matrix form and can be used by experimentalists for analysis of similar reactions proceeding through the subthreshold resonance.

Let us consider now the resonant reaction

$$\begin{aligned} a + A \rightarrow F_{s} \rightarrow b +B \end{aligned}$$

(173)

with $Q>0$, proceeding through an intermediate resonance, which is a resonance in the exit channel f and a subthreshold bound state $F_{s}= (a\,A)_{s}$ in the initial channel i. We assume also that $Q- \varepsilon _{i(s)} >0$, that is, the channel f is open at the subthreshold bound-state pole in the channel i.

We consider two interfering levels, $\tau =1\,$ and $\,2$, and two channels in each level. All the quantities related to the levels $\tau =1$ and 2 have additional subscripts 1 or 2, correspondingly. We assume that the level $\tau =1$ corresponds to the subthreshold state in the channel $i=a+A$, which decays to a resonant state corresponding to the level $\tau =1$ in the channel $f=b+B$. The level 2 describes the resonance in the channel $a+A$, which decays into the resonant state in the channel $f= b+ B$. The level $\tau =2$ lies higher than the level $\tau =1$ but both levels do interfere. The reaction amplitude is given by

$$\begin{aligned} T_{f\,i}&=-2\,i\,e^{-\,i(\delta _{i}^{hs} - \sigma _{i}^{C}+ \delta _{f}^{hs} - \sigma _{f}^{C}) }\, \nonumber \\&\quad \sqrt{P_{f}}\,\sqrt{ P_{i} }\sum \limits _{\lambda \,\tau }\gamma _{f_{\nu }}\,\big [{{\mathcal{A}}}^{-1}\big ]_{\nu \,\tau }\,\gamma _{i\,\tau } \end{aligned}$$

(174)

with

$$\begin{aligned} \big [{{\mathcal{A}}}\big ]_{\nu \,\tau }&= (-\varepsilon _{i}^{(s)} - E_{i} )\,\delta _{\nu \,\tau } \nonumber \\&\quad - \sum \limits _{c=i,f}\,\gamma _{c\,\nu }\, \gamma _{c\,\tau }\,\big [{{\hat{S}}}_{c}(E_{c}) - {{\hat{S}}}_{c}(-\varepsilon _{i}^{(s)}) + i\,P_{c} \big ]. \end{aligned}$$

(175)

The corresponding astrophysical $S(E_{i})$ factor is

$$\begin{aligned} S(E_{aA})(keVb)&= \frac{{{\hat{J}}}_{F_{s}}}{{{\hat{J}}}_{a}\,{{\hat{J}}}_{A}}\,\lambda _{N}^{2}\,\,m_{au}^{2}\,e^{2\,\pi \,\eta _{i}}\,\frac{20\,\pi }{\mu _{i}} \,P_{f}\,P_{i}\,\nonumber \\&\quad \Big |\sum \limits _{\nu \,\tau }\,\gamma _{f\,\nu }\,\big [{{\mathcal{A}}}^{-1}\big ]_{\nu \,\tau }\,\gamma _{i\,\tau }\,\Big |^{2}, \end{aligned}$$

(176)

where $J_{F_{s}}$ is the spin of the subthreshold resonance.

8 Astrophysical factor of $\mathbf {^{13}\textrm{C}(\alpha ,\,{{\textrm{n}}})^{16}\textrm{O}}$ reaction

8.1 Astrophysical reaction $\mathbf {^{13}\textrm{C}(\alpha ,\,{{\textrm{n}}})^{16}\textrm{O}}$

It is now time to demonstrate how the equations presented in the previous section for the reaction amplitude proceeding through the subthreshold resonance can be used for the analysis of the important astrophysical reaction $^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}$ reaction, which is considered to be the main neutron supply to build up heavy elements from iron-peak seed nuclei in AGB stars. At temperature $0.9 \times 10^{8}$ K the so-called Gamow window (Illiadis [26], Bertulani and Kajino [27]) of the $^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}$ reaction is within $\approx 140 - 230$ keV with the most effective energy at $\approx 190$ keV. The dominant contribution to the $^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}$ reaction at astrophysical energies comes from the state ${}^{17}\textrm{O}(1/2^{+}, E_{x}=6356 \pm 8 \, \textrm{keV})$, where $E_{x}$ is the excitation energy. Taking into account that the $\alpha - {}^{13}\textrm{C}$ threshold is located at 6359.2 keV one finds that this $1/2^{+}$ level is the located at $E_{\alpha \,{}^{13}\textrm{C}} = -3 \pm 8$ keV, that is, it can be or subthreshold bound state or a resonance (Tilley et al. [28]). This location of the level ${}^{17}\textrm{O}(1/2^{+})$ was adopted in (Heil et al. [29]). If this level is the subthreshold bound state, then its reduced width is related to the ANC of this level.

However, Faestermann et al. [30] determined that this level is actually a resonance located at $E_{\alpha \,{}^{13}\textrm{C}} = 4.7 \pm 3$ keV with the total observable width of $\Gamma =136 \pm 5$ keV. Note that $\Gamma _{\alpha }$ of this resonance with $l_{i}=1$ is negligibly small because it contains the penetrability factor $P_{1}$. Hence, $\Gamma = \Gamma _{n}$. If this level is a resonance located slightly above the threshold, then the reduced width is related to the resonance partial $\alpha$ width. This resonance is not of a Breit–Wigner type, and it does not make sense to use the ANC as a characteristic of this resonance.

Here we present the calculations of the astrophysical S-factors for the $^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}$ using the equations derived above. We fit the data (Tippella and La Cognata [31]) using both assumptions that the threshold level $1/2^{+}$ is the subthreshold state located at $-3$ keV and the resonance state at 4.7 keV. For the subthreshold state we use parameters from Heil et al. [29], while for the resonance state we adopted parameters from Faestermann et al. [30]. The resonances included in the analysis of this reaction are ($\,1/2^{+},\,l_{i}=1,\,E_{x}=6.356$ MeV), ($\,5/2^{-},\,l_{i}=2,\,E_{x}=7.165$ MeV), ($\,3/2^{+},\,l_{i}=1,\,E_{x}=7.216$ MeV), ($5/2^{+},\,l_{i}=3,\,E_{x}=7.379$ MeV) and ($5/2^{-},\,l_{i}=2,\,E_{x}=7.382$ MeV). Only two resonances, the second and the last one have the same quantum numbers and do interfere. Their interference can be taken into account using the S-factor given by Eq. (176). For non-interfering resonances we use the sum of the S-factors corresponding to different resonances.

In Fig. 3 we presented the S-factors contributed by four different resonant states located at $E_{\alpha \,{}^{13}\textrm{C}}>0$. All the parameters of these resonances are taken from Heil et al. [29]. We only slightly modified the $\alpha$-particle width of the wide resonance at $E_{\alpha \,{}^{13}\textrm{C}}=0.857$ MeV taking it to be 0.12 keV. The adopted channel radii are $R_{ch(\alpha \,{}^{13}\textrm{C})}= 7.5$ fm and $R_{ch(n\,{}^{16}\textrm{O})}= 6.0$ fm.

Fig. 3

The S-factors for the $^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}$ reaction as a function of the $\alpha -{}^{13}\textrm{C}$ relative kinetic energy proceeding through four resonances: black dotted-dashed line -($\,5/2^{-},\,l_{i}=2,\,E_{x}=7.165$ MeV; solid red line- ($\,3/2^{+},\,l_{i}=1,\,E_{x}=7.216$ MeV); dashed brown line-($5/2^{+},\,l_{i}=3,\,E_{x}=7.379$ MeV); dotted blue line- ($5/2^{-},\,l_{i}=2,\,E_{x}=7.382$ MeV). All the resonant parameters are taken from Heil et al. [29]. First published in Mukhamedzhanov et al. [32]

Figure 3 shows that the contributions of all the narrow resonances are negligible compared to the wide one (red solid line in Fig. 3). That is why we do not take into account the interference between two narrow $5/2^{-}$ resonances. Thus eventually we can take into account only the wide resonance ($\,3/2^{+},\,l_{i}=1,\,E_{x}=7.216$ MeV) and the near threshold level ($\,1/2^{+},\,l_{i}=1,\,E_{x}=6.356$ MeV).

8.2 Threshold level $\,{1/2^{+},\,l=1,\,E_{x}=6.356}$ MeV

Now, we discuss the threshold level corresponding to the excitation energy $E_{x}=6.356$ MeV. Until appearance of the work Faestermann et al. [30] this level was considered to be the subthreshold resonance located at $E_{\alpha \,{}^{13}\textrm{C}} = -3$ keV. However, Faestermann et al. [30] showed that this level was shifted to the continuum and is found to be a real resonance located at $E_{\alpha \,{}^{13}\textrm{C}}= 4.7$ keV. The astrophysical factor contributed by this $1/2^{+}$ state depends on the reduced width in the entry channel $\alpha -{}^{13}\textrm{C}$ of the $^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}$ reaction and the reduced width in the exit channel $n-{}^{16}\textrm{O}$. If we assume that the level $E_{x}=6.356$ MeV is the subthreshold bound state then its reduced width in the $\alpha$-channel is expressed in terms of the ANC for the virtual decay ${}^{17}\textrm{O}(1/2^{+},E_{\alpha \,{}^{13}\textrm{C}} = -3\,\,\textrm{keV} ) \rightarrow \alpha + {}^{13}\textrm{C }$. The latest measurement of this subthreshold state ANC (Avilla et al. [33]) gave ${{\tilde{C}}}_{\alpha \,{}^{13}\textrm{C}}^{2} = 3.6 \pm 0.7$ fm${}^{-1}$, which is the square of the Coulomb renormalized ANC of the subthreshold bound state. it is useful to remind readers that at very small binding energies, the ANC of the subthreshold bound state becomes very large due to the Coulomb-centrifugal barrier. If the subthreshold bound state is located at $E_{\alpha \,{}^{13}\textrm{C}}=-3$ keV, then the renormalization factor is $\Gamma (1+ l+ \eta ^{(s)})/l!=2.406 \times 10^{84}$ for the $\,\alpha -{}^{13}\textrm{C}\,$ relative orbital angular momentum $l=1.\,$ Here $\eta ^{s}$ is the Coulomb parameter of the bound state. That is why it is more convenient to work with the Coulomb renormalized ANC rather than with the ANC:

$$\begin{aligned} {{\tilde{C}}}_{l}^{2}=\Big ( \frac{l!}{\Gamma (1+ l+ \eta ^{(s)})}\Big )^{2}\,C_{l}^{2}. \end{aligned}$$

(177)

Note that usually, the barrier factor decreases the cross-section, but the barrier effect on the ANC has the opposite effect.

In the R-matrix approach the appropriate quantity, which we need to calculate the astrophysical S-factor, is the observable reduced width $\gamma _{l}^{2}$ related to the ANC by Eq. (145). To calculate the reduced width for the subthreshold bound state it is more convenient to exploit

$$\begin{aligned} { \gamma }_{l}^{2}&= \frac{C_{l}^{2}\,W_{-\,\eta ^{(s)},\,l+1/2}^{2}(2\,\kappa _{s}\,R_{ch} )}{2\,\mu \,R_{ch}} \end{aligned}$$

(178)

$$\begin{aligned}&= \frac{{{\tilde{C}}}_{l}^{2}\,{{\tilde{W}}}_{-\,\eta ^{(s)},\,l+1/2}^{2}(2\,\kappa _{s}\,R_{ch})}{2\,\mu \,R_{ch}}. \end{aligned}$$

(179)

For the subthreshold bound state located at $-3$ keV and the channel radius $R_{ch}=7.5$ fm $\;W_{-\,\eta ^{(s)},\,l+1/2}(2\,\kappa _{s}\,R_{ch})=2.44122 \times 10^{-86}$ while

$$\begin{aligned}&{{\tilde{W}}}_{-\,\eta ^{(s)},\,3/2}^{2}(2\,\kappa _{s}\,R_{ch}) \nonumber \\&\quad = \frac{\Gamma (1+ l+ \eta ^{(s)})}{l!}\, W_{-\,\eta ^{(s)},\,3/2}^{2}(2\,\kappa _{s}\,R_{ch}) = 0.0587. \end{aligned}$$

(180)

Correspondingly,

$$\begin{aligned}&C_{\alpha \,{}^{13}\textrm{C}}\,W_{-\,\eta ^{(s)},\,l+1/2}(2\,\kappa _{s}\,R_{ch})\nonumber \\&\quad = {{\tilde{C}}}_{\alpha \,{}^{13}\textrm{C}}\,{{\tilde{W}}}_{-\,\eta ^{(s)},\,l+1/2}(2\,\kappa _{(s)}\,R_{ch})\nonumber \\&\quad = 0.111 \, \textrm{fm}{}^{-1/2}. \end{aligned}$$

(181)

Thus the subthreshold reduced width is not affected by the Coulomb barrier because the significant increase of the ANC by the Coulomb barrier is compensated by the corresponding decrease of the Whittaker function. Hence Eq. (179) is very appropriate for the practical calculations for subthreshold states.

The reduced width changes very little as a function of the binding energy if we assume that the threshold level $1/2^{+}$ is the bound state. This circumstance can be used to find the reduced width of the nearby resonance state. First, we generate the $\alpha -^{13}\textrm{C}$ single-particle bound-state wave function with the binding energy 3 keV. To this end, one can use the $\alpha -^{13}\textrm{C}$ Woods-Saxon potential. The generated bound state has three nodes at $r>0$. Following the R-matrix procedure, the adopted internal region is taken to be $0 \le r \le R_{ch}$, where $R_{ch}=5.2$ fm is the location of the last peak of the internal wave function. The calculated wave function is normalized over the internal region. The obtained value can reasonably estimate the single-particle reduced width amplitude. After that we adopt the binding energy as low as 0.1 keV and repeat all the calculations using the well-depth procedure, which finds the potential depths corresponding to the selected bound state. The value of the single-particle reduced width decreased only by $2.5\%$ compared to the value for the 3 keV binding energy. Because the reduced width of the resonance state at 4.7 keV is unknown and we are not able to reproduce this state using a single-particle Woods-Saxon potential, as we did for the bound states, we assume that the reduced width for the resonance state is close to the reduced width for the 3 keV binding energy, which is 3.3 keV${}^{1/2}$ for the ANC ${{\tilde{C}}}_{\alpha \,{}^{13}\textrm{C}}=1.9$ fm${}^{-1/2}$ and $R_{ch}=7.5$ fm. After that we can fit the indirect THM data ( Tippella and La Cognata [31]) assuming that the threshold state is the resonance 4.7 keV varying the reduced width in the interval $\big (2.81-3.6 \big )\,$ keV${}^{1/2}$ at $R_{ch}= 7.5$ fm.

Fig. 4

Astrophysical S-factor for the $^{13}\textrm{C}(\alpha ,\,n)^{16}\textrm{O}$ reaction as a function of the $\alpha - {}^{13}\textrm{C}$ relative kinetic energy. Square black boxes, solid green dots and shaded orange band are data from Refs. Drotlieff et al. [36], Heil et al. [29] and Tippella and La Cognata [31], respectively. Red solid lines correspond to our calculations for the fit to the lower and upper limits of the TH data considering $1/2^{+}$ state as $-3$ keV subthreshold resonance with $\Gamma _{n} = 158.1$ keV [29]. The lower and upper limits of the square of the ANC are 2.89 fm$^{-1}$ and 4.7 fm$^{-1}$, respectively. Whereas, the blue dotted-dashed lines correspond to the current fit to TH data, considering $1/2^{+}$ state as 4.7 keV threshold resonance with $\Gamma _{n} = 136$ keV (Faestermann et al. [30]). The corresponding lower and upper values of observable reduced width are 2.81 keV$^{1/2}$ and 3.6 keV$^{1/2}$, respectively. For our calculations we have used $R_{\alpha \,{}^{13}\textrm{C}}= 7.5$ fm and $R_{n\,{}^{16}\textrm{O}}= 6.0$ fm. The insert in the figure shows enlarged low-energy S-factor. First published in Mukhamedzhanov et al. [32]

Figure 4 shows the S-factor for the reaction ${}^{13}\textrm{C}(\alpha ,\,n){}^{16}\textrm{O}$ assuming that the threshold level is the 4.57 keV resonance. Our numerical values of the S(0) factors are:

• (1) for $1/2^{+}$, $-3$ keV and $\Gamma _{n}= 158.1$ keV [29], $S(0)=7.62 _{-1.23}^{+2.65}\times 10^{6}$ MeVb;

• (2) for $1/2^{+}$, 4.7 keV and $\Gamma _{n}= 136$ keV [30], $S(0)=7.51 _{-1.1}^{+2.96}\times 10^{6}$ MeVb. Thus, even the TH data, which provides the astrophysical factor at significantly lower energies than direct measurements [29], cannot answer the question whether the threshold level is a subthreshold bound state or resonance.

9 Connection between Breit–Wigner resonance width and ANC of mirror resonance and bound states from Pinkston–Satchler equation

9.1 Introduction

The width of a narrow resonance can be expressed in terms of the ANC of the Gamow–Siegert wave function (Sect. 3.1). That is why we can extend the relationship between the ANCs of mirror bound states to the relationship between resonance widths and ANCs of the mirror nuclei (Timofeyuk et al. [34], Mukhamedzhanov [35]). The calculated resonance widths and the ANCs depend strongly on the choice of the nucleon–nucleon (NN) force, but the ratios of the resonance widths and the ANCs for mirror bound states should not depend on the adopted NN force, see for details review [1]. Another important feature of the mirror nuclei is the similarity of the internal mirror wave functions. Let us consider a mirror pair in two-body potential model: $\,B_{1} =(a_{1}\,A_{1})\,$ in the resonance state and the loosely bound nucleus $\,B_{2}=(a_{2}\,A_{2})$. The mirror resonance state is obtained by replacing one of the neutrons with a proton. The additional Coulomb interaction pushes the bound-state level into a resonance level. The resonance and binding energy of the mirror states are significantly smaller than the depth of the nuclear potential. The Coulomb interaction is almost a constant in the nuclear interior. Hence, in the nuclear interior, which all that matters to determine the ratio of the resonance width and the ANC of the mirror state, the radial behavior of the mirror wave functions is very similar, and they differ only by normalization. In the outer region, the resonant and bound-state wave functions vary significantly.

Below, using the Pinkston–Satchler equation (Pinkston and Satchler [37], Philpott et al. [38]), which has been used in Sect. 2.9, review [1], for the ANCs of the mirror bound states, we will obtain the ratio of the resonance width and the ANC of the mirror bound state. This equation had been successfully employed by Nollett [39] to determine the resonance widths of light nuclei ($5 \le A \le 9$). He used the ab initio variational Monte Carlo method to calculate the many-body wave functions in the interaction region. Timofeyuk and Descouvemont [40] applied the Pinkston–Satchler equation with the shell-model based sorce term to calculate the resonance widths. The obtained here the ratio of the resonance width and the ANC of the mirror bound state is expressed in terms of the ratio of the Wronskians containing the overlap functions of the mirror resonance and bound states in the internal region. In this region, the radial behavior of the mirror overlap functions is very similar and can be calculated quite accurately using ab initio approach. Suppose these overlap functions are not available. In that case, as an approximation, they can be replaced by the mirror resonance and bound state wave functions calculated using the two-body potential model with the same potentials for the resonance and bound states. In the Wronskian method, which is developed here, one needs the wave functions only in the internal region, in which it is very convenient to use the R-matrix method.

Assuming that the radial behavior of the mirror resonant and bound-state wave functions is identical in the nuclear interior, one can replace the Wronskian ratio for the resonance width and the ANC of the mirror bound state with the equation, which does not require knowledge of the internal resonant and bound-state wave functions (Timofeyuk et al. [34]).

The connection between the ANC and the resonance width of the mirror resonance state provides a powerful indirect method to obtain information that is unavailable directly. If, for instance, the resonance width is unknown, one can find it through the known ANC of the mirror state and vice versa. For example, near the edge of the stability valley, neutron binding energies become so small that the mirror proton states are resonances. The relationship between the mirror resonance width and the ANC allows us to find the resonance width from the ANC of the mirror bound state. Also loosely bound states $\alpha + A$ become resonances in the mirror nucleus $\alpha + B$, where charge $Z_{B}e > Z_{A}e$. Using the method developed below, one can find missing quantities, the resonance width of the narrow resonance state, or the mirror ANC.

9.2 Resonance width from Pinkston–Satchler equation

In Sect. 2.9 [1] the relationships between the mirror proton and neutron ANCs was derived using the Pinkston–Satchler equation. Here these relationships are extended for the ratio for the resonance width and the ANC of the mirror bound state in terms of the Wronskians, which follows from the Pinkston–Satchler equation.

Repeating step by step the derivation in Sect. 2.9.1, review [1], we arrive at the desired equation, which expresses the ANC of the narrow resonance state in terms of the source term:

$$\begin{aligned} C^{B}_{aA\,{l_B}\,{j_B}\,J_{B}}\,&= i\,\frac{\mu _{aA}}{k_{aA(R)}}\, \nonumber \\&\quad \int \limits _{0}^{R_{ch}}\,\textrm{d}r_{aA}\,r_{aA}\,\phi _{l_{B}}^{C}(k_{aA(0)},\,r_{aA})\,Q_{l_{B}j_{B}J_{a}J_{A}J_{B}}(r_{aA}), \end{aligned}$$

(182)

where $\,\phi _{l_{B}}^{C}(k_{aA(0)},\,r_{aA})\,$ is the regular Coulomb scattering wave function (review [1]). Using Eqs. (2.75), review [1], and (47) one gets the expression of the resonance width for narrow resonances in terms of the source term:

$$\begin{aligned}&e^{-\,i\,\delta _{l_{B}}^{hs}(k_{aA(0)})}\,\sqrt{\frac{\mu _{aA}}{k_{aA(0)}}\,\Gamma _{aA\,l_{B}j_{B}J_{B}}}\,\nonumber \\&\quad = 2\,\frac{\mu _{aA}}{k_{aA(0)}}\,\int \limits _{0}^{R_{ch}}\,\textrm{d}r_{aA}\,r_{aA}\,F_{l_{B}}(k_{aA(0)},\,r_{aA})\,Q_{l_{B}j_{B}J_{a}J_{A}J_{B}}(r_{aA}), \end{aligned}$$

(183)

where the Coulomb-nuclear phase shift is replaced by the sold-sphere phase taken at the real part of the resonance momentum $\,k_{aA(0)}$. Equations (182) and (183) provide the ANC or resonance width of the narrow resonance, which may depend on the channel radius $R_{ch}$. For practical calculations in the next subsection we express the resonance width in terms of the Wronskian as it was done for the ANC of the bound state in subsection (2.91), review [1].

9.3 Resonance width in terms of Wronskian

The advantage of Eq. (183) is that to calculate the resonance width one needs to know the microscopic resonant wave functions only in the nuclear interior where the ab initio methods are more accurate than in the external region. That is why Eq. (183) is so important if microscopic resonant wave functions are available. Now it will be shown that the radial integral in Eq. (183) can be transformed into the Wronskian at $r_{aA}= R_{ch}$. Again, repeat all the steps used in Sect. (2.9.1) [1] we arrive at the final expression for the ANC of the resonance state in terms of the Wronskian:

$$\begin{aligned} C_{aA\,\,{l_B}\,{j_B}\,J_{B}}^{B}&= \frac{i}{2\,k_{aA(0)}}\, \mathcal{W}[r_{aA}\,I_{aA\,\,{l_B}\,{j_B}\,J_{B}}^B({r_{aA}}),\,\phi _{l}(k_{aA(0)},r_{aA}]\Big |_{r_{aA}=R_{ch}} \nonumber \\&=\,\frac{1}{k_{aA(0)}}\,e^{\pi \,\eta _{aA(0)}/2}\,e^{-i\,\pi \,l_{B}/2}\nonumber \\&\quad \mathcal{W}[r_{aA}\,I_{aA\,\,{l_B}\,{j_B}\,J_{B}}^B({r_{aA}}),\,e^{i\,\sigma _{l}^{C}}F_{l_{B}}(k_{aA(0)},\,r_{aA})]\Big |_{r_{aA}=R_{ch}}. \end{aligned}$$

(184)

In view of Eq. (47), we get for the resonance width of the narrow resonance:

$$\begin{aligned} \sqrt{\frac{\mu _{aA}\,\Gamma _{aA\,l_{B}\,j_{B}\,J_{B}}}{k_{aA(0)}}}&=\frac{e^{i\,\delta _{l_{B}}^{hs}(k_{aA(0)})}}{k_{aA(0)}}\, \nonumber \\&\quad \mathcal{W}[r_{aA}\,I_{aA\,\,{l_B}\,{j_B}\,J_{B}}^B({r_{aA}})\,F_{l_{B}}(k_{aA(0)},\,r_{aA})]\Big |_{r_{aA}=R_{ch}}. \end{aligned}$$

(185)

The resonance width calculated using the Wronskian expression (185) depends on the channel radius and reaches a constant value as $R_{ch}$ increases. However, the sensitivity of the ratio of the resonance width and the ANC of the mirror bound state to the variation of the channel radius is significantly weaker than that of the resonance width and the ANC separately. It allows one to use the microscopic or potential-model wave functions in the internal region to calculate the ratio of the resonance width and the ANC of the mirror bound state. In the next section we present three different equations of this ratio and practical calculations.

9.4 Ratio of resonance width and ANC of mirror bound state in different approximations

In this part three different equations for the ratio of the resonance width and the ANC of the mirror bound state are presented. Let $B_{1}=(a_{1}\,A_{1})$ and $B_{2}=(a_{2}\,A_{2})$ be mirror nuclei. Then the quantum numbers in both nuclei are the same. We also assume that the channel radius $R_{ch}$ is the same for both mirror nuclei. Using Eqs. (2.229), (2.74), (2.227), review [1], and Eq. (185) we can express the ratio of the resonance width and the ANC of the mirror bound state as the ratio of the corresponding Wronskians:

$$\begin{aligned}&\qquad \qquad \qquad \frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}} = \,\sqrt{\frac{2\,E_{a_{1}A_{1}(0)}}{\mu _{a_{1}A_{1}}}} \nonumber \\&\qquad \qquad \qquad \quad \times \,\frac{{\,\big |\kappa _{a_{2}A_{2}}\,\mathcal{W}[{r_{{a_1}{A_1}}}\,{I_{{a_1}{A_1}\,\,{l_B}\,{j_B}\,{J_B}}}({k_{{a_1}{A_1}(0)}},\,{r_{{a_1}{A_1}}}),\,F_{l_{B}}({k_{{a_1}{A_1}(0)}},\,{r_{{a_1}{A_1}}})]{\big |^2}\,{\Big |_{{r_{{a_1}{A_1}}} = {R_{ch}}}}}}{{{{\big |k_{a_{1}A_{1}(0)}\,\mathcal{W}[{r_{{a_2}{A_2}}}\,{I_{{a_2}{A_2}\,\,{l_B}\,{j_B}\,{J_B}}}({\kappa _{{a_2}{A_2}}},\,{r_{{a_2}{A_2}}}),\,F_{l_{B}} (i{\kappa _{{a_2}{A_2}}},\,{r_{{a_2}{A_2}}})]\big |}^2}\,{\Big |_{{r_{{a_2}{A_2}}} = {R_{ch}}}}}}, \end{aligned}$$

(186)

where the ratio $\frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}}$ is dimensionless, $E_{a_{1}A_{1}(0)}$ and $\mu _{a_{1}A_{1}}$ are expressed in MeV.

Equation (186) allows one to determine the resonance width if the ANC of the mirror bound state is known and vice versa. To calculate the ratio $\frac{\Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{1}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}}$ one needs the microscopic radial overlap functions. If these radial overlap functions are not available then one can use a standard potential-model approximation for the overlap functions:

$$\begin{aligned}&I_{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}(k_{a_{1}A_{1}(0)},\,{r_{aA}})\nonumber \\&\qquad \approx {\mathtt S}_{a_{1}A_{1}}^{1/2}\, \phi _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}(k_{a_{1}A_{1}(0)},\,{r_{a_{1}A_{1}}}), \end{aligned}$$

(187)

$$\begin{aligned}&I_{a_{2}A_{2}\,\,{l_B}\,{j_B}\,J_{B}}(\kappa _{a_{2}A_{2}},\,{r_{aA}})\nonumber \\&\qquad \approx {\mathtt S}_{a_{2}A_{2}}^{1/2}\, \phi _{a_{2}A_{2}\,\,{l_B}\,{j_B}\,J_{B}}(\kappa _{a_{2}A_{2}},\,{r_{a_{2}A_{2}}}), \end{aligned}$$

(188)

where ${\mathtt S}_{a_{1}A_{1}}$ and ${\mathtt S}_{a_{2}A_{2}}$ are the SFs of the mirror resonance and bound states $(a_{1}A_{1})$ and $(a_{2}A_{2})$, respectively. $\phi _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}(k_{a_{1}A_{1}(0)},\,{r_{a_{1}A_{1}}})$ is a real internal resonant wave function calculated in the two-body model $(a_{1} \, A_{1})$ using some phenomenological potential, for example, Woods-Saxon one, which supports the resonance state under consideration. $\phi _{a_{2}A_{2}\,\,{l_B}\,{j_B}\,J_{B}}(\kappa _{a_{2}A_{2}},\,{r_{a_{2}A_{2}}})$ is the two-body bound-state wave function of the bound state $(a_{2}\,A_{2})$, which is also calculated using the same nuclear potential as the mirror resonance state. If the mirror symmetry holds then ${\mathtt S}_{a_{1}A_{1}} \approx {\mathtt S}_{a_{2}A_{2}}$ and one gets an approximated $\frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}}$ ratio in terms of the Wronskians, which does not contain the overlap functions:

$$\begin{aligned}&\frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}}\, \approx \,\sqrt{\frac{2\,E_{a_{1}A_{1}(0)}}{\mu _{a_{1}A_{1}}}} \nonumber \\&\quad \times \frac{\big |\kappa _{a_{2}A_{2}}\,\mathcal{W}[\phi _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}(k_{a_{1}A_{1}(0)},\,{r_{a_{1}A_{1} } }),\,F_{l_{B}}(k_{a_{1}A_{1}(0)},\,r_{a_{1}A_{1}})]\big |^{2}\,\Big |_{r_{a_{1}A_{1}}=R_{ch}}}{\big |k_{a_{1}A_{1}(0)}\,\mathcal{W}[\phi _{a_{2}A_{2}\,\,{l_B}\,{j_B}\,J_{B}}(\kappa _{a_{2}A_{2}},\,r_{a_{2}A_{2}} ),\,F_{l_{B}}(i\,\kappa _{a_{2}A_{2}},\,r_{a_{2}A_{2}})]\big |^{2}\,\Big |_{r_{a_{2}A_{2}}=R_{ch}}}. \end{aligned}$$

(189)

We can further simplify Eq. (189). The Coulomb interaction varies very little in the nuclear interior and its effect leads only to shifting of the energy of the bound state to the continuum. Hence, it can be assumed that $F_{l_{B}}(k_{a_{1}A_{1}(0)},\,r_{a_{1}A_{1}})$ and $F_{l_{B}}(i\,\kappa _{a_{2}A_{2}},\,r_{a_{2}A_{2}})$ behave similarly in the nuclear interior except for the overall normalization, that is

$$\begin{aligned} {F_{{l_B}}}({k_{{a_1}{A_1}(0)}},\,{r_{{a_1}{A_1}}}) \approx \frac{{{F_{{l_B}}}({k_{{a_1}{A_1}(0)}},\,{R_{ch}})}}{{{F_{{l_B}}}(i\,{\kappa _{{a_2}{A_2}}},\,{R_{ch}})}}\,F_{{l_B}}(i\,{\kappa _{{a_2}{A_2}}},\,{r_{{a_1}{A_1}}}). \end{aligned}$$

(190)

Then

$$\begin{aligned}&\frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}} \approx \sqrt{\frac{2\,E_{a_{1}A_{1}(0)}}{\mu _{a_{1}A_{1}}}} \,{\Bigg |\frac{{{F_{{l_B}}}({k_{{a_1}{A_1}(0)}},\,{R_{ch}})}}{{{F_{{l_B}}}(i\,{\kappa _{{a_2}{A_2}}},\,{R_{ch}})}} \Bigg |^2} \nonumber \\&\qquad \times \frac{{\Big | \kappa _{a_{2}A_{2}}\,\mathcal{W}\big [{\phi _{{a_1}{A_1}\,\,{l_B}\,{j_B}\,{J_B}}}({k_{{a_1}{A_1}(0)}},\,{r_{{a_1}{A_1}}}),\,F_{{l_B}}(i\,{\kappa _{{a_2}{A_2}}},\,{r_{{a_1}{A_1}}})\big ]\,{\Big |^2}\,{\Bigg |_{{r_{{a_1}{A_1}}} = {R_{ch}}}}}}{{{{\Big |k_{a_{1}A_{1}(0)}\,\mathcal{W}\big [{\phi _{{a_2}{A_2}\,\,{l_B}\,{j_B}\,{J_B}}}({\kappa _{{a_2}{A_2}}},\,F_{l_{B}}(i\,\kappa _{a_{2}A_{2}},\,r_{a_{2}A_{2}})}\big ]\Big |^2}\,{\Bigg |_{{r_{{a_2}{A_2}}} = {R_{ch}}}}}}. \end{aligned}$$

(191)

Neglecting further the difference between the mirror wave functions

${\phi _{{a_1}{A_1}\,\,{l_B}\,{j_B}\,{J_B}}}({k_{{a_1}{A_1}(0)}},\,{r_{{a_1}{A_1}}})$ and ${\phi _{{a_2}{A_2}\,\,{l_B}\,{j_B}\,{J_B}}}({\kappa _{{a_2}{A_2}}},\,{r_{{a_2}{A_2}}})$ in the nuclear interior we obtain the approximate expression for $\frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}}\,$:

$$\begin{aligned}&\frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}} \approx \sqrt{\frac{2\,E_{a_{1}A_{1}(0)}}{\mu _{a_{1}A_{1}}}} \,{\Bigg |\frac{{{F_{{l_B}}}({k_{{a_1}{A_1}(0)}},\,{R_{ch}})}}{{{F_{{l_B}}}(i\,{\kappa _{{a_2}{A_2}}},\,{R_{ch}})}} \Bigg |^2} . \end{aligned}$$

(192)

This equation provides the easiest way to determine $\frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}}$ because to calculate it one needs to know only the Coulomb wave functions for the resonant and mirror bound states.

In descending accuracy we can rank Eq. (186) as the most accurate. Taking into account that the microscopic overlap functions (calculated in the no-core-shell-model (see Navratil et al. [41] and references therein) or oscillator shell-model (Timofeyuk [42]) are accurate in the nuclear interior, using Eq. (186) one can determine the ratio $\frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}}$ quite accurately. If the microscopic overlap functions are not available one can use Eq. (189). Then follows Eq. (191) and finally Eq. (192). Note that Eq. (192) is valid only in the region where the mirror resonant and bound state wave functions do coincide or very close. The advantage of this equation is that it allows one to calculate the ratio without using the mirror wave functions and extremely simple to use.

Because for the cases considered below the internal microscopic resonance wave functions are not available, the $\frac{ \Gamma _{a_{1}A_{1}\,\,{l_B}\,{j_B}\,J_{B}}}{({C}_{a_{2}\,A_{2}\,\,{l_B}\,{j_B}\,J_{B}}^{B_{2}})^{2}}$ ratio is calculated using Eqs. (189) and (192). It allows one to determine the accuracy of both equations.

10 Comparison of resonance widths and ANCs of mirror states

Below a few examples of the application of Eqs. (189) and (192) are presented. To simplify the notations from now on the quantum numbers in the notations for the resonance width and the ANC are dropped and just simplified notations are used: $\Gamma _{a_{1}A_{1}}$ and ${C}_{a_{2}\,A_{2}}$. Equation (189) gives $\Gamma _{a_{1}A_{1}}/({C}_{a_{2}\,A_{2}})^{2}$ in terms of the ratio of the Wronskians and provides an exact value for given two-body mirror resonant and bound-state wave functions. Equation (192) gives the $\Gamma _{a_{1}A_{1}}/({C}_{a_{2}\,A_{2}})^{2}$ ratio in terms of the Coulomb scattering wave functions at the real resonance momentum $k_{{a_1}{A_1}(0)}$ and the imaginary momentum of the bound state $i\,\kappa _{{a_2}{A_2}}$ at the channel radius $R_{ch}$. Hence, to determine the ratio $\Gamma _{a_{1}A_{1}}/({C}_{a_{2}\,A_{2}})^{2}$ using Eq. (192) one does not need to know the mirror resonant and bound-state wave functions. However, to use this equation one should check whether the mirror wave functions are close. To demonstrate the convergence of the calculated ratio $\Gamma _{a_{1}A_{1}}/({C}_{a_{2}\,A_{2}})^{2}$ as $R_{ch}$ increases the channel radius $R_{ch}$ has been deliberately increased.

10.1 Comparison of resonance width for $\mathbf {{}^{13}\textrm{N}(1d_{5/2}) \rightarrow {}^{12}\textrm{C}(0.0\,\textrm{MeV}) + p}$ and mirror ANC for virtual decay $\mathbf {{}^{13}\textrm{C}(1d_{5/2}) \rightarrow {}^{12}\textrm{C}(0.0\,\textrm{MeV}) + n}$

As the first example we consider the isobaric analogue states $1d_{5/2}$ in the mirror nuclei ${}^{13}\textrm{N}$ and ${}^{13}\textrm{C}$. The resonance energy of ${}^{13}\textrm{N}(1d_{5/2})$ is $E_{p{}^{12}\textrm{C}(0)} =1.6065$ MeV with the resonance width of $\Gamma _{p\,{}^{12}\textrm{C}}= 0.047 \pm 0.0008$ MeV (Ajzenberg-Selove [43]). The neutron binding energy of the mirror state ${}^{13}\textrm{C}(1d_{5/2})$ is $\varepsilon _{n{}^{12}\textrm{C}} = 1.09635$ MeV with the experimental ANC $C_{n{}^{12}\textrm{C}}^{2}= 0.0225$ fm${}^{-1}$ (Liu et al. [44]). The experimental ratio is ${\Gamma _{{p\,^{12}}{\textrm{C}}}}/C_{{n\,^{12}}{\textrm{C}}}^2 = (1.1 \pm 0.2) \times {10^{ - 2}}$.

Fig. 5

Solid red line: The radial wave function of the $(p{}^{12}\textrm{C})_{1d_{5/2}^{+}}$ resonance state; dash blue line: the radial wave function of the mirror $(n{}^{12}\textrm{C})_{1d_{5/2}^{+}}$ bound state. r is the distance between N, where $N=p,n$, and the c.m. of ${}^{12}\textrm{C}$. First published in Mukhamedzhanov [35]

Figure 5 shows the radial wave functions of the mirror states. Following the R-matrix procedure, both wave functions are normalized to unity over the internal volume with the radius $R_{ch}=3$ fm. We see that the mirror wave functions are very close at distances $r \le 4$ fm what confirms the mirror symmetry of $(p{}^{12}\textrm{C})_{1d_{5/2}^{+}}$ and $(n{}^{12}\textrm{C})_{1d_{5/2}^{+}}$ systems.

The similarity of the internal mirror wave functions can be explained. In the nuclear interior the depth of the nuclear potential is much larger than the resonance and binding energies. Hence in the nuclear interior the mirror resonance and bound-state solutions of the Schrödinger equation corresponding to states with the same quantum numbers but different energies should be very close.

Fig. 6

The grey band is the experimental $\frac{{{\Gamma _{p{\,^{12}}{\textrm{C}}}}}}{{{{({{C}_{n{\,^{12}}{\textrm{C}}}})}^2}}}$ ratio of the resonance width of the resonance state ${}^{13}\textrm{N}(1d_{5/2}^{+})$ and the ANC of the mirror bound state ${}^{13}\textrm{C}(1d_{5/2}^{+})$; the red dash-dotted-dotted line and the red dash-dotted lines are the low and upper limits of this experimental ratio; the green dotted line is the adopted experimental value of the ratio $\frac{{{\Gamma _{p{\,^{12}}{\textrm{C}}}}}}{{{{({{C}_{n{\,^{12}}{\textrm{C}}}})}^2}}}= (1.1 \pm 0.2) \times {10^{ - 2}}$; the solid red line is the $\frac{{{\Gamma _{p{\,^{12}}{\textrm{C}}}}}}{{{{({{C}_{n{\,^{12}}{\textrm{C}}}})}^2}}}$ ratio as a function of $R_{ch}$ calculated using Eq. (189); the blue dotted line is the $\frac{{{\Gamma _{p{\,^{12}}{\textrm{C}}}}}}{{{{({{C}_{n{\,^{12}}{\textrm{C}}}})}^2}}}$ ratio calculated as a function of $R_{ch}$ using Eq. (192). First published in Mukhamedzhanov [35]

In Fig. 6 are shown the $\frac{{{\Gamma _{p{\,^{12}}{\textrm{C}}}}}}{{{{({{C}_{n{\,^{12}}{\textrm{C}}}})}^2}}}$ ratios calculated using Eqs (189) and (192), which are compared with the experimental ratio. We see that the calculated ratios are quite close to the experimental one. The $\frac{{{\Gamma _{p{\,^{12}}{\textrm{C}}}}}}{{{{({{C}_{n{\,^{12}}{\textrm{C}}}})}^2}}}$ ratio calculated using the simplified Eq. (192) shows the $R_{ch}$ dependence and is equal to 0.0141 at the peak at $R_{ch}=3.95$ fm. In the case under consideration the bound-state wave function does not have nodes at $r>0$. That is why the $\frac{{{\Gamma _{p{\,^{12}}{\textrm{C}}}}}}{{{{({{C}_{n{\,^{12}}{\textrm{C}}}})}^2}}}$ ratio calculated using Eq. (189) is a smooth function of $R_{ch}$. This equation gives $\frac{{{\Gamma _{p{\,^{12}}{\textrm{C}}}}}}{{{{({{C}_{n{\,^{12}}{\textrm{C}}}})}^2}}}=0.0135$ at $R_{ch}= 4$ fm, which differs very little from its correct asymptotic value of 0.0143. Our calculations show that the simple Eq. (192) can give the results close to the Wronskian method.

The ratio $\frac{{{\Gamma _{p{\,^{12}}{\textrm{C}}}}}}{{{{({{C}_{n{\,^{12}}{\textrm{C}}}})}^2}}}$ for the $1d_{5/2}^{+}$ was also calculated by Timofeyuk and Descouvemont [45] using the microscopic cluster model for mirror ${}^{13}\textrm{C}(1d_{5/2}^{+})$ and ${}^{13}\textrm{N}(1d_{5/2}^{+})$ states. The obtained ratios are $0.0124 \pm 0.0001$ for two-cluster model and 0.0130 for the four-cluster model. Both values are in a good agreement with the Wronskians ratio 0.0135.

10.2 Comparison of resonance width for $\mathbf {{}^{18}\textrm{Ne}(1^{-}) \rightarrow {}^{14}\textrm{O}(0.0\,\textrm{MeV}) + \alpha }$ and mirror ANC for virtual decay $\mathbf {{}^{18}\textrm{O}(1^{-}) \rightarrow {}^{14}\textrm{C}(0.0\,\textrm{MeV}) + \alpha }$

Here is determined the ratio ${\Gamma _{{\alpha \,^{14}}{\textrm{O}}}}/C_{{\alpha \,^{14}}{\textrm{C}}}^2$ for the mirror states ${}^{18}\textrm{Ne}(1^{-})$ and ${}^{18}\textrm{O}(1^{-})$. The resonance energy is $E_{\alpha {}^{14}\textrm{O}}=1.038$ MeV. The binding energy of the bound state ${}^{18}\textrm{O}(1^{-})$ is $\varepsilon _{\alpha {}^{14}\textrm{C}} = 0.027$ MeV. The resonance width and the ANC of the mirror states are unknown.

The purpose of this section is to show that the ratio ${\Gamma _{{\alpha \,^{14}}{\textrm{O}}}}/C_{{\alpha \,^{14}}{\textrm{C}}}^2$ does not depend on the number of the nodes of the mirror wave functions. The potential model search showed that for the given resonance energy and binding energy for $l=1$ the mirror wave functions have at $r>0$ the number of nodes $N=4$ or 6. The normalization region of the mirror wave functions is $r \le 7.2$ fm for $N=6$ and $r \le 6.73$ fm for $N=4$. In Figs.  7 and  8 are shown the radial wave functions and the ratio ${\Gamma _{{\alpha \,^{14}}{\textrm{O}}}}/C_{{\alpha \,^{14}}{\textrm{C}}}^2$ for the number of the nodes $N=4$ and 6. The presence of the nodes in the alpha-particle wave functions decreases the contribution of the nuclear interior making the contribution of the surface area $r> 6$ fm dominant. That is why for the mirror-conjugated $\alpha$-particle states the accuracy of Eq. (192) improves.

One can see that the mirror wave functions practically coincide up to $r=15$ fm. It means that the simplified Eq. (192) can be used up to 15 fm. The ratio ${\Gamma _{{\alpha \,^{14}}{\textrm{O}}}}/C_{{\alpha \,^{14}}{\textrm{C}}}^2$ calculated using Eq. (189) is the same for $N=4$ and 6. Because the mirror wave functions practically identical in the external region the ratio ${\Gamma _{{\alpha \,^{14}}{\textrm{O}}}}/C_{{\alpha \,^{14}}{\textrm{C}}}^2$ calculated using the Wronskian method (Eq. (189)) has an asymptote. The calculated for $N=4,\,6$ ratio reaches its asymptotic value at $R_{ch}=7.5$ fm which is ${\Gamma _{{\alpha \,^{14}}{\textrm{O}}}}/C_{{\alpha \,^{14}}{\textrm{C}}}^2= 3.48\,\times 10^{52}$. The maximum of ${\Gamma _{{\alpha \,^{14}}{\textrm{O}}}}/C_{{\alpha \,^{14}}{\textrm{C}}}^2$ calculated using Eq. (192) at $R_{ch}= 9$ fm is $3.42\,\times 10^{52}$. This comparison demonstrates again that in the absence of the microscopic internal overlap functions both the Wronskian and the simplified method given by Eq. (192) can be used and give very close results.

Fig. 7

Panel (a): the mirror radial wave functions for $N=6$; the solid red line is the $(\alpha {}^{14}\textrm{O})_{1^{-}}$ resonance wave function; the dashed blue line is the radial wave function of the mirror $(\alpha {}^{14}\textrm{C})_{1^{-}}$ bound-state. r is the distance between the $\alpha$-particle and the c.m. of the nucleus. Panel (b): notations are the same as in panel (a) but for $N=4$. First published in Mukhamedzhanov [35]

Fig. 8

Panel (a): the $\frac{{{\Gamma _{\alpha {\,^{14}}{\textrm{O}}}}}}{{{{({{C}_{\alpha {\,^{14}}{\textrm{C}}}})}^2}}}$ ratio for the resonance state ${}^{18}\textrm{Ne}(1^{-})$ and the mirror bound state ${}^{18}\textrm{O}(1^{-})$ for $N=6$; the solid red line is the $\frac{{{\Gamma _{\alpha {\,^{14}}{\textrm{O}}}}}}{{{{({{C}_{\alpha {\,^{14}}{\textrm{C}}}})}^2}}}$ ratio as a function of $R_{ch}$ calculated using Eq. (189); the blue dashed line is the $\frac{{{\Gamma _{\alpha {\,^{14}}{\textrm{O}}}}}}{{{{({{C}_{\alpha {\,^{14}}{\textrm{C}}}})}^2}}}$ ratio calculated as a function of $R_{ch}$ using Eq. (192). Panel (b): notations are the same as in panel (a) but for $N=4$. First published in Mukhamedzhanov [35]

11 Analytical methods of determination of resonance parameters

Analysis of the S-matrix pole structure is a powerful method in quantum physics. The structure of the S-matrix in the complex momentum (or energy) plane correspond to bound, virtual and resonance states, see Fig. 2 and Eq. (31). The relation between the S-matrix and the Jost functions $\mathcal{F}_{l}^{(\pm )}(k)$ is given by

$$\begin{aligned} {{\mathbb {S}}}_{l}(k)= \frac{\mathcal{F}_{l}^{(-)}(k)}{\mathcal{F}_{l}^{(+)}(k)}. \end{aligned}$$

(193)

The conventional numerical method for bound states is to search for solutions, which have only an outgoing wave at pure imaginary momenta in the upper half momentum plane. The corresponding wave function is an exponentially decreasing solution when $r \rightarrow \infty$. Virtual or resonance states are described by the wave functions containing only the outgoing waves asymptotically, which exponentially increase due to the complex momenta. To describe resonance states the Gamow–Siegert wave function can be used, see 2.3.

A few different techniques to determine the resonance energy, width and resonance wave function based on the solution of the Schrödinger equation have been previously suggested. One of them is Zel’dovich’s normalization procedure [14], which we discussed in Sect. 2.3. Another method is the modified CSM (see Appendix C). In this method the normalization of the resonant wave function is achieved using the rotation of the integration countour over r from $R_{max}$ to the complex plane, where the nuclear potential is cut to zero. First, we refer to the method of solution of the radial Schroödinger equation to determine resonances suggested by Vertse et al. [46] (GAMOW code). The method is designed to find poles corresponding to resonances and subthreshold resonances. In this method the complex eigenvalue and the Gamow wave function can be found by integration of the Schrödinger equation imposing the boundary conditions in the origin and the asymptotic region. An improved version of the the GAMOW code has been presented by Iharu et al. [47] (code ANTI), which was designed to determine parameters of broad resonances by introducing complex Woods-Saxon potential.

A pole search has also been used by Michel et al. [48] by solution of the Schrödinger equation with the short range interaction for the scattering wave function. The method allows one to find resonances and even subthreshold resonances.

11.1 The resonance states of $\mathbf {^{15}\textrm{F}(1/2^+,\, 5/2^+)}$

Below we illustrate how different theoretical approaches can be used to determine the parameters of the resonances ${}^{15}\textrm{F}(1/2^{+},\,5/2^{+})$ testing the predictive power of the used methods. The final goal is a comparison of the theoretical predictions with the available experimental data on the ${}^{15}\textrm{F}$ levels.

The resonance ${}^{15}\textrm{F}(1/2^{+})$ is broad. Determination of a broad resonance parameters is a well known unsolved problem in physics. The resonance energy and width for a broad resonance $^{15}\textrm{F}(1/2^+)$ are not defined uniquely and there are many prescriptions, which have been used in literature (Barker [49]). The definitions depend not only on the model used, say potential, R-matrix, microscopic, but even within a given model the prescriptions for the resonance parameters can be different (Barker [49, 50]). That is why when any compilation includes the broad resonance parameters, the reference should be done to the prescriptions used to determine these parameters. The reason for this ambiguity is that for broad resonances in the physical region the nonresonant contribution becomes comparable with the resonant one. In this case the determined resonance energy and width depend on how much of the background is included into the resonant part. The only way to determine correctly the resonance energy and width is to single out the resonance pole explicitly in the function fitting the experimental data. It is realized in the S-matrix pole method.

Here two approaches are addressed based on the definition of the resonance energy $E_{R}= E_{0} - i\,\Gamma /2$ as the energy at which the S-matrix has a pole on the second energy sheet (low half of the momentum plane): the potential approach based on the solution of the radial Schrödinger equation and the analytical expression for the S-matrix. The first one gives the most accurate definition of the resonance energy and width within the potential model, while the second one even more general because it is based only on the analyticity and the symmetry of the S-matrix.

We remind that a resonance corresponds to the pole of the S-matrix at $k_{R} = k_{0} - i\,k_{I}$ located in the fourth quadrant of the momentum complex plane. Correspondingly the resonance energy is

$$\begin{aligned} E_{R}= \frac{k_{R}^{2}}{2\,\mu }= E_{0} - i\,\frac{\Gamma }{2}, \end{aligned}$$

(194)

where

$$\begin{aligned} E_{0}= \frac{k_{0}^{2} - k_{I}^{2}}{2\,\mu }, \end{aligned}$$

(195)

and

$$\begin{aligned} \Gamma = \frac{ 2\,k_{0}\,k_{I} }{\mu }. \end{aligned}$$

(196)

Let us discuss the location of broad resonances and their qualification in more detail. For broad resonances $k_{I}$ becomes comparable with $k_{0}$. If $\,k_{0} > rsim k_{I}\,$ then $E_{0} >0$ and the broad resonance is located in the fourth quadrant of the momentum plane, which corresponds to the resonant pole located in the fourth quadrant on the second Riemann sheet of the energy plane. Such resonances are called observable. Owing to large $k_{I}$ (or resonance width $\Gamma$), their impact on the cross-section or scattering phase shift is weakened, and the non-resonant amplitude or phase shift (non-resonant background) becomes essential. The general expression for the elastic scattering S-matrix given by Eq. (31) in a vicinity of a single resonance can be rewritten as

$$\begin{aligned} {{\mathbb {S}}}_{l}^{CN}(k)&= e^{2\,i\,(\delta _{l}^{p}(k) + \delta _{R}(k) + \delta _{a}(k))}. \end{aligned}$$

(197)

$$\begin{aligned} \delta _{R}(k)&= -\arctan {\frac{k_{I}}{k - k_{0}}} \end{aligned}$$

(198)

$$\begin{aligned}&=-\left[ \frac{\pi }{2} - \arctan {\frac{k - k_{0}}{k_{I}}}\right] \end{aligned}$$

(199)

is the resonant scattering phase shift,⁶ and

$$\begin{aligned} \delta _{a}(k) =-\arctan {\frac{k_{I}}{k + k_{0}}}. \end{aligned}$$

(200)

For $k_{I} > k_{0}$ corresponding to $E_{o} <0$, the resonant pole is located in the third quadrant on the second energy sheet. These broad resonances, due to large $\Gamma$, are far from the negative real energy axis and are not observable and called unphysical resonances.

For narrow resonances, $k_{I}<< k_{0}$, the phase shift $|\delta _{a}(k)|<< 1$ can be neglected. In this case, the standard method, which we call the phase shift method (or “$\delta =\pi /2$” rule), entails the resonance energy $E_0$ the value at which the scattering phase $\delta (k)$ passes through $\pi /2$. The resonant width is evaluated from the formula $\Gamma =2/(d\delta /dE)$ at $E=E_0$ or as the energy interval corresponding to change of $\delta$ from $\pi /4$ to $3\pi /4$.

However, for broad resonances $\delta _{a}(k)$ cannot be neglected and the total non-resonant scattering phase shift $\delta _{p}(k) + \delta _{a}(k)$ becomes dependent on the resonant parameters. This the non-resonant scattering phase shift may be a large negative so that the total phase shift $\delta (k)$ cannot reach $\pi /2$ at $k = k_{0}$ making the $\pi /2$ method non-applicable. When calculating the elastic cross-section or scattering phase shift in the presence of the broad resonance due to the importance of the non-resonant phase shift, the cross-section depends not only on the resonance parameters $E_{0}$ and $\Gamma$ but also on the potential adopted.

Here as a test case, we select resonances representing the ground state $1/2^{+}$ and the first exited state $5/2^{+}$ in ${}^{15}\textrm{F}$. McCleskey et al. [51] showed that for the mirror ${}^{15}\textrm{C}$ states at standard geometrical parameters $r_{0}= 1.25$ fm and $a=0.65$ fm the extracted phenomenological SFs are close to unity. Hence the $1/2^{+}$ and $5/2^{+}$ states in ${}^{15}\textrm{C}$, which are mirror states in ${}^{15}\textrm{F}$, are close to the single-particle ones. Therefore, the potential approach is appropriate to describe these states and the same Woods-Saxon potential can be utilized to describe the mirror levels in ${}^{15}\textrm{C}$ and ${}^{15}\textrm{F}$ (Goldberg et al. [52]).

The energy at which the absolute value of the internal wave function reaches its maximum can be identified as the resonance energy. We call this the $|\Psi _{max}|$ method. Goldberg et al. [52] defined the width of the resonance by the energy interval over which the amplitude falls by $\sqrt{2}$ relative to the maximum of the $|\Psi _{max}|$. For comparison, one can also use the $\pi /2$ method.

We also apply the potential S-matrix pole method by solving the Schrödinger equation with the Woods-Saxon potential for both ${}^{15}\textrm{F}$ resonance states with the $J^{\pi } = 1/2^+$ and $5/2^+$. Zero of the the Jost function $\,\mathcal{F}_{l}^{(+)}(k) =0\,$ at complex energy give us the resonance pole, see Eq. (193). We note that in the standard approach, the scattering wave function is calculated at real energies, where the non-resonant contribution is significant for broad resonances, while the Gamow–Siegert wave function is calculated at the complex energy corresponding to the resonant pole of the S-matrix located on the second Riemann energy sheet. As a first approximation, to determine the complex resonance energy $E_R^{1}=E_{0}^{1} -i\Gamma ^{1}/2$ the phase shift method is used (or the $|\Psi _{max}|$ method when the $\delta =\pi /2$ method is non-applicable). After that, the Schrödinger equation near the complex energy $E_R^{1}=E_0^{1}-i\Gamma ^{1}/2$ is solved. The final result of this search is the complex energy $E_R$, at which the coefficient of the incoming wave vanishes. Also, the S-matrix pole search is utilized using the analytical representation (197) for the S-matrix (see explanation below).

The S-matrix pole method results for the energies and widths of the resonance states given in Table 1 are compared with the previous results obtained using the $\delta =\pi /2$ and $|\Psi _{max}|$ methods (Goldberg et al. [52]). The position E and the width $\Gamma$ of the broad resonance $1/2^{+}$ depends on the calculation method: the S-matrix pole method gives the values of the resonance energy and width smaller and more accurate than the $\delta =\pi /2$ and $|\Psi _{max}|$ methods. It is worth noting that the corrected value of 1.227 MeV for the resonance energy of the ground state of ${}^{15}\textrm{F}$ is very close to the lower limit obtained using the isobaric multiplet mass equation (Fortune [53] ).

Table 1 Energy and width of the resonances for the ${}^{15}\textrm{F}$ states with $J^p = 1/2^+$ (the ground state) and $5/2^+$ (the first exited state) calculated by the use of three different methods (see the text)

An important test of the S-matrix pole method is comparison of the single-particle ANC determined as an amplitude of the tail of the normalized Gamow–Siegert function with the ANC determined from the residue of the scattering amplitude at the pole corresponding to the resonance. For the normalization of the Gamow–Siegert wave function Zel’dovich regularization method is used (Baz’ et al. [14]). Both methods resulted in the same single-particle ANCs $(-0.123 + i\,0.153) \,\,\textrm{fm}^{-1/2}$ and $(0.115 + i\,0.067) \,\,\textrm{fm}^{-1/2}$ for the $1/2^{+}$ and $5/2^{+}$ states, respectively.

11.2 Model-independent determination of energy and width of the broad resonance $\mathbf {\frac{1}{2}^{+}}$ in $\mathbf {^{15}\textrm{F}}$

The limitations of the potential model and the existence of the phase-equivalent potentials call for a cross-check of the energy and width for the broad resonance determined from the potential approach. We define these resonance parameters using the model-independent representation of the elastic scattering S-matrix given by Eq. (197). Since the experimental $2s_{1/2}$ phase shift for ${}^{14}\textrm{O} +p$ scattering in the resonance energy region is not available, we generate the “quasi-experimental” $2s_{1/2}$ phase shift using the Woods-Saxon potential from Goldberg et al. [52], which reproduces the ${}^{14}\textrm{O} + p$ resonance scattering. Its geometry is $r_{0}=1.17$ fm, $a=0.735$ fm, $r_{C}=1.21$ fm and the depth $V_{0} = 53.52$ MeV. The phase shift is shown in Fig 9. Using the S-matrix pole method from the solution of the Schrödinger equation we find the resonance energy for this potential $E_{0}= 1.198$ MeV and the resonance width $\Gamma = 0.530$ MeV. Now we demonstrate that using Eq. (197) we can fit the “quasi-experimental” phase shift and determine the resonance energy and width. The potential phase shift in Eq. (197) is approximated by the polynomial $\delta _{p}(k)= \sum \nolimits _{n = 0}^3 {{b_n}{{(k - {k_s})}^n}}$. So, we have 6 fitting parameters including 4 coefficients $b_{n}$, $\,E_{0}$ and $\Gamma$. The final result does not depend on the choice of the center of the Taylor expansion $k_{s}$ and practically not sensitive to the starting values of $E_{0}$ and $\Gamma$. We take here the starting values $k_{s}= 0.25$ fm$^{-1},$ $\,E_{0}=1.45$ MeV and $\Gamma = 1.276$ MeV obtained from the $\delta = \pi /2$ method, Table 1. The fit to the “qausiexperimental” phase shift gives the final resonance energy $E_{0}= 1.194$ MeV and $\Gamma = 0.531$ MeV what is in a perfect agreement with the results obtained using the potential S-matrix pole method. For the starting search values $E_{0}=1.6$ Mev and $\Gamma =1.276$ MeV we get the fitted energy $E_{0}= 1.198$ MeV and $\Gamma = 0.532$ MeV. Thus Eq. (197) allows one to obtain the energy and width of the broad resonance using, for example, as input parameters the resonance and width obtained by the $\delta =\pi /2$, $\,|\Psi _{max}|$. The model-independent result obtained from Eq. (197) gives very close values to the potential S-matrix pole. Assigning a $10\%$ uncertainty to the “quasi-experimental” phase shift results in a similar uncertainty in the determined “quasi-experimental” phase shift resonance energy and width.

Fig. 9

The ${}^{14}\textrm{O}+ p$ $\,2\,s_{1/2}$ scattering phase shift generated by the Woods-Saxon potential from [52] and used as the “quasi-experimental phase shift”. First published in Mukhamedzhanov et al. [54]

11.3 Comparison with ${\textbf{R}}$-matrix approach

The resonant S-matrix obtained from the R-matrix contains the nonresonant contribution through the energy dependence of the level shift and resonance width. The extrapolation of these functions to the complex energy plane makes them complex. Hence they loose their physical meaning. Thus the R-matrix approach is not designed for extrapolation to the resonant pole.

Here we apply the R-matrix approach to determine the energy and the width of the resonance with the S-matrix pole method. For an isolated resonance in the single-level, single-channel R-matrix approach the Coulomb-modified nuclear scattering S-matrix is ( Eq. (87) in simplified notations)

$$\begin{aligned} {{\mathbb {S}}}_{l}^{CN}(E)=e^{-2\,i\,\delta _{l}^{hs}}\,\frac{E_{0} - E + i\,\frac{\Gamma _{l}(E)}{2}}{ E_{0} - E - i\,\frac{\Gamma _{l}(E)}{2}}. \end{aligned}$$

(201)

In contrast to the Breit–Wigner equation, the resonance width in the R-matrix approach depends on the energy. This dependence means that the S-matrix in the R-matrix is richer than the Breit–Wigner equation: it also includes the non-resonant background, which is contributed by the hard-sphere phase shift and the energy dependence of the resonance width. For narrow resonance ($\Gamma (E_{0})<< E_{0}$) the pole in Eq. (201) $E_{R} \approx E_{0} - i\,\Gamma (E_{0})/2$. For a broad resonance this resonance energy is not a pole of the S-matrix. The equation for the resonant pole in this case is given by $E_{R} = E_{0} - i\,\Gamma (E_{R})/2$. At complex $E_{R}$ $\,\,\Gamma (E_{R})$ becomes complex and looses its meaning of the width. For a broad resonance in the R-matrix method the resonance energy is defined as $E_{R}= E_{0} - i\,\Gamma (E_{0})$, which is not a pole of Eq. (201). Hence, for broad resonances, the difference between the resonance energy from the S-matrix pole method and the R-matrix method is expected.

To compare the results for the R-matrix and S-matrix pole methods for the $s_{1/2}^{+}$ resonance we use the phase shift generated by the Woods-Saxon potential from Goldberg et al. [52] as the “quasi-experimental” one and determine the resonance energy and width by fitting the R-matrix phase shift to the “quasi-experimental”. The results are shown in Table 1. The R-matrix resonance energy and width depend on $R_{ch}$. At $R_{ch}=4.5$ fm the R-matrix are close to $|\Psi _{max}|$ results. At $R_{ch}=6.0$ the R-matrix results are lower than the $|\Psi _{max}|$ ones. Both R-matrix and $|\Psi _{max}|$ methods determine the resonance energy from the data at real energies where for broad resonances the contribution of the background becomes important. The S-matrix pole method determines the resonance energy and width by extrapolating the data to the pole in the complex energy (momentum) plane. In the vicinity of the pole the resonant contribution becomes dominant compared to the background and determination of the resonance parameters is more accurate than in the physical region.

12 Theory of transfer reactions populating resonance states

12.1 Introduction

Production of unstable nuclei close to proton and neutron drip lines has become possible in recent years, making deuteron stripping reactions (d, p) and (d, n) on these nuclei (in inverse kinematics) not only more feasible as beam intensity increases but also a unique tool to study unstable nuclei and astrophysical $(n,\,\gamma )$, $\,(p,\gamma )$ and $(p,\,\alpha )$ processes. The deuteron stripping reactions populating the resonance states of final nuclei are an important and challenging part of reactions on unstable nuclei.

The standard method of analyzing the nucleon transfer reactions populating bound states for a long time was the distorted-wave-Born approximation (DWBA). By standard DWBA, I mean the approach in which the one-step transfer matrix element is evaluated with incoming and outgoing distorted waves calculated by fitting the deuteron and proton elastic scattering with local optical potentials. The transition operator contains finite range effects and the full complex remnant term. The main idea of the DWBA is that the transition matrix element is so small that one can use the first-order perturbation theory. Since the nuclear potential is quite large by itself ($\sim 100$ MeV), the smallness of the transition operator can be fulfilled if the reaction is peripheral enough that the nondiagonal matrix element representing the transfer reaction amplitude becomes small.

However, an adequate theory for transfer reactions to resonance states has yet to be developed because the resonance wave function is large in the nuclear interior, where different channels are coupled in the nuclear interior. The stripping pattern to resonances can differ from stripping to bound states. In the outer region, the resonance wave function is the Gamow–Siegert wave function, whose asymptotic is given by the outgoing Coulomb scattered wave. To regularize the reaction matrix elements, one can use the Zel’dovich regularization procedure (see Sect. 2) or CSM (see Appendix C). Nowadays, the standard DWBA is being replaced by more advanced approaches such as continuum discretized coupled channels (CDCC) (Rawitscher et al. [55], Kamimura et al. [56] Austern et al. [57], Yahiro et al. [58]), adiabatic distorted wave (ADWA) (Johnson and Soper [59]), coupled reaction channels (CRC) and the coupled channels in Born approximation (CCBA) available in FRESCO code (Thompson [60]).

For more than 50 years, transfer reactions to bound states, and deuteron stripping in particular, have been used to determine the spectroscopic factors, which measure the weight of the single-particle state in the overlap function of the initial and final nuclei. That is why there was always a temptation to develop a theory of stripping into resonant states that is fully similar to stripping into bound states. For example, Bunakov et al. [61] assumed that the SF could be extracted from deuteron stripping into resonance states. In this case, the SF is the ratio of the observable and single-particle resonance widths. However, the SF is not observable and depends on the single-particle potential used to calculate the single-particle width. Mukhamedzhanov and Kadyrov [62] showed that SFs are not invariant under finite-range unitary transformations and, hence, in the exact approach, nuclear reactions cannot be a tool to determine spectroscopic factors (review [1]). However, there is model-independent information, which can be extracted from deuteron stripping reactions. I mean the ANCs (resonance widths), which are the amplitudes of the tails of the Gamow–Siegert wave functions and are invariant under finite-range unitary transformations. The uncertainties of the ANCs extracted from (d, p) reactions are investigated by Lovell and Nunes [63] and Timofeyuk and R. C. Johnson [64].

Below we describe a theory of deuteron stripping that will solve the problems mentioned above for the deuteron stripping to resonant states. We start from the consideration of the conventional DWBA amplitude and then consider the CDCC one. By splitting the post and prior forms into the internal post, surface and external prior form we can analyze the convergence of the resonant DWBA amplitude. The details of the surface-integral formalism were addressed in (Kadyrov et al. [65], Mukhamedzhanov [66]). Modification of the FRESCO by Thompson allows one to analyze contribution of the internal post form, surface term and the external prior form (Escher et al. [67]).

12.2 Stripping to resonance state. Post form of DWBA

Let us consider the deuteron stripping reaction

$$\begin{aligned} d+A \rightarrow p+ F \rightarrow p+b+B, \end{aligned}$$

(202)

proceeding through the intermediate resonance in the subsystem $F=n+A=b+B$. Figure 10 shows the skeleton diagram describing the mechanism of reaction (202).

Fig. 10

The skeleton diagram describing the stripping reaction Eq. (202) proceeding through the resonance state in the subsystem $F=n+A=b+B$

In this subsection, we consider the post-form DWBA amplitude of reaction (202), which we split into the internal and external parts in the subspace over the relative coordinate between the transferred n and A. Owing to the choice of the transition operator in the post-form, the internal part turns out to be small. The outer part, parameterized in terms of the resonance width (or, equivalently, ANC), will be transformed into the dominant surface integral encircling the interior volume and small external prior DWBA amplitude. As a starting point, we consider the post-form of the reaction amplitude

$$\begin{aligned}&\mathcal{M}^{(post)}({P},\,{{\textbf {k}}}_{dA}) = <\Phi _{f}^{(-)}|\Delta V_{pF} \big |\Psi _{i}^{(+)}>. \end{aligned}$$

(203)

Here $\,\Psi _{i}^{(+)}\,$ is the exact scattering wave function in the initial state with the two-body $d + A$ incident wave, $\,\Phi _{f}^{(-)}=\chi _{pF}^{(-)}\,\Psi _{bB }^{(-)}$ is the channel wave function in the exit state $p+ b+B$, $\Psi _{bB }^{(-)}$ is the exact scattering wave function with the incident wave in the channel $b + B.$ $\,\Delta {V}_{pF}= V_{pA} +V_{pn} - U_{pF}\,$ is the transition operator in the post form, $V_{ij}$ is the interaction potential between nuclei i and j, $\,U_{ij}$ is the optical potential between nuclei i and j,  $\,\chi _{ij}^{(+)} \equiv \chi _{{{\textbf {k}}}_{ij}}^{(+)}({{\textbf {r}}}_{ij})$ is the distorted wave describing the relative motion of particles i and j interacting via the optical potential $U_{ij}$ with the relative momentum ${{\textbf {k}}}_{ij}$.

Because we consider the stripping to the resonance state, which decays into two fragments b and B, there are three particles ( $p,\,b$ and B ) in the final state. Hence, the kinematics of the final state of the reaction depends on two Jacobian momenta, for which we adopt the relative momentum of two fragments b and B, and the momentum corresponding to the relative motion of the exiting proton and the center of mass of the system $b + B$. Thus the deuteron stripping amplitude depends on the momentum ${P}=\{{{\textbf {k}}}_{pF},\,{{\textbf {k}}}_{bB}\}$, which is the six-dimensional momentum conjugated to the Jacobian coordinates of the system $p + b + B\,$ $\,{ X}=\{{{\textbf {r}}}_{pF},\,{{\textbf {r}}}_{bB}\}$.

We remind the reader that the exact wave function $\Psi _{i}^{(+)}$ is fully antisymmetrized, but the channel wave function $\Phi _{f}^{(-)}$ is not antisymmetrized with respect to the exchange of the exiting proton and nucleons in the system $b+B$. However, the scattering wave function $\,\Psi _{bB}^{(-)}$ in $\Phi _{f}^{(-)}$ is fully antisymmetrized. We can drop the antisymmetrization in the channel wave function because of the fully antisymmetrized exact wave function in the initial state and fully symmetric transition operator.

To obtain the post form of the DWBA from Eq. (203) we replace $\Psi _{i}^{(+)}$ with the channel wave function $\,\phi _{d}\,\phi _{A}\,\chi _{dA}^{(+)}$ in the initial $d + A$ state:

$$\begin{aligned} \mathcal{M}^{DW(post)}({P},\,{{\textbf {k}}}_{dA})= <\chi _{pF}^{(-)}\,\Psi _{bB }^{(-)}|\,\Delta \,V_{pF}|\phi _{d}\,\phi _{A}\,\chi _{dA}^{(+)}>. \end{aligned}$$

(204)

Note that the integration in Eq. (204) is taken over all the internal coordinates of nucleus A.

To further simplify Eq. (204) we introduce the approximate projector $|\phi _{A}> <\phi _{A}|$. Then we can reduce $\mathcal{M}^{DW(post)}$ to

$$\begin{aligned} \mathcal{M}^{DW(post)}({P},\,{{\textbf {k}}}_{dA})= <\chi _{pF}^{(-)}\,\Upsilon _{bB;nA }^{(-)}|\,\Delta {{\overline{V}}}_{pF}|\phi _{d}\,\chi _{dA}^{(+)}>, \end{aligned}$$

(205)

where $<\Upsilon _{bB;nA}^{(-)}| = < \Psi _{bB }^{(-)}|\phi _{A}>\,$ is the reaction component (in the simplified notations omitting quantum numbers) of the overlap function. The antisymmetrization factor between the neutron and the nucleons of nucleus A is absorbed into $\Upsilon _{bB;\,nA }^{(-)}$. We also use

$$\begin{aligned}<\phi _{A}|\Delta \,V_{pF}|\phi _{A}>\,=\, <\phi _{A}|V_{pA}|\phi _{A}> + V_{pn} - U_{pF}. \end{aligned}$$

(206)

The potential $<\phi _{A}|V_{pA}|\phi _{A}>$ is replaced by the optical potential $U_{pA}$ to get the standard post-form DWBA transition operator $\Delta \,{{\overline{V}}}_{pF}= U_{pA} + V_{pn} - U_{pF}.$ Also it useful to remind that $\chi _{pF}^{(-)*} \equiv \chi _{ - {{\textbf {k}}}_{pF} }^{(+)}$ and $\Upsilon _{bB;\,nA }^{(-)*} \equiv \Upsilon _{(bB;nA),\, -{{\textbf {k}}}_{nA}}^{(+)}.$ Here we need to address one very important point about Eq. (205). The bra state of the matrix element contains the overlap function $\,\Upsilon _{bB;\,nA}^{(-)}.\,$ In the external region the radial behavior of this overlap function is determined by the outgoing wave $\,O_{l'}(k_{c'},r_{c'})\,$ in the exit channel $c'=n+A.\,$ The amplitude of the outgoing wave is the S-matrix element corresponding to the reaction $b+B \rightarrow n+A.\,$ For the scattering near the resonance the momentum $k_{c'}$ in the outgoing wave can be taken equal to the real part of the resonance momentum in the channel $c':$ $\,k_{c'}= k_{0(c')}.\,$ For narrow resonances the outgoing wave can be replaced by the Gamow–Siegert wave function.

Now we transform this volume integral into the surface one following Sect. 8, review [1]. First, we adopt ${{\textbf {r}}}_{nA}$ and ${{\textbf {r}}}_{pF}$ as Jacobian variables and split the configuration space over ${{\textbf {r}}}_{nA}$ into the internal and external regions, while the integral over the second Jacobian variable, ${{\textbf {r}}}_{pF}$, is taken over all the coordinate space. Splitting the reaction amplitude into internal and external amplitudes, we get

$$\begin{aligned} \mathcal{M}^{DW(post)}({P},\,{{\textbf {k}}}_{dA})&= \mathcal{M}_{int}^{DW(post)}({P},\,{{\textbf {k}}}_{dA}) \nonumber \\&\quad + \mathcal{M}_{ext}^{DW(post)}({P},\,{{\textbf {k}}}_{dA}) , \end{aligned}$$

(207)

where the internal amplitude $\mathcal{M}_{int}^{DW(post)}$ is given by

$$\begin{aligned}&\mathcal{M}_{int}^{DW(post)}({P},\,{{\textbf {k}}}_{dA}) \nonumber \\&\quad = <\chi _{pF}^{(-)}\,\Upsilon _{bB;nA}^{(-)}|\,\Delta \,{{\overline{V}}}_{pF}| \phi _{d}\,\chi _{dA}^{(+)}>\Big |_{r_{nA} \le R_{ch(nA)}}. \end{aligned}$$

(208)

Correspondingly, the external amplitude is given by

$$\begin{aligned}&\mathcal{M}_{ext}^{DW(post)}({P},\,{{\textbf {k}}}_{dA}) \nonumber \\&\quad = <\chi _{pF}^{(-)}\,\Upsilon _{bB;nA}^{(-)}|\,\Delta \,{{\overline{V}}}_{pF}|\phi _{d}\,\chi _{dA}^{(+)}>\Big |_{r_{nA} > R_{ch(nA)}}. \end{aligned}$$

(209)

Here $R_{ch(nA)}$ is the channel radius in the channel $n+A$ similar to the one introduced in the R-matrix approach, which separates the internal and external regions.

The splitting of the amplitude into the internal and external parts in the subspace over the Jacobian variable ${{\textbf {r}}}_{nA}$ is natural and evident. The overlap function $\Upsilon _{pB;n A }^{(-)}({{\textbf {r}}}_{nA})$ is the only object in the reaction amplitude which provides spectroscopic information about the resonance in the system $n+A$. Owing to the structure of the transition operator, the external post-form matrix element $\mathcal{M}_{ext}^{DW(post)}$ is dominant compared to a small contribution coming from the internal part $\mathcal{M}_{int}^{DW(post)}$. This simple observation stems from the following.

In the internal matrix element, $r_{nA} \le R_{ch(nA)}$, owing to the absorption of the protons inside nucleus $F=(n\,A)$, effective $r_{pn} \sim r_{pA}\approx r_{pF}> R_{F}$, where $R_{F}$ is the radius of nucleus F. For the protons outside of F and neutrons inside or on the surface of A each nuclear interaction in the operator $\Delta \,{{\overline{V}}}_{pF} =\,U_{pA} + V_{pn} - U_{pF}$ is small. Potential $U_{pF}$ is arbitrary, and often $U_{pF}$ is chosen to compensate for $U_{pA}$ so that the transition operator reduces to $V_{pn}$. Because the DWBA is the first order perturbation theory, minimizing the whole transition operator $\Delta \,{{\overline{V}}}_{pF}$ provides smaller higher order terms and better serves the theory. This choice is more preferable in the formalism presented here and we adopt $U_{pF}$, which minimizes $\Delta \,{{\overline{V}}}_{pF} = U_{pA} + V_{pn} - U_{pF}$ at $r_{nA} \le R_{ch(nA)}$ making the contribution from the internal matrix element small compared to the external one.

The external post-form matrix element ($r_{nA} > R_{ch(nA)}$) is dominant. We transform $\mathcal{M}_{ext}^{DW(post)}$ into an alternative form, which has a clear advantage for stripping to resonance states as discussed below, when convergence becomes the main impediment.

Now we proceed to the transformation of the volume integral, defining the external matrix element in terms of the dominant surface integral encircling the sphere at $r_{nA}=R_{ch(nA)}$ and a small, owing to the structure of the transition operator in the prior form (see Eq. (216)), external prior-form volume integral. Note that the transformation is exact within the DWBA formalism.

To transform the external volume integral to the surface one, we rewrite the transition operator as

$$\begin{aligned} \Delta \,{{\overline{V}}}_{pF}&= U_{pA} + V_{pn} - U_{pF}\nonumber \\&= [V_{pn} + U_{dA}] - [U_{pF}] + (U_{pA} - U_{dA}). \end{aligned}$$

(210)

The bracketed operators are the right-hand-side operators in the Schrödinger equations for the initial and final channel wave functions in the external region (over the variable ${{\textbf {r}}}_{nA}$):

$$\begin{aligned} (E- {{\hat{T}}})\,\phi _{d}\,\chi _{dA}^{(+)} = (V_{pn} + U_{dA})\,\phi _{d}\,\chi _{dA}^{(+)} \end{aligned}$$

(211)

and

$$\begin{aligned} \,\Upsilon _{bB;nA }^{(-)*}\,\chi _{pF}^{(-)*}(E - {\overleftarrow{{\hat{T}}}})= U_{pF}\,\Upsilon _{bB;nA}^{(-)*}\,\chi _{pF}^{(-)*}. \end{aligned}$$

(212)

To derive Eq. (212) we took into account that at $r_{nA} > R_{nA(ch)}$ $\Upsilon _{bB;nA }^{(-)*}(E_{n\,A} - {\overleftarrow{{\hat{T}}}}_{nA})=0$, where $E_{ij}$ and ${{\hat{T}}}_{i\,j}$ are the relative kinetic energy and relative kinetic energy operator of the relative motion of i and j. These equations imply the following connection between the external post-form DWBA amplitude and the matrix element $\mathcal{M}_{S}^{DW}$ containing the surface integral:

$$\begin{aligned} \mathcal{M}_{ext}^{DW(post)}({P},\,{{\textbf {k}}}_{dA})&= \mathcal{M}_{S}^{DW}({P},\,{{\textbf {k}}}_{dA}) \nonumber \\&\quad + \mathcal{M}_{ext}^{DW(prior)}({P},\,{{\textbf {k}}}_{dA}) , \end{aligned}$$

(213)

where

$$\begin{aligned}&\mathcal{M}_{ext}^{DW(prior)}({P},\,{{\textbf {k}}}_{dA})\nonumber \\&\quad = <\chi _{pF}^{(-)}\,\Upsilon _{bB;nA}^{(-)}|\,\Delta \,{{\overline{V}}}_{dA} |\phi _{d}\,\chi _{dA}^{(+)}>\Big |_{r_{nA} > R_{ch(nA)}} \end{aligned}$$

(214)

and

$$\begin{aligned} \mathcal{M}_{S}^{DW}({P},\,{{\textbf {k}}}_{dA})&= <\chi _{pF}^{(-)}\,\Upsilon _{bB;nA}^{(-)}|\,{\overleftarrow{{\hat{T}}}} \nonumber \\&\quad - {\overrightarrow{{\hat{T}}}}|\phi _{d}\,\chi _{dA}^{(+)}>\Big |_{r_{nA} > R_{ch(nA)}}. \end{aligned}$$

(215)

Here the transition operator in the prior form $\Delta \,{{\overline{V}}}_{dA}$ in the external region, where the nuclear $n-A$ interaction disappears, takes the form

$$\begin{aligned} \Delta \,{{\overline{V}}}_{dA} = U_{pA} - U_{dA}. \end{aligned}$$

(216)

Then the total post DWBA amplitude reduces to

$$\begin{aligned} \mathcal{M}^{DW(post)}(P,\,{{\textbf {k}}}_{dA})&= \mathcal{M}_{int}^{DW(post)}(P,\,{{\textbf {k}}}_{dA}) \nonumber \\&\quad + \mathcal{M}_{ext}^{DW(prior)}(P,\,{{\textbf {k}}}_{dA})\nonumber \\&\quad + M_{S}^{DW}(P,\,{{\textbf {k}}}_{dA}). \end{aligned}$$

(217)

Let us discuss the advantage of this new form of the DWBA amplitude for the deuteron stripping to resonance state(s). Because the internal part $\mathcal{M}_{int}^{DW(post)}$ is given by the volume integral, its calculation requires the knowledge of $\Upsilon _{bB;nA}^{(int)(-)}$ in the internal region. The model dependence of this function in the nuclear interior ($r_{nA} \le R_{ch(nA)}$), where different coupled channels do contribute, brings one of the main problems and the main uncertainty in the calculation of the internal matrix element. However, as discussed in sec. (3.4) [1], this matrix element gives a small contribution to the total post-form amplitude $\mathcal{M}^{DW(post)}$ owing to the structure of the transition operator $\Delta \,{{\overline{V}}}_{pF}$ and constrain $r_{nA} \le R_{ch(nA)}$. These arguments are also valid when considering the stripping into resonance states. A proper choice of the optical potential $U_{pF}$ and the channel radius $R_{ch(nA)}$ may significantly reduce the contribution from the internal post-form DWBA amplitude. Owing to the structure of the transition operator $\Delta \,{{\overline{V}}}_{dA}$, the external matrix element $\mathcal{M}_{ext}^{DW(prior)}$ in the prior form is also small and in some cases with a reasonable choice of the channel radius $R_{ch(nA)}$ even can be neglected. Note that to keep $\mathcal{M}_{int}^{DW(post)}$ small, the channel radius $R_{ch(nA)}$ cannot be too large and, to keep $\mathcal{M}_{ext}^{DW(prior)}$ small, cannot be too small. Thus with the optimal choice of the channel radius, the dominant part is the surface part $\mathcal{M}_{S}^{DW}$, which contains only one volume integral over ${{\textbf {r}}}_{pF}$.

The idea of replacing the volume integral over ${{\textbf {r}}}_{nA}$ with the surface one reminds the Gauss law in electrodynamics when the volume integral of the charge density is replaced by the surface integral determining the electric field flux through the surface surrounding the volume integral. Using the surface-integral representation, we can transform a large internal volume integral (it is large because the internal resonance wave function is peaked in the nuclear interior) into a small post-form volume integral over ${{\textbf {r}}}_{nA}$ and large surface integral. In our case, the surface integral determines the neutron flux through the nuclear surface. However, we have the three-body problem, $p,\,n$ and nucleus A, and only the neutron is transferred. Since the proton is not transferred in the deuteron stripping reaction, the volume integral over ${{\textbf {r}}}_{pF}$ is taken over all the coordinate space.

Equation (217) presenting a new form of the DWBA amplitude for stripping to resonance states is quite important for analyzing the stripping to resonance. In this sense, the usage of the external prior-form amplitude $\mathcal{M}_{ext}^{DW(prior)}$ has a clear benefit because it is small and better converges than the external post form. Also the internal amplitude $\mathcal{M}_{int}^{DW(post)}$ is small. The main contribution to $\mathcal{M}^{DW(post)}$ comes from the surface term $\mathcal{M}_{S}^{DW}$. Using the R-matrix representation of the overlap function $\Upsilon _{bB;nA}^{(-)*}$ we can express the total DWBA amplitude in terms of the reduced width amplitudes, level matrix, boundary condition, and the channel radius ( Mukhamedzhanov [66]), Escher et al. [67]). These parameters are used in a standard R-matrix method to analyze binary resonant reactions $n + A \rightarrow b + B$. Since the reaction under consideration is the deuteron stripping, the presence of the deuteron in the initial state and exiting proton causes the distortions. That is why the reaction amplitude, in addition to the R-matrix parameters describing the binary subprocess, contains additional factors: distorted waves in the initial and the final state. Hence we can call the obtained expression for the DWBA amplitude a generalized R-matrix for the deuteron stripping to resonance states.

12.3 Stripping to resonance state: prior form of DWBA

Here we show how to derive Eq. (217) from the prior DWBA amplitude, which is

$$\begin{aligned}&\mathcal{M}^{DW(prior)}(P,\,{{\textbf {k}}}_{dA}) = <\chi _{pF}^{(-)}\,\Psi _{bB}^{(-)}| \,\Delta \,{{\overline{V}}}_{dA}|\phi _{d}\,\chi _{dA}^{(+)}>, \end{aligned}$$

(218)

where $\Delta \,{{\overline{V}}}_{dA} =<\phi _{A}|V_{pA}|\phi _{A}> + <\phi _{A}|V_{nA}|\phi _{A}> - U_{dA}.$ As usually, we split the amplitude into internal and external parts

$$\begin{aligned} \mathcal{M}^{DW(prior)}(P,\,{{\textbf {k}}}_{dA})&= \mathcal{M}_{int}^{DW(prior)}(P,\,{{\textbf {k}}}_{dA}) \nonumber \\&\quad + \mathcal{M}_{ext}^{DW(prior)}(P,\,{{\textbf {k}}}_{dA}), \end{aligned}$$

(219)

with

$$\begin{aligned}&\mathcal{M}_{int}^{DW(prior)}(P,\,{{\textbf {k}}}_{dA}) \nonumber \\&\quad = <\chi _{pF}^{(-)}\,\Psi _{bB}^{(int)(-)}\,|\,\Delta \,{{\overline{V}}}_{dA}|\phi _{d}\,\chi _{dA}^{(+)}>\Big |_{r_{nA} \le R_{ch(nA)}} \end{aligned}$$

(220)

and

$$\begin{aligned}&\mathcal{M}_{ext}^{DW(prior)}(P,\,{{\textbf {k}}}_{dA}) \nonumber \\&\quad = <\chi _{pF}^{(-)}\,\Psi _{bB}^{(ext)(-)}\,|\,\Delta \,{{\overline{V}}}_{dA}|\phi _{d}\,\chi _{dA}^{(+)}>\Big |_{r_{nA} > R_{ch(nA)}}. \end{aligned}$$

(221)

The external matrix element $\mathcal{M}_{ext}^{DW(prior)}$ in the prior form is small and, in some cases, with a reasonable choice of the channel radius $R_{ch(nA)}$ can be neglected. It is important to analyze the stripping to resonance states because the outer part in the post form doesn’t converge. In this sense, using the prior form in the outer part has a clear benefit. The main contribution to the prior-form amplitude $M^{DW(prior)}$ comes from the internal part $\mathcal{M}_{int}^{DW(prior)}$. Since the volume integral gives the internal part, its calculation requires the knowledge of $\Psi _{bB}^{(int)(-)}$ in the internal region. The model dependence of this function in the nuclear interior ($r_{nA} \le R_{ch(nA)}$), where different coupled channels do contribute, brings one of the main problems and main uncertainty in the calculation of the internal matrix element. Using the surface integral, we can rewrite the volume integral of the internal matrix element in terms of the volume integral in the post form and the dominant surface integral taken over the sphere at $r_{nA}=R_{ch(nA)}$. With a reasonable choice of the channel radius $R_{ch(nA)}$, the contribution from the internal volume integral in the post form can be minimized to make it significantly smaller than the surface matrix element. The latter can be expressed in terms of the R-matrix parameters - the observable reduced width amplitude (ANC), boundary condition, and channel radius (Mukhamedzhanov [66]). Repeating the steps outlined in Sect. 12.2 we get

$$\begin{aligned} \mathcal{M}_{int}^{DW(prior)}(P,\,{{\textbf {k}}}_{dA})&= \mathcal{M}_{int}^{DW(post)}(P,\,{{\textbf {k}}}_{dA}) \nonumber \\&\quad + \mathcal{M}_{S}^{DW}(P,\,{{\textbf {k}}}_{dA}). \end{aligned}$$

(222)

Here $\mathcal{M}_{int}^{DW(post)}$ has been previously considered and is given by Eq. (208) while $\mathcal{M}_{S}^{DW}$ takes the form

$$\begin{aligned} \mathcal{M}_{S}^{DW}(P,\,{{\textbf {k}}}_{dA})&= -<\chi _{pF}^{(-)}\,\Upsilon _{bB;nA}^{(ext)(-)}|\,{\overleftarrow{{\hat{T}}}}\nonumber \\&\quad - {\overrightarrow{{\hat{T}}}}\,|\phi _{d}\,\chi _{dA}^{(+)}>\Big |_{r_{nA} \le R_{ch(nA)}}, \end{aligned}$$

(223)

where $\Upsilon _{nA}^{(ext)(-)}= <\Psi _{bB}^{(ext)(-)}|\phi _{A}>$. The fact that the volume integral in this equation is the internal one makes transforming this volume matrix element to the surface much easier than for the post form. The transition operator $T= T_{pF} + T_{nA}$. At $r_{nA} \le R_{ch(nA)}$ and $r_{pF} \rightarrow \infty$ the integrand in Eq. (223) vanishes exponentially due to the presence of $\phi _{d}$. Hence the operator $T_{pF}$ is Hermitian (self-adjoint), and applying the integration by parts over $r_{pF}$ twice, we get

$$\begin{aligned}&<\chi _{pF}^{(-)}\,\Upsilon _{bB;nA}^{(ext)(-)}|\,{\overleftarrow{{\hat{T}}}}_{pF} - {\overrightarrow{{\hat{T}}}}_{pF}\,|\,\phi _{d}\,\chi _{dA}^{(+)}>\Big |_{r_{nA} \le R_{ch(nA)}} =0. \end{aligned}$$

(224)

Thus $\mathcal{M}_{S}^{DW}(P,\,{{\textbf {k}}}_{dA})$ reduces to

$$\begin{aligned} \mathcal{M}_{S}^{DW}(P,\,{{\textbf {k}}}_{dA})&= <\chi _{pF}^{(-)}\,\Upsilon _{bB;nA}^{(ext)(-)}|\,{\overleftarrow{{\hat{T}}}}_{nA} \nonumber \\&\quad - {\overrightarrow{{\hat{T}}}}_{nA}\,| \phi _{d}\,\chi _{dA}^{(+)}>\Big |_{r_{nA} \le R_{ch(nA)}}. \end{aligned}$$

(225)

Using the Green’s theorem we can transform this volume integral into the surface one. Note that the volume integral over ${{\textbf {r}}}_{nA}$ is constrained by the sphere with the radius $r_{nA}= R_{ch(nA)}$. Hence, only one surface integral appears with $r_{nA}= R_{ch(nA)}$.

Now we can see an important advantage of the prior form versus the post one by comparing Eqs. (220) and (221) with the corresponding post-form Eqs. (208) and (209). The difference is in the transition operators. In the post form, due to the structure of the transition operator $\Delta \,{{\overline{V}}}_{pB},$ the internal part can be minimized. The dominant contribution in the post form comes from the external amplitude, where we must deal with the convergent problem. In the prior form, the transition operator makes the internal amplitude dominant compared to small external one. Note that in both forms, post and prior, the dominant part contains the surface term: the outer amplitude in the post form and the internal one in the prior form. It explains why one should use the prior form in which the problem with convergence does not appear for analysis of transfer reactions.

12.4 Advancing DWBA

The more advanced than DWBA are ADWA and CDCC method.

12.4.1 ADWA

ADWA was formulated for the deuteron stripping (pickup) reactions (Johnson and Soper [59]). The idea is to improve the DWBA amplitude by effectively considering the deuteron breakup channel in the initial state. It is achieved by using the $d-A$ distorted wave, which satisfies the two-body $d+A$ Shrödinger equation with the optical potential $U_{dA}(r_{dA}) = U_{pA}(r_{dA}) + U_{nA}(r_{nA})$. Each nucleon-nucleus optical potential is calculated at half the initial dA relative kinetic energy. Different modifications of the ADWA are considered in [64].

12.4.2 CDCC

We consider the deuteron stripping reaction

$$\begin{aligned} d + A \rightarrow p + n + A, \end{aligned}$$

(226)

proceeding through the resonant sub-reaction $n + A \rightarrow F^{*} \rightarrow n + A$. To treat the stripping to resonance states we use the prior formalism, in which the exact scattering wave function appears in the final state rather than in the initial one. Then the reaction amplitude in the three-body model $p+N+A$ takes the form:

$$\begin{aligned}&{{\mathcal {M}}}^{(prior)} \,= <\Psi _{f}^{(-)}\big | U_{pA} + V_{nA} -U_{dA}\big | \phi _{d}\,\chi _{dA}^{(+)}>, \end{aligned}$$

(227)

where $\Psi _{f}^{(-)}$ is the $p+n+A$ scattering wave function in the final state. The prior-form of the CDCC amplitude is obtained by replacing $\Psi _{f}^{(-)}$ with the CDCC wave function:

$$\begin{aligned}&{{\mathcal {M}}}_{conv}^{CDCC(prior)} \,= <\Psi _{f}^{CDCC(-)}\big | U_{pA} + V_{nA} -U_{dA}\big | \phi _{d}\,\chi _{dA}^{(+)}>. \end{aligned}$$

(228)

The CDCC method, rather than solving three-body Faddeev coupled equations, reduces the problem to a single Schrödinger equation with the effective Hamiltonian The final-state CDCC wave function can be written as

$$\begin{aligned} \Psi _{f}^{CDCC(-)}({{{\varvec{\rho }}}}_{pF},\,{{\textbf {r}}}_{nA})&= \,\sum \limits _{i=0}^{i_{max}}\,\phi _{nA}^{(i)}({{\textbf {r}}}_{nA})\,\chi _{{{\textbf {k}}}_{pF}}^{(i)(-)}({{{\varvec{\rho }}}}_{pF})\nonumber \\&\quad + \,\sum \limits _{j=1}^{j_{max}}\, {{\overline{\psi }}}_{ {{\textbf {k}}}_{nA} }^{(j)(-)}({{\textbf {r}}}_{nA})\,{{\overline{\chi }}}_{ {{\textbf {k}}}_{pF}(\textbf{k}_{nA}) }^{(j)(-)}({{{\varvec{\rho }}}}_{pF}). \end{aligned}$$

(229)

Here $\phi _{nA}^{(i)}({{\textbf {r}}}_{nA})$ is the i-th bound state wave function of the system $F=(nA)$ with $i=0$ corresponding to the ground state and $\chi _{{{\textbf {k}}}_{pF}}^{(i)(-)}({{{\varvec{\rho }}}}_{pF})$ are the functions, which describe the relative motion of p and the $\,(n\,A)\,$ pair in the i-th bound state. ${{\overline{\psi }}}_{{{\textbf { k}}}_{nA} }^{(j)(-)}({{\textbf {r}}}_{nA})$ is the $n-A$ scattering wave function obtained by averaging continuous breakup states in the j-th bin and $\,{{\overline{\chi }}}_{{{\textbf {k}}}_{pF}(\textbf{k}_{nA}) }^{(j)(-)}({{{\varvec{\rho }}}}_{pF})\,$ is the wave function describing the relative motion of the proton and the c.m. of the system $n+ A$ in the continuum in the j-th bin. In Eq. (229) the relative momentum $\,{{\textbf {k}}}_{pF}({{\textbf {k}}}_{nA})\,$ of the particles p and F is related to the $n-A$ relative momentum ${{\textbf {k}}}_{nA}$ via the energy conservation law:

$$\begin{aligned} E= E_{dA} - \varepsilon _{pn} = E_{pF} - \varepsilon _{nA}= \frac{k_{pF}^{2}}{2\,\mu _{pF}} + \frac{k_{nA}^{2}}{2\,\mu _{nA}}. \end{aligned}$$

(230)

The $n-A$ interaction is taken as a real single-particle potential $V_{nA}$, which can support the resonance in the $n-A$ system. The corresponding scattering wave function is orthogonal to the bound states generated by this potential.

Note that in practical application we need to use ${{\overline{\psi }}} _{{{\textbf {k}}}_{nA}s\,m_{s}\,m''_{s}}^{(j)( - )*}({{\textbf {r}}}_{nA})$, which is expressed in terms of the binned radial wave function ${{\overline{u}}}_{k_{nA}\,s\,l_{nA}\,J_{F}}^{(j)(+)}(r_{nA})$ given by (Thompson [60], Thompson annd Nunes [68])

$$\begin{aligned}&{{\overline{u}}}_{k_{nA}\,s\,l_{nA}\,J_{F}}^{(j)(+)}(r_{nA}) = \sqrt{\frac{2}{\pi \,N_{s\,l_{nA}\,J_{F}}^{(j)}}}\,\int \limits _{k_{nA}^{(j-1)}}^{k_{nA}^{(j)}}\,\textrm{d}k_{nA} \nonumber \\&\quad \times g_{s\,l_{nA}\,J_{F}}^{(j)}(k_{nA})\,u_{k_{nA}\,s\,l_{nA}\,J_{F}}^{(+)}(r_{nA}) , \end{aligned}$$

(231)

where the radial scattering wave function $\,u_{k_{nA}s\,l_{nA},J_{F}}^{(j)(+)}(r_{nA})\,$ describes the resonance scattering in the bin covering the resonant region. $g_{s\,l_{nA}\,J_{F}}^{(j)}(k_{nA})$ is the weight function. The normalization constant is

$$\begin{aligned} N_{s\,l_{nA}\,J_{F}}^{(j)}= \int \limits _{k_{nA}^{(j-1)}}^{k_{nA}^{(j)}}\,\textrm{d}\,k_{nA}\, |g_{s\,l_{nA}\,J_{F}}^{(j)}(k_{nA})|^{2}. \end{aligned}$$

(232)

The adopted normalization constant $\,N_{s\,l_{nA}\,J_{F}}^{(j)}$ makes an orthonormal set ${{\overline{u}}}_{k_{nA}\,s\,l_{nA}\,J_{F}}^{(j)(+)*}(r_{nA})$ when all the intervals $(k_{nA}^{j-1},\,k_{nA}^{(j)})$ are non-overlapping.

The next important step is adoption of the weight function $g_{s\,l_{nA}\,J_{F}}^{(j)}(k_{nA})$. Two different prescriptions can be used for the weight function for resonant and non-resonant bins (Thomson and Nunes [68]). One can use for the non-resonant bins

$$\begin{aligned} g_{s\,l_{nA}\,J_{F}}^{(j)}(k_{nA}) \,= \,e^{-i\,\delta _{s\,l_{nA}\,J_{F}}(k_{nA})} \end{aligned}$$

(233)

and for the resonance bin

$$\begin{aligned} g_{s\,l_{nA}\,J_{F}}(k_{nA})=e^{i\delta _{s\,l_{nA}\,J_{F}}(k_{nA})}\sin (\delta _{s\,l_{nA}\,J_{F}}(k_{nA})), \end{aligned}$$

(234)

where $\delta _{s\,l_{nA}\,J_{F}}(k_{nA})$ is the $n-A$ elastic scattering phase shift. For this phase shift we adopt the hard-sphere scattering phase shift $\delta _{l_{nA}}^{hs}$ in the channel $n + A$, see Eq. (64).

12.5 Stripping to resonance state: reaction $\mathbf {{}^{16}\textrm{O}(d,\,p){}^{17} \textrm{O}(1d_{3/2})}$

Now we proceed to the calculation of the stripping to resonance state. We select the reaction ${}^{16}\textrm{O}(d,\,p){}^{17}\textrm{O}(1d_{3/2})$ at $E_{d}=36$ MeV populating a resonance state $E_{x}=5.085$ MeV, which corresponds to the resonance level at 0.94 MeV. Hence $A={}^{16}\textrm{O}$ and the resonance orbital angular momentum is $l_{nA}=2$. In all the calcullations shown below we use the single-particle approach for the $n-A$ resonant scattering wave function calculated in the Woods-Saxon potential with the radial parameter $r_{o}=1.25$ fm and diffuseness $a=0.65$ fm. All the calculations of the differential cross-sections were performed using the FRESCO code by Thompson [60]. For the binned functions see Thompson and Nunes [68].

In the first calculation we compare the post and prior calculations. The post and prior ADWA and prior CCBA (coupled channel Born approximation) are used for comparison. The prior ADWA is the standard prior DWBA in which the initial deuteron potential is given by the sum of the optical $U_{PA}$ and $U_{nA}$ potentials calculated at half of the deuteron energy using the zero-range Johnson-Sopper prescription [59]. In the prior-form CCBA amplitude the transition operator is taken to be $\Delta \,{{\overline{V}}}_{dA}$ and the final-state wave function can be derived from Eq. (229). To do it we use the partial wave expansion of the binned $n-A$ continuum scattering wave function leaving only the resonance partial wave $l_{nA}=2$. The adopted bin covers the resonance region and $\chi _{ {{\textbf {k}}}_{pF}(\textbf{k}_{nA}) }^{(res)(-)}({{{\varvec{\rho }}}}_{pF})$ corresponding to the resonance bin has asymptotically both incident and outgoing waves. The continuum resonance wave function component is coupled with two bound states in ${}^{17}\textrm{O}$: the ground state $1d_{5/2}$ and the first excited state $2s_{1/2}$. These terms are given by the sum over $i=0,1$ in Eq. (229). Thus schematically our final-state CCBA wave function coincides with the CDCC wave function, see Eq. (229):

$$\begin{aligned} \Psi _{f}^{CDCC(-)}({{{\varvec{\rho }}}}_{pF},\,{{\textbf {r}}}_{nA})&= \,\phi _{nA}^{(0)}({{\textbf {r}}}_{nA})\,\chi _{{{\textbf {k}}}_{pF}}^{(0)(-)}({{{\varvec{\rho }}}}_{pF})\, \nonumber \\&\quad + \phi _{nA}^{(1)}({{\textbf {r}}}_{nA})\,\chi _{{{\textbf {k}}}_{pF}}^{(1)(-)}({{{\varvec{\rho }}}}_{pF}) \nonumber \\&\quad + {{\overline{\psi }}}_{ {{\textbf { k}}}_{nA},\,l_{nA}=2 }^{(res)(-)}({{\textbf {r}}}_{nA})\,\chi _{ {{\textbf {k}}}_{pF}(\textbf{k}_{nA}) }^{(res)(-)}({{{\varvec{\rho }}}}_{pF}). \end{aligned}$$

(235)

Here, for simplicity, we omitted spins. The radial and momentum spherical harmonics are absorbed into ${{\overline{\psi }}}_{ {{\textbf { k}}}_{nA} }^{(res)(-)}({{\textbf {r}}}_{nA})$. The distorted waves $\chi _{{{\textbf {k}}}_{pF}}^{(0)(-)}({{{\varvec{\rho }}}}_{pF})$ and $\chi _{{{\textbf {k}}}_{pF}}^{(1)(-)}({{{\varvec{\rho }}}}_{pF})$ have only outgoing waves.

The results of the calculations are shown in Fig.  11. Dependence of the peak value of the normalized differential cross-section $R_{X}$ on the $r_{nA}^{min}$ (blue short (ADWA) and long dashed (CCBA) lines) shows that the prior form converges pretty fast being dominantly contributed by the region $r_{nA} \lesssim 5$ fm. The ADWA and CCBA lines (red dotted and green dash), which show the dependence of $R_{X}$ on $r_{nA}^{max}$ confirm that the prior form practically converges at $r_{nA}^{max}= 5 fm$ with small oscillations at higher $r_{nA}$. Because the ADWA and CCBA calculations used the ADWA prescriptions, the difference between both methods determines the effect of the coupling of the continuum resonant wave function in the final state with two bound states. As we see, this effect is not significant. The cross-section of the post form (solid red line) demonstrates very slow convergence despite using the bin functions, which have additional $r_{nA}^{-1}$ dependence. Thus Fig. 11 confirms our conclusion made in Sect. 12.3 about the advantage of the prior form over the post form when analyzing the resonance (d, p) reactions.

Fig. 11

Dependence of the normalized ADWA and CCBA differential cross-sections $\,R_{x}\,$ on $\,r_{nA}\,$ for the deuteron stripping to resonance $\,{}^{16}\textrm{O}(d,\,p){}^{17}\textrm{O}(1d_{3/2})\,$ at $\,E_{d}=36\,$ MeV. Blue short and long light-blue dash-dotted lines – the ratios $\,R_{X}\,$ of the peak prior ADWA and CCBA differential cross-sections, correspondingly, in which the radial integral over $r_{nA}$ is calculated for $r_{nA} \ge r_{nA}^{min}$, to the full differential cross-section. Similarly, magenta dotted and green dashed lines are the ratios $\,R_{X}\,$ of the peak prior ADWA and CCBA differential cross-sections, correspondingly, in which the radial integral over $r_{nA}$ is calculated in the inteval $0 \le r_{nA} \le r_{nA}^{max}$, to the full differential cross-section. The red solid line is the $R_{X}$ dependence on $r_{nA}^{max}$ calculated for the post ADWA form. Hence $r_{nA}$ on the abscissa is $\,r_{nA}^{min}$ for the blue short and long dashed lines and $r_{nA}^{max}$ for the dotted magenta, dashed green and solid red lines. First published in Mukhamedzhanov et al. [69]

Fig. 12

Angular distributions for the deuteron stripping to resonance $\,{}^{16}\textrm{O}(d,\,p){}^{17}\textrm{O}(1d_{3/2})\,$ at $\,E_{d}=36\,$ MeV. Red solid line is the DWBA, blue short dashed line is the ADWA, green dashed line is the CCBA. All the angular distributions are normalized in the region of the forward peak to the experimental one -red dots [70]. First published in Mukhamedzhanov et al. [69]

Figure 12 depicts the angular distributions for the reaction $\,{}^{16}\textrm{O}(d,\,p){}^{17}\textrm{O}(1d_{3/2})\,$ at $E_{d}=36$ using prior DWBA, ADWA and CCBA. As we can see, the impact of the coupling of the continuum resonance wave function with the bound states has little effect on the angular distributions. In the single-particle potential approach for the resonant scattering wave function the normalization of the theoretical cross-section to the experimental one determines the SF. From the normalization of the calculated differential cross-sections to the experimental one we determined the SFs: ${\mathtt S}= 0.89$ for the DWBA, ${\mathtt S}=0.66$ for the ADWA and ${\mathtt S}=0.73$ for the CCBA. Using the single-particle neutron partial resonance width $\Gamma _{sp}=128$ keV, we get for the observable neutron widths $\Gamma _{n}=113.9$ keV for the DWBA, $\Gamma _{n}= 84.5$ keV for the ADWA and $\Gamma _{n}=93.4$ keV for the CCBA. The observed experimental value is $\Gamma _{n}=96 \pm 5$ keV. Thus the prior CCBA and ADWA can be used to determine the observable partial resonance widths.

Figure 13, which is important for the corroboration of our theoretical findings, checks the dependence of the extracted neutron resonance width on the radius $r_{0}$ of the $n-A$ Woods-Saxon potential, which supports the resonance state $\textrm{O}(1d_{3/2})$. This test shows how peripheral the deuteron stripping to resonance is. At each $1.0 \le r_{0} \le 1.7$ we calculated the CCBA differential cross-section, normalized it to the exterimental one in the stripping peak in the angular distribution and determined the SF, which is the normalization factor. For each $r_{0}$ from the derivative of the calculated scattering phase shift we determine the single-particle neutron resonance width and multiplying it by the determined SF we find the observable resonance width shown in Fig. 13. The determined neutron resonance width $\Gamma _{n}$ varies with variation of $r_{0}$ in the realistic interval $1.0-1.6$ fm by $\pm 7\%$ from the experimental value of 96 keV. Such a relatively small variation proves that the reaction under consideration is significantly peripheral. From Fig. 11 follows that the dominant contribution comes from the surface area of the target nucleus ${}^{16}\textrm{O}$. Figure 14 confirms this observation demonstrating, as it is expected for peripheral reactions (see Sect. IX, review [1]) strong $r_{0}$ dependence of the SF. Evidently, the dependence on $r_{0}$ of the SF is much stronger than of $\Gamma _{n}$.

Fig. 13

Solid red line- dependence on $r_{0}$ of the neutron resonance width extracted from the CCBA calculations of the $\,{}^{16}\textrm{O}(d,\,p){}^{17}\textrm{O}(1d_{3/2})\,$ reaction at $E_{d}=36$ MeV. The blue dashed line is the experimental neutron resonance width of the $1d_{3/2}$ resonance in ${}^{17}\textrm{O}$ and the blue strip is the resonance width’s experimental uncertinty. First published in Mukhamedzhanov et al. [69]

Fig. 14

Solid red line- dependence on $r_{0}$ of the SF extracted from the CCBA calculations of the $\,{}^{16}\textrm{O}(d,\,p){}^{17}\textrm{O}(1d_{3/2})\,$ reaction at $E_{d}=36$ MeV. First published in Mukhamedzhanov et al. [69]

From Fig. 13 one can determine the radial parameter $r_{0}=1.35$ fm at which the extracted width coincides with the exeprimental one. Taking into account that at $r_{0}=1.35$ fm the calculated $\Gamma _{n}$ coincides with the experimental one we can determine the SF ${\mathtt S}_{nA}^{F}= 0.66 ^{+0.25}_{- 0. 1}$.

13 Radiative capture processes

13.1 Introduction

Radiative capture reactions in which a nucleus fuses with another one accompanied by the emission of the electromagnetic radiation, play a very crucial role in nuclear astrophysics. It is impossible to overestimate the contribution of these reactions in stellar nucleosynthesis in stars, stellar energy production (the Q-values for these reactions are positive except for the processes involving nuclei far off the valley of stability), in the explosive conditions found in novae, X-ray bursts, and supernovae. The radiative capture reactions caused by the electromagnetic interaction are significantly slower than reactions induced by the strong interactions. Hence these slow reactions control the rate and time of cycles of nucleosynthesis. At higher temperatures the intensity of high energy thermal photons becomes so large that these photons can induce the inverse reactions. These inverse reactions are called photodisintegreation processes. For the first time the role of the radiative capture reactions in the pp chain and CN cycle was addressed in Bethe and Critchfield [71] and Bethe [72].

There are different types of the radiative capture reactions:

• 1. Direct radiative capture

  $$\begin{aligned} a+ A \rightarrow B+\gamma , \end{aligned}$$

  (236)

  which is the one step process leading to the ground or excited bound states of B. The energy of the emitted photon is $E_{\gamma }= E + \varepsilon _{aA}$, where $E=E_{aA}$ is the $a-A$ relative kinetic energy in the continuum and $\varepsilon _{aA}$ is the $a-A$ binding energy in the final state state.

• 2. Resonant radiative capture reactions are two-step reactions. On the first step a resonance is formed, $a+A \rightarrow B^{*}$, which decays by emitting $\gamma$ to the ground or excited bound states of B. The energy of the emitted photon is $E_{\gamma }= E + \varepsilon _{aA}$. Owing to the resonance width, the energy of the emitted photon can deviate $E_{\gamma }= E_{0} + \varepsilon _{aA},\,$ where $E_{0}$ is the real part of the $a-A$ resonance energy $E_{R} =E_{0}- i\Gamma /2$, $\Gamma$ is the resonance width.

• 3. Two-step resonant radiative capture through a subthreshold resonance, which is a subthreshold bound state, see Sect. 6.2. The energy of the emitted photon is $E_{\gamma } = \varepsilon _{aA} - \varepsilon _{s}$, where $\varepsilon _{s}=\varepsilon _{aA}$ is the binding energy of the $a-A$ subthreshold state.

In nuclear astrophysics many important nucleon capture reactions take place through resonance states which then decay to bound states. The total capture cross-section for such reactions is then given by the interference of resonant and non-resonant contributions. Many theoretical models for resonant and non-resonant cross-sections require proper knowledge of the initial and final state, the nature and multipolarity of the transition, and the radiative width (Lane and Thomas [18], Holt et al. [73], Barker [22]).

For many nuclei, radiative capture reactions are the only p- or $\alpha$-capture processes with positive Q-values. Hence the reaction rates of these reactions are crucial for determining the stellar energy production. The radiative capture reactions represent the most practical application of the indirect ANC method in nuclear astrophysics. One of the main input parts of the radiative capture amplitude is the radiative width, one of the important observables whose precise value is required to determine the resonance capture cross-sections accurately and which is often the main source of uncertainty. That is why we start our discussion from the radiative width amplitudes.

To calculate the radiative width the R-matrix approach is often used (Lane and Thomas [18], Holt et al. [73], Barker and Kajino [22], Mukhamedzhanov et al. [74], Mukhamedzhanov and Pang [75]). In the R-matrix approach, the radiative width amplitude is given by the sum of the nuclear internal and external (channel) parts. The channel radiative width amplitude depends only on one model parameter, namely, the channel radius, and for a given channel radius, the channel radiative width amplitude is model-independent. Apart from this, to calculate the channel radiative width amplitude, one needs to know two observables: the ANC of the final bound state and partial resonance width. Therefore, with precise knowledge of these quantities, the channel radiative width amplitude can be calculated quite accurately. The channel radiative width amplitude is a complex quantity, and its imaginary part puts a lower limit on the radiative width (Eq. (234), review paper [1]). Contrary, the internal radiative width amplitude is a real and model-dependent quantity. The internal radiative width amplitude is usually a fitting parameter in the R-matrix method.

The combination of the peripheral transfer reactions allowing one to determine the ANCs and the radiative capture reactions whose amplitudes are parameterized in terms of the ANSs extracted from the transfer reactions is the essence of the indirect ANC method in nuclear astrophysics. In what follows, we present useful R-matrix equations for radiative capture amplitudes and then present two different examples of using the indirect ANC method to determine the astrophysical factors.

13.2 Radiative capture resonance to bound state

In the R-mtrix approach, the radiative capture amplitude for “resonance $\rightarrow$ bound state transition” is given by the radiative capture amplitude for “resonance $\rightarrow$ bound state” transition for multi-level case (it can be extended for multi-channel case) is given by

$$\begin{aligned} \mathcal{T}_{fi}^{R}(E)&= -i\,e^{-i(\delta _{l_{i}} - \sigma _{l_{i}}^{C})}\,2\,P_{l_{i}}(k, R_{ch})\,k_{\gamma }^{L+1/2}\,\nonumber \\&\quad \sum \limits _{\nu \,\tau }\,{{{\tilde{\gamma }}}}_{ \gamma \,\nu \,J_{f}}^{J_{i}}(E)\,[\textbf{A}(E)]_{\nu \,\tau }\, {{{\tilde{\gamma }}}}_{\tau }^{J_{i}}\,. \end{aligned}$$

(237)

Here $\textbf{A}(E)$ is the level matrix ( see Eq. (62) simplified here by considering only the single-channel case), ${{{\tilde{\gamma }}}}_{\tau }^{J_{i}}$ is the formal reduced resonance width ampliitude of the level $\tau$ and ${{{\tilde{\gamma }}}}_{\gamma \,\nu \,J_f}^{J_i}$ is the formal reduced radiative width amplitude of the level $\,\nu \,$ with the level energy $E_{\nu }$ ( Barker and Kajino [22], Mukhamedzhanov and Pang [75]):

$$\begin{aligned} {{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f}^{J_i}(E)&= \sqrt{\frac{2\,\lambda _N\,m_{au}\,R_{ch}}{137}}\, \sqrt{\frac{(L+1){{\hat{L}}}}{L}}\,\nonumber \\&\quad \frac{1}{({{\hat{L}}})!!}\,R_{ch}^{L+1/2}\,\mu ^L\,Z_{eff(L)aA}\,\sqrt{({{\hat{l}}}_{i})({{\hat{J}}}_{f})} \nonumber \\&\qquad \times (-1)^{L+l_f+I+J_i}\,<l_i\, 0\,\, L\, 0|l_{f}\,0\nonumber \\&>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \frac{1}{R_{ch}^{L+1}}\, \nonumber \\&\quad \int _0^{\infty } dr r^{L+2}\,I_{aA\,l_{f}\,s_{i}\,J_{f}}^{B}(r)\, \Psi _{\nu \,l_{i}\,s_{i}\,J_{i}}(k,\,r) \nonumber \\&= {{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f (int)}^{J_i} - {{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f (ch)}^{J_i}(E), \end{aligned}$$

(238)

where ${{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f (int)}^{J_i}$ and ${{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f (ch)}^{J_i}(E),$ are the internal and external formal reduced radiative width amplitudes, respectively.

We consider the non-spin-flip transition, that is, the channel spin $s_{i}$ is conserved in the transition. $\lambda _{N}=0.2118$ is the nucleon Compton wave length, $m_{au}=931.5$ MeV is the atomic mass unit. $<l_i\, 0\,\, L\, 0|l_{f}\,0>$ is the Clebsch-Gordan coefficient, $\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ I &{} J_i &{} J_f\end{array}\right\}$ is $6\,j$-symbol. $\{l_{i}\,s_{i}\,J_{i}\}$ ($\{l_{f}\,s_{i}\,J_{f}\}$) is the set of quantum number describing the initial resonance state i (final bound state f). Also $\Psi _{\nu \,l_{i}\,s_{i}\,J_{i}}(k_{\nu },r)$ is the R-matrix resonance radial scattering wave function of the the level $\nu$, $I_{aA\,l_{f}\,s_{i}\,J_{f}}^{B}(r)$ is the radial overlap function of the bound-state wave functions of nuclei $B,\,a$ and A.

In the R-matrix the configuration space is split into the internal and external regions. Correspondingly, the resonance radiative capture amplitude is split into internal and external amplitudes:

$$\begin{aligned} \mathcal{T}_{fi}^{R}(E)= \mathcal{T}_{fi(int)}^{R}(E) - \mathcal{T}_{fi(ext)}^{R}(E), \end{aligned}$$

(239)

where

$$\begin{aligned} \mathcal{T}_{fi(int,ch)}^{R}(E)&= -i\,e^{-i(\delta _{l_{i}} - \sigma _{l_{i}}^{C})}\,2\,P_{l_{i}}(k_{i}, R_{ch})\,k_{\gamma }^{L+1/2}\,\nonumber \\&\quad \sum \limits _{\nu \,\tau }\,{{{\tilde{\gamma }}}}_{ \gamma \,\nu \,J_{f}\,(int,ch)}^{J_{i}}\,[\textbf{A}(E)]_{\nu \,\tau }\, {{{\tilde{\gamma }}}}_{\tau }^{J_{i}} \end{aligned}$$

(240)

13.2.1 Internal reduced radiative width

We consider now the internal radiative capture amplitude. First, from Eq. (238) follows that in the internal region

$$\begin{aligned}&{{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f\,(int)}^{J_i} = \sqrt{\frac{2\,\lambda _N\,m_{au}\,R_{ch}}{137}}\, \sqrt{\frac{(L+1){{\hat{L}}}}{L}}\,\frac{1}{({{\hat{L}}})!!}\,R_{ch}^{L+1/2}\,\mu ^L \nonumber \\&\quad \times \,Z_{eff(L)aA} \,\sqrt{({{\hat{l}}}_{i})({{\hat{J}}}_{f})} (-1)^{L+l_f+I+J_i}\,<l_i\, 0\,\, L\, 0|l_{f}\,0> \nonumber \\&\quad \times \left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \frac{1}{R_{ch}^{L+1}} \int _0^{R} dr r^{L+1}\,I_{aA\,l_{f}\,s_{i}\,J_{f}}^{B}(r)\, u_{\nu \,l_{i}\,s_{i}\,J_{i}}(k_{\nu },r). \end{aligned}$$

(241)

Here

$$\begin{aligned} Z_{eff(L)ij}= \mu ^{L}\,\Big (\frac{Z_{i}}{m_{i}^{L}} + (-1)^{L}\,\frac{Z_{j} }{m_{j}^{L} }\Big ) \end{aligned}$$

(242)

determines the effective charge for the electric transition of the multipolarity L in the system $i+j$, $\,\mu \equiv \mu _{ij}.$

The internal resonance radial wave function $\,u_{\nu \,l_{i}\,s_{i}\,J_{i}}(k_{\nu },r)\,$ of level $\,\nu \,$ in the initial channel $\,i\,$ has been already introduced in Sect. 4.2. In the R-matrix approach, $\,u_{\nu \,l_{i}\,s_{i}\,J_{i}}(k_{\nu },r)\,$ is a real wave function, which is calculated at the level energy $E_{\nu }$ and momentum $k_{\nu }$, and is normalized to unity over the internal region $0 \le r \le R_{ch}$, where $r \equiv r_{aA}.\,$ If a few levels do contribute to the radiative capture amplitude, we can select the energy of one of the levels equal to the corresponding real part of the resonance energy $E_{\nu }= E_{0}$ ($k_{\nu }=k_{0}$), while all other energy levels are considered to be fitting parameters. Then we can calculate $\,u_{\nu \,l_{i}\,s_{i}\,J_{i}}(k_{\nu },r)\,$ at the real part of the resonance energy $E_{0}$. The radial overlap function can be approximated by

$$\begin{aligned} I_{aA\,l_{f}\,s_{i}\,J_{f}}^{B}(r)= {\mathtt S}_{l_f\,s_{i}\,J_f }^{1/2}\,\phi _{l_f\,s_{i}\,J_f}(r) = {\mathtt S}_{l_f\,s_{i}\,J_f }^{1/2}\,\frac{\varphi _{l_f\,s_{i}\,J_f}(r)}{r} , \end{aligned}$$

(243)

where ${\mathtt S}_{l_f\,s_{i}\,J_f }$ is the SF of the final bound state, $\phi _{l_f\,s_{i}\,J_f}$ is the single-particle bound-state wave function normalized to unity over the entire region $0 \le r < \infty$, $\varphi _{l_f\,s_{i}\,J_f}(r)$ is the reduced bound-state wave function. Then the single-particle reduced width amplitude is

$$\begin{aligned} {{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f\,(int)}^{J_i(sp)}&= \sqrt{\frac{2\,\lambda _N\,m_{au}\,R_{ch}}{137}}\,R_{ch}^{L+1/2}\,\mu ^L\, Z_{eff(L)aA}\,\sqrt{\frac{(L+1){{\hat{L}}}}{L}} \nonumber \\&\quad \times \frac{1}{({{\hat{L}}})!!}\,\sqrt{({{\hat{l}}}_{i})({{\hat{J}}}_{f})} (-1)^{L+l_f+I+J_i}\,\nonumber \\&<l_i\, 0\,\, L\, 0|l_{f}\,0>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \frac{1}{R_{ch}^{L+1}} \nonumber \\&\quad \times \int _0^{R} dr r^{L}\,\varphi _{l_f\,s_{i}\,J_f}(r)\,u_{\nu \,l_{i}\,s_{i}\,J_{i}}(k_{0},r). \end{aligned}$$

(244)

We can rewrite it in a more symmetric form, which will also be suitable for the “subthreshold resonance $\rightarrow$ bound state” transition. To this end, we rewrite the reduced single-particle bound-state wave function, which is normalized to unity over the entire space, as

$$\begin{aligned} \varphi _{l_f\,s_{i}\,J_f}(r) = \frac{\varphi _{l_f\,s_{i}\,J_f}'(r)}{\big [\int _{0}^{\infty }\,\textrm{d}r\,[\varphi _{l_f\,s_{i}\,J_f}'(r)]^{2}\big ]^{1/2}}, \end{aligned}$$

(245)

where we assume that the single-particle wave function $\varphi _{l_f\,s_{i}\,J_f}'(r)$ is not normalized to untiy and its normalization is provided by the normalization integral added in the denominator. From

$$\begin{aligned} \int \limits _{0}^{\infty }\,\textrm{d}r\,[\varphi _{l_f\,s_{i}\,J_f}'(r)]^{2}&= \int \limits _{0}^{R_{ch}}\,\textrm{d}r\,[\varphi _{l_f\,s_{i}\,J_f}'(r)]^{2} \nonumber \\&\quad \times \Big (1 + [{{{\tilde{\gamma }}}}^{J_{f}(sp)}]^{2}\textrm{d}{{\hat{S}}}_{l_{f}}/ \textrm{d}E\Big |_{E=-\varepsilon _{f}}\Big ) \end{aligned}$$

(246)

follows that

$$\begin{aligned}&\varphi _{l_f\,s_{i}\,J_f}(r) = \frac{\varphi _{l_f\,s_{i}\,J_f}'(r)}{\Big (\int _{0}^{R_{ch}}\,\textrm{d}r\,[\varphi _{l_f\,s_{i}\,J_f}'(r)]^{2}\Big )^{1/2}\,N_{f}^{1/2}} = \frac{u_{l_f\,s_{i}\,J_f}(r)}{N_{f}^{1/2}}, \end{aligned}$$

(247)

where $u_{l_f\,s_{i}\,J_f}(r)$ is the final state bound-state wave function normalized to unity over the internal region, and

$$\begin{aligned} N_{f}= 1 + [{{{\tilde{\gamma }}}}^{J_{f}(sp)}]^{2}\textrm{d}{{\hat{S}}}_{l_{f}}/ \textrm{d}E\Big |_{E=-\varepsilon _{f}}. \end{aligned}$$

(248)

For the bound state

$$\begin{aligned} {{\hat{S}}}_{l_{f}}=i\,\kappa _{f}\,R_{ch}\, \frac{\textrm{d}\ln [O_{l_{f}}(i\,\kappa _{f},r)]}{\textrm{d}r}\Big |_{r=R_{ch}}. \end{aligned}$$

(249)

Note that

$$\begin{aligned}{}[ {{{\tilde{\gamma }}}}^{J_{f}(sp)}]^{2}&= \frac{1}{2\,\mu \,R_{ch}}\,\frac{[\varphi _{l_f\,s_{i}\,J_f}'(R_{ch})]^{2}}{ \int \limits _{0}^{R_{ch}}\,\textrm{d}r\,[\varphi _{l_f\,s_{i}\,J_f}'(r)]^{2}} \nonumber \\&= \frac{1}{2\,\mu \,R_{ch}}\,[u_{l_f\,s_{i}\,J_f}(R_{ch})]^{2} \end{aligned}$$

(250)

is the formal reduced width of the bound state $B=(a\,A)$ with the binding energy $\varepsilon _{f}$ to which decay of the resonance occurs. Then

$$\begin{aligned}&{{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f\,(int)}^{J_i(sp)} = \sqrt{\frac{2\,\lambda _N\,m_{au}\,R_{ch}}{137}}\,R_{ch}^{L+1/2}\,\nonumber \\&\quad \mu ^L\, Z_{eff(L)aA}\,\sqrt{\frac{(L+1){{\hat{L}}}}{L}} \nonumber \\&\qquad \times \frac{1}{({{\hat{L}}})!!}\,\sqrt{({{\hat{l}}}_{i})({{\hat{J}}}_{f})} (-1)^{L+l_f+s_{i}+J_i}\,\nonumber \\&\quad <l_i\, 0\,\, L\, 0|l_{f}\,0>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \frac{1}{R_{ch}^{L+1}} \nonumber \\&\qquad \times \int _0^{R} dr r^{L}\,u_{l_f\,s_{i}\,J_f}(r)\,u_{\nu \,l_{i}\,s_{i}\,J_{i}}(k_{0},r)\,\frac{1}{N_{f}^{1/2}} \end{aligned}$$

(251)

and

$$\begin{aligned} {{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f\,(int)}^{J_i} = {\mathtt S}_{l_f\,s_{i}\,J_f }^{1/2}\,{{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f\,(int)}^{J_i(sp)}. \end{aligned}$$

(252)

Note that ${{{\tilde{\gamma }}}}_{\gamma \,\nu \, J_f\,(int)}^{J_i}$ is a real quantity.

We repeat now the steps developed in Sect. 6.1 and show how to obtain the observable reduced widths from the single-particle ones. Let us consider a simple single-level case taking into account only level $\tau$ in a single-particle approximation. Then

$$\begin{aligned} \mathcal{T}_{fi(int)}^{R(sp)}(E)&= -i\,e^{-i(\delta _{l_{i}} - \sigma _{l_{i}}^{C})}\, \nonumber \\&\quad \times \frac{2\,P_{l_{i}}(k, R_{ch})\,k_{\gamma }^{L+1/2}\, {{{\tilde{\gamma }}}}_{\gamma \,\tau \,J_{f}\,(int)}^{J_{i}(sp)}\,{{{\tilde{\gamma }}}}_{\tau }^{J_{i}(sp)}}{E_{\tau } - E - \big [{{{\tilde{\gamma }}}}_{\tau }^{J_{i}(sp)}\big ]^{2}[{{\hat{S}}}_{l_{i}}(E) - B_{l_{i}} - i\,P_{l_{i}}(E,R_{ch}]}, \end{aligned}$$

(253)

where (Lane and Thomas [18])

$$\begin{aligned} {{\hat{S}}}_{l_{i}}(E)= k\,R_{ch}\,\frac{F_{l_{i}}(k,r)\,\frac{\textrm{d}F_{l_{i}}(k,r)}{\textrm{d}r} + G_{l_{i}}(k,r)\,\frac{\textrm{d}G_{l_{i}}(k,r)}{\textrm{d}r}}{F_{l_{i}}^{2}(k,r) + G_{l_{i}}^{2}(k,r)}\Big |_{r=R_{ch}}, \end{aligned}$$

(254)

$E_{\tau }$ is the energy level of the $\tau$ level. Adopting $E_{\tau }= E_{0}$, where $E_{0}$ is the real part of the resonance close to the level $\tau$, for $E \rightarrow E_{0}$ Eq. (253) takes the form

$$\begin{aligned} \mathcal{T}_{fi(int)}^{R(sp)}(E)&= -i\,e^{-i(\delta _{l_{i}} - \sigma _{l_{i}}^{C})} \nonumber \\&\quad \times \frac{ 2\,P_{l_{i}}(k, R_{ch})\,k_{\gamma }^{L+1/2}\, {\gamma }_{\gamma \,\tau \,J_{f}(int)}^{J_{i}(sp)}\,{\gamma }_{\tau }^{J_{i}(sp)} }{E_{0} - E - i\,P_{l_{i}}(E,R_{ch})\,\big [\gamma _{\tau }^{J_{i}(sp)}\big ]^{2}}. \end{aligned}$$

(255)

Here the observable resonance reduced single-particle width is

$$\begin{aligned} \big [{\gamma }_{\tau }^{J_{i}(sp)}\big ]^{2} = \frac{\big [{{{\tilde{\gamma }}}}_{\tau }^{J_{i}(sp)}\big ]^{2} }{1 + \big [{{{\tilde{\gamma }}}}_{\tau }^{J_{i}(sp)}\big ]^{2}\textrm{d}{{\hat{S}}}_{l_{i}}/ \textrm{d}E\Big |_{E=E_{0}} } \end{aligned}$$

(256)

and

$$\begin{aligned}&[ {{{\tilde{\gamma }}}}_{\tau }^{J_{i}(sp)}]^{2} = \frac{1}{2\,\mu \,R_{ch}}\,[u_{\tau \,l_i\,s_{i}\,J_i}(R_{ch})]^{2} \end{aligned}$$

(257)

is the formal resonance reduced single-particle width.

The observable reduced internal single-particle radiative width reduces to the symmetric form regarding the initial and final wave functions:

$$\begin{aligned} \gamma _{\gamma \,\tau \, J_f\,(int)}^{J_i(sp)}&= \frac{{{{\tilde{\gamma }}}}_{\gamma \,\tau \, J_f\,(int)}^{J_i(sp)}}{N_{i}^{1/2}}\nonumber \\&= \sqrt{\frac{2\,\lambda _N\,m_{au}\,R_{ch}}{137}}\,R_{ch}^{L+1/2}\,\mu ^L\, Z_{eff(L)aA}\,\nonumber \\&\quad \times \sqrt{\frac{(L+1){{\hat{L}}}}{L}} \frac{1}{({{\hat{L}}})!!}\,\sqrt{({{\hat{l}}}_{i})({{\hat{J}}}_{f})} (-1)^{L+l_f+s_{i}+J_i}\,\nonumber \\&<l_i\, 0\,\, L\, 0|l_{f}\,0>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \frac{1}{R_{ch}^{L+1}} \nonumber \\&\quad \times \frac{1}{N_{f}^{1/2}\,N_{i}^{1/2}}\,\int _0^{R} dr r^{L}\,u_{l_f\,s_{i}\,J_f}(r)\,u_{\tau \,l_{i}\,s_{i}\,J_{i}}(k_{0},r), \end{aligned}$$

(258)

where

$$\begin{aligned}&N_{i}=1 + \big [{{{\tilde{\gamma }}}}_{\tau }^{J_{i}(sp)}\big ]^{2}\textrm{d}{{\hat{S}}}_{l_{i}}/ \textrm{d}E\Big |_{E=E_{0}}. \end{aligned}$$

(259)

Then

$$\begin{aligned} \big [{\gamma }_{\gamma \,\tau \,J_{f}(int)}^{J_{i}}\big ]^{2} = {\mathtt S}_{l_f\,s_{i}\,J_f }\, {\mathtt S}_{l_i\,s_{i}\,J_i}\, \big [{\gamma }_{\gamma \,\tau \,J_{f}(int)}^{J_{i}(sp)}\big ]^{2} \end{aligned}$$

(260)

and we can write the internal amplitude for the “resonance $\rightarrow$ bound state” transition in terms of the observable quantities:

$$\begin{aligned}&\mathcal{T}_{fi(int)}^{R}(E) = -i\,e^{-i(\delta _{l_{i}} - \sigma _{l_{i}}^{C})} \nonumber \\&\quad \times \frac{ 2\,P_{l_{i}}(k,\,R_{ch})\,k_{\gamma }^{L+1/2}\, {\gamma }_{\gamma \,\tau \,J_{f}\,(int)}^{J_{i}}\,{\gamma }_{\tau }^{J_{i}} }{E_{0} - E - i\,P_{l_{i}}(E,R_{ch})\,\big [{\gamma }_{\tau }^{J_{i}(sp)}\big ]^{2}}. \end{aligned}$$

(261)

Thus the amplitude $\,\mathcal{T}_{fi(int)}^{R}(E)\,$ can be rewritten in a symmetric form containing factors $N_{f}$ and $N_{i}$ for both the bound and resonance states. It is important because the bound-state wave function was originally normalized to unity over the entire coordinate space. In contrast, the internal resonance wave function $u_{l_{i}\,s_{i}\,J_{i}}(k_{0},r)$ is normalized to unity only over the internal region. Transformation (246) allows us to express the normalization integral over the entire space in terms of the normalization integral over the internal region.

We remind that the internal radiative width $\Gamma _{\gamma J_f\,(int)}^{J_i}(E)$ is given by

$$\begin{aligned} \Gamma _{\gamma J_f\,(int)}^{J_i}(E)=2\,k_{\gamma }^{{{\hat{L}}}}\,\Big |\gamma _{\gamma J_f\,(int)}^{J_i}\Big |^2. \end{aligned}$$

(262)

Note that $\,\gamma _{\gamma J_f\,(int)}^{J_i}\,$ is calculated at fixed energy $E=E_{0}.$ That is why the energy dependence of $\,\Gamma _{\gamma J_f\,(int)}^{J_i}(E)\,$ on the initial $a-A$ energy E is entirely due to the factor $\,k_{\gamma }^{{{\hat{L}}}}.$ Equation (258) can be generalized for the “subthreshold resonance $\rightarrow$ bound state” radiative capture.

13.2.2 Channel reduced radiative width

The observable channel radiative width amplitude, which determines the radiative capture from resonance to the ground state occuring at $r> R_{ch}$, has been introduced in review paper [1] and is given by (in the current notations)

$$\begin{aligned}&\gamma _{\gamma \,\tau \,J_{f}\,(ch) }^{J_{i} }(E) = \sqrt{\frac{\lambda _{N}\,m_{au}}{137\,E} }\,\sqrt{ \frac{(L+1)\,{{{\hat{L}}}} }{L} }\,\frac{1}{ {{\hat{L}}}!!}\,\nonumber \\&\quad \mu ^{L}\,Z_{eff(L)aA}\, (R_{ch})^{L+1/2}\,C_{ aA\,l_{f}s_{i}J_{f}}^{B}\,\sqrt{({{\hat{l}}}_{i})({{\hat{J}}}_{f})} \nonumber \\&\qquad \times \sqrt{ \Gamma _{aA\,\tau \,l_{i}s_{i} }^{J_{i}}(E) } \, \sqrt{P_{l_{i} }(k, R_{ch}) }\,\nonumber \\&\quad \Big ([F_{ l_{i}}(k, R_{ch})]^{2} + [G_{l_{i}}(k, R_{ch})]^{2} \Big )\, W_{-\eta _{f}^{bs}, l_{f}+1/2} \nonumber \\&\qquad \times (2\,\kappa _{f}\,R_{ch})\,<l_{i}0\,L0|l_{f}0>\,(-1)^{L+l_f+s_{i}+J_i}\,\nonumber \\&\quad <l_i\, 0\,\, L\, 0|l_{f}\,0>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \,J_{L}(l_{f},l_{i};k). \end{aligned}$$

(263)

Here we explicitly indicated that, in contrast to $\gamma _{\gamma J_f\,(int)}^{J_i},\,$ the channel radiative width dependes on the energy E. Also $\,C_{ aA\,l_{f}s_{i}J_{f}}^{B}$ is the ANC for the virtual decay/synthesis $\,B \leftrightarrow a+A,\,$ $\,W_{-\eta _{f}^{bs}, l_{f}+1/2}(2\,\kappa _{f}\,R_{ch})$ is the Whittaker function, which describes the radial behavior of the bound-state wave function $B=(a\,A)$ at $\,r_{aA} > R_{ch}$, $\,\eta _{f}^{bs}= Z_{a}\,Z_{A}\,\mu /(137\,\kappa _{f})$ is the Coulomb parameter of the bound state $B=(aA)$, $Z_{i}\,$ is the number of protons in nucleus i, $\,\kappa _{f}= \sqrt{2\,\mu \,\varepsilon _{f}}\,$ is the wave number of the bound state $(aA).\,$ $\,\Gamma _{aA\,\tau \,l_{i}s_{i}}^{J_{i}}(E)$ is the resonance width of the level $\tau ,\,$ which can be calculated through the following equation:

$$\begin{aligned} \Gamma _{aA\,\tau \,l_{i}s_{i} }^{J_{i}}(E)=\frac{P_{l_i}(E, R_{ch})}{P_{l_i}(E_{0}, R_{ch})}\,\Gamma _{aA\,\tau \,l_{i}s_{i} }^{J_{i}}(E_{0}), \end{aligned}$$

(264)

where $\,\Gamma _{aA\,\tau \,l_{i}s_{i} }^{J_{i}}(E_{0})\,$ is the observable resonance width of the level $\tau .$

Also

$$\begin{aligned} J_{L}(l_{f}, l_{i}; k)&= J_{L}''(l_{f},l_{i};k) \nonumber \\&\quad + i\frac{F_{ l_{i}}(k, R_{ch})\,G_{l_{i}}(k, R_{ch})}{F_{ l_{i}}^{2}(k, R_{ch}) + G_{l_{i}}^{2}(k, R_{ch})} \,J_{L}'(l_{f},l_{i}), \end{aligned}$$

(265)

$$\begin{aligned} J_{L}''(l_{B},l_{i};k)&= \frac{1}{R_{ch}^{L+1} }\,\int \limits _{ R_{ch} }^{\infty }\,\textrm{d}r\,r^{L}\, \frac{ W_{-\eta _{f}^{bs}, l_{f}+1/2}(2\,\kappa _{f}\,r) }{ W_{-\eta _{f}^{bs}, l_{f}+1/2}(2\,\kappa _{f}\,R_{ch})}\,\nonumber \\&\quad \frac{ F_{ l_{i}}(k, r)\,F_{ l_{i}}(k, R_{ch}) + G_{l_{i}}(k, r)\,G_{l_{i}}(k, R_{ch}) }{ F_{ l_{i}}^{2}(k, R_{ch}) + G_{l_{i}}^{2}(k, R_{ch}) } , \end{aligned}$$

(266)

$$\begin{aligned} J_{L}'(l_{f},l_{i};k)&= \frac{1}{R_{ch}^{L+1} }\,\int \limits _{ R_{ch} }^{\infty }\,\textrm{d}r\,r^{L}\, \frac{ W_{-\eta _{f}^{bs}, l_{f}+1/2}(2\,\kappa _{f}\,r) }{ W_{-\eta _{f}^{bs}, l_{f}+1/2}(2\,\kappa _{f}\,R_{ch})} \nonumber \\&\quad \times \Big [\frac{ F_{ l_{i}}(k, r)}{F_{ l_{i}}(k, R_{ch})} - \frac{G_{l_{i}}(k, r)}{G_{l_{i}}(k, R_{ch})} \Big ]. \end{aligned}$$

(267)

Note that the channel radiative width amplitude, in contrast to the internal one, is complex.

Equation (263) is used in the R-matrix analysis. After simple manipulations using Eqs. (A.23) and (A.26), review [1], and Eq. (71)) this equation can be reduced to

$$\begin{aligned}&\gamma _{\gamma \,\tau \,J_{f}(ch) }^{J_{i} }(E) = e^{-(\delta _{l_{i}}^{hs} - \sigma _{l_{i}}^{C})}\, \sqrt{\frac{\lambda _{N}\,m_{au}}{137\,E} }\,\sqrt{ \frac{(L+1)\,{{{\hat{L}}}} }{L} }\,\frac{1}{ {{\hat{L}}}!!}\,\nonumber \\&\quad \mu ^{L}\,Z_{eff(L)aA}\, (R_{ch})^{L+1/2}\,C_{ aA\,l_{f}s_{i}J_{f}}^{B}\,\sqrt{({{\hat{l}}}_{i})({{\hat{J}}}_{f})} \nonumber \\&\qquad \times \sqrt{ \Gamma _{aA\,\tau \,l_{i}s_{i}}^{J_{i} }(E) } \,\sqrt{k\,R_{ch}}\,<l_{i}0\,L0|l_{f}0>\,(-1)^{L+l_f+s_{i}+J_i}\,\nonumber \\&\quad <l_i\, 0\,\, L\, 0|l_{f}\,0>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \nonumber \\&\quad \frac{1}{R_{ch}^{L+!}}\,\int \limits _{R_{ch}}^{\infty }\textrm{d}r\,r^{L}\,,W_{-\eta _{f}^{bs}, l_{f}+1/2}(2\,\kappa _{f}\,r)\, O_{l_{i}}(k,r). \end{aligned}$$

(268)

Note that in the potential approach the R-matrix phase shift $-(\delta _{l_{i}}^{hs} - \sigma _{l_{i}}^{C})$ should be replaced by the potential phase shift $\delta _{l_{i}}^{p}$, which can be calculated using an adopted nuclear + Coulomb potentials.

The channel reduced radiative width is given by

$$\begin{aligned} \Gamma _{\gamma \,\tau \,J_f\,(ch)}^{J_i}(E) =2\,k_{\gamma }^{{{\hat{L}}}}\,\Big |\gamma _{\gamma \,\tau \, J_f\,(ch)}^{J_i}(E)\Big |^2 \end{aligned}$$

(269)

and the total radiative width is

$$\begin{aligned} \Gamma _{\gamma \,\tau \,J_f}^{J_i}(E)=2\,k_{\gamma }^{{{\hat{L}}}}\,\Big |\gamma _{\gamma \,\tau \, J_f}^{J_i}(E)\Big |^2. \end{aligned}$$

(270)

It is clear from Eq. (268) that to calculate the channel reduced radiative width amplitude $\gamma _{\gamma \,\tau \,J_{f}\,(ch) }^{J_{i} }(E)$ we need to know only two experimentally measurable quantities, the ANC, $C_{ aA\,l_{f}s_{i}J_{f}}^{B}$, and the resonance width $\, \Gamma _{aA\,\tau \,l_{i}s_{i} }^{J_{i}}(E_{0}).\,$ Thus, the ANC plays an important role in determining the reduced radiative width because the ANC determines the normalization of the channel contribution. Assuming that the experimental radiative width $\Gamma _{\gamma \,\tau \,J_{f}}^{J_{i}}(E_{0})$, the ANC of the bound state, and the observable resonance width $\Gamma _{aA\,\tau \,l_{i}\,s_{i}}^{\,J_{i}}(E_{o})$ are known, we can determine the internal reduced radiative width amplitude

$$\begin{aligned} \gamma _{\gamma \,\tau \,J_{f}\,(int)}^{J_{i}}&= \textrm{Re}\,\gamma _{ \gamma \,\tau \,J_{f}\,(ch)}^{J_{i} }(E_{0}) \nonumber \\&\quad \pm \sqrt{ \Gamma _{ \gamma \,\tau \,J_{f} }^{J_{i}}(E_{0}) - [\textrm{Im}\,\gamma _{\gamma \,\tau \,J_{f}\,(ch) }^{J_{i} }(E_{0}) ]^{2}} \end{aligned}$$

(271)

with two possible solutions.

The total resonance amplitude for the radiative capture “resonance $\rightarrow$ bound state”, which includes the internal and channel parts is given by

$$\begin{aligned} \mathcal{T}_{fi}^{R}(E) = -i\,e^{-i(\delta _{l_{i}} - \sigma _{l_{i}}^{C})}\, \frac{ 2\,P_{l_{i}}(k_{i}, R_{ch})\,k_{\gamma }^{L+1/2}\, {\gamma }_{\gamma \,\tau \,J_{f}}^{J_{i}}\,{\gamma }_{\tau }^{J_{i}} }{E_{0} - E - i\,P_{l_{i}}(E,R_{ch})\,\big [{\gamma }_{\tau }^{J_{i}(sp)}\big ]^{2}}. \end{aligned}$$

(272)

13.2.3 Radiative capture through subthreshold resonance

Now we consider the radiative capture to the ground state through the subthreshold resonance. We remind that the subthreshold resonance is a near threshold bound state. At relative $a-A$ energy E close to the threshold the tail of the subthreshold state extending to positive energies. Hence the capture to the bound state at positive initial energies is contributed by the subthreshold bound state. Again, as for the radiative capture “resonance $\rightarrow$ bound state”, the reduced single-particle radiative width amplitude for the radiative capture for the “subthreshold bound state $\rightarrow$ bound state” is

$$\begin{aligned} \gamma _{\gamma \, J_f}^{J_i(s)}(E)= \gamma _{\gamma \,J_f\,(int)}^{J_i(s)} - \gamma _{\gamma \,J_f\,(ch)}^{J_i(s)}(E). \end{aligned}$$

(273)

Here the superscript s stands for the subthreshold bound state. The reduced internal radiative width amplitude is given by

$$\begin{aligned} {{{\tilde{\gamma }}}}_{\gamma \,J_f\,(int)}^{J_i (s)}&= \sqrt{\frac{2\,\lambda _N\,m_{au}\,R_{ch}}{137}}\,\sqrt{\frac{(L+1){{\hat{L}}}}{L}}\,\frac{1}{({{\hat{L}}})!!}\, R_{ch}^{L+1/2}\,\mu ^L\, Z_{eff(L)aA} \nonumber \\&\qquad \times \sqrt{({{\hat{l}}}_{i})({{\hat{J}}}_{f})} (-1)^{L+l_f+s_{i}+J_i}\,\nonumber \\&\quad <l_i\, 0\,\, L\, 0|l_{f}\,0>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \frac{1}{R_{ch}^{L+1}} \nonumber \\&\qquad \times {\mathtt S}_{l_f\,s_{i}\,J_f}^{1/2}\, {\mathtt S}_{l_{i}\,s_{i}\,J_{i}}^{1/2}\,\frac{1}{N_{f}^{1/2}}\,\int _0^{R} dr r^{L}\,u_{l_f\,s_{i}\,J_f}(r)\,u_{l_{i}\,s_{i}\,J_{i}}(r), \end{aligned}$$

(274)

where the wave function of the final bound state $u_{l_f\,s_{i}\,J_f}(r)$ and the wave funcion of the subthreshold bound state $\,u_{l_{i}\,s_{i}\,J_{i}}(r)\,$ are normalized over the internal region ($r < R_{ch}$).

Then observable reduced radiative width amplitude for the transition “subthreshold bound state $\rightarrow$ bound state”

$$\begin{aligned} \gamma _{\gamma \,J_f\,(int)}^{J_i(s)}&= \frac{{{{\tilde{\gamma }}}}_{\gamma \,J_f\,(int)}^{J_i (s)}}{N_{i}^{1/2}} \nonumber \\&= \sqrt{\frac{2\,\lambda _N\,m_{au}\,R_{ch}}{137}}\sqrt{\frac{(L+1){{\hat{L}}}}{L}}\,\frac{1}{({{\hat{L}}})!!} \nonumber \\&\quad \times \,R_{ch}^{L+1/2}\,\mu ^L\, Z_{eff(L)aA}\,\sqrt{({{\hat{l}}}_{i})({{\hat{J}}}_{f})} (-1)^{L+l_f+s_{i}+J_i}\,\nonumber \\&<l_i\, 0\,\, L\, 0|l_{f}\,0>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \frac{1}{R_{ch}^{L+1}} \nonumber \\&\qquad \times {\mathtt S}_{l_f\,s_{i}\,J_f}^{1/2}\, {\mathtt S}_{l_{i}\,s_{i}\,J_{i}}^{1/2}\,\frac{1}{N_{f}^{1/2}\,[N_{i}^{s}]^{1/2}}\,\nonumber \\&\quad \int _0^{R} dr r^{L}\,u_{l_f\,s_{i}\,J_f}(r)\,u_{l_{i}\,s_{i}\,J_{i}}(r). \end{aligned}$$

(275)

Since now the initial i channel is the subthreshold bound state, $\,N_{i}^{s}\,$ is defined by the equations

$$\begin{aligned} N_{i}^{s}&= 1 + [{{{\tilde{\gamma }}}}^{J_{i}(s)(sp)}]^{2}\textrm{d}{{\hat{S}}}_{l_{i}}^{s}/ \textrm{d}E\Big |_{E=-\varepsilon _{s}}, \end{aligned}$$

(276)

$$\begin{aligned} {{\hat{S}}}_{l_{i}}^{s}&=i\,\kappa _{s}\,R_{ch}\, \frac{\textrm{d}\ln [O_{l_{i}}(i\,\kappa _{s},r)]}{\textrm{d}r}\Big |_{r=R_{ch}}. \end{aligned}$$

(277)

The reduced observable channel radiative width amplitude is given by

$$\begin{aligned} \gamma _{\gamma \,J_{f}\,(ch) }^{J_{i}(s) }(E)&= \sqrt{\frac{\lambda _{N}\,m_{au}}{137\,E} }\,\sqrt{ \frac{(L+1)\,{{{\hat{L}}}} }{L} }\,\frac{1}{ {{\hat{L}}}!!}\,\mu ^{L}\,Z_{eff(L)aA} \nonumber \\&\qquad \times (R_{ch})^{L+1/2}\,C_{ aA\,l_{f}s_{i}J_{f}}^{B(s)}\,\sqrt{ \Gamma _{aA\,l_{i}s_{i} }^{J_{i}(s)}(E)}\, \sqrt{P_{l_{i} }(k, R_{ch}) } \nonumber \\&\quad \Big ([F_{ l_{i}}(k, R_{ch})]^{2} + [G_{l_{i}}(k, R_{ch})]^{2} \Big )\, W_{-\eta _{f}^{bs}, l_{f}+1/2}(2\,\kappa _{f}\,R_{ch}) \nonumber \\&\qquad \times (-1)^{L+l_f+s_{i}+J_i}\,<l_i\, 0\,\, L\, 0|l_{f}\,0>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \,J_{L}(l_{f},l_{i};k), \end{aligned}$$

(278)

where the resonance width $\,\Gamma _{aA\,l_{i}s_{i}}^{J_{i}(s)}\,(E)$ of the subthreshold resonance is defined in Eq. (149). In the current notations it takes the form

$$\begin{aligned} \Gamma _{aA\,l_{i}\,s_{i}}^{J_{i}(s)}(E)&= P_{l_{i}}(E,R_{ch})\,\frac{1}{\mu \,R_{ch}} [C_{aA\,l_{i}\,s_{i}\,J_{i}}^{B(s)}]^{2}\nonumber \\&\quad \,W_{-\,\eta ^{s}\,l_{i}+1/2}^{2}(2\,\kappa _{s},\,R_{ch}) \nonumber \\&=2\,P_{l_{i}}(E,R_{ch})\,[\gamma ^{J_{i}(s)}]^{2}. \end{aligned}$$

(279)

Here $C_{aA\,l_{i}\,s_{i}\,J_{i}}^{B(s)},\,$ $\,\kappa _{s}$ and $\eta ^{s}$ are the ANC, wave number and the Coulomb parameter of the subthreshold bound state. $W_{-\eta _{i}^{bs}, l_{i}+1/2}(2\,\kappa _{s}\,R_{ch})$ is the Whittaker function of the subthreshold state determining the radial behavior of the subthreshold bound state at $r >R_{ch}$ where we can neglect the nuclear $a-A$ interaction. $\gamma ^{J_{i}(s)}={\mathtt S}_{l_{i}\,s_{i}\,J_{i}}^{1/2}\,\gamma ^{J_{i}(s)(sp)} \,$ is the observable reduced width amplitude of the subthreshold resonance:

$$\begin{aligned} \gamma ^{J_{i}(s)} = \frac{{{{\tilde{\gamma }}}}^{J_{i}(s)}}{[N_{i}^{s}]^{1/2}}. \end{aligned}$$

(280)

The amplitude of the resonance capture to the ground state, which proceeds through the subthreshold resonance, is

$$\begin{aligned}&\mathcal{T}_{fi}^{(s)(sp)}(E) = -i\,e^{-i(\delta _{l_{i}} - \sigma _{l_{i}}^{C})}\, \nonumber \\&\quad \times \frac{2\,P_{l_{i}}(k_{i}, R_{ch})\,k_{\gamma }^{L+1/2}\, {{{\tilde{\gamma }}}}_{\gamma \,\tau \,J_{f}\,(int)}^{J_{i}(s)(sp)}\,{{{\tilde{\gamma }}}}_{\tau }^{J_{i}(s)(sp)}}{-\varepsilon _{s} - E - \big [{{{\tilde{\gamma }}}}_{\tau }^{J_{i}(sp)}\big ]^{2}[{{\hat{S}}}_{l_{i}}^{s}(E) - B_{l_{i}} - i\,P_{l_{i}}(E,R_{ch}]}. \end{aligned}$$

(281)

13.2.4 Resonance and radiative width

The resonance width at any $E>0$ defined in Eq. (264) in simplified notations is

$$\begin{aligned} \Gamma ^{J_{i}}(E)=\frac{P_{l_i}(E, R_{ch})}{P_{l_i}(E_{0}, R_{ch})}\,\Gamma ^{J_{i}}, \end{aligned}$$

(282)

where the observable resonance width is $\Gamma ^{J_{i}}=\Gamma ^{J_{i}}(E_{0}).$

The total observable radiative width $\,\Gamma _{\gamma J_f}^{J_i}=\Gamma _{\gamma J_f}^{J_i}(E_{0})\,$ is given by the modulus square of the total reduced radiative width amplitude,

$$\begin{aligned} \Gamma _{\gamma J_f}^{J_i}=\Big |\gamma _{\gamma J_f}^{J_i}\Big |^2=\Big |\gamma _{\gamma J_f\,(int)}^{J_i} - \gamma _{\gamma J_f\,(ch)}^{J_i}(E)\Big |^2, \end{aligned}$$

(283)

which further can be written as

$$\begin{aligned} \Gamma _{\gamma J_f}^{J_i}&=\Big |\gamma _{\gamma J_f\,(int)}^{J_i} - {\text{ R }e}\Big [\gamma _{\gamma J_f\,(ch)}^{J_i}(E)\Big ]\Big |^2 \nonumber \\&\quad + \Big ({\text{ I }m}\Big [\gamma _{\gamma J_f\,(ch)}^{J_i}(E)\Big ]\Big )^2. \end{aligned}$$

(284)

${\text{ R }e}\Big [\gamma _{\gamma J_f\,(ch)}^{J_i}(E)\Big ]$ (real part) and real $\gamma _{\gamma J_f\,(int)}^{J_i}$ can interfere either constructively or destructively. Therefore, $({\text{ I }m}\Big [\gamma _{\gamma J_f\,(ch)}^{J_i}(E)\Big ])^{2}$ gives the lower limit of the radiative width $\Gamma _{\gamma J_f}^{J_i}$.

The radiative width at $E>0$ can be found from

$$\begin{aligned} \Gamma _{\gamma J_f}^{J_i}(E) = \Bigg (\frac{E+\varepsilon _{f}}{E_0+\varepsilon _{f}}\Bigg )^{{{\hat{L}}}}\,\Gamma _{\gamma J_f}^{J_i}. \end{aligned}$$

(285)

For the decay of the subthreshold resonance to the lower lying bound state, the energy dependence of the radiative width is given by

$$\begin{aligned} \Gamma _{\gamma J_f}^{J_i(s)}(E) = \Bigg (\frac{E+\varepsilon _{f}}{\varepsilon _{f}- \varepsilon _{s}}\Bigg )^{{{\hat{L}}}}\,\Gamma _{\gamma J_f}^{J_i(s)}, \end{aligned}$$

(286)

where $\Gamma _{\gamma J_f}^{J_i(s)}=\Gamma _{\gamma J_f}^{J_i(s)}(-\varepsilon _{s}).$

13.3 Non-resonant radiative capture amplitude

In the R-matrix method the internal non-resonant amplitude is absorbed into the internal resonance term, so that the non-resonant capture amplitude is entirely determined by the channel (external) term (review [1])

$$\begin{aligned} \mathcal{T}_{fi}^{NR}(E)&= -i\,2\, \sqrt{\frac{\lambda _{N}\,m_{au}}{137\,E} }\,e^{-i(\delta _{l_{i}}^{hs} - \sigma _{l_{i}}^{C}) }\,\nonumber \\&\quad \mu ^{L}\,Z_{eff(L)aA}\,\sqrt{ \frac{ (L+1){{{\hat{L}}}} }{L} } \frac{1}{ {{{\hat{L}}}}!! } \nonumber \\&\qquad \times \,(k_{\gamma }\,R_{ch})^{L+1/2}\,\sqrt{ P_{l_{i}}(E) }\,(-1)^{L+l_f+s_{i}+J_i}\,\nonumber \\&<l_i\, 0\,\, L\, 0|l_{f}\,0>\,\left\{ \begin{array}{ccc} L &{} l_f &{} l_i\\ s_{i} &{} J_i &{} J_f\end{array}\right\} \nonumber \\&\qquad \times C_{ aA\,l_{f}s_{i}J_{f}}^{B}\, W_{-\eta _{f}^{bs}, l_{f}+1/2}(2\,\kappa _{f}\,R_{ch})\,\nonumber \\&\quad F_{ l_{i}}(k, R_{ch})\, G_{l_{i}}(k, R_{ch}) \,J'(l_{i},l_{f}) \end{aligned}$$

(287)

containing the same ANC as the channel reduced radiative width amplitude $\, \gamma _{ \gamma \,J_{B}\,(ch)}^{J_{xA} }(E)$. Such a normalization of the channel radiative width and non-resonant amplitudes is physically transparent. Both quantities describe peripheral processes and, hence, contain the tail of the overlap function, whose normalization is given by the corresponding ANC. Thus in the R-matrix, the ANC controls the overall normalization of the channel radiative width and the non-resonant radiative capture amplitude. It underscores the ANC’s important role in analyzing radiative capture reactions.

13.4 Radiative capture reaction ${\mathbf { {}^{11}\textrm{C}(p,\,\gamma ){}^{12}\textrm{N}}}$

As the first example of the application of the indirect ANC method within the framework of the R-matrix formalism we discuss now the radiative capture process $\,{}^{11}\textrm{C}(p,\,\gamma ){}^{12}\textrm{N}.\,$ This reaction depletes ${}^{11}\textrm{C}$ affecting the chain ${}^{11}{C}(\beta ^{+}\,\nu ){}^{11}\textrm{B}(p,\alpha ){}^{8}\textrm{Be}({}^{4}\textrm{He}, {}^{4}\textrm{He})$, which provides an alternative pass to bypass $3\,\alpha$ process (Wiescher et al. [76]).

In the ${}^{11}\textrm{C} (p,\gamma ){}^{12}\textrm{N}$ reaction, direct capture into the ground state of ${}^{12}\textrm{N}$ and resonant capture into the first and second excited states, which are resonances, dominate the reaction rate at stellar energies. The low-lying energy levels of ${}^{12}\textrm{N}$ relevant for the E1 resonant and direct radiative capture process ${}^{11}\textrm{C} (p,\gamma ){}^{12}\textrm{N}$ are shown in Fig. 15.

Fig. 15

Low-lying energy levels of ${}^{12}\textrm{N}$ relevant for the E1 resonant and direct radiative capture processes ${}^{11}\textrm{C}(p,\gamma ){}^{12}\textrm{N}$. The dashed lines leading to the ground state are the E1 transitions. The solid lines leading to the resonances show the proton capture by ${}^{11}\textrm{C}$ populating the resonances ${}^{12}\textrm{N}(2^{+})$ and ${}^{12}\textrm{N}(2^{-})$

The parameters of these resonances are: $J_{1}^{\pi }=2^{+},\,E_{(1)0}=0.359\, \textrm{MeV},\,l_{1}=1$ with the resonance width $\Gamma _{p\,{}^{11}\textrm{C}\,1\,1}^{2}=0.0025$ MeV (here $l_{1}=1,\,s_{1}=1$ and $J_{1}=2$) and $\,J_{2}^{\pi }=2^{-},\,E_{(2)0}=0.589\, \textrm{MeV},\,l_{2}=0$ with $\Gamma _{p\,{}^{11}\textrm{C}\,0\,2}^{2}=0.118\,$ MeV. The third excited state corresponding to the resonance $J_{3}^{\pi }=1^{-},\,E_{(1)0}=1.199\, \textrm{MeV},\,l_{3}=0$ is located to far from the region of the astrophysical interest $E < 0.7$ MeV and its contribution is neglected.

Two proton ANCs of the ground state of ${}^{12}\textrm{N}$ were determined from the ${}^{14}\textrm{N}({}^{11}\textrm{C},\,{}^{12}\textrm{N}){}^{13}\textrm{C}$ peripheral transfer reaction using a 110 MeV ${}^{11}\textrm{C}$ radioactive beam (Tang et al. [77]): $[C_{p\,{}^{11}\textrm{C} 1\,1/2\,1}^{{}^{12}\textrm{N}}]^{2}= 1.4 \pm 0.2$ fm${}^{-1}$ and $[C_{p\,{}^{11}\textrm{C} 1\,3/2\, 1}^{{}^{12}\textrm{N}}]^{2}= 0.33 \pm 0.05$ fm${}^{-1}$, where $l_{f}= 1,\,s_{f}=1/2, 3/2$ and $J_{f}=1^{+}$.

The radiative width for the first resonance was set at $\Gamma _{\gamma \,1}^{2}= 2.6\,$ meV (Lefebvre [78]). The radiative width of the second resonance in ${}^{12}\textrm{N}$ decaying to the ground state has been a controversial subject theoretically. The latest measurement at RIKEN found this width to be $13.06 \pm 0.5$ meV (Minemura et al. [79]). It is informative to see how the measured ANC for ${}^{12}\textrm{N}$ imposes limits on the radiative width of the second resonance with respect to the experimental value. We find that $\Gamma _{\gamma \,J_{f}}^{J_{i}} =54$ meV for $R_{ch}=5.0$ fm. Taking into account the experimental value of the total radiative width, one can find the internal contribution from Eq. (271). There are two solutions, 15 and $112\,$ meV. Assuming that the second value is too high (Descouvemont [80]), we conclude that the internal part of the radiative width is $15\,$ meV, and destructive interference between the real parts of the channel and internal contributions gives the experimental value, $13\,$ meV. In this case, the channel contribution alone represents an upper limit for the radiative width, while the square of the imaginary part of the channel contribution, $1.8\,$ meV, gives a lower limit.

The relative phase between the direct capture amplitude and the channel contribution to the $\gamma$ width of the second resonance is fixed in the R-matrix approach, see Eqs. (287) and (263). Therefore, when the channel contribution to the $\gamma$ width dominates, the sign of the interference effects may be determined unambiguously. For ${}^{11}\textrm{C} (p,\,\gamma ){}^ {12}\textrm{N}$, we find that the nonresonant and resonant capture amplitudes interfere constructively below the resonance and destructively above it.

The summed astrophysical S-factor for interfering nonresonant capture and resonant capture through the broad second excited state was calculated from the measured ANC and the experimental resonance parameters using the R-matrix expressions presented in previous parts.

The total S-factor is

$$\begin{aligned} S_{tot}(E)&= S_{R1}(E) + S_{R2\,NR\,(s_{i}=2)}(E) \nonumber \\&\qquad + S_{NR\,(s_{i}=1)}(E). \end{aligned}$$

(288)

$$\begin{aligned} S_{R1}(E)&= 5\,\pi \,\lambda _{N}^{2}\frac{{{\hat{J}}}_{1}}{ {{\hat{J}}}_{a}\,{{\hat{J}}}_{A} }\,\mu \, m_{au}^{2}\,e^{2\,\pi \,\eta _{i}}\,|\mathcal{T}_{fi}^{R1}|^{2} \end{aligned}$$

(289)

is the S-factor for the capture through the first resonance.

$$\begin{aligned} S_{R2\,NR(s_{i}=2)}(E)= 5\,\pi \,\lambda _{N}^{2}\frac{{{\hat{J}}}_{1}}{ {{\hat{J}}}_{a}\,{{\hat{J}}}_{A} }\,\mu \, m_{au}^{2}\,e^{2\,\pi \,\eta _{i}}\,|\mathcal{T}_{fi}^{R2} + \mathcal{T}_{fi}^{NR}|^{2} \end{aligned}$$

(290)

is the S-factor due to the interference of the amplitude for the resonance capture through the second resonance with the direct (nonresonant) for the channel spin $s_{i}= 2.\,$ The direct capture S-factor $S_{NR\,(s_{i}=1)}(E)$ for the channel spin $s_{i}=1\,$ gives additional contribution.

The calculated S-factors for the ${\mathbf { {}^{11}\textrm{C}(p,\,\gamma ){}^{12}\textrm{N}}}$ radiative capture are shown in Fig. 16.

Fig. 16

$\,S$-factors of the $\,{}^{11}\textrm{C}(p,\,\gamma ){}^{12}\textrm{N}\,$ $\,E1\,$ radiative capture process. The black solid line is the total S-factor $S_{tot}(E).$ Also are shown the S-factors contributed by different transitions: magenta dotted line is the S factor $S_{R1}(E)$ for the capture to the ground state of ${}^{12}\textrm{N}$ through the first resonance $2^{+}$, purple dash-dotted line is the S-factor $S_{R2}(E)$ due to the capture through the second resonance $2^{-}$, blue dash-dotted-dotted line is the S-factor $S_{NR}(E)$ corresponding to the direct (nonresonant) capture, cyan short-dash line is the S-factor $\,S_{R2\,NR(s_{i}=2)}(E)\,$ corresponding to the transition from the second resonance and direct capture for the channel spin $s_{i}=2$ and their interference. First published in Tang et al. [77]

13.5 Radiative capture ${\mathbf { {}^{20}\textrm{Ne}(p,\,\gamma ){}^{21}\textrm{Na}}}$

The ${}^{20}\textrm{Ne}(p, \gamma ){}^{21}\textrm{Na}$ reaction, which is the first reaction of the Ne-Na cycle, is dominated by the capture to the ground state ($J^{\pi } =3/2^{+}, E_{x}= 0.00\,\textrm{MeV}$) through the tail of the subthreshold resonance ($J^{\pi }=1/2^{+},\,=E_{x}=2425\, \textrm{keV},\, \varepsilon = 7.1 \pm 0.6\, \textrm{keV}).\,$ Direct capture to this subthreshold state gives smaller contribution. Direct captures to other bound states are negligible. The overall normalization of the direct captures to the subthreshold state in ${}^{21}\textrm{Na}$ is defined by the corresponding ANC. Simultaneously this ANC determines also the proton partial width of the subthreshold resonance. In order to determine the ANCs for the ground and subthreshold state, the ${}^{20}\textrm{Ne}({}^3\textrm{He, d}){}^{21}\textrm{Na}1/2^{+},\, 2425\, \textrm{keV})$ proton transfer reaction has been measured at an incident energy of 26.3 MeV of $\,{}^{3}\textrm{He}$. The determined the square of the ANC for the ground state is $[C_{p\,{}^{20}\textrm{Ne} 2\,1/2\,3/2}^{{}^{21}\textrm{Na}}]^{2} =0.20$ fm${}^{-1}$ and for the subthreshold state is $[C_{p\,{}^{20}\textrm{Ne} 0\,1/2\,1/2}^{{}^{21}\textrm{Na}}]^{2} =7.36 \times 10^{33}$ fm${}^{-1}.$ The adopted observable subthreshold resonance width for the decay “subthreshold resonance $\rightarrow$ ground state” taken at $E=-0.007$ keV is $0.16 \times 10^{-6}$ eV, which provides the best fit to the experimental data from Rolfs at al. [81].

Figure 17 shows the calculated the astrophysical factor for ${}^{20}\textrm{Ne}(p,\gamma ){}^{21}\textrm{Na}$. This analysis confirms that the resonant capture through the subthreshold state at $-7.1 \pm 0.6$ keV and direct capture to this state give dominant contribution to the low-energy S-factor. The presence of the near-threshold bound state at $E=-0.007$ MeV causes a sharp increase of the S-factor toward $E=0$. Thus, the S-factor behaves like there is a resonance at $E=0$. That is why the subthreshold bound state can be called the subthreshold resonance.

13.6 ${\mathbf { {}^{15}\textrm{N}(p,\,\gamma ){}^{16}\textrm{O} }}$ radiative capture reaction in the ${\textbf{R}}$-matrix approach and the ANC

Another instructive example of the role of the ANC in the analysis of the astrophysical radiative capture is the ${}^{15}\textrm{N} +p \rightarrow {}^{16}\textrm{O} + \gamma \,$ radiative capture process. We also provide a practical guide on how one can analyze radiative capture reactions for two-channel and two-level case in which the interference effects between resonances and direct capture amplitudes ought to be taken into account. The $^{15}\textrm{N}(p,\gamma )^{16}\textrm{O}$ reaction provides the path to form $^{16}\textrm{O}$ in stellar hydrogen burning, thus transforming the CN cycle into the CNO bi-cycle and CNO tri-cycle. In stellar environments, the $^{15}\textrm{N}(p,\gamma )^{16}\textrm{O}$ reaction proceeds at very low energies, where it is dominated by resonant capture to the ground state through the first two interfering $J^{\pi }=1^{-}\,$ $\,s-$wave resonances at $E_{0_{1}}=312$ and $E_{0_{2}}=964$ keV, where $E_{0}$ is the real part of the resonance energy in the c.m. system. There is also a small contribution from the direct capture to the ground state of ${}^{16}\textrm{O}$, which turns out to play an important role due to the interference with the resonant amplitudes. Figure  18 shows the energy levels for the resonant and direct transitions $p+{}^{\textrm{15}}\textrm{N} \rightarrow {}^{16}\textrm{O}$.

Fig. 17

$\,S$-factors of the $\,{}^{20}\textrm{Ne}(p,\,\gamma ){}^{21}\textrm{Na}.\,$ The magenta solid squares and magenta dash-dotted curve are the experimental data points (Rolfs at al. [81]) and our result for direct capture to the subthreshold state, respectively; the cyan solid diamonds and cyan dash curve are the experimental data points (Rolfs at al. [81]) and our result for capture to the ground state through the subthreshold resonance, respectively; the black solid curve is our total astrophysical factor. First published in Mukhamedzhanov et al. [82]

Fig. 18

Low-lying energy levels of ${}^{16}\textrm{O}$ relevant for the E1 resonant and direct radiative capture processes ${}^{15}\textrm{N}(p,\gamma ){}^{16}\textrm{O}$. The dashed lines leading to the ground state are the E1 transitions. The solid lines leading to the resonances show the proton capture by ${}^{15}\textrm{N}$ populating the resonances ${}^{16}\textrm{O}(1^{-})$

The measurement of the ANC for the ${}^{16}\textrm{O} \rightarrow {}^{15}\textrm{N} + p$ using the ${}^{15}\textrm{O}({}^{3}\textrm{He},\,d){}^{16}\textrm{O}$ peripheral transfer reaction induced by the 25.74 MeV ${}^{3}\textrm{He}$ beam was reported by Mukhamedzhanov et al. [83]. This ANC has been used to fix the non-resonant contribution to the $^{15}\textrm{N}(p,\gamma )^{16}\textrm{O}$ capture and it was found that it was impossible to fit the low-energy data from Rolfs and Rodney [84]. Moreover, it was underscored that to fit these experimental data one needs to increase the ANC almost by an order of magnitude. The calculated astrophysical factor using the two-level, two-channel R-matrix approach led to $S(0)= 36.0 \pm 6.0$ keVb, which is significantly smaller than $S(0)=64 \pm 6$ keVb reported by Rolfs and Rodney [84] but in agreement with the older measurements in Hebbard [85]. Correspondingly, it was found that for every $2200 \pm 300$ cycles of the main CN cycle, one CN catalyst is lost due to the $^{15}\textrm{N}(p,\gamma )^{16}\textrm{O}$ reaction, rather than $1200 \pm 100$ cycles determined from experimental data (Rolfs and Rodney [84]). These results were confirmed later by Barker [86]. Two advanced measurements of the astrophysical factor for the $^{15}\textrm{N}(p,\gamma )^{16}\textrm{O}$ were performed at the LUNA underground accelerator facility at the Gran Sasso laboratory (Bemmerer et al. [87, 88]) covering only the low-energy region, $E \le 230$ keV, where E is the relative $\,p-{}^{15}\textrm{N}\,$ energy. Another study of $^{15}\textrm{N}(p,\gamma )^{16}\textrm{O}$, which has been reported in LeBlanc et al. [89], was performed over a wide energy range at the Notre Dame Nuclear Science Laboratory (NSL) and the LUNA II facility. The obtained $S(0)= 39.6 \pm 2.6$ keVb is in a perfect agreement with the prediction $S(0)=36.0 \pm 6.0$ keVb (Mukhamedzhanov et al. [83]) obtained using the R-matrix fit and the indirect ANC method. In the case under consideration, in the R-matrix approach the ANC determines the overall normalization of the non-resonant radiative capture amplitude and the channel (external) part of the radiative width amplitudes of the both resonances involved. These amplitudes are small and any sizable impact on the astrophysical factor can be achieved only by a significant variation of the ANC. Note that the contribution of the non-resonant amplitude increases toward low energies, which is the region of the astrophysical interest.

The expression for the astrophysical factor in the R-matrix method for the case under consideration can be written as (Barker and Kajino [22], Lane and Thomas [18]):

$$\begin{aligned} S(E)(keVb)&= \frac{\pi \,\lambda _{N}^{2}}{2}\,\frac{ {{\hat{J}}}_{i} }{ {{\hat{J}}}_{x}\,{{\hat{J}}}_{A} }\,\frac{m_{au}^{2}}{\mu }\,e^{2\,\pi \,\eta _{aA}}\,10\,\Big |[ e^{-i(\delta _{l_{i}}^{hs} - \sigma _{l_{i}}^{C}) } \nonumber \\&\quad \times \sum \limits _{\nu ,\tau = 1,2} (\gamma _{\nu \,\gamma \, \,J_{f}(int)}^{J_{R}} \pm \gamma _{\nu \,\gamma \,J_{f}(ext)}^{J_{i}}(E) )\,\nonumber \\&\quad \big [{\mathcal{A}}^{-1}\big ]_{\nu \tau }\,\gamma _{aA\,\tau \,l_{i}s_{i}J_{i}}(E) \nonumber \\&\quad + \,\, \mathcal{T}_{ fi}^{NR}(E) + \,U_{BG}(E)]\Big |^{2}, \end{aligned}$$

(291)

where $a=p,\,$ $\,A={}^{15}\textrm{N}$, $\,B={}^{16}\textrm{O},\,$ $\mu =\mu _{aA},\,$ $\,\nu ,\,\tau =1,2$ are coupled levels, $\,J_{a}=J_{A}=1/2,\,$ $\,J_{i}=J_{R}=1\,$ is the spin of the resonance. The channel spin of the resonance $\,s_{i}=s_{R}= s_{f}=1,\,$ $l_{i}=l_{R}=0$. In the channel $p+{}^{15}\textrm{N}$ for the ground state of $\,{}^{16}\textrm{O}\,$ we have $l_{f}=1,\,J_{f}=0$. The same quantum numbers are assigned for the direct E1 transition to the ground state, which interferes with the resonant E1 transition. $\,\mathcal{T}_{ fi}^{NR}(E)\,$ is the non-resonant transition R-matrix amplitude, see Eq. (287), and $\mathcal{T}_{fi}^{BG}(E)$ is the R-matrix amplitude of the background resonance.

13.7 ANC in R-matrix paradigm

Nuclear data are important input into nuclear astrophysics. When resonances contribute the analysis of the data usually are being done within the R-matrix approach. The R-matrix analysis includes fitting parameters, like particle and radiative reduced widths, resonance energies, channel radii and boundary conditions. Besides, often non-resonant processes also contribute to the reaction mechanism. For example, the radiative capture amplitude in the R-matrix approach consists of three terms: the internal resonance amplitude, which describes the radiative capture as the process in which the incident particle penetrates through the barrier into the internal region of a target, from which radiative decay to lower lying levels occurs; the external resonance amplitude describing the formation of the resonance in the external region of target with subsequent $\gamma$ decay and the non-resonant direct capture amplitude, which describes the transition from the initial continuum to a bound state by emitting $\gamma$ without the formation of the resonance. This non-resonant term in the R-matrix approach is contributed only by the matrix element in the external region, i.e. at distances larger than the channel radius, because the internal part of the non-resonant amplitude is included into the internal resonance amplitude. The normalization of the last two amplitudes is governed by the ANC. Thus the presence of the external resonant and non-resonant direct radiative captures adds an additional parameter into the R-matrix fit. Definitely the most reliable information can be obtained if one performs simultaneous R-matrix fit in all the open channels or uses available information, which has been obtained from other open channels analysis. This information allows us to fix or constrain reduced widths in some open channels. Since the ANCs in many cases are available from independent experimental data or theoretical calculations, it is always important to fix or significantly constrain the variation of the ANC. As a practical application of the procedures described above we analyze the astrophysical $^{15}\textrm{N}(p,\gamma )^{16}\textrm{O}$ reaction.

13.7.1 Unconstrained fits to all the data points

Now we perform two unconstrained fits A(113) to the Notre Dame-LUNA data (LeBlanc et al. [89]) adding a background resonance. All the parameters except for the ANC, channel radii and the background resonance energy are allowed to vary. To determine the resonance parameters, the fits are performed with two boundary conditions. First, we have searched for the best fit for the boundary condition $\,B_{c}=S_{c}(E_{2})$, where $\,E_{2}$ is the energy of the second level, which is taken to be equal to the second resonance energy $E_{2}= E_{0_{2}}=0.956$ MeV while the first level is varied to get the best fit. We find the best fit at $E_{1}=0.1662$ MeV. The energy of the included background resonance is 5.07 MeV, the proton reduced width amplitude of the background resonance is $\gamma _{p(BG)}= -0.3$ MeV${}^{1/2}$ and the $\alpha$ reduced width amplitude $\gamma _{\alpha (BG)}= 0.07$ MeV${}^{1/2}$. In the fit A(113) the search for the best fitting has been performed using unconstrained variation of other parameters. After that we can find the observable partial resonance widths for level $\nu =2$ and channel c using the standard R-matrix equation

$$\begin{aligned} \Gamma _{\nu \, c}= \frac{2\,\gamma _{\nu \, c}^{2}\,P_{c}(E_{{0_{\nu }}})}{1+ \sum \nolimits _{c' = p,\alpha } {\gamma _{\nu \, c'}^2\,\frac{{d{S_{c'}}}}{{dE}}{|_{E = {E_{{0_{\nu }}}}}}}}. \end{aligned}$$

(292)

Here $E_{0_{\nu }}$ is the real part of the resonance energy of the level $\nu$.

In the second unconstrained fit A(113), we have searched for the best fit with the boundary condition $\,B_{c}=S_{c}(E_{1})$, where the energy of the first level $E_{1}$ is near the first resonance at $E_{0_{1}}=0.3104$ MeV adopted in LeBlanc et al. [89] while the second level is varied to get the best fit. For this boundary condition we find the best fit at $E_{1}=0.30872$ MeV and $E_{2}= 1.0576$ MeV. To get the observable widths we use Eq. (292). In Fig. 19 we demonstrate the astrophysical factors S(E) obtained from these two unconstrained A(113) fits with the background resonance included. The red solid line is the fit corresponding to the boundary condition at $E_{2}= 0.956$ MeV with the normalized ${{{\tilde{\chi }}}}^{2}= 1.84$. For the fit A(113) with the boundary condition at $E_{1}=0.30872$, the blue dotted-dashed line, we obtain ${{{\tilde{\chi }}}}^{2}= 1.76$ with $S(0)=37.2$ keVb. This fit goes slightly lower than the red line at low energies better reproducing the low-energy trend of the data. The magenta solid line represents the non-resonant S(E) factor for the ANC $C_{p\,{}^{15}\textrm{N}}^{{}^{16}\textrm{O}}=14.154$ fm${}^{-1/2}$ which has been used for both fits. Thus adopting a physical ANC we correctly fix the normalization of the external direct capture amplitude and the channel radiative width amplitude, and adding the background pole we are able to get a perfect fit.

Fig. 19

The astrophysical S(E) factor for the $^{15}\textrm{N}(p,\gamma )^{16}\textrm{O}$ reaction. The black squares are experimental data from Ref. [89]. The red solid line is our unconstrained R-matrix fit A(113) with the boundary condition $B_{c}=S_{c}(E_{2})$, which takes into account four interfering amplitudes: two $1^{-}$ resonances at $E_{0_{1}}=312$ and $E_{0_{2}}=964$ keV, a nonresonant term, and background resonance at $E_{ 0_{(BG)} }=5.07$ MeV. The blue dotted-dashed line is our unconstrained R-matrix fit A(113) similar to the previous one but with the boundary condition $B_{c}=S_{c}(E_{1})$. The magenta solid line is the non-resonant S(E) factor for the ANC$\,\,C_{p\,{}^{15}\textrm{N}}^{{}^{16}\textrm{O}}=14.154$ fm${}^{-1/2}$. From Mukhamedzhanov et al. [74]

The added background resonance interferes with resonant and non-resonant terms and takes effectively into account the cumulative contributions from distant $1^{-}$ levels. It is demonstrated how thorough R-matrix analysis should be done applying the procedures used by Barker [86].

13.7.2 Constrained fits to all data points

Now we discuss two constrained fits B(113). The goal of these fits is to demonstrate that fixing some parameters at values obtained from previous works, we still can get as good fits as unconstrained ones but with better physical parameters.

In the constrained fits B(113) the procedure is the same as described before for the unconstrained fits. In these fits, in addition to the fixed channel radii in the proton and $\alpha$ channels, $R_{(ch(p))} = 5.03$ fm and $R_{(ch(\alpha ))}= 7.0$ fm, the ANC $C_{p\,{}^{15}\textrm{N}}^{{}^{16}\textrm{O}}=14.154$ fm${}^{-1/2}$ and the background resonance energy $E_{R_{BG}}= 5.07$ MeV, we also fix $\gamma _{\nu \, c}$, $\,c=p,\,\alpha$, when the boundary condition is chosen near the resonance energy $E_{R_{\nu }}$. These reduced widths are taken from the analysis of the direct ${}^{15}\textrm{N}(p,\alpha ){}^{12}\textrm{C}$ data (Rolfs and Rodney [84], Barker [86]), and indirect Trojan Horse data (La Cognata et al. [90]). First, we adopt the boundary condition near the second resonance at $E_{2}= 0.956$ MeV with the energy of the first level $E_{1}= 0.170$ MeV. For the best fit we get ${{{\tilde{\chi }}}}^{2}=1.93$ and $S(0)=38.8$ keVb. The radiative width for the background pole is found to be $\Gamma _{\gamma (BG)}=129.3$ eV.

To determine the parameters for the first resonance we use the boundary condition $B_{c}=S_{c}(E_{1})$ near the first resonance $E_{1}=0.30872$ MeV and found from the fit the second energy level $E_{2}=1.0576$ MeV. The rest is the same as in fit A(113). The radiative width for the background resonance is $\Gamma _{\gamma (BG)}=283.1$ eV. For the best constrained fit with the boundary at the first resonance we get $S(0)=37.2$ keVb with ${{{\tilde{\chi }}}}^{2}=1.74$. We note that the total $\chi ^{2}$ for the unconstrained fit A(113) with the boundary condition $B_{c}=S_{c}(E_{1})$ is slightly smaller than for the corresponding constrained fit B(113). However, because for the constrained fit the number of the fitting parameters are smaller than for the unconstrained one the normalized ${{{\tilde{\chi }}}}^{2}$ for the constrained fit is slightly smaller than for the unconstrained.

In Fig. 20 the S(E) factors are shown for both constrained fits B(113). The constrained fits B(113) have parameters which better agree with the previous estimations (Barker [86]) than unconstrained fits A(113).

Fig. 20

The astrophysical S(E) factor for the $^{15}\textrm{N}(p,\gamma )^{16}\textrm{O}$. The red solid line is the constrained fit B(113) with the boundary condition $B_{c}=S_{c}(E_{2}=0.956\, \textrm{MeV})$, the blue dotted-dashed line is the constrained fit B(113) with the boundary condition $B_{c}=S_{c}(E_{1}= 0.30872\, \textrm{MeV})$. The black squares are experimental data from LeBlanc et al. [89]. The ANC is $C=14.154$ fm${}^{-1/2}$. From Mukhamedzhanov et al. [74]

Appendices

Appendices

Appendix A: Rigged Hilbert space

A rigged Hilbert space is the so-called Gel’fand triplet (Gelfand and Vilenkin [15], Maurin [16])

$$\begin{aligned} \mathcal{{{\textbf{G}}}} \subset \mathcal{H}=\mathcal{H}^{\dagger } \subset \mathcal{{{\textbf{G}}}} ^{\dagger }. \end{aligned}$$

(A.1)

Here $\mathcal{H}$ is the completion of a linear space ${\mathbf \Psi }$ with a norm defined as a scalar product. Completed linear space $\,\mathcal{H}\,$ means that the Cauchy sequences converge in the norm topology. A linear space $\mathcal{{{\textbf{G}}}}$ is the completion of $\,{\mathbf \Psi }\,$ in the topology stronger than the norm topology, that is, $\mathcal{{{\textbf{G}}}}$ is dense in $\,\mathcal{H}.\,$ In other words, it means that every point of $\mathcal{H}$ either belongs to $\mathcal{{{\textbf{G}}}}$ or is a limit point of $\mathcal{{{\textbf{G}}}}$. The topology of the space $\mathcal{{{\textbf{G}}}}$ is more stronger then the norm topology because the operators corresponding to the observables are continuous while in the norm topology of $\mathcal{H}$ are not necessarily continuous. Thus $\mathcal{{{\textbf{G}}}}$ is a subspace of $\mathcal{H}$. $\mathcal{H}^{\dagger }$ and $\,\mathcal{{{\textbf{G}}}} ^{\dagger }$ are spaces of antilinear functionals over the spaces $\mathcal{{{\textbf{G}}}}$ and $\mathcal{H}$. While $\mathcal{H}= \mathcal{H}^{\dagger }$ the space $\,\mathcal{{{\textbf{G}}}} ^{\dagger }\,$ contains eigenvalues belonging to the continuous spectrum and complex eigenvalues. Adding $\mathcal{{{\textbf{G}}}} ^{\dagger }$ allows us to deal with resonances. Gamow–Siegert states, which represent the generalized eigenvectors with the complex eigenvalues $E_{R}= E_{0}- i\,\Gamma /2$, do not belong to the Hilbert state $\mathcal{H}$. They describe decaying (irreversable) states in the time-dependent formalism and contain diverging asymptotic in the coordinate space and, hence, do not belong to the norm topology. The norm definition of the Gamow–Siegert eigenfunctions reguires a generalization. In a nutshell, to determine the norm of such vectors we need to introduce a regulator. The proof that such generalized norms can be defined for potentials with the Coulomb tail is given in Sect. 2.3.

Appendix B: Normallization of Gamow–Siegert wave functions

We prove here that Zel’dovich regularization procedure permits us to normalize the Gamow–Siegert resonance wave functions for Coulomb plus nuclear potentials:

$$\begin{aligned} \mathcal{I}_{0}^{\infty }=\lim \limits _{\beta \rightarrow +0}\int _{0}^{\infty }\,\textrm{d}r\,e^{-\beta \,r^{2} }\, [{{{\tilde{\varphi }}}}_{l}^{GS}(k,r)]^{*}\,\varphi _{l}^{GS}(k,\,r) =1. \end{aligned}$$

(B.1)

Note that

$$\begin{aligned} \mathcal{I}_{0}^{R}(\beta ,\,r) =\int _{0}^{R}\,\textrm{d}r\, e^{-\beta \,r^{2} }\, [{{{\tilde{\varphi }}}}_{l}^{GS}(k,r)]^{*}\,\varphi _{l}^{GS}(k,\,r) \end{aligned}$$

(B.2)

converges for any $R < \infty$.

It is important to show that the integral

$$\begin{aligned} \mathcal{I}_{R}^{\infty }(\beta ,\,\,r) =\int _{R}^{\infty }\,\textrm{d}r\, e^{-\beta \,r^{2} }\, [{{{\tilde{\varphi }}}}_{l}^{GS}(k,r)]^{*}\,\varphi _{l}^{GS}(k,\,r) \end{aligned}$$

(B.3)

converges for $\beta \rightarrow +0$.

The introduction of the regularization factor $\exp (-\beta \,r^{2})$ is necessary to provide the convergence of the normalization integral for $r \rightarrow \infty$ which otherwise diverges because $\exp (i\,k_{R}\,r)= \exp (i\,k_{0}\,r + k_{I}\,r)$. We split the integral (B.1) into two parts:

$$\begin{aligned} \mathcal{I}_{0}^{\infty }&= \int \limits _{0}^{R} \textrm{d}r\,\varphi _{l}^{GS}(r)\,[{{{\tilde{\varphi }}}}_{l}^{GS}(r)]^{*} \nonumber \\&\quad +C_{l}^{2}\,e^{- \pi \,\eta _{R}}\,\mathop {\lim }\limits _{\beta \rightarrow +0}\, \int \limits _{R}^{\infty } \textrm{d}r\,\frac{e^{i\,2\,k_{R}\,r}}{(2\,k_{R}\,r)^{i\,2\,\eta _{R}}}\,e^{-\beta \,r^{2}}. \end{aligned}$$

(B.4)

R is assumed to be large enough to approximate the Gamow–Siegert wave function by its leading asymptotic term (18) at $r > R$.

The integral over a finite interval $r \le R$ converges, and in this integral, we can take limit $\beta \rightarrow +0$. We must prove that the second integral can also be determined in the limit $\beta \rightarrow +0$. Taking into account that

$$\begin{aligned} \eta _{R}= \frac{\alpha }{k_{R}}= \frac{\alpha }{(k_{0})^{2}+(k_{I})^{2}}(k_{0} + i\,k_{I})= \lambda + i\,\delta , \end{aligned}$$

(B.5)

where $\alpha = Z_{a}\,Z_{A}\,e^{2}\,\mu$, and $\lambda ,\,\delta > 0$, we get

$$\begin{aligned} \mathcal{I}_{R}^{\infty }&=C_{l}^{2}\,\frac{e^{- \pi \,\eta _{R}}}{(2\,k_{R})^{i\,2\,\eta _{R}}}\,\mathop {\lim }\limits _{\beta \rightarrow +0}\, \int \limits _{R}^{\infty } \textrm{d}r\,\frac{e^{i\,2\,k_{R}\,r}}{r^{i\,2\,\eta _{R}}}\,e^{-\beta \,r^{2}} \nonumber \\&= C_{l}^{2}\,\frac{e^{- \pi \,\eta _{R}}}{(2\,k_{R})^{i\,2\,\eta _{R}}}\,\mathop {\lim }\limits _{\beta \rightarrow +0}\, \int \limits _{R}^{\infty } \textrm{d}r\,e^{i\,2\,k_{0}\,r}\, e^{2\,k_{I}\,r}\,r^{-2\,i\,\lambda } \nonumber \\&\quad \times r^{2\,\delta }\,e^{-\beta \,r^{2}}. \end{aligned}$$

(B.6)

For neutral particles there is only one exponentially diverging factor $e^{2\,k_{I}\,r}$ (for $r \rightarrow \infty$) in the integrand. Zel’dovich’s normalization procedure works for $k_{0} > k_{I}$. The presence of the oscillating exponential factor $\exp (i\,2\,k_{0}\,r)$ is crucial for Zel’dovich’s regularization. However, for charged particles at complex momentum k we have an additional diverging factor in the integrand, $r^{2\,\delta }$. We will show now that Zel’dovich’s method also works for the charged particles. To this end, one can rewrite Eq. (B.6) as the sum of two terms:

$$\begin{aligned} \mathcal{I}_{R}^{\infty }&=- C_{l}^{2}\,\frac{e^{- \pi \,\eta _{R}}}{(2\,k_{R})^{i\,2\,\eta _{R}}}\,\mathop {\lim }\limits _{\beta \rightarrow +0}\, \int \limits _{0}^{R} \textrm{d}r\,e^{i\,2\,k_{0}\,r}\, e^{2\,k_{I}\,r}\,r^{-2\,i\,\lambda } \nonumber \\&\quad \times r^{2\,\delta }\,e^{-\beta \,r^{2}} +C_{l}^{2}\,\frac{e^{- \pi \,\eta _{R}}}{(2\,k_{R})^{i\,2\,\eta _{R}}}\,\mathop {\lim }\limits _{\beta \rightarrow +0}\, \int \limits _{0}^{\infty } \textrm{d}r\,e^{i\,2\,k_{0}\,r}\, e^{2\,k_{I}\,r} \nonumber \\&\quad \times r^{-2\,i\,\lambda }\,r^{2\,\delta }\,e^{-\beta \,r^{2}}. \end{aligned}$$

(B.7)

The first term in this equation converges, and we can take the limit $\beta \rightarrow +0$ in this term. It is enough to consider the second term only. For $\textrm{Re}k_{R}^{2} >0$

$$\begin{aligned}&\mathop {\lim }\limits _{\beta \rightarrow +0}\, \int \limits _{0}^{\infty } \textrm{d}r\,e^{i\,2\,k_{R}\,r}\,r^{-2\,i\,\eta _{R}}\,e^{-\beta \,r^{2}}\nonumber \\&\quad = \mathop {\lim }\limits _{\beta \rightarrow +0}\,(2\beta )^{\frac{{2\,i\,\eta _{R} - 1}}{2}}\,\Gamma ( - 2\,i\,\eta _{R} + 1)\,e^{ - \frac{k_{R}^2}{2\beta }}\, D_{2\,i\,\eta _{R} - 1} (-\frac{2\,i\,k_{R}}{\sqrt{2\beta }}) \nonumber \\&\quad =\Gamma ( - 2\,i\,\eta _{R} + 1)( - i\,2\,k_{R})^{2\,i\,\eta _{R} - 1}. \end{aligned}$$

(B.8)

Thus, we have shown that Zel’dovich’s regularization can be used to determine the norm of the Gamow–Siegert wave functions for charged particles. Zel’dovich’s regularization method is not unique, and other regularization techniques can be used. In particular, more general exponential regulator $exp(-\beta \,r^{n}),\;n>2,$ can be used. It will allow one to include more resonances. Gamow–Siegert wave functions can also be normalized using the so-called complex scaling method (CSM).

Appendix C: Complex scaling method

Gamow–Siegert wave functions have another important advantage. Since asymptotically, they have only outgoing waves, we can use the complex scaling method (CSM) (Aguilar and Combes [91], Balslev and Combes [92], Simon [93, 94]). Note that this method is not applicable if the asymptotic wave function contains both incident and outgoing waves. We briefly discuss the CSM considering the two-body case. CSM (also called the complex-coordinate-rotation method) is based on the rotation of the radial coordinate in the complex r plane making a diverging radial wave function square integrable eigenfunction of the complex-scaled Hamiltonian.

This method consists of solving the Schrödinger equation on a ray in the first quadrant of the radial complex plane rather than on the real axis of the coordinate r. The axis rotation angle $\theta$ (if we neglect the potential singularities) is limited by the angle defined by the resonance parameters, see below. It is important that the CSM can be applied to the case of charged particles. This is true only for the point-like Coulomb-potential, which behaves like 1/r or for the Coulomb potential of a diffuse sphere. An application of this method to resonances in nuclear reactions was presented by Gyarmati and Kruppa [95]. The numerical realization of this method is a rather complex one.

Let us consider the coordinate rotation operator (known also as complex scaling operator)

$$\begin{aligned} {{\hat{U}}}= e^{i\,\theta \,r\frac{\partial }{{\partial r}}}. \end{aligned}$$

(C.1)

Then

$$\begin{aligned} {{\hat{U}}}f_{l}(k_{R},r)= f_{l}(k_{R},r\,e^{i\,\theta }) \end{aligned}$$

(C.2)

and

$$\begin{aligned} {{\hat{U}}}f_{l}(k_{R},r) {\mathop {\approx }\limits ^{r \rightarrow \infty }} e^{i[k_{R}\,r\,e^{i\,\theta _{R}} -\eta _{R}\,\ln (2\,k_{R}\,r\,e^{i\,\theta })]}. \end{aligned}$$

(C.3)

Let k be the resonance momentum

$$\begin{aligned} k=k_{R}=\sqrt{2\,\mu (E_{0} - i\Gamma /2)} =\sqrt{ 2\,\mu \,(E_{0}^{2} +\Gamma ^{2}/4)^{1/2} }\,e^{-i\,\nu }, \end{aligned}$$

(C.4)

where $\nu = (1/2)\arctan (\frac{\Gamma }{2\,E_{0}})$ is the phase of $k_{R}$. We have

$$\begin{aligned} k_{R}\,r\,e^{i\,\theta }= |k_{R}|\,r\,e^{i[\theta -\nu ]} \end{aligned}$$

(C.5)

and

$$\begin{aligned} e^{i\,k_{R}\,r\,e^{i\,\theta }}= e^{i\,|k_{R}|\,r\,cos[\theta -\nu ]} \,e^{-|k_{R}|\,r\,sin[\theta -\nu ]}. \end{aligned}$$

(C.6)

Thus the critical angle of the radius rotation is $\theta _{cr}= \nu = 1/2\arctan (\frac{\Gamma }{2\,E_{0}})$. For $\theta > \theta _{cr},\,$ the exponential term $\,\,e^{-|k_{R}|\,r\,sin[\theta -\nu ]}\,$ vanishes at $r \rightarrow \infty$.

The term $e^{-i\eta _{R}\,\ln (2\,k_{R}\,r\,e^{i\,\theta })}$, which represents the Coulomb correction to the asymptotic outgoing wave, can be reduced to

$$\begin{aligned} e^{-i\eta _{R}\,\ln (2\,k_{R}\,r\,e^{i\,\theta })} = e^{-i\eta _{R}\,\ln (2\,|k_{R}|\,r)}\,e^{\eta _{R}\,[\theta -\theta _{cr}]}. \end{aligned}$$

(C.7)

Hence the rotation of the radius in the complex plane generates in the Coulomb term $e^{-i\eta _{R}\,\ln (2\,k_{R}\,r\,e^{i\,\theta })}$ a constant factor $e^{\eta _{R}\,[\theta -\theta _{cr}]}.\,$ Hence we achieved what sought:

$$\begin{aligned} \lim \limits _{r \rightarrow \infty }{{\hat{U}}}f_{l}(k_{R},r) =0. \end{aligned}$$

(C.8)

The asymptotic convergence of the complex-scaled outgoing waves allows one to normalize the Gamow–Siegert resonance wave function but we are not going into more detail about that.