On the stability of superheavy nuclei

Abstract

Potential energy surfaces of even–even superheavy nuclei are evaluated within the macroscopic-microscopic approximation. A very rapidly converging analytical Fourier-type shape parametrization is used to describe nuclear shapes throughout the periodic table, including those of fissioning nuclei. The Lublin Strasbourg Drop and another effective liquid-drop type mass formula are used to determine the macroscopic part of nuclear energy. The Yukawa-folded single-particle potential, the Strutinsky shell-correction method, and the BCS approximation for including pairing correlations are used to obtain microscopic energy corrections. The evaluated nuclear binding energies, fission-barrier heights, and $Q_\alpha$ energies show a relatively good agreement with the experimental data. A simple one-dimensional WKB model à la Świa̧tecki is used to estimate spontaneous fission lifetimes, while $\alpha$ decay probabilities are obtained within a Gamow-type model.

1 Introduction

Superheavy nuclei (SHN) have been a challenge for nuclear physicists, both theoreticians and experimentalists, for the last five or six decades, but speculations about their existence go back to the end of the 19th and the beginning of the 20th century [1, 2]. An extensive review of the properties of these nuclei, including the papers dealing with this subject can be found in Ref. [3] and many other review papers as e.g. [4,5,6], which allow us to avoid giving a long list of theoretical and experimental papers related to SHN. We shall instead concentrate on the problem of extrapolating what we know from lighter nuclei to the region of superheavy elements. We would like, in particular, to demonstrate that a reliable prediction of nuclear ground-state masses is crucial for a dependable description of spontaneous fission and $\alpha$-decay probabilities. All calculations reported in this paper are based on the macroscopic-microscopic(macro-micro) model [7], and we show how using different modern liquid-drop (LD) type models impacts on our predictions of masses and fission barrier heights of the SHN. An analysis of the single-particle spectra obtained in different mean-field and self-consistent calculations shows that the magic numbers predicted for the region of SHN are very contingent on the model used. To take into account the degeneracy of single-particle levels turns out to be essential, when analyzing nuclear spectra. We will show that the nuclear shell-correction energy is, in this respect, a much better-suited tool to find the magic numbers in a given region of nuclei.

Our paper is organized as follows. The Fourier shape parametrization [8] that has been shown [9, 10] to provide an excellent description of the shape of nuclei throughout the nuclear chart, including the very elongated and necked-in forms that appear in very heavy fissile nuclei, is presented in some detail in Sect. 2. Section 3 introduces two models, namely the well known Lublin-Strasbourg Drop (LSD) [11] and one of the drop models presented in 2006 by Moretto et al. [12], to describe the macroscopic nuclear energy. The potential energy surfaces (PES) of the SHN are evaluated including the microscopic shell and pairing energy corrections. The analysis of the PES’s allows to determine the fission barrier heights and $Q_\alpha$ energy values which we present in Sect. 4. Spontaneous fission lifetimes as obtained in a simple WKB type model are compared in Sect. 5 with the available experimental data, while $\alpha$-decay lifetimes evaluated in a Gamow-type model are presented in Sect. 6. Section 7 finally gives some conclusions and outlooks.

2 Fourier shape parametrization

A proper low-dimensional description of the shape of a nucleus that can undergo fission is probably one of the most challenging tasks with which nuclear physicists have been confronted since the early paper of Bohr and Wheeler [13] on nuclear fission theory. Many different parametrizations have been proposed to describe the shapes of deformed nuclei (see Ref. [14] for an extensive review of frequently used parametrizations). In the present paper, we are using a straightforward and rapidly convergent Fourier type parametrization as first presented in Refs. [8, 9].

Fig. 1

Shape of a very elongated fissioning nucleus

A typical shape of a strongly elongated nucleus is shown in Fig. 1, where the distance $\rho _s(z)$ from the z-axis to its surface is displayed as a function of the z coordinate, while the dashed line shows a spheroid having the same length and volume. We assume that for axially symmetric shapes the function $\rho _s(z)$ is described by the following Fourier series:

$$\begin{aligned} \rho _s^2(z)= & {} R_0^2\! \sum \limits _{n=1}^\infty \left[ a_{2n} \cos \left( \frac{(2n-1) \pi }{2} \, \frac{z-z_{sh}}{z_0}\right) \right. \nonumber \\&+\left. a_{2n+1} \sin \left( \frac{2 n \pi }{2} \, \frac{z-z_{sh}}{z_0}\right) \right] ~, \end{aligned}$$

(1)

where the expansion coefficients $a_\nu$ are treated as free deformation parameters. The half-length $z_0$ of the shape is evaluated from the $a_\nu$ parameters imposing the condition that the volume of the nuclear shape needs to be conserved, while $z_{\mathrm{sh}}$ ensures that the center of mass of the deformed nucleus is located at the origin of the coordinate system, with $R_0$ being the radius of the spherical nucleus having the same volume.

Non-axial shapes can easily be taken into account by assuming that the cross-section of the nuclear surface perpendicular to the z-axis has the form of an ellipse with half-axis a and b. One can then define a non-axiality deformation parameter $\eta$ as:

$$\begin{aligned} \eta =\frac{b-a}{a+b}~. \end{aligned}$$

(2)

In the case of a non-axial nuclear shape the volume conservation condition implies that $\rho _s^2(z)=a(z)b(z)$. The following equation then gives the non-axial shape:

$$\begin{aligned} \varrho ^2(z,\varphi ) = \rho ^2_s(z) \, \frac{1-\eta ^2}{1+\eta ^2+2\eta \cos (2\varphi )}~, \end{aligned}$$

(3)

where one assumes that the non-axiality parameter $\eta$ is independent on z. The rapid convergence of the Fourier parametrization (1) for any realistic nuclear shape is striking, as has been demonstrated in Ref.  [9].

In practical calculations, instead of the $a_\nu$ deformation parameters, it is more convenient to use the following combinations:

$$\begin{aligned} \begin{array}{l} q_2 =a_2^{(0)}/a_2 - a_2/a_2^{(0)} ,\\ q_3=a_3 ,\\ q_4=a_4+\sqrt{(q_2/9)^2+(a_4^{(0)})^2} ,\\ q_5=a_5-(q_2-2)a_3/10 , \\ q_6=a_6-\sqrt{(q_2/100)^2+(a_6^{(0)})^2} , \end{array} \end{aligned}$$

(4)

where the $a_{2n}^{(0)}=(-1)^{n-1}32/[\pi (2n-1)]^3$ are the Fourier expansion coefficients of a sphere. The new $q_\nu$ deformation parameters have the following physical interpretation:

$\star \;$ $q_2$ : elongation of the nucleus,

$\star \;$ $q_3$ : left-right asymmetry,

$\star \;$ $q_4$ : neck formation,

$\star \;$ $q_5$ and $q_6$ regulate the deformation of fission fragments.

These parameters were chosen in such a way that the liquid-drop path to fission corresponds approximately to $q_3=q_4=q_5=q_6=0$ and the spherical shape is obtained when all $q_\nu$ vanish.

3 Total nuclear energy

We have performed calculations using the macro-micro model approach of the total nuclear energy [15]:

$$\begin{aligned} E_{\mathrm{tot}} = E_{\mathrm{mac}}+ E_{\mathrm{shell}}^\mathrm{p} + E_{\mathrm{shell}}^\mathrm{n} + E_{\mathrm{pair}}^\mathrm{p} + E_{\mathrm{pair}}^\mathrm{n}~, \end{aligned}$$

(5)

where $E_{\mathrm{mac}}$ is the macroscopic part of the energy, while $E_{\mathrm{shell}}$ and $E_{\mathrm{pair}}$ describe the microscopic shell and pairing energy corrections for protons and neutrons.

3.1 Liquid-drop type mass formula

In what follows, two types of macroscopic models have been used: the Lublin-Strasbourg Drop (LSD) [11] which has been shown to represent one of the most performant liquid-drop type models on the one hand, and one of the five LD formulas proposed in 2012 by Moretto et al. [12], namely the version (i) which has, contrary to most existing LD formulas, the same isospin-square dependence of the volume and surface terms and does not contain any curvature contribution. Both these modern versions of the nuclear LD model which have the particularity to reproduce rather well not only nuclear masses but also the fission-barrier heights in the actinide region [16], will allow us to compare their extrapolations from the known nuclear region to one of the superheavy nuclei.

The LSD model [11] contains, in addition to the traditional volume, surface, and Coulomb terms, a curvature and a congruence (Wigner) energy term

$$\begin{aligned} M_{\mathrm{LSD}}(Z,N;q_i)= & {} Z M_{\mathrm{H}} + N M_{\mathrm{n}} - b_{\mathrm{elec}} \, Z^{2.39} \nonumber \\[1.2ex]&+\, b_{\mathrm{vol}}\;\,(1 - \kappa _{\mathrm{vol}} \; I^2\,)\,A \nonumber \\&{ +\, b_{\mathrm{surf}}\,(1 - \kappa _{\mathrm{surf}} I^2\,)\,A^{2/3} B_{\mathrm{surf}}(q_i) } \nonumber \\&+\, b_{\mathrm{cur}}\;\,(1 - \kappa _{\mathrm{cur}} \; I^2\,)\,A^{1/3} B_{\mathrm{cur}}(q_i) \nonumber \\&{ +\, \frac{3}{5} \, \frac{e^2Z^2}{r_0^\mathrm{ch} A^{1/3}}\, B_{\mathrm{Coul}}(q_i)} -\, C_{4}\,\frac{Z^2}{A} \nonumber \\&+ E_{\mathrm{cong}}(Z,N) + E_{\mathrm{odd}} \nonumber \\&+ E_{\mathrm{micr}}(Z,N;q_i)~. \end{aligned}$$

(6)

Here the nuclear deformation is identified by the parameter set $\{q_i\}$ in (4), $I=(N-Z)/A\;$ is the reduced isospin, and $M_{\mathrm{n}}$ and $M_\mathrm{H}$ are respectively the masses of the neutron and the hydrogen atom. The coefficient of the electron-shell binding energy is $b_\mathrm{elec}= 0.00001433\;$MeV, and the odd–even term $E_{\mathrm{odd}}$ and the congruence (Wigner) energy, given as $E_{\mathrm{cong}}(Z,N)=10\exp (-4.2\,|I|)$ MeV, are taken from Ref. [17]. The ground-state microscopic-energy corrections $E_\mathrm{micr}(Z,N;q_i)$ are finally taken from the tables presented by Möller at al. in Ref. [18]. The remaining LD parameters of the LSD mass formula have been adjusted to obtain the best possible fit of the 2766 nuclear masses with Z$\ge$8 and N$\ge$8, experimentally known by the time of the mass fit of Ref. [11].

The LD type formulae [12] of Moretto and coworkers have the following form:

$$\begin{aligned}&M_{\mathrm{MLD}}(Z,N;q_i) = Z M_{\mathrm{H}} + N M_{\mathrm{n}}\nonumber \\&\quad +\left[ b_{\mathrm{vol}}A+a_{\mathrm{surf}}A^{2/3}B_{\mathrm{surf}}(q_i) +a_{\mathrm{cur}}A^{1/3}B_{\mathrm{cur}}(q_i)\right] \nonumber \\&\quad \cdot \left[ 1-\kappa |N-Z|(|N-Z|+2)/A^2\right] \nonumber \\&\quad +a_{\mathrm{Coul}}\frac{Z(Z-1)}{A^{1/3}}B_{\mathrm{Coul}}(q_i) \pm \frac{\delta }{\sqrt{A}}+E_{\mathrm{micr}}(Z,N;q_i). \nonumber \\ \end{aligned}$$

(7)

Here the volume, surface, and curvature terms carry the same reduced isospin dependence, and the electron binding energy is absent. The last two terms describe the odd–even mass difference and the microscopic correction energy, which is the same as in Eq. (6). The term $|N-Z|(|N-Z|+2)$ origins from the requirement that the nuclear part of the total energy has to depend on the square of the isospin of a nucleus: $<{\hat{\tau }}^2>=\tau (\tau +1)$, where $\tau ={|N-Z|/2}$, and $<{\hat{\tau }}^2>=|N-Z|(|N-Z|+2)/4$. Note that the linear term $|N-Z|$ in Eq. (7) corresponds to the Wigner (congruence) energy present in the Eq. (6). A standard deformation dependence of surface, curvature and Coulomb energies, absent in the original paper [12], is added in the present investigation.

Five different sets of parameters were fitted in Ref. [12] to 2076 nuclear masses but only one of them (i) with the parameters shown in the table below:

$a_{\mathrm{vol}}$ [MeV]	$a_{\mathrm{surf}}$ [MeV]	$a_{\mathrm{cur}}$ [MeV]	$\kappa$ [–]	$a_{\mathrm{Coul}}$ [MeV]	$\delta$ [MeV]
$-$ 15.597	17.32	0.0	1.8048	0.7060	11.4

is able to reproduce the experimental barrier heights with a quality similar to the one of the LSD model, as it was shown in Ref. [16]. In what follows, we will only consider this parameter set, labeled MLD hereafter, to compare its results with the ones of the LSD mass formula and to predict properties of SHN.

Fig. 2

Difference between the MLD and LSD estimates of nuclear masses. Crosses mark the experimentally known isotopes. Constant A values are represented by dashed lines, while the $\beta$-stable nuclei are to be found around the solid line

Fig. 3

Difference between the LD barrier heights evaluated using the LSD (6) and MLD (7) formulas

Fig. 4

Single-particle levels of the spherical nucleus $^{294}$Og evaluated using the Yukawa-folded (l.h.s.) and the Woods–Saxon (r.h.s) potential

The difference between the mass estimates obtained in the MLD and LSD models for actinide and superheavy nuclei is shown in Fig. 2. Crosses mark known isotopes. The solid line indicates the $\beta$-stability line, while dashed lines correspond to constant A values. The difference between both estimates is smaller than 0.2 MeV in actinide nuclei while it becomes slightly larger but does not exceed 0.6 MeV around the heaviest known SHN. $\alpha$-decay chains correspond to vertical lines in Fig. 2 with an almost constant energy difference between both mass estimates for known elements with Z$\ge$102, thus indicating that $\alpha$-decay $Q_\alpha$ energies will be very similar for both LD models in the SHN region.

Liquid-drop fission barrier heights evaluated using the MLD model turn out to be slightly larger than those of LSD, as can be seen in Fig. 3 but the difference does not exceed 0.2 MeV in the superheavy region.

The very close estimation of the masses and the barrier heights of the SHN obtained in both modern LD models gives a certain guarantee that our description of the macroscopic part of the energy is reasonably accurate.

3.2 Microscopic part of the energy

Strutinsky type shell corrections are obtained as usual by subtracting the average energy ${\widetilde{E}}$ from the sum of the energies $e_k$ of the occupied single-particle (s.p.) levels

$$\begin{aligned} \mathrm{E_{\mathrm{shell}}} = \sum \limits _{\mathrm{occ}} e_k - {\widetilde{E}} . \end{aligned}$$

(8)

The energies $e_k$ in (8) are the eigenvalues of a mean-field Hamiltonian with a mean-field potential [19]. The average energy ${\widetilde{E}}$ is evaluated using the Strutinsky prescription [7, 20, 21]. The pairing-energy correction is determined as the difference between the BCS energy and the s.p. energy sum from which the average pairing energy is subtracted [7]

$$\begin{aligned} E_{\mathrm{pair}} = E_{\mathrm{BCS}} - \sum \limits _{\mathrm{occ}} e_k - \widetilde{E}_{\mathrm{pair}}. \end{aligned}$$

(9)

In the BCS approximation, the ground-state energy of a system with an even number of particles is given by

$$\begin{aligned} E_{\mathrm{BCS}} = \sum _{k>0} 2e_k v_k^2 - G\left( \sum _{k>0}u_kv_k\right) ^2 - G\sum _{k>0} v_k^4 -{{\mathcal {E}}}_0^\varphi , \nonumber \\ \end{aligned}$$

(10)

where the sums run over the pairs of s.p. levels belonging to the pairing window defined below. The coefficients $v_k$ and $u_k=\sqrt{1-v_k^2}$ are the BCS occupation amplitudes, and ${{\mathcal {E}}}_0^\varphi$ is the energy correction due to the particle number projection performed in the GCM+GOA approximation [22]

$$\begin{aligned} {{\mathcal {E}}}_0^\varphi =\frac{\sum \nolimits _{k>0}[ (e_k-\uplambda )(u_k^2-v_k^2) +2\varDelta u_k v_k +Gv_k^4] / E_k^2}{\sum \nolimits _{k>0} E_k^{-2}}. \end{aligned}$$

(11)

Here, $E_k=\sqrt{(e_k-\uplambda )^2+\varDelta ^2}$ is the quasi-particle energy and $\varDelta$ and $\uplambda$ the pairing gap and Fermi energy, respectively. The average projected pairing energy, for a pairing window, of width $2\varOmega$, symmetric in energy relative to the Fermi level, is equal to

$$\begin{aligned} \widetilde{E}_{\mathrm{pair}}= & {} -\frac{1}{2}\,\tilde{g}\, {\tilde{\varDelta }}^2+\frac{1}{2}\tilde{g}\,G{\tilde{\varDelta }}\, \mathrm{arctan}\left( \frac{\varOmega }{{{\tilde{\varDelta }}}}\right) -\log \left( \frac{\varOmega }{{{\tilde{\varDelta }}}}\right) {\tilde{\varDelta }}\nonumber \\[3ex]&+\frac{3}{4}G\frac{\varOmega /{\tilde{\varDelta }}}{1+(\varOmega /{\tilde{\varDelta }})^2}/ \mathrm{arctan}\left( \frac{\varOmega }{{\tilde{\varDelta }}}\right) -\frac{1}{4}G ~ , \end{aligned}$$

(12)

where $\tilde{g}$ is the average single-particle level density at the Fermi surface and ${{\tilde{\varDelta }}}$ the average pairing gap corresponding to a pairing strength G

$$\begin{aligned} {{\tilde{\varDelta }}}=2\varOmega \exp \left( -\frac{1}{G\tilde{g}}\right) ~. \end{aligned}$$

(13)

All details of the calculation and the parameters used are described in Ref. [23], where an extended set of maps with the potential energy surfaces (PES) of superheavy nuclei are presented. This pairing energy as defined by Eq. (9) has of course to be evaluated separately for protons and neutrons as indicated by Eq. (5).

Fig. 5

Single-particle proton levels of the spherical nucleus $^{294}$Og evaluated self-consistently using the SkIII and SkM* Skyrme and Gogny D1S forces

Fig. 6

The same as in Fig. 5 but for neutrons

Fig. 7

Proton (top) and neutron (bottom) shell correction energies of the spherical actinide and superheavy nuclei obtained using the Yukawa-folded (l.h.s) and the Woods–Saxon (r.h.s) s.p. potentials

In our calculation, the single-particle spectra are obtained by diagonalization of a Hamiltonian with a Yukawa-folded (YF) potential [19, 24] with the same parameters as used in Ref. [18]. Its s.p. proton and neutron orbitals $|nlj\rangle$ of a spherical $^{294}$Og nucleus are compared in Fig. 4 with the levels evaluated using the Woods–Saxon (WS) potential with the so-called universal set of parameters of Ref. [25]. Both energy spectra are similar. The main difference is seen in the proton spectrum above the 2f7/2 levels corresponding to the magic number Z = 114, where the distance between the orbitals is slightly different. However, the situation is quite different when one compares these spectra with the ones evaluated in self-consistent models. In Figs. 5 and 6 they are compared to the proton and neutron spectra obtained self-consistently using the Skyrme SIII and SkM* and the finite-range Gogny D1S interaction. As one can see, the order of the proton’s orbitals obtained with the SIII set of parameters is similar to that of the YF potential. However, the energy distances between the levels are more considerable. The two other proton s.p. spectra obtained with the SkM* and D1S forces show different orders of the orbitals around the Fermi energy. Also, the energy gap corresponding to the magic number Z = 114 is smaller in these three self-consistent models than in the case of the Yukawa-folded mean-field potential. The energy gap corresponding to Z = 126 is most pronounced in the SkM* spectrum. The situation is similar in the neutron spectra, where energy gaps are visible around N = 168 and N = 184, but the sequence of orbitals frequently differs from model to model.

Comparing the different spectra, one should not forget, however, about the $2j+1$ degeneracy of the orbitals. The contribution of a single orbital to the shell energy depends obviously on its degeneracy and the energy distance from the Fermi level. The gaps observed in the energy spectra could be misleading. A better way to judge the magic numbers would be to compare the shell-correction energies corresponding to the different numbers of protons and neutrons. The proton (top) and neutron (bottom) shell correction energies evaluated with the Yukawa-folded (YF) and the Woods–Saxon (WS) s.p. potentials are presented in the l.h.s. and r.h.s. columns of Fig. 7, respectively. The proton magic number at Z = 114 is well visible in the proton shell correction energy which reaches there around -6 MeV for the YF potential and $-3.5$ MeV for the SW one. Similarly, a neutron magic number N = 178 appears in the neutron shell correction what is visible in both bottom panels. The neutron shell correction corresponding to this magic number is around $-4$ MeV in the YF case and $-5.5$ MeV for the WS potential. The shell corrections at the above proton and neutron magic numbers change slightly with the mass number A. The proton shell energy is negative for $110\lesssim \mathrm{Z}\lesssim 124$ and the neutron one for $164\lesssim \mathrm{N} \lesssim 184$, which indicates that nuclei in this range of proton and neutron numbers are spherical in the ground state. Of course, only the complete macroscopic-microscopic calculation can finally decide whether a given nucleus is spherical or deformed.

An extended set of 2D cross-sections of the 4D PES’s of superheavy nuclei obtained in our model can be found in Ref. [23]. The following section will show only a few examples of such maps.

4 Barrier heights and $Q_\alpha$ energies

Calculations have been carried out for the superheavy nuclei with $104\le \mathrm{Z}\le 128$ and $250\le \mathrm{A}\le 324$. The PES have been evaluated in the 4D deformation parameter space: $(\eta ,\,q_2,\,q_3,\,q_4)$.

Fig. 8

PES obtained using the LSD (top) and MLD liquid-drop (bottom) formula of $^{286}$Cn on the ($q_2,\eta$) plane

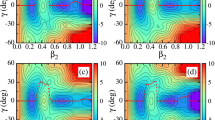
In Fig. 8 the ($q_2,\eta$) cross-section of the 4D potential energy surface of $\,^{286}$Cn [23] is shown using the LSD (top) and MLD (bottom) form of LD expression. The energies denoted on the layers are to be understood as relative to the LD energy of the spherical nucleus. The distance between layers (solid lines) is 2 MeV, while the intermediate dashed lines correspond to the half-layers. Both cross-sections (for LSD and MLD) in Fig. 8 have been evaluated by imposing left-right symmetry ($q_3=0$) and minimizing the energy in each ($q_2,\eta$) point with respect to $q_4$. The green lines marked by $\beta =0.3$ and $\gamma =10,\,30,\,60,\,120,\,150$ correspond to the frequently used ($\beta ,\,\gamma$) Bohr deformation parameters [26]. As one can see, both PES evaluated in different LD models are very close and give very similar estimates of the saddle point energy. The ground state of $^{286}$Cn turns out to be nearly spherical. The fission valley goes first via oblate ($\gamma =60^o$) shapes, then goes through a triaxial saddle point at ($\beta \approx 0.38,\,\gamma \approx 30^o$), and a non-axial second minimum ($\beta \approx 0.55,\,\gamma \approx 15^o)$ to a second also, non-axial saddle. Then at elongations $q_2\ge 0.8$ the fission valley returns to axially symmetric shapes ($\eta =\gamma =0$). Such a situation is typical for all SHN with Z$\ge 110$, which are spherical in the ground-state (see the collection of PES’s in Ref. [23]).

Fig. 9

PES obtained using the LSD (top) and MLD liquid-drop (bottom) formula of $^{286}$Cn on the ($q_2,q_3$) plane

The potential energy surface of $^{286}$Cn in the $(q_2, q_3)$ plane is shown in Fig. 9. The top panel corresponds again to the case where the LSD mass formula (5) is used, while the bottom part is obtained with the MLD liquid drop energy, Eq. (7). Both PES cross-sections are found to be very similar. A slightly smaller stiffness in the $q_3$ direction is observed in the MLD results at small elongations $q_2$, where the beginning of a valley which could probably lead to an $\alpha$-decay appears. We speak here about the beginning of such a valley since some more deformation parameters would be needed to describe with reasonable accuracy such a decay mode. Such valleys were also observed in the Gogny-HFB calculations presented in Ref. [27]. The main fission mode of $^{286}$Cn is a symmetric one since for a given $q_2$, the minimum of the energy corresponds to a reflection symmetric shape ($q_3=0$). Apart from this symmetric path to fission, two asymmetric valleys appear in Fig. 9. One is at $q_3=0.08$, and the second is very asymmetric ($q_3\approx 0.20$), which corresponds to a mass of the heavy fragment around A = 208. Note that the deformation-energy estimates obtained for very elongated shapes, close to the scission configuration ($q_2\approx 2.2$), are very close to each other in the LSD and MLD models.

Fig. 10

PES obtained using the LSD liquid-drop formula of $^{294}$Og on the ($q_2,\eta$) (top) ($q_2,q_3$) (bottom) planes

Similar cross-sections of the PES of the heaviest synthesized nucleus $^{294}$Og are shown in Fig. 10. Here we present only the results obtained with the LSD macroscopic energy since the MLD model gives very similar PES. A pronounced reduction of the saddle point energy, more significant than in the case of $^{286}$Cn, due to the breaking of axial and left-right reflection symmetries, is predicted in this isotope. The path to fission goes from a spherical ground-state via oblate-shapes, a triaxial and left-right asymmetric first saddle, a symmetric second minimum, and an asymmetric second saddle. Two fission valleys, the deeper one symmetric, the other one very asymmetric, corresponding to a mass of the heavy fragment around A = 208, lead to the scission configuration.

Fig. 11

Fission barriers heights of even–even superheavy nuclei with 104 $\le$ Z $\le$ 126

A significant reduction of the fission barrier height due to the non-axial and reflection degrees of freedom is observed in most superheavy nuclei. In Fig. 11 the fission-barrier heights $E_{\mathrm{B}}$ obtained with the LSD model for nuclei with $104\le Z\le 128$ and $250\le \mathrm{A}\le 324$ are displayed in the (A, Z) plane. These barrier heights defined as the difference between the highest saddle point and the ground state energy are evaluated using the flooding technique [28] in the 4D $(q_2,\,\eta ,\,q_3,\,q_4)$ deformation parameter space. As one can see, the highest barriers exceeding 8 MeV are found in the region with $112\le \mathrm{Z}\le 118$ and $280\le \mathrm{A} \le 294$. Above $\mathrm{A}\approx 310$ the barriers practically vanish. The experimental estimates of the lower limit of the barrier heights obtained in Ref. [29] for a few SHN are somewhat smaller than our predictions.

Fig. 12

Alpha decay energies $Q_\alpha$ of even–even superheavy nuclei with 104 $\le$ Z $\le$ 126

The theoretical values of the $Q_\alpha$ energies evaluated from the predicted mass difference of nuclei $^\mathrm{A}$X$_{\mathrm{Z}}$ and $^\mathrm{A-4}$Y$_{\mathrm{Z-2}}$ are compared in Fig. 12 with the experimental data (crosses) taken from Ref. [30]. The agreement of the theoretical values with the data is generally satisfactory, but with some exceptions, where the differences exceed 1 MeV.

5 Spontaneous fission lifetimes in a simple model

Let us remind the reader of the so-called topographical theorem of Myers and Świa̧tecki, which states that the mass of a nucleus at the saddle point is approximately equal to its macroscopic estimate. According to this statement, the fission barrier is equal to the difference between the saddle mass of the nucleus obtained in the macroscopic model and its experimental mass in the ground state. To verify that statement, a corresponding calculation was performed in Ref. [31] where the LSD mass formula, Eq. (6), was used to describe the macroscopic part of the binding energy. The fission barriers extracted experimentally for even–even actinide nuclei are compared in Fig. 13 with the estimates obtained using the topographical theorem and the LSD mass formula.

Fig. 13

Experimental fission barrier heights compared with the difference of the LSD saddle and the measured nuclear mass in the ground-state [31]

The results of this investigation are striking and prove the above idea of Myers and Świa̧tecki. The r.m.s. deviation between the prediction of such simple estimates and the data is only about 310 keV.

Fig. 14

Świa̧tecki systematics of the spontaneous fission lifetimes [32]

Fig. 15

Two-dimensional cross-section of 4D PES of $^{254}$Rf (top) with marked static path to fission (solid blue line). The potential barrier along this path is shown in the middle panel as a function of the relative distance between the mass-center of the fragments $s=r_{12}/R_0$. The dashed line shows the corresponding phenomenological mass parameter in the reduce mass units ($\mu$), found in Ref. [33]. The potential as function of the new coordinates x in which the mass parameter is constant ($B_{xx}=6\mu$) is drawn in the bottom panel. The dash-dotted line shows the approximation of this potential by two parabolas

In 1955 Świa̧tecki has made a famous systematic analysis [32] of the spontaneous fission lifetimes. He has noticed, in particular, that the quantity $\log _{10}\left( T^{\,\mathrm sf}_{1/2}/\mathrm{y}\right) + k\,\delta M$, where $\delta M=M_{\mathrm{exp}}-M^\mathrm{sph}_{\mathrm{LD}}$ and an adjustable parameter k, is almost a linear function of the fissility parameter for even–even nuclei. The lines representing the results for odd-A and odd–odd nuclei are then simply shifted by the so-called hindrance factor, as one can see in Fig. 14 taken from Ref. [32]. It was shown in Refs. [34, 35] that Świa̧tecki like systematics of spontaneous fission half-lives work surprisingly well for up-to-date experimental data for actinide nuclei up to Z=102, when one uses the LSD estimates of spherical nuclei [35]:

$$\begin{aligned} \log _{10}[T^{\,\mathrm sf}_{1/2}/\mathrm{y}]=-4.1\,Z+380.2 -7.7\,\delta M+ h~, \end{aligned}$$

(14)

where h is the hindrance factor equal to 0, 2.5, and 5 for even–even, odd-A, odd–odd nuclei, respectively.

The question arises, why the Świa̧tecki prescription for $T^{\,\mathrm sf}_{1/2}$ works so well? To answer this question, let us construct a simple model. The fission barrier of a given nucleus can be found by analyzing the static (minimal energy) or the dynamic (minimal action integral) [36] path of the PES in the multidimensional $\{q_i\}$ space, like the one presented in the top part of Fig. 15, where the ($q_2,q_4$) cross-section of the 4D PES of $^{254}$Rf is shown. The path (thick blue line) begins at the ground-state equilibrium point ($s_l$) and runs up to the exit point ($s_r$), where the energy is equal to the ground-state energy $E_0$. The fission barrier obtained along the static trajectory, where the energy has been minimized with respect to all deformation degrees of freedom except $q_2$, is presented in the middle panel of Fig. 15 as a function of the relative distance between the mass centers of both fragments $s=r_{12}/R_0$. The dashed line shows the phenomenological collective inertia $B_{ss}$ that enters, through the action integral, the calculation of the spontaneous fission lifetime (see below). It is clear that along the fission path, each deformation parameter $q_i(s)$ is a function of the path length s. The classical energy ${{\mathcal {H}}}$ of the nucleus is the sum of the kinetic and potential V energies:

$$\begin{aligned} {{\mathcal {H}}} = \frac{1}{2}B_{ss}(s)\dot{s}^2 + V(s)~, \end{aligned}$$

(15)

where $B_{ss}$ is the mass parameter and V the collective potential energy along the path s. A simple transformation from the s to a new x coordinate which conserves the kinetics energy:

$$\begin{aligned} x(s)=\int \limits _{s_{\mathrm{sph}}}^s \sqrt{\frac{B_{ss}(s')}{m}}\, ds', \end{aligned}$$

(16)

ensures that the mass parameter $B_{xx}=m$ corresponding to the new coordinate remains constant. One has assumed here that $x=0$ for the sphere. This transformation to a constant mass parameter is also valid in the quantum Hamiltonian when one does not take into account the derivatives of the $B_{ss}(s)$ parameter. The potential V[s(x)] in the new coordinate x, as shown in the bottom panel of Fig. 15, can be approximated by two (or more like in Ref. [33]) parabolas, one for each side of the barrier:

$$\begin{aligned} {\widetilde{V}}(x)= \left\{ \begin{array}{ll} V_{\mathrm{sadd}} - \frac{1}{2}\,C_l\, (x-x_{\mathrm{B}})^2~&{}\mathrm{for} ~x\,<\,x_{\mathrm{B}},\\ V_{\mathrm{sadd}} - \frac{1}{2}\,C_r\, (x-x_{\mathrm{B}})^2~&{}\mathrm{for} ~x\,>\,x_{\mathrm{B}}, \end{array}\right. \end{aligned}$$

(17)

how it is shown in the bottom part of Fig. 15.

The spontaneous fission half-life is then given by:

$$\begin{aligned} T^{\,\mathrm sf}_{1/2}=\frac{\ln 2}{nP}~, \end{aligned}$$

(18)

with

$$\begin{aligned} P=\frac{1}{1+\exp \{2S(L)\}}~, \end{aligned}$$

(19)

where the WKB action integral along the fission path L(x) is given by:

$$\begin{aligned} \begin{array}{rl} S(L) &{}= \displaystyle \int \limits ^{s_r}_{s_l} \sqrt{{2 \over \hbar ^2} \, B_{ss}[V(s) - E_0]}\, ds \\ &{}\approx \!\displaystyle \int \limits _{-x_l}^{x_r}\!\!\sqrt{\frac{2m}{\hbar ^2}[\widetilde{V}(x)-E_0]}\,dx~. \end{array} \end{aligned}$$

(20)

The penetration probability of the two (inverted parabola) barriers of height $E_{\mathrm{B}}$ is equal to:

$$\begin{aligned} S= & {} \frac{\pi }{2\hbar }E_{\mathrm{B}}\left( \sqrt{\frac{m}{C_l}} +\sqrt{\frac{m}{C_r}}\right) \nonumber \\= & {} \frac{\pi }{\hbar }E_{\mathrm{B}}\,\frac{\omega _l+\omega _r}{2\,\omega _l\,\omega _r} \equiv \frac{\pi }{\hbar }E_{\mathrm{B}}\,{{\tilde{\omega }}}^{-1}, \end{aligned}$$

(21)

where $\omega _l=\sqrt{C_l/m}$ and $\omega _r=\sqrt{C_r/m}$ are the inverted harmonic oscillator frequencies.

For $S\!\gg \! 1$ the logarithm of the spontaneous fission half-lives takes the form:

$$\begin{aligned} \log _{10} (T^{\,\mathrm sf}_{1/2})= & {} \frac{2\pi }{\hbar {{\tilde{\omega }}}}E_{\mathrm{B}} - \log _{10}[n\,\mathrm{ln}2]\nonumber \\\approx & {} \frac{2\pi }{\hbar {{\tilde{\omega }}}}(M_{\mathrm{sadd}}^\mathrm{LSD}-M_{\mathrm{exp}}) - \log _{10}[n\,\mathrm{ln}2], \end{aligned}$$

(22)

where n is the number of assaults against the fission barrier. The final formula for the spontaneous fission half-lives can then be written as

$$\begin{aligned} \log _{10}(T^{\,\mathrm sf}_{1/2})+\frac{4{\delta M}}{\hbar {{\tilde{\omega }}}}= \frac{4E_{\mathrm{B}}^\mathrm{LSD}}{\hbar {{\tilde{\omega }}}} - \log _{10}(n\,\mathrm{ln}2)~, \end{aligned}$$

(23)

where $\delta M=M_{\mathrm{exp}}-M_{\mathrm{LSD}}^{\,\mathrm sph}$. The above formula can be approximated similarly as it was done in Ref. [32]:

$$\begin{aligned} \log _{10}(T^{\,\mathrm sf}_{1/2}/\mathrm{s})-a\,\delta M=f(E_{\mathrm{B}})~, \end{aligned}$$

(24)

where $T^{\,\mathrm sf}_{1/2}$ is measured in seconds (s), a is a constant which has to be found, and $f(E_{\mathrm{B}})$ is an adjustable function which approximates the left side of this equation.

Fig. 16

Logarithm of the spontaneous fission half-lives corrected by the experimental and LSD mass difference as a function of the LSD barrier height

Fig. 17

Logarithm of the spontaneous fission half-lives predicted by formula (26) and the experimental data as a function of A

In Fig. 16 the l.h.s. of Eq. (24) is drawn as function of the barrier height for all experimentally known $T_{\mathrm{sf}}$. The coefficient a is found equal to 4.9 MeV$^{-1}$ and the function $f(E_{\mathrm{B}})$ (solid line in Fig. 16) is taken in the form of a second order polynomial

$$\begin{aligned} f(E_{\mathrm{B}})=-25.9+14.9\,E_{\mathrm{B}}-1.1\,E_{\mathrm{B}}^2~, \end{aligned}$$

(25)

where the coefficient of the polynomial have been obtained by a least-square fit to the data for nuclei with Z$\,\ge \,$90. The logarithm of the spontaneous fission half-lives can thus be approximated by

$$\begin{aligned} \log _{10}(T^{\,\mathrm sf}_{1/2}/\mathrm{s})= 4.9\,(M_{\mathrm{LSD}}^\mathrm{sph} -M_{\mathrm{exp}}) + f(E_{\mathrm{B}})~. \end{aligned}$$

(26)

The above theoretical estimate of $T^\mathrm{sf}_{1/2}$ is compared with the experimental data in Fig. 17 for nuclei from Th (Z$\,=\,$90) to Ds (Z$\,=\,$110).

As one can see, the simple one-dimensional WKB model reproduces the measured lifetimes quite well. Similar estimates of $T_{\mathrm{sf}}$ obtained using the MLD formula (7) are found to be very close to those obtained with the LSD masses.

6 Alpha decay lifetimes in the Gamow-like model

The lifetimes of nuclei decaying through $\alpha$ or cluster emission can be estimated quite accurately using a Gamow-like model [37] as shown in Ref. [38]. Let us recall here the main assumption of this model: The nucleus B decays into two parts: C, D:

$$\begin{aligned} ^{\mathrm{A}}B_{\,\mathrm Z} ~\longrightarrow ~ ^\mathrm{A_1}C_{\,\mathrm Z_1}~+~ ^\mathrm{A_2}D_{\,\mathrm Z_2}~, \end{aligned}$$

where the charges and the mass numbers of the daughter nucleus C and of the emitted nucleus D are denoted by (Z$_1$,A$_1$) and (Z$_2$,A$_2$), respectively.

Fig. 18

Potential barrier tunneling by $\alpha$ particle

A rectangular nuclear potential of depth $V_0$ and radius R for the nuclear part and a Coulomb potential V(r) for the outer part, as assumed in Ref. [38], is shown in Fig. 18. The emitted nucleus, as e.g. an $\alpha$-particle, has the energy $E_k$. The exit point from the barrier is denoted by b. The decay half-life is then given by:

$$\begin{aligned} T^{\,\alpha }_{1/2}=\frac{\ln 2}{\uplambda } \cdot 10^h \end{aligned}$$

(27)

where $\uplambda$ is the decay width and h is a hindrance factor needed to describe the decay of odd–even or odd–odd nuclei ($h=0$ for even–even nuclei). The decay width can be written as

$$\begin{aligned} \uplambda =\nu P~, \end{aligned}$$

(28)

where $\nu$ is the number of assaults against the barrier and P is the barrier penetration probability. In the WKB approximation [39] this probability is expressed by:

$$\begin{aligned} P=\exp {\biggl [-\frac{2}{\hbar }\int _{R}^{b} \sqrt{2\mu (V(r) -E_{\mathrm{k}})}\,dr\biggr ]}~, \end{aligned}$$

(29)

where $\mu$ is the reduced mass of the emitted particle. The exit point from the barrier b corresponds to the place where the Coulomb potential is equal to the kinetic energy $E_{\mathrm{k}}$:

$$\begin{aligned} b= {e^2\mathrm{Z}_1\mathrm{Z}_2\over E_{\mathrm{k}}} \end{aligned}$$

(30)

with $e^2 = 1.44\,\mathrm{fm\cdot MeV}$ beeing the square of the elementary charge.

Fig. 19

Theoretical estimates $\alpha$ decay half-life times of even–even heavy nuclei compared with the data (crosses). The experimental values of $T^\alpha _{1/2}$ and $Q_\alpha$ decay energies are taken here from Ref. [30]

The probability of tunneling of the Coulomb barrier of a spherical nucleus is given by:

$$\begin{aligned} P= & {} \exp \left\{ -\frac{2}{\hbar }\sqrt{2\mu Z_{1}Z_{2}e^{2}b}\right. \nonumber \\&\cdot \left. \left[ \arccos \sqrt{R/b} -\sqrt{{R/b}-\left( {R/b}\right) ^2}\right] \right\} . \end{aligned}$$

(31)

Here $R= r_0 (A_1^{1/3}+A_2^{1/3})$ is the radius of the square well shown in Fig. 18. It was assumed in Ref. [38] that the emitted particle is, in its ground-state, in a square well with relatively high walls like presented in Fig. 18. This assumption allows to use of the number of assaults per time-unit against the barrier corresponding to the ground state frequency of an infinite square well:

$$\begin{aligned} \nu \approx \frac{\pi \hbar }{2\mu R^2}~. \end{aligned}$$

(32)

Please note that the only one adjustable parameter in this model is the radius constant $r_0$ of the square well radius. A least-square fit performed in Ref. [38] to all known $\alpha$-decay lifetimes of even–even nuclei has given $r_0=1.21\;$fm. To describe the $\alpha$-decay of odd-A nuclei, an additional hindrance factor was fitted $h=0.216$. For odd–odd nuclei, the hindrance factor is simply doubled. The accuracy of reproducing the experimental data by this simple model is merely outstanding. It turns out to be better than that of Parkhomenko, and Sobiczewski obtained using the Viola-like formula, which contains for even–even nuclei four adjustable parameters [38, 40]. A similarly good accuracy for the reproduction of the probability of cluster [38], and proton decay [41] was obtained without any adjustment of the radius constant $r_0$. It could be mentioned that, recently, it was shown that a careful treatment of the preformation factor of alpha particle in the emitter helps to improve the calculation of the alpha-decay width (see e.g. Ref. [42]).

In Fig. 19 the logarithmic half-life $\log _{10}(T^\alpha _{1/2})$ for even–even superheavy nuclei is shown, where the experimental data for the lifetimes and $Q_\alpha$ are taken from Ref. [30]. It is shown that the theoretic calculations reproduces quite well the data if available.

Contrary to the estimates of Poenaru et al. [43] the cluster emission from the SHN is orders of magnitude less probable in our model [38, 44] than the one for $\alpha$-decay.

7 Conclusions

The following conclusions can be drawn from our investigation:

• The Fourier expansion of nuclear shapes offers a very effective way of describing nuclear deformations, both at the ground-state and in the vicinity of the scission configuration.

• Two modern liquid drop models: the LSD and MLD give very close estimates of nuclear masses, barrier heights, and $Q_\alpha$ energies of SHN,

• Further developments of the mean-field potentials are necessary since the present models predict very different magic numbers in superheavy nuclei,

• Shell and pairing effects at the ground-state determine the heights of fission barriers since the influence of these microscopic effects on the mass of a nucleus at the saddle point is practically negligible.

• Spontaneous fission lifetimes of nuclei are mostly determined by the microscopic energy correction at the ground-state and the macroscopic fission barrier height.

• A Simple WKB model with only one adjustable parameter, namely the radius constant $r_0$, describes well the alpha emission probabilities in SHN.

Langevin type calculations, based on the macro-micro model and the 3D Fourier shape parametrization, as well as the self-consistent method, are carried out in parallel by our group [23].