Excited states and staggering in $\varvec{\gamma }$-vibrational band built on the $\mathbf {11/2^{-}[505]}$ orbital of $\mathbf {^{~165}}$Er

Abstract

An extented Bohr Hamiltonian, by considering the Deformation-Dependent Mass Formalism with three different mass parameters one for each collective mode, is used to investigate the bands structure of the $^{165}$Er nucleus. By taking into account the Coriolis interaction, the staggering of $\gamma$ band energy levels built on the $11/2^{-}[505]$ orbital obtained within this theoretical approach has a similar behavior to that observed from experiment. E2 transition probabilities are also predicted for a future experimental test.

1 Introduction

One of the most fundamental issues in theoretical nuclear physics is being to describe collective states of atomic nuclei. In this context, Bohr-Mottelson Model [1, 2] provides a powerful tool to achieve such a goal alongside the Interacting Boson Model (IBM) [3]. Indeed, solving the Schrödinger equation corresponding to the collective Bohr Hamiltonian is one of the most reliable methods in studying the structure of deformed nuclei [4, 5]. So, many versions of Bohr Hamiltonian, using new concepts, are elaborated [6,7,8,9,10,11,12,13,14,15]. By analyzing experimental data and comparing them with theoretical calculations, such new approaches proved to be useful for a correct description of the properties of nuclei.

The presence of quadrupole shape oscillations is known to be the origin of $\beta$ and $\gamma$ bands in nuclei [2]. The $\beta$-band is caused by a shape oscillations in axially symmetric nuclei, while the $\gamma$-band is caused by non-axial shape oscillations. The energy staggering between the odd-even states of the gamma-vibration band are considered as one of the key observables to distinguish different modes of collective excitations [16,17,18].

In Ref. [19], the authors have studied the collective single-particle structure of the deformed odd nuclei using different mass parameters for different modes of motion in a nucleus, originating from Ref. [9], instead of the same mass parameter for all the vibration and rotation modes. This extended model was applied for the $^{163,165}$Er nuclei to calculate excited-state energies and E2 transition probabilities, but in a simple model where the quantum numbers K and $\varOmega$ of the projection of angular momentum of a nucleus and that of an external nucleon respectively, are good quantum numbers. Also, the Coriolis interaction had not been included in the Hamiltonian. This calculation did not show a staggering for the gamma band of $^{165}$Er which is observed in the experimental spectrum, especially when L (the total angular momentum of the nucleus) increases.

In our earlier work [20], we have studied the structure of nuclear excited states of four heavy odd mass nuclei $^{153,155}$Eu, $^{163}$Dy and $^{173}$Yb using an extended collective quadrupole Bohr Hamiltonian with different deformation-dependent mass parameters, where the mass parameters for the three collective mode motions are taken as different, and allowing the mass to depend on the nuclear deformation. The Coriolis interaction between the rotational and single-particle motions is taken into account in the case where K the projection of the angular momentum on the third axis connected with a nucleus and that of the external nucleon $\varOmega$ are not conserved. The Davidson potential [21] is used for $\beta$ shape and the harmonic oscillator potential for the $\gamma$ one.

The Er isotopes near the stability line have a large quadrupole deformation and exhibit both rotational and vibrational motions [22,23,24]. Thus, it is desirable to apply the model elaborated in Ref. [20] on the $^{165}$Er nucleus by calculating excited-state energies and E2 transition probabilities and then focus on the staggering in $\gamma$-band. The choice of this nucleus is due to the availability of experimental data for excited-state energies and for the $\gamma$-band especially.

The paper is organized in the following way: In Sect. 2 we give an outline of the used model. Numerical calculations for energy spectra compared with experimental data and for predicted E2 transition probabilities are presented and discussed in Sect. 3. In addition, an analysis of the staggering effect in $\gamma$-band is also presented. Finally, Sect. 4 is devoted to the conclusion.

2 Outline of the model

The Schrödinger equation corresponding to the Bohr Hamiltonian with three deformation-dependent mass coefficients for an odd-mass nucleus is given by [13, 15]

$$\begin{aligned}&\frac{\hbar ^2}{2\langle i|B_{0}|i\rangle }\left( \frac{-\sqrt{f}}{\beta ^4}\frac{\partial }{\partial \beta } \beta ^4 f \frac{\partial }{\partial \beta }\sqrt{f}-\frac{f^2}{\beta ^2 sin3\gamma } \frac{\partial }{\partial \gamma }sin3\gamma \frac{\partial }{\partial \gamma }\right. \nonumber \\&\quad \left. + \frac{f^2}{4\beta ^2}\sum _{k=1,2,3}\frac{(L_{k}-j_{k})^2}{sin^2(\gamma -\frac{2}{3}\pi k)}\right) \varPsi -f^2\beta \langle T\rangle (3j_{3}^2-j^2)\varPsi \nonumber \\&\quad +H_{p}\varPsi +V_{eff}\varPsi =E\varPsi , \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

(1)

with

$$\begin{aligned} V_{eff}= & {} V(\beta ,\gamma ) + \frac{\hbar ^2}{2\langle i|B_{0}|i\rangle }\left( \frac{1}{2}\left( 1-\delta -\lambda )f\nabla ^2f \right. \right. \nonumber \\&+\left. \left( \frac{1}{2}-\delta \right) \left( \frac{1}{2}-\lambda \right) \left( \nabla f\right) ^2 \right) , \qquad \qquad \qquad \end{aligned}$$

(2)

where $\langle i|B_{0}|i\rangle$ defines the mass parameters $B_{rot}$, $B_{\beta }$ and $B_{\gamma }$ for g.s. ($i\equiv g.s.$), $\beta$-vibrational state ($i\equiv \beta$) and $\gamma$-vibrational state ($i\equiv \gamma$) respectively [6]. f is the deformation function, it depends only on the radial coordinate $\beta$. Then, only the $\beta$ part of the resulting equation will be affected. L is the total angular momentum of the nucleus, $L_{1}$,$L_{2}$, and $L_{3}$ are its projections on the principal axes of the nucleus. j, $j_{1}$, $j_{2}$, and $j_{3}$ are the operator of a single nucleon external to the core, and its projections. $\langle T \rangle$ is the average value of a function of the distance between the single nucleon and the center of the nuclear core over internal states of the external nucleon, assuming zero nuclear surface oscillations [25, 26]. $H_{p}$ is the spherically symmetric part of the Hamiltonian of the external nucleon [25]. Originated from the construction procedure of the kinetic energy term within Deformation Dependent Mass Formalism (DDMF), $\delta$ and $\lambda$ are free parameters [11].

The potential is taken in this form

$$\begin{aligned} V(\beta ,\gamma )=U(\beta )+\frac{f^2}{\beta ^2}W(\gamma ), \end{aligned}$$

(3)

where

$$\begin{aligned} U(\beta )=V_{0}\Big (\frac{\beta }{\beta _{0}}-\frac{\beta _{0}}{\beta }\Big )^2 \end{aligned}$$

(4)

and

$$\begin{aligned} W(\gamma )=\frac{1}{2}(\beta _{0}^4C_{\gamma })\gamma ^2 \end{aligned}$$

(5)

$\beta _{0}$ is the position of the minimum of the potential in $\beta$, $C_{\gamma }$ is a free parameter, and $V_{0}$ represents the depth of the minimum, located at $\beta _{0}$.

For the deformation function, we use the following special form:

$$\begin{aligned} f=1+a\beta ^2,\qquad a<<1 \end{aligned}$$

(6)

where a is the deformation parameter. This specific form is required in the case of the Davidson potential (4) in order to get exact solvability in the framework of Supersymmetric Quantum Mechanics [11]. Other potentials require different forms for this function, see, for example, [12] for the Kratzer potential.

The eigenvalues of the Hamiltonian in Eq. (1) are determined by the following expression:

$$\begin{aligned} E_{n_{\beta }n_{\gamma }L|m|\tau }= & {} \frac{\hbar ^2}{2B_{\beta }}\Big (K_{0}+\frac{a}{2}(2+\frac{B_{\beta }}{B_{\gamma }}+2p+2q+pq)\nonumber \\&+2a(2+p+q)n_{\beta }+4an^2_{\beta }\Big )+\epsilon _{p}, \nonumber \\ \end{aligned}$$

(7)

where

$$\begin{aligned} q\equiv & {} q^\tau _{n_{\gamma }}(L,|m|)=\sqrt{1+4K_{-2}} \qquad \quad \nonumber \\ p\equiv & {} p^\tau _{n_{\gamma }}(L,|m|)=\sqrt{4\frac{B_{\beta }}{B_{\gamma }}-3+4\frac{K_{2}}{a^2}}, \end{aligned}$$

(8)

and

$$\begin{aligned} K_2= & {} \frac{a^2}{2}\Big [\Big (1+\frac{B_{\beta }}{B_{\gamma }}\Big )\Big (6\frac{B_{\beta }}{B_{\gamma }}+(1-2\delta )(1-2\lambda )\qquad \qquad \qquad \nonumber \\&+5(1-\delta -\lambda )\Big )+\frac{2B_{\beta }}{\hbar ^2}\varLambda \Big ]+\frac{2g_{\beta }}{\beta ^4_{0}}, \nonumber \\ K_0= & {} \frac{a}{2}\Big [\Big (1+\frac{B_{\beta }}{B_{\gamma }}\Big )\Big (8\frac{B_{\beta }}{B_{\gamma }}+5(1-\delta -\lambda )\Big )\nonumber \\&+\frac{4B_{\beta }}{\hbar ^2}\varLambda \Big ]-\frac{4g_{\beta }}{\beta ^2_{0}},\nonumber \\ K_{-2}= & {} \frac{B_{\beta }}{B_{\gamma }}\Big (1+\frac{B_{\beta }}{B_{\gamma }}\Big )+\frac{B_{\beta }}{\hbar ^2}\varLambda +2g_{\beta }, \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

(9)

where $g_{\beta }=\frac{B_{\beta }V_{0}\beta _{0}^2}{\hbar ^2}$, $\tau$ distinguishes different states of the same L, $n_{\beta }$ is the quantum number of $\beta$-vibrations, and $\epsilon _{p}$ is the corresponding energy of $H_{p}$ in units of $\hbar ^2/B_{\beta }\beta _{0}^2$ used here to be a parameter as in Ref. [27] which determines the distance between the single-particle spherical orbits.

The eigenvalues of the $\gamma$-vibrational part of the Hamiltonian plus the term of the rotational energy are determined by the following expression:

$$\begin{aligned} \frac{B_{\beta }}{\hbar ^2}\varLambda =\frac{2}{g}\frac{B_{\beta }}{B_{\gamma }}(1+2n_{\gamma }+|m|) +\frac{m^2}{3}\frac{B_{\beta }}{B_{\gamma }}+\varepsilon _{|m|L\tau }, \end{aligned}$$

(10)

where $g=\frac{1}{\beta _{0}^2}\frac{\hbar }{\sqrt{B_{\gamma }C_{\gamma }}}$ and $n_{\gamma }$ is the quantum number of $\gamma$-vibrations. The values of m are connected with K and $\varOmega$ through the condition $K - \varOmega = 2m$, where m should be an integer.

The following determinant is calculated in order to determine eigenvalues and eigenfunction of the rotational part of the Hamiltonian:

$$\begin{aligned} ||\langle LjKm|X| LjK'm'\rangle -\varepsilon _{|m|L\tau }\delta _{KK'}\delta _{mm'}||=0, \end{aligned}$$

(11)

where

$$\begin{aligned}&X=\frac{1}{3}\frac{B_{\beta }}{B_{rot}}\Big [L(L+1)+j(j+1)-L_{3}^2-j_{3}^2\nonumber \\&\qquad -2(L_{1}j_{1}+L_{2}j_{2})\Big ]-\frac{1}{3\xi }\Big [3j_{3}^2-j(j+1)\Big ], \end{aligned}$$

(12)

and $\xi =\frac{\hbar ^2}{6B_{\beta }\beta _{0}^3\langle T\rangle }$. Because of the quantum numbers K and $\varOmega$ which are not conserved in this present considerations, not only the diagonal elements of the Hamiltonian but also nondiagonal ones do contribute to the energies and E2 transition probabilities. The diagonal elements are given as follows:

$$\begin{aligned}&\langle LjKm|X| LjKm\rangle =\frac{1}{3}\frac{B_{\beta }}{B_{rot}}\Big [L(L+1)+j(j+1)-K^2\nonumber \\&\quad -(K-2m)^2-(-1)^{L-j} {\times } (L{+}1/2)(j{+}1/2)\delta _{K1/2}\delta _{m0}\Big ]\nonumber \\&\quad -\frac{1}{3\xi }\Big [3(K-2m)^2-j(j+1)\Big ].\qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$

(13)

The nondiagonal elements are

$$\begin{aligned}&\langle LjKm|X|LjK\pm m\rangle =\frac{1}{3}\frac{B_{\beta }}{B_{rot}}\Big [(L\mp K)(L\pm K+1)\Big ]^{1/2} \nonumber \\&\quad \times \Big [(j\mp K\pm 2m)(j\pm K\mp 2m+1)\Big ]^{1/2}. \qquad \end{aligned}$$

(14)

The bands are classified by the quantum numbers $n_{\beta }$, $n_{\gamma }$ and m, such as the g.s. band with $n_{\beta }=0$, $n_{\gamma }=0$, $m=0$; the $\beta$-band with $n_{\beta }=1$,$n_{\gamma }=0$, $m=0$; and the $\gamma$-band with $n_{\beta }=0$, $n_{\gamma }=0$,$m=1$.

The corresponding wave function is

$$\begin{aligned} \varPsi= & {} \beta ^{-(1+B_{\beta }/B_{\gamma })}R_{n_{\beta },L}(\beta )\qquad \qquad \qquad \qquad \qquad \nonumber \\&\times \sum _{{m}{K}}A_{LK}^{m\tau }\chi _{n_{\gamma }|m|}(\gamma )|LMjKm\rangle , \end{aligned}$$

(15)

where

$$\begin{aligned} R_{n_{\beta },L}(\beta )= & {} \beta ^{\frac{1}{2}(1+q)} (1+a\beta ^2)^{-n_{\beta }-\frac{1}{2}(1+\frac{B_{\beta }}{B_{\gamma }}) -\frac{1}{4}(p+q)}\nonumber \\&\times \phi (\beta ), \end{aligned}$$

(16)

with

$$\begin{aligned}&\phi (\beta )=N_{n_{\beta }}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \nonumber \\&\quad \times ~_{~ 2}F_1\left( -n_{\beta },-n_{\beta }-\frac{p}{2};-2n_{\beta } -\frac{(q+p)}{2};1+a\beta ^2\right) ,\nonumber \\ \end{aligned}$$

(17)

$$\begin{aligned}&\chi _{n_{\gamma },|m|}(\gamma )=N_{n_{\gamma },|m|}\gamma ^{|m|}e^{-\frac{\gamma ^2}{2g}}\qquad \qquad \nonumber \\&\quad \times ~_{~ 1}F_1\left( -n_{\gamma },1 +|m|,\frac{\gamma ^2}{g}\right) , \end{aligned}$$

(18)

and

$$\begin{aligned}&|LMjKm\rangle =\sqrt{\frac{2L+1}{16\pi ^2}}\Big [D^L_{MK}(\theta _{i})\varphi ^j_{K-2m}(x)\nonumber \\&\quad +(-1)^{L-j}D^L_{M-K}(\theta _{i})\varphi ^j_{-K+2m}(x)\Big ],\nonumber \\&\qquad \quad i=1,2 \, or \, 3. \end{aligned}$$

(19)

Here, $_{~ 2}F_1(-n_{\beta },-n_{\beta }-\frac{p}{2};-2n_{\beta }-\frac{(q+p)}{2};1+a\beta ^2)$ and

$_{~ 1}F_1(-n_{\gamma },1+|m|,\frac{\gamma ^2}{g})$ are hypergeometrical functions, $D(\theta _{i})$ is the Wigner function, $\varphi (x)$ is the wave function of single-particle state, $A_{LK}^{m\tau }$ are the coefficients of the expansion of the wave function [28], and $N_{n_{\beta }}$ with $N_{n_{\gamma },|m|}$ are normalization constants of radial and angular wave functions, respectively.

Table 1 The values of the parameters used in calculations

Table 2 The calculated values of $E(L_{g.s})/E(7/2_{g.s.}^-)$, $E(L_{\beta })/E(7/2_{g.s.}^-)$ and $E(L_{\gamma })/E(7/2_{g.s.}^-)$ compared with experimental data [22, 23, 31] for $^{165}$Er

Using the relationship between hypergeometric functions and generalized Jacobi polynomials on one side, and between hypergeometric functions and the Laguerre polynomials on the other side, we have

$$\begin{aligned} R(t)= & {} N_{n_{\beta }}2^{-(1+\frac{B_{\beta }}{B_{\gamma }})/2-(q+p)/4}a^{-(1+q)/4} \qquad \qquad \qquad \nonumber \\&\times (1-t)^{(1+2\frac{B_{\beta }}{B_{\gamma }}+p)/4}(1+t)^{(q+1)/4}P^{(q/2,p/2)}_{n_{\beta }}(t),\nonumber \\ t= & {} \frac{a\beta ^2-1}{a\beta ^2+1} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

(20)

and

$$\begin{aligned} \chi _{n_{\gamma },|m|}(\gamma )=N_{n_{\gamma },|m|}\gamma ^{|m|}e^{-\frac{\gamma ^2}{2g}}L_{n_{\gamma }}^{|m|}\big (\frac{\gamma ^2}{g}\big ), \end{aligned}$$

(21)

with

$$\begin{aligned}&N_{n_{\beta }}=(2a^{q/2+1}n_{\beta }!)^{1/2} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \nonumber \\&\quad \times \Bigg [\frac{\varGamma (n_{\beta }+\frac{q+p}{2}+1)\varGamma (2n_{\beta }+\frac{q+p}{2}+1+\frac{B_{\beta }}{B_{\gamma }})}{\varGamma (n_{\beta }+\frac{q}{2}+1)\varGamma (n_{\beta }\!+\!\frac{B_{\beta }}{B_{\gamma }}\!+\!\frac{p}{2})\varGamma (2n_{\beta }\!+\!\frac{q+p}{2}+1)}\Bigg ]^{1/2}\nonumber \\ \end{aligned}$$

(22)

and

$$\begin{aligned} N_{n_{\gamma },|m|}=\Big [\frac{2}{3}\frac{n_{\gamma }!}{g^{1+|m|}\varGamma (|m|+n_{\gamma })}\Big ]^{1/2}. \end{aligned}$$

(23)

B(E2) transition rate, taking into account the nonconservation of K [29], is given by

$$\begin{aligned}&B(E2;n_{\beta }Ln_{\gamma }K|m|\longrightarrow n'_{\beta }L'n'_{\gamma }K'|m'|)= \frac{5t^2}{16\pi }\nonumber \\&\quad \times \Big |\sum _{{K}{K'}}A_{LK}^{m\tau }A_{L'K'}^{m'\tau '}G\Big |^2 I^2_{n_{\beta }L,n'_{\beta }L'}C^2_{n_{\gamma },|m|,n'_{\gamma },|m'|}, \end{aligned}$$

(24)

where t is a scaling factor, $G=<L,K,2,K'-K|L',K'>$ is the Clebsch-Gordan coefficient dictating the angular momentum selection rules, while $I_{n_{\beta }L,n'_{\beta }L'}$ and $C_{n_{\gamma },|m|,n'_{\gamma },|m'|}$ are integrals over the shape variables $\beta$ and $\gamma$ with integration measures [13],

$$\begin{aligned}&I_{n_{\beta }L,n'_{\beta }L'}=\int \beta R_{n_{\beta },L}(\beta )R_{n'_{\beta },L'}(\beta ) \,\mathrm {d\beta }, \end{aligned}$$

(25)

$$\begin{aligned}&C_{n_{\gamma },|m|,n'_{\gamma },|m'|}=\int sin \gamma \chi _{n_{\gamma }|m|}\chi _{n'_{\gamma }|m'|}|sin 3\gamma |\mathrm {d\gamma }. \end{aligned}$$

(26)

3 Results and discussions

3.1 Excited-state energies

For this model, K and $\varOmega$ are not conserved, then the value of j affects the energy spectrum and the wave functions. $^{165}$Er has the $5/2^-[523]$ ground state determined from the Nilsson model [30] and a $\gamma$ band built on $11/2^{-}[505]$ orbital [23] giving importance to $f_{7/2}$ and $h_{11/2}$ orbits for the negative-parity states of this nucleus.

Fig. 1

The theoretical values of energy levels in units of $E(7/2_{g.s.}^-)$ in both cases with and without DDMF compared with experimental data [22, 23, 31] for $^{165}$Er

Both the excited-state energies E(L) and reduced transition probabilities $B(E_{2};L\rightarrow L')$ depend on the mass parameter ratios $B_{\beta }/B_{rot}$ and $B_{\beta }/B_{\gamma }$, and on the parameters $\xi$, g and $g_{\beta }$. Without taking into account DDMF, we determine the values of those free parameters with the condition that the value of $B_{\gamma }/B_{rot}$ to be close to 4 as it is the case for even-mass Er isotopes [8], by adjusting them in order to reproduce the optimal experimental spectrum. For this aim, we have used the root-mean-square (r.m.s) coefficient which describes the average deviation between theoretical predictions and experimental data:

$$\begin{aligned} \sigma =\sqrt{\frac{\sum _ {i=1}^{n}(E_i(exp)-E_i(th))^2}{(n-1)E(7/2^-_{g.s.})^2}}, \end{aligned}$$

(27)

where $E_i(exp)$ is the experimental energy of the $i^{th}$ level, $E_i(th)$ the corresponding theoretical value, n the maximum number of considered levels and $E(7/2_{g.s.}^-)$ the energy of the first excited state.

By introduction of DDMF, the optimal values of both parameters a and $\beta _{0}$ are evaluated through r.m.s fits of energy levels by making use of Eq. (27) for each band (g.s. , $\beta$ and $\gamma$-band). Note that, the values of the free parameters $\delta$ and $\lambda$ are null as in [11,12,13,14,15]. The obtained values of the parameters used in the calculation are given in Table 1. The large values of the position of the minimum of the potential $\beta _0$ are due to the dependence of the inertia coefficient on deformation. The inertia coefficient decreases with increase of $\beta$. It means that the velocity of the motion in $\beta$ is larger where deformation is larger, and smaller where deformation is smaller. Therefore, nucleus spends more time at smaller deformations. This decreases the effective value of deformation.

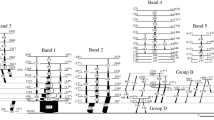
The comparison of the calculated values of energies $E(L_{g.s})$, $E(L_{\beta })$ and $E(L_{\gamma })$ in units of $E(7/2_{g.s.}^-)$ for the three bands with the available experimental data [22, 23, 31] is given in Table 2.

Fig. 2

Energy levels of $\gamma$-band as a function of parameter g in units of $E(7/2_{g.s.}^-)$ for differnt $L_{\gamma }$ for $^{165}$Er

Fig. 3

Energy levels of g.s.-band as a function of parameter g in units of $E(7/2_{g.s.}^-)$ for differnt $L_{g.s.}$ for $^{165}$Er

For the ground-state band, the calculated excited-state energies in units of $E(7/2_{g.s.}^-)$ are given for the sequence $9/2^{-},11/2^{-},...,45/2^{-}$ of spins and parities $L_{g.s.}^{\pi }$ for which the corresponding experimental values are available [22]. It shows that the theoretical results agree globally with experimental data. The value of the r.m.s coefficient presenting the deviations between experimental and theoretical data does not exceed $\sigma _{g.s.}=1.83$ bearing in mind that the presently adopted model is so complicated compared to that of the ref. [19]. It should also be noted that the introduction of DDMF allowed to increase the spacing between paired states as the angular momentum increases which is conform to the calculated spectrum of Ref. [27] for $^{153}$Eu and $^{155}$Eu nuclei while this pattern is not seen in experiment as we can observe in Fig. 1. For example, the differences of energies between every two neighboring levels $33/2^{-}$–$35/2^{-}$, $37/2^{-}$–$39/2^{-}$ and $41/2^{-}$–$43/2^{-}$ are respectively equal to 1.38, 1.13 and 0.90 in $E(7/2_{g.s.}^-)$ units while for the case without taken into account the DDMF it will be equal to 1.31, 1.03 and 0.79 respectively.

Fig. 4

The experimental and the theoreticals values of the quantity $S(L_{\gamma })$ given by Eq (28) obtained for the $\gamma$-band of $^{165}$Er plotted as functions of the angular momentum

For the $\beta$-band, only four states have been measured [31]. The calculated values of excited energies relative to $E(7/2_{g.s.}^-)$ energy are given up to the $L_{\beta }=41/2^{-}$ state. It is clearly shown that our results are closer to the experimental values ($\sigma _{\beta }= 0.27$).

Table 3 The theoretical predictions of $B(E_{2};L_{g.s.}+2 \rightarrow L_{g.s.})$ and $B(E_{2};L_{\beta } \rightarrow L_{g.s.})$ in units of $B(E_{2};9/2^-_{g.s.} \rightarrow 5/2^-_{g.s.})$ in both cases with and without DDMF for $^{165}$Er

The available experimental data for $E(L_{\gamma })/E(7/2_{g.s.}^-)$ of $\gamma$-band are up to $L_{\gamma }=31/2^{-}$ state [23]. The results of the calculations for this band are given up to $L_{\gamma }=47/2^{-}$ state. One can see that the agreement with the experiment is good ($\sigma _{\gamma }= 0.77$).

In the model of Ref. [19], the parameter g affects only the $\gamma$-band where the locations of the levels are very sensitive to it. For our model this parameter has also an effect on the locations of $\gamma$-band levels as shown in Fig. 2, where energy levels $E(L_{\gamma })$ as a function of parameter g in units of $E(7/2_{g.s.}^-)$ for different $L_{\gamma }$ are represented (while the other parameters are fixed as in Table 1). It has also an effect on the locations of high ground states band levels as shown in Fig. 3, where energy levels of g.s.-band as a function of parameter g in units of $E(7/2_{g.s.}^-)$ for differnt $L_{g.s.}$ are represented. In the right side of each figure are given the experimental energy levels, which are of course independent of the g axis, for each band.

3.2 Staggering in the $\varvec{\gamma }$-band

The staggering in the $\gamma$-band described by the discrete derivative of the energy as a function of the angular momentum given by the following quantity [32]:

$$\begin{aligned} S(L_{\gamma }) = E(L_{\gamma }) - 2E(L_{\gamma } - 1) + E(L_{\gamma } - 2), \end{aligned}$$

(28)

is studied in the ref [19]. But the performed theoretical calculations did not prove its existence, as was the case for the experiment, especially for higher $L_{\gamma }$ as we can see in Fig. 4. So, the adopted theory does not have enough complexity to recreate such high states. By using the same equation (28) we give the plot of the quantity $S(L_{\gamma })$ for our results for both cases with and without DDMF and compare them with experiment (Fig. 4).

It is clear that our model allowed us to reproduce well the shape of the staggering in the $\gamma$-band. By consediring the non-conservation of K and $\varOmega$ and by taking into account of the Coriolis interaction gave us this zigzaging effect while approaching the experimental form, especially for the high values of $L_{\gamma }$, while the introduction of DDMF increased the value of $S(L_{\gamma })$ for each level, giving almost coincidence with the experiment for the values of the lowest $L_{\gamma }$.

3.3 E2 transition probabilities

The calculated values of reduced E2 intraband transition probabilities for the ground-state band and interband E2 transition probabilities from $\beta$-band to the ground-state band in units of $B(E_{2};9/2_{g.s.}^- \rightarrow 5/2_{g.s.}^-)$ within and without the DDMF are given in Table 3. Within the DDMF, we have used the same optimal values of the two parameters a and $\beta _{0}$ previously obtained for the energy ratios in the ground-state band and $\beta$-band. For these transitions, we have $\varDelta m=0$. Then, the $\gamma$-integral part (Eq. (26)) reduces to the orthonormality condition of the $\gamma$-wave functions: $C_{n_{\gamma },|m|,n'_{\gamma },|m'|}=\delta _{n_{\gamma },n'_{\gamma }}\delta _{|m|,|m'|}$.

It is clearly shown that the inclusion of the DDMF decreases the E2 intraband transition probabilities for the ground-state band where the value of the deformation parameter is important. However, this behavior becomes clearer as the angular momentum increases too. For the case of interband E2 transition probabilities from $\beta$-band to the ground-state band, there is no effect of the introduction of DDMF. This is due to the value of the deformation parameter, obtained by the fit for the energy ratios of $\beta$-band, which tends towards zero.

4 Summary

In this paper we have recalculated the energy spectrum and transition rates for deformed odd-mass $^{165}$Er nucleus using an extented Bohr Hamiltonian, by considiring the Deformation-Dependent Mass Formalism with three different mass parameters for each collective mode in the case where the quantum numbers K and $\varOmega$ are not conserved and taking into account the Coriolis interaction. We have found a good agreement with the available experimental data for energy ratios. The values of reduced E2 transition probabilities, where the experimental data are not available, are given as predictions. The validity of this model was also proved by the fact that the shape of the staggering at higher spins in $\gamma$-band built on the $11/2^{-}[505]$ orbital is close to that obtained by the experiment. The effect of the parameter g on energy levels was also discussed. This parameter has a large effect on the $\gamma$-band as a whole. For this model such an effect is also observed in the ground state band which can be seen clearly when the angular momentum increases. We can also mention that, the fact that it is not possible to describe simultaneously neighboring even-even and odd nuclei in the framework of the considered model is much more interesting that a possibility to fit the data. Probably, it is an effect of the odd neutron occupying single particle state with large quadrupole moment.