Semi-classical approaches to heavy-ion reactions: fusion, rainbow, and glory

Abstract

A semi-classical approximation has been a powerful tool in understanding the dynamics of low-energy heavy-ion reactions. Here we discuss two topics in this regard, for which Mahir Hussein was a world leading pioneer. The first topic is heavy-ion fusion reactions of neutron-rich nuclei, in which the breakup process of the projectile nucleus plays a crucial role. The second is rainbow and glory scattering, for which characteristic oscillatory patterns in differential cross sections can be well understood in terms of intereferences among several semi-classical trajectories.

1 Introduction

The semi-classical approximation provides an intuitive view of various quantum mechanical phenomena in terms of classical concepts, such as a trajectory of a particle. This approximation works well when a variation of a potential within a wave length is negligibly small. The condition is satisfied when the energy and/or the mass of a particle is large. This is well fulfilled in heavy-ion reactions [1,2,3], for which a reduced mass for the relative motion between nuclei is in general large (but, see also Ref. [4] for the validity of the semi-classical approximation). As a matter of fact, angular distributions of elastic scattering can often be interpreted using classical trajectories. Also, a semi-classical coupled-channels method, in which quantal coupled-channels equations are solved along a classical trajectory, has been developed for inelastic scattering [5]. Moreover, the WKB formula for a penetrability has provided a convenient reference for heavy-ion fusion reactions at energies close to the Coulomb barrier. At the microscopic level, the time-dependent Hartree-Fock (TDHF) theory or the time-dependent density functional theory (TDDFT) [6, 7] can also be derived using the semi-classical approximation [8].

Mahir Hussein was an expert of the semi-classical approximation in the context of heavy-ion reactions, and carried out many pioneering works, as is well summarized in his textbook on nuclear reactions written with one of us (L.F.C.) [2]. In this paper, we shall discuss two topics among them. First is heavy-ion fusion reactions of neutron-rich nuclei. Here, the weakly bound nature of a projectile nucleus leads to complex features in the fusion dynamics. While a halo structure of a projectile nucleus naturally lowers the Coulomb barrier, the reaction dynamics is much more complicated due to the breakup process [9, 10]. Hussein was the first who discussed the role of breakup in fusion of weakly bound nuclei [11]. The second topic which we discuss in this paper is heavy-ion elastic scattering. Differential cross sections often exhibit characteristic oscillations. In the semi-classical approximation, such oscillations can be naturally interpreted as intereferences between several trajectories, such as intereferenes between a near-side and a far-side components of scattering amplitude [12], and intereferences between an internal wave and a barrier wave [13]. Among them, rainbow scattering is particularly important, as it probes a relatively inner region of an optical potential and thus it can be used to constrain the depth of a potential [14]. Glory scattering is another interesting phenomenon in which many classical trajectories coherently contribute to cross sections. In his own terms, Hussein mentioned “These effects (nuclear rainbow and glory scattering) are also common in atomic and molecular scattering, and have been reviewed extensively in the literature. Of course the commonest of all is the atmospheric rainbow and glory, a beautiful colorful dance of light and water” (at the workshop on occasion of Noboru Takigawa’s 60th birthday, November 2003, Sendai, Japan). Here in this paper we shall discuss the novel concept of glory in the shadow of rainbow, introduced by Hussein and his collaborators in Refs. [15, 16].

2 Fusion of weakly bound nuclei

2.1 A two-neutron halo nucleus $^{11}$Li

Nuclei far from the stability line are characterized by an extended density distribution due to weakly bound valence nucleons. Among such neutron-rich nuclei, the $^{11}$Li nucleus has been one of the most well studied nucleus since the discovery of its halo structure [17]. The two-neutron separation energy of this nucleus is indeed small, $S_{2n}=378\pm 5$ keV [18]. A strong low energy peak has been experimentally found in the Coulomb breakup spectrum [19], which is consistent with the small separation energy [20]. The low energy peak is due to the electric dipole (E1) excitation and thus has been referred to as a soft dipole mode. If one employs a three-body model with $^9$Li + n + n for the $^{11}$Li, the operator for the electric dipole excitation is proportional to $\mathbf {r}_1+\mathbf {r}_2$, where $\mathbf {r}_i$ is the coordinate of the i-th neutron measured from the core nucleus $^9$Li [21,22,23]. Using the cluster sum rule, the total E1 strength is thus proportional to the ground state expectation value of $\mathbf {R}^2$, where $\mathbf {R}=(\mathbf {r}_1+\mathbf {r}_2)/2$ is the center of mass of the valence neutrons with respect to the core nucleus. This implies that if one somehow supplies information on the distance between the two valence neutrons, $\mathbf {r}_{nn}=\mathbf {r}_1-\mathbf {r}_2$, one can combine those information to reconstruct the three-body geometry of the $^{11}$Li nucleus. This was done by Bertulani and Hussein, who used a HBT-type analysis of the two valence-halo particles correlation to extract the opening angle of the valence neutrons in $^{11}$Li to be $\theta _{nn}=66^{+22}_{-18}$ degrees [24]. See also Ref. [25], which used the matter radius to estimate $r_{nn}$ and obtained $\theta _{nn}=56.2^{+17.8}_{-21.3}$ degrees. These values are consistent with each other and both are smaller than the value of the uncorrelated case, that is, $90^\circ$, implying the existence of the dineutron correlation [22, 26, 27] in $^{11}$Li.

2.2 Sub-barrier fusion of $^{11}$Li

Heavy-ion fusion reactions take place by quantum tunneling at energies below the Coulomb barrier, and they are sensitive to details of nuclear structure of colliding nuclei. In particular, it has been well known that collective excitations of the colliding nuclei significantly enhance fusion cross sections at subbarrier energies [28,29,30,31,32]. A natural question is then how fusion cross sections are affected when a neutron-rich nucleus is used as a projectile. There are several aspects which one has to take into account. Those include:

• The extended density distribution of the projectile. This lowers the Coulomb barrier, enhancing fusion cross sections [33].

• The soft dipole excitation. Even though it may not carry a large collectivity [34], couplings to continuum may in general enhance fusion cross sections.

• The breakup process. It may hinder fusion cross sections since the lowering of the Coulomb barrier disappears. At the same time, it may also enhance fusion cross sections if couplings to a breakup channel dynamically lowers the Coulomb barrier [35, 36], in a similar way to well-known channel coupling effects for inelastic and transfer channels [30].

• The transfer processes. For neutron-rich nuclei, a transfer Q-value is likely positive, which may significantly influence fusion reactions [37]. It is still a challenge to take into account simultaneously both the transfer and the breakup processes in a theoretical calculation [38].

Among these effects, in this paper we particularly focus on the effect of breakup on heavy-ion fusion reactions. This problem was discussed for the first time by Hussein et al. [11]. Couplings to a breakup channel yields a dynamical polarization potential, $V_\mathrm{\scriptscriptstyle DPP}$, for the entrance channel. By taking into account the imaginary part of the dynamical polarization potential, Hussein et al. estimated fusion cross sections in the presence of a breakup channel as,

$$\begin{aligned} \sigma _{\mathrm{fus}}(E)= & {} \frac{\pi }{k^2}\sum _l(2l+1)\,\Bigg [ \frac{1}{2} \Big ( T_l(E+F) + T_l(E-F)\Big ) \nonumber \\&\times {\mathcal {P}}^\mathrm{\scriptscriptstyle S}_l(E), \end{aligned}$$

(1)

where E is the incident energy in the center of mass frame, $k=\sqrt{2\mu E/\hbar ^2}$ is the wave number for the relative motion, with $\mu$ being the reduced mass, and F is the strength of the coupling between the elastic channel and the soft dipole mode, taken at the barrier radius. The contribution from each partial wave involves the product of two factors. The first is the sum of the transmission probabilities through the barrier of the l-dependent potential for the collision energies $E\pm F$. The energy shifts, $\pm F$, account for the effects of couplings with the soft dipole mode in an approximate way [39, 40]. The second term is the probability of surviving the prompt breakup process. It is given by

$$\begin{aligned} {\mathcal {P}}^\mathrm{\scriptscriptstyle S}_l(E) = 1-{\mathcal {P}}_l^{\mathrm{bu}}(E), \end{aligned}$$

(2)

with ${\mathcal {P}}_l^{\mathrm{bu}}(E)$ being the breakup probability, estimated semi-classically as,

$$\begin{aligned} {\mathcal {P}}_l^{\mathrm{bu}}(E)=1-\exp \left[ 2\int ^\infty _{r_{0l}}W_\mathrm{\scriptscriptstyle DPP}(r)\frac{dr}{\hbar v(r)}\right] . \end{aligned}$$

(3)

Above, $r_{0l}$ is the outermost classical turning point for l, v(r) is the local velocity, and $W_\mathrm{\scriptscriptstyle DPP}$ is the imaginary part of the dynamical polarization potential. Notice that the exponent in this equation is a half of that in Ref. [11], by taking into account only the incoming part of the trajectory [41]. Since $W_\mathrm{\scriptscriptstyle DPP}$ is negative, in this approach fusion cross sections are suppressed due to the breakup.

Fig. 1

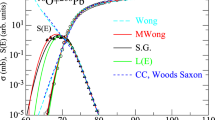
Fusion cross sections for the $^{11}$Li+$^{208}$Pb system. The dotted line is obtained with a single-channel calculation, while the dashed line is obtained by taking into account couplings to a soft dipole model excitation in $^{11}$Li. The solid line takes into account the breakup process in the semi-classical approximation, in addition to the couplings to the soft dipole excitation. Taken from Ref. [11]

Figure 1 shows fusion cross sections for $^{11}$Li+$^{208}$Pb, within different approximations. The solid line represents the cross section of Eq. (1), which takes into account both couplings to the soft dipole mode and the influence of prompt breakup. The dashed line corresponds to the cross section taking into account couplings to a soft dipole excitation in $^{11}$Li, but not survival probabilities ($F\ne 0$ but ${\mathcal {P}}^\mathrm{\scriptscriptstyle S}_l(E)= 1$). Finally, the dotted line corresponds to results of a one-channel calculation, which neglects all coupling effects ($F=0$ and ${\mathcal {P}}^\mathrm{\scriptscriptstyle S}_l(E)= 1$). Comparing the solid and the dotted lines, one concludes that the overall effect of the couplings is suppression of fusion above the Coulomb barrier and enhancement at sub-barrier energies. One can see also that, the cross section of Eq. (1) converges to the dashed line as the energy decreases well bellow the Coulomb barrier, meaning that in this energy limit the effects of prompt breakup become negligible, while the influence of the soft dipole mode remains.

Dasso and Vitturi [35] proposed a different approach to estimate breakup effects in $^{11}$Li+$^{208}$Pb fusion. They performed schematic coupled channel calculations involving two $^{11}$Li channels, corresponding to the elastic channel and the low-lying soft dipole mode, and a third channel for $^9$Li, associated with the breakup process. They found that the couplings with the soft mode make the fusion cross section much larger, at all collision energies. Further, they found that the inclusion of the $^9$Li channel in the coupled equations makes the cross section still larger.

These early calculations were based on very drastic approximations. Dasso and Vitturi treated the breakup channel only schematically. On the other hand, Hussein et al. evaluated the imaginary part of the polarization potential with several approximations, and completely neglected its real part. In reality, one has to take into account both the real and the imaginary parts of the dynamical polarization potential. The real part of the dynamical polarization potential is attractive at energies below the Coulomb barrier [42], and the coupling to the breakup process may lead to an enhancement. More quantitative theories were developed along the last 3 decades, including realistic quantum mechanical calculations, based on the continuum discretized coupled channel (CDCC) method [43,44,45]. A summary of these theories is presented below.

2.3 Further developments in the treatment of breakup in fusion

In collisions of neutron-halo projectiles, the experimental fusion cross section has contributions from captures of the whole projectile, and of the charged core, produced in prompt breakup. The two processes are experimentally indistinguishable. However, the latter contribution is expected to be small, owing to the higher Coulomb barrier for the charged fragment and also to its lower kinetic energy. This justifies the neglect of $^9$Li fusion in Ref. [11].

A different situation occurs in collisions of weakly bound projectiles that break up into two charged fragments. Some examples are the stable $^6$Li ($^4$He + $^2$H) and $^7$Li ($^4$He + $^3$H) nuclei, and the unstable $^8$B ($^7$Be + p). In such cases, the fusion of the whole projectile, known as complete fusion (CF), may, in principle, be experimentally distinguished from the fusion of one of the breakup fragments, known as incomplete fusion (ICF). Some experiments can determine also individual cross sections for the captures of the two breakup fragments. Then, the situation calls for more powerful theoretical models, that can predict cross sections for CF and also individual ICF cross sections for the two fragments, denoted by ICF$_\mathrm{\scriptscriptstyle 1}$ and ICF$_\mathrm{\scriptscriptstyle 2}$.

The first theory to evaluate CF and ICF cross sections was introduced in Ref. [46], which reported also measurements of CF and ICF cross sections in $^{6,7}$Li + $^{209}$Bi collisions. A detailed presentation of the theory can be found in Ref. [47]. It treats the collision by a classical three-body model, describing the motion of the target (T) and the two clusters of the projectile ($c_\mathrm{\scriptscriptstyle 1}$ and $c_\mathrm{\scriptscriptstyle 2}$) on the x-y plane. The time evolution of the system is determined by the Hamiltonian,

$$\begin{aligned} H= & {} \frac{\mathbf {p}_\mathrm{\scriptscriptstyle T}^2}{2m_\mathrm{\scriptscriptstyle T}}+\frac{\mathbf {p}_\mathrm{\scriptscriptstyle 1}^2}{2m_\mathrm{\scriptscriptstyle 1}} +\frac{\mathbf {p}_\mathrm{\scriptscriptstyle 2}^2}{2m_\mathrm{\scriptscriptstyle 2}}+ V_\mathrm{\scriptscriptstyle 12}\left( \mathbf {r}_\mathrm{\scriptscriptstyle 1}- \mathbf {r}_\mathrm{\scriptscriptstyle 2} \right) \nonumber \\&+ V_{\mathrm{\scriptscriptstyle 1T}}\left( \mathbf {r}_\mathrm{\scriptscriptstyle 1}-\mathbf {r}_\mathrm{\scriptscriptstyle T} \right) + V_{\mathrm{\scriptscriptstyle 2T}}\left( \mathbf {r}_\mathrm{\scriptscriptstyle 2}-\mathbf {r}_\mathrm{\scriptscriptstyle T} \right) . \end{aligned}$$

(4)

Above, $\mathbf {r}_\mathrm{\scriptscriptstyle T}$, $\mathbf {r}_\mathrm{\scriptscriptstyle 1}$ and $\mathbf {r}_\mathrm{\scriptscriptstyle 2}$ are vectors in the x-y plane, representing respectively the target, fragment $c_1$ and fragment $c_2$, and $\mathbf {p}_\mathrm{\scriptscriptstyle T}$, $\mathbf {p}_\mathrm{\scriptscriptstyle 1}$ and $\mathbf {p}_\mathrm{\scriptscriptstyle 2}$ are the corresponding momenta. The three potentials represent the interactions between the particles of the model ($T, c_\mathrm{\scriptscriptstyle 1}$ and $c_\mathrm{\scriptscriptstyle 2}$). The time evolution of the system begins with the projectile far apart from the target, where its interactions with the fragments depend only on the projectile-target relative vector, $\mathbf {R} = \mathbf {r}_\mathrm{\scriptscriptstyle P} - \mathbf {r}_\mathrm{\scriptscriptstyle T}$, with $\mathbf {r}_\mathrm{\scriptscriptstyle P} = (m_\mathrm{\scriptscriptstyle 1} \mathbf {r}_\mathrm{\scriptscriptstyle 1} + m_\mathrm{\scriptscriptstyle 2} \mathbf {r}_\mathrm{\scriptscriptstyle 2})/ (m_\mathrm{\scriptscriptstyle 1} + m_\mathrm{\scriptscriptstyle 2})$. The initial projectile-target momentum is given by the collision energy, whereas the initial values of $\mathbf {r}_\mathrm{\scriptscriptstyle 1}, \mathbf {p}_\mathrm{\scriptscriptstyle 1}, \mathbf {r}_\mathrm{\scriptscriptstyle 2}, \mathbf {p}_\mathrm{\scriptscriptstyle 2}$ are chosen randomly, from a distribution of positions and momenta given by the ground state (g.s.) wave function of the projectile. The calculations are performed for a mesh of impact parameters and the CF, ICF$_\mathrm{\scriptscriptstyle 1}$ and ICF$_\mathrm{\scriptscriptstyle 2}$ are determined from the final states of the three-body system. This model was used to predict CF and TF ($\mathrm{CF} + \mathrm{ICF}_\mathrm{\scriptscriptstyle 1} + \mathrm{ICF}_\mathrm{\scriptscriptstyle 2}$) cross sections. The results for the $^{6,7}$Li + $^{209}$Bi systems are shown in Fig. 2, in comparison with the data. Despite the simplicity of the model, it gives a reasonable account of the data at above-barrier energies. Of course, a classical model cannot describe sub-barrier fusion.

Fig. 2

CF and TF cross sections in the $^{6,7}$Li + $^{209}$Bi collisions of the classical model, in comparison with the data. The calculations and the data are from the work of Dasgupta et al. [46]

Diaz-Torres et al. [48, 49] developed a three-dimensional version of the classical model, in which the breakup of the projectile was treated as a stochastic process, based on a breakup function determined from sub-barrier breakup measurements [50], or from CDCC calculations. This model was implemented in the PLATYPUS computer code, available in the literature [51]. It was used to evaluate CF and ICF cross sections in the $^9$Be–$^{208}$Pb [48] and $^{6}$Li– $^{209}$Bi [52] collisions. Their results were compared with the data of Refs. [53] and [46, 54], respectively. The theoretical cross sections were shown to be in qualitative agreement with the above-barrier data.

Although the classical models give reasonable descriptions of the CF and ICF cross sections above the Coulomb barrier, they do not include quantum mechanical effects, like barrier tunnelling, which are essential at sub-barrier energies. The situation is improved in the semiclassical model (see e.g. Ref. [55]). The model is based on the same Hamiltonian of Eq. (4), but in the c.m. of the projectile-target system, and expressed in terms of the vectors $\mathbf {R}$ and $\mathbf {r} = \mathbf {r}_\mathrm{\scriptscriptstyle 1} - \mathbf {r}_\mathrm{\scriptscriptstyle 2}$. That is,

$$\begin{aligned} H=\frac{\mathbf {P}_\mathrm{\scriptscriptstyle \mathbf{R}}^2}{2\mu _\mathrm{\scriptscriptstyle PT}} + V_{\mathrm{\scriptscriptstyle 1T}}\left( \mathbf {R}, \mathbf {r} \right) + V_{\mathrm{\scriptscriptstyle 2T}}\left( \mathbf {R},\mathbf {r} \right) + h_0, \end{aligned}$$

(5)

where $h_0$ is the intrinsic Hamiltonian of the projectile,

$$\begin{aligned} h_0=\frac{\mathbf {p}_\mathrm{\scriptscriptstyle \mathbf{r}}^2}{2\mu _\mathrm{\scriptscriptstyle 12}} + V_{\mathrm{\scriptscriptstyle 12}}\left( \mathbf {r} \right) . \end{aligned}$$

(6)

In the above equations $\mathbf {P}_\mathrm{\scriptscriptstyle R}$ and $\mathbf {p}_\mathrm{\scriptscriptstyle r}$ are the momenta associated with $\mathbf {R}$ and $\mathbf {r}$, and $\mu _\mathrm{\scriptscriptstyle PT}$ and $\mu _\mathrm{\scriptscriptstyle 12}$ are the reduced masses of the projectile-target system and of the two clusters of the projectile. This Hamiltonian has both bound and scattering eigenstates, and its ground state is denoted by $\varphi _0$. The infinite space of scattering states is approximated by a finite set of wave packets, referred to as bins, by the CDCC method [43,44,45].

The projectile-target motion is treated by classical mechanics. The trajectory, $\mathbf {r}(t)$, is obtained solving the classical equations of motion with the Hamiltonian

$$\begin{aligned} {\mathcal {H}}_\mathrm{\scriptscriptstyle class} (\mathbf {R}) = \frac{\mathbf {P}_\mathrm{\scriptscriptstyle \mathbf{R}}^2}{2\mu _\mathrm{\scriptscriptstyle PT}} + {\overline{V}}(\mathbf {R}) , \end{aligned}$$

(7)

with

$$\begin{aligned} {\overline{V}}(\mathbf {R}) = \int d^3\mathbf {r}\ \big [ V_{\mathrm{\scriptscriptstyle 1T}}\left( \mathbf {R}, \mathbf {r} \right) + V_{\mathrm{\scriptscriptstyle 2T}}\left( \mathbf {R},\mathbf {r} \right) \big ]\ \left| \varphi _0(\mathbf {r}) \right| ^2. \end{aligned}$$

(8)

The intrinsic wave function of the projectile is expanded over the bound and continuum-discretized eigenstates of $h_0$, and the coefficients are found by solving the Schrödinger equation in the $\mathbf {r}$-space, with the time-dependent Hamiltonian

$$\begin{aligned} h(t)= & {} h_0 + V_{\mathrm{\scriptscriptstyle 1T}}\left( t, \mathbf {r} \right) + V_{\mathrm{\scriptscriptstyle 2T}}\left( t,\mathbf {r} \right) \\\equiv & {} h_0 + V_\mathrm{\scriptscriptstyle 1T}\left( \mathbf {R} (t), \mathbf {r} \right) + V_\mathrm{\scriptscriptstyle 2T}\left( \mathbf {R} (t),\mathbf {r} \right) . \end{aligned}$$

The CF cross section is then found multiplying the final populations of the bound states by transmission coefficients of the whole projectile through the barrier of ${\overline{V}}(\mathbf {R})$. The ICF cross section for each fragment, depends on the population of continuum states and transmission coefficients of the fragment through its interaction potential with the target. The association of CF and ICF with bound states and continuum states of the projectile was proposed in the quantum mechanical calculations of Hagino et al. [36], which is discussed later in this section. The semiclassical method was used to calculate CF and ICF cross sections in collisions of $^{6,7}$Li with $^{209}$Bi [56], $^{197}$Au and $^{159}$Tb [57]. The overall agreement between the theoretical CF cross sections and the data at near- and above barrier energies was reasonably good, while the predictions of ICF cross sections were poorer.

The most reliable calculations of fusion cross sections in collisions of weakly bound nuclei are based on the CDCC method. Standard CDCC calculations give only $\sigma _\mathrm{\scriptscriptstyle TF}$ [58,59,60,61]. It is extracted from $\sigma _\mathrm{\scriptscriptstyle R}$ through the relation,

$$\begin{aligned} \sigma _\mathrm{\scriptscriptstyle TF} = \sigma _\mathrm{\scriptscriptstyle R} - \sum _{\gamma \ne 0} \sigma _{\gamma } , \end{aligned}$$

(9)

where $\gamma \ne 0$ correspond to the nonelastic channels (the elastic is labelled by $\gamma = 0$), both bound and unbound (continuum discretized). In Eq. (9), $\sigma _\mathrm{\scriptscriptstyle R}$ is the total reaction cross section, given by the expansion

$$\begin{aligned} \sigma _\mathrm{\scriptscriptstyle R} = \frac{\pi }{k^2}\ \sum _{J} (2J+1)\ \left[ \, 1 - \left| S_0(J)\right| ^2\, \right] , \end{aligned}$$

(10)

where $S_0(J)$ is the elastic S-matrix in a collision with total angular momentum J.

However, Hagino et al. [36] proposed a CDCC based method that gives individual CF and ICF cross section in collisions of weakly bound nuclei. In their method, the TF cross section was evaluated directly by the expression,

$$\begin{aligned} \sigma _\mathrm{\scriptscriptstyle TF} = \frac{\pi }{k^2}\ \sum _{J} (2J+1)\ P_\mathrm{\scriptscriptstyle TF}(J). \end{aligned}$$

(11)

The TF probabilities were expressed as a sum of contributions from all channels (bound and unbound) involved in the CDCC equations. In each channel and for each J, this probability was determined by the flux that reaches the inner region of the barrier. The CF cross section was then associated with the contributions from the elastic channel (and from inelastic channels for bound excited states, if any), whereas the ICF cross section was given by the contribution from the bins. This method was used to study CF and ICF in the $^{11}$Be + $^{208}$Pb system. Their CDCC calculations were performed with real potentials, using the ingoing waves boundary conditions (IWBC) to account for fusion absorption. Comparing the obtained CF cross section with the fusion cross section without breakup couplings, they found enhancement at sub-barrier energies and suppression above the barrier.

Diaz-Torres and Thompson [62] used the same approach to evaluate CF and ICF for the same system. However, instead of IWBC, they used a short-range imaginary potential, W(R), depending exclusively on the distance between the centers of the projectile and the target. Thus, this potential is diagonal in channel space. The TF cross section was then given by the well known expression [2],

$$\begin{aligned} \sigma _\mathrm{\scriptscriptstyle TF} = \frac{k}{E}\ \sum _{\gamma ,\gamma ^\prime } \ \left\langle \psi _\gamma \left| \, - W_{\gamma \gamma ^\prime }\, \right| \psi _{\gamma ^\prime } \right\rangle , \end{aligned}$$

(12)

where $W_{\gamma \gamma ^\prime }$ are the matrix-elements of the imaginary potential and $\psi _\gamma$ is the projectile-target relative wave function in channel $\gamma$. Since $W_{\gamma \gamma ^\prime } = W_{\gamma \gamma }\cdot \delta _{\gamma ,\gamma ^\prime }$, the above expression reduces to

$$\begin{aligned} \sigma _\mathrm{\scriptscriptstyle TF} = \sum _{\gamma } \ \sigma _\mathrm{\scriptscriptstyle TF}^\mathrm{\scriptscriptstyle (\gamma )} \end{aligned}$$

(13)

with

$$\begin{aligned} \sigma _\mathrm{\scriptscriptstyle TF}^\mathrm{\scriptscriptstyle (\gamma )} = \frac{k}{E}\ \left\langle \psi _\gamma \left| \, W_{\gamma }\, \right| \psi _{\gamma } \right\rangle . \end{aligned}$$

(14)

The CF and ICF components of $\sigma _\mathrm{\scriptscriptstyle TF}$ where then evaluated by the method of Ref. [36]. That is, the cross sections $\sigma _\mathrm{\scriptscriptstyle CF}$ and $\sigma _\mathrm{\scriptscriptstyle ICF}$ were obtained restricting the sum of Eq. (13) to bound and to unbound channels, respectively. The calculations of Ref. [62] adopted a larger continuum space and took into account continuum-continuum couplings, neglected in Ref. [36], but qualitatively, they lead to the same conclusion, namely: enhancement of CF at sub-barrier energies and suppression above the barrier.

The calculations of Refs. [36, 62] have a limitation. They cannot be used in collisions of projectiles that break up into fragments of comparable masses. The association of ICF with unbound channels, where the two fragments tend to be far apart, is based on the assumption that the center of mass of the heavier fragment is very close to the center of the projectile. In this way, the imaginary potential absorbs the heavier fragment but not the lighter one. The method is justified in the case of $^{11}$Be, that breaks up into $^{10}$Be and a neutron, since the mass of the former is ten times larger than that of the latter. However, it cannot be used in collisions of nuclei like $^7$Li, that breaks up into a triton and an alpha particle. In this case the mass ratio is 4/3. To deal with this kind of weakly bound nuclei, it is necessary to use individual imaginary potentials for the two fragments. This generalisation has been carried out in a recent paper by Rangel et al. [63]. The extended method was applied to the $^7$Li + $^{209}$Bi system and the resulting CF and ICF cross sections were compared to the data of Dasgupta et al. [46, 54]. The theoretical predictions for both cross sections were in very good agreement with the data.

Another quantum mechanical method to evaluated $\sigma _\mathrm{\scriptscriptstyle CF}$ was recently proposed by Lei and Moro [64]. In a collision of a weakly bound projectile composed of fragments $c_\mathrm{\scriptscriptstyle 1}$ and $c_\mathrm{\scriptscriptstyle 2}$, the CF cross section was extracted from the expression,

$$\begin{aligned} \sigma _\mathrm{\scriptscriptstyle R} \simeq \sigma _\mathrm{\scriptscriptstyle CF} + \sigma _{\mathrm{inel}} + \sigma _\mathrm{\scriptscriptstyle EBU} + \sigma _\mathrm{\scriptscriptstyle NEB}^\mathrm{\scriptscriptstyle (c_1)} + \sigma _\mathrm{\scriptscriptstyle NEB}^\mathrm{\scriptscriptstyle (c_2)}, \end{aligned}$$

(15)

where $\sigma _\mathrm{\scriptscriptstyle R}$ is the total reaction cross section, $\sigma _{\mathrm{inel}}$ is the cross section for inelastic excitations, $\sigma _\mathrm{\scriptscriptstyle EBU}$ is the cross section for elastic breakup of the projectile, and $\sigma _\mathrm{\scriptscriptstyle NEB}^\mathrm{\scriptscriptstyle (c_i)}$ ($i=1,2$), is the cross section for nonelastic breakup, where fragment $c_i$ emerges from the interaction region and the target does not remain in its ground state (the other fragment may be captured by the target or collide inelastically with it). These cross sections were evaluated by different theoretical methods: $\sigma _\mathrm{\scriptscriptstyle R}$ and $\sigma _\mathrm{\scriptscriptstyle EBU}$ were determined by CDCC calculations with appropriate imaginary potentials, $\sigma _{\mathrm{inel}}$ was obtained through a standard coupled channel calculation involving the main collective states, and the nonelastic breakup cross sections were calculated by the spectator-participant inclusive breakup model of Ichimura, Austern, and Vincent (IAV) [45, 65, 66]. The IAV was used to calculate CF cross sections for the $^{6,7}$Li + $^{209}$Bi systems. The resulting cross sections at above-barrier energies were shown to be in good agreement with the data of Dasgupta et al. [46, 54]. We should also mention the work of Parkar et al. [67], were CF and ICF cross sections for the $^{6,7}$Li + $^{209}\mathrm{Bi}, ^{198}\mathrm{Pt}$ systems were obtained in approximate calculations with different short-range imaginary potentials. Their theoretical predictions were in reasonable agreement with the data of Refs. [46, 54] and [68, 69], respectively.

There are still other promising theoretical methods which have not yet been developed to the point of making quantitative predictions of CF and ICF data. Hashimoto et al. [70] proposed a CDCC-based method where the fusion cross sections were given by radial integrals of the fragment-target imaginary potentials, expressed in terms their separation vectors, $\mathbf {r}_1$ and $\mathbf {r}_2$. Then, the CF and ICF cross sections were respectively assigned to contributions from small and large values of $r_1$ and $r_2$ in the integrand. The same idea was used in a qualitative one-dimensional model proposed by Boseli and Diaz-Torres [71, 72], using position projected operators. The same authors proposed a time-dependent wave-packet approach to described collisions of three body systems, and performed calculations of $\sigma _\mathrm{\scriptscriptstyle CF}$ and $\sigma _\mathrm{\scriptscriptstyle ICF}$ for the $^6$Li + $^{209}$Bi system, within a schematic one-dimensional model. Their time-dependent method has also been used to study collisions of tightly bound systems [73, 74].

3 Elastic heavy-ion scattering

3.1 Rainbow and glory scattering

Let us next discuss elastic heavy-ion scattering. In the classical mechanics, the differential cross section is given by

$$\begin{aligned} \frac{d\sigma _{\mathrm{cl}}}{d\varOmega }=\frac{\lambda }{k^2\sin \theta } \left( \frac{d\varTheta (\lambda )}{d\lambda }\right) ^{-1}, \end{aligned}$$

(16)

where $\theta$ is a scattering angle, k is the wave number, and $\lambda$ is the angular momentum. $\varTheta (\lambda )$ is the scattering angle as a function of $\lambda$, that is, the deflection function. The classical cross section, Eq. (16), diverges at $d\varTheta (\lambda )/d\lambda =0$ as well as at $\sin \theta =0$, which are referred to as rainbow scattering and glory scattering, respectively. These are caustics in a sense that many angular momenta, $\lambda$, contribute coherently to scattering for a particular scattering angle $\theta$ and its vicinity.

In the semi-classical approximation, the deflection function $\varTheta (\lambda )$ is related to scattering phase shifts, $\delta _l$, for a partial wave l as [1],

$$\begin{aligned} \varTheta (\lambda )=2\frac{d\delta _l}{dl}\sim 2(\delta _{l+1}-\delta _l) \end{aligned}$$

(17)

with $\lambda =l+1/2$. Here, the phase shift $\delta _l$ is a sum of a nuclear phase shift $\delta ^{(N)}_l$ and the Coulomb phase shift $\delta ^{(C)}_l$, that is, $\delta _l=\delta ^{(N)}_l+\delta ^{(C)}_l$.

Fig. 3

The deflection function for the $\alpha$ + $^{90}$Zr scattering at energy $E_{\mathrm{lab}}=141.7$ MeV. It is obtained by neglecting the imaginary part of an optical potential of the Woods-Saxon form

Figure 3 shows a deflection function for $\alpha$ + $^{90}$Zr scattering at $E_{\mathrm{lab}}=141.7$ MeV in the laboratory frame. The phase shifts are evaluated with a Woods-Saxon potential with the depth, the range, and the diffuseness parameters of $V_0=117.5$ MeV, $R=1.267\times 90^{1/3}$ fm, and $a=0.783$ fm, respectively [75]. No imaginary part is included in the potential to draw the deflection function. One can see that the rainbow scattering takes place, at $\lambda =50.5$ with a rainbow angle of $\varTheta _R=4.34^\circ$ and at $\lambda = 31.5$ with $\varTheta _R=-73.4^\circ$. The former is due to a balance between the repulsive Coulomb interaction and an attractive nuclear interaction, and is referred to as the Coulomb rainbow scattering. On the other hand, the latter is due to purely a nuclear interaction, and is referred to as nuclear rainbow scattering. Scattering angles larger than $|\varTheta _R|$ are forbidden classically, but they are allowed in quantum mechanics due to the diffraction of a wave function; this is called shadow scattering. In addition to the rainbows, the deflection function crosses zero at $\lambda \sim 40$, that is the condition for (forward) glory scattering.

Fig. 4

(Top) The angular distribution for elastic $\alpha$+$^{90}$Zr scattering at $E_{\mathrm{lab}}=141.7$ MeV. It is given as a ratio to the Rutherford cross sections, $d\sigma _R(\theta )$. (Middle) The same as the top panel, but plotted in the linear scale for forward scattering angles. (Bottom) The absolute value of the nuclear scattering amplitude

The top panel of Fig. 4 shows the ratio of the differential cross sections to the Rutherford cross sections. To compute the cross sections, we include the imaginary part of the potential, with a Woods-Saxon parameterization with $W=21.02$ MeV, $R_w=1.267\times 90^{1/3}$ fm, and $a_w=0.783$ fm, together with the charge radius of $R_w=1.3\times 90^{1/3}$ fm for the Coulomb interaction [75]. This potential well reproduces the experimental data at $E_{\mathrm{lab}}=141.7$ MeV [75]. The cross sections show a bump around $\theta _{\mathrm{c.m.}}=45^\circ$, with an exponential fall off at larger scattering angles. This is a clear manifestation of the nuclear rainbow scattering. At angles smaller than the rainbow angle, there are two angular momenta which lead to the same scattering angle, as can be seen in the deflection function shown in Fig. 3. These two components interfere with each other, leading to a characteristic interference pattern given by the Airy function [1].

The middle panel of Fig. 4 shows the differential cross sections at forward angles in the linear scale. Here also one can see a characteristic interference pattern around $\theta _\mathrm{c.m.}=1.6^\circ$, which can be interpreted as the Coulomb rainbow scattering.

The bottom panel of Fig. 4 shows the absolute value of the nuclear scattering amplitude, $f_N(\theta )$. This quantity is enhanced at $\theta _{\mathrm{c.m.}}=0^\circ$, with characteristic oscillations. This is a manifestation of the glory scattering, for which the interference is originated from the contribution of the near-side component with $\theta$ and that of the far-side component with $-\theta$. In the semi-classical approximation, the nuclear scattering amplitude at forward angles is given by [1, 2],

$$\begin{aligned} f_N(\theta )\propto \sqrt{\frac{2\pi \theta }{\sin \theta }}\,J_0(\lambda _g\theta ), \end{aligned}$$

(18)

where $\lambda _g$ is the glory angular momentum at which the deflection function crosses zero. That is, the glory scattering is characterized by the zero-th order Bessel function, $J_0$.

Incidentally, the Rutherford cross section diverges at $\theta =0$ and it may not be straightforward to probe the forward glory scattering experimentally. Yet, one can still use the generalized optical theorem, that is, the sum-of-differences (SOD) method, to extract the nuclear scattering amplitude [15, 16, 76, 77]. The SOD cross section is defined as

$$\begin{aligned} \sigma _{\mathrm{SOD}}(\theta )=2\pi \int ^\pi _\theta \left( \frac{d\sigma _R}{d\varOmega '}-\frac{d\sigma }{d\varOmega '}\right) \, \sin \theta 'd\theta ', \end{aligned}$$

(19)

and is related to the total reaction cross section $\sigma _R$ and the nuclear scattering amplitude as

$$\begin{aligned}&\sigma _{\mathrm{SOD}}(\theta )\sim \sigma _{R} \nonumber \\&-\frac{4\pi }{k}|f_N(\theta )|\sin \left( \mathrm{arg} f_N(\theta )-2\delta ^{(C)}_0 +2\eta \ln \sin \frac{\theta }{2}\right) ,\nonumber \\ \end{aligned}$$

(20)

where $\eta$ is the Sommerfeld parameter. Here we have neglected small correction terms, which can be ignored when $\theta$ is small. Notice that one can also access to fusion cross sections by taking

$$\begin{aligned} \sigma '_{\mathrm{SOD}}(\theta )=2\pi \int ^\pi _\theta \left( \frac{d\sigma _R}{d\varOmega '}-\frac{d\sigma _\mathrm{qel}}{d\varOmega '}\right) \, \sin \theta 'd\theta ' \end{aligned}$$

(21)

in Eq. (19), where $d\sigma _{qel}/d\varOmega$ is the quasi-elastic cross section defined as a sum of elastic, inelastic, transfer, and breakup cross sections. In this case, $\sigma '_\mathrm{SOD}$ is related to fusion cross sections, $\sigma _{\mathrm{fus}}$, as [78],

$$\begin{aligned}&\sigma '_{\mathrm{SOD}}(\theta )\sim \sigma _{\mathrm{fus}} \nonumber \\&\quad -\frac{4\pi }{k}|f_N(\theta )|\sin \left( \mathrm{arg} f_N(\theta )-2\sigma _0 +2\eta \ln \sin \frac{\theta }{2}\right) . \end{aligned}$$

(22)

Fig. 5

(Upper panel) The angular distribution for elastic $^{16}$O + $^{208}$Pb scattering at $E_{\mathrm{lab}}=129.5$ MeV. It is given as a ratio to the Rutherford cross sections, $d\sigma _R(\theta )$. (Lower panel) The corresponding deflection function as a function of the angular momentum $\lambda$

In the $\alpha$ + $^{90}$Zr scattering shown in Fig. 3, the Coulomb rainbow angle is small and the forward scattering is actually affected both by the Coulomb rainbow scattering and by the glory scattering. The Coulomb rainbow is more clearly seen when a heavier nucleus is used as a projectile. In order to demonstrate this, the upper panel of Fig. 5 shows the elastic cross sections for the $^{16}$O + $^{208}$Pb system at $E_{\mathrm{lab}}=129.5$ MeV. The deflection function is also shown in the lower panel. To this end, we use the optical potential given in Ref. [79] (the deflection function is obtained using only the real part while the cross sections are calculated including both the real and the imaginary parts). The deflection function has a maximum at $\lambda =73.5$ with the rainbow angle of $48.9^\circ$. The scattering cross sections exhibit a characteristic Fresnel oscillation pattern, which can be interpreted as the Coulomb rainbow scattering (see Sec. 5.6 in Ref. [1] for a discussion on a relation between the Coulomb rainbow scattering and the Fresnel diffraction).

3.2 Glory in the shadow of rainbow

Even though Fig. 4 clearly shows the features of the nuclear rainbow and the glory scattering, the interference pattern becomes much more complex as the incident energy decreases. Moreover, the effect of absorption becomes more important. In particular, the deflection function may not cross zero but a minimum appears with a positive rainbow angle. This is illustrated in the upper panel of Fig. 6 for $\alpha +^{90}$Zr scattering at $E_{\mathrm{lab}}=40$ MeV. In this figure, the deflection function is decomposed into the barrier wave contribution and the internal wave contribution, where the former corresponds to the flux reflected at the barrier while the latter corresponds to the flux reflected at the innermost turning point [13]. The deflection function evaluated with a quantal calculation (the solid line) indicates that there is a crossover from the internal wave (the dot-dashed line) to the barrier wave (the dashed line) as the angular momentum increases, and that the barrier wave is responsible for the nuclear rainbow scattering for this system. An important feature is that the effect of nuclear interaction is not strong enough for the barrier wave so that the deflection function does not cross zero before it bends when the angular momentum decreases from the angular momentum for the Coulomb rainbow scattering. Interestingly, as shown in the lower panel of Fig. 6, the nuclear scattering amplitude still shows an enhancement at $\theta =0$ as in the glory scattering shown in the bottom panel of Fig. 4. That is, the nuclear scattering amplitude exhibits a similar behavior to glory scattering even though the deflection function does not cross zero.

Fig. 6

(Upper panel) The deflection function for $\alpha +^{90}$Zr scattering at $E_{\mathrm{lab}}=40$ MeV. The solid line is obtained with a quantum mechanical calculation. The dashed and the dot-dashed lines denote the deflection function for the barrier wave and the internal wave, respectively, obtained with the semi-classical approximation. The thin dashed line shows the deflection function for the pure Coulomb scattering. (Lower panel) The absolute value of the nuclear scattering amplitude. The solid line shows the result of the quantum mechanical calculation, while the dashed line is obtained with the semi-classical approximation. The dot-dashed line is obtained with a semi-classical formula which is valid at very small scattering angles. Taken from Ref. [16]

Fig. 7

A copy of a transparency which Mahir Hussein showed at the workshop on occasion of Noboru Takigawa’s 60th birthday (November 2003, Sendai, Japan)

In order to interpret this phenomenon, one of us (M.U.), together with Mahir Hussein, introduced a novel concept of glory in the shadow of rainbow [15, 16]. That is, when the deflection function does not cross zero, the zero scattering angle corresponds to the shadow region of the nuclear rainbow scattering. An important point is that the nuclear rainbow can still affect the zero angle scattering if the rainbow angle is small because of the diffractive nature of the wave function. Using the semi-classical approximation, one can actually derive the expression for the nuclear scattering amplitude for glory in the shadow of rainbow as [15, 16],

$$\begin{aligned} f_N(\theta )\propto \sqrt{\frac{2\pi \theta }{\sin \theta }}\, (A_+(\theta )J_0(\lambda _{\mathrm{NR}}\theta ) +iA_-(\theta )J_0(\lambda _{\mathrm{NR}}\theta )) \end{aligned}$$

(23)

with

$$\begin{aligned} A_\pm (\theta )= & {} \mathrm{Ai}(\xi _1)\pm \mathrm{Ai}(\xi _2), \end{aligned}$$

(24)

$$\begin{aligned} \xi _1= & {} \left( \frac{\varTheta ''_{\mathrm{NR}}}{2}\right) ^{-1/3}(\theta _\mathrm{NR}+\theta ), \end{aligned}$$

(25)

$$\begin{aligned} \xi _2= & {} \left( \frac{\varTheta ''_{\mathrm{NR}}}{2}\right) ^{-1/3}(\theta _\mathrm{NR}-\theta ), \end{aligned}$$

(26)

where $\mathrm{Ai}$ denotes the Airy function and $\lambda _{\mathrm{NR}}$ is the nuclear rainbow angular momentum at which the deflection function takes a minimum. $\theta _{\mathrm{NR}}$ and $\varTheta ''_{\mathrm{NR}}$ are the scattering angle and the curvature of the deflection function at $\lambda =\lambda _{\mathrm{NR}}$, respectively. Notice that Eq. (23) is indeed similar to the formula for glory scattering, Eq. (18), with a replacement of the glory angular momentum $\lambda _g$ with the nuclear rainbow angular momentum $\lambda _{\mathrm{NR}}$. In the bottom panel of Fig. 6, one can see that the semi-classical formula (the dashed line) well reproduces the quantum mechanical calculation (the solid line), supporting the concept of glory in the shadow of rainbow.

4 Summary

We have discussed the semi-classical approaches to low-energy heavy-ion reactions, focusing on heavy-ion fusion reactions of neutron-rich nuclei and the phenomena of nuclear rainbow and glory scattering in elastic heavy-ion scattering. Mahir Hussein significantly contributed to both topics, enhancing our understanding of the nature of low-energy heavy-ion reactions. We mention that fusion of neutron-rich nuclei are still important in connection to fusion in neutron stars, as well as syntheses of superheavy nuclei, especially attempts to reach the island of stability. Towards these goals, there are still many interesting topics to clarify in fusion of neutron-rich nuclei, such as an interplay between breakup and transfer.

We would like to close this paper by showing a parody of “what a wonderful world” which Hussein showed at the meeting for Takigawa (see Fig. 7 with slight modifications by us), since we feel that lyrics nicely reflects Hussein’s nature as a nuclear physicist.

• “What a Wonderful World” (with apologies to Louis Armstrong)

• I see trees of green, red roses too

• I see them bloom for me and you

• And I think to myself what a wonderful world

• I see skies of blue and clouds of white

• The bright blessed day, the dark sacred night

• And I think to myself what a wonderful world

• The colors of the RAINBOW so pretty in the sky

• And also on the faces of people going by

• I see Mahir shaking hands saying how do you do

• With a GLORY on his head telling the story of his life

• I hear babies crying, I watch them grow

• They’ll learn much more than we’ll never know

• And I think to myself what a wonderful world.