Fission barriers of actinide nuclei with nuclear density functional theory: influence of the triaxial deformation

Abstract

The fission pathway of even–even actinide nuclei have been systematically calculated using the deformation-constrained nuclear density functional theory beyond the second fission barriers within the UNEDF1 energy-density functionals (EDFs). Our calculated results show that, allowing for triaxial deformation, the second fission barriers are lowered by a few hundreds of keV to 2 MeV. For the heaviest actinides, it is found that inclusion of triaxial deformation reduces the outer barrier significantly.

1 Introduction

Since the 1950s, spontaneous fission has been understood as a process where heavy compound nuclei undergo a series of deformation changes or elongations, eventually splitting into two or three lighter daughter nuclei. The height ($E_{\mathrm{B}}$), and in general the shape, of the fission barrier of a nucleus is a fundamental quantity. Indeed, a number of observables related to the fission of a heavy nucleus as well as the fusion of two nuclei depend on $E_{\mathrm{B}}$ sensitively [1,2,3,4,5,6], such as the fission half life, and the fusion cross section. Whether a good description of $E_{\mathrm{B}}$ can be achieved in turn provides valuable constraints on the relevant nuclear model used.

From a perspective of nuclear mean-field model [7], the total energy ($E_{\mathrm{tot}}$) of a nucleus is a function of its intrinsic deformations [8, 9]. In the fission process, the compound system undergoes a complex shape trajectory towards scission, before splitting up. To determine the optimal/favored trajectory through which a fissioning nucleus most likely undergoes, one needs to perform extensive nuclear calculations as $E_{\mathrm{tot}}$ is a function of a large set of shape degrees of freedom. For example, in the recent macroscopic-microscopic calculations [10,11,12,13,14,15,16], one typically deals with 5 (or more) shape degrees of freedom, containing deformation points in the order of a few millions.

With the self-consistent mean-field models such as the nuclear density functional theory (DFT) [17,18,19,20,21,22,23,24], the relativistic mean field theory [26, 27], or the DFT with the finite-range Gogny force [28,29,30], performing the above-mentioned amount of separate calculations is nearly impossible. Instead, one picks a few important “active” deformation degrees of freedom to map out $E_{\mathrm{tot}}$, and releases the “background” deformations to be determined self-consistently through the variational process. To balance the needs for a fully minimized fissioning path with respect to the various shape degrees of freedom, and the huge amount of computing time, one frequently chooses the “active” deformations based on the physical insights. Frequently, the calculations enforce relevant symmetries on the fissioning nucleus due to limitations of computation resources.

For example, for the lowest-energy fission path of $^{240}$Pu using SkM* energy-density functional (EDF), it is known that the triaxial deformation is important for lowering the height of the first fission barrier (EB1). After the first fission barrier, the inclusion of the triaxial deformation has been shown to lower the second fission barrier [25]. Note, that the above-mentioned second fission barrier of $^{240}$Pu has been calculated with octupole moments being constrained to zero, rather than the one following the lowest-energy path. For enlongation larger than that corresponds to fission isomer until scission [29, 31, 32], the axially symmetric octupole deformation becomes important. The triaxial deformation has been shown to be unable to lower the second barrier of $^{240}$Pu with non-zero octupole deformation using SkM* EDF [25]. The existence of this reflection-asymmetric path is responsible for the dominance of the asymmetric fission in these actinide nuclei.

In this work, we plan to study the optimal trajectory of the fissioning actinide nuclei using the nuclear DFT. In particular, our goal is to see if the triaxial degree of freedom could still lower the second fission barrier before fission in the actinide nuclei. We notice that the triaxial deformation is important for lowering the second fission barriers for these nuclei in the relativistic mean field model [33, 34]. Section 2 briefly introduces the nuclear DFT calculation, and compares our results with existing calculations. In Sect. 3, we show the main results of the current work, before a summary in Sect. 4.

2 The model

We calculate $E_{\mathrm{tot}}$ using the nuclear DFT. Being a self-consistent mean-field theory, it allows for identifying the optimal deformation minimizing the binding energy self-consistently, given large enough model space. To access the full trajectory through which the fissioning nucleus undergoes, one needs to perform calculations where the quadrupole moments are constrained to the desired values. In this study, these calculations are performed using the symmetry-unrestricted solver HFODD (version 2.68f) [35]. In the current work, where we discuss the favored paths of fission through the double-humped energy curve of the actinide nuclei, we decide to adopt the more recent UNEDF1 EDF [36] which is fitted taking into account the excitation energies of the fission isomers of the actinides.

At each deformation point, defined by a set of constrained multipole moments, the Skyrme Hartree–Fock–Bogolyubov equations are solved, where $E_{\mathrm{tot}}$ of the system is always minimized with respect to the unconstraint moments (“background” deformation). In practice, this is done by constraining the obtained multipole moments $Q_{\lambda \mu }$ using the Augmented Lagrangian method (ALM) [37]. The quadrupole moments, $Q_{20}$ and $Q_{22}$ moments, are defined as follows

$$\begin{aligned} Q_{20}&=\langle 2\hat{z}^2-\hat{x}^2-\hat{y}^2 \rangle , \end{aligned}$$

(1)

$$\begin{aligned} Q_{22}&=\sqrt{3}\langle \hat{x}^2-\hat{y}^2 \rangle . \end{aligned}$$

(2)

The expectation value of the multipole moments, $\langle \hat{Q}_{\lambda \mu } \rangle$, with $\lambda >2$, are defined as

$$\begin{aligned} \langle \hat{Q}_{\lambda \mu } \rangle =\langle r^{\lambda }Y^*_{\lambda \mu }(\theta ,\phi )\rangle . \end{aligned}$$

(3)

In the current work, which includes $Q_{\lambda \mu }$ with the positive $\mu$, the real part of $\langle \hat{Q}_{\lambda \mu } \rangle$ has been used [38], namely

$$\begin{aligned} Q_{\lambda \mu }=\mathcal {R}\langle \hat{Q}_{\lambda \mu } \rangle , \quad for\quad \lambda >2. \end{aligned}$$

(4)

The HFODD code uses a set of three-dimensional (3D) harmonic oscillator (HO) basis which is particularly efficient for the calculation of nuclei with relatively smaller deformations. To compute systems involving large nuclear deformation (with long-axis-to-short axis ratio larger than 2), such as those involved in the fission process, it is essential to find the optimal parameters defining the HO basis.

To account for the deformed nucleus, HFODD allows for using a non-uniform HO basis in three space directions. It uses a set of numbers, $\beta _{\lambda \mu }$, as coefficients to expand the surface of the considered nucleus on the spherical harmonics [7]. Upon finding the (assumed) sharp edges in the three directions, $R_x, R_y, R_z$, one determines the frequencies according to

$$\begin{aligned} \omega _0^3&= \omega _x\omega _y\omega _z=(41 \times 1.2)^3 / A~\mathrm{MeV}, \end{aligned}$$

(5)

$$\begin{aligned} \omega _x R_x&= \omega _y R_y=\omega _z R_z. \end{aligned}$$

(6)

The $N_{\mathrm{max}}$ parameter adds limits on the largest number of the HO basis in the three directions by requiring $N_{x,y,z}<N_\mathrm{max}$. Finally, the $N_{\mathrm{states}}$ parameter limits the total number of 3D HO states. For an $N_{\mathrm{max}}$ that is large enough, the parameters, $N_{\mathrm{states}}$ and $\beta _{\lambda \mu }$, determine the largest number of the HO shells in the three Cartesian directions.

Ideally, at each quadrupole deformation, one should optimize the basis in such a way that it minimizes $E_{\mathrm{tot}}$ for sufficiently large total number of HO basis. However, this procedure would be computationally laborious. To limit the free deformation parameters, one first realizes that $\beta \equiv \beta _{20}$ is the most important one in determining the non-uniformity of the 3D HO basis. This is so because compared to other deformations in the fission process, elongation ($Q_{20}$) is by far the largest compared to the triaxial or octupole deformations.

In practice, the $\beta$ value is determined to follow the physical quadrupole deformation of the calculated nucleus [36, 39]. Here we adopt an empirical procedure. Namely, we use a few $\beta$ values to compute the full energy-$Q_{20}$ curves. An optimal $\beta$ value is then obtained for each $Q_{20}$ interval by examining whether it gives the lowest energy for that $Q_{20}$ interval.

Fig. 1

$E_{\mathrm{tot}}$ (with respect to the ground states) as functions of the $Q_{20}$ values of $^{240}$Pu using UNEDF1 EDF with the axial and reflection-symmetric deformations (a). A few $\beta$ values (0.3, 0.5, 0.8, 1.2, 1.5) for basis deformations are used to find out an optimal one at a certain deformation interval. The sub-plots b–e zoom in important local parts: the top areas of the two fission barriers, the minima for the ground states, as well as those of the fission isomers for better visualization

Figure 1a compares the energy-$Q_{20}$ curves of $^{240}$Pu for five different $\beta$ values using the UNEDF1 EDF. In these calculations, we consider only the variation of axially symmetric quadrupole moments $Q_{20}$ ($Q_{30}=0,Q_{22}=0$). Figure 1b–e zooms in the important local intervals of the full curves of Fig. 1a. We see from these figures a clear pattern that the optimal $\beta$ parameter minimizing $E_{\mathrm{tot}}$ seems to follow the growth of the physical deformation of the nucleus. Specifically, for the $Q_{20}$ in the interval of [0,75] b, a $\beta \approx 0.3$ is providing a lower $E_{\mathrm{tot}}$. Whereas for the $Q_{20}=75-200$ b, one needs a $\beta$ value of 0.5 or 0.8. For $E_{\mathrm{tot}}$ beyond the outer barrier ($Q_{20}>200$ b), one needs a $\beta >0.8$.

Fig. 2

The parameters used to specify the HO basis, adopted in this work (solid lines), as well as those adopted in Refs. [36, 39]

To illustrate the accuracy of our calculation, the other two sets of calculations using the continuous $\beta$ values (shown in Fig. 2b) are also performed. The first scheme in Fig. 2b shown by a solid red line with squares is from Ref. [36], where the $\omega _0$ and $\beta$ values vary with the desired expectation value of $Q_{20}$ according to

$$\begin{aligned} \omega _0 = \left\{ \begin{array}{ll} 0.1 \times Q_{20}e^{-0.02Q_{20}} + 6.5\, \mathrm {MeV} &{} \text {if }|Q_{20}|\le 30 \mathrm { b},\\ 8.14\, \mathrm { MeV} &{} \text {if }|Q_{20}| > 30 \mathrm { b},\\ \end{array} \right. \nonumber \\ \end{aligned}$$

(7)

and

$$\begin{aligned} \beta = A {Q^3_{20}}+B{Q^2_{20}}+C{Q_{20}}, \end{aligned}$$

(8)

with $A=3.16721\times 10^{-8}$ $\hbox {b}^{-3}$, $B=-2.75505\times 10^{-5}$ $\hbox {b}^{-2}$, $C=0.00954925$ $\hbox {b}^{-1}$. The other scheme is from Ref. [39], where the $\beta$ value is determined through

$$\begin{aligned} \beta = 0.05 \sqrt{Q_{20}}. \end{aligned}$$

(9)

From Fig. 2b we see that our scheme seems to be closer to that adopted in Ref. [36].

Fig. 3

$E_{\mathrm{tot}}$ (with respect to the ground state) of $^{240}$Pu as a function of $Q_{20}$, calculated using UNEDF1 EDF. The curves have been minimized with respect to $Q_{22}$ for $Q_{20}\le 100$ b; and with respect to $Q_{30}$ for $Q_{20}>100$ b. The three curves are obtained using the basis parameters shown in Fig. 2. The vertical dashed lines partition the graph into four $Q_{20}$ intervals where different $\beta$ parameters are used (see Fig. 2b)

Fig. 4

Similar curves as those in Fig. 3, except that this figure contains additional results with different ($N_{\mathrm{max}}, N_{\mathrm{states}}$) combinations. The energy curve calculated using a given ($N_{\mathrm{max}}, N_{\mathrm{states}}$) combination has been normalized with respect to the ground state

Fig. 5

$E_{\mathrm{tot}}$ (with respect to the ground state) as a function of the $Q_{20}$ value, calculated using UNEDF1 EDF. The curve with diamonds corresponds to a situation where both $Q_{20}$ and $Q_{30}$ values are constrained to 0; the one with circles is identical with those shown in Fig. 3; and the one with triangular symbols corresponds to the results where a minimization with respect to the $Q_{22}$ has been carried out for the outer barrier based on the curve with circles

Fig. 6

The two-dimensional total-energy surfaces of $^{240}$Pu as functions of $(Q_{20},Q_{30})$ (a) and $(Q_{20},Q_{22})$ (b) using the UNEDF1 EDF. The purple dots, which are resulted from the unconstrained calculations, denote the lowest-energy pathways

$E_{\mathrm{tot}}$ of $^{240}$Pu as a function of the $Q_{20}$ value, calculated using the three schemes as described above are summarized in Fig. 3. One can see that the energy obtained within these three schemes are fairly close to each other for the quadrupole moment concerned in the current work ($Q_{20}<250$ b). The same $\beta$ parameter used in the relevant deformation intervals are marked out. At the border of the discrete $\beta$ values, there appears to be a continuous variation of $E_{\mathrm{tot}}$. We have checked that the multipole moments vary continuously when the $\beta$ value varies.

The current survey shown in Figs. 1 and 3, indicates that all three schemes seem to provide reasonable precisions for the calculated energy curves. Our results in this section is necessary, for it numerically adds, in a way, justifications for the optimal parameters in the form shown in Eq. (7), especially for the $Q_{20}\ge 100$ b.

To examine the convergence of the calculation with respect to the $N_{\mathrm{states}}$ and $N_{\mathrm{max}}$ parameters, we show the results with the increase of them in Fig. 4. We see that for a fixed $N_{\mathrm{max}}$, increasing $N_{\mathrm{states}}$ from 1140 to 1540 results in the excitation energies (with respect to their respective ground states) at the top of the outer barrier being lowered by $\approx$150 keV. For a fixed $N_{\mathrm{state}}$, increasing $N_\mathrm{max}$ value from 20 to 31 results in a lowering of $E_{\mathrm{tot}}$ by $\approx$150 keV.

It has to be mentioned that even with the largest basis shown in Figs. 3 and 4, where ($N_{\mathrm{states}}, N_{\mathrm{max}}$)=(1540, 31), the absolute $E_{\mathrm{tot}}$ is still converging. Indeed, a Hartree-Fock calculation in the 3D Cartesian coordinate space with a large enough box, and a fine enough grid give $E_{\mathrm{tot}}$ about 1 MeV lower for $E_{\mathrm{II}}$ of $^{240}$Pu, compared to the current HFODD result with ($N_\mathrm{states}, N_{\mathrm{max}})=(1540, 31)$. Nevertheless, the results in the current section suggest that, with properly optimized basis, the relative $E_{\mathrm{tot}}$ with respect to the ground states can be adequately converged, as shown in Figs. 3 and 4. This justifies earlier studies using even smaller number of HO basis to calculate fission curves. Similar basis optimizations have been performed in Refs. [33, 36].

In this work, we choose to use $(N_{\mathrm{states}}, N_{\mathrm{max}})=(1140, 20)$. This choice is a compromise between the computing resources available and the precision needed. From Fig. 4, it can be said that the outer barrier is $\approx$300 keV overestimated using this set of basis. The lowering increases with the $Q_{20}$ value. The main conclusion that the additional $Q_{22}$ minimization brings down the heights of the outer barriers of actinide nuclei is independent from this limitation of basis number.

Fig. 7

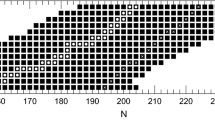
Similar quantities as those shown in Fig. 5, except that the calculations have been extended to a number of actinide nuclei with neutron number $N\le 146$. Specifically, the solid black curves in this plot correspond to the situation with red circles, and the dashed red curves correspond to the blue triangles shown in Fig. 5. The experimental data, denoted with horizontal lines, are extracted from Refs. [41, 42]

3 Results and discussions

In Fig. 5 we show $E_{\mathrm{tot}}$ with respect to the ground-state energies of $^{240}$Pu as a function of the $Q_{20}$ value from a value near the ground state ($Q_{20}\approx 30$ b) to a $Q_{20}>200$ b corresponding to a deformation beyond the second barrier. The different curves display the results with increasing restrictions on multipole moments being removed.

The green solid curve with squares takes into account only the $Q_{20}$ quadrupole moment, whereas the $Q_{22}$ and $Q_{30}$ values are constrained to be zero. The red solid line with circles shows the results where $Q_{30}$, which measures the axially symmetric octupole deformation, is allowed to deviate from zero. This energy curve is denoted with $E^{Q_{30}}(Q_{20})$. Further, the curve of $E^{Q_{30}}(Q_{20})$ is minimized with respect to the axially asymmetric quadrupole moment $Q_{22}$ (blue triangular symbol), which is denoted with $E^{Q_{30,22}}(Q_{20})$.

We see from Fig. 5 that the red line with circles allowing for asymmetric fission considerably brings down the outer fission barrier compared to the reflection-symmetric curve for $^{240}$Pu with the UNEDF1 EDF. Further removal of the constraint on the $Q_{22}$ value lowers the first fission barrier by about 3 MeV. We notice a small decrease in energy for the second fission barrier due to the additional inclusion of the triaxial degree of freedom. For $^{240}$Pu, the largest lowering is about 400 keV. With SkM* EDF [25] the inclusion of the $Q_{22}$ minimization has been shown to be unable to lower this second barrier along the lowest-energy path. Recently, a set of new parametrizations, SLy5sX have been obtained [40]. These new fits apply a constraint on the extracted surface term ($a_{\mathrm{surf}}$) in the fitting process. Using the SLy5sX EDFs, the calculated lowest-energy fission paths of $^{240}$Pu show nonzero $Q_{22}$, and a similar decrease of the heights of the outer barrier [40]. Similar results have also been obtained in relativistic mean field calculations [33, 34].

To better illustrate the effects of these two degrees of freedom, ($Q_{30}, Q_{22}$), on the second fission barrier, we plot the total-energy (with respect to the ground-state energies) surfaces of $^{240}$Pu as functions of ($Q_{20},Q_{30}$) in Fig. 6a, and as functions of ($Q_{20},Q_{22}$) in Fig. 6b. For Fig. 6a, the $Q_{22}$ values are constrained to be 0. The rest of the multipole moments other than $Q_{22}$ and $Q_{30}$ are unconstrained. We observe that the fission path denoted by the purple dots follows a mass-asymmetric (non-zero $Q_{30}$) path, which means that the mass distribution of the fission fragments of $^{240}$Pu is predominantly asymmetric. Along this asymmetric fission pathway, we plot $E_\mathrm{tot}$ in the $(Q_{20},Q_{22})$ plane, shown in Fig. 6b. We see a clear favorable path around the second fission barrier with $Q_{22}\ne 0$ at $Q_{20}\sim 130$ b.

Figure 7 displays the potential energies as functions of the $Q_{20}$ values for a few Th, U, Pu, and Cm isotopes with $N\le 146$. For the solid black lines, the results with the $Q_{20}$ smaller than the values corresponding to the fission isomers are obtained with the $Q_{22}$ values being minimized. Whereas the $Q_{30}$ values are zero by asking the HFB problem to conserve the parity symmetry. For the $Q_{20}$ values larger than the values corresponding to the fission isomers, the $Q_{22}$ values are constrained to zero using ALM. Here, the $Q_{30}$ values are allowed to deviate from zero by removing the parity symmetry. The dashed red lines differ from the solid black ones by the fact that, for the $Q_{20}$ values larger than the one corresponding to the fission isomers, an additional $Q_{22}$ minimization has been performed based on the solid black lines.

Fig. 8

The ($Q_{20}, Q_{22}$) (upper), and ($Q_{20},Q_{30}$) (lower) values along the lowest-energy fission paths for nuclei in Fig. 7

For $^{230,232}$Th, where the ground states might have nonzero $Q_{30}$ values, we have performed calculations where the $Q_{30}$ is constrained to a few finite values, while other multipole moments, such as $Q_{20}$, are unconstrained. We note that, for both nuclei, the ground states have $Q_{30}=0$. The energy curve for $^{230}$Th is flat in the $Q_{30}$ direction, indicating a ground state with nonzero $Q_{30}$, when the parity projection is performed on the currently obtained HFB ground state.

For some of the heaviest isotopes calculated in Fig. 7, experimental data¹ exist for the inner barrier heights (EB1), the excitation energies of the fission isomers ($E_{\mathrm{II}}$), and the outer barrier heights (EB2), which are marked out in the plots by blue, purple, and green lines, respectively. Figure 8 shows the $(Q_{20}, Q_{30})$ and the $(Q_{20}, Q_{22})$ values corresponding to $E^{Q_{30,22}}(Q_{20})$ curves in Fig. 7. We see a similar pattern in these curves where a $(Q_{20}, Q_{22})$-path around the second barrier appears by having a non-zero $Q_{22}$ value. The lowering in the height of the second barrier is relatively small ($<400$ keV) as compared to their heavier isotopes, as will be shown below.

For the heavier U, Pu, Cm, and Cf isotopes, the same quantities as those in Figs. 7 and  8 are plotted in Figs. 9 and 10, respectively. Compared to their lighter isotopes, EB2 values of these nuclei are lowered more significantly by having nonzero $Q_{22}$ values near the outer barrier. For $^{248,250}$Cm, $^{248-254}$Cf, the second barriers become thinner when the axial symmetry is relaxed. From Fig. 10 it can be seen that the largest deviations of the $Q_{22}$ values from zero is around 7 b for these Cm and Cf nuclei.

Fig. 9

The same as Fig. 7, except for selected actinide nuclei with $N>146$

From Fig. 10, an interesting observation is that, the appearance of the non-zero $Q_{22}$ around the top of the second fission barriers is accompanied with the decrease of the slopes of the $Q_{30}$ values as functions of the $Q_{20}$ values. This effect is particularly significant for the heaviest Cm and Cf isotopes, compared to the rest of the actinide nuclei studied here. In Fig. 11, we plot the $Q_{22,32,42,30,40}$ multipole moments along the paths with and without the $Q_{22}$ minimization. We notice that the removal of the axial symmetry results in the nonzero values for the high-order ($\lambda >2$) non-axial multipole moments.

Figure 12 shows the proton and neutron pairing energies of $^{254}$Cf with and without the $Q_{22}$ minimization near the outer barrier. If the fission barrier follows the $Q_{22}=0$ path, there seems to be an enhancement of the neutron pairing energy near the barrier. But this enhancement is reduced by a minimization on the $Q_{22}$ values. The fairly large different neutron pairing energies ($\Delta E^{\mathrm{n}}_{\mathrm{pairing}}\le 3$ MeV) along the paths with and without axial asymmetry indicate different underlying single-particle structures. This may suggest some adjustments of the predicted half lives when the $Q_{22}$ value is allowed to deviate from zero.

Fig. 10

The same as Fig. 8, except for nuclei in Fig. 9

Fig. 11

The $Q_{22}$, $Q_{32}$, $Q_{42}$, $Q_{30}$, and $Q_{40}$ values of $^{254}$Cf as a function of the $Q_{20}$ value, near the outer fission barrier. The dashed lines correspond to the pathways with $Q_{22}=0$

Table 1 lists EB1, $E_{\mathrm{II}}$, and EB2 values extracted from Figs. 7 and 9. For EB1 and EB2 values, the numbers are measured from the ground states, which are zeros, to the highest points of the maxima. A comparison can be made with experimental data [41, 42]. Since the UNEDF1 EDF is fitted taking into account $E_{\mathrm{II}}$ values, we focus on the influence of the $Q_{22}$ minimization on EB2 values. We have added results from Ref. [36], where $Q_{22}$ minimization is not taken into account. Together with our results suppressing $Q_{22}$, there are four columns in Table 1 for EB2 values.

Table 1 EB1, $E_{\mathrm{II}}$, and EB2 values extracted from Figs. 7, and 9. The columns with “exp.” are from Refs. [41, 42]. For EB2 values (the last 4 columns), we add the results without $Q_{22}$ (red dashed lines in Figs. 7, and 9). For comparison, we also add the axial results from Ref. [36] for EB2

Comparing our results with $Q_{22}=0$ (“Axial”) with that of Ref. [36], we see that our results are higher by $<200$ keV. This is due to the fact that we use $N_{\mathrm{max}}=20$, instead of $N_{\mathrm{max}}=31$, which has been used in Ref. [36]. For $^{242,244}$Pu, $^{244-248}$Cm, the $Q_{22}$ minimization brings the curves closer to the experimental data. In particular, EB2 values are lowered by about 1 MeV for $^{248}$Cm, which is much closer to experimental data compared to the axial results.

Fig. 12

The proton and neutron energies as a function of $Q_{20}$ near the outer fission barrier. The dashed lines denote quantities along a path with $Q_{22}=0$

However, one has to be careful interpretating the seemingly closeness to the data for EB2 values, when the $Q_{22}$ minimization is allowed. First, as noted before, the experimental data for EB1, $E_{\mathrm{II}}$, and EB2 [41, 42] are extracted by fitting them, through model calculations, to calculate a number of observables. These observables are confronted with direct experimental data, such as the cross sections of the slow-neutron induced fission reactions. Hence, these indirect data may serve as references for the current static calculations. To evaluate the success of such calculations, one needs to compute the direct observables, such as the fission half live, which is our future work.

Second, the heights of the outer barriers of these actinides may have been overestimated by about 300 keV due to the limited number of basis, see the discussions of Figs. 3 and 4. Nevertheless, it is reasonable to say that the inclusion of $Q_{22}$ minimization brings the outer barrier heights closer to data for $^{248}$Cm. For the even heavier actinides, one needs to take into account of the triaxial degree of freedom near the outer barrier when performing potential-energy surface calculations.

4 Summary

To summarize, we apply the deformation-constrained nuclear density-functional theory (DFT), using the UNEDF1 energy-density functional (EDF), to the description of the fission barriers of even–even actinide nuclei. To find out the lowest $E_{\mathrm{tot}}$ that follows the optimal fission pathways, we adopt a set of parameters where the $\beta$ value takes a stepped function with the $Q_{20}$ value of the nucleus. With this choice of parameter, our results are very close to those of previous studies about the fission barriers of $^{240}$Pu and reproduce the experimental data reasonably well.

In order to study the impact of the $Q_{22}$ moments on the outer fission barrier of the actinide nuclei, we conduct systematic constraint calculations of the lowest-energy fission pathways for these nuclei. It is found that the outer barriers calculated using the UNEDF1 EDF are lowered by including the minimization of the $Q_{22}$ value. The lowering increases with neutron and proton numbers. For the heaviest isotopes of the Cm and Cf isotopes, the width of the barriers are also reduced. This work indicates the importance of triaxial deformation for calculating fission properties which depend on the precise fission pathway such as the half-lives and the fusion cross sections and so on. Our future work will study how the inclusion of the triaxial degree of freedom near the outer barrier would impact the predicted fission half lives and fission yields.