INTRODUCTION

Establishing the structure–property relationships is one of the main goals of basic research in the field of membranes and membrane technologies [1]. Regarding ion-exchange membranes (IEMs), two types of models used as a theoretical basis for considering this problem can be distinguished. Models of the first type called “solution–diffusion” models [2–4] suggest that the transported substances dissolve in the membrane material and then are transferred through the membrane by the action of concentration or potential gradients, if any. Generally, the driving force causing the transport of ions in the membrane material is the gradient of electrochemical potential [5, 6].

The term “solution–diffusion” is used in contrast to the “pore flow” term, which refers to models considering the membrane as a system of flow-through pores. In such models, the transport of particles is described inside a separate pore filled with a solution [2, 7]. At the same time, the uneven distribution of concentrations and potential in the cross section perpendicular to the pore walls is considered. The unevenness is due to the fact that the pore walls have an electric charge imparted to them by fixed ions. In particular, such models take into account the presence of the electrical double layer (EDL) adjacent to the pore wall.

In the “solution–diffusion” models, the membrane is most often considered a homogeneous medium [8–10], namely, a uniform swollen sponge consisting of a polymer matrix with fixed ions which charge is compensated by the charge of the internal solution containing counterions and coions [8]. Such a homogeneous medium is often called charged gel [8]. However, there is a class of models that consider the presence in a membrane of at least two phases, the phase that includes a polymer or a crystalline matrix, which often carries a fixed electric charge balanced by mobile ions present in this phase, and the phase of solution between membrane pores [4, 11–18]. One of such models is the microheterogeneous model [19–25]. The model is based on a simplified representation of the membrane structure, according to which the IEM characteristics are determined by the properties of two phases. The gel phase is a microporous swollen medium, which includes both a polymer matrix with fixed groups and a charged solution of mobile counterions (and fewer coions) compensating the charge of fixed groups. The second phase is an electrically neutral solution (identical to the external solution), which fills the intergel spaces: membrane structural defects, macropores, and the central part of mesopores. This model attracts interest because it can describe almost all transport properties of homogeneous and heterogeneous membranes using a small set of parameters. Therefore, the microheterogeneous model is widely used to process and interpret the concentration dependences of specific electrical conductivity [10, 13, 25–27], diffusion permeability [20, 28, 29], electrolyte sorption [21, 27, 30], swelling [27], and other IEM characteristics.

Unfortunately, the basic microheterogeneous model is applicable only in the concentration range of 0.1–1 mol/L. The applicability of the microheterogeneous model to dilute solutions is limited primarily because of the assumption that the volume fractions of membrane phases are independent on the concentration of the external electrolyte. However, in classical electrochemistry, it is well known [31] that the length of the diffuse part of the electrical double layer depends on the concentration of the solution bordered by the charged surface. In the case of IEMs, EDL is formed in the pores of the swollen membrane and, as shown recently by Porozhnyy and coworkers [32, 33], it can have a noticeable effect on membrane transport characteristics. In the aforementioned papers, a modification of the basic microheterogeneous model is presented, which takes into account the presence of nanoparticles in the membrane pores, the surface of which may have an electric charge. Using this model, it has been shown that the features of the concentration dependences of the electrical conductivity and diffusion permeability of membranes with immobilized nanoparticles, as well as the growth of membrane selectivity, are due to the substitution of a part of the internal electroneutral solution with a nonconducting phase (body or core of the particle) and the electrical double layer at the nanoparticle charged surface.

This study deals with improving the basic microheterogeneous model.

The aim of the study is to take into account possible changes in the volume of the diffuse region of the electrical double layer in pores of an ion-exchange membrane and analyze the effect of this factor on both the electrical conductivity of the membranes, depending on the concentration of an external NaCl solution, and the membrane pore geometry and size. From the viewpoint of the above-mentioned classification, the proposed model can be called hybrid; on one hand, it takes into account the presence of mobile ions in the solution and gel phases (as the “solution–diffusion” model) and, on the other hand, it takes into account the presence of EDL in the membrane pore space as it is used in the “pore flow” models.

THEORETICAL

Basic Microheterogeneous Model

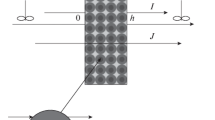
According to the basic microheterogeneous model [20], the ion-exchange membrane consists of two phases: the gel phase and that of an electroneutral solution with volume fractions fg and fs, respectively (fg + fs = 1). The model assumes that the intrapore electroneutral solution is identical to the external solution. The basic idea of simulating ion transport in a membrane represented in the form of several phases is to ascribe certain physicochemical properties to each region (phase) and describe properties of the membrane as a whole as a function of the properties of individual regions (the effective medium theory). Fig. 1

Fig. 1.
figure 1

Schematic representation of the structure of the ion-exchange membrane at the nanometer scale in accordance with the microheterogeneous model (adapted from [34]).

Full size image

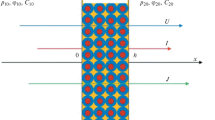
The flux of ions of the ith type in a two-phase system is proportional to the electrochemical potential gradient \(\frac{{d{{\mu }_{i}}}}{{dx}}{\text{:}}\)

$${{j}_{i}} = - L_{i}^{{{\text{mb}}}}\frac{{d{{\mu }_{i}}}}{{dx}},$$
((1))

where \(L_{i}^{{{\text{mb}}}}\) is the effective conductivity coefficient characterizing the multiphase system. The value of dx in Eq. (1) can be interpreted as the distance between two parallel planes perpendicular to the transport axis x, which correspond to the electrochemical potentials \({{\mu }_{i}}\left( x \right)\) and \({{\mu }_{i}}\left( {x + dx} \right)\), respectively [34]. The dx value should be significantly smaller than the membrane thickness d (to justify the application of differential equations), but noticeably larger than the characteristic size of an element of a separate phase to provide the layer between the x and x + dx planes to be “representative” and include all membrane phases and all structure features.

According to the microheterogeneous model [20],

$$L_{i}^{{{\text{mb}}}} = {{\left[ {{{f}_{{\text{g}}}}{{{\left( {L_{i}^{{\text{g}}}} \right)}}^{\alpha }} + {{f}_{{\text{s}}}}{{{\left( {L_{i}^{{\text{s}}}} \right)}}^{\alpha }}} \right]}^{{\frac{1}{\alpha }}}},$$
((2))

where \(L_{i}^{{\text{g}}}\) and \(L_{i}^{{\text{s}}}\) are the conductance coefficients of the gel and solution phases, respectively; \(\alpha \) is the structural parameter characterizing the mutual arrangement of the membrane phases (Fig. 2): \( - 1 \leqslant \alpha \leqslant + 1\), with α = −1 corresponding to the sequential arrangement of the phases and \(\alpha = + 1\) corresponding to the parallel one.

Fig. 2.
figure 2

Extreme cases of the location of phases in the membrane and the corresponding values of the parameter α.

Full size image

The parameters \(L_{i}^{{\text{g}}}\) and \(L_{i}^{{\text{s}}}\) are determined from the diffusion coefficients \(D_{i}^{{\text{g}}}\) and \(D_{i}^{{\text{s}}}\) (it is assumed that the diffusion coefficients are independent on the concentration) in the corresponding phases:

$$L_{i}^{{\text{g}}} = \frac{{D_{i}^{{\text{g}}}c_{i}^{{\text{g}}}}}{{RT}},$$
((3))
$$L_{i}^{{\text{s}}} = \frac{{D_{i}^{{\text{s}}}c_{i}^{{\text{s}}}}}{{RT}},$$
((4))

where \(c_{i}^{{\text{g}}}\) and \(c_{i}^{{\text{s}}}\) are the concentration of ions in the gel phase and in the intergel solution, respectively; R is the universal gas constant; T is the temperature; and \(D_{i}^{{\text{s}}}\) and \(c_{i}^{{\text{s}}}\) relate to electrically neutral interpore solution, which is considered identical to the external solution.

The gel and intergel solution phases are in local equilibrium. Then the concentration of ions in the gel phase \(c_{i}^{{\text{g}}}\) is related to the concentration in the intergel solution \(c_{i}^{{\text{s}}}\) through the Donnan relation:

$$\frac{{{{{\left( {c_{ + }^{{\text{g}}}} \right)}}^{{\frac{1}{{{{z}_{ + }}}}}}}}}{{{{{\left( {c_{ - }^{{\text{g}}}} \right)}}^{{\frac{1}{{{{z}_{ - }}}}}}}}} = {{K}_{{\text{D}}}}\frac{{{{{\left( {c_{ + }^{{\text{s}}}} \right)}}^{{\frac{1}{{{{z}_{ + }}}}}}}}}{{{{{\left( {c_{ - }^{{\text{s}}}} \right)}}^{{\frac{1}{{{{z}_{ - }}}}}}}}},$$
((5))

where KD is the Donnan constant, z+ and z– are charges of ions in the electrolyte solution, the subscript “+” means counterions (in the case of cation-exchange membranes), and “−” means coions.

In the case when the ion-exchange capacity of the gel phase of the membrane is much higher than the concentration of electrolyte sorbed by this phase, the Donnan ratio (5) can be simplified and rewritten (for a binary electrolyte) as [20]:

$$c_{ - }^{{\text{g}}} = \frac{{{{K}_{{\text{D}}}}}}{{{{Q}^{{\text{g}}}}}}{{c}^{2}},$$
((6))
$$c_{ + }^{{\text{g}}} = {{Q}^{{\text{g}}}} + c_{ - }^{{\text{g}}},$$
((7))

where is the concentration of electrically neutral solution; Qg is the ion-exchange capacity of the gel phase (concentration of charged fixed groups per unit volume of the gel), which is defined as the ratio of the ion-exchange capacity of the membrane Qmb to the volume fraction of the gel phase:

$${{Q}^{{\text{g}}}} = \frac{{{{Q}^{{{\text{mb}}}}}}}{{{{f}_{{\text{g}}}}}}.$$
((8))

It follows from Eqs. (1)–(4) that \(L_{i}^{{{\text{mb}}}}\) depends on the concentration of the external solution, the remaining parameters in the first approximation being assumed to be independent of the concentration. For a particular membrane system, some of these parameters can be found as table values (the value of \(D_{i}^{{\text{s}}}\) is assumed to be equal to the value in the free solution). The remaining parameters of the microheterogeneous model can be determined from experimental data. The algorithm for finding these parameters is described in [20]. According to it, the diffusion coefficient of counterions in the gel phase \(D_{ + }^{{\text{g}}}\) and the volume fraction of the intergel solution in the membrane fs can be found from the electrical conductivity of the membranes as a function of concentration in log–log coordinates (in the first approximation, fs is the slope of this dependence); the diffusion coefficient of co-ions in the gel phase \(D_{ - }^{{\text{g}}}\) and the structural parameter \(\alpha \) can be found from the concentration dependence of the diffusion permeability; the ion-exchange capacity of the gel Qg can be found from the total ion-exchange capacity Qmb; the Donnan constant is found from the data on the sorption of electrolytes.

Using the set of parameters described above, various membrane properties can be described, such as transport numbers of ions (Eq. (9)), diffusion permeability (Eq. (10)), and electrical conductivity (Eq. (11)):

$$t_{ + }^{{{\text{mb}}}} = \frac{{L_{ + }^{{{\text{mb}}}}}}{{L_{ + }^{{{\text{mb}}}} + L_{ - }^{{{\text{mb}}}}}},$$
((9))
$$P_{{{\text{dif}}}}^{{{\text{mb}}}} = 2t_{ + }^{{{\text{mb}}}}L_{ - }^{{{\text{mb}}}}\frac{{RT}}{c},$$
((10))
$${{\kappa }^{{{\text{mb}}}}} = {{\left[ {{{f}_{{\text{g}}}}{{{\left( {{{\kappa }^{{\text{g}}}}} \right)}}^{\alpha }} + {{f}_{{\text{s}}}}{{{({{\kappa }^{{\text{s}}}})}}^{\alpha }}} \right]}^{{\frac{1}{\alpha }}}},$$
((11))

where \({{\kappa }^{{\text{g}}}} = \left( {L_{ + }^{{\text{g}}} + L_{ - }^{{\text{g}}}} \right){{F}^{2}}\) and \({{\kappa }^{{\text{s}}}} = \left( {L_{ + }^{{\text{s}}} + L_{ - }^{{\text{s}}}} \right){{F}^{2}}\) are the electrical conductivity of the gel region and that of electroneutral solution, respectively.

The electrical conductivity attracts the greatest interest in this work, because it is one of the main properties of membranes determining their practical application.

Effect of Electrical Double Layer

Figure 3 schematically shows the distribution of the concentration of ions at the pore wall of the membrane in equilibrium solution. The central part of the pore is filled with an electroneutral solution. The electrical double layer is formed near the pore walls, inside which the distribution of cations and anions concentrations is uneven. The EDL consists of a dense part (Helmholtz layer) with the thickness \({{\lambda }_{{\text{H}}}}\) being approximately equal to the diameter of the hydrated counterion and the diffuse part with a thickness on the order of the Debye length LD [31].

Fig. 3.
figure 3

Distribution of ion concentrations at the pore wall in the membrane: x = 0 is the plane passing through the centers of fixed ions; x = λH is the plane passing through the centers of the hydrated counterions closest to the fixed groups (λH = 0.6–0.8 nm) (Helmholtz plane); x = λB is the plane representing the boundary between the regions with high and low mobility of ions and molecules: the outer boundary of the gel phase.

Full size image

The thickness of the dense part of the EDL does not depend on the concentration of the external solution and is determined by the concentration of fixed groups. Bjerrum [35] showed that the dependence of the probability of finding an ion in a layer with thickness da at distance a from the central (fixed) ion has a distinct minimum at \({{\lambda }_{{\text{B}}}} = \frac{{\left| {{{z}_{ + }}{{z}_{ - }}} \right|{{e}^{2}}}}{{4\pi \varepsilon {{\varepsilon }_{0}}kT}},\) where \({{\varepsilon }_{0}}\) is the electric constant, \(\varepsilon \) is the relative dielectric constant of the solvent, e is the electron charge, and k is the Boltzmann constant. At a shorter distance from the central ion, mobile ions oppositely charged relative to it have a kinetic energy insufficient to move away from the central ion and form ion pairs with it according to Bjerrum. Ions that are at a greater distance from the central ion quite easily diffuse into the solution and are considered free. As applied to ion-exchange materials, we consider the fixed ion to be the central Bjerrum ion.

Thus, counterions that occur at a distance shorter than λB are considered to be associated and have low mobility, while counterions at a greater distance are considered free, having the same mobility as ions in the external solution. The distinguishing of two states of counterions determined by their distance from a fixed ion, where the Bjerrum length is a critical parameter, is the central point of the Manning condensation theory [36] developed for polyelectrolyte solutions. Counterions that are located at a distance shorter than λB are “condensed” near the ions fixed on the polymer chain and are “associated” in contrast to the more distant “free” counterions. Kamcev and coworkers [6, 37–39] recently proposed a model that is based on the Manning theory [36] and makes it possible to calculate adequately the concentration of electrolyte sorbed in gel ion-exchange materials.

The Debye length increases with dilution of the solution and can be calculated by the following approximate equation:

$${{L}_{{\text{D}}}} = {{\left( {\frac{{\varepsilon {{\varepsilon }_{0}}RT}}{{2{{F}^{2}}c}}} \right)}^{{\frac{1}{2}}}},$$
((12))

where F is the Faraday constant.

The size of membrane pores can be different. Micropores, mesopores, and macropores are distinguished in the literature. As a parameter characterizing each type of pores, we will use the ratio of the pore radius rp to the theoretical value of LD on the inner wall of the pore calculated by Eq. (12). In the case of micropores, rp<LD (usually rp < 1 nm); for mesopores, it is characteristic that rp> LD but rp and LD must have values of the same order; for macropores, rp >> LD (rp> 50 nm).

With increasing electrolyte concentration, the value of LD decreases in accordance with Eq. (12). In concentrated electrolyte solutions (>1 mol/L), the calculated value of LD is small compared to λB. Therefore, all ions that compensate for the charge of fixed ions are associated. The value of λB in experimental homogeneous gel membranes [40] in the case of 1 : 1 electrolyte is 1.2 nm according to Kamcev et al. [39]. In the framework of the proposed model, this length determines the boundary separating the gel phase (in which the ions are “associated” and their mobility is significantly reduced) and the solution phase (in which the ion mobility is considered the same as in a free solution).

Therefore, it follows that the selectivity of mesopores should decrease with an increase in concentration of the external solution. On the other hand, LD increases to reach 10–20 nm with dilution, thereby makes even relatively large mesopores highly selective.

In the basic microheterogeneous model, the entire EDL refers to the gel phase, the volume fraction of which is considered constant and independent on the concentration of the external electrolyte solution. Here, we propose to separate a part of the diffuse domain of the EDL (located at a distance of >λB from the fixed ion) from the gel phase and assign it to the solution phase. Hereinafter, all parameters characterizing the charged region of the solution, in which the ions have the same mobility as in the free solution, will be denoted by subscript “D”. Thus, compared to the basic version of the microheterogeneous model [20], the solution phase is divided into two areas: the region of the electroneutral solution filling the central part of the inter-gel spaces, and the charged region intermediate between the electroneutral solution and the gel phase. As indicated above, the gel phase (together with polymer chains, fixed groups, and associated counterions) will also include a slow-moving part of EDL with thickness λB. Since in the first approximation λB is independent on the concentration of the solution, the volume fraction of the gel fg is considered constant.

In contrast to the basic microheterogeneous model, we will assume that the average concentration of counterions in the gel phase (for definiteness, the cation-exchange membrane) is equal to the concentration of fixed groups only at high solution concentrations (approximately >1 mol/L), when the thickness of the diffuse part of EDL can be neglected:

$$c_{ + }^{{\text{g}}} \approx {{Q}^{{\text{g}}}}.$$
((13))

In this case, all counterions are in the immediate vicinity of fixed groups, at a distance not exceeding \({{\lambda }_{{\text{B}}}},\) where their mobility is substantially lower than the mobility in the free solution [41]. The number of moles of counterions in the gel phase under these conditions is equal to QgfgVtot, where \({{V}_{{{\text{tot}}}}}\) is the total volume of the membrane.

When the solution is diluted, a part of the counterions move away from the fixed ions by a distance exceeding λB [41] and pass into the “mobile” part of EDL, where their mobility does not differ from the mobility in the free solution. The number of moles of counterions in this region is \(c_{ + }^{{D\,\,{\text{av}}}}{{V}_{D}},\) where \(c_{ + }^{{D\;{\text{av}}}}\) is the average concentration of counterions in the “mobile” part of EDL and \({{V}_{D}}\) is its volume. The concentration of counterions (cations) in the gel phase becomes lower than in the case of the concentrated solution:

$$\begin{gathered} c_{ + }^{{\text{g}}} = \frac{{n_{{\text{ + }}}^{{\text{g}}}}}{{{{f}_{{\text{g}}}}{{V}_{{{\text{tot}}}}}}} \\ = \frac{{{{Q}^{{\text{g}}}}{{f}_{{\text{g}}}}{{V}_{{{\text{tot}}}}} - c_{ + }^{{D\;{\text{av}}}}{{V}_{D}}}}{{{{f}_{{\text{g}}}}{{V}_{{{\text{tot}}}}}}} = {{Q}^{{\text{g}}}} - c_{ + }^{{D\;{\text{av}}}}\frac{{{{f}_{D}}}}{{{{f}_{{\text{g}}}}}}, \\ \end{gathered} $$
((14))

where \(f_{D}^{{}}\) is the volume fraction of the “mobile” part of EDL.

Let us consider the boundary between the pore wall and the solution (Fig. 3). The pore wall carries fixed anions, the charge of which is compensated by the charge of mobile cations and anions present in the solution. Let the coordinate of cations passing through the centers of the pores nearest to the wall to be x = 0. According to the Gouy–Chapman theory, the distribution of ions in a solution is described by the Poisson–Boltzmann equation. The potential difference between x = 0 and x = ∞ is:

$${{\varphi }^{{\text{g}}}} = \frac{{RT}}{F}\ln \frac{{c_{{\text{ + }}}^{{\text{g}}}}}{{{{c}_{0}}}},$$
((15))

where \(c_{ + }^{{\text{g}}}\) and φg refer to x = 0; x = ∞ refers to the electroneutral (real or virtual [12, 42]) solution balanced with the membrane fragment under consideration. Assuming that the potential and concentration change continuously, these values are approximately equal to the respective values in the gel phase, i.e. \(c_{ + }^{{\text{g}}}\) ≈ Qg.

In order to find the charge and concentration in EDL, we use the exact solution of the Poisson and Boltzmann equations [28]:

((16))

where \(\Phi = \frac{{F\varphi }}{{2RT}}\) is the dimensionless potential in an arbitrary point of EDL at a distance x from the plane passing through the centers of counterions closest to the pore wall and \({{\Phi }^{{\text{g}}}} = \frac{{F{{\varphi }^{{\text{g}}}}}}{{2RT}}\) is the potential in this plane of x = 0. Finding (numerically) the value of \(\Phi \) for point x from Eq. (16), the concentration of cations and anions for this point can be easily calculated using the Boltzmann equation:

((17))

Substituting x = xB into Eq. (16), we find the potential corresponding to the Bjerrum plane. Next, we can find the average integral values of the concentrations of “associated” ith ions in the Bjerrum layer \(c_{i}^{{{\text{av}}\,{\text{B}}}}\) and “free” ions \(c_{i}^{{D\,{\text{av}}}}\) in the “moving” part of the EDL bounded by the point x = xB on one side and by the center of the pore x = rp on the other side, where rp is the pore radius:

$$c_{i}^{{{\text{av}}\,{\text{B}}}} = \int\limits_0^{{{x}_{{\text{B}}}}} {c{{e}^{{ - 2{{z}_{i}}\Phi }}}} dx,\,\,\,\,c_{i}^{{D\,{\text{av}}}} = \int\limits_{{{x}_{{\text{B}}}}}^{{{r}_{p}}} {c{{e}^{{ - 2{{z}_{i}}\Phi }}}} dx.$$
((18))

Integration in accordance with Eqs. (18) was performed numerically. The resulting average concentrations were used to calculate the electrical conductivity of the gel phase κg and the “mobile” EDL region of the solution that fills the pore \({{\kappa }_{D}}{\text{:}}\)

$$\begin{gathered} {{\kappa }_{{\text{g}}}} = \frac{{{{F}^{2}}}}{{RT}}\left( {z_{ + }^{2}D_{ + }^{{\text{g}}}c_{ + }^{{\text{g}}} + z_{ - }^{2}D_{ - }^{{\text{g}}}c_{ - }^{{\text{g}}}} \right), \\ {{\kappa }_{D}} = \frac{{{{F}^{2}}}}{{RT}}\left( {z_{ + }^{2}D_{ + }^{{\text{s}}}c_{ + }^{{D\,{\text{av}}}} + z_{ - }^{2}D_{ - }^{{\text{s}}}c_{ - }^{{D\,{\text{av}}}}} \right), \\ \end{gathered} $$
((19))

where the concentration of counter-ions in the gel phase is calculated using Eq. (14), assuming fD to be fs = 1 − fg. Thus, since the ion concentration distribution functions are smooth (Boltzmann distribution) in terms of this modified model, the electroneutral part of the solution is not distinguished specifically.

The concentration of coions (anions) in the gel phase \(c_{ - }^{{\text{g}}}\) is calculated by the Donnan equation (Eq. (6)) as it is done in the basic model.

The specific electrical conductivity of the membrane, taking into account the presence of the gel phase and the “mobile” region of EDL in the membrane (it is obligatory to include the region of the electroneutral solution), is calculated in accordance with the theory of effective medium [11] and a formula similar to Eq. (11) as follows:

$${{\kappa }^{{{\text{mb}}}}} = {{\left( {{{f}_{{\text{g}}}}\kappa _{{\text{g}}}^{\alpha } + {{f}_{{\text{s}}}}\kappa _{D}^{\alpha }} \right)}^{{\frac{1}{\alpha }}}}.$$
((20))

The total surface area of EDL and, accordingly, the volume fraction of the “mobile” region of EDL depends on the membrane pore geometry. In this paper, we consider three main pore shapes that are most common in the literature: flat (Fig. 4a), cylindrical (Fig. 4b), and spherical (Fig. 4c).

Fig. 4.
figure 4

Geometry of electrical double layers in (a) flat, (b) cylindrical, and (c) spherical pores.

Full size image

For each of the pore geometries, we calculated the specific conductivities of the solution in the pore (\({{\kappa }_{D}}\)) and gel phase of the membrane (κg), as described above, as well as the specific conductivity of the membrane (Eq. (20)) as functions of the concentration of the external solution. The following quantities were used as parameters for the calculation: the volume fractions of the gel phase fg and the “intergel” solution fs, the diffusion coefficients of ions in both phases (it is believed that the diffusion coefficients \(D_{i}^{{\text{s}}}\) in the mobile part of EDL are the same as in the free solution, and the diffusion coefficients \(D_{i}^{{\text{g}}}\) characterize the ion mobility both in microporous medium and in the Bjerrum layer near the walls of mesopores and macropores), pore radius rp (in the case of a flat pore it is equal to half the distance between opposite walls), structural parameter α, the Donnan constant KD (characterizing equilibrium sorption of coions by the gel phase), and membrane ion-exchange capacity Q. Thus, compared with the basic microheterogeneous model, only one parameter is added, namely the effective pore radius.

EXPERIMENTAL

The studies were performed using a specially prepared homogeneous cation-exchange membrane, similar in structure and composition to commercial IEM NafionTM (DuPont). The method for obtaining such membranes is described in [43, 44]. An 8% solution of perfluorosulfonated polymer MF-4SK in dimethylformamide (Plastpolimer, Russia) was dispersed by ultrasound (frequency 35 kHz) using a Bandelin Sonorex device for 2 h. Characteristics of the polymer MF-4SK: lithium form, equivalent weight 1100, ion-exchange capacity 0.9 meq/g. The resulting homogeneous suspension was poured into a glass Petri dish. The solvent was removed during multistage drying: at 80, 90, 100, and 120°C (for 1 h at each step) followed by 80°C for 4 h. The formed film was carefully separated from the glass bottom of the Petri dish and hot-pressed for 3 min under a pressure of 5 MPa and at a temperature of 110°C to improve the mechanical properties. The resulting membrane was placed for 90 min in a 5% HCl solution, washed in a large volume of deionized water to get free of the acid, and conditioned at room temperature. Before the tests, the membrane was equilibrated with a 0.005 mol/L NaCl solution.

The average thickness of the sample made was 199 ± 1 μm.

The specific conductivity of membranes (κmb) was calculated from data on the resistance of membranes measured by the mercury-contact method in the ac frequency range of 50–500 kHz. This method is convenient to study thin polymer films, as it provides an ideal contact between the electrode and the membrane sample. In addition, this method has no restrictions on the concentration of the equilibrium solution or water content in the sample under study [45]. The current frequency that ensures the zero value of the imaginary component of the measuring cell impedance was chosen individually for each concentration of the equilibrium solution [23].

The value of the specific conductivity was calculated by the formula:

$${{\kappa }^{{{\text{mb}}}}} = \frac{l}{S}\frac{1}{{{{R}^{{{\text{mb}}}}}}},$$
((21))

where l is the membrane thickness, Rmb is the measured resistance, and S is the membrane area.

The measurements were carried out using a TESLA BM 507 impedance meter with NaCl solution concentrations varied from 0.005 to 0.2 mol/L.

RESULTS AND DISCUSSION

Figure 5 shows the experimental and calculated concentration dependences of the specific electrical conductivity of the membrane under study in NaCl solutions. The calculations were carried out using the base and modified models for flat, cylindrical, and spherical pores. The structural-kinetic parameters of the membrane used for the calculations are listed in Table 1. These parameters were chosen on the basis of the following considerations. As in the case of Nafion membrane [46], the fluorocarbon and ether chains are the basis of the polymer obtained (hydrophobic part) and, in the swollen state, form pores which have functional sulfo groups on their walls. These pores linked by a system of narrower channels contain hydrated cations and thus represent the hydrophilic part of the membrane. Thus, the membrane under discussion (as well as the Nafion membrane) has a cluster–channel morphology and is homogenous on the micrometer scale. According to DSC data [47], pores dominating in MF-4SK membranes have the radius of about 6 nm, but there are also pores with a larger diameter. The results of standard contact porosimetry reported in [47] give the following characteristic values of the effective pore radii in MF-4SK: 2, 11, and even 16 nm. The size of these pores can vary depending on the membrane prefabrication conditions. This is evidenced by the results of determining the volume fraction of the intergel solution fs from the concentration dependences of the electrical conductivity in terms of the basic microheterogeneous model: the fs values of this membrane fall in the range from 0.05 [20, 48, 49] to 0.15 [48, 50]. The value of this structural parameter for the studied sample MF-4SK adopted in this work is 0.13. The parameter fs was determined in this study (with an error of ±0.02) graphically as the slope of the experimental concentration dependence of the specific conductivity plotted in log–log coordinates in the concentration range of >0.1 mol/L, where the basic microheterogeneous model is approximately valid. The relatively high value of this parameter is indirect evidence for the presence of sufficiently large pores in the sample under study, which is natural in the case of membrane fabrication by casting (see Experimental). The values of the structural parameter α, the Donnan constant KD, and the diffusion coefficients of chloride (coion) \(D_{ - }^{{\text{g}}}\) and sodium (counterion) \(D_{ + }^{{\text{g}}}\) ions in the membrane are characteristic of homogeneous membranes [28]. The values of the diffusion coefficients of these ions in solution \(D_{ - }^{{\text{s}}}\) and \(D_{ + }^{{\text{s}}}\) were taken from the handbook [51].

Fig. 5.
figure 5

Experimental (squares) and calculated (lines) concentration dependences of the specific electrical conductivity of the membrane under study in a NaCl solution. The calculations were performed using the base (dashed line) and modified (solid curves) models for (1) flat, (2) cylindrical, and (3) spherical pores. The calculation parameters are given in Table 1.

Full size image
Table 1.   Structural-kinetic parameters of the membrane used for calculations in accordance with the basic and modified microheterogeneous models
Full size table

Comparison of experimental results and calculations using the basic microheterogeneous model shows that this model describes the electrical conductivity of membranes in the region of high NaCl concentrations (Fig. 5). However, in the region of dilute solutions, the values of electrical conductivity calculated using this model are underestimated compared with experimental data, and the difference between them increases with decreasing concentration of the equilibrium solution.

The values closest to our experimental results found for the specific conductivity give the results of calculations using a modified model made for flat pores (Fig. 5, curve 1). This result agrees with the data presented in [52]. In this work, it was shown that the model considering the membrane as a system of locally flat tape-like pores describes the processes that proceed during the swelling of perfluorinated membranes.

Calculations performed on the assumption that pores have a cylindrical or spherical shape give higher membrane conductivity values compared to flat pores providing that the effective pore radius have the same value of 6 nm (Fig. 5). This rise is due to a decrease in the volume fraction of the electroneutral solution in the order flat pore > cylindrical pore > spherical pore and an increase of the volume fraction of the charged solution in the pore in the same order.

It should be noted that when the solution concentration is about 0.01 mol/L, the rate of decrease in electrical conductivity when diluting solution is significantly reduced and in solutions whose concentration is less than millimolar, the value of κmb becomes almost constant. This type of dependence agrees with the experimental results obtained by Kamcev et al. [10] using methods specially developed by them for application in the region of dilute solutions.

Our calculation results on the effect of the radius (in the case of flat pores) on the concentration dependence of the electrical conductivity of the membrane are shown in Fig. 6. The basic microheterogeneous model is built without taking into account the pore size; therefore, it gives the same dependence close to a straight line for all the pore radius values (in the case under consideration, α = 0.01) in the logκmb–logc coordinates. The use of the modified microheterogeneous model results in that the lower the pore radius, the higher is the membrane electric conductivity, since the volume fraction of the highly conducting charged solution localized in the “moving” part of EDL increases with decreasing pore radius. At low values of rp and sufficiently low concentrations of the solution, the EDLs that are forming at the opposite walls of the pore overlap and the concentration distribution of ions in the pore becomes close to uniform. Therefore, the membrane conductivity remains almost constant with dilution starting from a certain concentration of the external solution (Fig. 6). The smaller the value of rp, the higher is the concentration of counterions in the pore, approaching the concentration of fixed ions.

Fig. 6.
figure 6

Experimental (squares) and calculated (lines) concentration dependences of the specific electrical conductivity of the membrane under study in NaCl solution. Calculations are made for pores with a flat geometry. The dashed line corresponds to the calculation according to the base microheterogeneous model; the solid lines represents the calculation using the modified microheterogeneous model. The arrow shows the direction of increasing rp= 1, 3, 6, 10, 20, and 30 nm.

Full size image

CONCLUSIONS

The microheterogeneous model has been modified by taking into account the contribution of the electrical double layer on the internal pore walls of the ion-exchange membrane to the electrical conductivity of the membrane. The resulting model describes the experimental concentration dependence of the electrical conductivity of the cation-exchange homogeneous perfluorocarbon membrane MF-4SK in the region of dilute NaCl solutions, at least in the range up to 0.01 mol/L, for which experimental data is available. The lower limit of the adequacy of the basic microheterogeneous model is the concentration of approximately 0.1 mol/L, at which the thickness of the diffuse part of EDL is slightly larger than that of the Bjerrum layer, in which the ion mobility is strongly limited due to the electrostatic interaction with fixed ions. The new version of the microheterogeneous model uses an additional parameter, namely the effective pore radius, which was absent in the basic version. It has been shown theoretically that the value of the effective pore radius has practically no effect on the specific conductivity of membranes in relatively concentrated (>0.1 mol/L) salt solutions. In dilute solutions, the size of the average pore radius determines the rate of decrease in the membrane conductivity with a decrease in salt concentration, as well as the threshold concentration of the solution, starting from which the membrane conductivity ceases to decrease. The larger the effective pore radius, the stronger is the decreases in electrical conductivity and the lower is the threshold concentration of the equilibrium salt solution.

FUNDING

This work was supported by the Russian Science Foundation, project no. 17-19-01486.