On the Number of Eigenvalues of the Lattice Model Operator in One-Dimensional Case

Abstract

It is considered a model operator $h_{\mu}(k),$ $k\in\mathbb{T}\equiv(-\pi,\pi]$, corresponding to the Hamiltonian of systems of two arbitrary quantum particles on a one-dimensional lattice with a special dispersion function that describes the transfer of a particle from one site to another interacting by a some short-range attraction potential $v_{\mu}$, $\mu=(\mu_{0},\mu_{1},\mu_{2},\mu_{3})\in\mathbb{R}^{4}_{+}$. The number of eigenvalues of the operator $h_{\mu}(k),$ $k\in\mathbb{T}$ depending on the energy of the particle interaction vector $\mu\in\mathbb{R}^{4}_{+}$ and the total quasi-momentum $k\in\mathbb{T}$ is studied.

1 INTRODUCTION

In the continuous case, the study of spectral properties of the total Hamiltonian of a system of two particles is reduced to investigating the two-particle Schrödinger operator by separating the energy of motion of the center of mass so that the two-particle bound states are eigenvectors of the energy operator with a separated total momentum (in this case, such type operator does not actually depend on the values of the total momentum) [1]. For the lattice case, the separation of the center of mass of the system corresponds to the realization of the Hamiltonian as a laminated operator, i.e., as the direct integral of the family of energy operators $h(k)$ of two particles, depending on the values of the total quasi-momentum $k$ on the $d$-dimensional torus $\mathbb{T}^{d}\equiv(-\pi,\pi]^{d}$ [2].

The two-particle Schrödinger operator $h_{\mu}(k)$, $k\in\mathbb{T}^{3}$, associated with the Hamiltonian of a system of two identical particles (bosons) interacting with the pair contact potential of attraction with interaction energy $\mu>0$ was considered in [3]. It was shown that the operator has either a single eigenvalue or no eigenvalues depending on the values of the interaction energy $\mu>0$ and the total quasi-momentum $k\in\mathbb{T}^{3}$ of the system of two particles.

In the cases of two bosons or two fermions moving on the lattice and interacting only at the nearest neighbouring sites, the exact number of eigenvalues of the corresponding two-particle Schrödinger operator $h_{\mu}(k)$, $\mu>0$, $k\in\mathbb{T}^{d}$, $d=1,2$ was found in [4, 5]. In addition, in the papers [6–10] the spectral properties of the one-particle Hamiltonian describing the motion of one quantum particle on a lattice in an external field were studied. The number of eigenvalues and their locations were investigated depending on the values of the interaction energy $\lambda,\mu\in\mathbb{R}$ ($\mu^{2}+\lambda^{2}>0$).

In the papers [11, 12], systems of two arbitrary quantum particles on a three-dimensional lattice with some selected dispersion relations interacting with pair attraction potentials were considered. The dependence of the number of eigenvalues of the family of operators $h_{\mu}(k)$, $k\in\mathbb{T}^{3}$, $\mu=(\mu_{1},\ldots,\mu_{N})\in\mathbb{R}^{N}_{+}$ on the particle interaction energy $\mu\in\mathbb{R}^{N}_{+}$ and the total quasi-momentum $k\in\mathbb{T}^{3}$ was investigated.

In the paper [13] was considered a system of two arbitrary quantum particles on a one-dimensional lattice with specially selected dispersion relations describing the transfer of a particle from the site $s=0$ to the sites $s=\pm 2n$, $n\in\mathbb{N}$ interacting with the pair attraction potential. Moreover, in accordance with the dispersion relations, the interaction potential $v_{\mu}$, $\mu=(\mu_{0},\mu_{1},\ldots,\mu_{N})\in\mathbb{R}^{N+1}_{+}$ was chosen so that the Fredholm determinant corresponding to the operator $h_{\mu}(k)$ was reduced to the product of the Fredholm determinants of the operators $h_{\mu_{l}}(k)$ and $l\in\{0,1,\ldots,N\}.$ The number of eigenvalues of the operator $h_{\mu}(k)$ was investigated depending on the interaction energy of particles and the total quasi-momentum $k\in\mathbb{T}$. Conditions for the existence of the eigenvalues (counting multiplicities) of the operator $h_{\mu}(k)$ lying to the left of the essential spectrum were established.

In this paper, we consider the model operator $h_{\mu}(k)$, $k\in\mathbb{T}$, corresponding to the Hamiltonian of a system of two arbitrary quantum particles on a one-dimensional lattice with special even dispersion relations describing the transfer of a particle from the site $s=0$ to sites $s=\pm 2$, interacting with the pair short-range attraction potential. In this case, the energy of pair interactions of particles is an even function and takes no more than four values $\mu_{0},$ $\mu_{1},$ $\mu_{2}$ and $\mu_{3}$.

Let us study the number of eigenvalues of the energy operator $h_{\mu}(k)$ depending on the energy vector of pair interactions of particles $\mu=(\mu_{0},\mu_{1},\mu_{2},\mu_{3})\in\mathbb{R}^{4}_{+}$ and the total quasi-momentum $k\in\mathbb{T}$ of the system of two particles.

Since the operator $h_{\mu}(k),$ $k\in\mathbb{T}$ is decomposed into the direct sum of the operators $h_{\mu,e}(k)$ and $h_{\mu,o}(k)$ acting in the Hilbert spaces of even and odd functions, respectively, it suffices to study the discrete spectra of these operators.

Further, using properties of the dispersion relations, we represent the Fredholm determinant $\Delta_{e}(\mu,k;z)$ $\Big{(}\Delta_{o}(\mu,k;z)\Big{)}$ of the operator $h_{\mu,e}(k)$ $\Big{(}h_{\mu,o}(k)\Big{)}$ as a product of the Fredholm determinants $h^{(1)}_{\mu,e}(k)$ and $h^{(2)}_{\mu,e}(k)$($h^{(1)}_{\mu,o}(k)$ and $h^{(1)}_{\mu,o}(k)$) depending only on two pairs of parameters $(\mu_{0},\mu_{2})$ and $(\mu_{1},\mu_{3})$, respectively. Moreover,

$$\Delta_{e}(\mu,k;z)=\prod\limits_{\gamma=1}^{2}\Delta^{(\gamma)}_{e}(\mu_{\gamma-1},\mu_{\gamma+1},k;z)\quad\textrm{and}\quad\Delta_{o}(\mu,k;z)=\prod\limits_{\gamma=1}^{2}\Delta^{(\gamma)}_{o}(\mu_{\gamma-1},\mu_{\gamma+1},k;z)$$

and

$$h_{\mu,e}(k)=h^{(1)}_{\mu,e}(k)\oplus h^{(2)}_{\mu,e}(k),\quad h_{\mu,o}(k)=h^{(1)}_{\mu,o}(k)\oplus h^{(2)}_{\mu,o}(k).$$

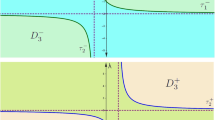
Therefore, the number of eigenvalues actually depends only on values of two pairs $(\mu_{\gamma-1},\mu_{\gamma+1})$, $\gamma=1,2$ and quasi-momentum $k\in\mathbb{T}$. Further, a geometric explanation of the conditions for the existence of eigenvalues with respect of two pairs $(\mu_{\gamma-1},\mu_{\gamma+1})$, $\gamma=1,2$ is given. We split the plane $O\mu_{0}\mu_{2}$ $\Big{(}O\mu_{1}\mu_{3}\Big{)}$ of parameters $\mu_{0},\mu_{2}\in\mathbb{R}_{+}$ $\Big{(}\mu_{1},\mu_{3}\in\mathbb{R}_{+}\Big{)}$ (see Fig. 1 and 2) into two components $\mathbb{E}^{(1)}_{1}$ and $\mathbb{E}^{(1)}_{2}$($\mathbb{E}^{(2)}_{1}$ and $\mathbb{E}^{(2)}_{2}$) and also into two components $\mathbb{O}_{0}^{(1)}$ and $\mathbb{O}_{1}^{(1)}$(into three components $\mathbb{O}_{0}^{(2)},$ $\mathbb{O}_{1}^{(2)}$ and $\mathbb{O}_{2}^{(2)}$). Moreover, the operators $h^{(\gamma)}_{\mu,e}(k)$ and $h^{(\gamma)}_{\mu,o}(k)$ acting in Hilbert spaces of even and odd functions have $\eta$ and $\rho$ eigenvalues on the left threshold of the essential spectrum, respectively, for $(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{E}^{(\gamma)}_{\eta},$ $\eta=1,2$ and $(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{O}^{(\gamma)}_{\rho},$ $\rho=0,1,2$.

Thus, this geometrical approach allows us to establish lower and upper bounds for the number of eigenvalues of the operator $h_{\mu}(k)$, $k\in\mathbb{T}$.

Fig. 1

Fig. 2

Remark that the obtained results clarify and generalize the results of the works [6, 7], and also show the complex dependence of the number of eigenvalues on the parameters of operators.

2 FORMULATION OF THE MAIN RESULTS

Let ${\mathbb{Z}}$ be the set of integers and $\ell^{2}(\mathbb{Z}\times\mathbb{Z})$ be the Hilbert space of square-summable functions on $\mathbb{Z}\times\mathbb{Z}.$

The model operator $\hat{h}_{\mu}$, corresponding to the Hamiltonian of a system of two arbitrary quantum particles on a one-dimensional lattice, in the coordinate representation, is defined as a bounded self-adjoint operator acting in $\ell^{2}(\mathbb{Z}\times\mathbb{Z})$ by $\hat{h}_{\mu}=\hat{h}_{0}-\hat{v}_{\mu},$ where

$$(\hat{h}_{0}\hat{\psi})(n_{1},n_{2})=\sum_{s\in\mathbb{Z}}\,\Big{[}\hat{\varepsilon}_{1}(s)\hat{\psi}(n_{1}+s,n_{2})+\hat{\varepsilon}_{2}(s)\hat{\psi}(n_{1},n_{2}+s)\Big{]},$$

$$(\hat{v}_{\mu}\hat{\psi})(n_{1},n_{2})=\hat{v}_{\mu}(n_{1}-n_{2})\hat{\psi}(n_{1},n_{2}).$$

Here $\hat{\varepsilon}_{1}(\cdot)$, $\hat{\varepsilon}_{2}(\cdot)$ are dispersion functions describing the transfer of particles from a site to neighbouring sites and $\hat{v}_{\mu}(\cdot)$ is a pair interaction potential of particles defined on $\mathbb{Z}$ as

$$\hat{\varepsilon}_{i}(s)=\begin{cases}\frac{1}{m_{i}},\quad\textrm{if}\quad s=0,\\ -\frac{1}{2m_{i}},\quad\textrm{if}\quad s=\pm 2,\\ 0,\quad\textrm{otherwise},\end{cases}\quad\textrm{and}\quad\hat{v}_{\mu}(s)=\begin{cases}2\pi\mu_{0},\quad\textrm{if}\quad s=0,\\ \pi\mu_{l},\quad\textrm{if}\quad s=\pm l,\quad l=1,2,3,\\ 0,\quad\textrm{otherwise},\end{cases}$$

where $m_{i}>0$ is the mass of the $i$-th particle, $i=1,2$ and $\mu_{n}\geq 0$, $n=0,1,2,3$.

Let $L^{2}(\mathbb{T}\times\mathbb{T})$ be the Hilbert space of square-integrable functions on $\mathbb{T}\times\mathbb{T},$ $\mathbb{T}=(-\pi;\pi]$. The transition from the coordinate representation of the Hamiltonian $\hat{h}_{\mu}$ to the momentum one $h_{\mu}$ is realized by the Fourier transform (see, [2])

$$\mathcal{F}:\ell^{2}(\mathbb{Z}\times\mathbb{Z})\to\,L^{2}(\mathbb{T}\times\mathbb{T}),\quad(\mathcal{F}\hat{\psi})(p)=\frac{1}{2\pi}\sum_{s\in\mathbb{Z}^{2}}\hat{\psi}(s)e^{i(p,s)}.$$

The momentum representation $h_{\mu}$ as a model operator in $L^{2}(\mathbb{T}\times\mathbb{T})$ is of the form

$$h_{\mu}:=\mathcal{F}\hat{h}_{\mu}\mathcal{F}^{-1}=\mathcal{F}\hat{h}_{0}\mathcal{F}^{-1}+\mathcal{F}\hat{v}_{\mu}\mathcal{F}^{-1}.$$

Two-particle problem on a lattice with dispersion relations $\varepsilon_{1}(k_{1})$ and $\varepsilon_{2}(k_{2})$, $k_{1},k_{2}\in\mathbb{T},$ in the momentum representation is reduced to study the effective one-particle problem by separating the total quasi-momentum $k=k_{1}+k_{2}$ of the two particles and the von Neumann expansion: the two-particle Hilbert space $L^{2}(\mathbb{T}\times\mathbb{T})$ is represented as a direct integral associated to the discrete abelian group $\mathbb{Z}$ by shift operators

$$L^{2}(\mathbb{T}\times\mathbb{T})=\int\limits_{k\in\mathbb{T}}\oplus L^{2}(\mathbb{T})dk.$$

Hence, the total two-particle Hamiltonian $h_{\mu}$ appears to be decomposable [14] and

$$h_{\mu}=\int\limits_{\mathbb{T}}\oplus\tilde{h}_{\mu}(k)dk$$

holds, where the quasi-momentum $k$ of a system of two particles runs through the first Brillouin zone $\mathbb{T}=\mathbb{R}/(2\pi\mathbb{Z})$. The layer operator $\tilde{h}_{\mu}(k)$ continuously depends on $k\in\mathbb{T}$. Bound states $\psi_{e,k}$ of the operator $\tilde{h}_{\mu}(k)$ are solutions of the following Schrödinger equation

$$\tilde{h}_{\mu}(k)\psi_{e,k}=e(k)\psi_{e,k},\quad\psi_{e,k}\in L^{2}(\mathbb{T}).$$

Therefore, the spectrum $\sigma(h_{\mu})$ of the operator $h_{\mu}$ expressed in terms of the spectrum of the layer Schrödinger operators $\tilde{h}_{\mu}(k)$ with a fixed quasi-momentum, i.e.,

$$\sigma(h_{\mu})=\cup_{k\in\mathbb{T}}\sigma(\tilde{h}_{\mu}(k))=\cup_{j=1}\cup_{k\in\mathbb{T}}\{e_{j}(k)\}\cup\sigma(\tilde{h}_{0}(k)),$$

where $e_{j}(k)$, $j=1,2,\ldots$ are eigenvalues of the layer operator $\tilde{h}_{\mu}(k).$

Using the unitary operator $U:L^{2}(\mathbb{T})\rightarrow L^{2}(\mathbb{T})$ (see [13])

$$(Uf)(p)=f\left(p-\frac{\theta(k)}{2}\right),\quad\theta(k)=\arccos\frac{\frac{1}{m_{1}}+\frac{1}{m_{2}}\cos 2k}{\sqrt{\frac{1}{m^{2}_{1}}+\frac{2}{m_{1}m_{2}}\cos 2k+\frac{1}{m^{2}_{2}}}},$$

we reduce the problem of investigating spectral properties of $\tilde{h}_{\mu}(k)$ to the study of the family of operators $h_{\mu}(k),$ $k\in\mathbb{T},$ acting in the Hilbert space $L^{2}(\mathbb{T})$ as $h_{\mu}(k)=h_{0}(k)-\mathbf{v}_{\mu},$ where $h_{0}(k)$ is the multiplication operator by the function $\mathcal{E}_{k}(\cdot)$ defined as

$$\mathcal{E}_{k}(p)=\frac{1}{m_{1}}+\frac{1}{m_{2}}-a(k)\cos 2p,\quad\ a(k)=\sqrt{\frac{1}{m^{2}_{1}}+\frac{2}{m_{1}m_{2}}\cos 2k+\frac{1}{m^{2}_{2}}}$$

and $\mathbf{v}_{\mu}$ is the integral operator with kernel $v_{\mu}(p-s)=\sum\limits_{n=0}^{3}\mu_{n}\cos n(p-s),$ i.e.,

$$(\mathbf{v}_{\mu}f)(p)=\sum_{n=0}^{3}\int\limits_{\mathbb{T}}\mu_{n}\cos n(p-s)f(s)ds,\quad f\in L^{2}({\mathbb{T}}).$$

According to the Weyl’s theorem on the stability of the essential spectrum [16] the essential spectrum $\sigma_{\textrm{ess}}(h_{\mu}(k))$ of the operator $h_{\mu}(k)$ remains unchanged under a compact perturbation $\mathbf{v}_{\mu}$ and coincides with the spectrum of the unperturbed operator $h_{0}(k)$:

$$\sigma_{\textrm{ess}}(h_{\mu}(k))=\sigma(h_{0}(k))=[m(k),M(k)],$$

where

$$m(k)=\min\limits_{p\in\mathbb{T}}\,\mathcal{E}_{k}(p)=\frac{1}{m_{1}}+\frac{1}{m_{2}}-a(k),\quad M(k)=\max\limits_{p\in\mathbb{T}}\,\mathcal{E}_{k}(p)=\frac{1}{m_{1}}+\frac{1}{m_{2}}+a(k).$$

If $\mathbf{v}_{\mu}\geq 0,$ then

$$(h_{\mu}(k)f,f)\leq(h_{0}(k)f,f)\leq M(k)(f,f),\qquad f\in L^{2}(\mathbb{T}).$$

Therefore, the operator $h_{\mu}(k)$ has no eigenvalues lying to the right of the essential spectrum, that is, $\sigma(h_{\mu}(k))\cap(M(k),\infty)=\emptyset.$

Remark 1. Let $L^{2}_{e}(\mathbb{T})\subset L^{2}(\mathbb{T})$ and $L^{2}_{o}(\mathbb{T})\subset L^{2}(\mathbb{T})$ be subspaces of even and odd functions, respectively. It is known that the equality $L^{2}(\mathbb{T})=L^{2}_{e}(\mathbb{T})\oplus L^{2}_{o}(\mathbb{T})$ holds. Hilbert spaces $L^{2}_{e}(\mathbb{T})$ and $L^{2}_{o}(\mathbb{T}$) are invariant under the self-adjoint operator $h_{\mu}(k).$ We denote by $h_{\mu,e}(k)$ and $h_{\mu,o}(k)$ the restrictions $h_{\mu}(k)\big{|}_{L^{2}_{e}(\mathbb{T})}$ and $h_{\mu}(k)\big{|}_{L^{2}_{o}(\mathbb{T})}$ of the operator $h_{\mu}(k)$ to $L^{2}_{e}(\mathbb{T})$ and $L^{2}_{o}(\mathbb{T}),$ respectively. The operators $h_{\mu,e}(k)$ and $h_{\mu,o}(k)$ act on $L^{2}_{e}(\mathbb{T})$ and $L^{2}_{o}(\mathbb{T})$ by the formulas $h_{\mu,e}(k)=h_{0}(k)-\mathbf{v}_{\mu,e}$ $h_{\mu,o}(k)=h_{0}(k)-\mathbf{v}_{\mu,o},$ respectively, where $\mathbf{v}_{\mu,e}$ and $\mathbf{v}_{\mu,o}$ are integral operators given as

$$\mathbf{v}_{\mu,e}f(p)=\sum_{n=0}^{3}\int\limits_{\mathbb{T}}\mu_{n}\cos np\cos nsf(s)ds,\quad f\in L^{2}_{e}({\mathbb{T}}),$$

$$\mathbf{v}_{\mu,o}f(p)=\sum_{n=0}^{3}\int\limits_{\mathbb{T}}\mu_{n}\sin np\sin nsf(s)ds,\quad f\in L^{2}_{o}({\mathbb{T}}).$$

Hence,

$$\sigma(h_{\mu}(k))=\sigma(h_{\mu,e}(k))\cup\sigma(h_{\mu,o}(k))\quad\textrm{and}\quad\sigma_{d}(h_{\mu}(k))=\sigma_{d}(h_{\mu,e}(k))\cup\sigma_{d}(h_{\mu,o}(k)).$$

We set

$$c_{nm}(k;z)=\int\limits_{\mathbb{T}}\frac{\cos nq\cos mqdq}{\mathcal{E}_{k}(q)-z},\quad c_{n}(k;z)=c_{nn}(k;z),\quad n,m=0,1,2,3$$

(1)

and

$$s_{lr}(k;z)=\int\limits_{\mathbb{T}}\frac{\sin lq\sin rqdq}{\mathcal{E}_{k}(q)-z},\quad s_{l}(k;z)=s_{ll}(k;z),\quad l,r=1,2,3.$$

(2)

Note that the function $\mathcal{E}_{k}(\cdot)$ has a non-generated minimum only at the points $p=0$ and $p=\pi$. Therefore, the integral

$$\int\limits_{\mathbb{T}}\frac{\sin^{2}lqdq}{\mathcal{E}_{k}(q)-m(k)},\quad l=1,2,3$$

is convergent and positive. Denote

$$\mu_{l}(k)=\Big{(}s_{l}\big{(}k;m(k)\big{)}\Big{)}^{-1}=\frac{a(k)}{l\pi},\quad l=1,2,3.$$

To formulate results on the number and locations of eigenvalues of the operators $h_{\mu,e}(k)$ and $h_{\mu,o}(k)$ we introduce the following partitions for parameters $\mu_{0},\mu_{2}\in\mathbb{R}_{+}$ and $\mu_{1},\,\mu_{3}\in\mathbb{R}_{+}$:

$$\mathbb{R}_{+}^{2}=\mathbb{E}^{(1)}_{1}\cup\mathbb{E}^{(1)}_{2}=\mathbb{O}_{0}^{(1)}\cup\mathbb{O}_{1}^{(1)}\quad\textrm{and}\quad\mathbb{R}_{+}^{2}=\mathbb{E}^{(2)}_{1}\cup\mathbb{E}^{(2)}_{2}=\mathbb{O}_{0}^{(2)}\cup\mathbb{O}_{1}^{(2)}\cup\mathbb{O}_{2}^{(2)},$$

where

$$\mathbb{E}^{(\gamma)}_{1}=\left\{(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{R}_{+}^{2}:\,\mu_{\gamma+1}\leq\mu_{2}(k)+\frac{\mu_{2}^{2}(k)}{\mu_{\gamma-1}-\mu_{2}(k)}\right\},$$

$$\mathbb{E}^{(\gamma)}_{2}=\left\{(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{R}_{+}^{2}:\,\mu_{\gamma+1}>\mu_{2}(k)+\frac{\mu_{2}^{2}(k)}{\mu_{\gamma-1}-\mu_{2}(k)}\right\},$$

$$\mathbb{O}_{0}^{(1)}=\left\{(\mu_{0},\mu_{2})\in\mathbb{R}_{+}^{2}:\,\mu_{2}\leq\mu_{2}(k)\right\},\quad\mathbb{O}_{1}^{(1)}=\left\{(\mu_{0},\mu_{2})\in\mathbb{R}_{+}^{2}:\,\mu_{2}>\mu_{2}(k)\right\},$$

$$\mathbb{O}_{0}^{(2)}=\left\{(\mu_{1},\mu_{3})\in\mathbb{R}_{+}^{2}:\mu_{1}<3\mu_{2}(k),\quad\mu_{3}\leq\mu_{2}(k)+\frac{\mu_{2}^{2}(k)}{\mu_{1}-3\mu_{2}(k)}\right\},$$

$$\mathbb{O}_{1}^{(2)}=\left\{(\mu_{1},\mu_{3})\in\mathbb{R}_{+}^{2}:\mu_{1}<3\mu_{2}(k),\quad\mu_{3}>\mu_{2}(k)+\frac{\mu_{2}^{2}(k)}{\mu_{1}-3\mu_{2}(k)}\right.$$

$$\left.\hskip 71.13189pt\textrm{or}\quad\mu_{1}>3\mu_{2}(k),\quad\mu_{3}\leq\mu_{2}(k)+\frac{\mu_{2}^{2}(k)}{\mu_{1}-3\mu_{2}(k)}\right\},$$

$$\mathbb{O}_{2}^{(2)}=\left\{(\mu_{1},\mu_{3})\in\mathbb{R}_{+}^{2}:\mu_{1}>3\mu_{2}(k),\quad\mu_{3}>\mu_{2}(k)+\frac{\mu_{2}^{2}(k)}{\mu_{1}-3\mu_{2}(k)}\right\}.$$

The following theorems describe the number of the eigenvalues of the operators $h_{\mu,e}(k)$ and $h_{\mu,o}(k)$.

Theorem 1. Let either $m_{1}\neq m_{2}$ and $k\in\mathbb{T}$ or $m=m_{1}=m_{2}$ and $k\neq\pm\frac{\pi}{2}$.

1. If $(\mu_{0},\mu_{2})\in\mathbb{E}^{(1)}_{\alpha},$ $(\mu_{1},\mu_{3})\in\mathbb{E}^{(2)}_{\beta},$ $\alpha,\beta=1,2,$ then the operator $h_{\mu,e}(k)$ has exactly $\alpha+\beta$ eigenvalues (counting multiplicities) lying to the left of the essential spectrum.

2. If $(\mu_{0},\mu_{2})\in\mathbb{O}_{\alpha}^{(1)},$ $(\mu_{1},\mu_{3})\in\mathbb{O}_{\beta}^{(2)},$ $\alpha=0,1$ , $\beta=0,1,2,$ then the operator $h_{\mu,o}(k)$ has exactly $\alpha+\beta$ eigenvalues (counting multiplicities) lying to the left of the essential spectrum.

Theorem 2. Let $m=m_{1}=m_{2}$ and $k=\pm\frac{\pi}{2}$ . Then the operators $h_{\mu,e}(k)$ and $h_{\mu,o}(k)$ have exactly four and three eigenvalues (counting multiplicities), respectively, lying to the left of the essential spectrum.

The following theorem sets the lower and upper bounds for the number of eigenvalues of the operator $h_{\mu}(k)$.

Theorem 3. 1. Let either $m_{1}\neq m_{2}$ and $k\in\mathbb{T}$ or $m=m_{1}=m_{2}$ and $k\neq\pm\frac{\pi}{2}$ . Then for each $k\in\mathbb{T}$ the operator $h_{\mu}(k)$ has at least two and at most seven eigenvalues (counting multiplicities) lying to the left of the essential spectrum.

2. Let $m=m_{1}=m_{2}$ and $k=\pm\frac{\pi}{2}$ . Then the operator $h_{\mu}(k)$ has exactly seven eigenvalues (counting multiplicities) lying to the left of the essential spectrum.

Remark 2. Let the conditions of the Theorem 3 (1) be fulfilled. If $(\mu_{0},\mu_{2})\in\mathbb{P}_{\alpha},$ $\alpha=1,2,3$ and $(\mu_{1},\mu_{3})\in\mathbb{Q}_{\beta},$ $\beta=1,...,4$, then for each $k\in\mathbb{T}$ the operator $h_{\mu}(k)$ has exactly $\alpha+\beta$ eigenvalues (counting multiplicities) lying to the left of the essential spectrum, where

$$\mathbb{P}_{1}=\mathbb{E}^{(1)}_{1}\cap\mathbb{O}_{0}^{(1)},\qquad\mathbb{P}_{2}=\mathbb{E}^{(1)}_{1}\cap\mathbb{O}_{1}^{(1)},\qquad\mathbb{P}_{3}=\mathbb{E}^{(1)}_{2}\cap\mathbb{O}_{1}^{(1)},$$

$$\mathbb{Q}_{1}=\mathbb{E}^{(2)}_{1}\cap\mathbb{O}_{0}^{(2)},\quad\mathbb{Q}_{2}=\mathbb{E}^{(2)}_{1}\cap\mathbb{O}_{1}^{(2)},\quad\mathbb{Q}_{3}=\mathbb{E}^{(2)}_{2}\cap\mathbb{O}_{1}^{(2)},\quad\mathbb{Q}_{4}=\mathbb{E}^{(2)}_{2}\cap\mathbb{O}_{2}^{(2)}.$$

3 PROOF OF THE MAIN RESULTS

Introduce the function $\Delta(k;\cdot):=\Delta_{\mu}(k;\cdot)$ defined in ${\mathbb{C}}\backslash[m(k),M(k)]$ as

$$\Delta(k;z)=\Delta_{e}(k;z)\Delta_{o}(k;z),$$

(3)

where

$$\Delta_{e}(k;z)=\Delta^{(1)}_{e}(k;z)\Delta^{(2)}_{e}(k;z),\quad\Delta_{o}(k;z)=\Delta^{(1)}_{o}(k;z)\Delta^{(2)}_{o}(k;z),$$

(4)

$$\Delta^{(\gamma)}_{e}(k;z)=\Big{(}1-\mu_{\alpha}c_{\alpha}(k;z)\Big{)}\Big{(}1-\mu_{\beta}c_{\beta}(k;z)\Big{)}-\mu_{\alpha}\mu_{\beta}c_{\alpha\beta}^{2}(k;z),$$

(5)

$$\Delta^{(\gamma)}_{o}(k;z)=\Big{(}1-\alpha\mu_{\alpha}s_{\alpha}(k;z)\Big{)}\Big{(}1-\mu_{\beta}s_{\beta}(k;z)\Big{)}-\alpha\mu_{\alpha}\mu_{\beta}s_{\alpha\beta}^{2}(k;z),$$

(6)

$\alpha=\gamma-1$, $\beta=\gamma+1$, $\gamma=1,2.$ The relation between zeros of $\Delta(k;\cdot)$ and eigenvalues of the operator $h_{\mu}(k)$ is established by the following lemma.

Lemma 1. For any $k\in\mathbb{T}$, the number $z<m(k)$ is an $m$-multiple eigenvalue of the operator $h_{\mu}(k)$ if and only if $z$ is a zero of $\Delta(k;\cdot)$ with multiplicity $m$.

A similar lemma was proved in [13].

Corollary 1. For any $(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{R}_{+}^{2}$ , $\gamma=1,2$ and $k\in\mathbb{T}$ , the number $z<m(k)$ is an eigenvalue of the operator $h^{(\gamma)}_{\mu,e}(k)$ ( $h^{(\gamma)}_{\mu,o}(k)$ ) if and only if it is a zero of the function $\Delta^{(\gamma)}_{e}(k;\cdot)$ ( $\Delta^{(\gamma)}_{o}(k;\cdot)$ ), $\gamma=1,2$ . Moreover, each eigenvalue of the operator $h^{(\gamma)}_{\mu,e}(k)$ ( $h^{(\gamma)}_{\mu,o}(k)$ ) is simple (see offer below 3), where

$$h^{(\gamma)}_{\mu,e}(k)=h_{0}(k)-\mathbf{v}^{(\gamma)}_{\mu,e},\quad h^{(\gamma)}_{\mu,o}(k)=h_{0}(k)-\mathbf{v}^{(\gamma)}_{\mu,o},\quad\gamma=1,2,$$

$\mathbf{v}^{(\gamma)}_{\mu,e}$ and $\mathbf{v}^{(\gamma)}_{\mu,o}$ are the integral operators defined as

$$\big{(}\mathbf{v}^{(\gamma)}_{\mu,e}f\big{)}(p)=\int\limits_{\mathbb{T}}\Big{(}\mu_{\gamma-1}\cos(\gamma-1)p\cos(\gamma-1)s+\mu_{\gamma+1}\cos(\gamma+1)p\cos(\gamma+1)s\Big{)}f(s)ds,$$

$$\big{(}\mathbf{v}^{(\gamma)}_{\mu,o}f\big{)}(p)=\int\limits_{\mathbb{T}}\Big{(}\mu_{\gamma-1}\sin(\gamma-1)p\sin(\gamma-1)s+\mu_{\gamma+1}\sin(\gamma+1)p\sin(\gamma+1)s\Big{)}f(s)ds.$$

Proposition 1. I. For any $k\in\mathbb{T}$, the functions $c_{nm}(k;\cdot),$ $n+m=0,2,4,6,$ $n,m=0,1,2,3$ and $s_{lr}(k;\cdot),$ $l+r=2,4,6,$ $l,r=1,2,3$ are analytic in $\mathbb{C}\backslash[m(k),M(k)]$, and positive, increasing monotonically in $(-\infty,m(k))$.

II. Let either $m_{1}\neq m_{2}$ and $k\in\mathbb{T}$ or $m=m_{1}=m_{2}$ and $k\neq\pm\frac{\pi}{2}$. Then for any $\mu_{\gamma-1}\geq 0,$ $\mu_{\gamma+1}\geq 0,$ $\gamma=1,2$ the equalities (asymptotic expansions)

$$\Delta^{(\gamma)}_{e}(k;z)=\mathbf{E}^{(\gamma)}_{-\frac{1}{2}}(k)\big{(}m(k)-z\big{)}^{-\frac{1}{2}}+\mathbf{E}^{(\gamma)}_{0}(k)+O\big{(}(m(k)-z)^{\frac{1}{2}}\big{)},\quad z\rightarrow m(k)-0,$$

(7)

$$\Delta^{(\gamma)}_{o}(k;z)=\mathbf{O}^{(\gamma)}_{0}(k)+O\big{(}(m(k)-z)^{\frac{1}{2}}\big{)},\quad z\rightarrow m(k)-0$$

(8)

hold, where

$$\mathbf{E}^{(\gamma)}_{-\frac{1}{2}}(k)=\frac{\sqrt{\pi}\Big{[}\mu_{\gamma-1}\mu_{\gamma+1}-(\mu_{\gamma-1}+\mu_{\gamma+1})\mu_{2}(k)\Big{]}}{\sqrt{\mu_{2}^{3}(k)}},$$

$$\mathbf{E}^{(\gamma)}_{0}(k)=\frac{2\mu_{2}^{2}(k)+\Big{[}(\gamma-1)\mu_{\gamma-1}+(\gamma+1)\mu_{\gamma+1}\Big{]}\mu_{2}(k)-(\gamma+1)\mu_{\gamma-1}\mu_{\gamma+1}}{2\mu_{2}^{2}(k)},$$

$$\mathbf{O}^{(\gamma)}_{0}(k)=\frac{2\mu_{2}^{2}(k)-\Big{[}(\gamma-1)\mu_{\gamma-1}+(\gamma+1)\mu_{\gamma+1}\Big{]}\mu_{2}(k)+(\gamma-1)\mu_{\gamma-1}\mu_{\gamma+1}}{2\mu_{2}^{2}(k)}.$$

Proof. I. The positivity of the functions $c_{n}(k;\cdot),$ $n=0,1,2,3$ and $s_{l}(k;\cdot),$ $l=1,2,3,$ defined by (1) and (2), directly follows from the nonnegativity of the integrands and the monotonicity of the Lebesgue integral.

Let’s represent the functions $c_{02}(k;\cdot),$ $c_{13}(k;\cdot)$ and $s_{13}(k;\cdot)$ as

$$c_{02}(k;z)=\frac{1}{a(k)}\int\limits_{-\pi}^{\pi}\frac{\cos 2q}{A-\cos 2q}dq,\quad c_{13}(k;z)=\frac{1}{a(k)}\int\limits_{-\pi}^{\pi}\frac{\cos q\cos 3q}{A-\cos 2q}dq,$$

$$s_{13}(k;z)=\frac{1}{a(k)}\int\limits_{-\pi}^{\pi}\frac{\sin q\sin 3q}{A-\cos 2q}dq,$$

where $A:=1+\frac{m(k)-z}{a(k)}>1$ for $z<m(k)$. One can easily check that

$$\int\limits_{-\pi}^{\pi}\frac{\cos 2q}{A-\cos 2q}dq=2\pi\frac{A-\sqrt{A^{2}-1}}{\sqrt{A^{2}-1}},$$

$$\int\limits_{-\pi}^{\pi}\frac{\cos q\cos 3q}{A-\cos 2q}dq=\frac{\pi}{\sqrt{A^{2}-1}}\frac{A-\sqrt{A^{2}-1}+1}{A+\sqrt{A^{2}-1}},$$

$$\int\limits_{-\pi}^{\pi}\frac{\sin q\sin 3q}{A-\cos 2q}dq=\frac{\pi}{\sqrt{A^{2}-1}}\frac{\sqrt{A^{2}-1}-(A-1)}{A+\sqrt{A^{2}-1}}.$$

From these and the inequality $A>1$, it follows that the functions $c_{02}(k;\cdot),$ $c_{13}(k;\cdot)$ and $s_{13}(k;\cdot)$ are positive for $z<m(k)$.

The positivity of the derivatives of the functions $c_{n}(k;\cdot),$ $n=0,1,2,3$ and $s_{l}(k;\cdot),$ $l=1,2,3$ in $z$ also follows from the nonnegativity of the integrands and the monotonicity of the Lebesgue integral.

The derivatives of the functions $c_{02}(k;\cdot),$ $c_{13}(k;\cdot)$ and $s_{13}(k;\cdot)$ in $z$ are represented as

$$\frac{\partial c_{02}(k;z)}{\partial z}=\frac{1}{a(k)}\int\limits_{-\pi}^{\pi}\frac{\cos 2q}{\big{(}F(z)-\cos 2q\big{)}^{2}}dq,$$

$$\frac{\partial c_{13}(k;z)}{\partial z}=\frac{1}{a(k)}\int\limits_{-\pi}^{\pi}\frac{\cos q\cos 3q}{\big{(}F(z)-\cos 2q\big{)}^{2}}dq,$$

$$\frac{\partial s_{13}(k;z)}{\partial z}=\frac{1}{a(k)}\int\limits_{-\pi}^{\pi}\frac{\sin q\sin 3q}{\big{(}F(z)-\cos 2q\big{)}^{2}}dq,$$

where $F(z):=\big{(}m^{-1}_{1}+m^{-1}_{2}-z\big{)}/a(k)>1$ for $z<m(k)$. Hence, we have

$$\frac{\partial c_{02}(k;z)}{\partial z}=\frac{2}{a(k)}\int\limits_{0}^{\pi}\frac{\cos 2q}{\big{(}F(z)-\cos 2q\big{)}^{2}}dq.$$

Representing the integral as a sum of two integrals over the intervals $[0,\frac{\pi}{2}]$ and $[\frac{\pi}{2},\pi],$ in the second integral making the change of variable $q:=q+\frac{\pi}{2}$ and using the identity $\cos(x-\pi)=-\cos x$ we get

$$\frac{2}{a(k)}\int\limits_{0}^{\pi}\frac{\cos 2q}{(F(z)-\cos 2q)^{2}}dq=\frac{8F(z)}{a(k)}\int\limits_{0}^{\frac{\pi}{2}}\frac{\cos^{2}2q}{\big{(}F(z)-\cos 2q\big{)}^{2}}dq>0.$$

The nonnegativity of the integrands and the monotonicity of the Lebesgue integral imply the positivity of $\partial c_{02}(k;z)/\partial z.$ Therefore, the function $c_{02}(k;\cdot)$ monotonically increases in $(-\infty,m(k))$. The monotonicity of the functions $c_{13}(k;\cdot)$ and $s_{13}(k;\cdot)$ is proved similarly.

II. We prove assertion II of the Proposition 1 for $\gamma=1.$ For the case $\gamma=2$, the proof is similar to that of part I. Note that for $\gamma=1$ the equalities (5) and (6) have the following forms

$$\Delta^{(1)}_{e}(k;z)=\Big{(}1-\mu_{0}c_{0}(k;z)\Big{)}\Big{(}1-\mu_{2}c_{2}(k;z)\Big{)}-\mu_{0}\mu_{2}c_{02}^{2}(k;z),\quad\Delta^{(1)}_{o}(k;z)=1-\mu_{2}s_{2}(k;z).$$

Computing the integrals in (1) and (2), we obtain the following equalities

$$c_{0}(k;z)=\frac{\sqrt{2}\pi\big{(}m(k)-z\big{)}^{-\frac{1}{2}}}{\sqrt{a(k)}}f(k;z),$$

$$c_{02}(k;z)=\frac{\sqrt{2}\pi\big{(}m(k)-z\big{)}^{-\frac{1}{2}}}{\sqrt{a(k)}}f(k;z)-\frac{2\pi}{a(k)}+\frac{\sqrt{2}\pi\big{(}m(k)-z\big{)}^{\frac{1}{2}}}{\sqrt{a^{3}(k)}}f(k;z),$$

$$c_{2}(k;z)=\frac{\sqrt{2}\pi\big{(}m(k)-z\big{)}^{-\frac{1}{2}}}{\sqrt{a(k)}}f(k;z)-\frac{2\pi}{a(k)}+\frac{2\sqrt{2}\pi\big{(}m(k)-z\big{)}^{\frac{1}{2}}}{\sqrt{a^{3}(k)}}g(k;z)-\frac{2\pi\big{(}m(k)-z\big{)}}{a^{2}(k)},$$

$$s_{2}(k;z)=\frac{2\pi}{a(k)}-\frac{2\sqrt{2}\pi\big{(}m(k)-z\big{)}^{\frac{1}{2}}}{\sqrt{a^{3}(k)}}g(k;z)+\frac{2\pi\big{(}m(k)-z\big{)}}{a^{2}(k)},$$

where

$$f(k;z)=\frac{1}{g(k;z)},\quad g(k;z)=\sqrt{1+\frac{m(k)-z}{2a(k)}}.$$

Further, expanding the functions $f(k;z)$ and $g(k;z)$ in Taylor series in neighbourhood of the point $z=m(k)$, we obtain

$$f(k;z)=1-\frac{1}{4a(k)}\Big{(}m(k)-z\Big{)}+O\Big{(}(m(k)-z)^{2}\Big{)},\quad z\rightarrow m(k)-0,$$

$$g(k;z)=1+\frac{1}{4a(k)}\Big{(}m(k)-z\Big{)}+O\Big{(}(m(k)-z)^{2}\Big{)},\quad z\rightarrow m(k)-0.$$

Using these equations, we obtain the following asymptotic expansions

$$c_{0}(k;z)=\frac{\sqrt{2}\pi}{\sqrt{a(k)}}\Big{(}m(k)-z\Big{)}^{-\frac{1}{2}}-\frac{\sqrt{2}\pi}{4\sqrt{(a(k))^{3}}}\Big{(}m(k)-z\Big{)}^{\frac{1}{2}}+O\Big{(}(m(k)-z)^{\frac{3}{2}}\Big{)},\quad z\rightarrow m(k)-0,$$

$$c_{02}(k;z)=\frac{\sqrt{2}\pi}{\sqrt{a(k)}}\Big{(}m(k)-z\Big{)}^{-\frac{1}{2}}-\frac{2\pi}{a(k)}+\frac{3\sqrt{2}\pi}{4\sqrt{(a(k))^{3}}}\Big{(}m(k)-z\Big{)}^{\frac{1}{2}}+O\Big{(}(m(k)-z)^{\frac{3}{2}}\Big{)},$$

$$z\rightarrow m(k)-0,$$

$$c_{2}(k;z)=\frac{\sqrt{2}\pi}{\sqrt{a(k)}}\Big{(}m(k)-z\Big{)}^{-\frac{1}{2}}-\frac{2\pi}{a(k)}+\frac{7\sqrt{2}\pi}{4\sqrt{(a(k))^{3}}}\Big{(}m(k)-z\Big{)}^{\frac{1}{2}}$$

$$-\frac{2\pi}{a^{2}(k)}\Big{(}m(k)-z\Big{)}+O\Big{(}(m(k)-z)^{\frac{3}{2}}\Big{)},\quad z\rightarrow m(k)-0,$$

$$s_{2}(k;z)=\frac{2\pi}{a(k)}-\frac{2\sqrt{2}\pi}{\sqrt{(a(k))^{3}}}\Big{(}m(k)-z\Big{)}^{\frac{1}{2}}+O\big{(}m(k)-z\big{)},\quad z\rightarrow m(k)-0.$$

Substituting these expansions into (5) and (6), respectively, we obtain the relations (7) and (8) for $\gamma=1.$ $\Box$

Proposition 2. I. For any $\mu_{n}\geq 0,$ $n=0,1,2,3$ and $k\in\mathbb{T}$, the function $1-\mu_{n}c_{n}(k;\cdot)$ has a unique zero $\zeta_{n}(k)\in(-\infty,m(k))$, i.e.,

$$1-\mu_{n}c_{n}(k;\zeta_{n}(k))=0,\quad n=0,1,2,3.$$

(9)

II. Let either $m_{1}\neq m_{2}$ and $k\in\mathbb{T}$ or $m=m_{1}=m_{2}$ and $k\neq\pm\frac{\pi}{2}$ . Then for any $\mu_{l}\geq 0,$ $l=1,2,3$ and $k\in\mathbb{T}$ the following statements are true:

1. If $\mu_{l}\leq\mu_{l}(k)$ , then the function $1-\mu_{l}s_{l}(k;\cdot),$ $l=1,2,3$ has no zeros in $(-\infty,m(k))$ .

2. If $\mu_{l}>\mu_{l}(k)$ , then the function $1-\mu_{l}s_{l}(k;\cdot),$ $l=1,2,3$ has a single zero $\xi_{l}(k)<m(k)$ .

Proof. I. By virtue of the Proposition 1 for fixed $\mu_{n},$ $n=0,1,2,3$ and $k\in\mathbb{T}$ the function $1-\mu_{n}c_{n}(k;\cdot)$ continuous and monotonically decreases in $(-\infty,m(k)).$ In addition, the equalities

$$\lim\limits_{z\rightarrow-\infty}\big{(}1-\mu_{n}c_{n}(k;z)\big{)}=1,\quad\lim\limits_{z\rightarrow m(k)-0}\big{(}1-\mu_{n}c_{n}(k;z)\big{)}=-\infty$$

hold. This implies statement I of Proposition 2.

II.1. By virtue of the Proposition 1 for fixed $\mu_{l},$ $l=1,2,3$ and $k\in\mathbb{T}$ the function $1-\mu_{l}s_{l}(k;\cdot)$ is continuous and monotonically decreases in $(-\infty,m(k)).$ In addition, the following relations

$$\lim\limits_{z\rightarrow m(k)-0}\big{(}1-\mu_{l}s_{l}(k;z)\big{)}=1-\mu_{l}s_{l}(k;m(k))=1-\frac{\mu_{l}}{\mu_{l}(k)}\geq 0\quad\textrm{as}\quad 0<\mu_{l}\leq\mu_{l}(k)$$

hold. Hence,

$$1-\mu_{l}s_{l}(k;z)>1-\mu_{l}s_{l}(k;m(k))\geq 0\quad\textrm{for}\quad z<m(k).$$

II.2. Let $\mu_{l}>\mu_{l}(k),$ $l=1,2,3$. Since the function $s_{l}(k;\cdot)$ is continuous and monotone, taking into account the relations

$$\lim\limits_{z\rightarrow-\infty}\big{(}1-\mu_{l}s_{l}(k;z)\big{)}=1,$$

$$\lim\limits_{z\rightarrow m(k)-0}\big{(}1-\mu_{l}s_{l}(k;z)\big{)}=\big{(}1-\mu_{l}s_{l}(k;m(k))\big{)}=1-\frac{\mu_{l}}{\mu_{l}(k)}<0,$$

we obtain statement II.2. $\Box$

Note that $rank(\mathbf{v}^{(\gamma)}_{\mu,e})=2$($rank(\mathbf{v}^{(\gamma)}_{\mu,o})\leq 2$), $\gamma=1,2$. Therefore, the following lemma holds.

Lemma 2. The operator $h^{(\gamma)}_{\mu,e}(k)$($h^{(\gamma)}_{\mu,o}(k)$), $\gamma=1,2$ has at most two eigenvalues (counting multiplicities) lying to the left of $z=m(k)$.

Note that by virtue of the corollary 1 and the relation (3) the study of the zeros of the function $\Delta(k;\cdot)$ reduces to study of zeros of the functions $\Delta^{(\gamma)}_{e}(k;\cdot)$ and $\Delta^{(\gamma)}_{o}(k;\cdot)$, $\gamma=1,2$, defined by (5) and (6), respectively.

We set

$$\eta^{(\gamma)}_{\min}(k)=\min\{\eta_{\gamma-1}(k),\eta_{\gamma+1}(k)\},\quad\eta^{(\gamma)}_{\max}(k)=\max\{\eta_{\gamma-1}(k),\eta_{\gamma+1}(k)\},\quad\gamma=1,2$$

and

$$\xi_{\min}(k)=\min\{\xi_{1}(k),\xi_{3}(k)\},\qquad\xi_{\max}(k)=\max\{\xi_{1}(k),\xi_{3}(k)\}.$$

The following proposition completely describe locations of the eigenvalues of the operators $h_{\mu,e}(k)$ and $h_{\mu,o}(k)$.

Proposition 3. Let either $m_{1}\neq m_{2}$ and $k\in\mathbb{T}$ or $m=m_{1}=m_{2}$ and $k\neq\pm\frac{\pi}{2}$. Then for any $(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{R}_{+}^{2}$, $\gamma=1,2$ the following statements are true:

I. If $(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{E}^{(\gamma)}_{1}$ , then the function $\Delta_{e}^{(\gamma)}(k;\cdot)$ has a single zero in $z_{e}^{(\gamma 1)}(k)<m(k)$ . Moreover, $z_{e}^{(\gamma 1)}(k)<\eta^{(\gamma)}_{\min}(k)$ .

II. If $(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{E}^{(\gamma)}_{2}$ , then the function $\Delta_{e}^{(\gamma)}(k;\cdot)$ has only two zeros $z_{e}^{(\gamma 1)}(k)<m(k)$ and $z_{e}^{(\gamma 2)}(k)<m(k)$ . Moreover, the inequalities

$$z_{e}^{(\gamma 1)}(k)<\eta^{(\gamma)}_{\min}(k)\leq\eta^{(\gamma)}_{\max}(k)<z_{e}^{(\gamma 2)}(k)$$

hold.

III. If $(\mu_{0},\mu_{2})\in\mathbb{O}_{0}^{(1)}$ ( $(\mu_{1},\mu_{3})\in\mathbb{O}_{0}^{(2)}$ ), then the function $\Delta_{o}^{(1)}(k;\cdot)$ ( $\Delta_{o}^{(2)}(k;\cdot)$ ) has no zeros in $(-\infty,m(k))$ .

IV. If $(\mu_{0},\mu_{2})\in\mathbb{O}_{1}^{(1)}$ ( $(\mu_{1},\mu_{3})\in\mathbb{O}_{1}^{(2)}$ ), then the function $\Delta_{o}^{(1)}(k;\cdot)$ ( $\Delta_{o}^{(2)}(k;\cdot)$ ) has a single zero $z_{o}^{(1)}(k)<m(k)$ ( $z_{o}^{(21)}(k)<m(k)$ and $z_{o}^{(21)}(k)<\xi_{\min}(k)$ ).

V. If $(\mu_{1},\mu_{3})\in\mathbb{O}_{2}^{(2)}$ , then the function $\Delta_{o}^{(2)}(k;\cdot)$ has only two zeros $z_{o}^{(21)}(k)<m(k)$ and $z_{o}^{(22)}(k)<m(k)$ . Moreover, the inequalities

$$z_{o}^{(21)}(k)<\xi_{\min}(k)\leq\xi_{\max}(k)<z_{o}^{(22)}(k)$$

hold.

Proof. I. By the statement I of the Proposition 2, the functions $1-\mu_{\gamma-1}c_{\gamma-1}(k;\cdot)$ and $1-\mu_{\gamma+1}c_{\gamma+1}(k;\cdot),$ $\gamma=1,2$ decrease monotonically and have unique zeros $\eta_{\gamma-1}(k)$ and $\eta_{\gamma+1}(k)$ in $(-\infty,m(k))$, respectively. Therefore for any $z<\eta^{(\gamma)}_{\min}(k),$ we have

$$1-\mu_{\gamma-1}c_{\gamma-1}(k;z)>1-\mu_{\gamma-1}c_{\gamma-1}(k;\eta_{\gamma-1}(k))=0,$$

$$1-\mu_{\gamma+1}c_{\gamma+1}(k;z)>1-\mu_{\gamma+1}c_{\gamma+1}(k;\eta_{\gamma+1}(k))=0.$$

From these and the statement I of the Proposition 3, we obtain the inequality

$$\frac{\partial\Delta^{(\gamma)}_{e}(k;z)}{\partial z}=-\mu_{\alpha}\frac{\partial c_{\alpha}(k;z)}{\partial z}\Big{(}1-\mu_{\beta}c_{\beta}(k;z)\Big{)}-\mu_{\beta}\frac{\partial c_{\beta}(k;z)}{\partial z}\Big{(}1-\mu_{\alpha}c_{\alpha}(k;z)\Big{)}$$

$${}-2\mu_{\alpha}\mu_{\beta}c_{\alpha\beta}(k;z)\frac{\partial c_{\alpha\beta}(k;z)}{\partial z}<0,\quad\alpha=\gamma-1,\quad\beta=\gamma+1,\quad\gamma=1,2$$

for all $z<\eta^{(\gamma)}_{\min}(k)$, i.e., the function $\Delta^{(\gamma)}_{e}(k;\cdot)$ decreases monotonically in $(-\infty,\eta^{(\gamma)}_{\min}(k)).$ The equalities (1), (5) and (9) imply the equalities

$$\lim\limits_{z\rightarrow-\infty}\Delta_{e}^{(\gamma)}(k;z)=1,\quad\Delta_{e}^{(\gamma)}(k;\eta^{(\gamma)}_{\min}(k))=-\mu_{\alpha}\mu_{\beta}c_{\alpha\beta}^{2}(k;\eta^{(\gamma)}_{\min}(k))<0$$

(10)

for $\alpha=\gamma-1,$ $\beta=\gamma+1,$ $\gamma=1,2.$ Therefore, there exists a unique number $z_{e}^{(\gamma 1)}(k)<\eta^{(\gamma)}_{\min}(k)$ such that $\Delta_{e}^{(\gamma)}(k;z_{e}^{(\gamma 1)}(k))=0.$

The function $\Delta_{e}^{(\gamma)}(k;\cdot)$ has no zeros in the interval $(\eta^{(\gamma)}_{\min}(k),m(k)),$ namely

$$\Delta_{e}^{(\gamma)}(k;z)<0\quad\textrm{for}\quad z\in(\eta^{(\gamma)}_{\min}(k),m(k)).$$

(11)

Indeed, assuming contrary, for $(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{E}^{(\gamma)}_{1},$ $\gamma=1,2$ and $\eta\in(\eta^{(\gamma)}_{\min}(k),m(k))$ the inequality $\Delta_{e}^{(\gamma)}(k;\eta)\geq 0$ is executed. Then by virtue (10) and $\lim\limits_{z\rightarrow m(k)-0}\Delta_{e}^{(\gamma)}(k;z)<0,$ according to continuity $\Delta_{e}^{(\gamma)}(k;\cdot),$ it has at least two zeros (counting multiplicities) in $(\eta^{(\gamma)}_{\min}(k),m(k))$, hence by (5) the function $\Delta_{e}^{(\gamma)}(k;\cdot)$ has at least three zeros in $(-\infty,m(k)),$ which contradicts the assertion of the Lemma 2.

By virtue of the Lemma 2, the inequality (11) implies that the function $\Delta_{e}^{(\gamma)}(k;\cdot)$ has no zeros in $(\eta^{(\gamma)}_{\min}(k),m(k)),$ which proves the assertion I of the proposition.

II. Since the condition of this item gives the relations

$$\lim\limits_{z\rightarrow m(k)-0}\Delta_{e}^{(\gamma)}(k;z)=+\infty$$

and $\Delta_{e}^{(\gamma)}(k;z)<0$ for $z\in(z_{e}^{(\gamma 1)}(k),\eta^{(\gamma)}_{\max}(k))$, the function $\Delta_{e}^{(\gamma)}(k;\cdot)$ has a zero $z=z_{e}^{(\gamma 2)}(k)$ on $(\eta^{(\gamma)}_{\max}(k),m(k))$. This $z=z_{e}^{(\gamma 2)}(k)$ is a single zero in $(\eta^{(\gamma)}_{\max}(k),m(k))$, since by the Lemma 2 the operator $h^{(\gamma)}_{\mu,e}(k)$, $\gamma=1,2$ has at most two eigenvalues.

III. Let $z<m(k).$ By the statement I of the Proposition 1 the functions $s_{n}(k;\cdot),$ $n=1,2,3$ and $s_{13}(k;\cdot)$ monotonically increase in $(-\infty,m(k))$. Therefore, by virtue of the statement II.1 of the Proposition 2, the following inequalities $s_{13}(k;z)<s_{13}(k;m(k))$ and

$$1-\mu_{n}s_{n}(k;z)>1-\mu_{n}s_{n}(k;m(k))\geq 0\quad\textrm{for}\quad z<m(k)$$

hold. Hence, from (6) and $(\mu_{\gamma-1},\mu_{\gamma+1})\in\mathbb{O}_{0}^{(\gamma)}$, $\gamma=1,2$, we have

$$\Delta_{o}^{(1)}(k;z)>\Delta_{o}^{(1)}(k;m(k))\geq 0,$$

$$\Delta^{(2)}_{o}(k;z)>\Big{(}1-\mu_{1}s_{1}(k;m(k))\Big{)}\Big{(}1-\mu_{3}s_{3}(k;m(k))\Big{)}-\mu_{1}\mu_{3}s_{13}^{2}(k;m(k))\geq 0.$$

Therefore, the function $\Delta_{o}^{(\gamma)}(k;\cdot)$, $\gamma=1,2$ does not have zeros in $(-\infty,m(k))$.

The assertions IV and V of the proposition are proved similarly. $\Box$

Proof of the Theorem 1. 1. Let $z<m(k)$. According to the statements I and II of the Proposition 3, we have

$$\Delta_{e}^{(1)}(k;\cdot)=\begin{cases}\text{ has a single zero }\quad\text{ if}\quad(\mu_{0},\mu_{2})\in\mathbb{E}^{(1)}_{1},\\ \text{ has only two zeros }\quad\text{ if}\quad(\mu_{0},\mu_{2})\in\mathbb{E}^{(1)}_{2},\end{cases}$$

$$\Delta_{e}^{(2)}(k;\cdot)=\begin{cases}\text{ has a single zero }\quad\text{ if}\quad(\mu_{1},\mu_{3})\in\mathbb{E}^{(2)}_{1},\\ \text{ has only two zeros }\quad\text{ if}\quad(\mu_{1},\mu_{3})\in\mathbb{E}^{(2)}_{2}.\end{cases}$$

By the Lemma 1, taking into account the representations (3)–(6) and statement 1 of the Theorem 1, the operator $h_{\mu,e}(k)$ has $\alpha+\beta,$ $\alpha,\beta=1,2$ eigenvalues for $(\mu_{0},\mu_{2})\in\mathbb{E}^{(1)}_{\alpha}$ and $(\mu_{1},\mu_{3})\in\mathbb{E}^{(2)}_{\beta}$.

2. Let $z<m(k)$. By the statements III–V of the Proposition 3, we have

$$\Delta_{o}^{(1)}(k;\cdot)=\begin{cases}\text{ has no zeros }\quad\text{ if}\quad(\mu_{0},\mu_{2})\in\mathbb{O}_{0}^{(1)},\\ \text{ has a single zero }\quad\text{ if}\quad(\mu_{0},\mu_{2})\in\mathbb{O}_{1}^{(1)},\end{cases}$$

$$\Delta_{o}^{(2)}(k;\cdot)=\begin{cases}\text{ has no zeros }\quad\text{ if}\quad(\mu_{1},\mu_{3})\in\mathbb{O}_{0}^{(2)},\\ \text{ has a single zero }\quad\text{ if}\quad(\mu_{1},\mu_{3})\in\mathbb{O}_{1}^{(2)},\\ \text{ has only two zeros }\quad\text{ if}\quad(\mu_{1},\mu_{3})\in\mathbb{O}_{2}^{(2)}.\end{cases}$$

The statement 2 of Theorem 1 follows from the Lemma 1. $\Box$

Proof of the Theorem 2. Let $m=m_{1}=m_{2}$ and $k=\pm\frac{\pi}{2}$. In this case, the function $\mathcal{E}_{k}(\cdot)$ does not depend on $p\in\mathbb{T},$ that is, $\mathcal{E}_{k}(p)=m(k)=\frac{2}{m}.$ This implies $c_{02}(k;z)=c_{13}(k;z)=s_{13}(k;z)=0$. Elementary calculations show that the functions $\Delta_{e}(k;\cdot)$ and $\Delta_{o}(k;\cdot)$, determined by (4), have the forms

$$\Delta_{e}(k;z)=\prod\limits_{n=0}^{3}\phi_{n}(k;z)\quad\textrm{and}\quad\Delta_{o}(k;z)=\prod\limits_{l=1}^{3}\psi_{l}(k;z),$$

where

$$\phi_{0}(k;z)=1-\mu_{0}\frac{2\pi m}{2-zm},\quad\phi_{n}(k;z)=\psi_{n}(k;z)=1-\mu_{n}\frac{\pi m}{2-zm},\quad n=1,2,3.$$

Due to the continuity and monotonicity of the function $\phi_{n}(k;\cdot)$(resp. $\psi_{l}(k;\cdot)$), taking into account the equalities

$$\lim\limits_{z\to\frac{2}{m}-0}\phi_{n}(k;z)=-\infty,\quad\lim\limits_{z\to-\infty}\phi_{n}(k;z)=1$$

$$\left(\textrm{resp.}\quad\lim\limits_{z\to\frac{2}{m}-0}\psi_{l}(k;z)=-\infty,\quad\lim\limits_{z\to-\infty}\psi_{l}(k;z)=1\right),$$

we conclude that the function $\phi_{n}(k;\cdot)$ $\big{(}$respectively, $\psi_{l}(k;\cdot)\big{)}$ has a unique zero in $(-\infty,m(k)).$ Therefore, the function $\Delta_{e}(k;\cdot)$(respectively, $\Delta_{o}(k;\cdot)$) has four zeros $z^{(0)}_{e}(\mu_{0})=\frac{2}{m}-2\pi\mu_{0},$ $z^{(n)}_{e}(\mu_{n})=\frac{2}{m}-\pi\mu_{n},$ $n=1,2,3$(resp. three zeros $z^{(l)}_{o}(\mu_{l})=\frac{2}{m}-\pi\mu_{l},$ $l=1,2,3$) in the interval $(-\infty,m(k)).$

According to the Lemma 1, we obtain the proof of the assertion of the Theorem 2. $\Box$

The proof of the Theorem 3 follows from the Lemma 1, Proposition 3 and Theorems 1, 2.