Experimental and Analytical Study of Gas Resonance Oscillations in the Closed Tube with the Cross-Section Jump

Abstract

The results of study of gas resonance oscillations in the closed tube with the cross-section jump are presented. The dependence of oscillation amplitude of gas pressure on the resonance frequency at different amplitude of piston displacement is plotted. The good agreement between the theoretical calculation of environmental pressure and the obtained experimental data is shown.

1 INTRODUCTION

The numerous technological processes from the most diverse areas are associated with the nonlinear environmental oscillations [1, 2]. The theoretical and experimental study of gas resonance oscillations in the tubes are particularly considered in the review [3]. It is necessary to admit that in works [4–6] devoted to the gas oscillations in the closed tube, which were studied by means of different modes and at close range of the first natural frequency, the theoretical calculations are performed by means of different methods though using solutions and transformations taken from [7, 8]. The resonance oscillations of gas in tube with the conic and suddenly reducing socket are analyzed in works [9, 10]. It is shown that geometrical features of resonators influence the oscillations intensifying them and causing the strong nonlinearity. Moreover, they may result in the waveform distortion and resonance frequency displacement [11]. The analytical and experimental study of nonlinear oscillations of gas in the closed tube with the step-like cross-section on the resonance frequency and at different amplitudes of piston displacement is presented in this work.

2 EXPERIMENTAL UNIT AND METHOD

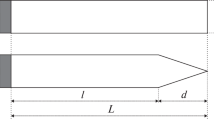
The experimental unit is shown in Fig. 1. ES-1-150-type electrodynamic vibration generator 1 that is produced by Dongling Vibration Company [12] represents the main element of unit. The vibration generator operates at frequencies $\nu$ ranging from 120 to 135 Hz with a maximum amplitude movement of $l_{0}=0.5\times 10^{3}$ m in this work. The environmental disturbance is produced by piston 3, which vibrates in the cylinder 4 (radius $R_{1}=0.05$ m and height $L_{1}=0.038$ m) connected to the glass tube 5 (length $L_{0}=1.06$ m and radius $R_{0}=0.018$ m). Such design feature allows intensifying the media oscillations in the tube if compared to the uniform tube under the same conditions. To consider the design features of the unit we introduce the computed length of tube $L$ and the effective amplitude of piston displacement $l$:

$$L=L_{0}+m^{2}(L_{1}+l_{0}),\quad m=\frac{R_{1}}{R_{0}},\quad l=m^{2}l_{0}.$$

(1)

Thus, the specified values (1) will be used instead of tube length $L_{0}$ and amplitude of piston displacement $l_{0}$ in the further assumptions and calculations.

Fig. 1

Experimental unit. (1) Vibration generator, (2) vibrating table, (3) piston, (4) cylinder, (5) quartz tube, (6) oscillograph, (7) voltage amplifier, (8) pressure indicator, (9) acceleration indicator, (10) controller.

The vibration generator is driven by 10 VENZO 880 controller produced by DynaTronic Corporation with the help of closed-loop system IEPE of AP2037-100 acceleration indicator 9 produced by Global Test Company and computer software. The pressure disturbance is measured with the help of 8530C-15 indicator 8 produced by Bruel and Kjaer Company. The signal of bridge voltage amplifier 7 of ENDEVCO type (model 136) manufactured by Bruel and Kjaer Company is sent to the digital oscillographs 6 of DSO type produced by Agilent Technologies Company.

3 RESULTS AND THEIR DISCUSSION

The theoretical resonance frequency was estimated according to the known dependence [13]

$$\nu_{1}=\frac{c_{0}}{2L(1+\beta^{\prime})},\quad\beta^{\prime}=\frac{1}{R_{0}\sqrt{2}}\sqrt{\frac{\mu}{\rho_{0}\omega}}\left(1+\frac{\kappa-1}{\sqrt{Pr}}\right),$$

where $R_{0}$ is equilibrium speed of sound, $\beta^{\prime}$ is absorption coefficient, $\kappa$ is adiabatic exponent, $Pr$ is Prandtl number, $\mu$ is dynamic viscosity, $\rho_{0}$ is undisturbed media density, $\omega$ is circular frequency. The result of experimental conditions is presented by $\nu_{1}=128.06$ Hz. Due to the obtained oscillograms of gas pressure oscillations for different amplitudes of piston displacement (Fig. 2), it was determined that experimentally found resonance frequency is 128 Hz being equal to the rated one. It is seen on the oscilograms that the form of pressure wave for all studied amplitudes and excitation frequencies is the same. As the resonance is approached, the pressure amplitude increases to its maximum value. The small nonlinearity which is preserved away from the resonance is observed. The increase of gas pressure amplitude may be also admitted in the course of increasing of piston displacement amplitude.

Fig. 2

Oscillograms of gas pressure disturbances at different times depending on the amplitude of piston displacement near the resonance frequency $\nu_{1}=128$ Hz.

To analytically describe the forced oscillations of gas in the tube we use the continuity and Navier–Stocks equations as well as entropy variations [6] which after some transformations [7, 8] carried out due to the boundary conditions of piston and closed tube end

$$x=0,\quad u=0;\quad x=L,\quad u_{p}=\omega l\cos{\omega t}$$

are equated to the following

$$C-\frac{(\cot^{2}\omega t+1)^{-1/2}}{2}=\left(g(\omega t)-\frac{2r}{\pi}\right)^{2}-\alpha\pi^{-1/2}\int\limits_{0}^{\infty}g(\omega t-\omega\xi)(\omega\xi)^{-1/2}d(\omega\xi),$$

(2)

where $\xi$ is variable arising in the course of evaluation, $C$ is integration constant, $g(\omega t)$ function depends on parameter $\varepsilon$ as $g(\omega t)=\varepsilon^{-1/2}h(t),$ which characterizes the amplitude of gas oscillations

$$\varepsilon=-\frac{4l}{(\kappa+1)L\cos(\omega L/c_{0})},$$

$r$ is non-dimensional frequency and $\alpha$ is friction coefficient

$$r=\frac{\pi c_{0}\varepsilon^{-1/2}}{(\kappa+1)\omega L\cot(\omega L/c_{0})},\quad\alpha=\frac{4\beta^{\prime}}{\kappa+1}\left(\frac{2}{\varepsilon}\right)^{1/2}.$$

To calculate the swing amplitude of gas pressure we use the energy method [7]

$$\left\langle\dot{E_{p}}\right\rangle=\left\langle\dot{E_{w}}\right\rangle+\left\langle\dot{E_{n}}\right\rangle,$$

where $\left\langle\dot{E_{p}}\right\rangle$ is average energy in the course of vibration, which is created by the piston per time unit; $\left\langle\dot{E_{w}}\right\rangle$, $\left\langle\dot{E_{n}}\right\rangle$ is energy dissipation rate as a result of wall and nonlinear losses respectively.

Let us differentiate (2) in time multiplying it on $-\omega\rho_{0}c_{0}^{2}h(t)/\pi$ and averaging according to the period of oscillation. We obtain the following after some transformations

$$-\frac{\omega}{2\pi}\rho_{0}c_{0}^{2}l\omega\int\limits_{t_{s}}^{t_{s}+2\pi/\omega}h(t)\cos\omega tdt=-\frac{\omega}{\pi}\rho_{0}c_{0}^{2}(\kappa+1)L\int\limits_{t_{s}}^{t_{s}+2\pi/\omega}h(t)h^{\prime}(t)\left[h(t)-\frac{2r}{\pi}\varepsilon^{1/2}\right]dt$$

$${}+\frac{\omega}{2\pi}\rho_{0}c_{0}^{2}\beta L\int\limits_{t_{s}}^{t_{s}+2\pi/\omega}h(t)\int\limits_{0}^{\infty}h^{\prime}(t-\xi)\xi^{-1/2}d\xi dt.$$

(3)

Here $t_{s}$ corresponds to the average time of compression, $2\pi/\omega$ is period of piston oscillations. There is a term determining the piston work $\left\langle\dot{E_{p}}\right\rangle$ in the left member of equation (3). The first term of the right member corresponds to the energy dissipation caused by the nonlinear losses $\left\langle\dot{E_{n}}\right\rangle$, the second term is an energy dissipation rate $\left\langle\dot{E_{w}}\right\rangle$ caused by the wall losses [6]. In fact, the tube influenced by the frictional force from the side of gas vibrates in the coordinate system, which is resting toward the pressure wave

$$\tau_{w}=-\mu\frac{\partial{u_{b}}}{\partial{y}}\bigg{|}_{w},$$

(4)

where $u_{b}$ is speed in the boundary layer, which may be defined, from Stokes equation

$$\frac{\partial{u_{b}}}{\partial{t}}=v\frac{\partial^{2}{u_{b}}}{\partial{y^{2}}}$$

in case of the following boundary conditions: $u_{b}=-u_{1}(x,t)$, $y=0$; $u_{b}=0$, $y=\infty$.

The work performed by the tube walls per time unit is calculated by the integration of $\tau_{w}u_{1}$ product over the surface of tube walls, which is then determined by averaging the cross-section and time. Thus, we obtain

$$\left\langle\dot{E_{w}}\right\rangle=-\frac{2\mu}{R}(1+\frac{\kappa-1}{\sqrt{Pr}})\frac{\omega}{2\pi}\int\limits_{0}^{L}\int\limits_{t_{s}}^{t_{s}+2\pi}u_{1}(x,t)\left(\frac{\partial{u_{b}}}{\partial{y}}\right)dxdt,$$

where $(\kappa-1)/\sqrt{Pr}$ component considers the influence of gas heat conduction.

We assume that wall losses are so small that $h$ to time dependence is the same as of the nonviscous gas. Then we may take $h=h_{0}\left[2r/n+\cos(\omega t/2-\pi/4)\right],$ where $h_{0}$ is value which is to be determined. After calculating some equation terms (4) we get

$$\left\langle\dot{E_{w}}\right\rangle=\rho_{0}c_{0}^{3}h_{0}^{2}b,\quad\text{where}\quad b=1.982\frac{\pi}{R\sqrt{\rho_{0}\omega/\mu}}\left(1+\frac{\kappa-1}{\sqrt{Pr}}\right),$$

(5)

$$\left\langle\dot{E_{n}}\right\rangle=\rho_{0}c_{0}^{3}h_{0}^{3}d,\quad\text{where}\quad d=2(\kappa-1)\left[\frac{1}{3}\cos^{3}\Delta_{0}+\left(\frac{2r}{\pi}\right)^{2}(1-\varepsilon^{1/2})\cos\Delta_{0}\right].$$

(6)

Thus, the energy produced by the piston for the saw-toothed wave is $3/4$ of the total energy being equal to

$$\left\langle\dot{E_{p}}\right\rangle=\rho_{0}c_{0}^{3}h_{0}\varepsilon a,\quad\text{where}\quad a=\frac{3\kappa+3}{8}\left(\cos\Delta_{0}+\frac{\cos 3\Delta_{0}}{3}\right).$$

(7)

Substituting the equations (5)–(7) in (3), we obtain the following equation

$$h_{0}^{2}+mh_{0}-n\varepsilon=0,$$

(8)

where $m=b/d$, $n=a/d$. The solution of equation (8) relating to $h_{0}$ determines the dimensionless amplitude of pressure disturbance $\Delta p=2\rho_{0}c_{0}^{2}h_{0}.$

The theoretical dependence and experimental data relating to the swing amplitude of gas pressure and amplitude of piston displacement toward the resonance frequency are shown in Fig. 3. As we can see the results of theoretical calculations are in good agreement with the obtained experimental data in case of oscillations available across the entire range of piston displacement amplitudes. The discrepancy does not exceed $10\%$. In the course of increasing of excitation amplitude (over $0.25\times 10^{-3}$ m) the experimental values are just above the theoretical ones. This is explained by the greater influence of nonlinearity in case of high oscillation amplitudes in the resonance, which are seen on oscillograms in Fig. 2. Moreover, to analyze the influence of oscillation intensity the obtained experimental results were approximated by the power function $\Delta p=Al_{0}^{n}.$ Consequently, the constant values and power coefficients become $A=0.2$, $n=0.85$ for these experiments in case of gas oscillation on the resonance frequency $\nu_{1}=128$ Hz. It should be noted that power coefficient $n$ for the shock wave mode is 0.5 [7], and for shock-free wave mode is close to 1 [13]. Thus, the transient oscillation mode is observed in these experiments.

Fig. 3

Dependence of pressure disturbance $\Delta p$ on amplitude of piston dispalcement $l_{0}$ at an resonance frequency $\nu_{1}=128$ Hz.

4 CONCLUSION

The nonlinear oscillations of gas in the closed tube with the step-like cross-section are studied in vicinity to resonance at different amplitudes of piston displacement. It is defined that presence of step-like cross-section allows intensifying the media oscillations without shockwaves. The good agreement of theoretical and experimental data is obtained.