1 INTRODUCTION

The effect of the average ambient pressure \({p_{m}=(p_{1}+p_{2})}\) on bending in the classical thin plate theory [1–11] seems to be negligible. Herein \({p_{1}}\) and \({p_{2}}\) are overpressures applied to bottom and top surfaces respectively. It was shown [12–15] that the transverse distributed load \(q\) depends not only on the change in pressure \({p_{e}=p_{2}-p_{1}}\), but also on the deformation of the plate itself. Thus, the expression for the distributed transverse load on a circular plate of thickness \(h\) in the linear approximation has the form [13]

$$q=p_{e}+p_{m}h\nabla^{2}w,\quad\nabla^{2}=\frac{1}{r}\frac{d}{dr}\left({r\frac{d}{dr}}\right).$$
(1)

In this case, it is assumed that the contour area of the plate is isolated from the action of overpressures \(p_{1}\) and \(p_{2}\). With a small relative thickness of the plate, a large ratio of the average pressure to the modulus of elasticity of the material, the effect of the second component in (1) should be taken into account [12–15].

The linear bending of a rectangular plate with finite ratio of sides was studied in [14]. In this article an equation for a transverse distributed load is derived based on the theory of elasticity. The variability effect of the curvature of the middle surface and different boundary conditions on the value of the transverse distributed force, deflection, and critical forces was also researched. If it is taken into account the deformations in the plane of the middle surface induced by compression along the thickness under the action of the average pressure \(p_{m}\), then in the absence of displacement on the supports, the compressing forces arise. Herewith in the plane problem for a circular plate, the radial stress has the form: \(\sigma_{r}^{0}=-\nu p_{m}\) [15]. In the development of [15], in this work the nonlinear system of differential equations and the boundary conditions for the stress function corresponding to the problem are written in a more general form.

2 PROBLEM DEFINITION

Let us consider the static axisymmetric elastic bending of a circular plate of radius \(c\) and thickness \(h\). The lower and upper surfaces of the plate are affected by the gas pressures \(p_{0}+p_{1}\) and \(p_{0}+p_{2}\), where \(p_{0}\) is the atmospheric pressure, \(p_{1},p_{2}\) are the uniform overpressures. The pressures \(p_{1}\) and \(p_{2}\) can be both positive and negative, in the latter case, we have \(\mid p_{1}\mid<p_{0}\), \(\mid p_{2}\mid<p_{0}\). It is assumed that pressures \(p_{1}\), \(p_{2}\) remain unchanged, when the plate is bending. The edge of the plate is isolated from the action of overpressures (only \(p_{0}\) acts). Prior to the application of pressures \(p_{1}\), \(p_{2}\) the plate under an all-round pressure \(p_{0}\) is in an unstressed plane state. The effect of gas densities on the transverse load is not taken into account. The direction of the load \(q\), and deflection \(w(r)\) are positively down.

In accordance with Kirchhoff’s hypotheses, the system of nonlinear equations of the bending about the deflection functions \(w(r)\) and stresses \(\Phi(r)\) has the form [7]

$$D\frac{d(\nabla^{2}w)}{dr}-\frac{h}{r}\frac{d\Phi}{dr}\frac{dw}{dr}=\Psi,\quad\frac{d(\nabla^{2}\Phi)}{dr}+\frac{E}{2r}\left({\frac{dw}{dr}}\right)^{2}=0,$$
(2)
$$D=\frac{Eh^{3}}{12(1-\nu^{2})},\quad\sigma_{r}=\frac{d\Phi}{rdr},\quad\sigma_{\varphi}=\frac{d^{2}\Phi}{dr^{2}},\quad\Psi=\frac{1}{r}\int\limits_{0}^{r}{qrdr}.$$

Taking into account \(q\) from (1), the load function \(\Psi\) can be written as

$$\Psi=\frac{p_{e}r}{2}+p_{m}h\frac{dw}{dr}.$$
(3)

Since considerable values \(p_{m}\) of average pressure are allowed in the considered approach, it is necessary to take into account the effect of strain \(\varepsilon_{z}^{0}\) in the plane of the middle surface due to compression in thickness under the action of average pressure subject to a condition that the plate contour does not move in the direction of the radius. In the first equation (2), instead of the radial stress \({d\Phi}\mathord{\left/{\vphantom{{d\Phi}{(rdr)}}}\right.\kern-1.2pt}{(rdr)}\), it is necessary to substitute the sum of the stresses \({d\Phi}\mathord{\left/{\vphantom{{d\Phi}{(rdr)}}}\right.\kern-1.2pt}{(rdr)}+\sigma_{r}^{0}\) due to the bending of the plate and its compression in thickness.

Further down, for the deflection function \(w\), the conditions of simple supported of the plate along the contour [7]

$$w=0,\quad\frac{d^{2}w}{dr^{2}}+\frac{\nu}{r}\frac{dw}{dr}=0\quad(r=c)$$
(4)

and clamped

$$w=0,\quad{dw}\mathord{\left/{\vphantom{{dw}{dr}}}\right.\kern-1.2pt}{dr}=0\quad(r=c)$$
(5)

will be used. For radial stresses on the middle surface the boundary condition (BC) in general form is considered

$$(\sigma_{r}+\sigma_{r}^{0})h=-K(u+u^{0}),$$
(6)

where by \(K\) we denote the support stiffness \((r=c)\) with radial displacement of the plate. BC (6) can be written separately for the bending problem

$$\sigma_{r}h=-Ku$$
(7)

and for the plane problem

$$\sigma_{r}^{0}h=-Ku^{0}.$$
(8)

For the stress function \(\Phi\), the condition (7) has the form

$$\frac{h}{r}\frac{d\Phi}{dr}=-\frac{Kr}{E}\left(\frac{d^{2}\Phi}{dr^{2}}-\frac{\nu}{r}\frac{d\Phi}{dr}\right)\quad(r=c).$$
(9)

Expression \(\sigma_{r}^{0}\) has been define, taking into account the dependencies between deformations and stresses in the plane problem for a circular plate

$$\sigma_{z}^{0}=\frac{E}{1-v^{2}}(\varepsilon_{z}^{0}+\nu\varepsilon_{r}^{0}+\nu\varepsilon_{\varphi}^{0}),\quad\sigma_{r}^{0}=\frac{E}{1-v^{2}}(\varepsilon_{r}^{0}+\nu\varepsilon_{\varphi}^{0}+\nu\varepsilon_{z}^{0}),\quad\varepsilon_{r}^{0}=\varepsilon_{\varphi}^{0}={u^{0}}\mathord{\left/{\vphantom{{u^{0}}r}}\right.\kern-1.2pt}r$$
(10)

and the expression for the compression stress across the plate thickness,

$$\sigma_{z}^{0}=-p_{m}.$$
(11)

We obtain from (10), (11)

$$\varepsilon_{z}^{0}=-(1-\nu^{2})\frac{p_{m}}{E}-2\nu\frac{u^{0}}{r},\quad\sigma_{r}^{0}=-\nu p_{m}+E\nu_{1}\frac{u^{0}}{r},\quad\nu_{1}=\frac{1+\nu-2\nu^{2}}{1-\nu^{2}}.$$
(12)

Eliminating from (8) and the second relation (12) the displacement \(u^{0}\) for \(r=c\), we have

$$\sigma_{r}^{0}=-\frac{\nu p_{m}}{(1+\eta)},\quad\eta=\frac{E\nu_{1}h}{Kc}.$$
(13)

The \(\eta\) parameter represents the ratio of the tensile stiffness of the plate to the stiffness of the support device. When this ratio is small \((\eta\ll 1)\), from (13) the condition of no radial displacement \((u^{0}=0)\) and \(\sigma_{r}^{0}=-\nu p_{m}\) is obtained. With a low stiffness of the support \((\eta\rightarrow\infty)\), the condition of free displacement \(\sigma_{r}^{0}=0\) follows. For \(\eta=1\), we have \(\sigma_{r}^{0}=-\frac{\nu p_{m}}{2}\).

From the equilibrium equation in stresses for the plane problem \(\frac{d\sigma_{r}^{0}}{dr}+\frac{\sigma_{r}^{0}-\sigma_{\varphi}^{0}}{r}=0\) taking into account (10) we have \(\frac{d\sigma_{r}^{0}}{dr}=0\), \(\sigma_{r}^{0}=const\). From the condition (13) it follows that \(\sigma_{r}^{0}=-\frac{\nu p_{m}}{(1+\ eta)}\) over the entire radius of the plate. Thus, instead of the system of equations (2) and considering (3), we have the following nonlinear system of equations

$$D\frac{d(\nabla^{2}w)}{dr}-h\frac{dw}{dr}\left(\frac{d\Phi}{rdr}+p_{m}(1-\frac{\nu}{1+\eta})\right)=\frac{p_{e}r}{2},\quad\frac{d(\nabla^{2}\Phi)}{dr}+\frac{E}{2r}\left({\frac{dw}{dr}}\right)^{2}=0.$$
(14)

System (14) is supplemented by the boundary conditions (4), (9) or (5), (9) and the boundedness conditions for the functions \(\sigma_{r}\) and \(\theta=-\frac{dw}{dr}\) for \(r=0\).

3 SMALL DEFLECTIONS OF A CIRCULAR PLATE

In the case of a linear problem from (14) we have the equation

$$\frac{d(\nabla^{2}w)}{dr}-\frac{p_{m}h(1-\frac{\nu}{1+\eta})}{D}\frac{dw}{dr}=\frac{p_{e}r}{2D}.$$
(15)

In the case (4), making an approximate solution in the form [7]

$$w=f\left({1-2a\frac{r^{2}}{c^{2}}+ab\frac{r^{4}}{c^{4}}}\right),\quad a=\frac{3+\nu}{5+\nu},\quad b=\frac{1+\nu}{3+\nu}.$$
(16)

and, integrating (15) by the Bubnov–Galerkin method, we obtain the following expression for the relative defection in the center of the plate

$$\xi=\frac{f}{h}=\frac{3q^{\ast}(1-\nu^{2})}{16ab(1+\alpha)},\quad\alpha=\frac{3(1-\nu^{2})p_{m}c^{2}}{4Eh^{2}\beta}(1-\nu/(1+\eta)),\quad\beta=\frac{b(3-2b)}{6-8b+3b^{2}}.$$
(17)

Thus, the dimensionless parameter \(\alpha\) determines the contribution of the second term in equation (15).

The clamped conditions of the contour (5) are satisfied with the deflection function [7]

$$w=f({1-{r^{2}}/{c^{2}}})^{2}.$$
(18)

Relative sag equals to

$$\xi=\frac{f}{h}=\frac{3(1-\nu^{2})q^{\ast}}{16(1+\alpha)},\quad q^{\ast}=\frac{p_{e}}{E}\left({\frac{c}{h}}\right)^{4}\mbox{, }\alpha=\frac{3p_{m}c^{2}}{4Eh^{2}}(1-\nu^{2})(1-\nu/(1+\eta)).$$
(19)

From the expressions (17), (19) it is possible to visualize that the influence of the parameter \(\alpha\) is the greatest in the case of the simple supported, this is explained by the fact that the sign of the curvature of the middle surface of the simple supported plate does not change over the entire surface, as opposed to clamped.

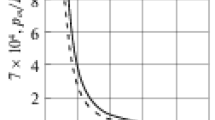
Figure 1 shows the dependence of the average pressure \(p_{m}/E\) on the parameter of the plate wall thinness \(c/h\) for the parameter \(\alpha=10^{-2}\) . The dashed line corresponds to the dependence at \(\eta\ll 1\), the dotted line represents to \(\eta=1\), the solid line describes to \(\eta\rightarrow\infty\). Curves 1 and 2 describe the dependencies for simple supported and clamped, respectively. For the values of the average pressure and thin-walled parameters that define the areas above the curves in Fig. 1, the effect of the average pressure for bending must be taken into account.

figure 1

Fig. 1.

The \(\alpha\) parameter and the average pressure have the least effect on the bending under one-sided pressure. Let \(p_{1}=0\), \(p_{m}=p_{2}/2\). We limit the value of \(p_{2}\) to the applicability of linear equation (15) and its solutions (17), (19). Setting \(\xi\leq 1\) in (17), (19), we obtain, respectively

$$\frac{p_{2}}{E}\leq\frac{16ab(1+\alpha)}{3(1-\nu^{2})}(h/c)^{4},\quad\frac{p_{2}}{E}\leq\frac{16(1+\alpha)}{3(1-\nu^{2})}(h/c)^{4}.$$
(20)

Taking into account (20), \(p_{m}=p_{2}/2\), (17), (19), we have the largest possible values of the parameter \(\alpha\) at the BC of the simple supported and clamped of the plate contour, respectively:

$${\alpha}=\frac{2}{\beta(c/h)^{2}/(ab(1-\nu/(1+\eta)))-2},\quad{\alpha}=\frac{2}{(c/h)^{2}/(1-\nu/(1+\eta))-2}.$$
(21)

Assuming in (21) that \(\alpha=0.01\), we find that for clamped of the plate contour and \(c/h\leq 12\), \(\eta\ll 1\) the point in Fig. 1 is above the curve, and for \(c/h>12\), \(\eta\ll 1\) it is below the curve (there is no effect of average pressure). This is explained by the fact that with a decrease in the relative thickness, the bending stiffness and the permissible one-sided pressure quickly fall. Moreover, the ratio \(p_{m}/E\) is also small.

Table 1 shows the values of the \(\alpha\) parameter for three pressure options \(p_{1},p_{2}\) at the same change in pressure \(p_{e}=10^{-3}\) bar, elastic modulus \(E=2\cdot 10^{6}\) bar and thin-walled parameter \(c/h=300\).

Table 1. Effect of boundary conditions and average pressure on the \(\alpha\) parameter
Full size table

It has been seen from (17), (19) and table that at large and close pressures \(p_{1}\) and \(p_{2}\), when the average pressure \(p_{m}\) is large and the difference \(p_{2}-p_{1}\) is small, the greatest deviation of the parameter \(\alpha\) from the classical value \(\alpha=0\) and the effect on bending are realized (for the same values of \(E\), \(c\), \(h\)). Note that the modulus of the parameter \(\alpha\) increases with decreasing support stiffness.

4 NONLINEAR BENDING

We take the same approximating functions for deflection \(w\) as in the linear solution. In the case of a clamped edge, substituting functions (18) in the second equation (14), we obtain the following expression bounded at \(r=0\) [7]

$$\frac{d\Phi}{dr}=-\frac{Ef^{2}r^{3}}{c^{4}}\left({1-\frac{2r^{2}}{3c^{2}}+\frac{r^{4}}{6c^{4}}}\right)+\frac{Cr}{2}.$$

Condition (9) implies

$$C=\frac{Ef^{2}}{3c^{2}}\left(\frac{3Eh+Kc(5-3\nu)}{Eh+Kc(1-\nu)}\right).$$

For \(K\rightarrow\infty\) \((u(c)=0)\) we have \(C=\frac{Ef^{2}(5-3\nu)}{3c^{2}(1-\nu)}\); for \(K=0\) \((\sigma_{r}(c)=0)\) we obtain \(C=\frac{Ef^{2}}{c^{2}}\). Let us substitute the expressions into the system of equations (14):

$$\frac{d(\nabla^{2}w)}{dr}=\frac{32fr}{c^{4}},\quad\frac{dw}{dr}=-\left({\frac{4fr}{c^{2}}}\right)\left({1-\frac{r^{2}}{c^{2}}}\right),$$
$$\frac{d^{2}\Phi}{dr^{2}}=\frac{Ef^{2}}{6c^{2}}\left({\frac{Kc(5-3\nu)+3Eh}{Kc(1-\nu)+Eh}-\frac{18r^{2}}{c^{2}}+\frac{20r^{4}}{c^{4}}-\frac{7r^{6}}{c^{6}}}\right).$$

After integration by the Bubnov–Galerkin method, we obtain the equation

$$\frac{2}{21}(7A-12)\xi^{3}+\frac{16(1+\alpha)}{3(1-\nu^{2})}\xi=q^{\ast},\quad A=\frac{Kc(5-3\nu)+3Eh}{Kc(1-\nu)+Eh},$$
(22)

where \(q^{\ast}\) and \(\alpha\) are presented in (19).

With simple supported (16) we have \(\frac{d\Phi}{dr}=-\frac{Ef^{2}a^{2}r^{3}}{c^{4}}\left({1-\frac{2br^{2}}{3c^{2}}+\frac{b^{2}r^{4}}{6c^{4}}}\right)+\frac{Cr}{2}.\) From the condition of fixing the points of the contour of the plate (9), we determine

$$C=\frac{Ef^{2}a^{2}}{3c^{2}}\left(\frac{(Eh-\nu Kc)(6-4b+b^{2})+Kc(18-20b+7b^{2})}{Eh+Kc(1-\nu)}\right).$$

In particular, for \(K\rightarrow\infty\) \((u(c)=0)\) we have

$$C=\frac{Ef^{2}a^{2}}{3c^{2}(1-\nu)}\left(6(3-\nu)-4b(5-\nu)+b^{2}(7-\nu)\right);$$

for \(K=0\) \((\sigma_{r}(c)=0)\) we obtain

$$C=\frac{Ef^{2}a^{2}}{3c^{2}}\left(6-4b+b^{2}\right).$$

Using the Bubnov–Galerkin method, we obtain the equation for \(\xi\)

$$8a^{3}e\xi^{3}+\frac{16ab(1+\alpha)}{3(1-\nu^{2})}\xi=q^{\ast},$$
(23)

where

$$e=\frac{Ab}{12\beta}-\frac{14-28b+21b^{2}-7b^{3}+b^{4}}{7(3-2b)},\quad A=\frac{(Eh-Kc\nu)(6-4b+b^{2})+Kc(18-20b+7b^{2})}{Kc(1-\nu)+Eh},$$

\(q^{\ast}\), \(\alpha\) correspond to (17). The equation (23) for \(\nu=0.3\), \(K\rightarrow\infty\) has the form

$$2.660\xi^{3}+1.437(1+\alpha)\xi=q^{\ast},\quad\alpha=1.8\frac{p_{m}}{E}\left({\frac{c}{h}}\right)^{2}.$$

For \(K=0\) from (23) it follows:

$$0.377\xi^{3}+1.437(1+\alpha)\xi=q^{\ast},\quad\alpha=2.6\frac{p_{m}}{E}\left({\frac{c}{h}}\right)^{2}.$$

In Fig. 2a shows nonlinear dependencies \(q^{*}(\xi)\) for various cases of fixing edges in a simple supported plate: \(K\rightarrow\infty\) (solid line), \(K=0\) (dash-dotted line). Linear solutions are shown in Fig. 2b, the solid line shows the dependencies taking into account the compression of the plate in thickness. It can be seen that for a fixed value of \(K\) and \(q^{\ast}\), an increase in the parameters \(\alpha\) leads to a decrease in the deflection, and for negative values of \(\alpha\), the deflection increases.

figure 2

Fig. 2

In a nonlinear solution, the effect of average pressure can be significant even in the case of one-sided pressure [13]. Taking for example \(\nu=0.3,p_{1}=0,p_{m}={p_{2}}\mathord{\left/{\vphantom{{p_{2}}2}}\right.\kern-1.2pt}2\) represent (23) as

$$2.660\xi^{3}+1.437(1+\alpha)\xi=q^{\ast},\quad q^{\ast}=\left({{p_{2}}\mathord{\left/{\vphantom{{p_{2}}E}}\right.\kern-1.2pt}E}\right)\left({c\mathord{\left/{\vphantom{ch}}\right.\kern-1.2pt}h}\right)^{4},\quad\alpha\approx\left({{0.9p_{2}}\mathord{\left/{\vphantom{{0.9p_{2}}{E}}}\right.\kern-1.2pt}{E}}\right)\left({c\mathord{\left/{\vphantom{ch}}\right.\kern-1.2pt}h}\right)^{2}.$$
(24)

We will restrict the deflection in the center of the plate to four thicknesses \((\xi=4)\).Then from (24) it follows

$$\alpha\approx\frac{148}{(c/h)^{2}-5.2}.$$
(25)

From the expression (25) it can be seen that for \(c/h\geq 122\), when \(\alpha=10^{-2}\), there is no effect of the average pressure on bending, while, for example, for \(c/h=12\), there is a noticeable influence \((\alpha\approx 1)\).

5 CONCLUSION

Thus, the effect on bending of the average overpressure \({p_{m}=(p_{1}+p_{2})/2}\) on the surface of a thin circular plate has been determined by the dimensionless parameter \({\alpha=\kappa(p_{m}/E)(c/h)^{2}(1-\nu/(1+\eta))}\). The effect essentially depends on the boundary conditions on the contour of the plate through the coefficient \(\kappa\), for example, for \({\nu=0.3}\), \({\eta\ll 1}\) when clamped we have \({\kappa=0.48}\), with simple support we obtain \({\kappa=1.84}\). Herein, the parameter \(\eta\) determines the ratio of the plate tensile stiffness to the support device stiffness. For \({\alpha\ll 1}\), the classical theory of bending of thin plates is valid.