On Gradient-Like Flows on Seifert Manifolds

Abstract

We consider a class of gradient-like flows on three-dimensional closed manifolds whose attractors and repellers belongs to a finite union of embedded surfaces and find conditions when the ambient manifold is Seifert.

1 INTRODUCTION AND STATEMENTS OF RESULTS

Let $M^{n}$ be a closed $n$-manifold. A flow $f^{t}$ on $M^{n}$ is called Morse-Smale if its non-wandering set consists of a finite set of hyperbolic equilibria and closed trajectories, and invariant manifolds of equilibria and closed trajectories have only transversal intersection. A Morse-Smale flow is called gradient-like if its non-wandering set does not contain closed trajectories.

Recall that a Morse index of hyperbolic equilibrium $p$ is the number equal to the dimension of the unstable manifold $W^{u}_{p}$ of $p$.

We suppose that $n=3$ and the manifold $M^{3}$ is oriented. Let us denote by $\Omega_{f^{t}}$ the set of all equilibria of gradient-like flow $f^{t}$ on $M^{3}$ and by $\Omega^{i}$, the set of equilibria of Morse index $i\in\{0,1,2,3\}$. Equilibria of Morse indices $0$ and $3$ are called nodes $($sinks and sources, respectively), equilibria of Morse indices $1,2$ are called saddles. Set $\Sigma=\Omega^{1}\cup\Omega^{2}$.

The following notation introduced similar to [2].

Definition 1. A gradient-like flow $f^{t}$ on $M^{3}$ has surface dynamics (belongs to a class $GSD(M^{3}))$ if the set $\Sigma$ can be represented as the union of two disjoint subsets $\Sigma_{a}$, $\Sigma_{r}$ such that each connected component of the sets $\mathcal{A}_{f^{t}}=W^{u}_{{\Sigma_{a}}}\cup\Omega^{0}$, $\mathcal{R}_{f^{t}}=W^{s}_{{\Sigma_{r}}}\cup\Omega^{3}$ is an oriented locally flat surface ¹ .

In [1] a topology of manifolds admitting flows from $GSD(M^{3})$ was studied. In particular it was proved, that $M^{3}$ is a mapping torus, that is $M^{3}$ is diffeomorphic to a quotient space $M_{g_{f^{t}},\tau_{f^{t}}}=\mathbb{S}_{g_{f^{t}}}\times[0,1]/\sim$ of the direct product of an oriented surface $S_{g_{f^{t}}}$ of a genus $g_{f^{t}}$ and the interval $[0,1]$ under an equivalence relation $(z,1)\sim(\tau_{f^{t}}(z),0)$, where $\tau_{f^{t}}:S_{f^{t}}\to S_{f^{t}}$ is an orientation preserving diffeomorphism.

In this paper we clarify the structure of ambient manifolds for flows from $GSD(M^{3})$ under the condition that invariant manifolds of saddle equilibria have simple asymptotic behavior (see definition 2). Main results of the paper are the following.

Theorem 1. If invariant manifolds of saddle equilibria of a flow $f^{t}\in GSD(M^{3})$ have simple asymptotic behavior, then the manifold $M^{3}$ is Seifert and gluing map $\tau_{f^{t}}$ is periodic.

Theorem 2. For any oriented surface $\mathbb{S}_{g}$ and any orientation preserving periodic diffeomorphism $\tau:\mathbb{S}_{g}\to\mathbb{S}_{g}$ there exists a gradient-like flow $f^{t}\in GSD(M^{3})$ with simple asymptotic behavior of invariant manifolds of saddles, and $M^{3}$ is the mapping torus $M^{3}_{\tau}$.

2 AUXILIARY FACTS AND BASIC DEFINITIONS

In [2, Theorems 1, 2], [4, Lemma 1, Theorem 1] the topology of manifolds admitting gradient-like cascades with surface dynamics was studied. Since a time one shift along trajectories of gradient-like flow with surface dynamics is such a cascade then results of these papers can be adopted to flows in the following way.

Proposition 1. Let $f^{t}\in GSD(M^{3})$ then there exist integers $k_{f^{t}},g_{f^{t}}\geq 0$ and an orientation preserving diffeomorphism $\tau_{f^{t}}$ of an oriented surface $\mathbb{S}_{g_{f^{t}}}$ of a genus $g_{f^{t}}$ such that:

1. Sets $\mathcal{A}_{f^{t}},\mathcal{R}_{f^{t}}$ consist of the same number $k_{f^{t}}$ of connected components, each of which is homeomorphic to $\mathbb{S}_{g_{f^{t}}}$.

2. Each connected component of the set $\mathcal{A}_{f^{t}}(\mathcal{R}_{f^{t}})$ is an attractor (repeller) ²

3. The closure of each connected component of the set $M^{3}\setminus(\mathcal{A}_{f^{t}}\cup\mathcal{R}_{f^{t}})$ is homeomorphic to the direct product $\mathbb{S}_{g_{f^{t}}}\times[0,1]$.

4. The manufold $M^{3}$ is diffeomorphic to the quotient space $M_{g_{f^{t}},\tau_{f^{t}}}=\mathbb{S}_{g_{f^{t}}}\times[0,1]/\sim$ under the equivalence relation $(z,1)\sim(\tau_{f^{t}}(z),0)$.

Let $\sigma\in\Sigma$. Recall that a connected component of the stable (unstable) manifold $W^{s}_{\sigma}\setminus\sigma$ ($W^{u}_{\sigma}\setminus\sigma$) is called the stable $($unstable$)$ separatrix of $\sigma$.

Let $\sigma^{1}\subset\Omega^{1},\sigma^{2}\subset\Omega^{2}$ be points such that $W^{u}_{\sigma^{2}}\cap W^{s}_{\sigma^{1}}\neq\varnothing$. According to [3] any connected component of the intersection $W^{u}_{\sigma^{2}}\cap W^{s}_{\sigma^{1}}\neq\varnothing$ is called heteroclinic trajectory.

Let $V$ be a connected component of the set $M^{3}\setminus(\mathcal{A}_{f^{t}}\cup\mathcal{R}_{f^{t}})$. Then, due to Proposition 1 there exist connected components $A,R$ of $\mathcal{A}_{f^{t}},\mathcal{R}_{f^{t}}$, respectively, such that $\partial V=A\cup R$. Set $\Omega_{A}=\Omega_{f^{t}}\cap A,\Omega^{i}_{A}=\Omega^{i}\cap A,\ i\in\{0,1,2\}$, $\Omega_{R}=\Omega_{f^{t}}\cap R,\Omega^{j}_{R}=\Omega^{j}\cap R,\ j\in\{1,2,3\}$. Then the following equalities hold: $A=\bigcup\limits_{p\in\Omega_{A}}W^{u}_{p}$, $R=\bigcup\limits_{p\in\Omega_{R}}W^{s}_{p}.$

Due to [5, Theorem 2.3] and [2, Lemmas 1, 2] the following statement is true.

Proposition 2. Let $\sigma^{1}\in\Omega^{1}_{A}$ and $\omega\in\Omega^{0}_{A}$ . Then:

1. $W^{u}_{\sigma^{1}}\subset A$ and exist points $\omega_{+},\omega_{-}\in\Omega^{0}_{A}$ (it is possible, $\omega_{+}=\omega_{-}$) such that $cl\ W^{u}_{\sigma^{1}}\setminus W^{u}_{\sigma^{1}}=\omega_{+}\cup\omega_{-}$.

2. there exist points $\sigma^{2}_{+},\sigma^{2}_{-}\in\Omega^{2}_{A}$ (it is possible, $\sigma^{2}_{+}=\sigma^{2}_{-}$ ) such that the set $W^{s}_{\sigma^{1}}\cap(W^{u}_{\sigma^{2}_{+}}\cup W^{u}_{\sigma^{2}_{-}})$ consists of exactly two different heteroclinic trajectories.

3. there exists a point $\sigma^{1}_{*}\in\Omega^{1}_{R}$ such that $\omega\subset cl\ W^{u}_{\sigma^{1}_{*}}$.

Similar statement is true for points $\sigma^{2}\in\Omega^{2}_{R}$ and $\alpha\in\Omega^{3}_{R}$ with formal change of symbols $A,0,1,2,s,u$ by $R,3,2,1,u,s$, respectively.

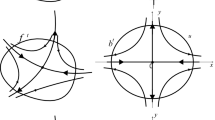
Definition 2. We say that invariant manifolds of saddle equilibria of a flow $f^{t}\subset GSD(M^{3})$ have simple asymptotic behavior if for any triple of connected components $A\subset\mathcal{A}_{f^{t}},R\subset\mathcal{R}_{f^{t}},V\subset M^{3}\setminus(\mathcal{A}_{f^{t}}\cup\mathcal{R}_{f^{t}})$ such that $\partial V=A\cup R$ the following conditions hold (see Figure 1 ):

Fig. 1

Simple asymptotic behavior of invariant manifolds of saddle equilibria.

1. for any two different points $\sigma^{1}_{r,1},\sigma^{1}_{r,2}\in\Omega^{1}_{R}$ the closures of separatrices $l^{u}_{\sigma^{1}_{r,1}}$, $l^{u}_{\sigma^{1}_{r,2}}\subset V$ contain different points $\omega_{1},\omega_{2}\subset\Omega^{0}_{A}$;

2. for any two different points $\sigma^{2}_{a,1},\sigma^{2}_{a,2}\in\Omega^{2}_{A}$ the closures of separatrices $l^{s}_{\sigma^{2}_{a,1}},l^{s}_{\sigma^{2}_{a,2}}\subset V$ contain different points $\alpha_{1},\alpha_{2}\subset\Omega^{3}_{R}$;

3. for any point $\sigma^{1}_{a}\subset\Omega^{1}_{A}$ there exists exactly one point $\sigma^{2}_{r}\subset\Omega^{2}_{R}$ such that the intersection $W^{s}_{\sigma^{1}_{a}}\cap W^{u}_{\sigma^{2}_{r}}\cap V$ is not empty; for any point $\sigma^{2}_{r}\subset\Omega^{2}_{R}$ there exists exactly one point $\sigma^{1}_{a}\subset\Omega^{1}_{A}$ such that $W^{s}_{\sigma^{1}_{a}}\cap W^{u}_{\sigma^{2}_{r}}\cap V$ is not empty;

4. for any points $\sigma^{1}_{a}\in\Omega^{1}_{A},\sigma^{2}_{r}\in\Omega^{2}_{R}$ the intersection $W^{s}_{\sigma^{1}_{a}}\cap W^{u}_{\sigma^{2}_{r}}\cap V$ is either empty or consists of exactly one heteroclinic curve.

Let us denote by $GSDS(M^{3})$ the subset of $GSD(M^{3})$ consisting of flows with the simple asymptotic behavior of separatrices.

3 CELLS OF $GSDS$-FLOWS

For a flows $f^{t}\in GSDS(M^{3})$ let us denote by $\Gamma_{A}$ ($\Gamma_{R}$) a union of all equilibria, one-dimensional separatrices and heteroclinic trajectories of $f^{t}$ that belong to $A(R)$ and by $f^{t}_{A}$ ($f^{t}_{R}$) the restriction of $f^{t}$ on $A(R)$. The set $\Gamma_{A}$ is support for a graph whose vertices are equilibria, and edges are one-dimensional separatrices and heteroclinic trajectories. Let us denote by $E(\Gamma_{A})$ the set of connected components of the set $\Gamma_{A}\setminus\Omega_{A}$.

Definition 3. A connected component of the set $A\setminus\Gamma_{A}$ ($R\setminus\Gamma_{R}$) is called two-dimensional cell of the flow $f^{t}_{A}$ $(f^{t}_{R})$.

It follows from proposition 2 the description of all possible types of two-dimensional cells (see Figure 2).

Fig. 2

Two-dimensional cells of $GSD$-flows.

Proposition 3. The boundary $\partial a$ of a two-dimensional cell $a$ of the flow $f^{t}_{A}$ have one of the following type:

$a_{1})$ $\partial a$ consists of a sink $\omega_{a}\in\Omega^{0}_{A}$, saddles $\sigma^{1}_{a,+},\sigma^{1}_{a,-}\in\Omega^{1}_{A}$, separatrices $l^{u}_{\sigma^{1}_{a,+}},l^{u}_{\sigma^{1}_{a,-}}$ of $\sigma^{1}_{a,+},\sigma^{1}_{a,-}$ whose closures contain $\omega_{a}$, a saddle $\sigma^{2}_{a}\in\Omega^{2}_{A}$, and heteroclinic curves $\gamma_{\sigma^{2}_{a},\sigma^{1}_{a,+}}\subset W^{u}_{\sigma^{2}_{a}}\cap W^{s}_{\sigma^{1}_{a,+}}$, $\gamma_{\sigma^{2}_{a},\sigma^{1}_{a,-}}\subset W^{u}_{\sigma^{2}_{a}}\cap W^{s}_{\sigma^{1}_{a,-}}$;

$a_{2})$ $\partial a$ consists of a sink $\omega_{a}$, an unstable manifold $W^{u}_{\sigma^{1}_{a}}$ of a point $\sigma^{1}_{a}\in\Omega^{1}_{A}$ whose closure contain $\omega_{a}$, a saddle $\sigma^{2}_{a}\in\Omega^{2}_{A}$ and a heteroclinic curve $\gamma_{\sigma^{2}_{a},\sigma^{1}_{a}}\subset W^{u}_{\sigma^{2}_{a}}\cap W^{s}_{\sigma^{1}_{a}}$;

$a_{3})$ $\partial a$ consists of a sink $\omega_{a}$, a saddle $\sigma^{1}_{a}$, a separatrix $l^{u}_{\sigma^{1}_{a}}$ such that $\omega_{a}\in cl\ l^{u}_{\sigma^{1}_{a}}$, a saddle $\sigma^{2}_{a}\in\Omega^{2}_{A}$ and heteroclinic curves $\gamma^{+}_{\sigma^{2}_{a},\sigma^{1}_{a}},\gamma^{-}_{\sigma^{2}_{a},\sigma^{1}_{a}}\subset W^{u}_{\sigma^{2}_{a}}\cap W^{s}_{\sigma^{1}_{a}}$.

The boundary $\partial r$ of any two-dimensional cell $r$ of $f^{t}_{R}$ has exactly one of the following three types:

$r_{1})$ $\partial r$ consists of a source $\alpha_{r}\in\Omega^{3}_{R}$, saddles $\sigma^{2}_{r,+},\sigma^{2}_{r,-}\in\Omega^{2}_{R}$, separatrices $l^{s}_{\sigma^{2}_{r,+}},l^{s}_{\sigma^{2}_{r,-}}$, whose closures contain $\alpha_{r}$, a saddle $\sigma^{1}_{r}\in\Omega^{1}_{A}$ and heteroclinic curves $\gamma_{\sigma^{2}_{r,+},\sigma^{1}_{r}}\subset W^{u}_{\sigma^{2}_{+}}\cap W^{s}_{\sigma^{1}_{r}}$, $\gamma_{\sigma^{2}_{r,-},\sigma^{1}_{r}}\subset W^{u}_{\sigma^{2}_{r,-}}\cap W^{s}_{\sigma^{1}_{r}}$;

$r_{2})$ $\partial r$ consists of a source $\alpha_{r}$, a stable manifold $W^{s}_{\sigma^{2}_{r}}$ of a saddle $\sigma^{2}_{r}\subset\Omega^{2}_{R}$ whose closure contains $\alpha_{r}$, a saddle $\sigma^{1}_{r}\subset\Omega^{1}_{R}$ and a heteroclinic curve $\gamma_{\sigma^{2}_{r},\sigma^{1}_{r}}\subset W^{u}_{\sigma^{2}_{r}}\cap W^{s}_{\sigma^{1}_{r}}$;

$r_{3})$ $\partial r$ consists of a source $\alpha_{r}$, a saddle $\sigma^{2}_{r}\subset\Omega^{2}_{R}$, a separatrix $l^{u}_{\sigma^{2}_{r}}$ whose closure contains $\alpha_{r}$, a saddle $\sigma^{1}_{r}\subset\Omega^{1}_{R}$, and heteroclinic curves $\gamma_{\sigma^{2}_{r},\sigma^{1}_{r}},\gamma_{\sigma^{2}_{r},\sigma^{1}_{r}}\subset W^{u}_{\sigma^{2}_{r}}\cap W^{s}_{\sigma^{1}_{r}}$.

Let us denote by $\Gamma_{A}^{u}$ a subset of $\Gamma_{A}$ that contains all one-dimensional separatrices of saddles from the set $\Omega^{1}_{A}$.

Proposition 4. $\Gamma_{A}^{u}$ is connected.

Proof. Let us choose a set of pair-wise disjoint disks $\{D_{q}\}_{q\in\Omega^{2}_{A}}$ bounded by circles that meet trajectories of $f^{t}_{A}$ transversally and such that $q\in int\ D_{q}$, $D_{q}\in W^{u}_{q}$ for any $q\in\Omega^{2}_{A}$. Set $U=A\setminus\bigcup\limits_{q\in\Omega^{2}_{q}}int\ D_{q}$. By definition the set $U$ is connected, $f^{t}(U)\subset int\ f^{s}(U)$ while $t>s$, and $\Gamma_{A}^{u}\subset int\ U$. Moreover, $\Gamma_{A}^{u}=\bigcap\limits_{t\geq 0}f^{t}(U)$. Then $\Gamma_{A}^{u}$ is connected as an the intersection of compact connected nested sets. $\Box$

Definition 4. Let $f^{t}\in GSDS(M^{3})$. A connected component of $M^{3}\setminus\bigcup\limits_{p\in\Sigma}(cl\ W^{u}_{p}\cup cl\ W^{s}_{p})$ is called three-dimensional cell of the flow $f^{t}$.

Proposition below immediately follows from the definition 2 of the class $GSDS(M^{3})$.

Proposition 5. Let $f^{t}\subset GSDS(M^{3})$. Then for any three-dimensional cell $C^{3}$ of $f^{t}$ its boundary $\partial C^{3}$ has one of types $v_{1}$ , $v_{2}$, $v_{3}$:

$v_{1})$ The intersection $\partial C^{3}\cap A$ is a two-dimensional cell with the boundary of type $a_{1})$, the set $\partial C^{3}\cap R$ is a two-dimensional cell of type $r_{1})$, the set $\partial C^{3}\cap V$ consists of a separatrix $l^{u}_{\sigma^{1},r}$ such that $\omega_{a}\subset cl\ l^{u}_{\sigma^{1},r}$, a separatrix $l^{s}_{\sigma^{2},a}$ such that $\alpha_{r}\subset cl\ l^{s}_{\sigma^{2},a}$, heteroclinic curves $\gamma_{\sigma^{2}_{r,-},\sigma^{1}_{a,-}}$, $\gamma_{\sigma^{2}_{r,+},\sigma^{1}_{a,+}}$, a subset of the manifold $W^{u}_{\sigma^{2}_{r,-}}\cap V$ bounded by curves $\gamma_{\sigma^{2}_{r,-},\sigma^{1}_{r}},\gamma_{\sigma^{2}_{r,-},\sigma^{1}_{a,-}}$, a subset of the manifold $W^{u}_{\sigma^{2}_{r,+}}\cap V$ bounded by curves $\gamma_{\sigma^{2}_{r,+},\sigma^{1}_{r}},\gamma_{\sigma^{2}_{r,+},\sigma^{1}_{a,+}}$, a subset of the manifold $W^{s}_{\sigma^{1}_{a,-}}\cap V$ bounded by curves $\gamma_{\sigma^{2}_{a},\sigma^{1}_{a,-}},\gamma_{\sigma^{2}_{r,-},\sigma^{1}_{a,-}}$, and a part of the manifold $W^{s}_{\sigma^{2}_{r,+}}\cap V$ bounded by curves $\gamma_{\sigma^{2}_{a},\sigma^{1}_{a,-}},\gamma_{\sigma^{2}_{r,+},\sigma^{1}_{a,+}}$.

$v_{2})$ The intersection $\partial C^{3}\cap A$ is a two-dimensional cell of type $a_{2}$), the set $\partial C^{3}\cap R$ is a two-dimensional cell of type $r_{3}$, the set $\partial C^{3}\cap V$ is defined similar to the item $v_{1})$.

$v_{3})$ The intersection $\partial C^{3}\cap A$ is a two-dimensional cell of type $a_{3})$ , the set $\partial C^{3}\cap R$ is a two-dimensional cell of type $r_{2}$ , the set $\partial C^{3}\cap V$ is defined similar to the item $v_{1})$ (see Figure 3 ).

Fig. 3

Three-dimensional cells of GSDS-flows.

For any set of connected components $A\subset\mathcal{A}_{f^{t}},R\subset\mathcal{R}_{f^{t}},V\subset M^{3}\setminus(\mathcal{A}_{f^{t}}\cup\mathcal{R}_{f^{t}})$ such that $\partial V=A\cup R$ let us denote by $\mathcal{C}^{2}_{A}$, $\mathcal{C}^{2}_{R}$, $\mathcal{C}^{3}_{V}$ the set of all cells of dimension two and three that belongs to $A$, $R$, $V$, respectively. Let us choose an arbitrary component $A\subset\mathcal{A}_{f^{t}}$ and denote by $V_{1},\dots,V_{2k_{f^{t}}}$ all pair-wise disjoint connected components of the set $M^{3}\setminus(\mathcal{A}_{f^{t}}\cup\mathcal{R}_{f^{t}})$. We will suppose that indices are chosen in such a way that $\mathop{cl}(V_{i})\cap\mathop{cl}(V_{i+1})\neq\varnothing$ for any $i\in\{1,\dots,2k_{f^{t}}-1\}$ and $\mathop{cl}(V_{2k_{f^{t}}})\cap\mathop{cl}(V_{1})\supset A$. Then the following proposition holds.

Proposition 6. For any two-dimension cell $c^{2}\subset A$ of the flow $f^{t}$ there is a sequence $C^{3}_{1},\dots,C^{3}_{2k_{f^{t}}}$ of three-dimensional cells such that $\mathop{cl}(C^{3}_{1})\cap A=\mathop{cl}(c^{2})$ , $C^{3}_{i}\subset V_{i}$ , $i\in\{1,\dots,2k_{f^{t}}\}$ and the intersections $\mathop{cl}(C^{3}_{i})\cap\mathop{cl}(C^{3}_{i+1})\setminus A$ , $i\in\{1,\dots,2k_{f^{t}}-1\}$ , $\mathop{cl}(C^{3}_{2k_{f^{t}}})\cap A$ are non-empty and each of them consists of a closure of two-dimensional cell.

Lemma 1. There is a well-defined one-to-one map $\mu_{A}:\mathcal{C}^{2}_{A}\to\mathcal{C}^{2}_{A}$ which assigns to each cell $c^{2}\in\mathcal{C}^{2}_{A}$ a cell $\tilde{c}^{2}$ belonging to the intersection $\mathop{cl}(C^{3}_{2k_{f^{t}}})\cap A$ . Moreover, $\mu_{A}$ induces orientation preserving homeomorphism $h_{A}:A\to A$ with the following properties:

1. $h_{A}(\Omega^{i}_{A})=\Omega^{i}_{A}$, $i\in\{0,1,2\}$;

2. $h_{A}(cl\ c^{2})=cl\ \mu_{A}(c^{2})$ for any cell $c^{2}\in\mathcal{C}^{2}_{A}$;

3. there exist an integer $m>0$ such that for ant arc $l\in\Gamma_{A}\setminus\Omega^{i}_{A}$ equalities $h_{A}^{m}(l)=l$, $h_{A}^{i}(l)\neq l$ hold for any natural $i<m$.

Proof. Let $c^{2}\subset A$, $C^{3}_{1},\dots,C^{3}_{2k_{f^{t}}}$ is a sequence of three-dimensional cells defined in Proposition 6 for $c^{2}$, and $\tilde{c}^{2}$ is a two-dimensional cell belonging to the intersection $cl\ C^{3}_{2k_{f^{t}}}\cap A$. Set $\mu_{A}(c^{2})=\tilde{c}^{2}$.

Suppose that $c^{2}$ has type $a_{1}$ (see Proposition 3). Let us choose an orientation on the boundary $\partial c^{2}$ of $c^{2}$ in such a way that if we going around it in counterclockwise direction (in the positive direction) provided that the observer is in the region $V$, the cell $c^{2}$ remains to the left from $\partial c^{2}$. If the cell $c^{2}$ has type $a_{2}$ ($a_{3}$) we choose the similar orientation on the closed curve consisting of closures of unstable separatrices of saddle point $\sigma^{1}_{c^{2}}\in\partial c^{2}$ (closures of heteroclinic curves joining points $\sigma^{2}_{c^{2}},\sigma^{1}_{c^{2}}\in\partial c^{2}$). Thus we obtain a finite set $\mathcal{E}_{A}$ of oriented simple closed curves cutting the surface $A$ into open disks. Since $A$ is oriented then for any arc $l\subset\partial c^{2}\cap\partial\tilde{c}^{2}$ the orientations of $\partial c^{2},\partial\tilde{c}^{2}$ induce opposite orientations on $l$.

let us construct an orientation preserving homeomorphism $h_{c^{2}}:cl\ c^{2}\to cl\ (\mu_{A}(c^{2}))$ in the following way.

Denote by $\mathbb{B}^{2}\subset\mathbb{R}^{2}$ the standard unit disk with the center in the Origin $O$ and by $\mathbb{S}^{1}$ the boundary of $\mathbb{B}^{2}$.

Let $e_{c^{2}}:\mathbb{B}^{2}\to cl\ c^{2}$ and $e_{\mu_{A}(c^{2})}:\mathbb{B}^{2}\to cl\mu_{A}(c^{2})$ be homeomorphisms preserving the orientation of the unit circle and such that $e_{c^{2}}(\mathbb{S}^{1})$ and $e_{\mu_{A}(c^{2})}(\mathbb{S}^{1})\in\mathcal{E}_{A}$. Without lost of generality suppose that if $c^{2}$ is a cell of type $a_{2}$ ($a_{3}$) then $e_{c^{2}}(O)=\sigma^{2}_{c^{2}}$ ($e_{c^{2}}(O)=\omega_{c^{2}}$) and $e_{c^{2}}(r_{x})=\gamma_{\sigma^{2}_{c^{2}},\sigma^{1}_{c^{2}}}(e_{c^{2}}(r_{x})=l^{u}_{\sigma^{1}_{c^{2}}})$, where $r_{x}\in\mathbb{B}^{2}$ is the interval joining the center $O$ of $\mathbb{B}^{2}$ with a point $x\in\mathbb{S}^{1}$.

Let us denote by $g^{1}_{c^{2},\mu_{A}(c^{2})}:\mathbb{S}^{1}\to\mathbb{S}^{1}$ an orientation preserving homeomorphism with following property: if $p\in\Omega^{i}_{A}\cap\partial c^{2},$ where $i\in\{0,1,2\}$, then there is $p^{\prime}\in\Omega^{i}_{A}\cap\partial\mu_{A}(c^{2})$ such that $g^{1}_{c^{2},\mu_{A}(c^{2})}(e^{-1}_{c^{2}}(p))=e^{-1}_{\mu_{A}(c^{2})}(p^{\prime})$.

Let $g^{2}_{c^{2},\mu_{A}(c^{2})}:\mathbb{B}^{2}\to\mathbb{B}^{2}$ be a homeomorphism given in the polar coordinates $\varphi,r$ by the formula $g^{2}_{c^{2},\mu_{A}(c^{2})}(\varphi,r)=(g^{1}_{c^{2},\mu_{A}(c^{2})}(\varphi),r)$. At last define a homeomorphism $h_{c^{2},\mu_{A}(c^{2})}:cl\ c^{2}\to cl\ \mu_{A}(c^{2})$ by $h_{c^{2},\mu_{A}(c^{2})}=e_{\mu_{A}(c^{2})}g^{2}_{c^{2},\mu_{A}(c^{2})}e^{-1}_{c^{2}}$. By construction $h_{c^{2},\mu_{A}(c^{2})}$ satisfy the following conditions:

1. $h_{c^{2},\mu_{A}(c^{2})}$ preserves the orientation of boundaries of cells $c^{2},\mu_{A}(c^{2})$;

2. $h_{c^{2},\mu_{A}(c^{2})}(\partial c^{2}\cap\Omega^{i}_{A})=\partial\mu_{A}(c^{2})\cap\Omega^{i}_{A}$.

Let $\hat{c}^{2}$ be a two-dimensional cell such that $\partial c^{2}\cap\partial\hat{c}^{2}\neq\emptyset$. Let us define an orientation preserving homeomorphism $g^{1}_{\hat{c}^{2},\mu_{A}(\hat{c}^{2})}:\mathbb{S}^{1}\to\mathbb{S}^{1}$ in such a way that:

1. for any $p\in\Omega^{i}_{A}\cap\partial\hat{c}^{2}$, $i\in\{0,1,2\}$, there is $p^{\prime}\in\Omega^{i}_{A}\cap\partial\mu_{A}(\hat{c}^{2})$ such that $g^{1}_{\hat{c}^{2},\mu_{A}(\hat{c}^{2})}(e^{-1}_{\hat{c}^{2}}(p))=e^{-1}_{\mu_{A}(\hat{c}^{2})}(p)$;

2. $g_{\hat{c}^{2},\mu_{A}(\hat{c}^{2})}(e^{-1}_{\hat{c}^{2}}(x))=e^{-1}_{\mu_{A}(\hat{c}^{2})}(h_{c^{2},\mu_{A}(c^{2})}(x))$ for any point $x\in\partial c^{2}\cap\partial\hat{c}^{2}$.

At last, let us define a homeomorphism $h_{\hat{c}^{2},\mu_{A}(\hat{c}^{2})}:cl\ \hat{c}^{2}\to cl\ \mu_{A}(\hat{c}^{2})$ similar to $h_{c^{2},\mu_{A}(c^{2})}$ and continue the process until we run out all cells from the set $\mathcal{C}^{2}$. The agreement of orientations of the boundaries of all cells guarantees that in the finale we get an orientation preserving homeomorphism $h_{A}:A\to A$. It follows from construction and Proposition 5 that homeomorphism $h_{A}$ satisfies to items 1, 2 of the Lemma.

Let us prove the item 3.

Since the set $\Omega_{A}$ is finite then for any point $p\in\Omega_{A}$ there exists an integer $m_{p}>0$ such that $h^{m_{p}}_{A}(p)=p$ and $h^{i}_{A}(p)\neq p$ for any natural $i$ less than $m_{p}$. For any curve $l\subset\Gamma_{A}\setminus\Omega_{A}$ and a cell $c^{2}\in\mathcal{C}^{2}_{A}$ denote similar numbers by $m_{l},m_{c^{2}}$.

Let $p\in\Omega^{1}_{A}$ and $\mathcal{L}_{p}$ be the set of arcs from the set $\Gamma_{A}\setminus\Omega_{A}$ the closures of which contain the point $p$. It follows from Lemma 2 that the set $\mathcal{L}_{p}$ consists exactly on four arcs and a pair of them belongs to the unstable manifold of $p$, and the other pair belongs to the intersection of the two-dimensional unstable manifold of $p$ with $A$. Let $d^{2}_{p}\subset A$ be a disk such that $d^{2}_{p}\cap\Omega_{A}=p$, $p\in int\ d^{2}_{p}$, and any arc $l^{i}_{p}\in\mathcal{L}_{p}$ intersects the boundary $\partial d^{2}_{p}$ of $d^{2}_{p}$ at the single point $z^{i}_{p}$. Let us choose an orientation of the curve $\partial d^{2}_{p}$ and suppose, without loss of the generality, that when one goes along the curve from the point $z^{1}_{p}$ to point $z^{4}_{p}$ in positive direction then points $z^{2}_{p},z^{3}_{p}$ appears on order of the numbering decreasing. Then the points belonging to the stable and the unstable manifolds of $p$ alternate. Then $m_{l^{1}_{p}}=m_{l^{3}_{p}},m_{l^{2}_{p}}=m_{l^{4}_{p}}$, and $m_{l^{1}_{p}},m_{l^{2}_{p}}\in\{m_{p},2m_{p}\}$. Since $h_{A}$ is orientation preserving then the order of the points of the intersection of arcs $h^{m_{p}}_{A}(l^{i}_{p})$ with $h^{m_{p}}_{A}(d^{2}_{p})$ coincides with the order of points $\{z^{i}_{p}\}$. Then $m_{l^{1}_{p}}=m_{l^{2}_{p}}$.

Let us show that for any pair $l,l^{\prime}\in\Gamma_{A}\setminus\Omega_{A}$ the equality $m_{l}=m_{l^{\prime}}$ holds. The set $\Gamma_{A}\setminus\Omega_{A}$ can be presented as a disjoint unit of the subsets $\mathcal{L}^{u}_{A}$ and $\mathcal{L}^{s}_{A}$ consisting of one-dimensional separatrices and heteroclinic trajectories of the flow $f^{t}$ respectively. Let us prove the statement for the arcs from $\mathcal{L}^{u}_{A}$. Then from this fact and the previous paragraph one gets that all numbers $m_{l}$ are equal to each other.

Let $\mathcal{L}_{\omega}\subset\mathcal{L}^{u}_{A}$ be a set of one-dimensional separatrices of the flow $f^{t}_{A}$ whose closures contain the sink $\omega$, and $k_{\omega}$ be the number of arcs in the set $\mathcal{L}_{\omega}$. Denote by $d^{2}_{\omega}\subset W^{s}_{\omega}$ a disk such that $p\in int\ d^{2}_{\omega}$ and $\partial d^{2}_{\omega}$ intersects each separatrix $l\in\mathcal{L}_{\omega}$ at the single point. Let us choose an orientation on the curve $\partial d^{2}_{\omega}$ and numbering of the point of the intersection of the arcs from $\mathcal{L}_{\omega}$ in order induces by the chosen orientation. Let $j=1,2,\dots$. The homeomorphism $h^{jm_{\omega}}$ preserves the set $\mathcal{L}_{\omega}$ and the orientation of $A$, hence it sends any three consecutive points from the set $\{z^{i}_{\omega}\}$ into points of the intersection of curves from $\mathcal{L}_{\omega}$ with $h^{jm_{\omega}}(\partial d^{2}_{\omega})$ following in the same order. Then $m_{l^{i}_{\omega}}=m_{l^{j}_{\omega}}$ for $i,j\in\{1,\dots,k_{\omega}\}$.

Now the coinciding of all periods of curves from the set $\mathcal{L}_{A}$ follows from the connectedness of the set $\Gamma_{A}^{u}$ consisting of closures of all one-dimensional separatrices laying in $A$, that was proven in Proposition 4. $\Box$

3.1 Construction of Seifert Fibration of the Ambient Manifold

Let us recall that a homeomorphism $\tau\colon\mathbb{S}_{g}\to\mathbb{S}_{g}$ of the closed oriented surface $S_{g}$ is called a periodic homeomorphism of the period $r>1$ if $\tau^{r}(x)=x$ for any point $x\in\mathbb{S}_{g}$, and $\tau^{l}\neq Id$ if $l\in(0,r)$. A number $\mu_{x}>0$ such that $\tau^{\mu_{x}}(x)=x$ and $\tau^{l}(x)\neq x$ form any $l\in(0,\mu_{x})$ is called the period of the point $x$. Due to [6] the set $X_{\tau}\subset S_{g}$ of points whose period less that $r$ is finite.

Topological classification of oriented preserving periodic homeomorphisms of surfaces is obtained by Nielsen in [6].

Lemma 2. There exists a periodic homeomorphism $\tau:A\to A$ such that $\tau(cl\ c^{2})=h_{A}(cl\ c^{2})$ for any cell $c^{2}\subset\mathcal{C}_{A}$, where $h_{A}:A\to A$ is a homeomorphisms defined in Lemma 1, and $X_{\tau}\subset\Omega_{A}$.

Proof. For a point $p\in\Omega_{A}$ set $\tau(p)=h_{A}(p)$. Let $\mathcal{L}_{0}\subset\Gamma_{A}\setminus\Omega_{A}$ be a set of all arcs such that $h$ does not send any arc from $\mathcal{L}_{0}$ to the arc from $\mathcal{L}_{0}$. For any arc $l_{0}\in\mathcal{L}_{0}$ set $l_{i}=h^{i}_{A}(l_{0})$, $i\in\{1,\dots,m_{l_{0}}-1\}$. Remark that the boundary of any arc $l\in\Gamma_{A}\setminus\Omega_{A}$ contains exactly one saddle point $\sigma_{1}(l)$ of the flow $f^{t}$ whose Morse index equals one. Denote by $e_{i}\colon[0,1]\to cl\ l_{i}$ a homeomorphisms such that $e_{i}(0)=\sigma_{1}(l_{i})$. For $i\in\{0,\dots,m_{l_{0}}-1\}$, $x\in l_{i}$ set $\tau(x)=e_{i+1}(e^{-1}_{i}(x))$, for $x\in l_{m_{l_{0}}-1}$ set $\tau(x)=e_{0}(e^{-1}_{m_{l_{0}}-1}(x))$. By construction the map $\tau$ is periodic on $\Gamma_{A}$. Then it is possible to extend it into the set $\mathcal{C}^{2}$ similar to construction of the homeomorphism $h_{A}$ in the proof of Lemma 1. $\Box$

Let $\nu,\mu$ be co-prime integers, $0\leq\nu<\mu$, and $\theta:\mathbb{B}^{2}\to\mathbb{B}^{2}$ be a rotation of the disk $\mathbb{B}^{2}$ by the angle $2\pi\frac{\nu}{\mu}$. Denote by $N^{3}=\mathbb{B}^{2}\times[0,1]/_{\sim}$ the quotient space by means of equivalence relation $(x,1)\sim(\theta(x),0)$, $x\in\mathbb{B}^{2}$.

Recall that a manifold $M^{3}$ is called Seifert manifold if $M^{3}$ is fibered into circles and any fiber has a neighborhood in $M^{3}$ fiber by fiber homeomorphic to $N^{3}$.

Proof of Theorem 1. Let us show that $M^{3}$ is a Seifert manifold. Due to Proposition 6 for any two-dimensional cell $c^{2}\subset A$ of the flow $f^{t}_{A}$ there exists a sequence $C^{3}_{1},\dots,C^{3}_{2k_{f^{t}}}$ of three-dimensional cells such that $\mathop{cl}(C^{3}_{1})\cap A=\mathop{cl}(c^{2})$, $C^{3}_{i}\subset V_{i}$, $i\in\{1,\dots,2k_{f^{t}}\}$, and intersections $\mathop{cl}(C^{3}_{i})\cap\mathop{cl}(C^{3}_{i+1})\setminus A$, $i\in\{1,\dots,2k_{f^{t}}-1\}$, $\mathop{cl}(C^{3}_{2k_{f^{t}}})\cap A$ are non-empty and consist of a closures of two-dimensional cells. Let $\tau:A\to A$ be a periodic homeomorphism constructed in Lemma 2.

Denote by $Q_{c^{2}}$ a union of closures of all three-dimensional cells belonging to the obtained sequence and set $X_{c^{2}}=\{x\in cl\ c^{2}:x=\tau(x)\}$. It follows from Propositions 3, 5 that there exists a continuous map $g_{c^{2}}:\mathbb{B}^{2}\times[0,1]\to Q_{c^{2}}$ such that:

1. $g_{c^{2}}(\mathbb{B}^{2}\times\{0;1\})\subset A$;

2. $g_{c^{2}}(\mathbb{B}^{2}\times\{0\})=cl\ c_{2}$;

3. $g_{c^{2}}(z,1)=\tau(g_{c^{2}}(z,0))$ for any point $z\in\mathbb{B}^{2}$;

4. the restriction of $g_{c^{2}}$ on $\mathbb{B}^{2}\times[0,1]\setminus\widetilde{X}$, where $\widetilde{X}=\{(z,1),z\in\mathbb{B}^{2},g_{c^{2}}(z,1)\subset X_{c^{2}}\}$, is a homeomorphism.

Let $c^{2}_{0}\in\mathcal{C}^{2}_{A}$ be an arbitrary cell. If $\tau=id$ then the map $g_{c^{2}_{0}}$ induces a continuous fibration $\mathcal{F}_{c^{2}_{0}}$ of the set $Q_{c^{2}_{0}}\setminus X_{c^{2}_{0}}$ into circles. If $\tau\neq id$ then the map $g_{c^{2}_{0}}$ induces a continuous fibration of the set $Q_{c^{2}_{0}}\setminus X_{c^{2}_{0}}$ into segments $I_{c^{2}_{0}}=\{g_{c^{2}_{0}}(z\times[0,1]),z\notin g^{-1}_{c^{2}_{0}}(X)\cap\mathbb{B}^{2}\times\{0\}\}$ supplemented with a finite set of circles $S_{c^{2}_{0}}=\{g_{c^{2}_{0}}(z\times[0,1]),z\in g^{-1}_{c^{2}_{0}}(X)\cap\mathbb{B}^{2}\times\{0\}\}$. In this case set $\mathcal{F}_{c^{2}_{0}}=I_{c^{2}_{0}}\cup S_{c^{2}_{0}}$.

Suppose that the cell $c^{2}_{1}\in\mathcal{C}^{2}_{A}\setminus c^{2}_{0}$ is such that $cl\ c^{2}_{0}\cap cl\ c^{2}_{1}\neq\emptyset$ and $Q_{c_{1}^{2}}$ is the closure of the sequence of three-dimensional cells of the flow $f^{t}$ described above, and the set $\widetilde{F}_{1}\subset(\partial\mathbb{B}^{2})\times[0,1]$ is such that $g_{c^{2}_{0}}(\widetilde{F}_{1})\subset Q_{c_{1}^{2}}$. It follows from Proposition 5 that $\widetilde{F}_{1}$ is homeomorphic to the disk. Therefore there exists a continuous map $g_{c^{2}_{1}}:\mathbb{B}^{2}\times[0;1]\to Q_{c_{1}^{2}}$ that consists with $g_{c^{2}_{0}}$ on the set $\widetilde{F}_{1}$ and satisfy the conditions 1–4 above (if to replace $c^{2}$ with $c^{2}_{1}$ in the notations). Denote by $\mathcal{F}_{c^{2}_{1}}$ a fibration of the set $Q^{2}_{c^{2}_{1}}$ induced by $g_{c^{2}_{1}}$ and continue the process of constructing the fibration in a similar way until all two-dimensional cells are exhausted.

Since the homeomorphism $\tau$ is periodic then after a finite number of steps we obtain a fibration $\mathcal{F}_{A}$ of $M^{3}$ into circles. Let us show that this fibration is Seifert. Denote by $X_{\tau}$ the set of points from $A$ (possibly, empty) whose period with respect to $\tau$ is less than the period $m_{\tau}$ of $\tau$. Due to Lemmas 1, 2 $X_{\tau}\subset\Omega_{A}$.

Two cases are possible: 1) $X_{\tau}$ is non-empty, then $\tau$ is not identity; 2) the set $X_{\tau}$ is empty.

Let us consider the case 1). Let $q\in X_{\tau}$ and $u_{q}\subset A$ be a neighborhood of $q$ wish does not contain any equilibria different from $q$. Suppose that $q$ is fixed point of $\tau$ (if period $m_{q}$ of $q$ greater then one then $\tau$ move to $\tau^{m_{q}}$ and apply the similar reasoning). Denote by $L_{q}$ a set of all arcs from $\mathcal{L}_{A}$ whose closures contain $q$. It follows from the construction of $\tau$ that the set $L_{q}$ contains at least two arcs. Let $l_{1},l_{2}\subset L_{q}$ be arcs that belongs to a boundary of the same cell $c^{2}_{*}$ and $\nu\in\{1,\dots,m_{\tau}-1\}$ be such a number that $l_{2}=\tau^{\nu}(l_{1})$. Let us choose a point $x_{1}\in l_{1}$ and join it with the point $x_{2}=\tau^{\nu}(x_{1})$ by an arc $b_{q}$ without self-intersections such that the interior of $b_{q}$ belongs to the set $c^{2}_{*}\cap u_{q}$. Set $S_{q}=\bigcup\limits_{i=0}^{m-1}\tau^{i}(b_{q})$. By construction, $S_{q}$ is $\tau$-invariant simple closed curve bounding a disk $D_{q}\subset u_{q}$, such that $q\in int\ D_{q}$. Since $\tau|_{S_{q}}$ is orientation preserving and periodic then there exists a homeomorphism $h_{q}:S_{q}\to\mathbb{S}^{1}$ which topologically conjugates $\tau|_{S_{q}}$ with the rotation $\theta|_{\mathbb{S}^{1}}$ of the circle $\mathbb{S}^{1}=\partial\mathbb{B}^{2}$ with an angle $2\pi\frac{n}{m_{\tau}}$, where $n,m_{\tau}$ are co-prime. A homeomorphism $h_{q}$ can be extended into a homeomorphism $H_{q}:D_{q}\to\mathbb{B}^{2}$ which conjugates $\tau|_{D_{q}}$ with the periodic rotation $\theta:\mathbb{B}^{2}\to\mathbb{B}^{2}$.

Denote by $\lambda_{x}$ a fiber of the fibration $\mathcal{F}_{A}$ passing through the point $x\in A$, and by $N_{q}$ a neighborhood of the fiber $\lambda_{q}$ generated by the fibers of the fibration $\mathcal{F}_{A}$ passing through points of $D_{q}$. Let us extend the homeomorphism $H_{q}:D_{q}\to\mathbb{B}^{2}$ up to a fiber by fiber homeomorphism $G_{q}:N_{q}\to N_{\theta}$, where $N_{\theta}=\mathbb{B}^{2}\times[0,1]/_{\sim}$ is the quotient space of $\mathbb{B}^{2}\times[0,1]$ by means of equivalence relation $(x,1)\sim(\theta(x),0)$, $x\in\mathbb{B}^{2}$. For this, remark that the orientation of any segment $z\times[0,1]$, $z\in\mathbb{B}^{2}$ induces the orientation of the closed curve $(z\times[0,1])/_{\sim}$ in $N_{\theta}$. Similar, the homeomorphisms $g_{c^{2}}$ induce the orientations of fibers generated the set $N_{q}$. Let $x\in D_{q},y\in\lambda_{x}$ be points such that there exists an arc $\hat{\lambda}_{x,y}\subset\lambda_{x}$ joining points $x,y$ and such that the movement along this arc from $x$ to $y$ is agreed with the orientation of the fiber $\lambda_{x}$ and $\hat{\lambda}_{x,y}\cap d_{p}=x$. Denote by $|\hat{\lambda}_{x,y}|$ the length of the arc $\hat{\lambda}_{x,y}$ and by $x^{\prime}\in\mathbb{B}^{2},\lambda^{\prime}_{x^{\prime}},y^{\prime},\hat{\lambda}^{\prime}_{x^{\prime},y^{\prime}},|\hat{\lambda}^{\prime}_{x^{\prime},y^{\prime}}|$ similar objects for the manifold $N_{\theta}$. Set $G(y)=y^{\prime}$, where $y^{\prime}$ is a point such that $\frac{|\hat{\lambda}_{x,y}|}{|\hat{\lambda}_{x,\tau(x)}|}=\frac{|\hat{\lambda}^{\prime}_{x^{\prime},y^{\prime}}|}{|\hat{\lambda}^{\prime}_{H_{q}(x),\theta(H_{q}(x))}|}$.

For an arbitrary point $p\in A\setminus X_{\tau}$ there exists a closed neighborhood $D_{p}\subset A$ consisting of points of equal periods with respect to the map $\tau$. Denote by $N_{p}$ the neighborhood of the fiber $\lambda_{p}$ generated by the fibers of the fibration $\mathcal{F}_{A}$ passing though the points of $D_{p}$. Similar to the construction of $G_{q}$ one can construct fiber by fiber homeomorphism $G_{p}:N_{p}\to\mathbb{B}^{2}\times\mathbb{S}^{1}$.

In the case 2) for any points $p\in A$ reasoning are similar to ones above.

Thus, we have proved that the constructed bundle is a Seifert bundle.

Since $A$ is homeomorphic to the surface $\mathbb{S}_{g_{f^{t}}}$ we can identify it with $\mathbb{S}_{g_{f^{t}}}$. Then applying the techniques of the proof of the Theorem 1 one can immediately get the following statement.

Corollary 1. Manifold $M^{3}$ is diffeomorphic to the quotient space $\mathbb{S}_{g}\times[0,1]/_{\sim}$ of $\mathbb{S}_{g}\times[0,1]$ by equivalence relation $(z,1)\sim(\tau_{f^{t}}(z),0)$ , where $\tau:\mathbb{S}_{g_{f^{t}}}\to\mathbb{S}_{g_{f^{t}}}$ is the periodic homeomorphisms defined in Lemma 2.

4 REALIZATION

In this section we prove Theorem 2. Let $\mathbb{S}_{g}$ be an orientable surface of genus $g$ and $\tau:\mathbb{S}_{g}\to\mathbb{S}_{g}$ be an orientation preserving periodic diffeomorphism. Let us prove that there exists a gradient-like flow $f^{t}\in GSD(M^{3})$ with simple asymptotic behavior of invariant manifolds of saddles given on the mapping torus $M^{3}_{\tau}$.

According to [6] the orbit space $\mathbb{S}_{g}/_{\tau}$ is homeomorphic to an orientable surface $S_{g_{\tau}}$ of genus $g_{\tau}$ (a module surface) and the natural projection $p_{\tau}:\mathbb{S}_{g}\to S_{g_{\tau}}$ is $m_{\tau}$-branched covering everywhere except points of the set $X_{\tau}\subset\mathbb{S}_{g}$ consisting of points whose period is less then $m_{\tau}$. Any point $x\in X_{\tau}$ of period $m_{x}$ is a branch point of the order $\lambda_{x}=\frac{m_{x}}{m_{\tau}}$. It means that there exists a neighborhood $U_{x}\subset\mathbb{S}_{g}$ of the point $x$ and homeomorphisms $h_{x}:U_{x}\to\mathbb{C}$, $\chi_{x}:p_{\tau}(U_{x})\to\mathbb{C}$, where $\mathbb{C}$ is the complex plane, such that $h_{x}(x)=O$, $\chi_{x}(p_{\tau}(x))=O$ and $\chi(p_{\tau}(h^{-1}(z)))=z^{\lambda_{x}},z\in\mathbb{C}$.

Let us present the surface $S_{g_{\tau}}$ by an $4g_{\tau}-$polyhedron unfolding as it shown on the Figure 4, (a) and denote by $g^{t}$ a gradient-like flow on the surface $S_{g_{\tau}}$ with phase portrait shown on the Figure 4. If the set $X_{\tau}$ contains more than two fixed points then one can modify the flow $g^{t}$ as in shown on the Figure 4, (b), by adding pairs of a sink and a saddle in such a way that projections of all branch points belongs to equilibria of obtained flow (see [7, Theorem 3.1.2] for more details). We will denote the modified flow also by $g^{t}$. Then there exists a gradient-like flow $G^{t}$ on $S_{g_{\tau}}$ such that $p_{\tau}G^{t}=g^{t}p_{\tau}$, so trajectories of the flow $G^{t}$ are $\tau$-invariant.

Fig. 4

Construction of an axillary flow on the module surface.

Define on the segment $[0,1]$ a flow $\psi^{t}$ by equation $\dot{s}=\sin{\pi s}$, $s\in[0,1]$ and consider the flow $F^{t}$ on the direct product $\mathbb{S}_{g}\times[0,1]$ given by $F^{t}(z,s)=(G^{t}(z),\psi^{t}(s))$, $z\in\mathbb{S}_{g},s\in[0,1]$. Let $\pi_{\tau}:\mathbb{S}_{g}\times[0,1]\to M_{\tau}$ be the natural projection. Then the flow $f^{t}=\pi_{\tau}F^{t}\pi^{-1}_{\tau}$ is the desired flow.