1 INTRODUCTION

Reactions of ionic dissociation of molecules and reverse reactions of recombination of ions constitute an important component of many complex chemical processes occurring in various non-equilibrium natural or technological media. In particular, the concentration of ions in plasma is primarily determined by the competition between the reactions in question [1, 2]. The simplest examples of these reactions are collision induced dissociation (CID) of diatomic molecules to singly charged ions and recombination of singly charged atomic ions. The study of CID processes has an important place in chemical physics. For instance, there is a rich body of literature devoted to investigations of the dynamics of ionic dissociation of alkali halide molecules (first of all, of cesium halides) in collisions with rare gas and mercury atoms (as well as with a sulfur hexafluoride molecule) in crossed molecular beams, see the surveys [3–7] and the detailed bibliography [8]. These CID reactions proceed according to the schemes

$${\text{R}} + {\text{MX}} \to {\text{R}} + {{{\text{M}}}^{ + }} + {{{\text{X}}}^{ - }},$$
(1)
$${\text{R}} + {\text{MX}} \to {\text{R}}{{{\text{M}}}^{ + }} + {{{\text{X}}}^{ - }},$$
(2)

where M+ is an alkali ion, X– is a halide ion, and R is a neutral rare gas or mercury atom. The CID channel R + MX → RX– + M+ was observed in crossed molecular beam experiments for the system Xe + CsI only [9, 10]. Note that the cesium halides practically do not dissociate to neutral atoms [11]. The main tool of theoretical exploration of the reactions (1) and (2) is quasiclassical trajectory simulation on an adequate potential energy surface, see the surveys [4–7].

There are no experimental studies of the dynamics of the recombination reactions

$${{{\text{M}}}^{ + }} + {{{\text{X}}}^{ - }} + {\text{R}} \to {\text{MX}} + {\text{R}},$$
(3)
$${\text{R}}{{{\text{M}}}^{ + }} + {{{\text{X}}}^{ - }} \to {\text{MX}} + {\text{R}},$$
(4)

reverse to the CID reactions (1) and (2). Moreover, most certainly, experimental investigations of the dynamics of direct three-body recombination (3) are currently not possible at all. This is primarily due to the fact that it is extremely difficult to experimentally implement the intersection of three sufficiently intense beams or of two beams and a dense gas target. On the other hand, various dynamical characteristics of the reactions (3) with M+ = Cs+ have been examined in detail within the framework of the quasiclassical trajectory method [2, 7, 12–23]. The paper [22] presents the results of quasiclassical trajectory simulation of one of the reactions (4), namely, of the XeCs+ + Br– reaction. Note that the bimolecular reaction (4) is the final stage of one of the indirect recombination mechanisms known as the bound complex mechanism [2, 13, 24, 25].

Simulation of elementary atomic and molecular processes within the framework of the quasiclassical trajectory method is, as a rule, more illustrative than semiclassical or quantum mechanical calculations (and such simulation is fully justified if all the particles involved in the process are heavy enough). However, the use of hard sphere approximations sometimes enables one to achieve even greater visuality in the studies of atomic and molecular collisions. Within the framework of hard sphere models (impulsive models), the description of the motion of the particles in the zone of strong repulsive interaction is radically simplified. Namely, these particles are treated as balls which exchange energies and momenta at their contacts with each other according to the elastic impact law [4, 26–30] (inelastic encounters of balls are also sometimes considered). In addition, simulation of the particle motion outside the zone of strong repulsive interaction is also greatly simplified. The “ideology” of the hard sphere approximation, as well as the advantages and disadvantages of hard sphere models in comparison with full trajectory calculations, are discussed in detail in the works [26–28, 31] and partly in the works [4, 32]. As far as the authors know, the first attempt to study chemical reactions in the hard sphere approximation was made in the paper [33]. The report [28] contains an annotated list of 209 works (up to 1991, inclusive), in which one or another version of the hard sphere approximation is employed to examine various phenomena in chemical or atomic physics. Hard sphere models of the CID reactions (1) have been considered in many works [4, 9, 10, 26, 28, 34–38]. Hard sphere models have been used in the theory of atomic and molecular collisions in the gas phase until recently [29–32, 39–43].

In the works [31, 32], we proposed a hard sphere model of direct three-body recombination (3) and presented calculation results for the reactions

$${\text{C}}{{{\text{s}}}^{ + }} + {\text{B}}{{{\text{r}}}^{ - }} + {\text{R}} \to {\text{CsBr}} + {\text{R}}$$
(5)

with R = Ar, Kr, Xe, Hg for the ion approach energies and the third body energies in the range 1–10 eV typical for low temperature plasma [1]. This model includes instantaneous elastic encounters among the particles M+, X–, R, while the particle motion in the time intervals between the encounters (as well as before and after the series of the encounters) is described as the motion of the neutral atom R under no forces and the motion of the ions M+, X– under Coulomb attraction. The interaction potentials M+–R and X––R are not dealt with in any way in the model of [31, 32] (to be more precise, they have the form of infinite potential walls). A much simpler version of the hard sphere model of direct three-body recombination (3) is considered in [40]. The aim of the present paper is to describe a hard sphere model of bimolecular recombination (4) and calculation results for the same particles M+, X–, R as in the works [31, 32], i.e., for the reactions

$${\text{RC}}{{{\text{s}}}^{ + }} + {\text{B}}{{{\text{r}}}^{ - }} \to {\text{CsBr}} + {\text{R}}$$
(6)

with R = Ar, Kr, Xe, Hg, and for the same range 1–10 eV of collision energies. It is interesting that a hard sphere model of recombination is already contained in one of the first papers [44] devoted to applications of the hard sphere approximation in chemical physics. In the work [44], the so-called method of images is introduced to study the motions of three particles along a fixed straight line in piecewise constant potentials.

Within hard sphere simulation of bimolecular recombination (4), as well as of the reverse CID reaction (2) with the molecular ion formation, it is, of course, impossible to completely ignore the interaction potential between the particles R and M+.

In the case of CID (2), a model should include one or another criterion for the formation of the molecular ion (complex) RM+. Various versions of a hard sphere model of the reactions (2) were used in the works [4, 26, 45, 46] (see also [10, 36]). In these works, the criteria for the molecular ion formation (in the case of dissociation of the MX salt molecule) boil down, roughly speaking, to checking (possibly, several times) the inequality \(W < \varepsilon \), where W is the energy of the relative motion of the particles R and M+, while \(\varepsilon \) is the potential well depth of the M+–R interaction potential, i.e., the dissociation energy of the complex. The fulfillment of the inequality \(W < \varepsilon \) (or of some analogue of this inequality) immediately after the system leaves the zone of strong repulsive interaction (i.e., immediately after the termination of the series of elastic impacts among the particles R, M+, X–) is a criterion for the complex formation. The fulfillment of this inequality after the ions move away from each other in the Coulomb potential field for a great distance is a criterion for the complex “survival”. Hard sphere models of the reactions (2) that only involve a criterion for the complex formation were considered in the works [4, 26, 46]. Hard sphere models involving both criteria were dealt with in the works [26, 45, 46].

The hard sphere model of bimolecular recombination (4) proposed in the present paper is based on the following idealized description of the approach of the RM+ complex and the X– ion. Denote by r the internuclear distance in the complex. A realistic potential \(U(r)\) of the M+–R interaction with \(U( + \infty ) = 0\) is characterized by the equilibrium distance \({{r}_{m}}\), the depth \(\varepsilon \) of the potential well, and the distance \({{r}_{*}} > {{r}_{m}}\) at which the attraction force between the particles R and M+ is maximal and equal to \({{f}_{*}}{\text{:}}\)

$$\begin{gathered} U{\kern 1pt} '({{r}_{m}}) = 0,\,\,\,\,U({{r}_{m}}) = - \varepsilon , \\ U{\kern 1pt} {''}({{r}_{*}}) = 0,\,\,\,\,U{\kern 1pt} '({{r}_{*}}) = {{f}_{*}}. \\ \end{gathered} $$

At \(r = {{r}_{*}}\) the graph of the function \(U(r)\) has an inflection point. It is supposed in our model that the RM+ complex and the X– ion are approaching as follows: the center of mass of the complex and the X– ion move as two material points of the corresponding masses connected by Coulomb attraction, while the R atom and the M+ ion move around the center of mass of the complex as two material points connected by the potential \(U(r)\) in the absence of the X– ion. Such an approach of the RM+ complex and the X– ion takes place until the distance d between the center of mass of the complex and the X– ion becomes equal to the quantity \({{d}_{{\text{*}}}}\) defined by the equation

$$d_{*}^{{ - 2}} = {{f}_{*}}$$
(7)

(here and henceforth, the atomic units are used unless when stated otherwise). The relation (7) means that the Coulomb attraction force between the RM+ complex and the X– ion is equal to the maximal attraction force between the R atom and the M+ ion in the complex. After that, the R atom starts moving inertially, while the M+ and X– ions start moving as two balls connected by Coulomb attraction. After the equality \(d = {{d}_{*}}\) is achieved, the potential \(U(r)\) is no longer taken into account while considering the motion of the particles. As to the X––R interaction potential, we did not take it into account at any stage of the particle motion.

The prototype of this model is the method of patched conics in space dynamics [47–49]. Within the framework of this method, passive motion (motion without any engine thrust) of a spacecraft C in the gravitational field of two celestial bodies A and B of masses \({{m}_{{\text{A}}}} < {{m}_{{\text{B}}}}\) (for instance, of a planet and a star) is treated as Keplerian with respect to the body A inside the so-called sphere of influence of this body and as Keplerian with respect to the body B outside the sphere of influence of the body A. At the boundary of the sphere of influence, Keplerian trajectories are “patched” together according to sufficiently simple rules. The sphere of influence of the body A with respect to the body B is defined as the domain of locations of the spacecraft C where the inequality

$$\frac{{\left| {{{{\mathbf{g}}}_{{{\text{BC}}}}} - {{{\mathbf{g}}}_{{{\text{BA}}}}}} \right|}}{{\left| {{{{\mathbf{g}}}_{{{\text{AC}}}}}} \right|}} < \frac{{\left| {{{{\mathbf{g}}}_{{{\text{AC}}}}} - {{{\mathbf{g}}}_{{{\text{AB}}}}}} \right|}}{{\left| {{{{\mathbf{g}}}_{{{\text{BC}}}}}} \right|}}$$

holds, here \({{{\mathbf{g}}}_{{{\text{PQ}}}}}\) is the gravitational acceleration with which a body Q is attracted to a body P. In contrast to the sphere of influence, the sphere of attraction of the body A with respect to the body B (which is defined as the domain where the inequality \(\left| {{{{\mathbf{g}}}_{{{\text{BC}}}}}} \right| < \left| {{{{\mathbf{g}}}_{{{\text{AC}}}}}} \right|\) is valid) is not essential for space flight mechanics [47].

The literal analogue of the method of patched conics for the particles R = A, X– = B, and M+ = C (in the setup where one takes into account the potential \(U(r)\) of the interaction M+–R = C–A and the Coulomb potential of the interaction M+–X– = C–B) looks as follows. Since we neglect the interaction X––R = B–A, the “sphere of influence” of the R atom on the M+ ion with respect to the X– ion coincides with the “sphere of attraction” and is given by the inequality

$${{s}^{{ - 2}}} < \left| {U{\kern 1pt} '(r)} \right|,$$
(8)

where, as above, r is the M+–R internuclear distance, while s is the M+–X– internuclear distance. Inside this “sphere of influence”, the M+ ion and the R atom move around their common center of mass as two material points connected by the potential \(U(r)\). Outside the “sphere of influence” (8), the M+ and X– ions move around their common center of mass as two material points connected by Coulomb attraction.

The differences between our model and this exact analogue of the method of patched conics are as follows. In the inequality (8), we replace the distance s between the ions with the distance d between the X– ion and the center of mass of the M+–R system and replace the right-hand side with its maximal (for \(r > {{r}_{m}}\)) value \({{f}_{*}}.\) Thus, the equation of the “sphere of influence” of the R atom on the M+ ion with respect to the X– ion in our model has the form \({{d}^{{ - 2}}} < {{f}_{*}}.\) Moreover, whenever the M+ ion is located inside this “sphere of influence”, we suppose that the center of mass of the M+–R system and the X– ion move as a pair of material points connected by Coulomb attraction.

2 DESCRIPTION OF THE MODEL

As in the hard sphere model of direct three-body recombination (5) [31, 32], each of the particles Cs+, Br–, Ar, Kr, Xe, Hg was represented by a homogeneous ball of the mass corresponding to the actual atomic weight of the element in question. As the radii of the balls, we used the ionic radii of the ions Cs+ and Br– (1.67 and 1.96 Å, respectively [50]) and the atomic radii of the neutral atoms Ar, Kr, Xe, Hg (1.92 [51], 1.98 [52], 2.18 [52], and 1.55 Å [53], respectively). We employed the same Cs+–R interaction potentials as in the works [2, 7, 12–23] devoted to trajectory simulation of recombination (3) and (4) with M+ = Cs+.

The Cs+–R interaction potentials with R = Ar, Kr, Xe were given by the model [4, 34, 35]

$$U(r) = A{{e}^{{{{ - r} \mathord{\left/ {\vphantom {{ - r} {{\rho }}}} \right. \kern-0em} {{\rho }}}}}} - {{{{\alpha }_{{\text{R}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{\text{R}}}}} {2{{r}^{4}}}}} \right. \kern-0em} {2{{r}^{4}}}} - {C \mathord{\left/ {\vphantom {C {{{r}^{6}}}}} \right. \kern-0em} {{{r}^{6}}}},$$
(9)

where r is the internuclear distance, A and \(\rho \) are parameters of the repulsive wall in the Born–Mayer form (A is the calibration factor and \(\rho \) is the “softness” of the Cs+–R pair), C is the dispersion constant of the van der Waals interaction in the London approximation, and \({{\alpha }_{{\text{R}}}}\) is the polarizability of the R atom. The values of \({{\alpha }_{{\text{R}}}}\) are given in the works [9, 54–58]. The values of the parameters A, \(\rho \), and C were obtained on the basis of various sources [9, 56, 58–62] (as well as [10] in the case R = Xe). Some parameters are explicitly given in these works, while the other ones were computed to ensure the reproduction of the spectroscopic data, i.e., the location and depth of the potential well.

Following the works [26, 38, 46], we represented the Cs+–Hg interaction potential as the sum of the interaction potential of the isoelectronic system Xe–Hg (in the Lennard-Jones form) and the summand \({{ - {{\alpha }_{{{\text{Hg}}}}}} \mathord{\left/ {\vphantom {{ - {{\alpha }_{{{\text{Hg}}}}}} {2{{r}^{4}}}}} \right. \kern-0em} {2{{r}^{4}}}},\) where \({{\alpha }_{{{\text{Hg}}}}} = 34.4\) a.u. [54] is the polarizability of the mercury atom:

$$U(r) = {{D}_{0}}[{{({{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} r}} \right. \kern-0em} r})}^{{12}}} - 2{{({{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} r}} \right. \kern-0em} r})}^{6}}] - {{{{\alpha }_{{{\text{Hg}}}}}} \mathord{\left/ {\vphantom {{{{\alpha }_{{{\text{Hg}}}}}} {2{{r}^{4}}}}} \right. \kern-0em} {2{{r}^{4}}}}.$$
(10)

Here \({{r}_{0}}\) and \({{D}_{0}}\) are respectively the equilibrium distance and the potential well depth of the ground state of the Xe–Hg system. We used the values of these quantities determined experimentally in the paper [63] (the same values are given in the handbook [55]).

The values of all the parameters of the potentials (9) and (10) are compiled in Table 1 along with the equilibrium distance \({{r}_{m}}\), the depth \(\varepsilon \) of the potential well, and the distances \({{r}_{*}}\) and \({{d}_{*}} = f_{*}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}\) (see the equation (7)). Note that a detailed annotated bibliography of the works (up to 2016) on the interaction potentials in all the two-particle systems M+–X–, M+–R, X––R, and R–Hg (M+ being an alkali ion, X– a halide ion, and R a rare gas atom) is presented in the report [64].

Table 1.   Parameters of the Cs+–R interaction potentials (in the atomic units)
Full size table

We assumed that before the RM+ complex and the X– ion get close to each other at the critical distance \({{d}_{*}}\), the vibrational and rotational levels of the complex have Boltzmann distributions corresponding to a certain temperature T. The selection procedure for the initial conditions of a collision of the reactants RM+ and X– in our model at a fixed temperature T and a fixed collision energy \({{E}_{{{\text{col}}}}}\) was as follows.

In accordance with the brief characterization of the model given in the introduction, we supposed that at the initial time instant \(t = 0\), the distance between the center of mass of the RM+ complex and the X– ion is equal to \({{d}_{*}}\), while the energy of the relative motion of the complex and the ion is equal to \({{E}_{*}} = {{E}_{{{\text{col}}}}} + d_{*}^{{ - 1}}.\) To be more precise, we assumed that at \(t = 0\) the center of mass of the complex coincides with the origin of the fixed coordinate frame \(Oxyz\) and has zero velocity whereas the nucleus of the X– ion has the coordinates \(\left( {{{{\left( {d_{*}^{2} - b_{*}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},{{b}_{*}},0} \right)\) and the velocity \(( - {{({{2{{E}_{*}}} \mathord{\left/ {\vphantom {{2{{E}_{*}}} {{{\mu }_{{{\text{col}}}}}}}} \right. \kern-0em} {{{\mu }_{{{\text{col}}}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},0,0)\). Here \({{\mu }_{{{\text{col}}}}}\) is the reduced mass of the RM+ complex and the X– ion, while the distance \({{b}_{*}} \leqslant {{d}_{*}}\) is chosen randomly according to the rule \({{b}_{*}} = {{d}_{*}}{{\xi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\) (\(\xi \) being a random variable uniformly distributed between 0 and 1). The angular momentum conservation law implies that the impact parameter b of such a collision relates to the distance \({{b}_{*}}\) by the equality \(bE_{{{\text{col}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} = {{b}_{*}}E_{*}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}},\) so that

$$\begin{gathered} b = {{b}_{*}}{{({{{{E}_{*}}} \mathord{\left/ {\vphantom {{{{E}_{*}}} {{{E}_{{{\text{col}}}}}}}} \right. \kern-0em} {{{E}_{{{\text{col}}}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{b}_{{{\text{max}}}}}{{\xi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ {{b}_{{{\text{max}}}}} = {{d}_{*}}{{({{{{E}_{*}}} \mathord{\left/ {\vphantom {{{{E}_{*}}} {{{E}_{{{\text{col}}}}}}}} \right. \kern-0em} {{{E}_{{{\text{col}}}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $$
(11)

At impact parameters greater than \({{b}_{{\max }}}\), recombination in our model is impossible. Note that in the overwhelming majority of cases, while simulating elementary processes, the values of the impact parameters above which the reaction in question does not occur are determined by test calculations and cannot, strictly speaking, be indicated a priori. Such a situation also takes place for the hard sphere model of direct three-body recombination (3) proposed in the works [31, 32]. In the hard sphere model of bimolecular recombination (4) described in the present paper, the limit value \({{b}_{{\max }}}\) of the impact parameter is computed a priori, although via a quantity without an explicit physical meaning, namely, via the derivative \({{f}_{ * }}\) of the interaction potential in the RM+ complex at the inflection point (see the equation (7)).

As the collision energy \({{E}_{{{\text{col}}}}}\) grows from zero to infinity, the coefficient \({{({{{{E}_{*}}} \mathord{\left/ {\vphantom {{{{E}_{*}}} {{{E}_{{{\text{col}}}}}}}} \right. \kern-0em} {{{E}_{{{\text{col}}}}}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\) in (11) monotonically decreases from infinity to one and the value of \({{b}_{{\max }}}\) monotonically decreases from infinity to \({{d}_{*}}.\)

After \({{b}_{ * }}\) was selected, the coordinates and velocities of the M+ ion and the R atom in the RM+ complex at \(t = 0\) were chosen randomly on the basis of the Boltzmann distributions (at the temperature T) of the vibrational energy \({{E}_{{{\text{vib}}}}} = \omega ({v} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})\) and the rotational energy \({{E}_{{{\text{rot}}}}} = Bj(j + 1)\). Here \(\omega = {{[{{U{\kern 1pt} {''}({{r}_{m}})} \mathord{\left/ {\vphantom {{U{\kern 1pt} {''}({{r}_{m}})} {{{\mu }_{{{\text{lex}}}}}}}} \right. \kern-0em} {{{\mu }_{{{\text{lex}}}}}}}]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\) \(B = {{(2{{\mu }_{{{\text{lex}}}}}r_{m}^{2})}^{{ - 1}}}\), \({{\mu }_{{{\text{lex}}}}}\) is the reduced mass of the M+ ion and the R atom, while v and j are the vibrational and rotational quantum numbers. Otherwise speaking, we supposed that \({{E}_{{{\text{vib}}}}}\) and \({{E}_{{{\text{rot}}}}}\) are the energies of the harmonic oscillator and the linear rigid rotor, respectively, with the parameters corresponding to the interaction potential \(U(r)\) in the complex near the minimum point \(r = {{r}_{m}}\) where \(U(r) \approx {{\mu }_{{{\text{lex}}}}}{{\omega }^{2}}{{(r - {{r}_{m}})}^{2}}{\text{/}}2 - \varepsilon \). Of course, such a selection procedure for the energies \({{E}_{{{\text{vib}}}}}\) and \({{E}_{{{\text{rot}}}}}\) is not very precise, especially for potentials with such “shallow” potential wells as the M+–R interaction potentials, but the error associated with this circumstance is definitely smaller than the errors of the hard sphere approximation itself. If for the current values of v and j, the sum of the energies \({{E}_{{{\text{vib}}}}} + {{E}_{{{\text{rot}}}}}\) exceeded the depth \(\varepsilon \) of the potential well in the complex, then such values of v and j were rejected and the vibrational and rotational quantum numbers of the complex were chosen again. The entire selection procedure for the state of the complex at \(t = 0\) was carried out using the computer code presented in the report [65] on pages 59–61 (with minor changes due to the need to check the inequality \({{E}_{{{\text{vib}}}}} + {{E}_{{{\text{rot}}}}} < \varepsilon \) and due to another form of the potential).

If for the current collection of the values of the distance \({{b}_{ * }}\) and of the coordinates and velocities of the M+ ion and the R atom at \(t = 0\), the distance between the nuclei of some two particles out of M+, X–, R turned out to be less than the sum of the radii of those particles, then such a collection was rejected and the initial conditions of the collision were chosen again.

Thus, in our selection procedure for the initial conditions of a collision, the potential \(U(r)\) of the M+–R interaction is used in two ways, namely, to determine the distance \({{d}_{*}}\) and within the random choice of the coordinates and velocities of the M+ ion and the R atom.

Knowing the coordinates of the X– ion at \(t = 0\) pointed out above and the coordinates of the M+ ion, one can calculate the initial internuclear distance \({{s}_{*}}\) between the ions. The sum H of the initial energy of the relative motion of the RM+ complex and the X– ion (this energy being equal to \({{E}_{{{\text{col}}}}} + d_{*}^{{ - 1}}\)) and the initial energy of the Coulomb interaction of the ions (this energy being equal to \( - s_{*}^{{ - 1}}\)) in our model is not necessarily equal to \({{E}_{{{\text{col}}}}}\) and varies as one proceeds from one set of initial conditions to another. However, on the average, H differs little from \({{E}_{{{\text{col}}}}}\). Indeed, the location of the M+ ion at \(t = 0\) is determined by its distance \({{l}_{*}}\) to the origin (the center of mass of the complex) and by its location on the sphere centered at the origin and of radius \({{l}_{*}}\), the probability density of the occurrence of the nucleus of the M+ ion at any point of the sphere being constant and equal to \({{\left( {4\pi l_{*}^{2}} \right)}^{{ - 1}}}\) (if one neglects the condition that the balls representing the particles M+, X–, R should not “overlap”). On the other hand, the distance from the X– ion to the origin at \(t = 0\) is always equal to \({{d}_{*}},\) and the electrostatic field outside a uniformly charged sphere coincides with the field of the point charge equal to the total charge of the sphere and located at the center of the sphere [66] (the electrostatic field inside such a sphere vanishes). Consequently, the value \( - s_{*}^{{ - 1}},\) averaged over all the possible locations of the M+ ion with \({{l}_{*}} < {{d}_{*}},\) is equal to \( - d_{*}^{{ - 1}}.\)

After selecting the initial conditions of a collision RM+ + X–, further simulation of the particle motion, as was already noted in the introduction, was carried out in exactly the same way as in the hard sphere model of direct three-body recombination (3) [31, 32]. It was assumed that at a contact of any two balls representing the particles, their velocities instantly change according to the elastic impact law [4, 26–30]. In the time intervals between the encounters of the balls, the R atom and the center of mass of the ionic pair move under no forces, whereas the relative motion of the ions was determined by solving numerically the Newtonian equations of motion corresponding to a material point in the Coulomb potential field on a plane orthogonal to the conserved angular momentum vector \({\mathbf{L}} = {{\mu }_{{{\text{ion}}}}}[{\mathbf{s}},{\mathbf{\dot {s}}}]\) of the M+–X– system (the mass of the point being equal to the reduced mass \({{\mu }_{{{\text{ion}}}}}\) of the ions; \({\mathbf{s}}\) denotes the vector connecting the nuclei of the ions).

The equations of motion were integrated by the sixth order Adams–Bashforth method, while the first five integration steps (after selecting the initial conditions or after the latest encounter of two particles) were carried out by the fourth order Runge–Kutta method. The integration step length was set to be equal to 10 a.u. This turned out to be sufficient for conservation of the total internal energy \({{E}_{{{\text{tot}}}}} = {{{{\mu }_{{{\text{ion}}}}}{{{{\mathbf{\dot {s}}}}}^{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{{{\text{ion}}}}}{{{{\mathbf{\dot {s}}}}}^{2}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}\) and of the angular momentum L of the ionic pair M+–X– between two consecutive encounters with an accuracy up to \( \approx {\kern 1pt} 15\) significant digits. The instant of the impact was determined by a series of trial one-step backward integrations of the equations of motion by the fourth order Runge–Kutta method. The paper [32] explains in detail why we preferred numerical integration of the equations of motion to analytically solving the Kepler problem on the motion of a material point in the Coulomb potential.

The integration of the equations of motion was stopped and we proceeded to selecting the initial conditions of the next collision RM+ + X– as soon as the minimum of the two internuclear distances M+–R and X––R became larger than 250 a.u. If at this time instant the total internal energy \({{E}_{{{\text{tot}}}}}\) of the ionic pair turned out to be negative, recombination of the M+ and X– ions was regarded as having occurred (irrespective of the current internuclear distance s between the ions). The a priori minimum possible energy \({{E}_{{{\text{tot}}}}}\) corresponds to motionless tangent balls representing the M+ and X– ions. In the case of the Cs+ and Br– ions, it is equal to \( - 3.96684\) eV.

Note that while using the hard sphere model, one has to distinguish clearly between a collision of the particles (such a collision is understood as the whole process of interaction of the M+ and X– ions and the R atom from the initial time instant \(t = 0\) to the termination of integrating the equations of motion) and pairwise elastic encounters of the particles (there can be many such encounters within a single collision event). An encounter of the ions with each other does not affect the total internal energy \({{E}_{{{\text{tot}}}}}\) of the ionic pair; the energy \({{E}_{{{\text{tot}}}}}\) can only change at an encounter of one of the ions with the R atom.

3 RESULTS OF THE CALCULATIONS

For each of the four atoms R = Ar, Kr, Xe, Hg, for each of the three values of the temperature \(T = 500\), 1000, and 2000 K, and for each value of the collision energy \({{E}_{{{\text{col}}}}}\) from 1 to 10 eV with a step of 1 eV, we generated \(N = 500{\kern 1pt} 000\) collisions RCs+ + Br–. For each of the 120 triples \(({\text{R}},\;T,\;{{E}_{{{\text{col}}}}})\), the recombination probability is equal to \(P = {{{{N}_{0}}} \mathord{\left/ {\vphantom {{{{N}_{0}}} N}} \right. \kern-0em} N},\) where \({{N}_{0}}\) is the number of collisions ending in recombination of the Cs+ and Br– ions (such collisions will be said to be recombinative). It follows from the rule (11) of choosing the impact parameters b of the collisions that the recombination cross section \(\sigma \) can be computed by the formula

$$\sigma = \pi b_{{{\text{max}}}}^{2}P = \pi {{d}_{*}}\left( {{{d}_{*}} + E_{{{\text{col}}}}^{{ - 1}}} \right)P.$$
(12)

The standard error (also known as the mean error or the statistical error) of the probability P can be estimated as \({{[{{P(1 - P)} \mathord{\left/ {\vphantom {{P(1 - P)} N}} \right. \kern-0em} N}]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\) [67, 68].

The calculations show that the dynamics of recombination (6) in our model is weakly dependent on the temperature T (i.e., on the initial internal energy of the complex). We did not find any trend towards an increase or decrease in the recombination probability P as the temperature T grows. For each of the 40 pairs \(({\text{R}},\;{{E}_{{{\text{col}}}}})\), denote by \(\bar {P}\) the arithmetic mean of the three values of P obtained at \(T = 500\), 1000, and 2000 K, and by \(\Delta P\), the difference between the maximum and the minimum of these three values. The ratio \({{\Delta P} \mathord{\left/ {\vphantom {{\Delta P} {\bar {P}}}} \right. \kern-0em} {\bar {P}}}\) does not exceed 0.0238, 0.0196, 0.0374, and 0.0861 for R = Ar, Kr, Xe, and Hg, respectively. Moreover, the ratio \(\zeta = {{\Delta P} \mathord{\left/ {\vphantom {{\Delta P} {{{{[{{\bar {P}(1 - \bar {P})} \mathord{\left/ {\vphantom {{\bar {P}(1 - \bar {P})} N}} \right. \kern-0em} N}]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{[{{\bar {P}(1 - \bar {P})} \mathord{\left/ {\vphantom {{\bar {P}(1 - \bar {P})} N}} \right. \kern-0em} N}]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\) in our calculations does not exceed 4.3 (and in many cases it is several times smaller); in other words, the difference in the values of the probability P at different temperatures T is within the statistical error. The only exceptions are the cases R = Hg, \({{E}_{{{\text{col}}}}} = 1\) eV (\(\zeta = 25.4\)) and R = Hg, \({{E}_{{{\text{col}}}}} = 2\) eV (\(\zeta = 9.3\)). This is possibly due to the fact that the distance \({{d}_{ * }}\) for the interaction potential Cs+–Hg is noticeably less than that for the interaction potentials Cs+–Ar, Cs+–Kr, and Cs+–Xe (see Table 1).

As one expects, for each of the four atoms R (and for each of the three values of the temperature T), the recombination probability P and the cross section \(\sigma \) monotonically decrease as the collision energy \({{E}_{{{\text{col}}}}}\) grows. Figure 1 shows the dependences of the recombination probability P on \({{E}_{{{\text{col}}}}}\) at \(T = 1000\) K, while Fig. 2 displays the dependences of the recombination cross section \(\sigma \) on \({{E}_{{{\text{col}}}}}\) (i.e., the excitation functions) at \(T = 1000\) K. Due to the presence of the factor \({{d}_{*}} + E_{{{\text{col}}}}^{{ - 1}}\) in the formula (12), as the energy \({{E}_{{{\text{col}}}}}\) grows, the cross section \(\sigma \) decreases somewhat faster than the probability P. This is especially noticeable for small values of \({{E}_{{{\text{col}}}}}\). At \(T = 1000\) K, the ratio

$$Q_{P}^{{1,10}} = {{P({{E}_{{{\text{col}}}}} = 1\,\,{\text{eV}})} \mathord{\left/ {\vphantom {{P({{E}_{{{\text{col}}}}} = 1\,\,{\text{eV}})} {P({{E}_{{{\text{col}}}}} = 10\,\,{\text{eV}})}}} \right. \kern-0em} {P({{E}_{{{\text{col}}}}} = 10\,\,{\text{eV}})}}$$

is equal to 9.4, 6.06, 7.46, and 12.5 for R = Ar, Kr, Xe, and Hg, respectively, whereas the ratio

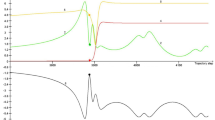
$$Q_{\sigma }^{{1,10}} = \sigma ({{E}_{{{\text{col}}}}} = 1\;{\text{eV}}){\text{/}}\sigma ({{E}_{{{\text{col}}}}} = 10\;{\text{eV}})$$

is equal to 15.8, 11.3, 13.1, and 25.9 for R = Ar, Kr, Xe, and Hg, respectively. Nevertheless, as \({{E}_{{{\text{col}}}}}\) grows, the hard sphere excitation function of the recombination reaction (6) with R = Xe in Fig. 2 recedes more slowly than the excitation function of the same reaction obtained in trajectory calculations [22] for the ground initial state (\({v} = j = 0\)) of the XeCs+ complex. This trajectory excitation function is also presented in Fig. 2 in the relative units chosen in such a way that the hard sphere cross section (at \(T = 1000\) K) and the trajectory cross section coincide for \({{E}_{{{\text{col}}}}} = 1\) eV. For the trajectory excitation function, \(Q_{\sigma }^{{1,10}} = 47.\)

Fig. 1.
figure 1

The dependences of the probability P of recombination (6) on the collision energy \({{E}_{{{\text{col}}}}}\) at \(T = 1000\) K. Lines 1, 2, 3, and 4 correspond to R = Ar, Kr, Xe, and Hg, respectively.

Full size image
Fig. 2.
figure 2

The excitation functions of recombination (6) at \(T = 1000\) K. Lines 1, 2, 3, and 4 correspond to R = Ar, Kr, Xe, and Hg, respectively. Line 5 represents (in arbitrary units) the excitation function of recombination (6) with R = Xe obtained in trajectory calculations [22].

Full size image

It is of interest to compare the probabilities P of bimolecular recombination (6) and the probabilities \({{P}_{3}}\) of three-body recombination (5) in the hard sphere approximation. Figure 3 shows the dependences of \({{P}_{3}}\) on the third body energy \({{E}_{{\text{R}}}}\) at the fixed ion approach energy \({{E}_{{\text{i}}}} = 1\) eV for the hard sphere model of recombination (5) from [32] in the case where the maximal values of the impact parameters \({{b}_{{\text{i}}}}\) and \({{b}_{{\text{R}}}}\) are equal to 80 and 40 a.u., respectively. For each of the four atoms R (especially for R = Ar), the dependence of \({{P}_{3}}\) on \({{E}_{{\text{R}}}}\) is characterized by a slower decrease in the recombination probability as the energy grows than the dependence of P on \({{E}_{{{\text{col}}}}}\). The ratio

$$\begin{gathered} Q_{{{{P}_{3}}}}^{{1,10}}({{E}^{0}}) \\ = {{{{P}_{3}}({{E}_{{\text{i}}}} = {{E}^{0}},\,\,{{E}_{{\text{R}}}} = 1\,\,{\text{eV}})} \mathord{\left/ {\vphantom {{{{P}_{3}}({{E}_{{\text{i}}}} = {{E}^{0}},\,\,{{E}_{{\text{R}}}} = 1\,\,{\text{eV}})} {{{P}_{3}}({{E}_{{\text{i}}}} = {{E}^{0}},\,\,{{E}_{{\text{R}}}} = 10\,\,{\text{eV}})}}} \right. \kern-0em} {{{P}_{3}}({{E}_{{\text{i}}}} = {{E}^{0}},\,\,{{E}_{{\text{R}}}} = 10\,\,{\text{eV}})}} \\ \end{gathered} $$

at \({{E}^{0}} = 1\) eV is equal to 2.11, 3.96, 5.34, and 6.04 for R = Ar, Kr, Xe, and Hg, respectively. These values are noticeably smaller than the values of the ratio \(Q_{P}^{{1,10}}\) at \(T = 1000\) K pointed out above. In the framework of quasiclassical trajectory simulation, we observed this phenomenon for the reactions (5) and (6) with R = Xe (see Fig. 1 in [22] where \({{E}^{0}} = 0.2\) eV). At \({{E}^{0}} \geqslant 2\) eV, the ratio \(Q_{{{{P}_{3}}}}^{{1,10}}({{E}^{0}})\) takes on even smaller values (and it is even less than one in some cases).

Fig. 3.
figure 3

The dependences of the probability \({{P}_{3}}\) of three-body recombination (5) on the third body energy \({{E}_{{\text{R}}}}\) at the fixed ion approach energy \({{E}_{{\text{i}}}} = 1\) eV for \({{b}_{{{\text{i}},\max }}} = 80\) a.u. and \({{b}_{{{\text{R}},\max }}} = 40\) a.u. in the hard sphere approximation [32]. Lines 1, 2, 3, and 4 correspond to R = Ar, Kr, Xe, and Hg, respectively.

Full size image

The opacity functions of the reactions (6) in our model, i.e., the dependences of the recombination probability on the impact parameter b for fixed values of T and \({{E}_{{{\text{col}}}}}\), are displayed in Fig. 4 at \(T = 1000\) K for the minimal (1 eV) and maximal (10 eV) collision energies \({{E}_{{{\text{col}}}}}\). These opacity functions were obtained as follows. The interval \(0 \leqslant b \leqslant {{b}_{{\max }}}\) where the parameter b ranges was divided into subintervals of length 1 a.u. (the last subinterval was of a smaller length), and the value of the opacity function at the center of a given subinterval \(\Xi \) is equal to the ratio of the number of recombinative collisions with b lying in \(\Xi \) to the number of all the collisions with b lying in \(\Xi \). The small oscillations in the lines of Fig. 4 are due to statistical uncertainties, and the differences between the opacity function at \(T = 500\) or 2000 K and the opacity function at \(T = 1000\) K do not exceed these uncertainties.

Fig. 4.
figure 4

The opacity functions of recombination (6) at \(T = 1000\) K. Lines 1, 2, 3, and 4 correspond to R = Ar, Kr, Xe, and Hg, respectively, for \({{E}_{{{\text{col}}}}} = 1\) eV. Lines 5, 6, 7, and 8 correspond to R = Ar, Kr, Xe, and Hg, respectively, for \({{E}_{{{\text{col}}}}} = 10\) eV.

Full size image

As is seen in Fig. 4, on the whole, the opacity functions for R = Kr, Xe, and Hg monotonically decrease as the parameter b grows (if one neglects the short initial piece of an increase at \({{E}_{{{\text{col}}}}} = 10\) eV). The behavior of the opacity functions for these atoms R at the intermediate values \(2 \leqslant {{E}_{{{\text{col}}}}} \leqslant 9\) eV of the collision energy is the same. On the other hand, for the lightest atom R = Ar (to which, in addition, there corresponds the largest distance \({{d}_{{\text{*}}}}\), see Table 1), the opacity function at \({{E}_{{{\text{col}}}}} = 1\) eV (as well as at \({{E}_{{{\text{col}}}}} = 2\) eV) is characterized by a sufficiently long initial piece where the recombination probability is constant, while at \({{E}_{{{\text{col}}}}} = 10\) eV (as well as at \(3 \leqslant {{E}_{{{\text{col}}}}} \leqslant 9\) eV), it is characterized by a sufficiently long initial piece where the recombination probability increases. The opacity functions of the reaction (6) with R = Xe obtained in the framework of trajectory simulation have a completely different shape. For example, the trajectory opacity function of this reaction at \({{E}_{{{\text{col}}}}} = 1\) eV shown in Fig. 5 of the paper [22] possesses a sharp (although “split”) maximum at \(b \approx 20\) a.u.

Fig. 5.
figure 5

The number of different types of collisions RCs+ + Br– among the \(500{\kern 1pt} 000\) collisions generated for the given atom R and the given collision energy \({{E}_{{{\text{col}}}}}\) at \(T = 1000\) K. Lines 1, 2, 3, and 4 present the number of types of recombinative collisions for R = Ar, Kr, Xe, and Hg, respectively. Lines 5, 6, 7, and 8 present the number of types of non-recombinative collisions for R = Ar, Kr, Xe, and Hg, respectively.

Full size image

What is an interesting peculiarity of the model in question of bimolecular recombination (4) is that the total internal energy \({{E}_{{{\text{tot}}}}}\) of the ionic pair M+–X– can be negative already at the initial time instant \(t = 0\). In the hard sphere model of three-body recombination (3) [31, 32] for ion approach energies \({{E}_{{\text{i}}}}\) of order 1 eV = 0.03675 a.u. and higher, this is impossible because in [31, 32], the initial internuclear distance between the ions is equal to \({{d}_{{\text{i}}}} = 250\) a.u., so that the initial total internal energy \({{E}_{{\text{i}}}} - 1{\text{/}}{{d}_{{\text{i}}}}\) of the ionic pair is always positive. Of course, the inequality \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) in the model proposed in the present paper does not imply that the corresponding collision is necessarily recombinative, since the subsequent encounters of the ions with the R atom can change the sign of \({{E}_{{{\text{tot}}}}}\). In our calculations related to the recombination reactions (6), we observed collisions with \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) for R = Kr, Xe, Hg only and at \({{E}_{{{\text{col}}}}} \leqslant 3\) eV only. Table 2 contains the numbers of collisions with \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) for various atoms R and for various values of the temperature T and the collision energy \({{E}_{{{\text{col}}}}}\).

Table 2. The number \({{N}_{0}}\) of collisions RCs+ + Br– with \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) (out of the total number \(N = 500{\kern 1pt} 000\) of all the collisions), the number \({{N}_{1}}\) of collisions with \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) and without encounters of the ions with the R atom, and the number \({{N}_{2}}\) of collisions with \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) and without encounters of the particles at all (semicolons separate the data for \({{E}_{{{\text{col}}}}} = 1\), 2, and 3 eV)
Full size table

As is seen in Table 2, for R = Kr and Xe, we only observed isolated collisions with \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) (and, moreover, at \({{E}_{{{\text{col}}}}} = 1\) eV only). On the other hand, for R = Hg, the number of collisions with \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) at \({{E}_{{{\text{col}}}}} = 1\) eV turned out to be substantial even for \(T = 500\) K. To explain this exceptional feature of mercury, estimate the minimal initial internuclear distance between the Cs+ ion and the R atom for which the inequality \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) is possible (recall that \({{\mu }_{{{\text{ion}}}}}\), \({{\mu }_{{{\text{lex}}}}}\), and \({{\mu }_{{{\text{col}}}}}\) are respectively the reduced mass of the ions, the reduced mass of the Cs+ ion and the R atom, and the reduced mass of the RCs+ complex and the Br– ion). We will suppose that the energy of the relative motion of the Cs+ ion and the R atom in the RCs+ complex at \(t = 0\) is equal to \({{E}_{T}} = {{k}_{{\text{B}}}}T\) where \({{k}_{{\text{B}}}}\) is the Boltzmann constant. In the coordinate frame we employ, the velocity of the Br– ion at \(t = 0\) is equal to \({{V}_{{{\text{Br}}}}} = {{(2{{E}_{ * }}{\text{/}}{{\mu }_{{{\text{col}}}}})}^{{1/2}}}\), while the velocity of the Cs+ ion is equal to \({{V}_{{{\text{Cs}}}}} = \lambda {{(2{{E}_{T}}{\text{/}}{{\mu }_{{{\text{lex}}}}})}^{{1/2}}}\) where \(\lambda \) is the mass ratio \({{m}_{{\text{R}}}}{\text{/}}({{m}_{{\text{R}}}} + {{m}_{{{\text{Cs}}}}})\). Of course, even at \({{E}_{{{\text{col}}}}} = 1\) eV and \(T = 2000\) K, the energy \({{E}_{T}}\) is considerably less than the energy \({{E}_{*}},\) and the velocity \({{V}_{{{\text{Cs}}}}}\) is much smaller than the velocity \({{V}_{{{\text{Br}}}}}\). The energy of the relative motion of the ions at \(t = 0\) cannot be less than \({{E}_{{{\text{crit}}}}} = {{\mu }_{{{\text{ion}}}}}{{({{V}_{{{\text{Cs}}}}} - {{V}_{{{\text{Br}}}}})}^{2}}{\text{/}}2\), so that for the occurrence of the inequality \({{E}_{{{\text{tot}}}}}(t = 0) < 0\), the initial internuclear distance \({{s}_{*}}\) between the ions should be smaller than \({{s}_{{{\text{crit}}}}} = 1{\text{/}}{{E}_{{{\text{crit}}}}}\) (and, moreover, \({{s}_{{{\text{crit}}}}}\) should be no less than the sum \({{s}_{0}}\) of the radii of the ions, this sum being equal to 6.85971 a.u.).

The initial distance between the center of mass of the RCs+ complex and the Br– ion is equal to \({{d}_{*}}.\) Consequently, for the inequality \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) to occur, the initial internuclear distance between the Cs+ ion and the R atom should be greater than the quantity \({{r}_{{{\text{crit}}}}}\) defined by the equation \(\lambda {{r}_{{{\text{crit}}}}} + {{s}_{{{\text{crit}}}}} = {{d}_{ * }}\), i.e., greater than the quantity \({{r}_{{{\text{crit}}}}} = ({{d}_{ * }} - {{s}_{{{\text{crit}}}}}){\text{/}}\lambda \). Easy calculations show that the values of \({{s}_{{{\text{crit}}}}}\) and \({{r}_{{{\text{crit}}}}}\) depend little on the temperature T and, moreover, the distance \({{s}_{{{\text{crit}}}}}\) depends little on the R atom as well. For instance, at \({{E}_{{{\text{col}}}}} = 1\) eV and \(T = 1000\) K, the distance \({{s}_{{{\text{crit}}}}}\) is equal to 18.84, 18.48, 21.64, and 18.57 a.u. for R = Ar, Kr, Xe, and Hg, respectively. However, the distance \({{d}_{ * }}\) for R = Hg is noticeably smaller than that for the three other atoms R (see Table 1), while the ratio \(\lambda \), on the contrary, is larger. Because of this, the distance \({{r}_{{{\text{crit}}}}}\) at \({{E}_{{{\text{col}}}}} = 1\) eV turns out to be small for R = Hg (for example, at \(T = 1000\) K, it is equal to 2.54 a.u.) and rather significant for R = Ar, Kr, Xe; at \(T = 1000\) K, it is equal to 62.56, 18.92, 16.27 a.u., respectively (the initial internuclear distance between the Cs+ ion and the Ar atom exceeding 62.56 a.u. is, of course, unrealizable). On the other hand, already at \({{E}_{{{\text{col}}}}} = 2\) eV, the distance \({{r}_{{{\text{crit}}}}}\) for R = Hg becomes considerably greater. For instance, at \(T = 1000\) K, one obtains \({{s}_{{{\text{crit}}}}} = 12.56\) a.u. and \({{r}_{{{\text{crit}}}}} = 12.54\) a.u. We observed a large number of collisions with \({{E}_{{{\text{tot}}}}}(t = 0) < 0\) for R = Hg and \({{E}_{{{\text{col}}}}} = 1\) eV only (see Table 2) precisely because this is the only pair \(({\text{R}},\;{{E}_{{{\text{col}}}}})\) characterized by small distances \({{r}_{{{\text{crit}}}}}\).

4 TYPES OF COLLISIONS

For each collision event RM+ + X–, the hard sphere model enables one to determine unambiguously the sequence of pairwise encounters of the balls representing the particles M+, X–, and R. Treating the M+ ion as the first particle, the X– ion as the second one, and the R atom as the third one, we will encode any such encounter by one of the six numbers 12, –12, 13, –13, 23, and –23 according to the following rule [31, 32]. An encounter of the particle no. i and the particle no. j (where \(j > i\)) is denoted by one of the numbers \( \pm (10i + j)\), the sign of the number coinciding with the sign of the total internal energy \({{E}_{{{\text{tot}}}}}\) of the ionic pair after the encounter. As was already noted at the end of Section 2, encounters of the codes ±12 do not alter the value of \({{E}_{{{\text{tot}}}}}\).

Within the framework of a recombinative collision, after all the encounters of the R atom with the ions, a bound ionic pair M+–X– remains. The parameters of the ellipse traced in this setup by the vector \({\mathbf{s}}\) connecting the nuclei of the ions can be easily computed in terms of the energy \({{E}_{{{\text{tot}}}}} < 0\) and the angular momentum L of the ionic pair [48, 49]. Denote by \({{s}_{\pi }}\) the pericenter radius of the ellipse (the minimal distance from a point of the ellipse to its focus) and by \({{s}_{0}}\), the sum of the radii of the balls representing the ions. Depending on which of the two inequalities \({{s}_{\pi }} > {{s}_{0}}\) or \({{s}_{\pi }} < {{s}_{0}}\) holds, in an isolated bound ionic pair M+–X–, either there are no encounters of the ions with each other at all or the ions undergo infinitely many encounters of the code –12. In our calculations pertaining to the recombination reactions (6), until the integration of the equations of motion was stopped according to the algorithm of Section 2, only a finite number (usually no more than ten) of such encounters of the code –12 had time to occur. We observed the maximal number of such final encounters of the code –12 for one of the collisions KrCs+ + Br– at \(T = 1000\) K and \({{E}_{{{\text{col}}}}} = 1\) eV. In this recombinative collision, after two encounters of the codes 12 and –23, before the integration of the equations of motion was terminated, 892 encounters of the ions with each other occurred. Within the framework of a non-recombinative collision, after all the encounters of the R atom with the ions, one more encounter of the ions with each other of the code 12 is possible.

As in the hard sphere model of three-body recombination (5) [31, 32], to each collision RCs+ + Br–, we will assign the sequence of the numbers encoding the pairwise encounters of the particles not taking into account the final encounters of the ions with each other (these encounters occur after all the encounters of the R atom with the ions). The resulting sequence of numbers, enclosed in parentheses, will be called the type of the collision. For example, a collision of the type (12, –23) is recombinative and includes an encounter of the ions with each other with \({{E}_{{{\text{tot}}}}} > 0\), an encounter of the Br– ion with the R atom changing the sign of the energy \({{E}_{{{\text{tot}}}}}\), and possibly some more encounters of the ions with each other of the code –12 (as in the collision KrCs+ + Br– mentioned above with 894 encounters of the particles). The recombinative collisions that do not include any encounter of the R atom with the ions constitute a separate type which will be conditionally denoted by \(( - \Omega )\). For such collisions \({{E}_{{{\text{tot}}}}}(t = 0) = {{E}_{{{\text{tot}}}}}(t = {{t}_{{{\text{end}}}}}) < 0\); they either do not include encounters of the particles at all or include several encounters of the code –12 (\({{t}_{{{\text{end}}}}}\) denotes the instant of termination of the integration of the equations of motion). The numbers \({{N}_{1}}\) in the penultimate column of Table 2 are the numbers of collisions of the type \(( - \Omega )\) in our calculations for various triples \(({\text{R}},\;T,\;{{E}_{{{\text{col}}}}})\). In the hard sphere model of three-body recombination (5) [31, 32], we did not observe collisions of the type \(( - \Omega )\) (see an explanation at the end of Section 3). The non-recombinative collisions that do not include any encounter of the R atom with the ions will be regarded as belonging to the type \((\Omega )\). For such collisions \({{E}_{{{\text{tot}}}}}(t = 0) = {{E}_{{{\text{tot}}}}}(t = {{t}_{{{\text{end}}}}}) > 0\); they either do not include encounters of the particles at all or include a single encounter of the code 12.

The “longest” type we met with was the sequence of 58 numbers equal to 13. We observed a single collision of this type. It was one of the non-recombinative collisions KrCs+ + Br– at \(T = 1000\) K and \({{E}_{{{\text{col}}}}} = 1\) eV. It included 58 encounters of the Cs+ ion with the Kr atom without a final encounter of the Cs+ and Br– ions.

Within the framework of hard sphere simulation of direct three-body recombination (5), we observed 34 types of recombinative collisions (all these types are listed in [31, 32]) and 61 types of non-recombinative collisions (these types are listed in [31]). In the hard sphere model of bimolecular recombination (6) described in the present paper, we met with considerably more different types of collisions.

The total number of collision events RCs+ + Br– in our calculations was equal to 4 × 3 × 10 × 500 000 = 6 × 107; here we take into account four distinct atoms R, three values of the temperature T, and ten values of the energy \({{E}_{{{\text{col}}}}}\). Of these 6 × 107 collisions, \({\text{1}}{\kern 1pt} {\text{863}}{\kern 1pt} {\text{030}}\) collisions (3.10505%) of 64 different types turned out to be recombinative. The number of types of non-recombinative collisions in our calculations was equal to 172, i.e., 2.6875 times more than the number of types of recombinative collisions. However, such a “variety” of types of bimolecular collisions occurs largely due to a very small number of collisions (both recombinative and non-recombinative) including long series of encounters of the code 13, i.e., encounters of the Cs+ ion with the R atom leaving the total internal energy \({{E}_{{{\text{tot}}}}}\) of the ionic pair positive. In the course of such collisions, the particles Cs+ and R which constituted the RCs+ complex at the beginning, for some more time undergo many encounters with each other under the influence of the Br– ion attracting the Cs+ ion. Apparently, the R atom in this case turns out to be “sandwiched” between the ions. Emphasize that such collisions are very rare. We observed only 4725 collisions (66 recombinative ones and 4659 non-recombinative ones) whose types start with five or more numbers 13; however, these collisions are categorized into 16 recombinative and 53 non-recombinative types. In addition, for 9 other non-recombinative collisions, the type ends with five or more numbers 13, these collisions being categorized into 7 different types.

The twenty most frequently occurring types of recombinative collisions are listed in Table 3 (in the descending order of the numbers of collisions belonging to the types in question). These 20 types cover 99.9204% of all the recombinative collisions. An overwhelming majority (69.9872%) of recombinative collisions belong to the types (–23) and (13, –23). In the course of these collisions, the total internal energy \({{E}_{{{\text{tot}}}}}\) of the ionic pair becomes negative due to an encounter of the R atom with the Br– ion, and this encounter may be preceded by an encounter of the R atom with the Cs+ ion leaving the energy \({{E}_{{{\text{tot}}}}}\) positive. In the hard sphere model of direct three-body recombination (5) [31, 32], the two most frequently occurring types of recombinative collisions were (–23) and (–13), while the type (13, –23) was only in third place. In the hard sphere model of bimolecular recombination (6), as is seen in Table 3, we observed recombinative collisions of the type (–13) as well, but this type is in 11th place in terms of the occurrence frequency. Since at \(t = 0\), the particles Cs+ and R constitute the RCs+ complex, their relative velocity is small (and remains not very large for some more time), so that with a high probability a single encounter between the R atom and the Cs+ ion only slightly changes the velocity of the Cs+ ion and leaves the sign of the energy \({{E}_{{{\text{tot}}}}}\) unaltered.

Table 3. The twenty most frequently occurring types of recombinative collisions
Full size table

The twenty most frequently occurring types of non-recombinative collisions are listed in Table 4 (also in the descending order of the numbers of collisions belonging to the types in question). These 20 types cover 99.9709% of all the non-recombinative collisions. The three most frequent types of non-recombinative collisions are the same types \((\Omega )\), (13), (23) as in the case of the hard sphere model of direct three-body recombination (5) [31, 32] (however, the proportions of occurrence of these types in the hard sphere model of three-body recombination were completely different). Together, these three types make up 94.8824% of all the non-recombinative collisions.

Table 4.   The twenty most frequently occurring types of non-recombinative collisions
Full size table

If one proceeds from the entire set of 6 × 107 collisions generated in our calculations to the \(500{\kern 1pt} 000\) collisions generated for individual triples \(({\text{R}},\;T,\;{{E}_{{{\text{col}}}}})\), then for some triples, the two most frequently occurring types of recombinative collisions and the three most frequently occurring types of non-recombinative collisions will be different.

For all the triples \(({\text{R}},\;T,\;{{E}_{{{\text{col}}}}})\), the most frequent type of recombinative collisions is (–23). However, for R = Ar and \({{E}_{{{\text{col}}}}} = 10\) eV at all the three values of the temperature T, as well as for R = Ar, \(T = 1000\) K, and \({{E}_{{{\text{col}}}}} = 9\) eV, the type second in terms of the frequency turns out to be (23, –13), while the type (13, –23) moves to third place. For R = Hg, the type (13, –23) never ranks second and is relegated to third, fourth, or fifth place depending on T and \({{E}_{{{\text{col}}}}}\). The second place type for R = Hg is almost always (12, –13). The exceptions are two triples \(({\text{Hg}},\;T,\;1\;{\text{eV}})\) with \(T = 1000\) and 2000 K. For these triples, the type of recombinative collisions that is second in terms of the frequency turns out to be \(( - \Omega )\). Let us note the probable cause of this peculiarity of mercury. As is explained at the end of Section 3, for R = Hg, smaller initial internuclear distances \({{s}_{ * }}\) between the ions are possible than for R = Ar, Kr, and Xe. Apparently, because of this, the following scenario has a better chance of occurring for mercury. The first encounter of the particles is an encounter of the ions with each other of the code 12 that preserves the energy \({{E}_{{{\text{tot}}}}}\) but strongly changes the velocities of both the ions. Thus, the velocities of the particles R and Cs+ begin to differ markedly. Then an encounter of these particles with each other happens. Again, this encounter greatly changes their velocities (in particular, that of the Cs+ ion), and the energy \({{E}_{{{\text{tot}}}}}\) becomes negative, i.e., the encounter of R and Cs+ turns out to be of the code –13.

The most frequent type of non-recombinative collisions for all the triples \(({\text{R}},\;T,\;{{E}_{{{\text{col}}}}})\) is \((\Omega )\), while the type second in terms of the frequency is (13). At the same time, for 24 triples \(({\text{R}},\;T,\;{{E}_{{{\text{col}}}}})\) with low collision energies \({{E}_{{{\text{col}}}}} \leqslant 4\) eV, the type (23) turns out to be not the third in terms of the frequency, but the fourth, fifth, or even sixth. In third place for these triples, there are the types (12, 13) or (13, 13). For the other 24 triples \(({\text{R}},\;T,\;{{E}_{{{\text{col}}}}})\) with \({{E}_{{{\text{col}}}}} \leqslant 4\) eV, the type (23) is in third place.

The number \({{n}_{1}}\) of different types of recombinative collisions and the number \({{n}_{2}}\) of different types of non-recombinative collisions among the \(500{\kern 1pt} 000\) collisions generated for each triple \(({\text{R}},\;T,\;{{E}_{{{\text{col}}}}})\) depend little on the temperature T and, on the whole, decrease as the collision energy \({{E}_{{{\text{col}}}}}\) grows. Figure 5 shows the dependences of these numbers on \({{E}_{{{\text{col}}}}}\) at \(T = 1000\) K. The ratio \({{{{n}_{2}}} \mathord{\left/ {\vphantom {{{{n}_{2}}} {{{n}_{1}}}}} \right. \kern-0em} {{{n}_{1}}}}\) lies in the range from 1.416 to 3.75 for all the triples \(({\text{R}},\;T,\;{{E}_{{{\text{col}}}}})\). In particular, for each triple, the number of types of non-recombinative collisions exceeds the number of types of recombinative collisions. In general, as is seen in Fig. 5, the greatest number of types of both recombinative and non-recombinative collisions is observed for R = Kr, followed by Ar, Xe, and Hg.

5 CONCLUSIONS

The calculations we carried out have shown that the proposed hard sphere model of the bimolecular recombination reactions (6) enables one to reproduce the most important feature of the dynamics of these reactions, namely, that the probability and the cross section of recombination decrease as the collision energy grows and that this decrease is faster than the decrease in the probability of three-body recombination (5) as the third body energy grows at a fixed value of the ion approach energy. On the other hand, the hard sphere opacity functions of the reactions (6) with R = Xe are very different from the opacity functions obtained in trajectory calculations [22].

Other meaningful dynamical aspects of the recombination reactions (3) and (4) are the distributions of the MX product by the vibrational and rotational energies, as well as the minimum possible total internal energy of the product, which characterizes (in the case of three-body recombination) the efficiency of the third body R as an acceptor of the excess energy of the ionic pair [7, 14, 17, 19, 20, 40]. However, in the framework of the hard sphere models of the reactions (3) and (4) proposed in the works [31, 32] and in the present paper, what is regarded as the reaction product is not a salt molecule MX but a pair of ions M+ and X– bound by the Coulomb potential. For such a pair, the total internal energy \({{E}_{{{\text{tot}}}}}\) is negative but the semiaxes of the ellipse traced by the vector \({\mathbf{s}}\) connecting the nuclei of the ions can be arbitrarily large. Therefore, it does not make much sense to consider the distribution of the energy \({{E}_{{{\text{tot}}}}}\), to decompose \({{E}_{{{\text{tot}}}}}\) into the vibrational and rotational components, and to calculate the minimum possible value of \({{E}_{{{\text{tot}}}}}\) in hard sphere simulation of the reactions (3) and (4).

At the same time, one of the goals of using hard sphere models in the theory of atomic and molecular collisions is to separate the effects of the particle masses from those of the structure of the potential energy surfaces (PES) [4, 26–28, 31, 40]. The results of the present paper suggest that the energy dependences of the probabilities of three-body and bimolecular recombination are affected by the PES relief to a much lesser extent than the peculiarities of the opacity functions. For a more comprehensive study of this issue, one has to carry out trajectory simulation of the reactions (6) with R = Ar, Kr, Hg as well as calculations in the framework of a hard sphere model with varying details of the Cs+–R interaction potentials (and also calculations with a formal change in the masses and radii of the particles, cf. [19–21]).

The construction of hard sphere models of direct three-body recombination of ions (3) in the works [31, 32] and of bimolecular recombination of ions (4) in the present paper allows one to suppose that hard sphere concepts can be used while describing such complicated recombination processes as ion-ion recombination reactions in the atmosphere [69, 70], the death of oxygen atoms in the atmosphere due to recombination with the participation of O2 and N2 molecules as the third bodies [71], or recombination of radicals in the polymer cage and in the bulk of polymers [72].