INTRODUCTION

Solving the heat equation with data on a timelike boundary (for example, see [1]) or some inverse problems for the heat equation (see [2]), we have to solve the convolution type Volterra integral equation of the first kind

$$ \int \limits ^t_0 K(t-s) f(s)\thinspace ds = g(t). $$
(1)

The distinctive feature of applications of this type is that (1) cannot be reduced to the Volterra integral equation of the second kind since the function \(K(t) \), as well as all its derivatives, vanishes at the point \(t=0 \).

Example 1\(. \) Consider the function \(K(t) = t^{-1/2} e^{-a/t} \) (see Fig. 1). In [1, 2] the cases are considered when the kernel is the same or more intricate but \(K(t)\) has similar behavior in the neighborhood of \(t=0\).

Fig. 1.
figure 1

The graph of \(K(t) \).

Full size image

In this case for the solution of (1) the regularization methods applied in [3-6] cannot be used since these methods require the condition \(K^{(n)}(0)\ne 0\) ( \(n \) is some natural). The Denisov method requires the knowledge of \(f(0) \), but this condition is not usually fulfilled in practice. The Tikhonov regularization method leads to the solution of a Fredholm equations of the first kind [7].

Basing on the quadrature method, we propose the numerical method for solving integral equation (1) and obtain an estimate of the error of the solution. Some example is presented of a numerical implementation of the method.

The particularity of the solution of the convolution type Volterra integral equation of the first kind by applying the quadrature integration method is that we need to use only a fixed time meshsize. The time meshsize cannot be too small since, otherwise, a solution of the integral equation will take more time than we can afford. The second particularity that should be taken into account in our case is the behavior of \(K(t)\). Usually, this function changes significantly in a small neighborhood of \(t=0 \), and then it has a fairly “calm” behavior.

Example 2\(. \) The kernel \(K(t) = t^{-1/2}e^{-a/t} \) attains the maximum value at \(t_{\max } = 2a \) after which \(K(t) \) decreases smoothly as \(t^{-1/2} \) (see Fig. 1). In practice the parameter \(a \) is very small (for example, \(a = 10^{-6} \) [2]); i.e., \(a \) is smaller than any reasonable time meshsize. Therefore, this imposes constraints on the construction of the quadrature formula.

In [8], another technique is proposed for solving the given integral equation. This result is based on an optimization approach and the theorem of existence (proved in [8]) of a solution of this equation in the class of functions that can be represented by a Fourier series whose coefficients tend to zero as \(k^{-(1+\gamma )}\), \(\gamma >0 \). Sufficiently complete information of the theory and practice of the solutions of integral equations of various types is collected in the books [7, 9, 10] and their electronic version [11].

1. CONSTRUCTION OF A QUADRATURE FORMULA

We follow the standard scheme for constructing a quadrature formula for the solution of integral equation (1) (for example, see [7]). We will seek a solution on the interval \([0,T] \). To construct a quadrature formula, it suffices to assume that

$$ g(0)=0, \qquad g(t)\in C[0,T], \qquad K(t)\in C[0,T], \qquad f(t)\in C[0,T]. $$

Let the number of nodes of the interval \([0,T] \) be \(N+1 \). We denote the nodes of the mesh by \(t_n \), \(n=\overline {0,N}\), and the meshsize by \(h = T/N\), \(t_n = hn \). Put \(K^n = K(hn) \), \(f^n = f(hn)\), and \(g^n = g(hn) \).

To construct a quadrature formula, we write (1) at \(t_k \) as follows:

$$ \int \limits ^{t_n}_0 K(t_n-s)f(s)\thinspace ds = g(t_n)$$

or

$$ \sum \limits ^n_{j=1}\ \int \limits ^{t_j}_{t_{j-1}} K(t_n - s) f(s)\thinspace d s = g(t_n).$$
(2)

Before proceeding with the construction of the quadrature formula, we make some assumptions:

1. Assume that \(K(t)\ne 0 \) (\(t\in (0,\tau ]\), where \(\tau \) is some positive real). This assumption is related to the Titchmarsh Theorem:

Theorem 1 [12, p. 352]\(. \) Let \(f(t) \) and \(K(t) \) belong to \( L(0,T)\), and let

$$ \int \limits ^t_0 K(t-s)f(s)\thinspace d s = 0$$

for almost all \(t\in (0,T)\). Then \(f(t)=0\) for almost all \(t \in (0,\theta ) \) and \( K(t)=0\) for almost all \(t\in (0,T-\theta )\).

The uniqueness of the solution of (1) if \(K(t)\not \equiv 0 \) in some neighborhood of zero on \([0,T] \) is a consequence of this theorem.

2. Assume that \(N \) is chosen so that \(h\le \tau \). We will need this assumption to use the mean value theorem below (see, for instance, [13]).

Theorem 2 \(. \) If \(K(t) \) is of constant sign in the interval \([0,\tau ]\) then there is \(\vartheta \in (0,\tau ) \) such that

$$ \int \limits ^{\tau }_0 K(s)f(s)\thinspace d s = f(\vartheta ) \int \limits ^{\tau }_0 K(s)\thinspace d s.$$

To construct the quadrature formula we will proceed under the assumption that the kernel \(K(t) \) is given analytically, while the function \(g(t) \) is the result of measurements and is given in a table.

We have already noted that \(K(t)\) is a rapidly varying function in a small neighborhood of zero (the radius of the neighborhood is much less than \(h \)) and changes smoothly on the rest of the interval. Using the above suggestions, let us approximate each integral by the midpoint rectangle formula:

$$ \int \limits ^{t_j}_{t_{j-1}} K(t_n - s)f(s)\thinspace d s = h K^{n-j+1/2} f^{j-1/2} + r^n_j, $$

where \(r^n_j\) is the approximation error and \(j < n\). The last integral is approximated as follows:

$$ \int \limits ^{t_n}_{t_{n-1}} K(t_n-s) f(s)\thinspace d s = f^{n-1/2} \int \limits ^h_0 K(s)\thinspace d s + r^n_n. $$

3. Suppose that for \(K(t) \) the following holds:

$$ \int \limits ^h_0 K(s)\thinspace d s = k(h),\qquad |k(h)|\ge c_0 h^{\alpha }, \qquad 0 < \alpha \le 1. $$
(3)

Example 3. Let \(K(t) = t^{-1/2} e^{-a/t} \). Then

$$ \int \limits ^h_0 K(s)\thinspace d s = 2 h^{1/2} e^{-a/h} - 2\sqrt {\pi a}\thinspace \mathrm {erfc}(\sqrt {a/h}). $$

Since \(a \ll h\), we have \(|k(h)|\ge h^{1/2}\).

Remark\(. \) If \(K(t) \) has no singularity in neighborhood of zero then we put \(\alpha = 1 \). In this case the method for approximating the definite integral on \([t_n, t_{n-1}]\) will not differ from the approximation method on each other interval \([t_j, t_{j-1}] \), \(j < n\).

From (2) we have

$$ \begin {gathered} k(h)f^{1/2} = g^1 + R^1, \\ h \sum \limits ^{n-1}_{j=1} K^{n-j+1/2} f^{j-1/2} + k(h) f^{n-1/2} = g^n + R^n, \qquad n\ge 2, \end {gathered}$$
(4)

where

$$ R^n = \sum \limits ^n_{j=1} r^n_j $$
(5)

is the approximation error (the remainder term in the quadrature) for (2).

Subtracting (4) with number \(n-1\) from (4) with number \(n \), we have

$$ \begin {gathered} \begin {aligned} k(h) f^{1/2} &= g^1 + R^1, \\ [h K^{3/2} - k(h)] f^{1/2} + k(h)f^{3/2} &= g^2-g^1 + R^2 - R^1, \end {aligned} \\ \begin {aligned} &h \sum \limits ^{n-2}_{j=1} [K^{n-j+1/2} - K^{n-j-1/2}] f^{j-1/2} \\ &\qquad \qquad {}+ [hK^{3/2} - k(h)] f^{n-3/2} + k(h)f^{n-1/2} = g^n - g^{n-1} + R^n - R^{n-1}, \quad n\ge 3.\qquad \end {aligned} \end {gathered}$$
(6)

4. Assuming that the remainder terms \(R^j \) are small, we obtain

$$ \begin {gathered} \begin {aligned} k(h) f^{1/2} &= g^1,\notag \\ [h K^{3/2} - k(h)] f^{1/2} + k(h) f^{3/2} &= g^2 - g^1, \end {aligned} \\ \begin {aligned} &h \sum \limits ^{n-2}_{j=1} \bigl [ K^{n-j+1/2} - K^{n-j-1/2} \bigr ] f^{j-1/2} + [h K^{3/2} - k(h)] f^{n-3/2} + k(h) f^{n-1/2} \\ &\qquad \qquad {}= g^n - g^{n-1}, \qquad n\ge 3, \end {aligned} \end {gathered} $$
(7)

which can be used for solving (1).

2. PRELIMINARY ESTIMATES

To obtain some estimates, it is necessary to assume that

$$ f(t)\in C^2 [0,T], \qquad |f^{(j)}(t)| \le F_{j}, \qquad K(t)\in C^2 [0,T], \qquad |K^{(j)}(t)| \le M_{j}, \qquad j=\overline {0,2}.$$

1. Estimate the difference \(h K^{3/2} - k(h)\). It is not hard to see that

$$ K^{3/2} = K^{1/2} + h K^{\prime }(\xi _1), \qquad \xi _1 \in (t_{1/2},t_{3/2}), $$
$$ \begin {aligned} &h K^{1/2} - k(h) = h K^{1/2} - \int \limits ^h_0 K(s)\thinspace ds = \int \limits ^h_0 (K^{1/2}-K(s))\thinspace ds \\ &\qquad {}= -\int \limits ^h_0 \bigg (K^{\prime }(h/2)(s-h/2) + \frac {1}{2} K^{\prime \prime }(\xi _2)(s-h/2)^2 \bigg )\thinspace ds = \frac {1}{24} K^{\prime \prime }(\xi _2)h^3, \qquad \xi _2 \in (0,t_{1/2}).\quad \end {aligned} $$

From these two equalities we have

$$ \bigl | hK^{3/2} - k(\zeta ) \bigr | \le h^2 c_1, $$
(8)

where \(c_1 = c_1 (M_1, M_2) \).

2. Estimate the difference \(K^{n-j+1/2} - K^{n-j-1/2}\). From

$$ K^{n-j+1/2} = K^{n-j-1/2} + hK^{\prime }(\xi _3), \qquad \xi _3 \in (t_{n-j-1/2}, t_{n-j+1/2}), $$

we obtain

$$ |K^{n-j+1/2} - K^{n-j-1/2}| \le h M_1. $$
(9)

3. Consider the remainder term in the quadrature when the integral in \([t_{j-1}, t_j]\) is approximated by the midpoint rectangle formula

$$ \int \limits ^{t_j}_{t_{j-1}} u(s)\thinspace d s = u(t_{j-1/2}) h + r^n_j, \qquad j < n.$$

We have the chain of equalities

$$ \begin {aligned} r^n_j &= \int \limits ^{t_j}_{t_{j-1}} u(s)\thinspace d s - hu(t_{j-1/2}) = \int \limits ^{t_j}_{t_{j-1}} [u(s) - u(t_{k-1/2})]\thinspace d s \\ &= \int \limits ^{t_j}_{t_{j-1}} \bigg [ u^{\prime }(t_{k-1/2})(s-t_{k-1/2}) + u^{\prime \prime }(\xi _j) \frac {(s-t_{k-1/2})^2}{2!} \bigg ]d s = u^{\prime \prime }(\xi _j) \frac {h^3}{24},\qquad \end {aligned} $$

where \(\xi _j\) is some point in \((t_{j-1},t_j) \).

Hence, for the quadrature remainder \(r^n_j \) it is easy to obtain the estimate

$$ \big |r^n_j \big |\le h^3 c_3, \qquad j < n. $$
(10)

Note that since \(u(s) \) is the product of the two functions \(K(t-s)f(s) \) (here \(t \) plays the role of some parameter) then \(c_3 = c_3(M_0,M_1,M_2,F_0,F_1,F_2)\).

3. AN ERROR ESTIMATE OF A SOLUTION

Let \(f(t) \) be the solution of (1) such that (6) holds at \(t_{j-1/2} \), \(j=\overline {1,N}\). Relation (7) is a system of linear algebraic equations with a triangular matrix that can be solved. Let its solution be \( \tilde {f}^{j-1/2}\). Put

$$ \Delta f^{j-1/2} = f^{j-1/2} - \tilde {f}^{j-1/2}.$$

Assume that \(g(t)\in C[0,T]\) and \(g(t) \) is defined with some error \(\tilde {\delta }(t) \); i.e.,

$$ |g_{\delta }(t) - g(t)| = |\tilde {\delta }(t)| \le \delta .$$

Subtracting (7) from (6), we obtain that for \(\Delta f^{j-1/2}\) the following relations hold:

$$ \begin {gathered} k(h)\Delta f^{1/2}=\tilde {\delta }^{1}+R^{1},\notag \\ [hK^{3/2}-k(h)]\Delta f^{1/2}+k(h)\Delta f^{3/2} =\tilde {\delta }^2 - \tilde {\delta }^1 + R^2 - R^1, \end {gathered} $$
(11)
$$ \begin {gathered} h\sum \limits ^{n-2}_{j=1} \bigl [ K^{n-j+1/2} - K^{n-j-1/2} \bigr ] \Delta f^{j-1/2} + \bigl [ hK^{3/2} - k(h) \bigr ] \Delta f^{n-3/2} + k(h) \Delta f^{n-1/2} \\ = \tilde {\delta }^n - \tilde {\delta }^{n-1} + R^n - R^{n-1}, \qquad n\ge 3. \quad \end {gathered} $$

From (11) we infer

$$ \begin {gathered} c_0 |\Delta f^{n-1/2}| \le h \sum \limits ^{n-2}_{j=1} |K^{n-j+1/2} - K^{n-j-1/2}| |\Delta f^{j-1/2}| + |hK^{3/2}-k(\zeta )| |\Delta f^{n-3/2}| \\ + |R^n| + |R^{n-1}| + 2\delta .\qquad \end {gathered}$$

Taking (5) and (8)-(10) into account, we obtain

$$ c_0 h^{\alpha } |\Delta f^{n-1/2}| \le h^2 M_1 \sum \limits ^{n-2}_{j=1} |\Delta f^{j-1/2}| + h^2 c_1 |\Delta f^{n-3/2}| + 2h^3 c_3 (n-1) + 2\delta .$$

Since \(T=Nh \) and \(n \le N \), we can simplify the estimate:

$$ c_0 h^{\alpha } |\Delta f^{n-1/2}| \le h^2 c_1 \sum \limits ^{n-1}_{j=1} |\Delta f^{j-1/2}| + 2 T c_3 h^2 + 2 \delta .$$

Dividing this by \(c_{0}h^{\alpha } \) and applying Gronwall’s Lemma, as a result we get

$$ |\Delta f^{n-1/2}| \le (h^{2-\alpha } c_4 + c_5 \delta /h) e^{h^{2-\alpha } n c_6} \le (h^{2-\alpha } c_4 + c_5 \delta /h^{\alpha }) {\rm e}^{h^{1-\alpha } T c_6}, $$

where \(c_4 = 2 T c_3/c_0\), \(c_5 = 2/c_0 \), and \(c_6 = c_1/c_0 \). On the right-hand side of the inequality one term tends to zero as \(h \to 0\), the second term can take different values with a mismatched tendency of \(\delta \) and \(h \) to zero. In this case \(h \) must agree with the error value \(\delta \); i.e., \(h \) is quasi-optimal [14]. Assuming that \(h_{*}=(\alpha c_{4}/(2-\alpha )c_{5})^{1/2}\delta ^{1/2}\), we have the estimate

$$ |\Delta f^{n-1/2}| \le c_7\thinspace \delta ^{1-\alpha /2},$$
(12)

where \(c_7 = 2(c_4 c_5/(2-\alpha ))^{1/2}{\rm e}^{h_{*}^{1-\alpha } T c_6}\).

4. THE TECHNIQUE TO IMPROVE (12)

Estimation (12) can be improved by assuming

$$ f(t)\in C^4 [0,T], \qquad |f^{(j)}(t)|\le F_j, \qquad K(t)\in C^4 [0,T], \qquad |K^{(j)}(t)|\le M_j, \qquad j=\overline {0,4}, $$

and/or

$$ g(t)\in C^1 [0,T], \qquad |g^{\prime }(t)-g^{\prime }_{\delta }(t)| \le \varepsilon .$$

In this case, the following equality holds (see the derivation of (10)):

$$ \begin {aligned} r^n_j &= \int \limits ^{t_j}_{t_{j-1}} u(s)\thinspace d s-u(t_*)h = \int \limits ^{t_j}_{t_{j-1}}[u(s)-u(t_*)]\thinspace d s \\ &= \int \limits ^{t_j}_{t_{j-1}} \bigg [ u^{\prime }(t_*)(s-t_*) + u^{\prime \prime }(t_*) \frac {(s-t_*)^2}{2!} + u^{(3)}(t_*) \frac {(s-t_*)^3}{3!} + u^{(4)}(\xi _k) \frac {(s-t_*)^4}{4!} \bigg ]d t \\ &= u^{\prime \prime }(t_*) \frac {h^3}{24} + u^{(4)}(\xi _j) \frac {h^5}{1920}, \end {aligned} $$
(13)

where, for short, \(t_{*} = t_{j-1/2} \) and \(\xi _j \in (t_{j-1},t_j) \). From (13) the next estimate is obtained:

$$ \bigg |r_j^n - u^{\prime \prime }(t_{j-1/2}) \frac {h^3}{24} \bigg | \le c_8 \frac {h^5}{1920}.$$
(14)

Since the integrand \( u(s)\) is a product of the two functions \(K(s) \) and \(f(t_n - s) \); therefore,

$$ c_{10} = c_{10}(M_0, M_1, M_2, M_3, M_4, F_0, F_1, F_2, F_3, F_4).$$

From (11) it follows that

$$ c_0 h^{\alpha } |\Delta f^{n-1/2}| \le h^2 M_1 \sum \limits ^{n-2}_{j=1} |\Delta f^{j-1/2}| + c_1 h^2 |\Delta f^{n-3/2}| + |R^n - R^{n-1}| + \varepsilon h.$$

Further, (14) allows us to estimate \(|R^n - R^{n-1}|\) and conclude that

$$ c_0 h^{\alpha } |\Delta f^{n-1/2}| \le h^2 M_1 \sum \limits ^{n-2}_{j=1} |\Delta f^{j-1/2}| + h^2 c_1 |\Delta f^{n-3/2}| + h^5 c_8 \frac {(n-1)}{1920}+\varepsilon h. $$

Then

$$ c_0 h^{\alpha } |\Delta f^{n-1/2}| \le h^2 c_1 \sum \limits ^{n-1}_{j=1} |\Delta f^{j-1/2}| + h^4 c_8 \frac {T}{1920} + \varepsilon h. $$

Let us divide this inequality by \(c_0 h^{\alpha } \) and apply the Gronwall’s lemma. Then we have

$$ |\Delta f^{n-1/2}| \le (h^{4-\alpha }c_9 + c_{10}\varepsilon h^{1-\alpha }) e^{h^{1-\alpha }Tc_{11}}, $$
(15)

where \(c_9 = (Tc_8/1920)/c_0 \), \(c_{10}=1/c_0 \), and \(c_{11}=c_1/c_0 \). Since, as \(h \) and \(\varepsilon \) tend to zero, both terms on the right hand side of (15) decrease; therefore, there is no need to choose a quasi-optimal meshsize.

5. A NUMERICAL EXPERIMENT

Let us give the three examples of solution of (1) by using (6). Consider \(K(t) = t^{-1/2}e^{-a/t} \) and \(a=10^{-5} \).

Put \(T=10\) and \(h=10^{-2} \). Consider the following three solutions of (1):

$$ f(t)=1,$$
(16)
$$ f(t)=t,$$
(17)
$$ \begin {gathered} f(t) = 1 + \sum _{j=1}^3 [a_j \sin (\omega _j t) + b_j \sin (\omega _j t)], \\ a_1=1/3, \qquad a_2=1/7, \qquad a_3=1/20, \qquad b_1=1/4, \qquad b_2=1/8, \qquad b_3=1/21, \notag \\ \omega _0 = 2\pi /T, \qquad \omega _1 = 2\omega _0, \qquad \omega _2 = 5\omega _0, \qquad \omega _3 = 20\omega _0. \notag \end {gathered}$$
(18)

The functions \( f(t)\) are chosen in such a way that in these cases it is easy to calculate the corresponding functions \(g(t) \) by using the equality

$$ \int \limits _0^t K(t-s)f(s)\thinspace d s = \int \limits _0^t K(s)f(t-s)\thinspace d s $$

and the property \(f(t-s) = f_{11}(t) f_{12}(s) - f_{21}(s) f_{22}(t)\). The corresponding integrals

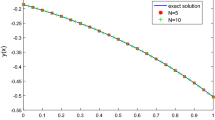
$$ \int \limits ^t_0 K(s)\thinspace d s, \qquad \int \limits ^t_0 K(s) f_{mn}(s)\thinspace d s $$

are calculated analytically or numerically by using the trapezoid formula with \(h=10^{-6}\). The calculation results are shown in Fig. 2. On the left-hand side of the picture the exact \(f_e(t)\) and computed \(f(t) \) solutions are given, while on the right-hand side the relative calculation error \(\Delta (t) = |f_e(t)-f(t)|/|f_e(t)| \) is shown. It is clear that as \(t \) grows, the relative error decreases. The largest relative error is obtained in the neighborhood of zero which, as shown by the numerical experiments, decreases as \(h\) decreases.

Fig. 2.
figure 2

Some examples of solutions of (1) by (6), when \(f(t)\) is given by (16) (see plot (a)), (17) (see plot (b)), or (18) (see plot (c)).

Full size image

Thus, \(f(t) \) is calculated at \(t_{j-1/2} \), \(j=\overline {1,N} \). At practice point of view, this is quite sufficient to evaluate the behavior of the unknown function. Nevertheless, if for some purpose we need to know the values of \( f(t)\) at points \(t_j \), \(j=\overline {1,N-1} \) then we can use the interpolation procedure. The extrapolation procedure can be used to find the value of \(f(t) \) at \(t_N \). However, judging by the behavior of the relative error (see Fig. 2), the extrapolation will not give a satisfactory result for \(t_0 = 0\).

To find the value of \(f(0)\), we use the equality that follows from (1):

$$ K(t) f(0) + \int \limits ^t_0 K(s) f^{\prime }(t-s)\thinspace d s=g^{\prime }(t).$$
(19)

Let \(t=h \) and let \(f(t) \) on the interval \([0,h] \) be approximated by the straight line \(at+b \). From (1) and (19) the two equalities follow:

$$ a(hk-m)+bk = g, \qquad ak+bK = g^{\prime },$$

where

$$ k = k(h) = \int \limits ^h_0 K(s)\thinspace d s, \qquad m = \int \limits ^h_0 s K(s)\thinspace d s, \qquad K = K(h), \qquad g=g(h), \qquad g^{\prime }=g^{\prime }(h). $$

From these it is easy to obtain that

$$ a = \frac {Kg-kg^{\prime }}{K(hk-m)-k^2}, \qquad b = \frac {(hk-m)g^{\prime }-gk}{K(hk-m)-k^2}.$$
(20)

Obviously,

$$ f(0)=b,\qquad f^{1/2} = \frac {1}{2} a h + b. $$
(21)

It remains to determine what value to take for \(g^{\prime } \). Since \(g(t) \) is given in tabular form, we have the two choices: (1) \(g^{\prime }=g^1 /h\) and (2) \(g^{\prime }=(g^2 - g^1)/h \). If you look at the behavior of the function \(K(t) \) in the interval \([0,2h] \) (see Fig. 1), then the second choice is preferable. Numerical experiments have shown that the second choice leads to the smaller computational errors. Which is the preferred choice for calculating \(f^{1/2} \): (1) the first formula from (7); or (2) the second expression from (21) Numerical calculations have shown that both expressions give comparable accuracy results when calculating \(f(t)\) in a neighborhood of zero, and then the calculation error decreases in the same way. Nevertheless, the second choice is preferable since it additionally allows us to compute the value of \(f(0) \).

Fig. 3.
figure 3

Some examples of solutions of (1) when the right-hand side of \(g(t)\) is defined with an error. The exact solution is given by the smooth line, and the solution when the right-hand side is defined with an error is depicted in a broken line.

Full size image

In Fig. 3 the result is presented of some solution of (1) when \(g(t) \) is defined with an error; i.e., instead of \(g(t) \), we consider \(g_{\varepsilon }(t) \) as follows:

$$ g_{\varepsilon }(t_j) = g(t_j)\bigg ( 1 + h\zeta _j \frac {P}{100} \bigg ). $$

Here \(\zeta _j\) is a random variable uniformly distributed in \([-1,1]\), while \(P \) is the error percentage, and the factor \(h \) ensures the inequality \(|g_{\varepsilon }(t_{j})-g^{\prime }(t_{j})| \le \varepsilon \). In the numerical experiment presented in Fig. 3, \(P = 20\% \) and the error with which the solution of (1) was obtained is at most \(10\%\).

CONCLUSION

In this article some algorithm is presented for solving the convolution type Volterra integral equation of the first kind by the quadrature-sum method. It is assumed that this integral equation of the first kind cannot be reduced to an integral equation of the second kind. For the relations we propose there is given the error estimate of the numerical solution.

We present the numerical experiments demonstrating the efficiency of the proposed algorithm. During calculations the solution of (1) was obtained at the points \(t_{j-1/2} \), \(j=\overline {1,N} \).

In practice it is quite sufficient to evaluate the behavior of the desired function. Nevertheless, if we need for some purpose to know the values of \(f(t) \) at \(t_j \) (\(j=\overline {1,N-1} \)) then we can use some interpolation procedure. The extrapolation procedure can be used to find \(f(t) \) at \(t_N \). To find the value of \(f(0) \), we give a simple formula in Section 5.