1. INTRODUCTION

Fluid flows, mixing, and heat transfer processes in curved ducts (CDs) and channels are common phenomena with a vast range of applications in fluids engineering like flow separation, heat exchangers, cooling systems, solar energy, electric generators, rocket engines, and many more. A fluid flow through a curved channel also attracts the interest of biomedical researchers and pharmaceutical industry due to real-life applications such as blood flow in the complex non-dichotomously curved network of the blood vessels. In a rotating curved channel, due to the influence of the channel curvature, a counter-rotating vortex motion is produced, which acts in the main flow direction and generates a twisted fluid flow in the curved passage, known as a secondary flow. Due to the centrifugal force and tangential fluid pressure at the outer concave wall, acting towards the curvature of the channel center, a supplementary pair of counter-rotating secondary vortices appear on the outer concave wall of the curved fluid passage, which are known as the Dean vortices [1]. Since the pioneering work by Dean [1], several researchers have studied these flows using experimental [2–4], numerical and experimental [5–8], analytical and experimental [9, 10], and numerical [11–16] techniques.

Since the nature of the Navier–Stokes equation is highly non-linear and the existence of multifarious solutions of a partial differential equation does not come as a surprise, the solution structure belonging to a combined flow bifurcation consists of a number of branches, which are generally influenced by the parameters of the governing equations, including the curvature and rotational effect of the channel. The literature is replete with numerous instances of detailed numerical computations of fundamental flows in a fluid flow. Daskopoulos and Lenhoff [17] studied a detailed bifurcation diagram of flow through a rectangular curved duct. A significant number of studies have been published on a fluid flow and energy distribution in a curved square or rectangular channel flow [14, 18–21]. Several researches were conducted on rotation and curvature of duct for a two-dimensional (2D) flow in a confined geometry. For instance, Selmi et al. [22] and Dennis and Ng [23] investigated the Coriolis and centrifugal force effects in curvature in a square duct. A comprehensive study of combined solution structure through a CSD was performed by Winters [24]. In connection with that study, Yanase et al. [15] conducted a magnificent research on a combined solution structure of incompressible flow through a CRD. They found a combined solution structure consisting of different steady solution structures and a relationship among them. A detailed pore-scale study on such systems by the spectrum-based method for a combined flow bifurcation (Holf and Pitchfork bifurcation) structure and their stability points are available in the literature [25]. Hasan et al. [26–28] applied the spectral method to develop a solution structure for non-isothermal flows through non-circular ducts. To obtain reliable and meaningful characteristics and to get better fundamental understanding of swirling flow and its thermal properties, Chandratilleke [29] used an advanced numerical simulation model based on 3D vortex structures. A review by Watanabe and Yanase [30] describes bifurcation phenomena, as well as linear stability of solutions, for a square geometry in both two- and three-dimensional analysis. Yanase et al. [31] and Wang and Yang [32] reported the structural fluctuation of steady solution structures at change in the truncation numbers and the stability for a curved square duct flow. Most of the previous studies focused on non-rotating geometries, and the researchers did not approach the effect of the Taylor number in the steady or transient solution along with the number of secondary near-wall vortices for increasing or decreasing the rotation, which is an important matter. Hence, motivated by these unresolved issues, the present study deals with the effects of rotation and curvature on a steady and unsteady fluid flow in a curved rectangular channel.

Yanase and Nishiyama [33] were the first to realize a time-dependent flow in a curved rectangular duct to observe oscillating behavior of flow in a curved channel. Several works related to the oscillating behavior in a confined geometry have been conducted. Yanase et al. [14] and recently Mondal et al. [34] investigated the oscillating behavior numerically. They have identified two types of oscillations: periodic and aperiodic oscillating flows, which appear with and without symmetry condition, respectively. Wang and Yang [6, 7] performed a detailed numerical analysis and experiment with an oscillating flow by using a flow visualization technique. Yamamoto et al.[3] developed an experimental technique, called visualization method, to solve the problem of secondary flow characteristics and flow structure through a curved square geometry. Mondal et al. [35, 36] obtained numerical prognosis for oscillation behavior by time advancement for a fully developed flow, considering square and rectangular configurations, and discussed details of transitions between periodic and aperiodic oscillating behaviors. Regarding the development of the axial velocity and secondary flow structure, Li et al. [8] used both experimental and numerical approach for a 3D flow in 120° curved rectangular ducts, varying the curvatures and aspect ratios.

To improve the understanding of thermo-fluid behavior and heat transfer in a curved channel, Chandratilleke and Nursubyakto [37] conducted a numerical analysis to explain properties of swirling flow through curved rectangular and elliptical ducts of different aspect ratios with the concave outer wall heated. Concerning the convective heat transfer, Norouzi et al. [38] performed numerical simulations assisted by the FDM to analyze the inertial flow and second-grade creeping flow of fluid in a curved square-shaped channel. To find the effects of secondary flow, Yanase et al. [39] simulated the heat transfer numerically for an oscillating flow through a curved duct of a rectangular cross-section. Sohn and Chang [40] calculated the heat transfer, as well as the friction factor, for straight ducts and revealed the effects of laminar viscosity in temperature-dependent fluids. Mondal et al. [41, 42] performed numerical prediction of the oscillating behavior of thermal flows through a curved square enclosure with impacts of rotation and heat transfer. The influence of the aspect on a transient fluid flow and energy distribution through a coiled rectangular channel was analyzed by Mondal et al. [43]. Zhang et al. [44] used a numerical procedure known as the second order finite difference method to investigate the time-dependent convective heat transfer and mixing behavior between two different geometries: an enclosure and an inner concentric circular cylinder. Very recently, Hasan et al. [45–48] demonstrated the heat transfer through a curved duct for different Dean and Taylor numbers and established a relationship between the typical flow behavior and enhancement of the heat transfer. The earlier studies admittedly illustrate the flow patterns and heat transfer characteristics in various geometries with rotation. Besides, the investigation considers only a low rotational speed; unsteady flow characteristics in the presence of centrifugal and heating-induced buoyancy forces and the Coriolis effects in a curved rectangular channel with high rotational speed are not considered, despite numerous engineering applications, e.g., plastic industry, metallic industry, gas turbines, etc. The key intention of the current study is to examine the perplexing flow behavior and energy distribution in a coiled rectangular duct with impact of rotation.

The main intention of the ongoing study is to explore the steady solution branches and investigate unsteady characteristics with heat-flux effects in the secondary flow structure. The study further presents and discusses a novel approach for a numerical scheme in identifying the onset of flow instability in a CRD, reflected by the appearance of Dean vortices.

2. PHYSICAL MODEL AND GOVERNING EQUATIONS

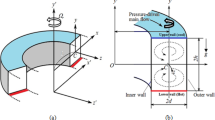
Consideration is given for a fully developed two-dimensional (2D) flow through a CRD. Figure 1 presents the cross-sectional view and coordinate system of the computational domain with necessary notations. The system rotates with the angular velocity \(\Omega_T\) about the \(y'\) axis. The bottom of the working system is heated, while the opposite side is at normal room temperature; the remaining walls are well insulated to prevent heat loss. The fluid passes uniformly in the \(z\) axis direction, as shown in Fig. 1. The governing equations for the flow and HT are as follows.

Fig. 1
figure 1

(a) Schematic representation of physical domain. (b) Cross-section of channel.

Full size image

Continuity equation:

$$\frac{\partial u'}{\partial r'}+\frac{\partial v'}{\partial y'} + \frac{u'}{r'}=0. $$
(1)

Momentum equations:

$$\frac{\partial u'}{\partial t'} + u'\frac{\partial u'}{\partial r'} + v'\frac{\partial u'}{\partial y'} - \frac{{w'}^2}{r'} -2\Omega_T w' = - \frac{1}{\rho} \frac{\partial P'}{\partial r'} + \upsilon \left[ \frac{\partial^2 u'}{\partial {r'}^2} + \frac{\partial^2 u'}{\partial {y'}^2} + \frac{1}{r'} \frac{\partial u'}{\partial r'} - \frac{{u'}}{{r'}^2} \right], $$
(2)
$$\frac{\partial v'}{\partial t'} + u'\frac{\partial v'}{\partial r'} + v'\frac{\partial v'}{\partial y'} = - \frac{1}{\rho} \frac{\partial P'}{\partial y'} + \upsilon \left[ \frac{\partial^2 v'}{\partial {r'}^2} + \frac{1}{r'} \frac{\partial v'}{\partial r'} + \frac{\partial^2 v'}{\partial {y'}^2} \right] + g\beta T', $$
(3)
$$\frac{\partial w'}{\partial t'} + u'\frac{\partial w'}{\partial r'} + v'\frac{\partial w'}{\partial y'} + \frac{u'w'}{r'} +2\Omega_T u' = - \frac{1}{\rho} \frac{1}{r'} \frac{\partial P'}{\partial z'} + \upsilon \left[ \frac{\partial^2 w'}{\partial {r'}^2} + \frac{\partial^2 w'}{\partial {y'}^2} + \frac{1}{r'} \frac{\partial w'}{\partial r'} - \frac{w'}{{r'}^2} \right]. $$
(4)

Energy equation:

$$\frac{\partial T'}{\partial {t}'}+u'\frac{\partial T'}{\partial r'}+v'\frac{\partial T'}{\partial y'}=\kappa \left[ {\frac{\partial ^2T'}{\partial r'^2}+\frac{1}{r'}\frac{\partial T'}{\partial r'}+\frac{\partial ^2T'}{\partial y'^2}} \right], $$
(5)

where \(r'=L+3x'\) and the dimensional velocity components can be decomposed into \(u'\), \(v'\), and \(w'\) in the \(x'\), \(y'\), and \(z'\) directions, respectively. The dimensional variables are made non-dimensional via use of the characteristic length \(d\) and velocity scale \(U_0 = \frac{\upsilon}{d}\). The resulting non-dimensional variables are defined as

$$u=\frac{u'}{U_0}, \quad v=\frac{v'}{U_0}, \quad w=\frac{\sqrt{2\delta}}{U_0}w', \quad x=\left(\frac{x'}{d}-\frac{1}{\delta}\right), \quad y=\frac{y'}{3d}, \quad z=\frac{z'}{d},$$
$$T=\frac{T'}{\Delta T'}, \quad t=\frac{U_0}{d}t', \quad \delta=\frac{d}{L}, \quad P=\frac{P'}{\rho U_0^2}, \quad G=-\frac{\partial P'}{\partial z'} \frac{d}{\rho U_0^2},$$

where \(u\), \(v\), and \(w\) are the non-dimensional velocity components in the \(x\), \(y\), and \(z\) directions, respectively; \(t\), \(P\), and \(\delta = \frac{d}{L}\) are for the time, pressure, and curvature, respectively, in the non-dimensional form. Henceforth, all the variables are non-dimensional, unless otherwise specified. The stream functions for the cross-sectional velocities have the following form:

$$\left. {\begin{array}{l} u= \displaystyle \frac{1}r\frac{\partial \psi}{\partial y}= \displaystyle \frac{1}{1+\delta x}\frac{\partial \psi}{\partial y}\, \\[2ex] v= \displaystyle \frac{1}r\frac{\partial \psi}{\partial x}=- \displaystyle \frac{1}{1+\delta x}\frac{\partial \psi}{\partial x} \ \end{array}} \right\} . $$
(6)

Then, the basic equations for \(w\), \(\psi \), and \(T\) are derived from the Navier–Stokes equations and energy equation as follows:

$$\left({1+\delta \,x} \right)\frac{\partial w}{\partial t}=Dn - \frac{1}{3}\frac{\partial (w,\psi)}{\partial (x,y)}-\frac{\delta ^2w}{1 + \delta \,x}+(1+\delta \,x)\Delta_2 w-\frac{\delta}{3(1+\delta \,x)}\frac{\partial \psi}{\partial y}w+\delta \frac{\partial \,w}{\partial \,x}-\delta \,Tr\frac{\partial \psi}{\partial y}, $$
(7)
$$\begin{array}{c} \left({\Delta_2- \displaystyle \frac{\delta}{1+\delta \,x}\frac{\partial}{\partial \,x}} \right)\, \displaystyle \frac{\partial \,\psi}{\partial \,t}=- \displaystyle \frac{1}{3(1 + \delta \,x)}\frac{\partial \,(\Delta_2 \,\psi ,\psi)}{\partial (x,y)}\, + \frac{\delta}{(1+\delta \,x)^2}\,\left[ {3\,\delta \frac{\partial ^2\psi }{\partial \,x^2}- \displaystyle \frac{3\delta ^2}{1+\delta \,x}\frac{\partial \psi }{\partial \,x}} \right] \\[3ex] + \displaystyle \frac{\delta}{3(1+\delta \,x)^2}\left[ { \displaystyle \frac{\partial \psi }{\partial y}\left({2\,\Delta_2 \,\psi- \displaystyle \frac{3\delta}{1+\delta \,x}\frac{\partial \psi}{\partial \,x}+\frac{\partial ^2\psi}{\partial \,x^2}} \right)} \right.\left. {-\frac{\partial \psi}{\partial \,x}\frac{\partial ^2\psi}{\partial x\,\partial y}} \right] \\[3ex] - \displaystyle \frac{2\delta}{1+\delta \,x}\frac{\partial}{\partial \,x}\Delta_2 \,\psi+ \displaystyle \frac{1}{3}w\,\frac{\partial \,w}{\partial \,y}+\Delta_2 ^2\psi \,-Gr\,\,\,(1+\delta \,x)\frac{\partial \,T}{\partial \,x} + \frac{1}{3}Tr\frac{\partial \,w}{\partial \,y}, \ \end{array} $$
(8)
$$\frac{\partial T}{\partial t}=\frac{1}{\Pr}\left({\Delta_2 T + \frac{\delta}{1+\delta x}\frac{\partial T}{\partial x}} \right) - \frac{1}{3(1+\delta x)}\frac{\partial (T,\psi)}{\partial (x,y)} , $$
(9)

where

$$\Delta_2 \equiv \frac{\partial ^2}{\partial \,x^2} + \,\frac{1}{9}\frac{\partial ^2}{\partial \,y^2}, \quad \frac{\partial (f,g)}{\partial (x,y)} \equiv \frac{\partial f}{\partial x}\frac{\partial g}{\partial y} - \,\frac{\partial f}{\partial y}\frac{\partial g}{\partial x}. $$
(10)

The system is therefore governed by the four non-dimensional parameters: the Dean number, Dn; the Taylor number, Tr; the Grashof number, Gr; the Prandtl number, Pr. They are included in Eqs. (7)–(9) defined as follows:

$$Dn=\frac{Gd^3}{\mu \upsilon}\sqrt {\frac{2d}{L}}, \quad Gr = \frac{\beta g\Delta Td^3}{\upsilon ^2}, \quad Tr=\frac{2\sqrt {2\delta} \Omega_T d^3}{\upsilon \delta}, \quad \mathrm{ Pr}=\frac{\upsilon}{\kappa}. $$
(11)

The no-slip boundary conditions for the fluid velocity are applied for \(w\) and \(\psi \) as follows:

$$w(\pm 1,y)=w(x,\pm 1)=\psi (\pm 1,y)=\psi (x,\pm 1)=\frac{\partial \psi}{\partial x}(\pm 1,y)=\frac{\partial \psi}{\partial y}(x,\pm 1) = 0 $$
(12)

and the temperature \(T\) is assumed to be constant on the walls:

$$T(x,1)=1,T(x,-1)=- 1,T(\pm 1,y)=- y . $$
(13)

There is a class of solutions that satisfy the following symmetry condition with respect to the horizontal plane \(y=0\):

$$\left. {{\begin{array}{l} w\left({x,y,t} \right) \Rightarrow w\left({x,-y,t} \right), \\ \psi (x,y,t) \Rightarrow -\psi (x,-y,t), \\ T(x,y,t) \Rightarrow -T(x,-y,t). \\ \end{array}}} \right\}$$
(14)

The solution which satisfies condition (14) is called asymmetric solution, otherwise it is an asymmetric solution. In the present study, \(Tr\,(-2500 \le Tr \le 2500)\) and \(\delta\, (0.001 \le \delta \le 0.5)\) vary, whereas Gr, Dn, and Pr are fixed: \(Gr=100\), \(Dn=1000\), and \(\mathrm{ Pr}=7.0\) (water).

3. NUMERICAL ANALYSIS

3.1. Numerical Procedure

In order to find out the numerical solution from Eqs. (7)–(9), we apply the spectral method [49] with the obtained non-dimensionalized momentum and energy equations. By this method, the variables are expanded into a series of functions consisting of the Chebyshev polynomials. That is, the expansion functions \(\varphi_n (x)\) and \(\psi_n(x)\)are stated as

$$\left. {\begin{array}{l} \varphi_n (x)=(1-x^2)C_n (x), \\ \psi_n (x)=(1-x^2)^2C_n (x). \\ \end{array}} \right\}$$
(15)

Here \(C_n (x)=\cos ({n\,\cos^{-1}(x)} )\) is the \(n\)th order Chebyshev polynomial. \(w({x,y,t})\), \(\psi ({x,y,t})\), and \(T({x,y,t})\) are expressed in terms of \(\varphi_n (x)\) and \(\psi_n(x)\) as follows:

$$\left. {\begin{array}{l} w(x,y,t)=\sum\limits_{m=0}^M {\sum\limits_{n=0}^N {w_{mn} (t)\,\phi _m (x)\,\phi_n (y)}}, \\ \psi (x,y,t)=\sum\limits_{m=0}^M {\sum\limits_{n=0}^N {\psi_{mn} (t)\,\psi_m (x)\,\psi_n (y)}}, \\ T(x,y,t)=\sum\limits_{m=0}^M {\sum\limits_{n=0}^N {T_{mn} (t )\,\phi_m (x)\,\phi_n (y)-y}}, \\ \end{array}} \right\}$$
(16)

where \(M\) and \(N\) represent the truncation numbers in the \(x\) and \(y\) directions, respectively, and \(w_{mn}\), \(\psi_{mn}\), and \(T_{mn}\) are the coefficients of the expansion. To obtain the time dependent evolution of \(\overline w_{mn}\), \(\overline \psi_{mn}\), and \(\overline T_{mn}\), we substitute required series expansion (16) into basic equations (7)–(9) by the collocation method. Consequently, a set of nonlinear algebraic equations for \(\overline w_{mn} \), \(\overline \psi _{mn}\), and \(\overline T_{mn}\) is found. The steady solutions are determined by the Newton–Raphson iteration method (N-RIM), assisted by the path continuation technique. To evade difficulty near the point of inflection for the steady solution branches, we use the following arc-length equation:

$$\sum\limits_{m=0}^M {\sum\limits_{n=0}^N {\left\{{\left({\frac{dw_{mn} }{ds}} \right)^2+\left({\frac{d\psi_{mn}}{ds}} \right)^2+\left( {\frac{dT_{mn}}{ds}} \right)^2} \right\}=1}}, $$
(17)

which is solved simultaneously with Eq. (19) using the N-RIM. An initial guess at the point \(s+\Delta s\) is considered starting from point \(s\) as follows:

$$\left. {\begin{array}{l} w_{mn} \left({s+\Delta s} \right)=w_{mn} \left(s \right) + \displaystyle \frac{dw_{mn} \left(s \right)}{ds}\Delta s ,\\[1ex] \psi_{mn} \left({s+\Delta s} \right)=\psi_{mn} \left(s \right) + \displaystyle \frac{d\psi_{mn} \left(s \right)}{ds}\Delta s, \\[1ex] T_{mn} \left({s+\Delta s} \right)=T_{mn} \left(s \right) + \displaystyle \frac{dT_{mn} \left(s \right)}{ds}\Delta s .\ \end{array}} \right\} $$
(18)

The convergence is ensured if \(\varepsilon_p ({\varepsilon_p < 10^{-10}})\) defined as

$$\varepsilon_p=\sum\limits_{m=0}^M {\sum\limits_{n=0}^N {\left[ {\left({w_{mn}^{\left({p+1} \right)}-w_{mn}^p} \right)^2+\left( {\psi_{mn}^{\left({p+1} \right)}-\psi_{mn}^p} \right)^2+\left( {T_{mn}^{\left({p+1} \right)}-T_{mn}^p} \right)^2} \right]}} $$
(19)

is taken suitably small.

3.2. Resistance Coefficient

The resistance coefficient \(\lambda \), called the hydraulic resistance coefficient, denotes the quantity of the flow state and is defined as follows:

$$\frac{P_1^\ast-P_2^\ast}{\Delta z^\ast}=\frac{\lambda}{d_h^\ast }\frac{1}{2}\rho \left\langle {w^\ast} \right\rangle ^2 , $$
(20)

where \(\left\langle ~~\right\rangle\) stands for the mean over the cross-section of the duct, \(d_h^\ast\) is the hydraulic diameter, \(\rho \) is the density, \(P_1^\ast\) and \(P_2^\ast\) are the pressure at upstream and downstream positions of the duct, respectively, and \(\left\langle {w^\ast} \right\rangle\) is the stream-wise main velocity:

$$\left\langle {w^\ast} \right\rangle=\frac{\nu}{4\sqrt {2\delta} d} \int\limits_{-1}^1 dx \int\limits_{-1}^1 \bar{w}(x,y,t)dy. $$
(21)

Since \(\frac{P_1^\ast-P_2^\ast}{\Delta z^\ast}=G\), \(\lambda \) is linked with the mean non-dimensional axial velocity \(\langle w \rangle = {\sqrt {2\delta} d\langle {w^\ast} \rangle} /\upsilon \) as follows:

$$\lambda=\frac{16\sqrt {2\delta} Dn}{3\langle w\rangle^2}. $$
(22)

3.3. Grid Sensitivity Test

Based on five test cases with truncation numbers \(M\) and \(N\), the comparative study is conducted at five truncation numbers in conjunction with Dn = 1000, Gr = 100, Tr = 200, and \(\delta=0.1\). The computational domain size in this research is \(14\times 42\), \(16\times 48\), \(18\times 54\), \(20\times 60\), and \(22\times 66\), i.e., \(N\) is chosen equal to \(3M\). The \(20\times 60\) grid resolution was sufficiently fine to ensure the accuracy of the present numerical computation, as shown in the table.

Fig. 2
figure 2

(a) Branching structure of SCs for \(\delta=0.1\), \(Dn = 1000\), \(Gr=100\), and \(0 \le Tr \le 2500\). (b) Velocity contours (top and bottom) and isotherm (middle) on SSB for various values of Tr.

Full size image

Values of \(Q\) and \(w(0,0)\) for various \(M\) and \(N\) atDn = 1000, Gr = 100, Tr = 200, and \(\delta=0.1\)

\(M\)

\(N\)

\(Q\)

\(w(0,0)\) 

14

42

580.3289478

1108.325360

16

48

581.0745552

1110.106655

18

54

581.0486605

1111.835302

20

60

581.0552044

1112.001216

22

66

581.0562282

1112.176767

Fig. 3
figure 3

(a) 1st steady branch for \(\delta=0.1\) and \(0 \le Tr \le 2500\). (b) Expansion at point \(c\). (c) Expansion at point \(e\). (d) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) on the 1st steady branch for different values of Tr.

Full size image
Fig. 4
figure 4

(a) 2nd steady branch for \(\delta=0.1\) and \(0 \le Tr \le 2500\). (b) Expansion at point \(b\). (c) Expansion at point \(c\). (d) Expansion at point \(d\). (e) Expansion at point \(e\). (f) Expansion at point \(f\).

Full size image
Fig. 5
figure 5

Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) on the 2nd steady branch at fixed value of Tr for \(\delta=0.1\). (a) Tr = 250, (b) Tr = 500, and (c) Tr = 750.

Full size image
Fig. 6
figure 6

(a) Schematic of the 3rd SB for \(\delta=0.1\) and \(0 \le Tr \le 2500\). (b) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) on the 3rd SB for different Tr.

Full size image
Fig. 7
figure 7

(a) The 4th SB for \(\delta=0.1\) and \(0 \le Tr \le 2500\). (b) Expansion at point \(b\). (c) Expansion at point \(c\). (d) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) on the 4th SB for different values of Tr.

Full size image
Fig. 8
figure 8

The 5th SSB and its expansion for \(\delta=0.1\) and \(0 \le Tr \le 2500\). (a) 5th SC. (b) Expansion at point \(b\). (c) Expansion at point \(e\). (d) Expansion around Tr = 1150.

Full size image
Fig. 9
figure 9

Contour plots of secondary flow (top) and axial velocity (bottom) on the 5th steady branch at fixed value of Tr for \(\delta = 0.1\). (a) Tr = 750. (b) Tr = 1000. (c) Tr = 1250.

Full size image
Fig. 10
figure 10

Vortex structure of secondary flows: number of vortices in (\(Tr\)-\(\theta\)) plane vs. Taylor number. (a) \(\delta = 0.001\). (b) \(\delta=0.1\). (c) \(\delta=0.5\).

Full size image
Fig. 11
figure 11

Time progress, phase space, and streamlines for Tr = 0 and \(\delta=0.1\). (a) Time advancement of \(\lambda\) with values of \(\lambda \) for steady solutions. (b) Phase portrait. (c) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(3.00\le t \le 7.50\).

Full size image
Fig. 12
figure 12

Time progress, phase space, and streamlines for Tr = 1000 and \(\delta=0.1\). (a) Time advancement of \(\lambda \) with values of \(\lambda \) for steady solutions. (b) Phase portrait. (c) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for 10.00 \( \le t \le 24.00\).

Full size image
Fig. 13
figure 13

Time progress, phase space, and streamlines for Tr = 1570 and \(\delta=0.1\). (a) Time advancement of \(\lambda \) with values of \(\lambda \) for steady solutions. (b) Phase-portrait. (c) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(7.50\le t \le 18.50\).

Full size image
Fig. 14
figure 14

Time progress, phase space, and streamlines for Tr = 1585 and \(\delta=0.1\). (a) Time advancement of \(\lambda \) at \(\lambda\) values for steady solutions. (b) Expansion of (a). (c) Phase portrait. (d) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(11.92 \le t \le 12.38\).

Full size image
Fig. 15
figure 15

Time progress, phase space, and streamlines for Tr = 2000 and \(\delta=0.1\). (a) Time advancement of \(\lambda \) at \(\lambda \) values for steady solutions. (b) Expansion of (a). (c) Phase portrait. (d) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(12.55 \le t \le 12.65\).

Full size image
Fig. 16
figure 16

Time progress, phase space, and streamlines for Tr = 2185 and \(\delta=0.1\). (a) Time advancement of \(\lambda \) at \(\lambda \) values for steady solutions. (b) Expansion of (a). (c) Phase-portrait. (d) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(12.49 \le t \le 12.59\).

Full size image
Fig. 17
figure 17

Time progress, phase space, and streamlines for Tr = 2188 and \(\delta=0.1\). (a) Time advancement of \(\lambda \). (b) Contour plots of secondary flow (left), energy distribution (middle). and axial velocity (right) at \(t=14.50\).

Full size image
Fig. 18
figure 18

Time progress, phase space, and streamlines for Tr = 2289 and \(\delta=0.1\). (a) Time advancement of \(\lambda \). (b) Contour plots of secondary flow (left), energy distribution (middle), and axial velocity (right) at \(t=10.00\).

Full size image

To obtain time-dependent solutions, we applied the Crank–Nicolson and Adams–Bashforth methods together with function expansion (16) and the collocation method, which are not shown here for brevity. Details of this method are available in [49] and [16].

4. RESULTS AND DISCUSSION

4.1. Structure of Steady Solutions

Here we present a detailed examination of combined flow structure in a steady solution branch for the curvature \(\delta=0.1\), discuss the flow configurations in various steady branches, and then sum up the results for other curvatures at the end of this section. After a rigorous survey, five branches of axisymmetric steady solutions are obtained for \(Dn=1000\) and \(Gr=100\) with \(0 \le Tr \le 2500\). The whole process for Tr values ranging from 0 to 2500 finds five branches of complex bifurcation structure of steady solutions, as presented in Fig. 2a. The five steady solution branches (SSBs) are referred to as the 1st, 2nd, 3rd, 4th, and the 5th branch, respectively; they are distinguished with different colors and lines. It is found that there exists no bifurcating connectivity among the solution curves (SCs).

4.1.1. Description of the 1st Steady Branch

The 1st steady solution branch (SSB) is solely illustrated by the solid line in Fig. 3a. The whole branching pattern is pointed out with six points: \(a\), \(b\), \(c\), \(d\), \(e\), and \(f\). starting point of the branch is \(a\) (Tr = 0). The turning points \(c\) and \(e\) are shown in Figs. 3b and 3c, respectively, where we see that the branch changes the direction smoothly at both points. Soon the branch again moves to its way of increasing Tr, and at point \(d\) (Tr = 1108.566) we find another turning, where the branch changes its direction again, decreases Tr up to point \(e\) (Tr = 793.75), and experiences another smooth turning, as shown in Fig. 3c, where the branch changes its direction again to larger Tr, then goes to point \(f\) (Tr = 1170.444), and finally arrives at point \(a\) (Tr = 0) with many turnings on its way. It is also noticed that more than one turning is found at points \(b\), \(c\), \(d\), and \(e\). After that, in order to observe the configurations and dissimilarities on this branch, we trace the streamlines of the secondary flow (SF), isotherms (energy distribution), and axial flow (AF) at different Tr, as presented in Fig. 3d, which shows that the branch consists of solutions with axisymmetric single-pair cell to axisymmetric multi-pair cell vortices.

Fig. 19
figure 19

Time progress, phase space, and streamlines for Tr = \(-10\) and \(\delta=0.1\). (a) Time advancement of \(\lambda \). (b) Phase portrait. (c) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(10.00 \le t \le 18.00\).

Full size image
Fig. 20
figure 20

Time progress, phase space, and streamlines for Tr = \(-1000\) and \(\delta=0.1\). (a) Time advancement of \(\lambda \). (b) Phase portrait. (c) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(12.00 \le t \le 17.00\).

Full size image
Fig. 21
figure 21

Time progress, phase space, and streamlines for Tr = \(-1970\) and \(\delta=0.1\). (a) Time advancement of \(\lambda \). (b) Phase portrait. (c) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(13.00 \le t \le 18.00\).

Full size image
Fig. 22
figure 22

Time progress, phase space, and streamlines for Tr = \(-1975\) and \(\delta=0.1\). (a) Time advancement of \(\lambda \). (b) Phase portrait. (c) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(14.37 \le t \le 14.70\).

Full size image

Additional vortices appear near the concave wall because of the Dean unstableness (centrifugal instability) as Tr increases, and these additional vortices, called Dean vortices, can only be seen in a rotating system, which plays a pivotal role for boosting of heat transfer. At small Tr, the swirling flow is a strongly axisymmetric single-pair cell. The curve starts with an axisymmetric single-pair cell at Tr = 0 and the branch turns into a multi-pair cell with increasing Tr. It is seen that the axial flow is moved a little bit towards the outer bend of the duct as Tr increases. In the presence of rotation and the fluid pressure on swirling-flows causing increasing the number of Dean vortices extensively change. Strong interaction of the heating-induced buoyancy force and the centrifugal force causes the flow axisymmetry, which induces secondary vortices. In this regard, the centrifugal force caused by the duct curvature produces two effects: the positive outward fluid pressure field and the tangential fluid motion, both transferred from the convex wall towards the concave wall.

The positive outward fluid motion, induced by the centrifugal effect, takes place against the outward pressure field and is superimposed on the main flow to create the secondary vortex flow structure. In the neighbourhood of the concave wall, the resultant action of the flow divergence, or pressure gradient along the axis (adverse outward pressure), and viscous effects decelerates the tangential fluid motion and constructs an inactive flow zone; the increase in the critical value of Dn, beyond a certain limit that the pressure gradient field along the axis (adverse outward pressure) becomes more and more stronger so that the direction of the tangential fluid flow reverses on the duct wall. Dean vortices appear in the motionless region near the outer wall if a weak local flow re-circulation is established; this flow condition is known as Dean’s hydrodynamic instability.

4.1.2. Description of the 2nd Steady Branch

The 2nd SSB for \(0 \le Tr \le 2500\) is explicitly shown by the solid line in Fig. 4a. This is the only branch that exists for the whole range of the Taylor number in this study. The 2nd branch is very entangled, e.g., experiencing many turnings in the region \(a \to b \to c \to d \to e \to f\). To observe the turning points \(b\), \(c\), \(d\), \(e\), and \(f\), we draw Figs. 4b–4f, respectively, with expansion. It should be noted that the branch changes its direction smoothly at all above mentioned turning points. Figures 5a–5c show the streamlines of SF, thermal profile (TF), and AF on the 2nd steady branch at Tr = 250, 500, and 750, respectively. The branch has many turnings on its way and it is found that the flow consists of symmetric 1-, 2-, 3-, 5-, 7-, 8-, 9-, and 10-pair cell vortex solutions. With increase in Tr, the AF is moved towards the concave wall of the duct.

4.1.3. Description of the 3rd Steady Branch

Figure 6a represents the 3rd SSB (line). As seen in Fig. 6a, the branch starts from point \(a\) (Tr = 0) and returns to the starting point with a single reversal at Tr = 1661.4769838. It is observed that the upper part (from point \(a\) to point \(b\)) and the lower part (from point \(b\) to point \(a)\) of the branch pass are very close to each other, as in the study by Mondal et al. [25] for a non-isothermal flow (no rotation case). Figure 6b shows streamlines of SF, TF, and AF on the 3rd SB at various values of Tr. As shown in Fig. 6b, the 3rd SB consists of asymmetric 1- and 2-pair cell solution. The patterns of the secondary flow in the lower part of the branch are opposite (mirror symmetric) to those in the upper part of the curve.

Fig. 23
figure 23

Time progress, phase space, and streamlines for Tr = \(-2500\) and \(\delta=0.1\). (a) Time advancement of \(\lambda \). (b) Phase portrait. (c) Contour plots of secondary flow (top), energy distribution (middle), and axial velocity (bottom) for \(11.57 \le t \le 11.68\).

Full size image
Fig. 24
figure 24

Schematic diagram of time-advancement solutions for \(0.001 \le \delta \le 0.5\) at positive and negative rotation.

Full size image

4.1.4. Description of the 4th Steady Branch

The fourth SSB is presented in Fig. 7a by the solid line. It is clear from the plot that the branch has three turning points: \(b\), \(c\), and \(d\). The curve turns very smoothly at points \(b\) (Tr = 1409.6155948) and \(c\) (Tr = 465.438993), as evidenced by Figs. 7b and 7c, which visualize the turning points more clearly. A more comprehensive analysis behind point \(d\) shows that the upper part (from point \(c\) to point \(d)\) and the lower part (from point \(d\) to point \(c)\) of the branch pass very close to each other, as in [25]. As seen in Fig. 7d, the 4th branch consists of axisymmetric single- and 2-pair cell vortex solutions. The SF patterns in the lower part of the branch are opposite to those of the upper part of the branch. The SF patterns are axisymmetric for every Tr except for those at point \(d\) (Tr = 1443.5633877). With increase in Tr, the AF is transferred to the concave bend of the duct.

4.1.5. Description of the 5th Steady Branch

The line in Fig. 8a plots the 5th SSB. Figures 8b–8d present expansions at points \(b\) and \(e\) and around Tr = 1150, respectively. Figures 8a and 8d elucidate the curve where it is twisted, experiencing many turnings at larger Tr. Moreover, the branch turns very smoothly at points \(b\) (Tr = 1629.6939) and \(e\) (Tr = 705.409022), as evidenced by Figs. 8b and 8c, respectively. Since the branch is very twisted, we consider fixed values Tr = 750, Tr = 1000, and Tr = 1250 for observing the streamline contours of the SF patterns and AF distribution as shown in Figs. 9a–9c, respectively. The figures show that the flow consists of symmetric 2-, 4-, 5-, 7-, 8-, and 11-pair cell solution. It should be noted that the 5th steady branch contains more than one solution at the same value of Tr.

A schematic representation of the vortex-structure of the secondary flows observed at various values of Tr for \(\delta =0.001\), 0.1, and 0.5 is presented in the (\(Tr\)–\(\theta\)) plane in Fig. 10. Figure 10a shows the vortex structure for the steady solutions at \(\delta=0.001\), Fig. 10b for \(\delta=0.1\), and Fig. 10c for \(\delta=0.5\). As seen in Fig. 10, 1- to 5-pair cell solutions were visible at the same value of Tr on various branches of steady solutions for different curvatures. It is seen that the maximum 5-pair cell is realized at Tr = 500 and Tr = 750 for \(\delta=0.1\). However, as the curvature grows, i.e., the duct becomes more curved, e.g., \(\delta=0.5\), the number of secondary vortices decreases and we get only 1-pair to 2-pair cell solutions. Figure 10b shows that there are many solutions at the same value of Tr, that is, the 2nd branch has many turnings at Tr = 250 and Tr = 500, as does the 5th branch at Tr = 750 and Tr = 1000. Again, from Fig. 10c it is also observed that the number of branches decreases gradually and the first branch exists above Tr = 500 only.

Fig. 25
figure 25

Schematic diagram of vortex structure of secondary flows for \(0.001 \le \delta \le 0.5\) and \(-2500 \le Tr \le 2500\).

Full size image
Fig. 26
figure 26

(a) TG at heated wall. (b) TG at cooling wall.

Full size image

4.2. Oscillating Behavior and Phase Spaces

4.2.1. Case I: Positive Rotation \((0 \le Tr \le 2500)\)

The results of oscillating behavior at \(\delta=0.1\) with Tr varying from 0 to 2500 are discussed in this subsection. In the interest of brevity, we present the oscillating behavior for \(\delta=0.1\) only. We calculate the oscillating behavior of \(\lambda\) for Tr = 0, Tr = 1000, Tr = 1570, Tr = 1585, Tr = 2000, Tr = 2185, Tr = 2188, and Tr = 2289 with the \(\lambda \) values for steady solutions for the above-mentioned Tr at \(\delta=0.1\), pointed out by straight lines of the same sort as used in Fig. 2a. It is found that the oscillating behavior is chaotic at Tr = 0, Tr = 1000, and Tr = 1570, as shown in Figs. 11a, 12a, and 13a, respectively. To be sure whether the flow is chaotic or not, we draw the phase space (PS) of the time-advancement solutions, as shown in Figs. 11b, 12b, and 13b in the \(\lambda-\gamma \) plane, where \(\gamma=\int \int\psi\,dx\,dy\). Figures 11c, 12c, and 13c suggest that the flow oscillates irregularly between the axisymmetric 5-pair cell and 6-pair cell, 5- and 9-pair cell, and 7- and 8-pair cell solutions for Tr = 0, Tr = 1000, and Tr = 1570, respectively, and the axial velocity that generated near the outer wall of the duct. In rotating plane-channel flows, the resulting force of the centrifugal, Coriolis, and buoyancy forces affects the fluid, and the flow becomes accelerated. It is seen that the chaotic solutions for Tr = 0, Tr = 1000, and Tr = 1570 move around \(\lambda = 0.142\), \(\lambda=0.215\), and \(\lambda=0.234\) and that the chaotic solutions for Tr = 0, Tr = 1000, and Tr = 1570 are independent on the initial condition. It is also observed that the chaotic solutions for Tr = 0, Tr = 1000, and Tr = 1570 fluctuate above all the steady solution branches, that is, the oscillating behaviors are very chaotic (Mondal et al. [25]).

The present study shows that as Tr is increased gradually, the chaotic flow transforms into the multi-periodic flow at Tr = 1585, 2000, and 2185. Figures 14a, 15a, and 16a display the multi-periodic flow. Figures 14b, 15b, and 16b show the multi-periodic flow to be more pronounced in comparison with Figs. 14a, 15a, and 16a. It is well justified by the PS diagrams presented in Figs. 14c, 15c, and 16c. Furthermore, the multi-periodic oscillations at Tr = 1585, Tr = 2000, and Tr = 2185 fluctuate above all the steady solutions, and the multi-periodic solutions at Tr = 1585, Tr = 2000, and Tr = 2185 move around \(\lambda = 0.234\), \(\lambda=0.249\), and \(\lambda=0.255\), respectively, the multi-periodic solutions being independent on the initial condition. Various flow patterns observed for Tr = 1585, Tr = 2000, and Tr = 2185 are presented in Figs. 14d, 15d, and 16d. It is also noticed that the time-dependent flow oscillates multi-periodically between the asymmetric 4-pair cell and 5-pair cell solutions at \(11.92\le t \le 12.38\) and 4-pair cell at \(12.55 \le t \le 12.65\), 3- and 4-pair cell solutions at \(12.49 \le t \le 12.59\). For Tr ranging between 2188 and 2289, the flow behavior changes to the steady state with asymmetric single-pair vortices noted, as shown in Figs. 17a, 17b, 18a, and 18b. From Fig. 17a, the steady solution and time advancement of the steady-state solution at Tr = 2188 are very close to each other. It is necessary to note that the transition from the multi-periodic flow to the steady state takes place between Tr = 2185 and Tr = 2188. If the Dean vortices are generated near the outer wall of the duct and the secondary flow becomes stronger, then the heat transfer occurring is greater than usual.

Fig. 27
figure 27

Experimental vs. numerical results. Left: Experimental result by Chandratilleke [51] for curved rectangular duct flow with aspect ratio of 2. Right: numerical result by authors.

Full size image

4.2.2. Case II: Negative Rotation \((-2500 \le Tr < 0)\)

The results of oscillating behavior for \(\delta=0.1\) with Tr varying from \(-2500\) to \(-10\) are discussed in this subsection. For brevity, we present oscillating behavior for \(\delta=0.1\). At Tr ranging from \(-10\) to \(-1970\), the flow oscillates irregularly with asymmetric 2-pair to 3-pair vortices at Tr = \(-10\) and Tr = \(-1000\) and 4-pair to 5-pair vortices at Tr = \(-1970\), as evidenced by Figs. 19a, 19c, 20a, 20c, 21a, and 21c, respectively. Figures 19b, 20b, and 21b plot the PS diagram to show the chaotic behavior. It is observed that the streamlines of the thermal profiles are consistent, i.e., the high temperature fluid near the bottom wall is forced upwards, and the convective heat generation is strengthened markedly throughout the area of the contours. With further increase in Tr in the negative direction, another flow transformation occurs at Tr = \(-1975\), where the chaotic flow turns into the multi-periodic flow, which is well evidenced by the SP plot with asymmetric 2-pair and 3-pair vortices at \(14.37 \le t \le 14.70\), as shown in Figs. 22a and 22c. If Tr is further increased, the multi-periodic flow remains unchanged, but with 3-pair and 4-pair vortices at Tr = \(-2500\), as shown in Figs. 23a and 23c. Figure 23b shows the PS diagram for clearer visualization; it can be seen that the flow is multi-periodic. It is perceived that the transition from the chaotic to multi-periodic oscillations occurs between Tr = \(-1970\) and Tr = \(-1975\).

4.3. Time Advancement and Vortex Structure

4.3.1. Time Advancement in the \((Tr\)–\(\delta)\) Plane

In this subsection, the distribution of diverse transient solutions obtained by TEv computations is offered in Fig. 24 in the \(Tr\)–\(\delta\) plane for \(-2500 \le Tr\le 2500\) and \(0.001 \le \delta \le 0.5\). Here the steady-state solution is denoted with circles, chaotic solution with crosses, multi-periodic solution with squares, and periodic solution with triangles. At \(\delta=0.001\) over a wide range of Tr (\(-1250\le Tr\le 1250\)), the chaotic flow is noticed. The oscillating chaotic flow, on the other hand, transforms into the multi-periodic one in the range for \(1585 \le Tr \le 2185\) and \(-2500 \le Tr\le -1975\) at \(\delta = 0.1\). It is interesting that in the small range \(-500 \le Tr\le 295\) at \(\delta=0.5\), four types of solutions occur in this region: chaotic, multi-periodic, periodic, and steady-state solutions, i.e., with weak rotation (positive or negative) and strong curvature, the flow state behaviors change quickly. In contrast, the steady-state solution occurs for \(295 \le Tr\le 2289\) and \(-2500 \le Tr \le -750\), (strong rotation, positive or negative), as the curvature is increased. It is clear that the oscillating behavior is chaotic at small curvature for weak or strong rotation, and consequently the flow transforms into the steady state via periodic and multi-periodic ones at strong rotation as the curvature is gradually increased in the rotating system.

4.3.2. Schematic Diagram of Vortex-Structure in the \((Tr\)–\(\delta)\) Plane

In this subsection, we show the vortex structure of the secondary flows for time-dependent solutions. Figure 25 represents the vortex structure of the flow state in the \(Tr\)–\(\delta \) plane for Tr varying from \(-2500\) to 2500 and the curvature ratio \(0.001 \le \delta \le 0.5\). The variation of the curvature with respect to Tr is plotted. Figure 25 clearly shows that the flow state has 1-pair to 5-pair vortices at various values of Tr. However, a closer observation reveals that the maximum 1-pair to 5-pair solutions are at the moderate curvature \(\delta=0.1\) and \(\delta=0.001\). As the value of Tr is increased, the number of vortices decreases. A more comprehensive analysis of Figs. 24 and 25 shows that 1-pair and 2-pair vortices exist in the steady-state region, whereas 1-pair to 6-pair vortices exist in the chaotic region. Therefore, it may be supposed that the enhancement of heat transfer for the chaotic flow is more pronounced than that for the steady-state or periodic flow and this is a result of many secondary vortices produced near the concave wall in the chaotic flow, which agrees well with the numerical result for a rotating curved duct in the literature [50]. However, the solution structure for steady branches, as well as characteristics of the flow transition, is still absent in the literature for a rotating CRD, as the present work shows clearly. Furthermore, this study gives a clear view regarding the CHT, hydrodynamic instability, and vortex generation in a curved duct. So far, no reliable technique for the Dean instability in a rectangular duct has been known in literature for such flows.

4.4. Convective Heat Transfer (CHT)

In this subsection, we discuss the effect of rotation of the system shown in Fig. 2 on the CHT from the heated wall to the fluid, which is quantitatively assessed by the temperature gradient (TG) at the differentially heated walls. In Figs. 26a and 26b, the variation of the temperature gradient \(\frac{\partial T}{\partial x}\) is plotted as a function of \(y\). As seen in Fig. 26a, the TG variation exhibits a much complex manner for the bottom wall. The TG magnitude on the bottom wall declines in the central zone around \(y=0\) from Tr = 300 to Tr = 900 and then decreases and fluctuates through small and medium amplitude oscillations (the number of oscillations increases with the rotation speed) around Tr = 1100 for the heating wall. On the other hand, at the bottom wall, the TG magnitude approaches to increase the zone other than the central zone when \(Tr\le 900\). In Fig. 26b, the TG magnitude at the top (cooled) wall increases slowly in the central zone around \(y=0\) from Tr = 300 to Tr = 700, and then the curve rapidly approaches to approximately flat shape (very small oscillations), and the magnitude decreases over the whole zone at the top wall for Tr = 900 and Tr = 1000. It is also seen that the peak TG appears in the centre at Tr = 1170. This happens owing to advection of the SF in the inward direction there, which is a reverse flow of the outward SF in the central zone. This result shows that heat transfer occurs mostly from the heated wall to the fluid as Tr increases.

4.5. Validation Test

In this subsection, validation of our numerical results in the present study is performed in Fig. 27 in comparison with experimental investigations by Chandratilleke [51]. The left figure presents the experimental results and the right one displays the numerical results for the curved rectangular duct. As can be seen, there is great similarity between the experimental data and our numerical results. Note that not enough experimental research has been found on a flow through a curved rectangular duct.

5. CONCLUSION

The current paper uses the spectral method to numerically explore the 2D flow characteristics and heat transfer through a tightly coiled duct with an aspect ratio of 3 by for the Taylor number \(-2500 \le Tr \le 2500\) and curvature \(0.001 \le \delta \le 0.5\). The lower wall of the duct is heated with cooling from the upper wall, the other walls being thermally insulated to prevent heat loss. Five branches of asymmetric steady solutions, comprising single-pair to 11-pair vortices, are found. To discuss the transient behavior, time advancement of the flow is performed and flow transition is well predicted through the phase space of the solutions, which shows that in the case of co-rotating system, a chaotic flow transforms into a steady state flow via a multi-periodic flow; in the case of counter-rotating system, however, a chaotic flow changes to a multi-periodic flow directly. Streamlines of the secondary flow, isotherms (energy distribution), and axial velocity are obtained for different values of Tr, and it is found that in the co-rotation case there exist a single-pair vortex for the steady-state, 3-pair to 5-pair vortices for the periodic or multi-periodic flow, and 3-pair to 5-pair vortices for the chaotic solution. In the counter-rotation case, however, there exist 2-pair to 5-pair vortices for the chaotic solution and 3-pair and 4-pair vortices for the multi-periodic solution. The present study shows that maximum 6-pair vortices appear at small curvature \((\delta=0.001)\), 11-pair vortices at moderate curvature, and maximum 2-pair vortices at strong curvature \((\delta=0.5)\). It is found that the number of secondary vortices decreases as Tr increases and increasing the secondary vortices makes the flow chaotic, multi-vortex solutions propagating at the outer concave wall; consequently, the chaotic flow is more effective for heat transfer in the fluid than the steady-state or periodic flow. The study clearly shows that the existence of axial velocity and wall pressure is greatly influenced by the Dean vortices. The present study also shows that the fluid mixing is certainly induced by the duct curvature and rotation, and as a consequence, the overall heat transfer becomes larger throughout the fluid in the curved channel.