1 INTRODUCTION

There have been a number of studies on the dynamics of two charged particles in the plane and in space in the presence of a uniform magnetic field [13, 14, 6]. In each of these, the symmetry group consists of rotations and translations in the plane (that is, \(\mathsf{SE}(2)\)), together with translations along the magnetic field direction in the spatial setting.

In this paper we consider a similar problem, but with the particles constrained to move on the surface of a sphere, with the magnetic field vector normal to the surface and of constant magnitude. This ensures the system has spherical symmetry; the symmetry group is therefore the group of rotations \(\mathsf{SO}(3)\).

Physically, this setup requires there to be a net magnetic charge within the sphere, for example, a magnetic monopole at the centre of the sphere. The motion of a charged particle in \(\mathbb{R}^{3}\) in the presence of a monopole is a well-studied topic, and goes back to Poincaré in 1896 [15] who showed that the motion of the particle is constrained to a circular cone. More recent work can be seen in, for example, [12] and [16]. Various generalisations of the Kepler problem to \(S^{3}\), among which is the addition of a spherical analog of the magnetic monopole, are studied in [3].

The traditional Lagrangian or Hamiltonian approach to studying systems in the presence of a magnetic field is to introduce a vector potential. However, on the sphere there is no globally defined vector potential (for topological reasons), so we use the alternative Hamiltonian approach which incorporates the magnetic field into the symplectic structure, similar to the treatment in [13, 14] and first introduced by Littlejohn [10].

Reduction and particle motion

We investigate the motion of one and two particles on a sphere in the presence of a centrally symmetric magnetic field using a Hamiltonian approach. Similarly to their conterparts with no magnetic vector field, the system with one particle is an integrable one; however, that is not the case for two particles.

For a single charged particle, the motion is either stationary or has circles as trajectories, with a simple relation between the velocity of the particle and the radius of the circle, depending on the strength of the magnetic field (Proposition 3.1).

For two particles, we adapt the well-known Hamiltonian approach for the similar non-magnetic problem [4, 2] to our setting and perform the Poisson reduction with respect to the \(\mathsf{SO}(3)\)-action, obtaining the reduced Hamiltonian, Hamilton’s equations and the Poisson structure. The latter is degenerate and possesses a Casimir function, the second first integral of motion, which involves the angular momentum and the strength of the magnetic field.

The reduced system is described in terms of the distance \(q\) between the particles, its conjugate variable \(p\) and the three components of the angular momentum in the body frame \((m_{1},m_{2},m_{3})\), similar to the analogous problem with no magnetic field [2]. The magnetic field \(B\) explicitly enters through the form of the Poisson structure.

The goal of this paper is to find the relative equilibrium states of the system. Solving the equations explicitly in the general case does not appear to be tractable, due to their complexity. Nonetheless, in Theorem 4.5 we establish the general existence of relative equilibria for arbitrary masses and charges of the two particles.

Identical particles

For calculations, we choose the explicit potential \(V(q)=e_{1}e_{2}\cot(q)\), where \(e_{1}\) and \(e_{2}\) are the charges of the particles. This function arises as a fundamental solution of the Laplace – Beltrami equation for the case of an electric field due to a single charged particle on a three-dimensional sphere \(S^{3}\). It also arises as an instance of the solutions of the generalised Bertrand problem of finding potentials depending only on geodesic distance and with closed orbits [8]. As physics dictates, the potential is repelling when the signs of the charges coincide and attracting when they differ.

Due to the complexity of the general form of the reduced system of equations, in Section 5 we limit our attention to the (tractable) case where the two particles are identical.

Solving the equations for identical particles explicitly gives four classes of relative equilibria. Two of these — called Type I relative equilibria — exist for all values of \((q,B)\) with \(q\neq\pi/2\), while the other two — those of Type II — exist only in a certain region of the \((q,B)\)-plane. The two Type I relative equilibria are related by an exchange of particles but the two Type II relative equilibria are genuinely different.

Reconstructing motion from the solutions of the reduced system of equations requires expressing the vector of angular velocity of the solutions and noticing that it has to be parallel to the value of the momentum map, \(\Phi\) for that configuration.

Fig. 1
figure 1

The two types of relative equilibrium for equal masses and equal charges, with \(V(q)=\cot(q)\). (See Fig. 10 for the case with opposite charges.)

Full size image

Type I relative equilibria exist with both acute and obtuse angles between the bodies (but not a right angle); in both cases, the motions of the particles are parallel in the sense that the axis of rotation is located to the side of the two particles, and the angles of the two particles with the axis of rotation are always different.

On the other hand, Type II relative equilibria have isosceles configurations: be they obtuse, acute or right-angled, the axis of rotation is always placed between the bodies, equidistant from both of the particles. They have another interesting property: the same geometric configuration can be occupied by two states with different rates of rotation, and hence different energy levels.

Employing the standard method of investigating linear stability of relative equilibria, we find the regions in the \((q,B)\)-plane for which the equilibria in question are stable or unstable.

Type I relative equilibria allow for an analytic solution of the region of stability, described in Section 5.5, where we show that larger inter-particle distances are more likely to be stable. In contrast, for Type II relative equilibria, we need to employ numerical methods to differentiate between stability and instability (see Section 5.6).

We finish the analysis of the stability by calculating the Hessians of different types of relative equilibrium and plotting them on a simplified version of the energy-momentum diagram.

In Section 6 we briefly discuss the setting with two particles of equal mass but opposite charge. Indeed, we note that there is a simple transformation of the phase space that takes the case of identical charges to the case of opposite charges, extending a similar observation in [7]. Due to the nature of the transformations required for the switch, all the relative equilibria are retained, together with their respective stability properties, but the actual motion of the particles will change.

The case of two identical particles with a cotangent potential has a limiting case when \(B\to 0\): the two-body problem with a repelling potential described in [7]. We draw comparisons to it throughout the paper, and in the first appendix we discuss the limiting case of relative equilibria: the right-angle ones. Type I relative equilibria do not exist for \(q=\frac{\pi}{2}\) when \(B\neq 0\), and Type II relative equilibria are not present for small values of \(B\). It turns out that different right-angled relative equilibria for the gravitational problem appear as limits of the equilibria of Type I when we approach the point \((q,B)=(\frac{\pi}{2},0)\) via different curves \(B=B(q)\).

2 THE SETUP

We begin by recalling some basic facts from electrodynamics.

The force acting on a non-relativistic particle with mass \(\mu\) and charge \(e\) in the presence of an electric field \(\mathbf{E}\) and a magnetic field \(\mathbf{B}\) is called the Lorenz force and is given by \(\mathbf{F}=e(\mathbf{E}+\mathbf{v}\times\mathbf{B})\), where \(\mathbf{v}\) is the velocity of the particle. In the absence of any other forces acting on the particle, Newton’s second law dictates that

$$\mu\mathbf{a}=e(\mathbf{E}+\mathbf{v}\times\mathbf{B}),$$
(2.1)

with \(\mathbf{a}\) denoting the acceleration of the particle.

Recall that from Maxwell’s equations (see, for example, [9]), \(\nabla\cdot\mathbf{B}=0\).

Using Hodge duality in \(\mathbb{R}^{3}\), \(\mathbf{B}\) can be represented as a two-form rather than a vector field: \(\mathbf{B}=\mathbf{B}_{3}\mathrm{d}x\wedge\mathrm{d}y+\mathbf{B}_{2}\mathrm{d}z\wedge\mathrm{d}x+\mathbf{B}_{1}\mathrm{d}y\wedge\mathrm{d}z\). The divergence-free nature of the vector field is then rephrased as stating that \(\mathbf{B}\) is a closed two-form.

Consider now two non-relativistic particles in \(\mathbb{R}^{3}\), with respective masses \(\mu_{1}\) and \(\mu_{2}\), charges \(e_{1}\) and \(e_{2}\), position vectors \(\mathbf{q}_{1}\) and \(\mathbf{q}_{2}\) and velocities \(\mathbf{v}_{1},\mathbf{v}_{2}\), and momenta \(\mathbf{p}_{1},\mathbf{p}_{2}\) (where \(\mathbf{p}_{i}=\mu_{i}\mathbf{v}_{i}\)).

It is well known that their motion is described by the trajectories of a Hamiltonian system on \(T^{\ast}\mathbb{R}^{3}\times T^{\ast}\mathbb{R}^{3}\), with Hamiltonian

$$\mathcal{H}=\frac{1}{2\mu_{1}}\left|\mathbf{p}_{1}\right|^{2}+\frac{1}{2\mu_{2}}\left|\mathbf{p}_{2}\right|^{2}+V(\mathbf{q}_{1},\mathbf{q}_{2})$$
(2.2)

and symplectic form

$$\omega=\left(\begin{array}[]{c|c}\begin{array}[]{c c}e_{1}\mathfrak{B}&0\\ 0&e_{2}\mathfrak{B}\end{array}&I_{6}\\ \hline-I_{6}&0\end{array}\right),$$
(2.3)

where \(\mathfrak{B}\) is the matrix

$$\mathfrak{B}=\begin{pmatrix}0&-B_{3}&B_{2}\\ B_{3}&0&-B_{1}\\ -B_{2}&B_{1}&0\end{pmatrix},$$
(2.4)

which represents the magnetic 2-form. The function \(V(\mathbf{q}_{1},\mathbf{q}_{2})\) is the potential energy of the system, born out of the interaction between the particles and the effect of any pre-existing electric field.

First, we note that, due to closedness of \(\mathbf{B}\), \(\omega\) is a closed form as well. Together with its obvious non-degeneracy and skew symmetry, this shows (2.3) and (2.2) form a Hamiltonian system.

To prove that this Hamiltonian system does indeed model the system, we need to demonstrate that the Hamiltonian equations obtained from (2.2) are equivalent to Newton’s second law, as written for each of the particles:

$$\left\{\begin{aligned} \displaystyle\dot{\mathbf{q}}_{1}&\displaystyle=\frac{1}{\mu_{1}}\mathbf{p}_{1},\\ \displaystyle\dot{\mathbf{q}}_{2}&\displaystyle=\frac{1}{\mu_{2}}\mathbf{p}_{2},\\ \displaystyle\dot{\mathbf{p}}_{1}&\displaystyle=-V^{\prime}(\mathbf{q}_{1},\mathbf{q}_{2})_{\mathbf{q}_{1}}+\frac{e_{1}}{\mu_{1}}\mathfrak{B}|_{\mathbf{q}_{1}}(\mathbf{p}_{1}),\\ \displaystyle\dot{\mathbf{p}}_{2}&\displaystyle=-V^{\prime}(\mathbf{q}_{1},\mathbf{q}_{2})_{\mathbf{q}_{2}}+\frac{e_{2}}{\mu_{2}}\mathfrak{B}|_{\mathbf{q}_{2}}(\mathbf{p}_{2}).\end{aligned}\right.$$
(2.5)

The first two lines in (2.5) are tautological expressions, being equivalent to the definitions of \(\mathbf{p}_{i}\). The second two are precisely Newton’s second law. Thus, Hamiltonian equations on two copies of the cotangent bundle of \(\mathbb{R}^{3}\) with the symplectic form given above are equivalent to Newton equations for particle motion.

Setup for two particles on the plane and in space

Here we recall briefly the approach to the problem taken by the authors in [6, 13, 14] and [10].

The study by Escobar-Ruiz and Turbiner [6] for two particles in the plane is based on a Lagrangian approach involving a vector potential for the magnetic field (that is, \(\mathbf{A}\) satisfying \(\mathbf{B}=\nabla\times\mathbf{A}\), or as differential forms, \(\mathbf{B}=\mathrm{d}\mathbf{A}\)).

Littlejohn [10] showed how to avoid the use of a vector potential by incorporating the magnetic field (as a 2-form) into the symplectic form, and then proceed directly with Hamilton’s formulation. This was used by him to study the guiding centre problem, and more pertinent for us, was also used by Pinheiro and MacKay [13, 14] in their studies of two particles in the plane and in space.

For a uniform magnetic field on the sphere, there is no vector potential (the existence of a vector potential implies the magnetic field has mean zero, by Stokes’ theorem), so we are obliged to use the Hamiltonian approach described above.

All the authors assume (as do we) that there is no external electric field, so that the potential is a function of the distance between the particles \(V(\mathbf{q}_{1},\mathbf{q}_{2})=V\left(\|\mathbf{q}_{1}-\mathbf{q}_{2}\|\right)\). Hamilton’s equations for the motion in the plane are still given by (2.5).

Particles are placed on the horizontal plane in [6] and [13] and in three-dimensional space in [14]. These systems have similarly structured symmetry groups, comprised of translations (in the plane or in space) and rotations in the \(x\)-\(y\)-plane.

The specific magnetic field studied in all cases is (as a 2-form) \(\mathbf{B}=B\mathrm{d}x\wedge\mathrm{d}y\), with \(B\) constant, which corresponds to a uniform magnetic field parallel to the \(z\)-axis.

3 MOTION OF ONE PARTICLE

Suppose that one particle of mass \(\mu\) and charge \(e\) is placed on a unit sphere.

We take \(V(\mathbf{q})=0\) and the magnetic vector field \(\mathbf{B}\) orthogonal to \(S^{2}\) of uniform strength \(B\); thus, it can be easily seen that the system possesses \(\mathsf{SO}(3)\)-symmetry.

It can be checked that the restriction of our system to \(T^{\ast}S^{2}\) will be a Hamiltonian system; this is a simple reasoning that we omit here.

Keeping notation as above, we may easily write the symplectic form (on \(T^{*}\mathbb{R}^{3}\), not restricted to \(T^{\ast}S^{2}\) in this notation) as

$$\omega=\begin{pmatrix}e\mathfrak{B}&I\\ -I&0\end{pmatrix},$$
(3.1)

where \(\mathfrak{B}\) is given in Eq. (2.4). The Hamiltonian and the momentum map on \(T^{*}S^{2}\) are

$$\mathcal{H}=\frac{1}{2\mu}|\mathbf{p}|^{2}$$
(3.2)
$$\Phi:T^{\ast}S^{2}\to\mathfrak{so}(3)^{\ast},\ \ \Phi(\mathbf{q},\mathbf{p})=-eB\mathbf{q}+\mathbf{q}\times\mathbf{p}.$$
(3.3)

The momentum map \(\Phi\) is a map from a four-dimensional space into a three-dimensional one and its fibres \(\Phi^{-1}(\eta),\ \eta\in\mathfrak{so}(3)^{\ast}\) are one-dimensional.

Additionally, the stabiliser of any non-zero element in \(\mathfrak{so}(3)^{\ast}\) is isomorphic to \(\mathsf{SO}(2)\) and has dimension one. Thus, as quotient spaces, all the reduced spaces \({\mathchoice{\raisebox{4.479932pt}{$\displaystyle{\Phi^{-1}(\eta)}$}\mskip-5.0mu \diagup\mskip-4.0mu \raisebox{-3.499947pt}{$\displaystyle{\mathsf{SO}(3)_{\eta}}$}}{\raisebox{4.479932pt}{$\textstyle{\Phi^{-1}(\eta)}$}\mskip-5.0mu \diagup\mskip-4.0mu \raisebox{-3.499947pt}{$\textstyle{\mathsf{SO}(3)_{\eta}}$}}{\raisebox{3.499947pt}{$\scriptstyle{\Phi^{-1}(\eta)}$}\mskip-5.0mu \diagup\mskip-4.0mu \raisebox{-3.499947pt}{$\scriptstyle{\mathsf{SO}(3)_{\eta}}$}}{\raisebox{3.499947pt}{$\scriptscriptstyle{\Phi^{-1}(\eta)}$}\mskip-5.0mu \diagup\mskip-4.0mu \raisebox{-3.499947pt}{$\scriptscriptstyle{\mathsf{SO}(3)_{\eta}}$}}}\) are single points, making any motion a relative (or absolute, in the case of a stationary particle) equilibrium.

Explicitly writing the formulae for the pre-image of an element in \(\mathfrak{so}(3)^{\ast}\) and finding the maximal Euclidean distance between any two points therein (keeping in mind that it has to be a circle) gives

Proposition 3.1

The trajectories of a non-relativistic charged particle on a unit sphere with a unform magnetic field are circles whose radius \(r\) is related to the velocity \(\mathbf{v}\) by the relation

$$r^{2}=\frac{\mu^{2}|\mathbf{v}|^{2}}{B^{2}e^{2}+\mu^{2}|\mathbf{v}|^{2}}.$$
(3.4)

In terms of angular velocity \(\boldsymbol{\omega}\) this is

$$r^{2}=1-\frac{e^{2}B^{2}}{\mu^{2}|\boldsymbol{\omega}|^{2}}.$$
(3.5)

The circle on which the particle moves is the intersection of the sphere with the cone given by Poincaré’s solution to the motion in \(\mathbb{R}^{3}\) of a charged particle in the presence of a monopole. Indeed, the expression for the momentum map in (3.3) is the restriction to \(T^{*}S^{2}\) of the one for the action of \(\mathsf{SO}(3)\) on \(T^{*}\mathbb{R}^{3}\) with symplectic form (3.1), which is

$$(\mathbf{x},\mathbf{p})\longmapsto-\frac{eB}{|\mathbf{x}|}\mathbf{x}+\mathbf{x}\times\mathbf{p}.$$

That this expression is a conserved quantity for the motion of a charged particle in the presence of a magnetic monopole was shown by Poincaré [15].

4 MOTION OF TWO PARTICLES

Now consider the setup with two particles of respective masses \(\mu_{1}\) and \(\mu_{2}\) and charges \(e_{1}\) and \(e_{2}\), located, once again, on a unit sphere.

As previously, we assume that no external electric fields are present, resulting in \(V(\mathbf{q}_{1},\mathbf{q}_{2})=V(||\mathbf{q}_{1}-\mathbf{q}_{2}||)\), and throughout we assume \(V^{\prime}(q)\neq 0\) for all \(q\in(0,\pi)\).

Following [2], we assume that \(\lim\limits_{q\to 0^{+}}V(q)\to\infty\) and \(\lim\limits_{q\to\pi^{-}}V(q)\to-\infty\) (or vice versa, when \(V(q)\) is an attracting potential). Thus, the configuration space of the problem is \(\mathcal{Q}=S^{2}\times S^{2}\setminus\Delta\), where \(\Delta\) is the union of the diagonal subset of \(S^{2}\times S^{2}\) and the subset that contains all the pairs of antipodal points.

The momentum map for the \(\mathsf{SO}(3)\) action on the phase space \(T^{*}\mathcal{Q}\) is the sum of those for each particle:

$$\Phi(\mathbf{q}_{1},\mathbf{q}_{2},\mathbf{p}_{1},\mathbf{p}_{2})=-B(e_{1}\mathbf{q}_{1}+e_{2}\mathbf{q}_{2})+\mathbf{q}_{1}\times\mathbf{p}_{1}+\mathbf{q}_{2}\times\mathbf{p}_{2}$$
(4.1)

For reduction, we follow along the lines of parametrisation used in [2, 4] and [7].

Any matrix in \(\mathsf{SO}(3)\) can be written using Euler angles in the form \(g(\theta,\phi,\psi)\) as

$$\displaystyle\left(\begin{array}[]{c c c}\cos(\phi)\cos(\psi)-\cos(\theta)\sin(\psi)\sin(\phi)&-\sin(\phi)\cos(\psi)-\cos(\theta)\sin(\psi)\cos(\phi)&\sin(\theta)\sin(\psi)\\ \cos(\phi)\sin(\psi)+\cos(\theta)\cos(\psi)\sin(\phi)&-\sin(\phi)\sin(\psi)+\cos(\theta)\cos(\psi)\cos(\phi)&-\sin(\theta)\cos(\psi)\\ \sin(\theta)\sin(\phi)&\sin(\theta)\cos(\phi)&\cos(\theta)\end{array}\right)$$
(4.2)

and any element of \(\mathfrak{so}(3)\) as

$$\xi=\left(\begin{array}[]{c c c}0&-\boldsymbol{\omega}_{3}&\boldsymbol{\omega}_{2}\\ \boldsymbol{\omega}_{3}&0&-\boldsymbol{\omega}_{1}\\ -\boldsymbol{\omega}_{2}&\boldsymbol{\omega}_{1}&0\end{array}\right).$$
(4.3)

Now, consider the two points in \(S^{2}\subset\mathbb{R}^{3}\), separated by a geodesic distance \(q\):

$$\mathbf{x}_{1}=\left(\begin{array}[]{c}0\\ 0\\ -1\end{array}\right),\quad\mathbf{x}_{2}=\left(\begin{array}[]{c}0\\ \sin(q)\\ -\cos(q)\end{array}\right).$$
(4.4)

It is straightforward to see that any configuration can be obtained by placing the two particles at an appropriate distance in the form above and then rotating them. Hence, the tangent bundle can be rewritten in terms of the angles \(\theta,\psi,\phi\), the coordinates on the Lie algebra \(\boldsymbol{\omega}_{1},\boldsymbol{\omega}_{2},\boldsymbol{\omega}_{3}\), the distance \(q\) and its rate of change \(\dot{q}\).

Due to the nature of our phase space, we can assume that that \(q\in I:=(0,\pi)\). The left trivialisation of \(T\mathsf{SO}(3)=\mathsf{SO}(3)\times\mathfrak{so}(3)\) allows us to write the parametrisation

$$\begin{array}{l}\displaystyle TI\times T\mathsf{SO}(3)\to T\mathcal{Q}\\ \displaystyle(q,\dot{q},\theta,\phi,\psi,\boldsymbol{\omega}_{1},\boldsymbol{\omega}_{2},\boldsymbol{\omega}_{3})\mapsto(g\cdot\mathbf{x}_{1},g\cdot\mathbf{x}_{2},g\xi\cdot\mathbf{x}_{1},g\xi\cdot\mathbf{x}_{2}+g\mathbf{x}_{2}^{\prime}\dot{q}),\end{array}$$
(4.5)

where \(g\) is given in (4.2). This gives \(\xi\) the physical meaning of angular velocity in the body frame [11].

Since the problem is not determined by a Lagrangian, to transfer to a set of conjugate variables we use a slightly modified method from the usual one (compare with the Lagrangian approach in [2]).

Let \(T\) denote the kinetic energy of the system (as rewritten in our reduced coordinates): \(T=\frac{\mu_{1}}{2}(\boldsymbol{\omega}_{1}^{2}+\boldsymbol{\omega}_{2}^{2})+\frac{\mu_{2}}{2}\left((\boldsymbol{\omega}_{1}+\dot{q})^{2}+(\sin(q)\boldsymbol{\omega}_{3}+\cos(q)\boldsymbol{\omega}_{2})^{2}\right)\) and introduce \(m_{i}=\frac{\partial T}{\partial\boldsymbol{\omega}_{i}}\) in place of the \(\boldsymbol{\omega}_{i}\).

Moving from \(TI\) to \(T^{\ast}I\) can be accomplished by taking \(p:=\frac{\partial T}{\partial\dot{q}}\). The relations between the variables are as follows:

$$\left\{\begin{aligned} \displaystyle\boldsymbol{\omega}_{1}&\displaystyle=\frac{1}{\mu_{1}}(m_{1}-p),\\ \displaystyle\boldsymbol{\omega}_{2}&\displaystyle=\frac{1}{\mu_{1}}(m_{2}-m_{3}\cot(q)),\\ \displaystyle\boldsymbol{\omega}_{3}&\displaystyle=\frac{1}{\mu_{1}}(\cot(q)(m_{3}\cot(q)-m_{2}))+\frac{1}{\mu_{2}}(m_{3}\csc^{2}(q)),\\ \displaystyle\dot{q}&\displaystyle=\frac{1}{\mu_{1}\mu_{2}}\left(p(\mu_{1}+\mu_{2})-\mu_{2}m_{1}\right).\end{aligned}\right.$$
(4.6)

The momentum map \(\Phi\) is, in the new set of variables,

$$\Phi(g,m_{1},m_{2},m_{3},q,p)\ =\ g\cdot\begin{pmatrix}m_{1}\\ m_{2}-Be_{2}\sin(q)\\ m_{3}+Be_{1}+Be_{2}\cos(q)\end{pmatrix}.$$
(4.7)

Since the symplectic form is not standard, we need to rewrite it according to the general rule: if the change of coordinates is given by a Jacobian matrix \(J\), the new symplectic structure will be \(\tilde{\omega}=(J)^{T}\omega J\). Keeping our choice of signs in line with [10], we write the Poisson structure as \(\tilde{\sigma}=-\left((J)^{T}\omega J\right)^{-1}\), and the Hamiltonian equations are consequently given by \(\tilde{\sigma}\cdot\mathrm{grad}\ \mathcal{H}\), with \(\mathrm{grad}\ \mathcal{H}\) rewritten in the new set of variables.

After performing the calculations, it can be observed that the last five equations form an independent subsystem:

$$\left\{\begin{aligned} \displaystyle\dot{m}_{1}&\displaystyle=-\frac{1}{\mu_{1}\mu_{2}}\left(\mu_{2}(m_{2}-m_{3}\cot q)(Be_{1}+m_{2}\cot q+m_{3})+Be_{2}\mu_{1}m_{3}\csc q-\mu_{1}m_{2}m_{3}\csc^{2}q\right),\\ \displaystyle\dot{m}_{2}&\displaystyle=\frac{1}{\mu_{1}\mu_{2}}\left(\mu_{2}(m_{1}-p)(Be_{1}+m_{3})+Be_{2}\mu_{1}p\cos(q)\right.\\ &\displaystyle\left.\quad+\mu_{2}m_{1}\cot q(m_{2}-m_{3}\cot q)-\mu_{1}m_{1}m_{3}\csc^{2}q\right),\\ \displaystyle\dot{m}_{3}&\displaystyle=\frac{1}{\mu_{1}\mu_{2}}\left(\mu_{1}(Be_{2}p\sin q)+\mu_{2}(m_{2}p-m_{1}m_{3}\cot q)\right),\\ \displaystyle\dot{q}&\displaystyle=\frac{1}{\mu_{1}\mu_{2}}\left(p(\mu_{1}+\mu_{2})-\mu_{2}m_{1}\right),\\ \displaystyle\dot{p}&\displaystyle=-\frac{1}{\mu_{1}\mu_{2}}\left(m_{3}\csc q(Be_{2}\mu_{1}+\csc q(\mu_{2}m_{2}-m_{3}(\mu_{1}+\mu_{2})\cot q))+\mu_{1}\mu_{2}V^{\prime}(q)\right).\end{aligned}\right.$$
(4.8)

The quintuple of coordinates \((m_{1},\ m_{2},\ m_{3},\ q,\ p)\) describes the system reduced with respect to the \(\mathsf{SO}(3)\)-action. From here on, we restrict our attention to these reduced equations.

The Hamiltonian is rotationally invariant, so its reduced form is obtained just by substitution of the new set of variables:

$$\displaystyle\mathcal{H}=\frac{1}{2\mu_{1}\mu_{2}}\biggl{(}\mu_{2}\left((m_{1}-p)^{2}+m_{2}^{2}\right)+m_{3}\left(-2\mu_{2}m_{2}\cot(q)+\mu_{1}m_{3}\csc^{2}q+\mu_{2}m_{3}\cot^{2}q\right)\biggr{)}$$
$$\displaystyle\quad{}+\frac{p^{2}}{2\mu_{2}}+V(q).$$

The non-zero Poisson brackets in the reduced variables are given by

$$\displaystyle\{m_{1},m_{2}\}=-m_{3}-B(e_{1}+e_{2}\cos(q)),\{m_{2},m_{3}\}=-m_{1},$$
$$\displaystyle\{m_{1},m_{3}\}=m_{2}-Be_{2}\sin(q),\{m_{2},p\}=Be_{2}\cos(q),$$
$$\displaystyle\{m_{3},p\}=Be_{2}\sin(q),\{q,p\}=1.$$
(4.10)

It can easily be seen that the Poisson structure (4) is generically of rank 4, and has a Casimir function given by the square of the momentum map:

$$\mathcal{C}=m_{1}^{2}+(m_{2}-Be_{2}\sin q)^{2}+(m_{3}+B(e_{1}+e_{2}\cos q))^{2}.$$
(4.11)

Remark 4.1

The limiting case of \(B=0\) takes these expressions to the reduced equations of motion for the two-body problem on a sphere from [2, 7] \((\)for details, see the Appendix\()\).

Remark 4.2

Note that the simultaneous change in the signs of \(B,m_{1},m_{2},m_{3},p\) is a time-reversing symmetry, for it takes the Poisson structure to its opposite while leaving \(\mathcal{H}\) invariant.

4.1 Relative Equilibria

Our primary goal is to describe and locate relative equilibria of the system. The condition for this is that the right-hand side of the system (4.8) equals 0.

Solving (4.8) gives \(p=m_{1}=0\) from the second and fourth equations. Assuming otherwise leads to a linear relation between \(m_{2}\) and \(m_{3}\), which ultimately yields \(V^{\prime}(q)=0\), contradicting our initial assumptions about the potential.

Substituting zero values of \(m_{1}\) and \(p\) into the equations, we obtain a system for \(m_{2}\) and \(m_{3}\), consisting of the first and the fifth equation from (4.8).

Solving the first equation for \(m_{2}\) yields

$$m_{2}=\frac{1}{2\mu_{2}}\tan(q)\left(m_{3}(\mu_{1}\csc^{2}q+\mu_{2}\cot^{2}q-\mu_{2})-Be_{1}\mu_{2}\pm\sqrt{A}\right),$$
(4.12)

where

$$\begin{array}{r}\displaystyle A\ =\ 4\mu_{2}m_{3}\displaystyle\cot(q)\csc(q)(\mu_{2}\cos(q)(Be_{1}+m_{3})-Be_{2}\mu_{1})\\ +\Bigl{(}-\mu_{2}(Be_{1}+m_{3})+\mu_{1}m_{3}\csc^{2}q+\mu_{2}m_{3}\cot^{2}q\Bigr{)}^{2}.\end{array}$$
(4.13)

Firstly, we note that the expression for \(m_{2}\) is indeterminate when \(q=\frac{\pi}{2}\), separating this into a special case.

Secondly, due to a square root being present in the expressions, the right-hand side of (4.13) is only defined for some values of \(m_{3}\). The inequality

$$\displaystyle A\geqslant 0$$
(4.14)

describes the permitted values of the variable.

A little rearrangement of the polynomial (4.13) shows that the coefficient of \(m_{3}^{2}\) is

$$\csc^{4}(q)\left(\mu_{1}^{2}+\mu_{2}^{2}+2\mu_{1}\mu_{2}\cos(2q)\right).$$

Note that, since this expression is always positive, all the “bad” values of \(m_{3}\) in (4.14) always lie between the two solutions of the equation \(A=0\).

Substituting (4.12) into the fifth equation of (4.8), we obtain for \(m_{3}\):

$$m_{3}\csc(q)\sec(q)\left(Be_{1}\mu_{2}-2Be_{2}\mu_{1}\cos(q)-2\mu_{1}m_{3}+m_{3}(\mu_{1}+\mu_{2})\csc^{2}q\pm\sqrt{A}\right)-\ 2\mu_{1}\mu_{2}V^{\prime}(q)=0.$$
(4.15)

In order to prove the existence of roots for (4.15), we employ the following observation: the value of \(A\) at \(m_{3}=0\) is \(B^{2}e_{1}^{2}\mu_{2}^{2}\), whence \(A\) is always positive at \(m_{3}=0\). Thus, the interval in \(m_{3}\) where the function on the left-hand side of (4.15) is not defined lies entirely to the left or to the right of \(m_{3}=0\).

Consider the two equations in (4.15). With appropriate arrangements, they both square to a fourth-degree polynomial in \(m_{3}\):

$$\displaystyle-4\mu_{1}m_{3}^{4}\csc^{4}(q)+4Bm_{3}^{3}\csc^{4}(q)(\text{$e_{1}$}\mu_{2}-\text{$e_{2}$}\mu_{1}\cos(2q)\sec(q))$$
$$\displaystyle\quad+2m_{3}^{2}\csc^{3}(q)\sec(q)\left(2B^{2}e_{2}\sin(q)(\text{$e_{2}$}\mu_{1}\cos(q)-\text{$e_{1}$}\mu_{2})-2\mu_{2}V^{\prime}(q)(\mu_{2}+\mu_{1}\cos(2q))\right)$$
(4.16)
$$\displaystyle\qquad+4B\mu_{2}m_{3}\csc(q)V^{\prime}(q)(2e_{2}\mu_{1}-\text{$e_{1}$}\mu_{2}\sec(q))+4\mu_{1}\mu_{2}^{2}V^{\prime}(q)^{2}=0.$$

At this point we employ a classical theorem:

Theorem 4.3 (Descarte’s rule of signs, [5])

The number of positive roots of a polynomial with real coefficients is equal to or less by an even number than the number of changes of sign of the coefficients of the polynomial in question, when written in the order of descending degree of the variable.

By looking at (4.16), it can be easily observed that, since \(\mu_{1}>0,\mu_{2}>0\), the highest coefficient is always negative and the lowest one is positive. Since the degree of the polynomial is 4, Descarte’s rule of signs, as applied to the polynomial of \(m_{3}\) and then \(-m_{3}\), gives that the first equation in (4.16) must have at least one positive and one negative root. But then at least one of them does not lie in the interval between the roots of (4.13). Hence, for (4.15), at least one solution always exists.

Now we fill in the gap by taking \(q=\frac{\pi}{2}\) where we can give a more precise statement depending on the value of \(V^{\prime}(\pi/2)\). Taking \(m_{1}=0,\ p=0,\ q=\frac{\pi}{2}\) in the system (4.8) gives us only two nontrivial equations:

$$\displaystyle\mu_{2}m_{2}(Be_{1}+m_{3})+Be_{2}\mu_{1}m_{3}-\mu_{1}m_{2}m_{3}= 0,$$
$$\displaystyle m_{3}(Be_{2}\mu_{1}+\mu_{2}m_{2})+\mu_{1}\mu_{2}V^{\prime}\left(\frac{\pi}{2}\right)= 0.$$
(4.17)

By analytically solving (4.17), one can check that it has real solutions if and only if

$$B^{4}e_{1}^{2}e_{2}^{2}+2B^{2}e_{1}e_{2}(\mu_{1}+\mu_{2})V^{\prime}\left(\frac{\pi}{2}\right)+(\mu_{1}-\mu_{2})^{2}V^{\prime}\left(\frac{\pi}{2}\right)^{2}\geqslant 0,$$
(4.18)

with two solutions if the left-hand side of (4.18) is strictly greater than 0, one if it is equal to 0 and none when it is less than zero.

Remark 4.4

From the explicit form of the solutions of (4.17)\((\)we omit the computations here\()\), it can be easily seen that the limiting case \(B=0\) agrees with the results for the two-body problem on a sphere from [2] and [7]: no relative equilibria exist when \(q=\frac{\pi}{2}\) unless \(\mu_{1}=\mu_{2}\).

Thus, we have demonstrated

Theorem 4.5

  1. 1)

    For each \(q\in(0,\pi)\setminus\{\pi/2\}\) , and for all non-zero values of \(B,\ e_{1},\ e_{2},\ \mu_{1},\ \mu_{2}\) and any smooth function \(V(q)\) there exists at least one relative equilibrium;

  2. 2)

    for \(q=\pi/2\) , there are precisely 0, 1 or 2 relative equilibria according as the discriminant in (4.18) is negative, zero or positive.

5 IDENTICAL PARTICLES

The most natural case to investigate closely is the case of two identical particles, that is, the one with \(e_{1}=e_{2}=1,\ \mu_{1}=\mu_{2}=1\). Without loss of generality we may assume \(B>0\), as \(B<0\) can be reduced to this via the time-reversing symmetry described in Remark 4.2. In this section we describe both the existence and stability of the relative equilibria for identical particles (in Section 6 we consider the setting where the particles have the same mass but opposite charges).

Our choice of the potential is \(V(q)=\cot(q)\). This gives \(V^{\prime}(q)=-\csc^{2}(q)<0\) and so describes a repelling force in accordance with the physics.

The reduced equations of motion (4.8) then read:

$$\left\{\begin{aligned} \displaystyle\dot{m}_{1}&\displaystyle=-(m_{2}-m_{3}\cot(q))(B+m_{2}\cot(q)+m_{3})-m_{3}\csc(q)(B-m_{2}\csc(q)),\\ \displaystyle\dot{m}_{2}&\displaystyle=m_{1}(B+2m_{3})-p(2B\sin^{2}\left(\frac{q}{2}\right)+m_{3})+m_{1}m_{2}\cot(q)-2m_{1}m_{3}\csc^{2}q,\\ \displaystyle\dot{m}_{3}&\displaystyle=p(B\sin(q)+m_{2})-m_{1}m_{3}\cot(q),\\ \displaystyle\dot{q}&\displaystyle=2p-m_{1},\\ \displaystyle\dot{p}&\displaystyle=\csc(q)\left(\csc(q)\left(-m_{2}m_{3}+2m_{3}^{2}\cot(q)+1\right)-Bm_{3}\right).\end{aligned}\right.$$
(5.1)

5.1 Classification of Relative Equilibria

We proceed to find stationary points of the system (5.1), which correspond to relative equilibria of the original system. The conditions \(\dot{m}_{2}=\dot{m}_{3}=\dot{q}=0\) imply \(p=m_{1}=0\) (as pointed out above for the more general case). If we then solve \(\dot{m}_{1}=0\) for \(m_{2}\) and substitute the two solutions of this into \(\dot{p}=0\), we obtain two quadratic equations (since \(A\) from (4.13) becomes a square) for \(m_{3}\). The four solutions can be split into 2 pairs leading to the following solutions (the analytic expressions were found using Mathematica).

$$\displaystyle\mathrm{Type\ I}:\left\{\begin{aligned} \displaystyle m_{1}&\displaystyle=0,\\ \displaystyle p&\displaystyle=0,\\ \displaystyle m_{2}^{\pm}&\displaystyle=\frac{2B\sin^{3}\left(\frac{q}{2}\right)\sin(q)\pm\cos^{\frac{3}{2}}\left(\frac{q}{2}\right)\cos(q)\sqrt{4\csc\left(\frac{q}{2}\right)+B^{2}\sec\left(\frac{q}{2}\right)\sin^{2}(q)\tan^{2}(q)}}{\sin\left(\frac{q}{2}\right)-\sin\left(\frac{3q}{2}\right)},\\ \displaystyle m_{3}^{\pm}&\displaystyle=\frac{1}{2}\left(B\sin(q)\tan(q)\mp\sqrt{\cos\left(\frac{q}{2}\right)}\sqrt{4\csc\left(\frac{q}{2}\right)+B^{2}\sec\left(\frac{q}{2}\right)\sin^{2}(q)\tan^{2}(q)}\right);\end{aligned}\right.$$
(5.2)
$$\displaystyle\mathrm{Type\ II}:\left\{\begin{aligned} \displaystyle m_{1}&\displaystyle=0,\\ \displaystyle p&\displaystyle=0,\\ \displaystyle m_{2}^{\pm}&\displaystyle=-2\sin^{4}\left(\frac{q}{2}\right)\csc(q)\left(B\pm\sqrt{B^{2}-2\csc^{2}\left(\frac{q}{2}\right)\csc(q)}\right),\\ \displaystyle m_{3}^{\pm}&\displaystyle=\sin^{2}\left(\frac{q}{2}\right)\left(B\pm\sqrt{B^{2}-2\csc^{2}\left(\frac{q}{2}\right)\csc(q)}\right).\end{aligned}\right.$$
(5.3)

It is convenient to express the existence and stability of all the solutions in (5.2) and (5.3) through the two “parameters”, \(B\) and \(q\).

Observe that, except for \(q=\pi/2\), the two solutions in (5.2) exist for all values of \(B\) and \(q\) — we refer to these as relative equilibria of Type I. It turns out (see Lemma 5.3 below) that the two Type I solutions are related by exchanging the (identical) particles.

For solutions (5.3) to exist, the expression under the square root needs to be positive. It is clear that for each value of \(q\in(0,\pi)\) when \(B\) is sufficiently large, there is a solution. We call these relative equilibria of Type II. More precisely, relative equilibria of Type II exist when \(B^{2}\geqslant 2\csc^{2}(q/2)\csc(q)\). Since we are assuming that \(B>0\), the threshold value of \(B\) is

$$B=2\sqrt{\frac{\csc(q)}{1-\cos(q)}}.$$
(5.4)

We will refer to the graph of (5.4), shown in Fig. 2, as “the threshold curve”.

The minimal value that the function above assumes is \(B=\frac{4}{3}3^{1/4}\) (which is approximately \(1.755\)) at \(q=\frac{2\pi}{3}\). The value of (5.4) at \(q=\frac{\pi}{2}\) is 2 (this fact will come useful later).

Note that for the values of \((q,B)\) on the threshold curve the two solutions from (5.3) coincide.

Fig. 2
figure 2

The threshold curve: only Type I solutions exist below the curve.

Full size image

We summarise the above discussion in the following existence theorem.

Theorem 5.1

For the system described above, with two identical particles, we have the following relative equilibria for values of \(B>0\) :

  1. 1)

    for every \(q\in(0,\pi)\setminus\left\{\frac{\pi}{2}\right\}\) there is a unique relative equilibrium of Type I, up to particle exchange, and none exists for \(q=\frac{\pi}{2}\) ;

  2. 2)
    1. (a)

      For \(0<B<\frac{4}{3}3^{1/4}\) there are no relative equilibria of Type II.

    2. (b)

      Let \(B=\frac{4}{3}3^{1/4}\) . Then for \(q=\frac{2\pi}{3}\) there is one relative equilibrium of Type II, while for \(q\neq 2\pi/3\) there are none.

    3. (c)

      Let \(B>\frac{4}{3}3^{1/4}\) . Then for \(q\in(q_{0},q_{1})\) there are two distinct relative equilibria of Type II, for \(q\in\{q_{0},q_{1}\}\) there is just one, while for \(q\not\in[q_{0},q_{1}]\) there are none, where \(q_{0},q_{1}\) denote the two solutions of \(2\sqrt{\frac{\csc(q)}{1-\cos(q)}}=B\) \((q_{0}\leqslant q_{1})\) .

Remark 5.2

For an arbitrary choice of the potential \(V(q)\) with \(V^{\prime}(q)\neq 0\) there are four solutions as well, with one pair existing for all values of \(B\) and \(q\) , and the second pair for the values above some threshold curve.

Before proceeding further with the analysis, we determine the effect of swapping the particles on the reduced space.

Lemma 5.3

The \(\mathbb{Z}_{2}\) -action of swapping the two identical particles is a symmetry of the system and induces a coordinate change on the reduced phase space which leaves \(q\) invariant and multiplies \((m_{1},m_{2},m_{3},p)^{T}\) by the matrix

$$\begin{pmatrix}-1&0&0&0\\ 0&-\cos(q)&-\sin(q)&0\\ 0&-\sin(q)&\cos(q)&0\\ -1&0&0&1\\ \end{pmatrix}.$$
(5.5)

Proof

Without loss of generality we can assume that the initial placement of our particles, and the one at which the exchange happens, is at the two points \(\mathbf{x}_{1}\) and \(\mathbf{x}_{2}\) from (4.4).

The matrix exchanging the said points is given by

$$\mathsf{SO}(3)\ni A_{0}:=\begin{pmatrix}-1&0&0\\ 0&-\cos(q)&-\sin(q)\\ 0&-\sin(q)&\cos(q)\end{pmatrix}.$$

With this in mind, the swapping can be written as \(g\mathbf{x}_{1}\mapsto gA_{0}\mathbf{x}_{1}\), with a similar relation for the second particle. Therefore, under this \(\mathbb{Z}_{2}\)-action we have for \(\dot{g}\) and \(\xi\)

$$\begin{array}{l}\displaystyle g\mapsto gA_{0},\\ \displaystyle\dot{g}\mapsto\dot{g}A_{0}+g\dot{A}_{0}=g\xi A_{0}+gA_{0}\xi_{0}=gA_{0}(A_{0}^{-1}\xi A_{0}+\xi_{0}),\end{array}$$

where \(\xi_{0}\) is the tangent element of the Lie algebra \(\mathfrak{so}(3)\) to the one-parameter subgroup \(A_{0}\) with varying \(q\).

Hence,

$$\xi\mapsto A_{0}^{-1}\xi A_{0}+\xi_{0}$$

or, explicitly,

$$\begin{pmatrix}0&-\boldsymbol{\omega}_{3}&\boldsymbol{\omega}_{2}\\ \boldsymbol{\omega}_{3}&0&-\boldsymbol{\omega}_{1}\\ -\boldsymbol{\omega}_{2}&\boldsymbol{\omega}_{1}&0\end{pmatrix}\mapsto\begin{pmatrix}0&\text{$\boldsymbol{\omega}_{2}$}\sin(q)-\text{$\boldsymbol{\omega}_{3}$}\cos(q)&-\text{$\boldsymbol{\omega}_{2}$}\cos(q)-\text{$\boldsymbol{\omega}_{3}$}\sin(q)\\ \text{$\boldsymbol{\omega}_{3}$}\cos(q)-\text{$\boldsymbol{\omega}_{2}$}\sin(q)&0&\dot{q}+\text{$\boldsymbol{\omega}_{1}$}\\ \text{$\boldsymbol{\omega}_{2}$}\cos(q)+\text{$\boldsymbol{\omega}_{3}$}\sin(q)&-\dot{q}-\text{$\boldsymbol{\omega}_{1}$}&0\\ \end{pmatrix}$$

The Jacobian matrix \(\mathcal{J}_{1}\) of this change in the variables \((\boldsymbol{\omega}_{1},\boldsymbol{\omega}_{2},\boldsymbol{\omega}_{3},\dot{q})\) is then

$$\begin{pmatrix}-1&0&0&-1\\ 0&-\cos q&-\sin q&0\\ 0&-\sin q&\cos q&0\\ 0&0&0&1\\ \end{pmatrix},$$

while the Jacobian \(\mathcal{J}_{2}\) of the transfer from \((\boldsymbol{\omega}_{1},\boldsymbol{\omega}_{2},\boldsymbol{\omega}_{3},\dot{q})\) to \((m_{1},m_{2},m_{3},p)\) in the case of identical particles is given by

$$\begin{pmatrix}1&0&0&-1\\ 0&1&-\cot(q)&0\\ 0&-\cot(q)&\cot^{2}q+\csc^{2}q&0\\ -1&0&0&2\\ \end{pmatrix}.$$

Finally, the final transformation matrix for the reduced conjugate coordinates is \(\mathcal{J}_{2}^{-1}\mathcal{J}_{1}\mathcal{J}_{2}\) and is explicitly given by (5.5), which is straightforwardly an involutory matrix.     \(\square\)

We apply Lemma 5.3 to the Type I relative equilibria and multiply the vector \((0,m_{2}^{+},m_{3}^{+},0)\) by (5.5), which maps it to \((0,m_{2}^{-},m_{3}^{-},0)\), and vice versa. Thus, the two solutions are the same up to changing the labelling of the particles, as claimed above.

5.2 Variation of Configurations for Type I Relative Equilibria

Here we briefly comment on how the relative equilibria of the non-magnetic 2-body problem on the sphere with a repelling potential [7] deform into the relative equilibria of Type I in the current problem, as mentioned in Remark 4.4.

Let \(\theta_{1}\) be the angle between the directed axis of rotation and the first particle and let \(\theta_{2}\) be the angle between that axis and the second particle. For given \(q\) we have \(\theta_{2}=\theta_{1}+q\).

With \(B=0\) there are two families of relative equilibria, the isosceles ones with \(\theta_{1}+\theta_{2}=\pi\) and the right-angled ones with \(\theta_{2}-\theta_{1}=q=\pi/2\) ([7], Theorem 2.1). These are the two lines shown in Fig. 3a.

Now with \(B>0\), for every \(q\ \neq\frac{\pi}{2}\) there will be a single relative equilibrium of Type I (as mentioned previously, up to a particle exchange). Therefore, \(\theta_{1}=\theta_{1}(q)\) and \(\theta_{2}=\theta_{1}(q)+q\). This relation is plotted on the \((\theta_{1},\theta_{2})\)-plane in Figs. 3b, 3c.

For negative values of \(B\), the two branches of the curve will lie in the remaining upper and lower quadrants formed by the lines in Fig. 3a.

Fig. 3
figure 3

Relative equilibria of Type I, plotted on the \((\theta_{1},\theta_{2})\)-plane for various values of \(B\). The plot of relative equilibria for \(B=0\) is provided in blue on the second and third picture for comparison.

Full size image

5.3 Reconstruction of Motion

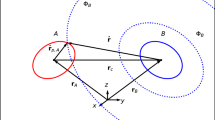
Explicit formulae for relative equilibria in reduced coordinates allow us to reconstruct the motion of the particles (see Fig. 1 for identical particles and Fig. 10 for the case with opposite charges). By the nature of relative equilibria, the said motion will be a rigid body type rotation of the particles around some fixed axis.

\(\boldsymbol{\omega}_{1}\),  \(\boldsymbol{\omega}_{2}\),  \(\boldsymbol{\omega}_{3}\) from (4.5) are the components of the body frame angular velocity vector of our system, which is parallel to the axis of rotation. Substituting the expressions for relative equilibria into (4.6), assuming that one particle is at the point \((0,0,-1)\) and the other at \((0,\sin(q),-\cos(q))\) (namely, the body frame) gives us the desired picture.

We explain the calculations in detail for relative equilibria of Type II: they can be repeated verbatim for Type I. Let us denote the angular velocity for \((m_{2}^{\pm},m_{3}^{\pm})\) by \((\boldsymbol{\omega}_{1}^{\pm},\boldsymbol{\omega}_{2}^{\pm},\boldsymbol{\omega}_{3}^{\pm})\). It is straightforward that \(\boldsymbol{\omega}_{1}^{\pm}=0\). The other two coordinates are given by

$$\begin{cases}\boldsymbol{\omega}_{2}^{+}\!=\!-\frac{1}{2}\tan\left(\frac{q}{2}\right)\!\left(B{+}\sqrt{B^{2}{-}2\csc^{2}\left(\frac{q}{2}\right)\csc(q)}\right),\\ \boldsymbol{\omega}_{3}^{+}\!=\!\frac{1}{2}\left(B+\sqrt{B^{2}-2\csc^{2}\left(\frac{q}{2}\right)\csc(q)}\right);\end{cases}\!\!\!\begin{cases}\boldsymbol{\omega}_{2}^{-}\!=\!-\frac{1}{2}\tan\left(\frac{q}{2}\right)\!\left(B{-}\sqrt{B^{2}{-}2\csc^{2}\left(\frac{q}{2}\right)\csc(q)}\right),\\ \boldsymbol{\omega}_{3}^{-}\!=\!\frac{1}{2}\left(B-\sqrt{B^{2}-2\csc^{2}\left(\frac{q}{2}\right)\csc(q)}\right).\end{cases}$$

It is easy to check that the two vectors \((\boldsymbol{\omega}_{2}^{+},\boldsymbol{\omega}_{3}^{+})\) and \((\boldsymbol{\omega}_{2}^{-},\boldsymbol{\omega}_{3}^{-})\) are parallel. One can easily deduce that the cosines of the angles between the axis of rotation and the two vectors \((0,-1)\) and \((\sin(q),-\cos(q))\) are equal (both of them are \(\cos(q/2)\)). Hence, we can conclude that relative equilibria of Type II are isosceles configurations. (This also follows from the fact that the reduced equilibria are fixed by the particle exchange symmetry.)

Identical manipulations with the formulae for the relative equilibrium of Type I give that the difference between \(\cos(\theta_{1})\) and \(\cos(\pi-\theta_{2})\) (the minimal angle between the axis of rotation and the coordinate vector of the second body) will be equal to \({B(\sec(q)+1)}/({\sqrt{B^{2}\sec^{2}(q)+2\csc^{3}(q))}}\), a function that is zero if and only if \(B=0\). Therefore, the two minimal angles between coordinate vectors and the axis of rotation are not equal unless the magnetic field is absent.

5.4 Energy-Casimir Map

Having the solutions of (5.1) of Types I and II, we want to approach the problem from a more physical angle: that of the energy-Casimir (or energy-momentum) map.

The first natural question to ask is that of the form of its image: namely, what does the set of values of \((\mathcal{C},\mathcal{H})\) look like? Since \(\mathcal{C}\geqslant 0\), it lies entirely in the right half-plane, including the boundary \(\mathcal{C}=0\).

To determine which values \(\mathcal{H}\) can assume with a fixed \(\mathcal{C}=C_{0}\), we assign specific values to our variables: \(m_{1}=\sqrt{C_{0}},\ m_{2}=B\sin(q),\ m_{3}=-B(1+\cos(q)),\ p=0\). At all of these points \(\mathcal{C}\) is indeed equal to \(C_{0}\), and \(\mathcal{H}\) is a function of \(q\), reduced to

$$\mathcal{H}(q)=\frac{1}{2}C_{0}+\cot(q)+B^{2}\cot^{2}\left(\frac{q}{2}\right).$$
(5.6)

This is a simple monotonic decreasing function of \(q\), with limits \(+\infty\) when \(q\to 0\) and \(-\infty\) when \(q\to\pi\). Therefore, the image of the energy-momentum map is the entire right half-plane in \((\mathcal{C},\mathcal{H})\).

Zero level set of the Casimir Because of the magnetic term in the momentum map or Casimir, it could be particularly interesting to ask about the zero level set. However, it turns out not to be so interesting!

The zero level set of the Casimir is given by \(m_{1}=0,\ m_{2}=B\sin(q),m_{3}=-B(1+\cos(q))\). After substituting these values (along with \(p=0)\) into the system (5.1), we obtain one equation in \(q\) for equilibrium points:

$$\csc(q)+2B^{2}\cot^{2}\left(\frac{q}{2}\right)=0,$$

which clearly has no solutions when \(q\in\left(0,\pi\right)\). Therefore, as Fig. 4 suggests, there are no equilibria on the zero level set of the Casimir.

The reduced system is described in terms of \(p\) and \(q\) only, and thus is integrable with just the Hamiltonian, which has the form

$$\mathcal{H}(q,p)=\frac{3}{2}p^{2}+B^{2}\cot^{2}\left(\frac{q}{2}\right)+\cot(q).$$
(5.7)

The level sets of this function are non-compact, and consequently all motion is unbounded.

5.4.1 Energy-Casimir bifurcation diagram

Figure 4 illustrates the set of singular values of the energy-Casimir map for a fixed value of \(B\), which form the “bifurcation diagram” (see also Fig. 8). It shows a relatively large-scale view and a close-up of a neighbourhood of the origin. Singular points of the energy-Casimir map are relative equilibria, so the curves shown are the energy-Casimir values on the set of relative equilibria.

Of the different curves shown, the uppermost one consists of obtuse Type I relative equilibria. Along this curve, as \(\mathcal{C}\to 0\) we have \(q\to\pi\) and \(\mathcal{H}\to-\infty\) (we have seen above that there are no equilibria for \(\mathcal{C}=0\)), and as \(\mathcal{C}\to\infty\) we have \(q\to\frac{\pi}{2}^{+}\) and \(\mathcal{H}\to\infty\).

The intermediate curve, with a cusp, represents acute Type I relative equilibria. As \(q\to 0,\ \mathcal{H}\to+\infty\), making up the lower branch of this curve; as \(q\to\frac{\pi}{2}^{-},\ \mathcal{H}\to+\infty\), forming its upper branch.

The lowest curve shows the image of the Type II relative equilibria. What is not shown at this scale is that the two branches of the Type II relative equilibria meet again in a second cusp point. If this diagram is shown at a scale which shows the entirety of the Type II relative equilibria, the two branches would be indistinguishable; for this reason we illustrate it with a schematic diagram in Fig. 8b. The blue and red parts of this curve correspond to \((m_{2}^{-},m_{3}^{-})\) and \((m_{2}^{+},m_{3}^{+})\) from (5.3), respectively.

Fig. 4
figure 4

Energy-momentum bifurcation diagram with \(B=2.5\); the red and blue curve corresponds to Type II relative equilibria, the others to Type I. See also Fig. 8.

Full size image

From the point of view of the reduced systems, with the Casimir \(\mathcal{C}\) as the natural parameter, the behaviour is as follows. For small values of \(\mathcal{C}\), the reduced space has just one (relative) equilibrium: an obtuse Type I configuration (which persists for all values of \(\mathcal{C}\)); as \(\mathcal{C}\) increases (assuming \(B>\frac{4}{3}3^{1/4}\)), two Type II relative equilibria appear from a saddle-node bifurcation and then, as \(\mathcal{C}\) increases further, there appears a pair of acute Type I relative equilibria, also in a saddle-node bifurcation. For a still larger value of \(\mathcal{C}\) the two Type II relative equilibria merge in yet another saddle-node bifurcation, and no longer exist for large values of \(\mathcal{C}\). The precise values of \(\mathcal{C}\) (and \(q\)) at which these three saddle-node bifurcations appear depend on the strength of the magnetic field.

We return to these bifurcation curves when looking at stability below.

5.5 Stability of Type I Relative Equilibria

A lengthy calculation shows that the characteristic polynomial of the linearised matrix of the system (5.1) is of the form \(x(-x^{4}+ax^{2}+b)\) (as it would be for every four-dimensional Hamiltonian system: the factor of \(x\) is due to the Casimir). Note that the coefficients \(a\) and \(b\) here are functions of \(B\) and \(q\).

Substituting \(y=x^{2}\), we obtain a quadratic equation: \(-y^{2}+ay+b=0\). Thus, for linear stability, both solutions of this equation must be negative. That is, three conditions need to be fulfilled:

  • the top of the parabola must be to the left of \(y=0\) (i. e., \(a<0\)),

  • the value of \(-y^{2}+ay+b\) at the top must be greater than 0 (i. e., \(a^{2}+4b>0)\),

  • the value of \(-y^{2}+ay+b\) at \(y=0\) must be less than 0 (i. e., \(b<0\)).

In this case, the conditions for stability can be written analytically.

Since the two relative equilibria of Type I are related by particle exchange (and the particles are identical) we only need perform calculations for one of the explicit solutions. By doing so, we obtain Fig. 5.

Fig. 5
figure 5

Stability for the relative equilibria of Type I: the coloured region is where the relative equilibria are linearly stable.

Full size image

Relative equilibria are linearly stable in the region coloured lilac and linearly unstable in the white-coloured one. The thick red line is where \(q=\frac{\pi}{2}\) for which there is no relative equilibrium.

In Fig. 5, the transition curve is obtained from the third condition for stability above (\(b=0\)) and is explicitly given by the expression \(B=\sqrt{\frac{\cos^{3}(q)(2+\cos(q))}{2\sin^{3}\left(q\right)\sin^{2}\left(\frac{q}{2}\right)}}\). Note that the graph meets the horizontal axis \(B=0\) at \(q=\frac{\pi}{2}\).

We have demonstrated

Proposition 5.4

For the system with identical particles, the linear stability of the relative equilibria of Type I \((\) solutions of (5.2) \()\) is as follows:

  • when \((q,B)\) is to the left of the graph \(B=\sqrt{\frac{\cos^{3}(q)(2+\cos(q))}{2\sin^{3}\left(q\right)\sin^{2}\left(\frac{q}{2}\right)}}\) , the relative equilibrium is linearly unstable;

  • when \((q,B)\) is to the right of the graph \(B=\sqrt{\frac{\cos^{3}(q)(2+\cos(q))}{2\sin^{3}\left(q\right)\sin^{2}\left(\frac{q}{2}\right)}},q\neq\frac{\pi}{2}\) , the relative equilibrium is linearly stable.

See Fig. 5 .

Remark 5.5

Almost all of the linearly stable Type I relative equilibria will probably be nonlinearly \((\)Lyapunov\()\) stable, by KAM theory; however, there are non-degeneracy conditions to check in the higher-order terms of the Hamiltonian near each relative equilibrium. For the non-magnetic \(2\)-body problem these conditions are checked numerically for many of the relative equilibria [2, Section 4.2.2]. We do not pursue this here.

5.6 Stability of Type II Relative Equilibria

Here, we employ the same method as the one from the previous section. However, it has not been possible to obtain analytic results for general values of \(q\) and \(B\) for these relative equilibria.

5.6.1 Points on the threshold curve

First, we investigate the stability on the line \(B=2\sqrt{\frac{\csc(q)}{1-\cos(q)}}\), where one can obtain analytic results. Here, as previously mentioned, the two relative equilibria of Type II, namely, \((m_{2}^{\pm},m_{3}^{\pm})\), coincide, and we are looking to determine whether the resulting one is stable.

We employ the standard method for establishing linear stability: linearising the system and taking \(B=2\sqrt{\frac{\csc(q_{0})}{1-\cos(q_{0})}}\) for some fixed \(q_{0}\).

Computing the characteristic polynomial of the matrix of the linearised system at any relative equilibrium on the threshold curve gives us

$$x\left(x^{2}+2\csc^{3}(q_{0})\right)\left(x^{2}+2(1+2\cos(q_{0}))\csc^{3}(q_{0})\right)=0$$

with the solutions

$$\displaystyle x=0,\ x=\pm\mathrm{\mathbf{i}}\sqrt{2}\csc^{\frac{3}{2}}(q_{0}),\ x=\pm\sqrt{-2(2\cot(q_{0})\csc^{2}(q_{0})+\csc^{3}(q_{0}))}.$$

The zero is due to the Casimir being conserved, so the other four roots determine the linear stability of the equilibrium on the reduced space; in particular, the sign of the expression under the root determines its linear stability.

It is greater than zero (rendering the equilibrium linearly unstable) when \(\frac{2\pi}{3}<q_{0}<\pi\) and less than 0 with a linearly stable equilibrium when \(0<q_{0}<\frac{2\pi}{3}\).

We have demonstrated

Proposition 5.6

For the values of \((q,B)\) on the threshold curve, the Type II equilibrium is

  • linearly stable if \((q,B)\) is to the left of \(\left(\frac{2\pi}{3},\frac{4}{3}3^{1/4}\right)\) ,

  • linearly unstable if \((q,B)\) is to the right of \(\left(\frac{2\pi}{3},\frac{4}{3}3^{1/4}\right)\) .

5.6.2 Stability of general relative equilibria of Type II

Now we position ourselves in the region strictly above the threshold curve. Again, we linearise the system at the equilibrium point and look at the zeros of the characteristic polynomial. However, due to the complexity of the equations we have to employ numerical methods.

We have performed the numerics for values of \(B\) less than 100, and found that up to this value the properties are always as shown in Fig. 6.

Fig. 6
figure 6

Stability of relative equilibria of Type II in terms of \(B\) and \(q\): in the dark purple regions, the corresponding relative equilibrium is linearly stable, while the blue colour denotes linear instability.

Full size image

As calculations demonstrate, the curves that separate the regions of stability from those of instability consist of degenerate relative equilibria; these are, in fact, the only degenerate relative equilibria of Type II. As will be discussed later, for a fixed value of \(B\) the Casimir function assumes its minima and maxima on the relative equilibria lying on the curves where stability changes.

In Fig. 7, the points A and B on the curve are the points where the Casimir is minimal and maximal, respectively, on the family of relative equilibria for that fixed value of the magnetic field strength \(B\). Stable relative equilibria lie to the left of these points and unstable ones to the right. These two points represent saddle-node bifurcations of the relative equilibria of Type II as the value of the Casimir is varied.

For both \((m_{2}^{+},m_{3}^{+})\) and \((m_{2}^{-},m_{3}^{-})\) the curves dividing the stability region from that of instability separate from the threshold curve at the point \((q,B)=\left(\frac{2\pi}{3},\frac{4}{3}3^{1/4}\right)\).

Fig. 7
figure 7

The values of \(\mathcal{C}\) for relative equilibria of Type II with a fixed \(B=1.9\). The blue (lower) part of the curve is given by \((m_{2}^{-},m_{3}^{-})\), the red (upper) one by \((m_{2}^{+},m_{3}^{+})\).

Full size image

5.6.3 Energy-Casimir map revisited

Fig. 8
figure 8

Energy-Casimir bifurcation diagrams with cusp points and signatures of the Hessian.

Full size image

With the newly acquired information about the stability, we cast another look at the energy-Casimir map. Figures 8a and 8b shows the set of singular values of this map, which are the images of the set of relative equilibria. The figure in (b) is schematic, as the two branches are very close in reality. The cusps on the curves, emphasised by dots, are the configurations at which the transition between stability and instability occurs. They represent saddle-node bifurcations when using the Casimir as a parameter. The cusps in (b) correspond to the points marked A and B in Fig. 7.

The topmost curve in Fig. 8a corresponds to the values of \(q>\pi/2\), the lower half of the bottom curve to the values of \(q\) less than the root (as solved for \(q\)) of \(B=\sqrt{\frac{\cos^{3}(q)(2+\cos(q))}{2\sin^{3}\left(q\right)\sin^{2}\left(\frac{q}{2}\right)}}\) for a fixed \(B\), and the upper half to the rest of the interval between the said root and \(\pi/2\). (The figure is very similar to ([2], Fig. 9), of which it is a continuation.)

We have simplified the form of the bifurcation diagram in Fig. 8b, but the essential features remain: the two solutions, one of which is linearly stable and the other linearly unstable, merge together at the two cusps in saddle-node bifurcations.

Figure 8 has the signatures of the Hessian of \(\mathcal{H}\), as restricted to the level sets of \(\mathcal{C}\) next to each part of the bifurcation diagram. Since the eigenvalues of the Hessian depend smoothly on \(B\) and \(q\) and the only points where the Hessian matrix has a zero eigenvalue are the cusp points (the only points where the matrix of the linearised system has a zero eigenvalue), it is sufficient to calculate the signature of the Hessian on each part of the diagram for a single value of \(B\) and \(q\). By continuity, the signatures will remain the same throughout the changes in \(B\) and \(q\).

It follows that the linearly stable (relative) equilibria in Proposition 5.6 are in fact nonlinearly stable.

Remark 5.7

It is curious that, for the Type I relative equilibria, the unstable configurations occur when the particles are closer together, but for the Type II relative equilibria, the unstable ones occur when they are further apart. However, in both cases, the unstable ones occur when the particles are further from the axis of rotation \((\) see Fig. 1 \()\) .

5.7 The Bifurcation Diagram

So far, we have described the existence of relative equilibria in terms of \(B\) and \(q\). This is a reasonable approach for presenting the results, but carries no physical meaning in terms of bifurcations of dynamical systems. Indeed, for each fixed value of \(B\), there is a 1-parameter family of reduced systems parametrised naturally by the Casimir. We therefore have two parameters: the Casimir (an “internal” parameter) and the magnetic field strength (an “external” parameter).

For relative equilibria of Type I, parametrised by \(B\) and \(q\), the explicit expression for the Casimir is

$$\frac{\cos(q/2)}{\sin^{3}(q/2)}\left(1+B^{2}\sin(q)\tan^{2}(q)\right),$$

which for all values of \(B\) tends to \(+\infty\) if \(q\to 0\) and to \(0\) if \(q\to\pi\), spanning all the values in between. Therefore, the region spanned by all possible Casimir values as \(B\) varies is the entirety of the first quadrant in the \((B,\mathcal{C})\)-plane.

The situation is more complicated when we pose the same problem for relative equilibria of Type II: once again, we have to resort to numerics due to the complexity of the computations. The image of the set of relative equilibria for \((m_{2}^{-},m_{3}^{-})\) is depicted in Fig. 9a. The darker blue region in the diagram denotes the locus of the points in the \((B,\mathcal{C})\) plane that are images of two relative equilibria.

Fig. 9
figure 9

Possible values of the Casimir for the two classes of relative equilibria of Type II, as a function of \(B\).

Full size image

For \((m_{2}^{+},m_{3}^{+})\) (Type II) the possible values of the Casimir lie inside the set depicted in Fig. 9b.

As can be noted, the region in the second diagram fits in the lighter area of the first one, which is clear since every point strictly inside the union of the two sets corresponds to two values of \(q\) and, therefore, to two relative equilibria.

The image in the \((B,\mathcal{C})\)-plane of the threshold curve is the transition between the two regions in Fig. 9 and is shown as a dark blue curve in both.

Since the values of the Casimir for the relative equilibria of Type II, as plotted against \(q\) (see Fig. 7) form a closed curve, the set of possible values of \(\mathcal{C}\) on the set of relative equilibria is bounded for every value of \(B\). Saddle-node bifurcations arise at the extreme points of \(\mathcal{C}\) on the curve.

These relative equilibria are degenerate; they coincide with the set of cusp points for Type II relative equilibria in Figs. 4 and 8 and, as the only degenerate relative equilibria of Type II, with the curves in Fig. 4 that separate the regions of stability and instability. Therefore, the bifurcation curve is the image of the said curves on the \((B,\mathcal{C})\) plane.

Indeed, since the relative equlibria on the bifurcation curve are degenerate, the only point where it can meet the threshold curve is the only degenerate relative equilibrium on the threshold curve: \(B=\frac{4}{3}3^{1/4},\mathcal{C}={20}/(3\sqrt{3})\), the left-most point on the image of the threshold curve in Fig. 9.

From the discussion above it can be easily seen that, for every fixed value of \(B\) and \(\mathcal{C}\) for which there are 2 relative equilibria of Type II, one of these is (linearly) stable and the other unstable.

6 OPPOSITE CHARGES

After describing in some detail the relative equilibria with equal charges, the next logical step is to investigate the case with opposite charges, thereby replacing the repelling potential by an attracting one. The following observation is based on ([7], Lemma 2.4), which there is stated for a Lagrangian system with no magnetic field, but applies equally well in the presence of a magnetic field.

On the configuration space \(\mathcal{Q}=S^{2}\times S^{2}\setminus\Delta\) (see Section 4), the involution \((\mathbf{q}_{1},\mathbf{q}_{2})\mapsto(\mathbf{q}_{1},-\mathbf{q}_{2})\) is antisymplectic on the second component. If this is combined with a change of sign of charge \(e_{2}\mapsto-e_{2}\) of the second particle, then the symplectic form in (2.3) is unchanged (we are not changing the sign of the magnetic field).

Write \(V_{1}(\mathbf{q}_{1},\mathbf{q}_{2})\) for the potential energy obtained from \(V(\mathbf{q}_{1},\mathbf{q}_{2})\) after changing \(e_{2}\) to \(-e_{2}\). Then, if \(V(\mathbf{q}_{1},\mathbf{q}_{2})=V_{1}(\mathbf{q}_{1},-\mathbf{q}_{2})\), then the involution transforms the Hamiltonian to itself. Under this condition, the involution will map the Hamiltonian system with potential energy \(V\) to the one with potential energy \(V_{1}\).

A case in point is \(V(\mathbf{q}_{1},\mathbf{q}_{2})=e_{1}e_{2}\cot(q)\) where \(q\) is the geodesic distance between \(\mathbf{q}_{1}\) and \(\mathbf{q}_{2}\) on the sphere. For then \(V_{1}(\mathbf{q}_{1},\mathbf{q}_{2})=e_{1}(-e_{2})\cot(q)\) and \(V(\mathbf{q}_{1},-\mathbf{q}_{2})=e_{1}e_{2}\cot(\pi-q)=-e_{1}e_{2}\cot(q)\).

The effect of this involution on the reduced coordinates is

$$(m_{1},m_{2},m_{3},q,p)\longmapsto(-m_{1},-m_{2},m_{3},\pi-q,-p)$$

(notice that \(m_{3}\) is unchanged). The Casimir is invariant, and so is the Hamiltonian provided the potential changes as discussed above. Each relative equilibrium, as well as its stability properties, for charges \((e_{1},e_{2})\) is therefore mapped to a relative equilibrium for charges \((e_{1},-e_{2})\), together with its stability properties, by this involution.

Now consider the specific potential \(V(q)=e_{1}e_{2}\cot q\) (repelling for like charges, attracting for charges of opposite sign). All the conclusions about the relative equilibria found in Section 5 carry over here, up to reflection of all the graphs with respect to the line \(q=\frac{\pi}{2}\). For example, the threshold curve becomes \(B=2\sqrt{\frac{\csc(q)}{1+\cos(q)}}\). In the same way, the relative equilibria are divided into two types, I and II, depending on domains of existence. We refer to them accordingly, depending on the one they coincide with via the involution described above.

The geometric differences with the case of identical particles is illustrated in Fig. 10. In particular, the new Type I relative equilibria have the axis between the particles, and the configuration continues to be asymmetric. (Compare with the analogous transformation in [7].)

Fig. 10
figure 10

The two types of relative equilibrium for equal masses and opposite charges, with \(V(q)=-\cot(q)\).

Full size image

Type II relative equilibria are no longer isosceles configurations in the sense we have used the term before; however, they retain a symmetry, with the axis of rotation lying to the side of the particle pair. As previously, the same geometric arrangement can be occupied by relative equilibria with two distinct rates of rotation (about the same axis), and hence two different energy levels.

The plots of the regions of stability and instability shown in Figs. 5 and 6 remain the same, except for a reflection in the line \(q=\pi/2\).

In particular (cf. Remark 5.7), relative equilibria with configurations that are closer to the axis of rotation are now more likely to be stable.