INTRODUCTION

The existence of three-nucleon forces (3NFs) is not doubted both in the standard meson-exchange picture [1] and in chiral perturbation theory [2]. Their strength and detailed structure are still under discussion.

The development of today’s most widely used 3NF models began in the 1970s and early 1980s and was based on the work by Fujita and Miyazawa [3].

Around the same time, the Urbana group found, that for a description of saturation of nuclear matter, a short range repulsive interaction is required. The force was then adjusted to reproduce the triton binding energy. This lead to a series of 3NF called Urbana. The most up-to-date version is called Urbana-IX [4].

Development of chiral effective field theory of interaction between nucleons provides a selfconsistent treatment of two-, three- and many-nucleon forces and exchange currents on the basis of symmetries of underlying theory of strong interactions—Quantum chromodynamics. This approach is widely applied for low energy nuclear physics and nuclear astrophysics. Necessary low-energy parameters of the theory have to be extracted from experimental data [5].

\(\Delta {{\sigma }_{{\text{L}}}}\) is the difference in the nd total cross section for beam and target spins parallel and anti-parallel to each other, with both spins aligned with the beam momentum axis. \(\Delta {{\sigma }_{{\text{T}}}}\) is similarly defined. Theoretical calculations predict that the Tucson-Melbourne three-nucleon force (TM-3NF) changes \(\Delta {{\sigma }_{{\text{L}}}}\) by 5–10% [7] from its value calculated using only NN interaction potentials.

The total cross-section difference \(\Delta {{\sigma }_{{\text{L}}}}\)(nd) was measured firstly at TUNL [8] for incident neutron energies of 5.0, 6.9 and 12.3 MeV. The results were compared to the theoretical predictions based on the CD Bonn NN potential calculations, with and without the inclusion of the TM-3NF, “but are not of sufficient precision to distinguish the presence or absence of three-nucleon force contributions to the cross-sections”.

1 EARLY EXPERIMENTS AT PRAGUE

At the Charles University Nuclear Center the measurements of \(\Delta {{\sigma }_{{\text{L}}}}\)(np) and \(\Delta {{\sigma }_{{\text{T}}}}\)(np) were performed using the transmission method, i.e., the relative difference in attenuation of a polarized neutron beam passing through a polarized proton target was measured.

A polarized neutron beam was based on the Van de Graaff electrostatic accelerator HV 2500 of the Nuclear Center, Charles University (now belongs to IEAP CTU), using the reaction T(d, n)4He with a deuteron beam (\({{E}_{{\text{d}}}} = 1.82\) MeV). To achieve a monoenergetic collimated neutron beam, the associated particle method was used [9]. The transversely polarized neutron beam with an energy \({{E}_{{\text{n}}}} = (16.2 \pm 0.1)\) MeV was emitted at an angle \({{\theta }_{{{\text{lab}}}}} = (62.0 \pm 0.7)^\circ \). The value of neutron polarization was \({{P}_{{\text{n}}}} = ( - 13.5 \pm 1.4)\% \). To get longitudinal polarization for the \(\Delta {{\sigma }_{{\text{L}}}}\) experiment, spin was rotated with the help of a permanent magnet of 0.5 Tm.

For these experiments, the frozen spin polarized target has been developed which includes a stationary cryostat with a dilution refrigerator, a movable magnetic system including a superconducting dipole magnet with a large aperture, a superconducting solenoid and electronic equipment for providing a dynamic polarization and NMR signal detection . The polarized sample of 20 cm\(^{3}\) in volume contained propanediol with paramagnetic Cr(V) impurity. The maximum obtained polarization was 93 and 98% for positive and negative values respectively. The target temperature in a frozen mode was about 20 mK. Under these conditions the proton spin relaxation was approximately 1000 h for positive polarization and 300 h for negative one (with a holding field of 0.37 T). The important peculiarity of the developed target was a big aperture for scattered neutrons detection (50° in the vertical plane and almost 360° in the horizontal plane). The polarization direction is defined by the orientation of the holding field. A detailed description of the target can be found in [10].

A phase-shift analysis has been performed to extract the value of the 3S1–3D1 mixing parameter \({{\epsilon }_{1}}\). The result is \({{\epsilon }_{1}} = (1.36 \pm 0.66)^\circ \). The physical results obtained in Prague permit a new view to the earlier data in this energy range. Earlier, experimental results of other authors (Bonn, Erlangen, Triangle Universities) supported the hypothesis on the minimum value of \({{\epsilon }_{1}}\) in the vicinity of 15 MeV. Our results disproved this. which is in good accord not only with the other experimental data in this energy range, but with model predictions, in [11, 12].

2 NEW EXPERIMENTS AT PRAGUE

Now the proton polarized target (PPT) has been transformed into the frozen spin deuteron polarized target (DPT). DPT is a facility consisting of a 3He/4He dilution refrigerator, 3He and 4He pumping system, two superconducting magnets providing longitudinal and transverse deuteron polarizations and a PC-controlled equipment to build-up and measure the target polarization. Deuterated 1, 2 propanediol with a paramagnetic Cr(V) impurity having a spin concentration about \({{10}^{{20}}}\) cm–3 is used as a target material.

A system providing the microwave pumping of deuteron polarization consists of a microwave generator, a wave guide inside and outside the dilution refrigerator, and a multimode cavity containing the target material. The microwave generator is a 4 mm wavelength oscillator using an ATT diode placed inside the invar cavity, an output power is above 100 mW. A frequency tuning in 73.0–75.5 GHz range is provided by the cavity piston. The frequency modulation \({\text{of}}\) the microwave power is necessary to obtain higher deuteron polarization.

The universal system of polarization measurement was created: PC based Liverpool type Q-meter has been put into operation in order to enlarge a range of nuclei whose polarization can be measured. The maximum deuteron vector polarization achieved was 40%. The DPT was described in detail in [13, 14].

Experience showed that all components of the DPT as well as the accelerator worked well. Unfortunately, the intensity of the neutron beam was not sufficient. The attempts to increase the intensity brought problems in the stability of the measured values, and the systematic error increased. It was suspected that the electronics used is responsible (many old modules are still present in the system). Several measurement runs were performed, in order to diagnose the sources of the measurement instabilities. In these runs, individual parts of data acquisition system were analyzed and as a result, better solution has been found (triggering the time-to-digit converter TDC by the coincidence signal of neutron with alpha particle rather than the alpha-particle itself). This improvement was tested with an accelerator and gave bette results. The systematic errors were lowered and the number of events per second was increased 3–4 times. The second reason for the large uncertainties is the polarization of the deuteron target, which is lower than expected. The average polarization achieved has been \( \simeq \,29\% \).

The last experiments showed that the polarization and intensity of the neutron beam and also the deuteron polarization of the target are insufficient for achieving the necessary accuracy on the measurement of the cross-section difference. Now a modernization of the facility is in progress with the aim to increase the deuteron polarisation of the polarized target and the intensity and polarization of the neutron beam. We will replace our current target material (propanediol) with the novel material, trityl-doped butanol. With this material, polarizations as high as \( \simeq \,80\% \) were achieved by the Mainz group [15]. But, in order to use new target materials it is necessary to improve the stability and precision of existing dynamical nuclear polarization apparatus. The linewidth of the resonance of trityl is approximately three times narrower compared to the ones of usually used materials. So we must make a new generator with the required parameters. Also we should test the homogeneity of the superconducting solenoid and correct the field if necessary. The solution to the problem of instability and low statistics would be the increase of the polarisation and intensity of the neutron beam. To improve the parameters of the neutron beam it is proposed to use the reaction T(\(\vec {d}\),n)4He with polarized deuterons of an energy 100–150 keV. This can be achieved using Kaminsky’s proposal [16, 17].

3 POLARIZED DEUTERONS

The first proposal concerning nuclear polarization of protons (deuterons, tritons) via a pick-up of polarized ferromagnetic electrons from a magnetized foil was made by Zavoiskii in 1957 [18]. The method includes adiabatic transition of atoms from a high magnetic field to a low magnetic field of an order 1 mT, so that the electron polarization of the atoms is transferred to the nuclei by hyperfine interaction.

Kaminsky used the effect of channeling of an unpolarized deuteron beam through a magnetized single-crystal Ni foil to produce deuterium atoms with electron polarization. A beam of deuterons with a half angle of 0.01° was incident on a Ni(110) foil \( \approx \,2\,\,\mu {\text{m}}\) thick within 0.1° of the [110] direction.

We calculated the critical acceptance angle of channeling according to [19]. For the exit energy 200 keV of deuterons (or deuterium atoms) and the \(\left\langle {110} \right\rangle \) direction of Ni, this angle equals 2.3°. For the angle 0.1° relatively to the [110] direction, axially channeled ions have the transverse energy less then the potential barrier between adjacent rows and are restrained to travel in a single axial channel. This type of channeling is named hyperchanneling. These ions will have lower energy losses than ions which wander from a channel to a channel (normal channeling).

It was produced 500 nA/cm2 of channeled deuterium atoms with an energy of 100–200 keV with nuclear polarization \({{P}_{{zz}}} = - 0.32 \pm 0.010\) (without a significant lattice damage for 25 h of operating time). To test the proposal of Zavoiskii the author passed deuterons through magnetized polycrystalline foils and observed no polarization.

The paper contains a few details about the experimental setup, in particular, the magnitude of the deuteron beam current, its diameter, which is important for practical applications. One can find the diameter of the beam in the description of the patent [18], it equals 1 mm. Hence the current of polarized deuterium atoms does not exceed 5 nA. To form such a beam the length of the system of focusing should be several meters [20].

Feldman et al. [21] made polarization measurements with an experimental arrangement similar to that of Kaminsky. Their data qualitatively agree with Kaminsky’s data (\({{P}_{{zz}}} = - 0.14 \pm 0.06\)). Also, as in Kaminsky’s experiment, no effect was seen for polycrystalline foils.

In addition, Feldman et al. attempted to observe the effect using thin polycrystalline foils of Fe. No effect was seen, possibly because of the presence of fairly thick (50–100 Å) surface oxide layers.

Ebel [22] tried to explain this high observed polarization by postulating that once a deuteron has captured a spin-up electron inside the crystal, the probability of its losing this electron would be small since the spin-up 3d-band states are filled. A captured spin-down electron, on the other hand, could readily be lost since the spin-down 3d-band states in the crystal are not filled. This would give rise to a pumping of electrons from spin-down to spin-up atomic states of deuterium.

Brandt and Sizmann [24], however, pointed out that stable bound electronic states could not exist in deuterium atoms passing through metals at these velocities. They proposed instead that the electron capture took place in the tail of the electron density distribution at the crystal surface where the density was low enough for bound states to be stable.

Later, Kreussler and Sizmann [24] confirmed that at high energies (more than 250 keV/amu) neutralization took place chiefly in the bulk of the crystal and the surface effects were important at lower energies.

Quite a different electron field-emission experiment [25] on Ni showed that electrons emitted along the [100], [110], and [137] directions had predominantly spin-up direction (along the magnetic field), but when emitted along the [111] direction they had spin-down direction. This can explane the absence of polarization in experiments of Kaminsky and Feldman with policrystalline Ni targets.

Rau and Sizmann [26], who also used the T(d, n)4He reaction, measured polarization of the nuclei in neutral deuterium atoms created by electron capture during reflection of a 150-keV D+ beam incident at glancing angles (<0.4°) on the surface of magnetized Ni crystals. The results show that the electron spin orientation is predominantly parallel to the magnetizing field for electrons on the (100), (110), and (111) surfaces and antiparallel in the (120) surface. On the (110) surface the electron polarization is \(P = 96\% \) [27]. This gives the negative tensor polarization, which corresponds to the results of Kaminsky.

On the other hand, there is evidence for polarization of \(1s\) electrons (\({{P}_{{1s}}} = 0.10 \pm 0.03\)) attached to F ions as they emerge from magnetized polycrystalline Fe layers [28].

It was found that a vacuum of \(2 \times {{10}^{{ - 8}}}\) Torr was necessary in order to see polarization effects. If the vacuum was allowed to deteriorate to \(5 \times {{10}^{{ - 6}}}\) Torr, the polarization gradually vanishes, presumably as a result of the build-up of thin layers of surface contaminants.

It was supposed [23] that the role of channeling is not obvious. The ion which goes out of channel can perturb the equilibrium electron distribution at the surface. This can decrease the electron polarization.

It can be assumed that the absence of polarization in the experiment with a polycrystal is due to the fact that electrons on different planes of microcrystals have a different sign of polarization and, upon averaging, will create zero polarization of atoms. Although another explanation is possible, connected with the formation of “dead layers” [29, 30].

4 EXPERIMENTAL SETUP

An experimental setup has been developed to research the possibility in limited space to produce the beam of nuclear-polarized deuterium atoms with energies of 100–300 keV with intensity enough to measure \(\Delta {{\sigma }_{{\text{T}}}}\) and \(\Delta {{\sigma }_{{\text{L}}}}\) for reasonable time. The deuteron beam with an energy up to 300 keV was produced by the Van de Graaff electrostatic accelerator HV 2500 of the IEAP CTU).

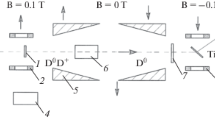
The scheme and photo of the experimental setup is shown in Figs. 1, 2. We propose to apply the Sona method, zero-field transitions, with the total transfer of the electron polarization to deuterons in the atomic beam [31]. The magnetic field is directed along the foil plane (vertically), so we must use Sona transitions with vertical magnetic fields [32]. Earlier this method was proposed by Ehrenstein [33]. This is different from the usual configuration with longitudinal magnet fields. We use two permanent magnets with a length 15 and 6 cm between them with a changing gap between the poles along the beamline (\({{B}_{{\max }}} = 0.07\) T). Oppositely directed magnetic fields of the two magnets do not allow deflect charged deuterons that didn’t pick up an electron. Therefore, we added a permanent magnet 70 mT with a strong field in front of the system of the Sona magnets. Ultimately, electrostatic plates were not used. Vacuum was better then \({{10}^{{ - 4}}}\) Pa.

Fig. 1.
figure 1

Scheme of the polarized deuteron source; (1) nickel foil, (2) permanent magnet (0.07 T), (3) solid state detector, (4) goniometer, (5) polarizing permanent magnets (for Sona transitions), (6) electrostatic plates, (7) CD2 target of the polarimeter.

Full size image
Fig. 2.
figure 2

Photo of the experimental setup.

Full size image

The single-crystal nickel foils of thickness 0.5–2 μm with size \(1 \times 1\) cm2 are grown epitaxially on NaCl crystals cleaved to expose the (110) plane (produced by Princeton Scientific Corp.). The substrate was dissolved by water and the Ni foils were floated on a stainless steel ring mounted on the goniometer. The working diameter of the foil was 6 mm, the diameter of the deuteron beam was about 4 mm, and the deuteron current was up to 0.5 μA. The Ni foil and the TiT target of a polarimeter are placed in oppositely directed magnetic fields. Figure 1 shows the polarimeter permanent magnet of 70 mT.

The tensor polarization was measured with TiT target by registration of the angular distribution of α-particles emitted in the reaction T\({{(d,n)}^{4}}\)He [36]. In this experiment we used only the first magnet of the Sona transition system and the polarimeter was in a weak field of 1 mT. Theoretically, tensor polarization in this configuration is \({{P}_{{33}}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}\). The cross section equals [36]:

$$\sigma (\vartheta ) = {{\sigma }_{0}}\left[ {1 - \frac{f}{4}(3{{{\cos }}^{2}}\vartheta - 1){{P}_{{zz}}}} \right],$$
(1)

where \(\vartheta \) is the center-of-mass angle between the outgoing particle (α or neutron) and the polarisation axis. Experimenters usually assume that \(f = 1\), but there are indications that this assumption is not correct even at low energies. Haeberli pointed out [37] that the best value is \(f = 0.95 \pm 0.01\) at 100 keV.

The α-particles are counted by two solid state detectors positioned in a plane perpendicular to the beam and 90° to each other.

The ratio of the counting rates \(R = {{{{N}_{{\text{v}}}}N_{{\text{h}}}^{0}} \mathord{\left/ {\vphantom {{{{N}_{{\text{v}}}}N_{{\text{h}}}^{0}} {{{N}_{{\text{h}}}}N_{{\text{v}}}^{0}}}} \right. \kern-0em} {{{N}_{{\text{h}}}}N_{{\text{v}}}^{0}}}\) of the two detectors, vertical \({{N}_{{\text{v}}}}\), and horizontal \({{N}_{{\text{h}}}}\), is a measure of the tensor polarization of the deuterons in the deuterium atoms. Of course, these counting rates were related to the rates with a nonpolarized beam, produced by a copper foil, \(N_{{\text{v}}}^{0}\) and \(N_{{\text{h}}}^{0}\). For \({{N}_{{\text{v}}}}\) \(\vartheta = 0^\circ \) and \({{N}_{{\text{h}}}}\) \(\vartheta = 90^\circ \)

$${{P}_{{zz}}} = \frac{{4(1 - R)}}{{R + 2}}.$$
(2)

The absolute statistical error is

$$\Delta ({{P}_{{zz}}}) = \frac{{12R}}{{{{{(R + 2)}}^{2}}}}\sqrt {\frac{1}{{{{N}_{{\text{v}}}}}} + \frac{1}{{{{N}_{{\text{h}}}}}} + \frac{1}{{N_{{\text{v}}}^{0}}} + \frac{1}{{N_{{\text{h}}}^{0}}}} .$$
(3)

The count of alpha particles was about 1 pulse per a second. To get \(\Delta ({{P}_{{zz}}}) = 0.01\) the total count for \(N\) should be \( \approx 7 \times {{10}^{4}}\).

As a result, \({{P}_{{zz}}} = - 0.10 \pm 0.02\) (theoretical value is \({{P}_{{zz}}} = - 0.33\)) at the deuteron energy of 500 keV for the Ni foil thickness 1.5 μm (the deuterium atom energy is 250 keV). This corresponds to the deuteron vector polarization \({{P}_{z}} = 0.12\). The negative sign of tensor polarization also is in agreement with the result of Kaminsky. During this experiment the goniometer was at a random position. This means that nonchanneled atoms also polarized, at least, partly. We did not see polarization with policrystalline foils.

We started experiments with a channeled deuteron beam and found a second peak with a higher energy of deuterons at a certain position of the goniometer. It seems possible that the effect of channeling permits to increase the available deuterium current at the target and polarization.

5 NEUTRON BEAM

The deuterium beam in a strong magnetic field has vector polarization of deuterons up to the theoretical maximum \({{P}_{3}} = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}\) and zero tensor polarization.

If the tensor polarization is zero, then neutrons emitted at an angle of   90° in the center of mass system have the same value of vector polarization, as the original beam and the transverse direction in the horizontal plane [34]. Thus, the increase in polarization is approximately two times in comparison with the known method.

If we turn adiabatically the longitudinal polarization into the vertical plane with help of an additional magnet, then the neutrons emitted at 0° are theoretically will have a vertical polarization.

With the neutron emission angle \((83 \pm 0.5)^\circ \) the α‑particles associated with these neutrons are emitted at the angles \((90 \pm 4)^\circ \) for deuteron energies from 25 up to 200 keV. This defines the dimension of the α-particle detector. We can easily cut off the scattered deuteron of 200 keV from the α-particles with a thin foil.

If the target material TiT\(_{N}\) contains N = 1.5 tritium atoms/titanium atom, then the density of the target material is \({{\rho }_{{{\text{Ti}}{{{\text{T}}}_{N}}}}} = 0.85{{\rho }_{{{\text{Ti}}}}}{{(47.88 + 3.015N)} \mathord{\left/ {\vphantom {{(47.88 + 3.015N)} {47.88}}} \right. \kern-0em} {47.88}} = \) 4.19 g/cm3, where \({{\rho }_{{{\text{Ti}}}}} = 4.505\) g/cm3. The factor 0.85 arises from the 15% expansion which the titanium lattice undergoes during tritiation. In table 1 the values of the quantities \({{({{d{{E}_{{\text{d}}}}} \mathord{\left/ {\vphantom {{d{{E}_{{\text{d}}}}} {d\tau }}} \right. \kern-0em} {d\tau }})}_{{{{T}_{2}}}}}\), \({{({{d{{E}_{{\text{d}}}}} \mathord{\left/ {\vphantom {{d{{E}_{{\text{d}}}}} {d\tau }}} \right. \kern-0em} {d\tau }})}_{{{\text{Ti}}}}}\) and \(\sigma ({{E}_{{\text{d}}}})\), that have been utilized in the calculations are reported. The values of the quantities \({{({{d{{E}_{{\text{d}}}}} \mathord{\left/ {\vphantom {{d{{E}_{{\text{d}}}}} {d\tau }}} \right. \kern-0em} {d\tau }})}_{{{{T}_{2}}}}}\) and \({{({{d{{E}_{{\text{d}}}}} \mathord{\left/ {\vphantom {{d{{E}_{{\text{d}}}}} {d\tau }}} \right. \kern-0em} {d\tau }})}_{{{\text{Ti}}}}}\) have been obtained by interpolation from the data given in [35]. The total yield of neutrons per incident deuteron with an energy of \({{E}_{{\text{d}}}} = 200\) keV is given by integration on the deuteron energy in the target. As a result, the yield is \(Y = 3 \times {{10}^{{ - 5}}}\) neutrons per one deuteron, or \(1.5 \times {{10}^{7}}\) neutrons per steradian per one μA of deuterons, the deuteron range in the target is \(R \simeq 1.3\) μm, the activity of the TiT target is \( \simeq 0.45\) Ci/cm2.

Table 1.   Values of the functions \({{({{d{{E}_{{\text{d}}}}} \mathord{\left/ {\vphantom {{d{{E}_{{\text{d}}}}} {d\tau }}} \right. \kern-0em} {d\tau }})}_{{{{{\text{T}}}_{{\text{2}}}}}}}\), \({{({{d{{E}_{{\text{d}}}}} \mathord{\left/ {\vphantom {{d{{E}_{{\text{d}}}}} {d\tau }}} \right. \kern-0em} {d\tau }})}_{{{\text{Ti}}}}}\), and \(\sigma ({{E}_{{\text{d}}}})\) (for unpolarized deuterons) used in the calculation
Full size table

M. Kaminsky [16] obtained 0.5 μA/cm2 of channeled deuterium atoms with nuclear spin polarization without a significant lattice damage for approximately 25 h of operation time. At the beam radius of 0.5 mm we would have \( \simeq 4 \times {{10}^{{ - 3}}}\) μA of deuterium atoms. With a solid angle \(3 \times {{10}^{{ - 4}}}\) sterad the neutron beam would be 17 neutrons/s.

We can estimate the possibility of the \(\Delta \sigma \) experiment with this neutron intensity. According to [11, 12] statistical error for \(\Delta {{\sigma }_{{{\text{L}}{\text{,T}}}}}\) may be written as

$$\Delta {{\sigma }_{{{\text{L}}{\text{,T}}}}} = \frac{{\ln \xi ({\text{antiparallel}}) - \ln \xi ({\text{parallel}})}}{{\omega {{P}_{{\text{b}}}}{{P}_{{\text{t}}}}}},$$
(4)

where ω is deuteron surface density of polarized target (deuterons/cm2) \({{P}_{{\text{b}}}}\), \({{P}_{{\text{t}}}}\) are the polarization of the beam and target, respectively, and \(\xi = {{{{N}_{{\det }}}} \mathord{\left/ {\vphantom {{{{N}_{{\det }}}} {{{N}_{{{\text{mon}}}}}}}} \right. \kern-0em} {{{N}_{{{\text{mon}}}}}}}\), where \({{N}_{{{\text{det}}}}}\) and \({{N}_{{{\text{mon}}}}}\) are neutron counting rates of the detector and monitor, respectively. The monitor counts the neutron intensity before the polarized target.

Absolute statistical error is

$$\delta (\Delta \sigma ) = \frac{{\sqrt 2 }}{{\omega {{P}_{{\text{b}}}}{{P}_{{\text{t}}}}}}\sqrt {\frac{1}{{{{{\bar {N}}}_{{{\text{mon}}}}}t}} + \frac{1}{{{{{\bar {N}}}_{{\det }}}t}}} ,$$
(5)

where \({{\bar {N}}_{{{\text{mon}}{\text{,det}}}}} = \frac{1}{2}({{N}_{{{\text{mon}}{\text{,det}}}}}({\text{par}}.) + {{N}_{{mon,\det }}}({\text{antipar}}.)\)

For the polarized target (propanediol) \(\omega = 3 \times \) 10–4 mbarn–1. At \({{P}_{{\text{t}}}} = 0.8\) and \({{P}_{{\text{b}}}} = 0.6\), one obtains \({1 \mathord{\left/ {\vphantom {1 \omega }} \right. \kern-0em} \omega }{{P}_{{\text{b}}}}{{P}_{{\text{t}}}} \approx 7 \times {{10}^{3}}\) mbarn.

If the detector efficiency is \({{10}^{{ - 2}}}\), and solid angle \(3 \times {{10}^{{ - 4}}}\) sterad, then at \({{N}_{{{\text{mon}}}}} \simeq {{N}_{{\det }}} = 18 \times {{10}^{{ - 2}}}\) neutrons/s to get \({{\delta }_{{{\text{stat}}}}}(\Delta \sigma ) = 7\) mbarn it is necessary \(t = 6200\) h of data taking for two values of polarization sign.

At a neutron energy of 14 MeV \(\Delta {{\sigma }_{{\text{T}}}} \approx - 300\) mbarn. Inclusion of the 3NF decreases the cross section difference [7] to 20 mbarn, so we can detect this difference.

It seems that experiment would be too long with supposed polarized neutron beam and we must search the possibility to increase the intensity.

6 ADIABATICITY

When a beam moves in a magnetic field, there are two regions with opposite requirements for adiabaticity. If the field is approximately described by the relation

$${{B}_{z}}(x) = {{B}_{0}}(1 - {{2x} \mathord{\left/ {\vphantom {{2x} l}} \right. \kern-0em} l}),$$
(6)

then at the initial point \(x = 0\) the field must change slowly enough so that the spin can follow the direction of the field. To implement the Sona transition with the reversal of the magnetic field when passing through zero, it must change quickly enough so that the spin remains in a frozen state.

Quantitatively, for deuterium atoms moving perpendicular to the magnetic field, it looks like this. The angular velocity of rotation of the magnetic field \({{\omega }_{B}} = {{d\theta } \mathord{\left/ {\vphantom {{d\theta } {dt}}} \right. \kern-0em} {dt}}\), seen by an atom moving with velocity \(v\) at a distance \(z\) from the median plane, follows from the relations

$$\begin{gathered} \cot \theta = \frac{{{{B}_{z}}}}{{{{B}_{x}}}},\,\,\,{{B}_{x}} = z\frac{{d{{B}_{z}}}}{{dx}},\,\,\,\frac{1}{{{{{\sin }}^{2}}\theta }}\frac{{d\theta }}{{dx}} = \frac{1}{z}, \\ \frac{{d\theta }}{{dx}} = \frac{1}{z}\frac{{B_{x}^{2}}}{{B_{x}^{2} + B_{z}^{2}}}. \\ \end{gathered} $$
(7)

For the selected magnetic field model

$${{\omega }_{B}}(x) = \frac{{d\theta }}{{dx}}v = \frac{{4zv}}{{{{l}^{2}}[{{{(1 - {{2x} \mathord{\left/ {\vphantom {{2x} l}} \right. \kern-0em} l})}}^{2}} + {{4{{z}^{2}}} \mathord{\left/ {\vphantom {{4{{z}^{2}}} {{{l}^{2}}}}} \right. \kern-0em} {{{l}^{2}}}}]}}.$$
(8)

At the point of zero field, the angular velocity of rotation of the magnetic field is

$${{\omega }_{B}}({l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}) = {v \mathord{\left/ {\vphantom {v z}} \right. \kern-0em} z}.$$
(9)

The angular velocity of Larmor precession \({{\omega }_{{\text{L}}}}\) is equal to the difference between the energies of adjacent levels divided by \(\hbar \)

$$\begin{gathered} {{\omega }_{{\text{L}}}} = \frac{1}{\hbar }\left[ {\frac{{\Delta W}}{2} - {{\mu }_{e}}B(x) - \frac{{{{\mu }_{d}}B(x)}}{2}} \right. \\ \left. { - \,\,\frac{{\Delta W}}{2}\sqrt {1 + \frac{2}{3}X(x) + X{{{(x)}}^{2}}} } \right], \\ \end{gathered} $$
(10)

where

$$\begin{gathered} B(x) = \sqrt {{{B}_{z}}{{{(x)}}^{2}} + B_{x}^{2}} = {{B}_{0}}\sqrt {{{{\left( {1 - \frac{{2x}}{l}} \right)}}^{2}} + \frac{{4{{z}^{2}}}}{{{{l}^{2}}}}} , \\ X(x) = \frac{{B(x)}}{{{{B}_{c}}}}, \\ \end{gathered} $$

\({{\mu }_{{\text{e}}}} = - 9.274 \times {{10}^{{ - 24}}}\) J/T, \({{\mu }_{{\text{d}}}} = 4.331 \times {{10}^{{ - 27}}}\) J/T, \(\Delta W = 2.168 \times {{10}^{{ - 25}}}\) J, \({{B}_{{\text{c}}}} = 0.0117\) T.

Neglecting \({{\mu }_{{\text{d}}}}\), at the zero crossing point we get

$${{\omega }_{{\text{L}}}}({l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}) = \frac{{2\left| {{{\mu }_{{\text{e}}}}} \right|}}{{3\hbar }}B({l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}) = \frac{{2\left| {{{\mu }_{{\text{e}}}}} \right|}}{{3\hbar }}{{B}_{x}} = \frac{{2\left| {{{\mu }_{{\text{e}}}}} \right|}}{{3\hbar }}\frac{{2{{B}_{0}}z}}{l}.$$
(11)

The fast transition condition is \({{\omega }_{{\text{L}}}} \ll {{\omega }_{{\text{B}}}}\). For \({{B}_{0}} = 0.07\) T, \(z = 3\) mm, \(v = 4 \times {{10}^{6}}\) m/s one get \({{\omega }_{{\text{L}}}}({l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}) = 8.4 \times {{10}^{7}}\) rad/s and \({{\omega }_{{\text{B}}}}({l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}) = 1.3 \times {{10}^{9}}\) rad/s, i.e. the condition is met.

In general, the fast transition condition has the form

$$\frac{{{{B}_{x}}z}}{v} \ll \frac{{3\hbar }}{{2\left| {{{\mu }_{{\text{e}}}}} \right|}},\,\,\,\,\frac{{{{B}_{0}}{{z}^{2}}}}{{vl}} \ll \frac{{3\hbar }}{{4\left| {{{\mu }_{{\text{e}}}}} \right|}}.$$

For these parameters, we have \(5.6 \times {{10}^{{ - 13}}} \ll 8.5 \times {{10}^{{ - 12}}}\).

At the initial point for \(x = 0\)

$${{\omega }_{{\text{B}}}}(0) = \frac{{B_{x}^{2}v}}{{zB{{{(0)}}^{2}}}} \approx \frac{{4zv}}{{{{l}^{2}}}}.$$

For \(z = 3\) mm, \(l = 0.28\) m and \(v = 4 \times {{10}^{6}}\) m/s \({{\omega }_{{\text{B}}}}(0) = 6 \times {{10}^{5}}\) rad/s. The angular velocity of the Larmor precession is \({{\omega }_{{\text{L}}}} = 6.2 \times {{10}^{8}}\) rad/s i.e. the adiabaticity condition \({{\omega }_{{\text{B}}}} \ll {{\omega }_{{\text{L}}}}\) is satisfied.

Note that the adiabaticity condition is satisfied for \(x = 0.45l\): \({{\omega }_{{\text{B}}}} = 6.1 \times {{10}^{7}}\) rad/s, \({{\omega }_{{\text{L}}}} = 2.8 \times {{10}^{8}}\) rad/s. But for \(x = 0.49l\) (\(B = 1.4 \times {{10}^{{ - 3}}}\) T) \({{\omega }_{{\text{B}}}} = 2.1 \times \) 109 rad/s, \({{\omega }_{{\text{L}}}} = 8.2 \times {{10}^{7}}\) rad/s and \({{\omega }_{{\text{L}}}} \ll {{\omega }_{{\text{B}}}}\).

We should consider the presence of a superimposed transverse field \({{B}_{t}}\) in the zero-crossing from terrestrial magnetic field. This requires

$$\cot \theta = \frac{{{{B}_{z}}}}{{{{B}_{t}}}},\,\,\,\,\frac{1}{{{{{\sin }}^{2}}\theta }}\frac{{d\theta }}{{dx}} = \frac{{{{d{{B}_{z}}} \mathord{\left/ {\vphantom {{d{{B}_{z}}} {dx}}} \right. \kern-0em} {dx}}}}{{{{B}_{t}}}}.$$

For \(\theta = 90^\circ \) we get the condition of fast transition

$$\frac{{2{{\mu }_{{\text{B}}}}}}{{3\hbar }}{{B}_{t}} \ll \frac{{{{d{{B}_{z}}} \mathord{\left/ {\vphantom {{d{{B}_{z}}} {dx}}} \right. \kern-0em} {dx}}}}{{{{B}_{t}}v}},\,\,\,{{d{{B}_{z}}} \mathord{\left/ {\vphantom {{d{{B}_{z}}} {dx}}} \right. \kern-0em} {dx}} \gg B_{t}^{2}\frac{{2{{\mu }_{{\text{B}}}}}}{{3\hbar v}},$$

or \({{d{{B}_{z}}} \mathord{\left/ {\vphantom {{d{{B}_{z}}} {dx}}} \right. \kern-0em} {dx}} \gg 1.5 \times {{10}^{4}}B_{t}^{2}\). For \({{d{{B}_{z}}} \mathord{\left/ {\vphantom {{d{{B}_{z}}} {dx}}} \right. \kern-0em} {dx}} = 0.25\) T/m and \({{B}_{t}} \sim {{10}^{{ - 4}}}\) T and the condition \({{d{{B}_{z}}} \mathord{\left/ {\vphantom {{d{{B}_{z}}} {dx}}} \right. \kern-0em} {dx}} \gg 1.5 \times {{10}^{{ - 2}}}\) T/m is satisfied.

7 PERSPECTIVES

Kaminsky [16] pointed that the intensity of the polarized deuteron beam can probably be increased by relaxing of requirements on collimation of the emergent beam. We can work with in regime of beam channelling with a critical angle of approximately 2°. To reduce losses due to the divergence of the atomic beam, the size of the Sona magnets can be reduced. The calculation shows that this will not affect on adiabaticity. If the foil remains operational at a beam diameter of about 6 mm and an atomic current density of 500 nA/cm2 (our calculation shows that it is real for a deuteron beam 1 μA), the intensity of the flux of polarized deuterium atoms will increase and the data taking time will decrease by a factor of 6 and amounts to 1000 h. The foil should be cooled in this case.

We could not measure the deuteron vector polarization using the reaction D(\(d,p\))T [38] as cross section of the dd-reaction approximately two order lower then for dt-reaction.

The polarimeter target consistes of deuterated polyethylene with a thickness of about 2–3 μm on a Cu support. The protons produced in this reaction are detected by two surface barrier detectors, each having an effective area of 20 mm2.

The detectors are placed symmetrically at ±120° with respect to the beam axis, and the solid angle is \( \approx 1\) msr. In order to suppress the elastically scattered deuterons, 3H and 3He, each detector is masked with a 10-μm-thick aluminum foil.

For a vector polarized beam the particle intensities detected by two detectors placed on the right and on the left of the beam axis are proportional to the cross sections \({{\sigma }_{{\text{R}}}}(\theta )\) and \({{\sigma }_{{\text{L}}}}(\theta )\), respectively,

$${{\sigma }_{{\text{R}}}}(\theta ) = {{\sigma }_{{{\text{0R}}}}}(\theta )\left[ {1 - \frac{3}{2}{{P}_{z}}{{A}_{y}}(\theta )} \right]$$
(12)

and

$${{\sigma }_{{\text{L}}}}(\theta ) = {{\sigma }_{{{\text{0L}}}}}(\theta )\left[ {1 + \frac{3}{2}{{P}_{z}}{{A}_{y}}(\theta )} \right],$$
(13)

where \(\theta \) is the angle between the polarization vector and the beam direction, and \({{A}_{y}}(\theta )\) is the analyzing power for the reaction. The vector analyzing power \({{A}_{y}}(\theta )\) for 200 keV deuterons at an angle of 120° in the laboratory system is \(0.224 \pm 0.017\) [38].

Replacing the cross sections by the corresponding right and left detector intensities, \({{N}_{{\text{R}}}}\) and \({{N}_{{\text{L}}}}\), for polarized beam and \({{N}_{{{\text{0R}}}}}\), \({{N}_{{{\text{0L}}}}}\) for unpolarized beam, we obtain

$$\frac{{{{N}_{{\text{R}}}}(\theta )}}{{{{N}_{{\text{L}}}}(\theta )}}\frac{{{{N}_{{{\text{0L}}}}}(\theta )}}{{{{N}_{{{\text{0R}}}}}(\theta )}} = \frac{{1 - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}{{P}_{z}}{{A}_{y}}(\theta )}}{{1 + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}{{P}_{z}}{{A}_{y}}(\theta )}}.$$
(14)

Designating

$$\kappa = \frac{{{{N}_{{\text{R}}}}(\theta )}}{{{{N}_{{\text{L}}}}(\theta )}}\frac{{{{N}_{{{\text{0L}}}}}(\theta )}}{{{{N}_{{{\text{0R}}}}}(\theta )}},$$
(15)

one obtains

$${{P}_{z}} = \frac{{1 - \kappa }}{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}(\kappa + 1){{A}_{y}}(\theta )}}.$$
(16)

The statistical error is

$$\delta P_{z}^{2} = \frac{{16}}{{9{{{(\kappa + 1)}}^{4}}A_{y}^{2}}}\delta {{\kappa }^{2}} + \frac{{P_{z}^{2}}}{{A_{y}^{2}}}\delta A_{y}^{2},$$
(17)

where

$$\delta \kappa = \kappa \sqrt {\frac{1}{{{{N}_{{\text{R}}}}}} + \frac{1}{{{{N}_{{\text{L}}}}}} + \frac{1}{{{{N}_{{{\text{R0}}}}}}} + \frac{1}{{{{N}_{{{\text{L0}}}}}}}} .$$
(18)

According to the calculations, for the real magnetic field value the tensor polarization after the Sona transitions is not equal zero, \({{P}_{{zz}}} \approx 0.1\). In this case we use the general formula [39]

$$\begin{gathered} \sigma (\theta ,\phi ) = \left[ {1 + \frac{3}{2}\sin \beta \cos \phi {{P}_{z}}{{A}_{y}}(\theta )} \right. \\ \,\, - \cos \beta \sin \beta \sin \phi {{P}_{{zz}}}{{A}_{{xz}}}(\theta ) - \frac{1}{4}{{\sin }^{2}}\beta \cos 2{{P}_{{zz}}}{{A}_{{xx - yy}}}(\theta ) \\ + \left. {\,\,\frac{1}{4}(3{{{\cos }}^{2}}\beta - 1){{P}_{{zz}}}{{A}_{{zz}}}(\theta )} \right], \\ \end{gathered} $$
(19)

where \({{A}_{{xx - yy}}} = {{A}_{{xx}}} - {{A}_{{yy}}}\).

For a vertically polarized beam (\(\beta = 90^\circ \)), the reaction protons detected by two detectors, placed at left (\(\phi = 0^\circ \)) and right (\(\phi = 180^\circ \)) of the beam axis, are proportional to cross sections \({{\sigma }_{{\text{L}}}}(\theta )\) and \({{\sigma }_{{\text{R}}}}(\theta )\), respectively, where

$$\begin{gathered} {{\sigma }_{{\text{L}}}}(\theta ) = {{\sigma }_{{{\text{0L}}}}}(\theta ) \\ \times \,\,\left[ {1 + \frac{3}{2}{{P}_{z}}{{A}_{y}}(\theta ) - \frac{1}{4}{{P}_{{zz}}}{{A}_{{xx - yy}}}(\theta ) - \frac{1}{4}{{P}_{{zz}}}{{A}_{{zz}}}(\theta )} \right], \\ \end{gathered} $$
(20)
$$\begin{gathered} {{\sigma }_{{\text{R}}}}(\theta ) = {{\sigma }_{{{\text{0R}}}}}(\theta ) \\ \times \,\,\left[ {1 - \frac{3}{2}{{P}_{z}}{{A}_{y}}(\theta ) - \frac{1}{4}{{P}_{{zz}}}{{A}_{{xx - yy}}}(\theta ) - \frac{1}{4}{{P}_{{zz}}}{{A}_{{zz}}}(\theta )} \right]. \\ \end{gathered} $$
(21)

According to Ad’yasevich [40], at 300 keV \({{A}_{{zz}}} \approx {{A}_{{xx - yy}}} \approx 0\), at 400 keV \({{A}_{{zz}}} + {{A}_{{xx - yy}}} \approx 0\) and in this energy range additional terms can be neglected.

For deuteron with an energy of 200 keV the expected count rate is \( \sim \,2\) s–1 per 1 μA of neutral deuterium atoms on the target and \( \sim \,{{10}^{{17}}}\) cm–2 thickness of the target. The range in CD2 is 0.4 μm.

8 CONCLUSIONS

The experimental setup has been developed to produce the beam of deuterium atoms of energies 100–400 keV with polarized nuclei.

The final aim is to produce a polarized 14 MeV neutron beam with use the reaction T(\(d,n{{)}^{4}}\)He for measuring the neutron-deuteron total cross section differences \(\Delta {{\sigma }_{{\text{L}}}}(nd)\) and \(\Delta {{\sigma }_{{\text{T}}}}(nd)\) together with frozen-spin polarized deuteron target.

The measurement of the deuteron tensor polarization were carried out with use the Titan-Tritium target in the same reaction with registration of α-particles. Our result is \({{P}_{{zz}}} = - 0.10 \pm 0.02\) for weak magnetic field 1 mT on the target. This corresponds to the vector polarization \( \approx 0.24\).

The negative sign of tensor polarization, also, is in agreement with the result of Kaminsky. During this experiment the goniometer was at a random position. This means that nonchanneled atoms also polarized, at last means, particularly.

In first experiment the only one magnet of Sona transition system was used. Theoretically, the total inclusion of Sona system will increase the vector polarization up to 2/3.

The deuteron polarization in the polarized target can be increased from present 40 up to 80% by use trityl radical as a dopant to the target material.