Research and Development of the Polarized Deuteron Source for the Van de Graaff Accelerator

Abstract

An attempt is made to develop a polarized deuteron source suited for the Van de Graaff accelerator of Czech Technical University in Prague. We based on Kaminsky’s experiment on channeling deuterons through a Ni single crystal. The setup is described, which contains permanent magnets with a transversal magnetic field to increase the deuteron polarization using Sona-method (zero transition). The measurements of tensor polarization were carried out with TiT target. The result is ${{P}_{{zz}}} = - 0.12 \pm 0.04$ for a weak field at the target without channeling. The ultimate aim is to produce 14-MeV polarized neutrons which will be used jointly with the frozen-spin polarized deuteron target for measurement $\Delta {{\sigma }_{T}}$ and $\Delta {{\sigma }_{L}}$ asymmetries in the $nd$‑transmission experiment.

1 INTRODUCTION

Formally, measurement of spin-dependent parameters allows imposing additional constraints on the reaction mechanism and the structure of the micro-object under study. For example, measurements of $\Delta {{\sigma }_{T}}$ and $\Delta {{\sigma }_{L}}$ are necessary to determine the imaginary part of the $nd$ forward elastic scattering amplitude [1]. These measurements are important for the problem of 3-nucleon forces [2].

The total cross-section difference ${{(\Delta {{\sigma }_{L}})}_{d}}$ was measured at TUNL (North Carolina) [3] for the incident neutron energies of 5.0, 6.9 and 12.3 MeV.

In the previous experiments on $np$-scattering (Prague, Charles University) [4, 5], transversely polarized neutrons were produced as a secondary beam in the T${{(d,n)}^{4}}$He reaction with deuterons with energies up to 2.5 MeV [6]. The neutron beam with an energy ${{E}_{n}} = 16.2$ MeV was emitted at an angle ${{\theta }_{{{\text{lab}}}}} = 62.0^\circ .$ The neutron polarization was ${{P}_{n}} = - 0.135 \pm 0.014.$ To get longitudinal beam polarization in the ${{(\Delta {{\sigma }_{L}})}_{p}}$ experiment, the neutron spin was rotated with the help of a permanent magnet of 0.5 T m. The associated particle method was used in the experiments.

The planned experiments are continuation in the Czech Technical University in Prague of the previous measurements of the same quantities in $np$-scattering.

Preliminary experiments showed that the polarization and intensity of the neutron beam and also the deuteron polarization of the target are insufficient for achieving the necessary accuracy of the measurement of the cross-section difference [7]. To improve the parameters of the neutron beam, it is proposed to use the reaction T${{(d,n)}^{4}}$He with polarized deuterons with an energy of 100–150 keV. Also, we plan to replace the current target material (propanediol) with a novel material chemically doped with the trityl family radicals, which showed the deuteron polarization as high as ${{P}_{d}} = 0.80$ [8].

As to the polarized beam, the first proposal concerning the nuclear polarization via a pick-up of polarized ferromagnetic electrons was made by Zavoiskii in 1957 [9]. The method proposes adiabatic transition of atoms from a high magnetic field to a low magnetic field on the order of 1 mT where nuclei are polarized through the hyperfine interaction.

Here we rely on the results of the experiment by Kaminsky [10] on the production of nuclear polarized deuterium atoms by channeling a low energy deuteron beam through a magnetized single-crystal nickel foil.

In Kaminsky’s setup a beam of deuterons with a half angle of 0.01° was incident on a Ni(110) foil ≈2 μm thick within 0.1° of the [110] direction (the critical acceptance angle (1.6–1.8)°). This is a hyperchanneling regime. He obtained 500 nA/cm² of channeled deuterium atoms with an energy of 100–200 keV with nuclear polarization ${{P}_{{zz}}} = - 0.32 \pm 0.010$ (without a significant lattice damage for 25 h of operating time). To test Zavoiskii’ proposal the author passed deuterons through magnetized polycrystalline foils and observed no significant tensor polarization (i.e. ${{P}_{{zz}}} \approx 0$).

Feldman et al. [11] also made polarization measurements with an experimental arrangement very similar to that of Kaminsky. Their data qualitatively agree with Kaminsky’s data (${{P}_{{zz}}} = - 0.14 \pm 0.06$). Also, as in Kaminsky’s experiment, no effect was seen for polycrystalline foils. In addition, these authors attempted to observe an effect using thin polycrystalline foils of Fe. No effect was seen, possibly because of the presence of fairly thick (50–100 Å) surface oxide layers.

Quite a different electron field-emission experiment [12] on Ni showed that electrons emitted along the [100], [110] and [137] directions had predominantly spin-up (along the magnetic field), but when emitted along the [111] directiom they had a spin-down.

Rau and Sizmann [13], who also used the ³H(d,n)⁴He reaction, measured polarization of nuclei in neutral deuterium atoms created by electron capture during reflection of a 150-keV D⁺ beam incident at glancing angles (<0.4°) on the surface of magnetized Ni crystals.

The results show that the electron spin orientation is predominantly parallel to the magnetizing field for electrons in the (100), (110), and (111) surfaces and antiparallel in the (120) surface. In the (110) surface the electron polarization is $P = 96\%$ [14]. This explains the high polarization in Kaminsky’ experiment.

On the other hand, there is evidence for polarization of $1s$ electrons (${{P}_{{1s}}} = 0.10 \pm 0.03$) attached to F ions as they emerge from magnetized polycrystalline Fe layers [15].

It was found that a vacuum of 2 × 10^–8 Torr was necessary in order to see polarization effects. If the vacuum was allowed to deteriorate to $5 \times {{10}^{{ - 6}}}$ Torr, the polarization gradually vanishes, presumably as a result of the build-up of thin layers of surface contaminants.

2 THEORY

Ebel [16] tried to explain the high observed polarization by postulating that once a deuteron has captured a spin-up electron inside the crystal, the probability of its losing this electron would be small since the spin-up 3d-band states are filled. A captured spin-down electron, on the other hand, could readily be lost since the spin-down 3d-band states in the crystal are not filled. This would give rise to a pumping of electrons from spin-down to spin-up atomic states of deuterium.

Brandt and Sizmann [17], however, pointed out that stable bound electronic states could not exist in deuterium atoms passing through metals at these velocities. They proposed instead that the electron capture took place in the tail of the electron density distribution at the crystal surface where the density was low enough for bound states to be stable.

Later, Kreussler and Sizmann [18] discussed that at high energies (more than 250 keV/amu) neutralization took place chiefly in the bulk of the crystal and the surface effects were important at lower energies.

Kaminsky did not measure the polarization of nonchanneled atoms. We may suppose that the channeling is not essential, and the electron polarization in the neutral beam is determined by the polarization of the electrons at the surface.

3 EXPERIMENTAL SETUP

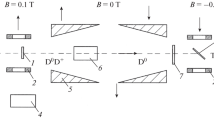
The scheme of the experimental setup is shown in Fig. 1. We propose to apply the Sona method, zero-field transitions with total transfer of the electron polarization to deuterons in the atomic beam [19]. We use two permanent magnets (2 × 20 cm) with a changing distance between the poles (${{B}_{{{\text{max}}}}} = 0.08$ T). The charged deuterons are deflected by the magnetic and electric fields. The Ni foil and the target of a polarimeter are placed in oppositely directed magnetic fields.

Fig. 1.

Scheme of the polarized deuteron source; (1) nickel foil, (2) permanent magnet (0.07 T), (3) solid state detector, (4) a goniometer, (5) polarizing permanent magnets (for the Sona transitions), (6) electrostatic plates, (7) the target of a polarimeter.

The magnetic field is directed along the foil plane (vertically), and we must use Sona transitions with vertical magnetic fields. This is different from the standard configuration.

The single-crystal nickel foils of thickness up to 2 μm are grown epitaxially on NaCl crystals cleaved to expose the (110) plane (produced by Princeton Scientific Corp.). The substrate was dissolved by water and the Ni foils were floated on the Cu disc mounted on the goniometer.

Vacuum of better then 10^–4 Pa was used.

The atomic beam in a strong magnetic field has vector polarization of deuterons up to the theoretical limit ${{P}_{3}} = {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ and zero tensor polarization.

If we pass the deuterium beam to a tritium target, 14-MeV neutrons of the $dt$-reaction produced at an angle of 90° (center of mass) have almost the same vector polarization as the deuterons [20].

4 POLARIMETRY

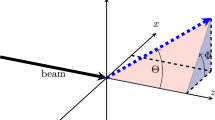
The deuteron vector polarization may be measured using the reaction D($d,p$)T [21]. The polarimeter target consisted of deuterated polyethylene with a thickness of about 2–3 μm on a Cu support. The protons produced in this reaction were detected by two surface barrier detectors, each having an effective area of 20 mm².

The detectors were placed symmetrically at ±120° with respect to the beam axis, and the solid angle was ≈1 msr. In order to suppress the elastically scattered deuterons, ³H and ³He, each detector was masked with a 10-μm-thick aluminum foil. For deuteron with an energy of 400 keV the expected count rate is 4 s^–1 per 1 μA of neutral deuterium atoms on the target. The range in CD₂ is 0.4 μm.

For a vector polarized beam the particle intensities detected by two detectors placed on the right and on the left of the beam axis are proportional to the cross sections ${{\sigma }_{{\text{R}}}}(\theta )$ and ${{\sigma }_{{\text{L}}}}(\theta ),$ respectively,

$${{\sigma }_{{\text{R}}}}(\theta ) = {{\sigma }_{{0{\text{R}}}}}(\theta )\left[ {1 - \frac{3}{2}{{P}_{z}}{{A}_{y}}(\theta )} \right],$$

((1))

and

$${{\sigma }_{{\text{L}}}}(\theta ) = {{\sigma }_{{0{\text{L}}}}}(\theta )\left[ {1 + \frac{3}{2}{{P}_{z}}{{A}_{y}}(\theta )} \right],$$

((2))

where ${{A}_{y}}(\theta )$ is the Cartesian analyzing power for the reaction.

Replacing the cross sections by the corresponding right and left detector intensities, ${{N}_{{\text{R}}}}$ and ${{N}_{{\text{L}}}},$ for polarized beam and ${{N}_{{0{\text{R}}}}},$${{N}_{{0{\text{L}}}}}$ for unpolarized beam, we obtain

$$\frac{{{{N}_{{\text{R}}}}(\theta )}}{{{{N}_{{\text{L}}}}(\theta )}}\frac{{{{N}_{{0{\text{L}}}}}(\theta )}}{{{{N}_{{0{\text{R}}}}}(\theta )}} = \frac{{1 - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}{{P}_{z}}{{A}_{y}}(\theta )}}{{1 + {{{{3 \mathord{\left/ {\vphantom {3 {2P}}} \right. \kern-0em} {2P}}}}_{z}}{{A}_{y}}(\theta )}}.$$

((3))

Designating

$$\kappa = \frac{{{{N}_{{\text{R}}}}(\theta )}}{{{{N}_{{\text{L}}}}(\theta )}} \times \frac{{{{N}_{{0{\text{L}}}}}(\theta )}}{{{{N}_{{0{\text{R}}}}}(\theta )}},$$

((4))

one obtains

$${{P}_{z}} = \frac{{1 - \kappa }}{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}(\kappa + 1){{A}_{y}}(\theta )}}.$$

((5))

The statistical error is

$$\delta P_{z}^{2} = \frac{{16}}{{9{{{(\kappa + 1)}}^{4}}A_{y}^{2}}}\delta {{\kappa }^{2}} + \frac{{P_{z}^{2}}}{{A_{y}^{2}}}\delta A_{y}^{2},$$

((6))

where

$$\delta \kappa = \kappa \sqrt {\frac{1}{{{{N}_{{\text{R}}}}}} + \frac{1}{{{{N}_{{\text{L}}}}}} + \frac{1}{{{{N}_{{{\text{R}}0}}}}} + \frac{1}{{{{N}_{{{\text{L}}0}}}}}} .$$

((7))

According to the calculations, for the real magnetic field value the tensor polarization after the Sona transitions is not equal zero, ${{P}_{{zz}}} \approx 0.1.$ In this case we use the general formula

$$\begin{gathered} \sigma (\theta ,\phi ) = \left[ {1 + \frac{3}{2}} \right.\sin\beta \cos\phi {{P}_{z}}{{A}_{y}}(\theta ) \\ - \,\,\cos\beta \sin\beta \sin\phi {{P}_{{zz}}}{{A}_{{xz}}}(\theta ) \\ \end{gathered} $$

((8))

$$\begin{gathered} - \frac{1}{4}{{\sin}^{2}}\beta \cos2\phi {{P}_{{zz}}}{{A}_{{xx - yy}}}(\theta ) \\ + \,\,\left. {\frac{1}{4}(3{{\cos}^{2}}\beta - 1){{P}_{{zz}}}{{A}_{{zz}}}(\theta )} \right], \\ \end{gathered} $$

((9))

For $\beta = 90^\circ$ and $\phi = 0^\circ$

$$\begin{gathered} {{\sigma }_{{\text{L}}}}(\theta ) = {{\sigma }_{{0{\text{L}}}}}(\theta ) \\ \times \,\,\left[ {1 + \frac{3}{2}{{P}_{z}}{{A}_{y}}(\theta ) - \frac{1}{4}{{P}_{{zz}}}{{A}_{{xx - yy}}}(\theta ) - \frac{1}{4}{{P}_{{zz}}}{{A}_{{zz}}}(\theta )} \right], \\ \end{gathered} $$

((10))

and for $\phi = 180^\circ$

$$\begin{gathered} {{\sigma }_{{\text{R}}}}(\theta ) = {{\sigma }_{{0{\text{R}}}}}(\theta ) \\ \times \,\,\left[ {1 - \frac{3}{2}{{P}_{z}}{{A}_{y}}(\theta ) - \frac{1}{4}{{P}_{{zz}}}{{A}_{{xx - yy}}}(\theta ) - \frac{1}{4}{{P}_{{zz}}}{{A}_{{zz}}}(\theta )} \right]. \\ \end{gathered} $$

((11))

According to Ad’yasevich [22], at 300 keV ${{A}_{{zz}}} = {{A}_{{xx - yy}}} \approx 0,$ at 400 keV ${{A}_{{zz}}} = - {{A}_{{xx - yy}}} = - 0.1$ and in this energy range additional terms can be neglected.

The measurements of deuteron vector polarization are in progress.

The tensor polarization was estimated with TiT target by measuring the angular distribution of $\alpha$-particles emitted in the reaction T${{(d,n)}^{4}}$He [23].

The cross section depends on the c.m. angle between the spin and the particle direction:

$$\sigma (\theta ) = {{\sigma }_{0}}\left[ {1 - \frac{1}{4}(3{{\cos}^{2}}\theta - 1){{P}_{{zz}}}} \right].$$

((12))

As a result, ${{P}_{{zz}}} = - 0.12 \pm 0.04$ (theoretical value is ${{P}_{{zz}}} = - 0.33$ at the deuteron energy of 500 keV for the foil thickness 1.5 μm (real energy is 250 keV). Feldman’s result is ${{P}_{{zz}}} = - 0.14 \pm 0.06.$ During the first experiments the goniometer was at a random position, and we used only one magnet of the Sona transition system.

5 ADIABATICITY

The polarized deuterium atoms enter a region where the value ${{B}_{z}} = {{B}_{0}}(1 - {{2x} \mathord{\left/ {\vphantom {{2x} L}} \right. \kern-0em} L})$ is decreasing , and if this decrease is slow enough (adiabatic), each state follows the corresponding energy line. Ionization at a low field gives ideally the deuteron tensor polarization ${{P}_{{zz}}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}$ and vector polarization ${{P}_{z}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}.$

We have to take into account the finite beam dimension, and therefore the presence of the transverse component ${{B}_{x}} = {{{{z}_{1}}d{{B}_{z}}} \mathord{\left/ {\vphantom {{{{z}_{1}}d{{B}_{z}}} {dx}}} \right. \kern-0em} {dx}} = - \tfrac{{2{{B}_{0}}}}{L}{{z}_{1}},$${{z}_{1}} = {{z}_{0}} + \alpha x,$${{B}_{y}} = 0.$ For estimate we set $\alpha = 0.$

A particle off-axis never “sees” a field going exactly to zero, but a field which in a “short” but finite time changes continuously its direction by 180°, taking its minimum value when it is normal to the beam direction.

We begin from the Schrödinger equation for movement along the axis $x$

$$\begin{gathered} \frac{{d\psi (x)}}{{dx}} = - \frac{i}{{\hbar v}}\hat {H}(x)\psi (x) \\ = - \frac{i}{{\hbar v}}[ - {{\mu }_{J}}{{{\hat {\sigma }}}_{J}}{\mathbf{B}}(x) - {{\mu }_{d}}{{{{\mathbf{\hat {S}}}}}_{d}}{\mathbf{B}}(x) + \frac{1}{3}\Delta W{{{\hat {\sigma }}}_{J}}{{{{\mathbf{\hat {S}}}}}_{d}}]\psi (x), \\ \end{gathered} $$

((13))

where $v = \sqrt {{{2{{E}_{d}}} \mathord{\left/ {\vphantom {{2{{E}_{d}}} {{{m}_{d}}}}} \right. \kern-0em} {{{m}_{d}}}}} ,$ for ${{E}_{d}} = 100$ keV, $v = 3 \times {{10}^{6}}$ m/s,

$$\begin{gathered} \psi (x) = {{C}_{1}}(x)\varphi _{e}^{ + }\varphi _{d}^{ + } + {{C}_{2}}(x)\varphi _{e}^{ + }\varphi _{d}^{0} + {{C}_{3}}(x)\varphi _{e}^{ + }\varphi _{d}^{ - } \\ + \,\,{{C}_{4}}(x)\varphi _{e}^{ - }\varphi _{d}^{ + } + {{C}_{5}}(x)\varphi _{e}^{ - }\varphi _{d}^{0} + {{C}_{6}}(x)\varphi _{e}^{ - }\varphi _{d}^{ - }. \\ \end{gathered} $$

((14))

The results of calculations are presented in Tables 1–3. The polarization values are P_z = |C₁|² + |C₄|² – ${{\left| {{{C}_{3}}} \right|}^{2}} - {{\left| {{{C}_{6}}} \right|}^{2}}$ and ${{P}_{{zz}}} = 1 - 3({{\left| {{{C}_{2}}} \right|}^{2}} + {{\left| {{{C}_{5}}} \right|}^{2}}).$

Table 1.   Zero transition

Table 2.   Zero transition

Table 3.   Transition to the field 1 mT

We make the approximate estimates, in which we compare the angular velocity of magnetic field and the spin precession. The angular velocity of the magnetic field rotation ω_B, as seen by a particle travelling with the velocity $v$ and at the distance $z$ from the central plane is following from the equation

$$\coth\theta = \frac{{{{B}_{x}}}}{{{{B}_{z}}}},\,\,\,\,\,\frac{1}{{{{\sin}^{2}}\theta }}\frac{{d\theta }}{{dx}} = \frac{1}{{{{z}_{1}}}},\,\,\,\,\frac{{d\theta }}{{dx}} = \frac{1}{{{{z}_{1}}}}\frac{{B_{z}^{2}}}{{B_{x}^{2} + B_{z}^{2}}}.$$

((15))

Generally,

$${{\omega }_{B}}(x) = \frac{{d\theta }}{{dx}}v = \frac{{4{{z}_{1}}v}}{{{{L}^{2}}[{{{(1 - {{2x} \mathord{\left/ {\vphantom {{2x} L}} \right. \kern-0em} L})}}^{2}} + {{4z_{1}^{2}} \mathord{\left/ {\vphantom {{4z_{1}^{2}} {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}}]}}.$$

((16))

In zero crossing point (${{B}_{x}} = 0$), the angular velocity of the rotation of the field ${{\omega }_{B}}$ is

$${{\omega }_{B}}({L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}) = \frac{v}{{{{z}_{1}}}}.$$

((17))

At $x = 0$ the velocity of the magnetic field rotation is

$${{\omega }_{B}}(0) = \frac{{4{{z}_{1}}v}}{{{{L}^{2}}(1 + {{4z_{1}^{2}} \mathord{\left/ {\vphantom {{4z_{1}^{2}} {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}})}}.$$

((18))

The angular velocity of the spin precession ${{\omega }_{P}}$ is

$$\begin{gathered} {{\omega }_{P}}(x) = \frac{1}{\hbar }\left[ {\frac{{\Delta W}}{2} - {{\mu }_{e}}B(x) - \frac{{{{\mu }_{d}}B(x)}}{2}} \right. \\ \left. { - \,\,\frac{{\Delta W}}{2}\sqrt {1 + \frac{2}{3}X(x) + X{{{(x)}}^{2}}} } \right], \\ \end{gathered} $$

((19))

where

$$\begin{gathered} B(x) = \sqrt {{{B}_{x}}{{{(x)}}^{2}} + B_{z}^{2}} = {{B}_{0}}\sqrt {{{{\left( {1 - \frac{{2x}}{L}} \right)}}^{2}} + \frac{{4z_{1}^{2}}}{{{{L}^{2}}}}} , \\ X(x) = \frac{{B(x)}}{{{{B}_{c}}}}. \\ \end{gathered} $$

((20))

The angular velocity of the precession in zero crossing is

$${{\omega }_{P}}({L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}) = \frac{{2{{\mu }_{e}}}}{{3\hbar }}B({L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}) = \frac{{2{{\mu }_{e}}}}{{3\hbar }}{{B}_{z}} = \frac{{2{{\mu }_{e}}}}{{3\hbar }}\frac{{2{{B}_{0}}z}}{L}.$$

((21))

For ${{B}_{0}} = 7 \times {{10}^{{ - 2}}}$ T, ${{z}_{1}} = 2$ mm, $L = 0.4$ m and the atom velocity $v = 4 \times {{10}^{6}}$ m/s, ${{\omega }_{B}}({L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}) = 2 \times {{10}^{9}}$ rad/s, and ${{\omega }_{P}}({L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}) = 3.9 \times {{10}^{7}}$ rad/s.

Thus, the velocity of precession of the atoms in the zero transition region $3.9 \times {{10}^{7}}$ rad/s is much less than the velocity of field rotation $2 \times {{10}^{9}}$ rad/s, i.e. the spin does not follow the field.

At $x = 0$ the velocity of the magnetic field rotation is ${{\omega }_{B}}(0) = 2 \times {{10}^{5}}$ rad/s, and the angular velocity of precession is ${{\omega }_{p}}(0) = 6.109 \times {{10}^{8}}$ rad/s.

So, we have adiabatic transition.

Fig. 2.

Photo of the experimental setup.

Fig. 3.

Goniometer.

Fig. 4.

Au-foil.

Fig. 5.

Magnets.

6 CONCLUSIONS

The experimental setup has been developed to produce the beam of deuterium atoms of energies 100–400 keV with polarized nuclei and to measure vector and tensor polarizations of deuterons.

The ultimate aim is to produce a highly polarized 14-MeV neutron beam for measuring the neutron-deuteron total cross section differences $\Delta {{\sigma }_{L}}(nd)$ and $\Delta {{\sigma }_{T}}(nd)$ using the frozen-spin polarized deuteron target (as first experiment).

To improve the parameters of the neutron beam it is proposed to use the reaction T${{(d,n)}^{4}}$He with polarized deuterons of an energy 100–150 keV.

For a nonchanneled beam (the goniometer is in a random position), the tensor polarization measurements were carried out with a TiT target in the reaction T${{(d,n)}^{4}}$He. Our result is ${{P}_{{zz}}} = - 0.12 \pm 0.04$ for weak field at the target. Feldman’s result is ${{P}_{{zz}}} = - 0.14 \pm 0.06.$

We continue experiments to get the nuclear polarized deuterium beam with an energy of about 150 keV and vector polarization up to 2/3 via pick-up of electrons in a magnetized single crystal nickel foil.