INTRODUCTION

Rare decays of bottom hadrons are of extreme importance both in precision tests of the Standard Model (SM) and in searches of New Physics (NP). A majority of such processes are due to the \(b \to s\) and \(b \to d\) Flavor-Changing Neutral Currents (FCNCs). Decays due to the \(b \to s\) quark transition are the most studied, as a lot of experimental measurements are already done. Similar decays induced by the \(b \to d\) FCNC are less attractive because there is still a little information about them. So, the \({{B}^{ + }} \to {{\pi }^{ + }}{{\mu }^{ + }}{{\mu }^{ - }}\) decay is one of such processes which is relatively well studied both theoretically and experimentally. Predictions including subleading contributions [1–3] give a better agreement with experimental data by the LHCb Collaboration [4]. It is also of interest to consider its tauonic counterpart, \({{B}^{ + }} \to {{\pi }^{ + }}{{\tau }^{ + }}{{\tau }^{ - }}\), as a decay to be searched for at the SuperKEKB factory and possibly at the LHC. In the paper we present theoretical analysis of this rare decay. We obtain SM predictions for the ditauon invariant mass distirbution and decay width for various types of form factor parameterizations of the \(B \to \pi \) transition. We estimate also the ratio \({{R}_{\pi }}(\tau /\mu )\) which is the ratio of the taounic branching fraction to the muonic one.

THEORY OF RARE SEMILEPTONIC \(B\)-MESON DECAYS

Theoretical analysis of rare \(B\)-decays is convenient to do within the framework of effective electroweak Hamiltonians. This theory is derived from the SM by integrating out heavy particles—the top quark and \(W\)‑, \(Z\)- and Higgs bosons [5, 6]. The rare \({{B}^{ + }} \to {{\pi }^{ + }}{{\ell }^{ + }}{{\ell }^{ - }}\) decay is induced by the \(b \to d\) FCNC Hamiltonian [5]:

$$\mathcal{H}_{{{\text{weak}}}}^{{b \to d}} = - \frac{{4{{G}_{F}}}}{{\sqrt 2 }}\sum\limits_{p = u,c} V_{{pd}}^{*}V_{{pb}}^{{}}\sum\limits_j {{C}_{j}}(\mu ){{\mathcal{P}}_{j}}(\mu ) + {\text{h}}{\text{.}}{\kern 1pt} {\text{c}}.,$$
(1)

where \({{G}_{F}}\) is the Fermi constant, \({{C}_{j}}(\mu )\) are Wilson coefficients, \({{\mathcal{P}}_{j}}(\mu )\) are the local \(b \to d\) transition operators, \({{V}_{{{{q}_{1}}{{q}_{2}}}}}\) is the CKM matrix element. The \({{\mathcal{P}}_{j}}(\mu )\) operator basis includes 10 operators [6]. The leading-order contribution to the \({{B}^{ + }} \to {{\pi }^{ + }}{{\ell }^{ + }}{{\ell }^{ - }}\) decay amplitude is given by the following operators:

$${{\mathcal{P}}_{{7\gamma }}} = \frac{e}{{16{{\pi }^{2}}}}\left[ {\bar {d}{{\sigma }^{{\mu \nu }}}({{m}_{b}}R + {{m}_{d}}L)b} \right]{{F}_{{\mu \nu }}},$$
(2)
$$\begin{gathered} {{\mathcal{P}}_{{9\ell }}} = \frac{\alpha }{{2\pi }}(\bar {d}{{\gamma }_{\mu }}Lb)\sum\limits_\ell (\bar {\ell }{{\gamma }^{\mu }}\ell ), \\ {{\mathcal{P}}_{{10\ell }}} = \frac{\alpha }{{2\pi }}(\bar {d}{{\gamma }_{\mu }}Lb)\sum\limits_\ell (\bar {\ell }{{\gamma }^{\mu }}{{\gamma }^{5}}\ell ), \\ \end{gathered} $$
(3)

where \(L,R = \left( {1 \mp {{\gamma }_{5}}} \right)/2\) are the fermionic left- and right-handed projectors, \({{F}_{{\mu \nu }}}\) is the electromagnetic field strength tensor, \({{m}_{b}}\) and \({{m}_{d}}\) are \(b\)- and \(d\)-quark masses, \({{\sigma }^{{\mu \nu }}} = i\left( {{{\gamma }_{\mu }}{{\gamma }_{\nu }} - {{\gamma }_{\nu }}{{\gamma }_{\mu }}} \right)/2\), and \(\alpha = {{e}^{2}}{\text{/}}(4\pi )\) is fine structure constant. The summation index \(\ell \) covers all the charged leptons.

The \(B \to \pi \) transition matrix elements are expressed in terms of three transition form factors \({{f}_{ + }}({{q}^{2}})\), \({{f}_{0}}({{q}^{2}})\), and \({{f}_{T}}({{q}^{2}})\), where \({{q}^{\mu }} = p_{B}^{\mu } - p_{\pi }^{\mu }\) is the four-momentum transferred to the lepton pair [7]:

$$\begin{gathered} \left\langle {\pi ({{p}_{\pi }})\left| {\bar {d}{{\gamma }^{\mu }}b} \right|B({{p}_{B}})} \right\rangle = {{f}_{ + }}({{q}^{2}})\left[ {p_{B}^{\mu } + p_{\pi }^{\mu } - \frac{{m_{B}^{2} - m_{\pi }^{2}}}{{{{q}^{2}}}}{{q}^{\mu }}} \right] \\ + \,\,{{f}_{0}}({{q}^{2}})\frac{{m_{B}^{2} - m_{\pi }^{2}}}{{{{q}^{2}}}}{\kern 1pt} {{q}^{\mu }}, \\ \end{gathered} $$
(4)
$$\begin{gathered} \left\langle {\pi ({{p}_{\pi }})\left| {\bar {d}{{\sigma }^{{\mu \nu }}}{{q}_{\nu }}b} \right|B({{p}_{B}})} \right\rangle \\ = i\left[ {\left( {p_{B}^{\mu } + p_{\pi }^{\mu }} \right){{q}^{2}} - {{q}^{\mu }}\left( {m_{B}^{2} - m_{\pi }^{2}} \right)} \right]\frac{{{{f}_{T}}({{q}^{2}})}}{{{{m}_{B}} + {{m}_{\pi }}}}, \\ \end{gathered} $$
(5)

where \({{m}_{B}}\) and \({{m}_{\pi }}\) are the \(B\)- and \(\pi \)-meson masses.

The \(B \to \pi {{\ell }^{ + }}{{\ell }^{ - }}\) differential branching fraction including subleading contributions can be presented as follows [2, 3]:

$$\begin{gathered} \frac{{d{\kern 1pt} {\text{Br}}{\kern 1pt} \left( {B \to \pi {{\ell }^{ + }}{{\ell }^{ - }}} \right)}}{{d{{q}^{2}}}} \\ = {{S}_{\pi }}\frac{{2G_{F}^{2}{{\alpha }^{2}}{{\tau }_{B}}}}{{3(4\pi {{)}^{5}}m_{B}^{3}}}{{\left| {{{V}_{{tb}}}V_{{td}}^{*}} \right|}^{2}}{{\lambda }^{{3/2}}}({{q}^{2}}){{F}^{{B\pi }}}({{q}^{2}})\sqrt {1 - \frac{{4m_{\ell }^{2}}}{{{{q}^{2}}}}} , \\ \end{gathered} $$
(6)
$$\begin{gathered} {{F}^{{B\pi }}}({{q}^{2}}) = F_{{97}}^{{B\pi }}({{q}^{2}}) + F_{{10}}^{{B\pi }}({{q}^{2}}), \\ \lambda ({{q}^{2}}) = (m_{B}^{2} + m_{\pi }^{2} - {{q}^{2}}{{)}^{2}} - 4m_{B}^{2}m_{\pi }^{2}, \\ \end{gathered} $$
(7)
$$\begin{gathered} F_{{97}}^{{B\pi }}({{q}^{2}}) = \left( {1 + \frac{{2m_{\ell }^{2}}}{{{{q}^{2}}}}} \right)\left| {C_{9}^{{{\text{eff}}}}({{q}^{2}}){\kern 1pt} f_{ + }^{{B\pi }}({{q}^{2}}) + \frac{{2{{m}_{b}}C_{7}^{{{\text{eff}}}}({{q}^{2}})}}{{{{m}_{B}} + {{m}_{\pi }}}}} \right. \\ {{\left. {{{ \times }^{{^{{^{{}}}}}}}f_{T}^{{B\pi }}({{q}^{2}}) + L_{A}^{{B\pi }}({{q}^{2}}) + \Delta C_{V}^{{B\pi }}({{q}^{2}})} \right|}^{2}}, \\ \end{gathered} $$
(8)
$$\begin{gathered} F_{{10}}^{{B\pi }}({{q}^{2}}) = \left( {1 - \frac{{4m_{\ell }^{2}}}{{{{q}^{2}}}}} \right){{\left| {C_{{10}}^{{{\text{eff}}}}{\kern 1pt} f_{ + }^{{B\pi }}({{q}^{2}})} \right|}^{2}} \\ + \,\,\frac{{6m_{\ell }^{2}}}{{{{q}^{2}}}}{\kern 1pt} \frac{{{{{\left( {m_{B}^{2} - m_{\pi }^{2}} \right)}}^{2}}}}{{\lambda ({{q}^{2}})}}{{\left| {C_{{10}}^{{{\text{eff}}}}{\kern 1pt} f_{0}^{{B\pi }}({{q}^{2}})} \right|}^{2}}, \\ \end{gathered} $$
(9)

where \({{S}_{\pi }}\) is an isospin factor of the final meson (\({{S}_{{{{\pi }^{ \pm }}}}} = 1\) and \({{S}_{{{{\pi }^{0}}}}} = 1/2\)), \(C_{{7,9,10}}^{{{\text{eff}}}}\) are the effective Wilson coefficients including the NLO QCD corrections [8], \(L_{A}^{{B\pi }}({{q}^{2}})\) is the Weak Annihilation (WA) contribution, and \(\Delta C_{V}^{{B\pi }}({{q}^{2}})\) are the Long-Distance (LD) ones.

WA contribution [9] has a significant impact only at the beginning of the \({{q}^{2}}\)-spectrum, and its accounting makes sense for the \({{B}^{ + }} \to {{\pi }^{ + }}{{e}^{ + }}{{e}^{ - }}\) and \({{B}^{ + }} \to {{\pi }^{ + }}{{\mu }^{ + }}{{\mu }^{ - }}\) decays. LD contributions are originated by two-body decays, \(B \to V\pi \), where \(V = {{\rho }^{0}},\omega ,\phi ,J{\text{/}}\psi ,\psi (2S)\) are neutral vector mesons, followed by the leptonic decays, \(V \to {{\ell }^{ + }}{{\ell }^{ - }}\) [1]. For the \({{B}^{ + }} \to {{\pi }^{ + }}{{\tau }^{ + }}{{\tau }^{ - }}\) decay considered, the dominant contribution from the \(\psi (2S)\)-meson should be taken into account only, and this analysis is postponed for another publication.

The differential branching fraction (6) involves three \(B \to \pi \) transition form factors (FFs). Among available FF parameterizations, we adopt the following three: the Boyd–Grinstein–Lebed (BGL) [10], Bourrely–Caprini–Lellouch (BCL) [11] and modified Bourrely–Caprini–Lellouch (mBCL) [12].

NUMERICAL RESULTS FOR \({{B}^{ + }} \to {{\pi }^{ + }}{{\tau }^{ + }}{{\tau }^{ - }}\) DECAY

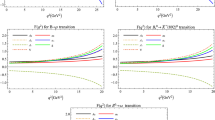
The dilepton invariant-mass distribution of the \({{B}^{ + }} \to {{\pi }^{ + }}{{\tau }^{ + }}{{\tau }^{ - }}\) decay for three types of the FF paramereterizations is presented in Fig. 1. As seen, theoretical predictions based on BGL parameterization are systematically above other types of parameterizations and the total branching fraction for BGL parameterization is the largest one (see Table 1). Our predictions for all the parameterizations in Table 1 are consistent with each other within uncertainties as well as with [13]. The ratios, \({{R}_{\pi }}(\tau {\text{/}}\mu )\), of the tauonic branching fraction to the muonic one are \(0.44 \pm 0.16\), \(0.31 \pm 0.12\), and \(0.37 \pm 0.15\) for the BGL, BCL, and mBCL parameterizations, respectively. As mentioned above, the largest ratio is for the BGL parameterization and the smallest one is for the BCL parameterization.

Fig. 1.
figure 1

The dilepton invariant-mass distribution of the \({{B}^{ + }} \to {{\pi }^{ + }}{{\tau }^{ + }}{{\tau }^{ - }}\) decay for BGL (upper left plot), BCL (upper right plot), and mBCL (bottom plot) FF parameterizations. The green areas indicate the uncertainty due to the factorization scale and CKM matrix element \({{V}_{{td}}}\).

Full size image
Table 1.   Theoretical predictions for the \({{B}^{ + }} \to {{\pi }^{ + }}{{\tau }^{ + }}{{\tau }^{ - }}\) total branching fraction
Full size table

CONCLUSIONS

Theoretical predictions for the \({{B}^{ + }} \to {{\pi }^{ + }}{{\tau }^{ + }}{{\tau }^{ - }}\) total branching fraction are obtained in the NLO for three types of the form factor parameterizations. The impact of the parameterization choice is strongly manifested by comparing BGL and BCL predictions and can be explained by the fact that FF expansion coefficients are determined in different \({{q}^{2}}\)-regions. Theoretical predictions for the semitauonic decay give a factor of 2 or 3 suppression in comparison with \({{B}^{ + }} \to {{\pi }^{ + }}{{\mu }^{ + }}{{\mu }^{ - }}\) already measured and it is an attractive process for experimental searches. Note that a detection of tauonic decays with a sufficient accuracy is planned by the Belle-II Collaboration on the scale of the integrated luminosity ~5 ab–1.