Rare Decays of Neutral B Mesons into Four Charged Leptons in the Standard Model

Abstract

As part of the Standard Model (SM), we present new theoretical predictions for the branching ratio and differential distributions for the ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ decay. We take into consideration the contributions ${{\rho }^{0}}(770)$ and $\omega (782)$ of resonances; the main contributions of four charmonium resonances: $\psi (3770)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$; the contributions of the tails from ${J \mathord{\left/ {\vphantom {J \psi }} \right. \kern-0em} \psi }$ and $\psi (2S)$ resonances; and the nonresonant contribution of the $b{\kern 1pt} \bar {b}$ pairs, bremsstrahlung, and the contribution of the weak annihilation. We use the model of vector meson dominance (VMD) for calculating resonances contributions.

INTRODUCTION

The investigation of four-lepton decays of neutral $B$ mesons is one of the main methods for testing the predictions of the Standard Model (SM) in higher orders of perturbation theory. From the structure of the Lagrangian describing the interaction of quarks with gauge bosons and the Higgs boson, it follows that, in the SM in the first order of the perturbation theory, neutral currents that change flavor (FCNC) are forbidden. Neutral currents that change the flavor of quarks can go into the SM in higher orders of perturbation theory due to loop corrections. Examples of FCNC processes are the decays of neutral $B$ mesons. This work is devoted to the study of decays of neutral $B$ mesons into four light charged leptons of different flavors in the final state, in particular, ultrarare decay ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$. There are currently two theoretical predictions for the characteristics of this decay [1, 2]. The experimental study of ultrarare decays of neutral $B$ mesons in the last 10 years has been carried out at the LHC [3–5].

1 DECAY AMPLITUDES ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$

Six main types of diagrams contribute to the decay amplitude ${{\bar {B}}_{d}}(p) \to {{\mu }^{ + }}({{k}_{1}}){{\mu }^{ - }}({{k}_{2}}){{e}^{ + }}({{k}_{3}}){{e}^{ - }}({{k}_{4}})$. The first corresponds to the situation when a virtual photon is emitted by a valence $\bar {d}$ quark of a ${{\bar {B}}_{d}}$ meson in one channel by a four-momentum and, in the other, the formation of a lepton pair occurs due to FCNC (see Fig. 1).

Fig. 1.

Diagrams corresponding to the emission of a virtual photon by the $\bar {d}$ quark of a ${{\bar {B}}_{d}}$ meson.

The second type of diagram refers to similar processes for a $b$ quark. In this case, the virtual photon is emitted by the valence $b$ quark of a ${{\bar {B}}_{d}}$ meson. Diagrams corresponding to these processes are shown in Fig. 2.

Fig. 2.

Diagrams corresponding to the emission of a virtual photon by the $b$ quark of a ${{\bar {B}}_{d}}$ meson.

The third and fourth types of diagrams are “penguin” diagrams arising from contributions of $u\bar {u}$ and $c\bar {c}$ pairs (see Fig. 3). Based on the general form of the Hamiltonian for the FCNC transition $b \to q{{\ell }^{ + }}{{\ell }^{ - }}$, the amplitude corresponding to the processes of emission of a virtual photon by the $d$ quark and contributions of $u\bar {u}$, $c\bar {c}$, and $b\bar {b}$ pairs can be represented in the following form:

$$\begin{gathered} \mathcal{M}_{{fi}}^{{(1234)}} = i{\kern 1pt} \sqrt 2 {{G}_{{\text{F}}}}\alpha _{{em}}^{2}{\kern 1pt} {{V}_{{tb}}}V_{{ts}}^{*}{{M}_{1}} \\ \times \,\,\left[ { - \frac{{{{a}^{{(VV)}}}}}{{M_{1}^{2}}}{\kern 1pt} {{\varepsilon }_{{\mu {\kern 1pt} \alpha {\kern 1pt} k{\kern 1pt} q}}} - i{{b}^{{(VV)}}}{\kern 1pt} {{g}_{{\mu \alpha }}} + 2i\frac{{{{c}^{{(VV)}}}}}{{M_{1}^{2}}}{{q}_{\alpha }}{{k}_{\mu }}} \right] \\ \times \,\,{{j}^{\mu }}({{k}_{2}},{\kern 1pt} {{k}_{1}}){\kern 1pt} {{J}^{\alpha }}({{k}_{4}},{\kern 1pt} {{k}_{3}}) + \left[ { - \frac{{{{a}^{{(VA)}}}}}{{M_{1}^{2}}}{{\varepsilon }_{{\mu \alpha kq}}}} \right. - i{{b}^{{(VA)}}}{{g}_{{\mu \alpha }}} \\ + \,\,2i\frac{{{{c}^{{(VA)}}}}}{{M_{1}^{2}}}{{q}_{\alpha }}{{k}_{\mu }} + \left. {i\frac{{{{g}^{{(VA)}}}}}{{M_{1}^{2}}}{\kern 1pt} {{k}_{\mu }}{{k}_{\alpha }}} \right]{{j}^{\mu }}({{k}_{2}},{{k}_{1}}){{J}^{{\alpha 5}}}({{k}_{4}},{{k}_{3}}){\kern 1pt} \\ + \,\,\left[ { - \frac{{{{a}^{{(AV)}}}}}{{M_{1}^{2}}}} \right.{{\varepsilon }_{{\mu \alpha kq}}} - i{{b}^{{(AV)}}}{{g}_{{\mu \alpha }}} + 2i\frac{{{{c}^{{(AV)}}}}}{{M_{1}^{2}}}{{q}_{\alpha }}{{k}_{\mu }} \\ + \,\,\left. {i\frac{{{{d}^{{(AV)}}}}}{{M_{1}^{2}}}{{q}_{\mu }}{{k}_{\alpha }}} \right]{{j}^{{\mu 5}}}({{k}_{2}},{{k}_{1}}){{J}^{\alpha }}({{k}_{4}},{{k}_{3}}){\kern 1pt} \\ + \,\,\left[ { - \frac{{{{a}^{{(AA)}}}}}{{M_{1}^{2}}}} \right.{\kern 1pt} {{\varepsilon }_{{\mu {\kern 1pt} \alpha {\kern 1pt} k{\kern 1pt} q}}} - i{{b}^{{(AA)}}}{\kern 1pt} {{g}_{{\mu \alpha }}} + 2i{\kern 1pt} \frac{{{{c}^{{(AA)}}}}}{{M_{1}^{2}}}{\kern 1pt} {{q}_{\alpha }}{{k}_{\mu }} \\ \left. { + \,\,i{\kern 1pt} \frac{{{{d}^{{(AA)}}}}}{{M_{1}^{2}}}{\kern 1pt} {{q}_{\mu }}{{k}_{\alpha }} + \left. {i{\kern 1pt} \frac{{{{g}^{{(AA)}}}}}{{M_{1}^{2}}}{\kern 1pt} {{k}_{\mu }}{{k}_{\alpha }}} \right]{\kern 1pt} {{j}^{{\mu {\kern 1pt} 5}}}({{k}_{2}},{\kern 1pt} {{k}_{1}}){\kern 1pt} {{J}^{{\alpha {\kern 1pt} 5}}}({{k}_{4}},{\kern 1pt} {{k}_{3}}){\kern 1pt} } \right], \\ \end{gathered} $$

(1)

where M₁ is weight, B_d is a meson, and four-momentums are given by equalities $q = {{k}_{1}} + {{k}_{2}}$ and $k = {{k}_{3}} + {{k}_{4}}$. The expressions for the currents are defined as

$$\begin{gathered} {{j}^{\mu }}({{k}_{2}},{\kern 1pt} {{k}_{1}}) = \bar {\mu }({{k}_{2}}){\kern 1pt} {{\gamma }^{\mu }}\mu ( - {{k}_{1}}),{\kern 1pt} {\kern 1pt} {{J}^{\alpha }}({{k}_{4}},{\kern 1pt} {{k}_{3}}) \\ = \bar {e}({{k}_{4}}){\kern 1pt} {{\gamma }^{\alpha }}{\kern 1pt} e( - {{k}_{3}}); \\ {{j}^{{\mu {\kern 1pt} 5}}}({{k}_{2}},{\kern 1pt} {{k}_{1}}) = \bar {\mu }({{k}_{2}}){\kern 1pt} {{\gamma }^{\mu }}{\kern 1pt} {{\gamma }^{5}}{\kern 1pt} \mu ( - {{k}_{1}}),{\kern 1pt} {\kern 1pt} {{J}^{{\alpha {\kern 1pt} 5}}}({{k}_{4}},{\kern 1pt} {{k}_{3}}) \\ = \bar {e}({{k}_{4}}){\kern 1pt} {{\gamma }^{\alpha }}{\kern 1pt} {{\gamma }^{5}}{\kern 1pt} e( - {{k}_{3}}). \\ \end{gathered} $$

Fig. 3.

Penguin diagrams corresponding to loop contributions of $c$ and $u$ quarks.

Form factors ${{a}^{{(IJ)}}} \equiv {{a}^{{(IJ)}}}({{x}_{{12}}},{\kern 1pt} {{x}_{{34}}})$, ${{b}^{{(IJ)}}} \equiv$ ${{b}^{{(IJ)}}}({{x}_{{12}}},{\kern 1pt} {{x}_{{34}}})$, ${{c}^{{(IJ)}}} \equiv {{c}^{{(IJ)}}}({{x}_{{12}}},{\kern 1pt} {{x}_{{34}}}),$ ${{d}^{{(IJ)}}} \equiv {{d}^{{(IJ)}}}({{x}_{{12}}},{\kern 1pt} {{x}_{{34}}})$, and ${{g}^{{(IJ)}}} \equiv {{g}^{{(IJ)}}}({{x}_{{12}}},{\kern 1pt} {{x}_{{34}}})$ are dimensionless, where $IJ = \{ VV,{\kern 1pt} VA,{\kern 1pt} AV,{\kern 1pt} AA\}$, ${{x}_{{12}}} = \frac{{{{q}^{2}}}}{{{{M}_{1}}}}$, and ${{x}_{{34}}} = \frac{{{{k}^{2}}}}{{{{M}_{1}}}}$. In this article, due to its cumbersome nature, the explicit form of these functions is not given.

The fifth kind of diagrams refers to bremsstrahlung, when a virtual photon is emitted by a lepton in the final state (see Fig. 4).

As an example of the amplitude of the bremsstrahlung process, which contributes to the decay amplitude ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$, we can give an expression describing the contribution the ${{\mu }^{ + }}{{\mu }^{ - }}$ pair emitted by the electron and positron in the final state:

$$\begin{gathered} \mathcal{M}_{{fi}}^{{(\mu )}} = i\sqrt 2 {{G}_{{\text{F}}}}\alpha _{{em}}^{2}{{V}_{{tb}}}V_{{ts}}^{*}(\bar {\mu }({{k}_{2}}){{\gamma }^{\mu }}\mu ( - {{k}_{1}})) \\ \times \,\,\left[ {i{\kern 1pt} {{d}^{{(VP)}}}({{x}_{{12}}},{{x}_{{123}}},{{x}_{{124}}}){\kern 1pt} {{k}_{\mu }}{\kern 1pt} (\bar {e}({{k}_{4}}){{\gamma }^{5}}e( - {{k}_{3}}))} \right. \\ \left. { + \,\,{{f}^{{(VT)}}}({{x}_{{12}}},{\kern 1pt} {{x}_{{123}}},{{x}_{{124}}}){{\varepsilon }_{{\mu \nu \alpha \beta }}}{{p}^{\nu }}(\bar {e}({{k}_{4}}){{\gamma }^{\alpha }}{{\gamma }^{\beta }}e( - {{k}_{3}}))} \right]. \\ \end{gathered} $$

(2)

A similar expression to describe the contribution of ${{e}^{ + }}{{e}^{ - }}$, pairs emitted by ${{\mu }^{ + }}$ and ${{\mu }^{ - }}$ in the final state, is obtained by replacing in the expression (2) of muon masses with electron masses in form factors ${{d}^{{(VP)}}}$ and ${{f}^{{(VP)}}}$.

Fig. 4.

Diagrams corresponding to the emission of a virtual photon by one of the leptons in the final state.

The sixth kind of diagrams corresponds to the contribution $u\bar {u}$ and $c\bar {c}$ pairs associated with weak annihilation processes (see Fig. 5).

Fig. 5.

Diagrams corresponding to weak annihilation processes.

Accounting for the contribution of weak annihilation processes gives the following amplitude structure:

$$\begin{gathered} \mathcal{M}_{{fi}}^{{(WA)}}{\kern 1pt} = i\frac{{32\sqrt 2 }}{{3\pi }}\frac{{{{G}_{{\text{F}}}}}}{{M_{1}^{3}}}\alpha _{{em}}^{2}{\kern 1pt} \left( {{{V}_{{ub}}}{\kern 1pt} V_{{ud}}^{*} + {{V}_{{cb}}}{\kern 1pt} V_{{cd}}^{*}} \right){\kern 1pt} {{a}_{1}}(\mu ){\kern 1pt} {{{\hat {f}}}_{{{{B}_{d}}}}} \\ \times \,\,\frac{1}{{{{x}_{{12}}}{\kern 1pt} {{x}_{{34}}}}}{\kern 1pt} {{\varepsilon }_{{\mu \alpha kq}}}(\bar {\mu }({{k}_{2}}){{\gamma }^{\mu }}\mu ( - {{k}_{1}})){\kern 1pt} (\bar {e}({{k}_{4}}){\kern 1pt} {{\gamma }^{\alpha }}e( - {{k}_{3}})), \\ \end{gathered} $$

where ${{\hat {f}}_{{{{B}_{d}}}}} = \frac{{{{f}_{{{{B}_{d}}}}}}}{{{{M}_{1}}}}$.

2 NUMERICAL RESULTS FOR DECAY ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$

Taking into account the contributions of all the diagrams discussed above, we calculated the partial width of the decay ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$. When obtaining the numerical value of this quantity, the EvtGen software package was used [6]. The expression for the partial decay width ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ can be given as

$$\begin{gathered} Br{\kern 1pt} \left( {{{{\bar {B}}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}} \right) \\ \approx \frac{{\alpha _{{em}}^{4}{\kern 1pt} {{{\left| {{{V}_{{tb}}}{\kern 1pt} V_{{td}}^{*}} \right|}}^{2}}}}{{3 \times {{2}^{{13}}} \times {{\pi }^{5}}}}{\kern 1pt} {{\tau }_{{{{B}_{d}}}}}{\kern 1pt} G_{{\text{F}}}^{2}M_{{{{B}_{d}}}}^{5}\frac{{{{N}_{0}}}}{{{{N}_{{{\text{tot}}}}}}}{\kern 1pt} {{\left| X \right|}^{2}}, \\ \end{gathered} $$

(3)

where ${{N}_{{{\text{tot}}}}}$ is the total number of events obtained by Monte Carlo integration, ${{N}_{0}}$ is the number of received events, and ${{\left| X \right|}^{2}}$ is the dimensionless maximum of the matrix element. Numerical values of parameters ${{N}_{{{\text{tot}}}}}$, ${{N}_{0}}$, and ${{\left| X \right|}^{2}}$ are obtained within the EvtGen software package. When calculating the partial decay width of ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$, areas ${J \mathord{\left/ {\vphantom {J \psi }} \right. \kern-0em} \psi }$ and $\psi (2S)$ resonances were excluded in accordance with the conditions $\left| {\sqrt {M_{1}^{2}{{x}_{{ij}}}} - m(\operatorname{Re} s)} \right| < 100\,\,{\kern 1pt} {\text{MeV}}$.

The value of the partial decay width ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$, calculated in the EvtGen package, turns out to be equal to

$${\text{B}}{{{\text{r}}}_{{{\text{EvtGen}}}}}{\kern 1pt} \left( {{{{\bar {B}}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}} \right) \approx (3.2 \pm 1.2) \times {{10}^{{ - 11}}}.$$

(4)

This value was obtained taking into account the contributions of $\rho (770)$ and $\omega (782)$ resonances.

Based on the theoretical study for the decay ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$, a model for the Monte Carlo generator EvtGen was created. With the help of this model, a set of differential characteristics of decay ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ was obtained. When calculating the differential characteristics, the contributions ${{\rho }^{0}}(770)$ and $\omega (782)$, $\psi (4040)$, $\psi (4160)$, $\psi (4415)$ and resonances and tails from ${J \mathord{\left/ {\vphantom {J \psi }} \right. \kern-0em} \psi }$ and $\psi (2S)$ resonances were considered; areas ${J \mathord{\left/ {\vphantom {J \psi }} \right. \kern-0em} \psi }$ and $\psi (2S)$ resonances were excluded in accordance with the conditions given above. The relative phase between all resonances in all calculations is equal to zero.

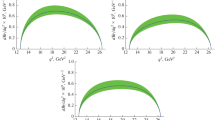
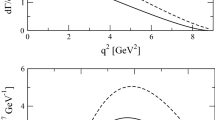
Distributions of the partial decay width ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ by variables ${{x}_{{12}}}$ and ${{x}_{{34}}}$ are shown in Fig. 6 (1, 2). The distributions for both variables are presented in the range $[0.0015,1.0]$; i.e., distribution shapes for the electron and muon channels in the region of small values ${{x}_{{ij}}}$ should be similar, as is shown in Fig. 6 (1, 2). In area ${{x}_{{ij}}} \to \left( {\frac{{{{M}_{\omega }}}}{{{{M}_{{{{B}_{d}}}}}}}} \right) \approx 0.022$ there is a peak from the $\omega (782)$ meson. Contributions from ${{\rho }^{0}}(770)$ resonances appear as a wide substrate to a narrow peak $\omega (782)$. Fig. 1 (3, 4) shows the distributions of the partial width of the decay ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ in angular variables ${{y}_{{12}}} \equiv \cos ({{\theta }_{{12}}})$ and ${{y}_{{34}}} \equiv \cos ({{\theta }_{{34}}})$, respectively.

Fig. 6.

(1) One-dimensional distribution of the partial decay width ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ variable ${{x}_{{12}}}$ (${{\mu }^{ + }}{{\mu }^{ - }}$ channel), (2) one-dimensional distribution of the partial decay width ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ by variable ${{x}_{{34}}}$ (${{e}^{ + }}{{e}^{ - }}$ channel), (3) distribution of the partial decay width ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ by variable $\cos ({{\theta }_{{12}}}) \equiv {{y}_{{12}}}$, and (4) distribution of the partial decay width ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ by variable $\cos ({{\theta }_{{34}}}) \equiv {{y}_{{34}}}$.

CONCLUSIONS

The main results of the work are presented in this section.

(i) As part of the SM, a prediction is obtained for the partial width of the decay ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ taking into account resonance contributions ${{\rho }^{0}}(770)$ and $\omega (782)$, $\psi (4040)$, $\psi (4160)$, $\psi (4415)$, resonances, tails from ${J \mathord{\left/ {\vphantom {J \psi }} \right. \kern-0em} \psi }$ and $\psi (2S)$ and nonresonant contributions, bremsstrahlung, and weak annihilation processes. Partial decay width ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$:

$${\text{Br}}{\kern 1pt} \left( {{{{\bar {B}}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}} \right) \approx (3.2 \pm 1.2) \times {{10}^{{ - 11}}}.$$

(ii) Various differential distributions for the decay ${{\bar {B}}_{d}} \to {{\mu }^{ + }}{{\mu }^{ - }}{{e}^{ + }}{{e}^{ - }}$ are built using a new Monte Carlo model created on the basis of the EvtGen generator.