INTRODUCTION

Decay of a metastable phase during first-order phase transition is accompanied by formation (or nucleation) of particles of a new phase. Under conditions of rapid establishment of the initial metastable state in a closed system, the phase transformation proceeds through several stages [1–3]. We will be interested in this communication in the first stage called the stage of nucleation (with formation of spectrum of new-phase particles of overcritical sizes and growth of the overcritical particles [2]) and the second stage called the stage of an intense collapse of the supersaturation of the metastable system [3].

The traditional approach to kinetic description of nucleation is based on the assumption that homogeneous nucleation of overcritical particles of a new phase in a closed system occurs uniformly over the volume of the system and is synchronous with decrease in the average supersaturation of the metastable phase [1–5]. This approach is called the mean-field supersaturation approximation. The mean-field supersaturation approximation also implies that the transfer of molecules of metastable phase into growing particles of new phase is stationary and proceeds rather slowly.

Below we will speak about nucleation and subsequent growth of overcritical liquid droplets in a supersaturated vapor and overcritical gas bubbles in a liquid solution supersaturated with dissolved gas [6–8]. We will consider the growth of overcritical particles of new phase to occur due to the diffusion of the metastable substance. In the mean-field supersaturation approximation, the end of the nucleation stage is determined by the moment when a relative decline in the initial supersaturation leads to the decrease in the nucleation rate by e times. The condition for the applicability of the mean-field supersaturation approximation at the end of the nucleation stage is provided by smallness of the average distance between overcritical particles compared to the size of the diffusion clouds surrounding the particles. In this communication, we will show that this condition of the applicability of the mean-field approximation can be reduced to a very strong inequality, to provide which in the case of droplet nucleation in a supersaturated vapor, the low volatility of the condensing liquid is required, and in the case of the stage of nucleation of overcritical gas bubbles in a supersaturated gas solution, we need an extremely low solubility of the gas in the degassing solution.

To take into account the effect of concentration inhomogeneity and nonstationary diffusion of a metastable substance into the overcritical particle of new phase, we previously developed an approach [9–15] based on the concept of the formation of a volume excluded for nucleation during the diffusion growth of a such particle. The excluded volume approach takes into account that, due to a decrease in the concentration of the available metastable substance, the nucleation of new particles is strongly suppressed in the diffusion shell surrounding an already formed particle. In other words, a spherical shell of a metastable substance of certain thickness around each overcritical particle can be excluded from the region of nucleation, while in the rest of the metastable system the intensity of supercritical particles nucleation remains at the initial level. For a particle growing in a self-similar diffusion regime [16–19], the volume excluded from the nucleation process is proportional to the particle volume.

In the excluded volume approach, the end of the nucleation stage corresponds to the time at which the sum of excluded volumes for individual particles becomes equal to the volume of the initial metastable system. In this communication, we will show that this condition does not mean a significant overlap of diffusion shells and complete mixing of the metastable substance of the system to its quasi-homogeneity. This condition can be satisfied at any initial supersaturation of the metastable phase and at any nucleation growth rate.

Although in the case of rapid diffusion growth of overcritical particles, the end of the nucleation stage corresponds to the fact that the spherical layers related to the excluded volumes of individual particles come into contact with each other, the local supersaturations near the outer boundary of the excluded volume decrease slightly by the end of this stage. It can be assumed that after this, at the second stage of the phase transition, the stage of intensive absorption of the metastable substance, each overcritical particle grows due to the consumption of the metastable substance only from its own layer. Estimates in favor of this assumption will be presented in the third section of the article.

1. APPROXIMATION OF THE MEAN-FIELD SUPERSATURATION

Below, we restrict ourselves to the case of homogeneous formation of one-component particles of a new phase in a homogeneous metastable system. The expression for the rate J of homogeneous nucleation of new phase particles at any point of the metastable phase can be written [1–5] as

$$J = C{e^{ - \Delta {F_c}}},$$
((1))

where C is the pre-exponential factor and ∆Fc is the minimal work of formation of an equilibrium (critical) particle expressed in thermal units kBT (kB is the Boltzmann constant, T is the absolute temperature of the system), which plays the role of the activation barrier for homogeneous nucleation. The quantities ∆Fc and C are functions of the supersaturation of the metastable phase ζ

$${\rm{\zeta }} \equiv {{n - {n_f}} \over {{n_f}}}$$
((2))

(n is the bulk concentration of metastable substance molecules, nf is their concentration at equilibrium of the initial and new phases with a flat interface) and can change with time along with this supersaturation during the nucleation stage. The factor C is a slowly varying function of supersaturation ζ compared to exp(–∆Fc). Therefore, the dependence of the activation barrier ∆Fc on supersaturation ζ is more important in nucleation kinetics. For homogeneous nucleation of droplets and bubbles in the framework of the classical theory of nucleation, we have the following expressions for the activation barriers [6]

$$\Delta F_c^{\left( {\rm{d}} \right)}{\rm{ = }}{{16\pi {\sigma ^3}} \over {3{{\left( {{k_{\rm{B}}}T} \right)}^3}n_l^2{{\left( {\ln \left( {1 + {\rm{\zeta }}} \right)} \right)}^2}}}{\rm{ }},$$
((3))
$$\Delta F_c^{\left( {\rm{b}} \right)}{\rm{ = }}{{16\pi {\sigma ^3}} \over {3{k_{\rm{B}}}TP_l^2{{\rm{\zeta }}^2}}}{\rm{ }}{\rm{,}}$$
((4))

where the superscripts (d) and (b) hereinafter refer to a droplet and, respectively, to a bubble, σ is the surface tension at the flat gas–liquid interface, nl is the number density of molecules in the liquid droplet, and Pl is the bulk pressure in the liquid solution around the bubble. For the appearance of the first overcritical nuclei within a reasonable waiting time, the height of the activation barrier must satisfy the condition ∆Fc ≤ 100.

Let us define the relative diminution of the supersaturation with time by the relation

$${\rm{\varphi }}(t) \equiv {{{{\rm{\zeta }}_0} - {\rm{\zeta }}(t)} \over {{{\rm{\zeta }}_0}}},$$
((5))

where ζ0 is the initial value of the supersaturation of the system (hereinafter, the subscript 0 indicates that the corresponding value was determined at the initial moment of time). Taking into account only constant and linear in φ(t) terms, ∆Fc(t) can be represented as an expansion

$$\Delta {F_c}\left( t \right) \approx \Delta {F_{c,0}} + {\rm{\Gamma \varphi }}\left( t \right),$$
((6))

Where

$${\rm{\Gamma }} \equiv - {{\rm{\zeta }}_0}{\left( {{{\partial \Delta {F_c}} \over {\partial {\rm{\zeta }}}}} \right)_0}.$$
((7))

Taking into account the relations (3) and (4), we find for a droplet and a bubble in the framework of the classical theory of nucleation

$${\Gamma ^{\left( {\rm{d}} \right)}}{\rm{ = }}{{32\pi {\sigma ^3}} \over {3{{\left( {{k_{\rm{B}}}T} \right)}^3}n_l^2{{\left( {\ln \left( {1 + {{\rm{\zeta }}_0}} \right)} \right)}^3}}}{\rm{ }}{{{{\rm{\zeta }}_0}} \over {1 + {{\rm{\zeta }}_0}}} = {{2{{\rm{\zeta }}_0}\Delta F_c^{\left( {\rm{d}} \right)}} \over {\left( {1 + {{\rm{\zeta }}_0}} \right)\ln \left( {1 + {{\rm{\zeta }}_0}} \right)}},$$
((8))
$${\Gamma ^{\left( {\rm{b}} \right)}}{\rm{ = }}{{32\pi {\sigma ^3}} \over {3{k_{\rm{B}}}TP_l^2{\rm{\zeta }}_0^2}} = 2\Delta F_c^{\left( {\rm{b}} \right)}.$$
((9))

We see from relations (8) and (9) that the quantity Г decreases with increasing supersaturation ζ0, but even at high supersaturations, when ∆Fc ≤ 100, we have double inequality 1 << Г ≤ 200, which justifies expansion (6).

In view of expansion (6), expression (1) for J(t) can be written as

$$J(t) = {J_0}\exp \left( { - {\rm{\Gamma \varphi }}\left( t \right)} \right),$$
((10))

where J0 = C0e–ΔFc,0. In the approximation of the mean-field supersaturation, the condition determining the moment tl of the end of the nucleation stage is taken as

$$\Gamma \varphi \left( {{t_1}} \right) = 1.$$
((11))

Taking into account definitions (2) and (3), we have

$${n_0} - n\left( t \right) = {\rm{\varphi }}(t)\left( {{n_0} - {n_f}} \right).$$
((12))

The change in the current amount of a metastable substance in the system equals V(n0 – n(t)), where V is the initial volume of the system. In view of expressions (8) and (9), the material balance conditions for the metastable substance at the end of the nucleation stage for condensation of vapor into droplets and for the degassing of the solution into bubbles can be written respectively as

$${n_l}{V_l}\left( {{t_1}} \right) = V{\left( {{n_0} - n\left( {{t_1}} \right)} \right)^{\left( {\rm{d}} \right)}} = {\left( {{{{n_0} - {n_f}} \over \Gamma }} \right)^{\left( {\rm{d}} \right)}}V,$$
((13))
$${n_g}{V_g}\left( {{t_1}} \right) = {\left( {{{{n_0} - {n_f}} \over \Gamma }} \right)^{\left( {\rm{b}} \right)}}V,$$
((14))

where ng is the number density of molecules in a gas bubble at pressure Pl, Vl(tl) and Vg(tl) are the total volumes of overcritical droplets and, accordingly, overcritical bubbles by the end of the first stage of nucleation. Expressions (13) and (14) can be rewritten as

$${V_l}\left( {{t_1}} \right) = {{{a_l}} \over \Gamma }V,\;{V_g}\left( {{t_1}} \right) = {{{a_g}} \over \Gamma }V,$$
((15))

where

$${a_l} \equiv {{{n_0} - {n_f}} \over {{n_l}}} = {\zeta _0}{{{n_f}} \over {{n_l}}} < < 1,$$
((16))
$${a_g} \equiv {{{n_0} - {n_f}} \over {{n_g}}} = {\zeta _0}{{{n_f}} \over {{n_g}}} = {\zeta _0}s < < 1,$$
((17))

s is the gas solubility.

The total volumes of droplets Vl(tl) and bubbles Vg(tl) can be represented as

$${V_l}\left( {{t_1}} \right) = {{4\pi } \over 3}\left\langle {{R^3}} \right\rangle _{{t_1}}^{\left( {\rm{d}} \right)}{N^{\left( {\rm{d}} \right)}}\left( {{t_1}} \right),\;{V_g}\left( {{t_1}} \right) = {{4\pi } \over 3}\left\langle {{R^3}} \right\rangle _{{t_1}}^{\left( {\rm{b}} \right)}{N^{\left( {\rm{b}} \right)}}\left( {{t_1}} \right),$$
((18))

where 4π/3‹R3›t1 is the volume of the overcritical particle averaged over the size distribution, and N(tl) is the total number of overcritical particles by the end of the nucleation stage. As a consequence of expressions (15) and (18), by the end of the nucleation stage, we find that the average concentration of droplets in the vapor and bubbles over the solution volume is equal respectively to

$${\left( {{{N\left( {{t_1}} \right)} \over V}} \right)^{\left( {\rm{d}} \right)}} = {{{a_l}} \over {{\Gamma ^{\left( {\rm{d}} \right)}}}}{3 \over {4\pi \left\langle {{R^3}} \right\rangle _{{t_1}}^{\left( {\rm{d}} \right)}}},\;{\left( {{{N\left( {{t_1}} \right)} \over V}} \right)^{\left( {\rm{b}} \right)}} = {{{a_g}} \over {{\Gamma ^{\left( {\rm{b}} \right)}}}}{3 \over {4\pi \left\langle {{R^3}} \right\rangle _{{t_1}}^{\left( {\rm{b}} \right)}}}.$$
((19))

Estimating the average distance \(\bar r\)(t1) between the particles of a new phase as

$${{4\pi } \over 3}{\left( {\bar r\left( {{t_1}} \right)} \right)^3}{{N\left( {{t_1}} \right)} \over V} \approx 1,$$

using relations (19), we obtain

$${\left( {\bar r\left( {{t_1}} \right)} \right)^{\left( {\rm{d}} \right)}} \approx {\left( {{{{\Gamma ^{\left( {\rm{d}} \right)}}} \over {{a_l}}}} \right)^{1/3}}{\left( {\left\langle {{R^3}} \right\rangle _{{t_1}}^{\left( {\rm{d}} \right)}} \right)^{1/3}},\;{\left( {\bar r\left( {{t_1}} \right)} \right)^{\left( {\rm{b}} \right)}} \approx {\left( {{{{\Gamma ^{\left( {\rm{b}} \right)}}} \over {{a_g}}}} \right)^{1/3}}{\left( {\left\langle {{R^3}} \right\rangle _{{t_1}}^{\left( {\rm{b}} \right)}} \right)^{1/3}}.$$
((20))

The condition for the applicability of the approximation of the mean-field supersaturation is requirement of the smallness of the distance \(\bar r\)(t1) compared to the sizes of diffusion clouds surrounding overcritical particles. For a droplet and a bubble of the maximum size, which is reached by the end of the nucleation stage at the quasi-stationary diffusion growth, we have

$${\left( {R_{\max }^2\left( {{t_1}} \right)} \right)^{\left( {\rm{d}} \right)}} = 2{D_g}{a_l}t_1^{\left( {\rm{d}} \right)},\;{\left( {R_{\max }^2\left( {{t_1}} \right)} \right)^{\left( {\rm{b}} \right)}} = 2{D_l}{a_g}t_1^{\left( {\rm{b}} \right)},$$
((21))

where Dg and Dl are the diffusion coefficients in the gas and liquid phases, respectively. Since the radius of the diffusion cloud rD equals rD = (2Dt1)1/2 , then, in view of relations (21), we find

$${\left( {{r_D}} \right)^{\left( {\rm{d}} \right)}} = {{{{\left( {{R_{\max }}\left( {{t_1}} \right)} \right)}^{\left( {\rm{d}} \right)}}} \mathord{\left/ {\vphantom {{{{\left( {{R_{\max }}\left( {{t_1}} \right)} \right)}^{\left( {\rm{d}} \right)}}} {a_l^{1/2}}}} \right. \kern-\nulldelimiterspace} {a_l^{1/2}}},\;{\left( {{r_D}} \right)^{\left( {\rm{b}} \right)}} = {{{{\left( {{R_{\max }}\left( {{t_1}} \right)} \right)}^{\left( {\rm{b}} \right)}}} \mathord{\left/ {\vphantom {{{{\left( {{R_{\max }}\left( {{t_1}} \right)} \right)}^{\left( {\rm{b}} \right)}}} {a_g^{1/2}}}} \right. \kern-\nulldelimiterspace} {a_g^{1/2}}}.$$
((22))

As follows from relations (20)–(22), the condition for applicability of the approximation of the mean-field supersaturation can be reduced to strong inequalities

$${\left( {{\Gamma ^{\left( {\rm{d}} \right)}}} \right)^{1/3}}a_l^{1/6} < < {{{{\left( {{R_{\max }}\left( {{t_1}} \right)} \right)}^{\left( {\rm{d}} \right)}}} \over {{{\left( {\left\langle {{R^3}} \right\rangle _{{t_1}}^{\left( {\rm{d}} \right)}} \right)}^{1/3}}}},\;{\left( {{\Gamma ^{\left( {\rm{b}} \right)}}} \right)^{1/3}}a_g^{1/6} < < {{{{\left( {{R_{\max }}\left( {{t_1}} \right)} \right)}^{\left( {\rm{b}} \right)}}} \over {{{\left( {\left\langle {{R^3}} \right\rangle _{{t_1}}^{\left( {\rm{b}} \right)}} \right)}^{1/3}}}}.$$
((23))

The expression for the average cubic radius of the overcritical particle at time t has the form

$${\left\langle {{R^3}} \right\rangle _t} = {{\int\limits_0^{R_{\max }^2\left( t \right)} {{R^3}f\left( {{R^2},t} \right)} d{R^2}} \over {\int\limits_0^{R_{\max }^2\left( t \right)} {f\left( {{R^2},t} \right)} d{R^2}}}.$$
((24))

Here f(R2,t) is the distribution function of the overcritical particles in square radii, which, in view of expressions (21), can be written as

$$f\left( {{R^2},t} \right) = \int\limits_0^t {\delta \left( {{R^2} - R_{\max }^2\left( {t - \tau } \right)} \right)} J\left( \tau \right)d\tau = {{{t_1}} \over {R_{\max }^2\left( {{t_1}} \right)}}J\left( {t - {{{R^2}{t_1}} \over {R_{\max }^2\left( {{t_1}} \right)}}} \right).$$
((25))

Introducing the average value of the distribution function \(\bar f\)(t) by the expression

$$\int\limits_0^{R_{\max }^2\left( t \right)} {\left( {f\left( {{R^2},t} \right) - \bar f\left( t \right)} \right)} d{R^2} = 0,$$
((26))

we have

$${\left\langle {{R^3}} \right\rangle _t} = {2 \over 5}R_{\max }^3\left( t \right) + {1 \over {\bar f\left( t \right)R_{\max }^2\left( t \right)}}\int\limits_0^{R_{\max }^2\left( t \right)} {{R^3}\left( {f\left( {{R^2},t} \right) - \bar f\left( t \right)} \right)} d{R^2}.$$
((27))

Since, according to relation (10), J(t) decreases monotonically with time, it is obvious that the function f(R2,t) is a monotonically increasing function of the variable R2. Accordingly, there exists a value R2 = R*2(t) such that f(R2,t) < \(\bar f\)(t) for R2 < R*2(t) and f(R2,t) > \(\bar f\)(t) for R2 > R*2(t). With this in mind, it is easy to verify that the integral term in the expression for ‹R3›t has a positive value, so that

$${\left\langle {{R^3}} \right\rangle _t} > {2 \over 5}R_{\max }^3\left( t \right).$$

Thus, by the time t1 of the end of the nucleation stage, we have

$${{{R_{\max }}\left( {{t_1}} \right)} \over {{{\left\langle {{R^3}} \right\rangle }^{1/3}}\left( {{t_1}} \right)}} < {\left( {{5 \over 2}} \right)^{1/3}}.$$

From here and from relations (23), the strong inequalities should be satisfied.

$$a_l^{1/6} < < {\left( {{5 \over {2{\Gamma ^{\left( {\rm{d}} \right)}}}}} \right)^{1/3}},\;a_g^{1/6} < < {\left( {{5 \over {2{\Gamma ^{\left( {\rm{b}} \right)}}}}} \right)^{1/3}}.$$
((28))

Taking into account the explicit classical relations (8), (9) for Г(d), Г(b) and definitions (16), (17), inequalities (28) can be rewritten in the form of conditions for vapor supersaturation ζ0 and the saturated vapor concentration nf characterizing the volatility of the liquid in the case of droplet nucleation and the conditions for gas supersaturation ζ0 in solution and gas solubility s in the case of bubble nucleation:

$${{{\rm{\zeta }}_0^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}n_f^{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-\nulldelimiterspace} 6}}} \over {{{\left( {1 + {{\rm{\zeta }}_0}} \right)}^{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}}\ln \left( {1 + {{\rm{\zeta }}_0}} \right)}} < {1 \over 3}{\left( {{{15} \over {64\pi }}} \right)^{1/3}}{{{k_{\rm{B}}}Tn_l^{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-\nulldelimiterspace} 6}}} \over \sigma },$$
((29))
$${\rm{\zeta }}_0^{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}{s^{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-\nulldelimiterspace} 6}}} < {1 \over 3}{\left( {{{15{k_{\rm{B}}}TP_l^2} \over {64\pi {\sigma ^3}}}} \right)^{1/3}}.$$
((30))

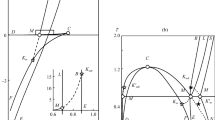
Figure 1 shows the surfaces of the left and right sides of inequality (29) as functions of the initial vapor supersaturation ζ0 and its concentration nf at equilibrium with the liquid phase. Figure 2 plots the dependences of the left and right parts of inequality (30) on the initial gas supersaturation ζ0 in solution and the gas solubility s. The temperature of the systems for both figures is 293 K. For calculations in Fig. 1, the values of the parameters for water were taken: nl = 3.34×1028 m–3, σ = 0.068 Nm–1. For calculations in Fig. 2, the parameters of ethanol as a solvent were taken: σ = 0.022 Nm–1, Pl = 105 Pa. As seen from Fig. 1, inequality (29) is satisfied only at sufficiently small values nf < 2.5×1022 m–3, which are more than an order of magnitude smaller than the tabular value nf = 5.78×1023 m–3 for water. Note that at nf < 2.5×1022 m–3 and ζ0 < 3, according to relations (3), (8) and (16), we have ∆F(d)c > 37.1, Г(d) > 42.8 and al < 2.2×10–6, while the critical radius Rc = 2σ/[nlkBTln(1+ζ0)] of droplets satisfies the inequality Rc > 7.5×10–10m. Figure 2 shows that inequality (30) is satisfied only at extremely low values of gas solubility s < 3×10–9. Note that for s < 3×10–9 and ζ0 < 300, according to Eqs. (9) and (17), we have Г(b) > 98 and ag < 2×10–6, while the critical bubble radius satisfies the inequality Rc = 2σ/(Plζ0) > 1.5×10–9 m.

Fig. 1.
figure 1

Illustration of the region of applicability of inequality (29) for the nucleation of droplets in a supersaturated vapor.

Full size image
Fig. 2.
figure 2

Illustration of the region of applicability of inequality (30) for the nucleation of gas bubbles dissolved in a liquid.

Full size image

Figures 1 and 2 illustrate that for typical values of the parameters for water and ethanol, which were taken to construct the left and right parts of inequalities (29) and (30), these inequalities cannot be satisfied within the framework of the classical theory, and the approximation of the average supersaturation field by the nucleation stage of supercritical nuclei is either not applicable or its applicability is very limited.

2. EXCLUDED VOLUME APPROACH

As noted in the Introduction, there is another approach to the theory of homogeneous nucleation that in the full extent takes into account the effects of concentration inhomogeneity and the nonstationarity of the diffusion of a metastable substance into the particles of a new phase. This approach is based on the idea of the formation of an excluded volume in the process of self-similar nonstationary diffusion growth [16–19] of overcritical particles of a new phase and is described in [9–15].

For a single overcritical particle of radius R growing in the self-similar regime, the value Vex(R) of the volume excluded from the nucleation process equals [9–15]

$${V_{ex}}\left( R \right) \equiv q{{4\pi } \over 3}{R^3},$$
((31))

where factor q is given by the expression

$$q = 3\int\limits_1^\infty {d\rho {\rho ^2}\left[ {1 - \exp \left( { - \Gamma {{\int\limits_\rho ^\infty {{{dx} \over {{x^2}}}\exp \left[ { - {b \over 2}\left( {{x^2} + {2 \over x} - 3} \right)} \right]} } \over {\int\limits_1^\infty {{{dx} \over {{x^2}}}\exp \left[ { - {b \over 2}\left( {{x^2} + {2 \over x} - 3} \right)} \right]} }}} \right)} \right]} ,$$
((32))

and does not depend on the size of the particle. In the self-similar mode of diffusion growth of a droplet or bubble, the parameter b determines the rate of their growth renormalized compared to (21):

$${\left( {{R^2}\left( t \right)} \right)^{\left( {\rm{d}} \right)}} = 2{D_g}{b^{\left( {\rm{d}} \right)}}t,\;{\left( {{R^2}\left( t \right)} \right)^{\left( {\rm{b}} \right)}} = 2{D_l}{b^{\left( {\rm{b}} \right)}}t$$
((33))

and is related to the parameters al and ag introduced in Section 1 by formulas (16) and (17) as

$${a_l} = {b^{\left( {\rm{d}} \right)}}\int\limits_1^\infty {{{dx} \over {{x^2}}}\exp \left[ { - {{{b^{\left( {\rm{d}} \right)}}} \over 2}\left( {{x^2} + {2 \over x} - 3} \right)} \right]} ,$$
((34))
$${a_g} = {b^{\left( {\rm{b}} \right)}}\int\limits_1^\infty {{{dx} \over {{x^2}}}\exp \left[ { - {{{b^{\left( {\rm{b}} \right)}}} \over 2}\left( {{x^2} + {2 \over x} - 3} \right)} \right]} .$$
((35))

In the limiting case, when al1/2 << 1 or ag1/2 << 1, we obtain from expression (34) or (35)

$${b^{\left( {\rm{d}} \right)}} \approx {a_l}\left( {1 + \sqrt {\pi {{{a_l}} \mathord{\left/ {\vphantom {{{a_l}} 2}} \right. \kern-\nulldelimiterspace} 2}} } \right)\;{\rm{or}}\;{b^{\left( {\rm{b}} \right)}} \approx {a_g}\left( {1 + \sqrt {\pi {{{a_g}} \mathord{\left/ {\vphantom {{{a_g}} 2}} \right. \kern-\nulldelimiterspace} 2}} } \right).$$

Estimates for the dependence of the factor q on b were considered in [14].

The excluded volume is a volume of spherical layer surrounding the overcritical particle of a new phase. According to relation (31), the outer radius Rex(R) of this layer is equal to

$${{R_{{\rm{ex}}}^3\left( R \right)} \mathord{\left/ {\vphantom {{R_{{\rm{ex}}}^3\left( R \right)} {{R^3}}}} \right. \kern-\nulldelimiterspace} {{R^3}}} = 1 + q.$$
((36))

Accordingly, the thickness ∆ex(R) = Rex(R) – R of this layer is

$${\Delta _{{\rm{ex}}}}\left( R \right) = {R_{{\rm{ex}}}}\left( R \right) - R = \left[ {{{\left( {1 + q} \right)}^{1/3}} - 1} \right]R.$$
((37))

Let us compare this value with the thickness ∆D(R) of the diffusion layer surrounding the overcritical particle. Since the growth time of a droplet or bubble up to radius R is determined from expression (33), we have

$$\Delta _{\rm{D}}^{\left( {\rm{d}} \right)}\left( R \right) = {\left( {2{D_g}{t^{\left( {\rm{d}} \right)}}\left( R \right)} \right)^{1/2}} = {R \mathord{\left/ {\vphantom {R {{{\left( {{b^{\left( {\rm{d}} \right)}}} \right)}^{1/2}}}}} \right. \kern-\nulldelimiterspace} {{{\left( {{b^{\left( {\rm{d}} \right)}}} \right)}^{1/2}}}},$$
((38))
$$\Delta _{\rm{D}}^{\left( {\rm{b}} \right)}\left( R \right) = {\left( {2{D_l}{t^{\left( {\rm{b}} \right)}}\left( R \right)} \right)^{1/2}} = {R \mathord{\left/ {\vphantom {R {{{\left( {{b^{\left( {\rm{b}} \right)}}} \right)}^{1/2}}}}} \right. \kern-\nulldelimiterspace} {{{\left( {{b^{\left( {\rm{b}} \right)}}} \right)}^{1/2}}}}.$$
((39))

Using relations (37) and (38), (39) for the ratio ∆ex/∆D, at any values of the parameter b, we find in the general form

$${{{\Delta _{{\rm{ex}}}}\left( R \right)} \over {{\Delta _{\rm{D}}}\left( R \right)}} = \left[ {{{\left( {1 + q} \right)}^{1/3}} - 1} \right]{b^{1/2}} \equiv \varepsilon .$$
((40))

As we can see, the ratio ∆ex/∆D does not depend on the size of the particle.

In the approach with the excluded volume, the end of the nucleation stage corresponds to the time t1, at which the sum of the excluded volumes for individual overcritical particles becomes equal to the initial volume of the system V. The average distance \(\bar r\)(t1) between particles can then be estimated as \(\bar r\)(t1) ~ Δex(Rmax(t1)). Accordingly, we can assume \(\bar r\)(t1)/ ΔD(Rmax(t1)) ~ ε and, by the value of ε, to estimate the degree of overlapping of the diffusion clouds of individual particles by the end of the nucleation stage. In particular, in the limiting case of small values of b, we obtain for the factor q, as shown in [14], the value q ≈ Г/b >> 1. Accordingly, in this case, taking into account the equality b ≈ a at small b, we have

$$\varepsilon = \left[ {{{\left( {1 + q} \right)}^{1/3}} - 1} \right]{b^{1/2}} \approx {\left( {{\Gamma \over a}} \right)^{1/3}}{a^{1/2}} = {\Gamma ^{1/3}}{a^{1/6}}.$$
((41))

As one can see, the sizes of diffusion clouds significantly exceed the distances between particles only if the condition Г1/3a1/6 << 1 is satisfied, which is equivalent to extremely stringent conditions (28) for the applicability of the approximation of the mean-field supersaturation. However, these conditions are not required under the excluded volume approach.

With an increase in the parameter b (i.e., with an increase in the rate of diffusion growth of overcritical particles of a new phase), which, according to Eqs. (34), (35) and (16), (17), is associated with an increase in the initial supersaturation of the system or an increase in the volatility of the condensed substance during droplet nucleation and an increase in gas solubility during bubble nucleation, the overlap of diffusion clouds at the end of the nucleation stage becomes less and less significant, and at sufficiently large b, this overlap is practically absent. In this case, the volume of the diffusion layer of the nucleus is close to the value of the corresponding excluded volume. In other words, the picture is radically different from that arising in the approximation of the mean-field supersaturation.

Everything that has been said in this section can be extended to the situation when the mode of self-similar non-stationary diffusion growth of overcritical particles of a new phase is itself establishing during the nucleation stage, i.e., the parameters b and q depend on the radius of the particle and reach their self-similar values by end of the nucleation stage. As shown in [20, 21], this can be the case when the Laplace pressure in overcritical gas bubbles is fully taken into account at high gas supersaturations and when bubbles are formed in a highly viscous liquid. A corresponding extension of the excluded volume theory was also made in [20, 21].

3. ENTERING THE STAGE OF INTENSE ABSORPTION OF A METASTABLE SUBSTANCE

At the second stage of the phase transition, the overcritical particles of new phase grow, intensively absorbing the excess of the matter of the metastable phase. The formation of new overcritical particles at this stage practically does not occur. The dynamics of this stage will, of course, substantially depend on the degree of diffusion nonstationarity, which is determined by the value of the parameter a. Being interested in the evolution of an ensemble of particles under conditions of strong nonstationarity, we will consider a system of bubbles, since the condition a >> 1, necessary for the significant role of nonstationarity, is relatively easily ensured in the case of degassing the solution.

As already noted, in the case of a strong nonstationarity of bubble growth, i.e., in a situation where the approximation of the mean-field supersaturation is obviously inapplicable, the end of the nucleation stage is reached to the moment when the spherical layers corresponding to the excluded volumes of individual bubbles come into contact with each other and practically do not overlap. As a consequence, it can be assumed that after this (at the next stage of intensive consumption of dissolved gas), each bubble grows due to the consumption of gas only from its own layer. If at the nucleation stage the bubbles grow in a self-similar mode, then for any bubble having a radius R(t1) by the time t1 of the end of this stage, the outer radius ~R(t1) of such a layer should be assumed equal to

$$\tilde R\left( {R\left( {{t_1}} \right)} \right) = \alpha R\left( {{t_1}} \right),$$
((42))

where α is a coefficient that depends on the degree of non-stationarity of the diffusion flow of dissolved gas particles (depends only on the parameter b). By the time t2 of the end of the second stage, the dissolved gas concentration in the layer surrounding the bubble decreases to a value close to nf, and the bubble radius at this stage will increase from R(t1) to R(t2). The corresponding solute material balance condition for an individual bubble can be written as

$$\left( {{n_0} - {n_f}} \right)\left( {{{\tilde R}^3}\left( {R\left( {{t_1}} \right)} \right) - {R^3}\left( {{t_1}} \right)} \right) = {n_g}{R^3}\left( {{t_2}} \right),$$
((43))

or, taking into account relations (17) and (42), as

$${R^3}\left( {{t_2}} \right) = = a\left( {{\alpha ^3} - 1} \right){R^3}\left( {{t_1}} \right).$$
((44))

As a consequence, for the ratio of the total bubble volumes Vg(t1) and Vg(t2) we have the estimate

$${{{V_g}\left( {{t_2}} \right)} \over {{V_g}\left( {{t_1}} \right)}} = a\left( {{\alpha ^3} - 1} \right).$$
((45))

In the excluded volume approach, the total volume of bubbles Vg(t1) by the end of the nucleation stage was previously determined by the expression [14]

$${V_g}\left( {{t_1}} \right) = {{{V_l}} \over q}.$$
((46))

By the time t2 of the end of the second stage, almost the entire excess of the dissolved gas passes into bubbles, and this fact leads to the relation (n0 – nf)Vl = ngVg(t2) or Vg(t2) = aVl. Then, taking into account expression (46), we obtain

$${{{V_g}\left( {{t_2}} \right)} \over {{V_g}\left( {{t_1}} \right)}} = aq.$$
((47))

Comparing two expressions (45) and (47) for the ratio Vg(t2)/Vg(t1), we arrive at the relation

$${\alpha ^3} = 1 + q.$$
((48))

Relation (48) allows us to rewrite equation (42) in the form

$${\tilde R^3}\left( {R\left( {{t_1}} \right)} \right) = \left( {1 + q} \right){R^3}\left( {{t_1}} \right).$$
((49))

Taking into account expression (36) given in Section 2, we obtain from relation (49)

$$\tilde R\left( {R\left( {{t_1}} \right)} \right) = {R_{ex}}\left( {R\left( {{t_1}} \right)} \right).$$
((50))

Thus, the idea that at the second stage of the phase transition each bubble grows, absorbing excess gas only from its nearest layer (the solution evolves as a cellular structure), is consistent with the solute balance condition.

CONCLUSIONS

In this communication, we have shown that the approximation of the mean-field supersaturation and stationarity of the diffusion growth of overcritical droplets in a supersaturated vapor or the diffusion growth of overcritical gas bubbles in a gaseous solution at the nucleation stage are either inapplicable, or their applicability is very limited by the extremely small values of parameters al and ag determined by the relations (16) and (17). Physically, these restrictions require a low volatility of the condensing liquid in the case of droplets, and an extremely low solubility of the gas in solution in the case of gas bubbles. Previously, it was assumed that the approximation of the mean-field of supersaturation and the stationarity of diffusion growth is more justified in the case of low supersaturations of a metastable system, but the estimates made in this work demonstrate the deterioration of the applicability of the theory with decreasing supersaturation. It is also shown in this work that kinetic description of phase transition based on the excluded volume approach is completely devoid of the limitations mentioned above. Such a description, allowing a significant nonstationarity of diffusion, leads to the end of the nucleation stage to formation of a cellular structure, which evolves at the next stage of intense depletion of the metastable system.