1. A method for constructing combined shock-capturing schemes that monotonically localize shock fronts and simultaneously preserve increased accuracy in domains of smoothness of the computed weak solutions was proposed in [1, 2]. A combined scheme involves a baseline nonmonotone scheme that has an increased order of convergence in the domains of influence of shock waves. The baseline scheme is used to construct a discrete solution in the entire computational domain. In high-gradient domains, where this solution exhibits spurious oscillations, it is corrected by numerically solving internal initial–boundary value problems with the help of a nonlinear flux correction (NFC) scheme. Examples of NFC schemes are MUSCL schemes [3], TVD schemes [4], WENO schemes [5], discontinuous Galerkin (DG) schemes [6], and CABARET schemes [7]. As a baseline scheme, a symmetric compact scheme [8] of the third order of weak approximation was used in [1] and the Rusanov–Burstein–Mirin (RBM) scheme [9, 10] of the third order of classical approximation was used in [2]; the second-order accurate CABARET scheme [7] on smooth solutions was applied as an internal NFC scheme. The basic disadvantage of the combined schemes constructed in [1, 2] is that the corresponding baseline and internal schemes have a widely different type, which leads to difficulties in implementing the numerical algorithm on the boundary of the internal computational domain. For this reason, a new combined scheme free of this disadvantage is proposed below. In this scheme, a nonmonotone third-order DG method [6] is used as a baseline algorithm and an NFC version of the same method is used as an internal algorithm.

2. Consider the quasilinear hyperbolic system of conservation laws

$${{{\mathbf{u}}}_{t}} + {\mathbf{f}}{{({\mathbf{u}})}_{x}} = 0,$$
((1))

where \({\mathbf{u}}(x,t)\) and \({\mathbf{f}}({\mathbf{u}})\) are the desired and given smooth vector functions, respectively.

For system (1), we set up the Cauchy problem with smooth periodic initial data

$${\mathbf{u}}(x,0) = {\mathbf{v}}(x) \equiv {\mathbf{v}}(x + X).$$
((2))

Assume that, for t > 0, problem (1), (2) has a unique bounded weak solution \({\mathbf{u}}(x,t)\) that contains a shock wave on an interval of period length X resulting from a gradient catastrophe.

The Cauchy problem (1), (2) is approximated by a discontinuous Galerkin method on a uniform spatial grid \({{x}_{i}} = ih\), where \(h = X{\text{/}}N\) is a constant mesh size and N is the number of grid cells on an interval of period length. A numerical solution is sought in the form of a piecewise polynomial function made up of polynomials in \(x\) of degree at most p in each spatial cell \([{{x}_{i}},{{x}_{{i + 1}}}] \in [0,X]\):

$$\begin{gathered} {{{\mathbf{U}}}_{i}}(x,t) = \sum\limits_{j = 0}^p {{{\mathbf{U}}}_{{ij}}}(t){{\varphi }_{{ij}}}(x), \\ x \in [{{x}_{i}},{{x}_{{i + 1}}}],\quad i = 0,1,...,N - 1, \\ \end{gathered} $$
((3))

where

$${{\varphi }_{{ij}}}(x) = {{\left( {\frac{{x - {{x}_{{i + 1/2}}}}}{h}} \right)}^{j}},\quad {{x}_{{i + 1/2}}} = \frac{{{{x}_{i}} + {{x}_{{i + 1}}}}}{2}$$

are the scalar basis functions and \({{{\mathbf{U}}}_{{ij}}}(t)\) are the desired vector functions.

The functions \({{{\mathbf{U}}}_{{ij}}}(t)\) are determined by solving the system of ordinary differential equations

$$\begin{gathered} \frac{d}{{dt}}\int\limits_{{{x}_{i}}}^{{{x}_{{i + 1}}}} {{{{\mathbf{U}}}_{i}}{{\varphi }_{{ik}}}dx - } \int\limits_{{{x}_{i}}}^{{{x}_{{i + 1}}}} {{\mathbf{f}}({{{\mathbf{U}}}_{i}})\varphi _{{ik}}^{'}dx} \\ \, + {{{\mathbf{F}}}_{{i + 1}}}{{\varphi }_{{ik}}}({{x}_{{i + 1}}}) - {{{\mathbf{F}}}_{i}}{{\varphi }_{{ik}}}({{x}_{i}}) = 0, \\ \end{gathered} $$
((4))

in which \({{{\mathbf{F}}}_{i}}(t)\) are the numerical fluxes given by the Rusanov–Lax–Friedrichs formulas

$$\begin{gathered} {{{\mathbf{F}}}_{i}}(t) = \frac{{{\mathbf{f}}({{{\mathbf{U}}}_{{i - 1}}}({{x}_{i}},t)) + {\mathbf{f}}({{{\mathbf{U}}}_{i}}({{x}_{i}},t))}}{2} \\ \, - a({{{\mathbf{U}}}_{{i - 1}}}({{x}_{i}},t),{{{\mathbf{U}}}_{i}}({{x}_{i}},t))\frac{{({{{\mathbf{U}}}_{i}}({{x}_{i}},t) - {{{\mathbf{U}}}_{{i - 1}}}({{x}_{i}},t))}}{2}, \\ \end{gathered} $$

where

$$\begin{gathered} a({{{\mathbf{U}}}_{{i - 1}}}({{x}_{i}},t),{{{\mathbf{U}}}_{i}}({{x}_{i}},t)) \\ = \mathop {\max }\limits_m \left( {{\text{|}}{{\lambda }_{m}}({{{\mathbf{U}}}_{{i - 1}}}({{x}_{i}},t)){\text{|}},{\text{|}}{{\lambda }_{m}}({{{\mathbf{U}}}_{i}}({{x}_{i}},t)){\text{|}}} \right), \\ \end{gathered} $$

and λm are the eigenvalues of the Jacobian matrix \({{{\mathbf{f}}}_{{\mathbf{u}}}}\) of system (1).

Since, in view of formula (3),

$$\frac{d}{{dt}}\int\limits_{{{x}_{i}}}^{{{x}_{{i + 1}}}} {{{{\mathbf{U}}}_{i}}{{\varphi }_{{ik}}}dx} = \sum\limits_{j = 0}^p {a_{{kj}}^{i}\frac{{d{{{\mathbf{U}}}_{{ij}}}}}{{dt}},\quad a_{{kj}}^{i} = \int\limits_{{{x}_{i}}}^{{{x}_{{i + 1}}}} {{{\varphi }_{{ik}}}{{\varphi }_{{ij}}}dx,} } $$

where the matrices \({{A}_{i}} = (a_{{kj}}^{i})\) are nonsingular, system (4) can be rewritten as

$$\begin{gathered} \frac{{d{{{\mathbf{U}}}_{{ij}}}}}{{dt}} = \sum\limits_{k = 0}^p b_{{jk}}^{i}{{{\mathbf{Y}}}_{{ik}}}, \\ j = 0,\;1,\;...,\;p,\quad i = 0,\;1,\;...,\;N - 1, \\ \end{gathered} $$
((5))

where

$${{{\mathbf{Y}}}_{{ik}}} = \int\limits_{{{x}_{i}}}^{{{x}_{{i + 1}}}} {{\mathbf{f}}({{{\mathbf{U}}}_{i}})\varphi _{{ik}}^{'}dx - {{{\mathbf{F}}}_{{i + 1}}}{{\varphi }_{{ik}}}({{x}_{{i + 1}}}) + {{{\mathbf{F}}}_{i}}{{\varphi }_{{ik}}}({{x}_{i}}),} $$

and \({{B}_{i}} = (b_{{jk}}^{i})\) is the inverse of the matrix Ai.

3. System (5) represents a differential-projective scheme of the discontinuous Galerkin method (differential in the time variable t and projective in the space variable x). In this paper, we study a third-order method, for which p = 1 and polynomials (3) at every time level \(n\) are linear functions of x:

$${\mathbf{U}}_{i}^{n}(x) = {\mathbf{U}}_{{i0}}^{n} + {\mathbf{U}}_{{i1}}^{n}\;\frac{{x - {{x}_{{i + 1/2}}}}}{h}\;,\quad {\mathbf{U}}_{{ij}}^{n} = {{{\mathbf{U}}}_{{ij}}}({{t}_{n}}).$$
((6))

The numerical time stepping is based on the third-order Runge–Kutta method on the uniform grid \({{t}_{n}} = n\tau \) with \(n \geqslant 0\), in which the constant time step is determined by the stability condition

$$\tau = \frac{{rh}}{{\mathop {\max }\limits_{m,i,n} {\text{|}}{{\lambda }_{m}}({\mathbf{U}}_{{i + 1/2}}^{n}){\text{|}}}},\quad {\mathbf{U}}_{{i + 1/2}}^{n} = {{{\mathbf{U}}}_{i}}({{x}_{{i + 1/2}}},{{t}_{n}}),$$

where \(r \in (0,1)\) is the Courant number. This discontinuous Galerkin method will be denoted by DG1.

Since the DG1 method has the third order for smooth solutions and does not belong to the class of NFC schemes, the numerical solution generated by it contains noticeable spurious oscillations arising in computing shock waves. These oscillations are suppressed using the Cockburn limiter [6], according to which each component \(U_{{i1}}^{n}\) of the vector solution \({\mathbf{U}}_{{i1}}^{n}\) in formula (6) is replaced by the quantity

$$V_{{i1}}^{n} = M(U_{{i1}}^{n},\alpha (U_{{i + 1,0}}^{n} - U_{{i0}}^{n}),\alpha (U_{{i0}}^{n} - U_{{i - 1,0}}^{n}));$$
((7))

here, \(\alpha \in [1,\;2]\) is a heuristic parameter chosen in test computations; \(U_{{l0}}^{n}\) are the corresponding components of the vectors \({\mathbf{U}}_{{l0}}^{n}\) for \(l = i - 1,\;i,\;i + 1\); and M is the minmod operator defined by the formula

$$M\left( {{{u}_{1}},{{u}_{2}},{{u}_{3}}} \right) = s\min \left( {{\text{|}}{{u}_{1}}{\text{|}},{\text{|}}{{u}_{2}}{\text{|}},{\text{|}}{{u}_{3}}{\text{|}}} \right),$$
((8))

where \(s = \text{sgn}({{u}_{i}})\) if all the numbers \({{u}_{i}}\) in (8) have the same sign and s = 0 if this condition does not hold. The DG1 methods with correction based on formula (7) with α = 1 and α = 2 are denoted by DG1A1 and DG1A2, respectively.

When the parameter α involved in the correction operator (7) is increased, the smoothing properties of this operator are reduced. Specifically, test computations show that DG1A1 completely suppresses the numerical oscillations arising at the shock front in the DG1 method, while DG1A2 method only partially suppresses these oscillations. The goal of this work is to perform a comparative analysis of the accuracy of DG1, DG1A1, and DG1A2 as applied to shock wave computation and, relying on this analysis and the approaches developed in [1, 2], to construct a combined discontinuous Galerkin scheme that monotonically localizes shock fronts and simultaneously preserves increased accuracy in domains of smoothness of the computed weak solutions.

4. As a particular hyperbolic system, we use the system of shallow water equations in the first approximation. In the case of a rectangular horizontal channel without bottom friction, its conservative has the form of (1), where

$${\mathbf{u}} = \left( {\begin{array}{*{20}{c}} H \\ q \end{array}} \right),\quad {\mathbf{f}}({\mathbf{u}}) = \left( {\begin{array}{*{20}{c}} q \\ {{{q}^{2}}{\text{/}}H + g{{H}^{2}}{\text{/}}2} \end{array}} \right).$$
((9))

Here, \(H(x,t)\) is the fluid depth, \(q(x,t)\) is the mass flow rate, and g is the acceleration of gravity. For system (1), (9), we consider Cauchy problem (2) with initial data

$$\begin{gathered} {v}(x,0) = a\sin \left( {\frac{{2\pi x}}{X} + \frac{\pi }{4}} \right), \\ H(x,0) = \frac{1}{{4g}}{{\left( {a\sin \left( {\frac{{2\pi x}}{X} + \frac{\pi }{4}} \right) + b} \right)}^{2}}, \\ \end{gathered} $$
((10))

where \({v} = q{\text{/}}H\) is the fluid velocity (this problem was considered in [1, 2]). The initial conditions (10) correspond to the following initial values of the invariants \({{w}_{1}} = {v} - 2c\) and \({{w}_{2}} = {v} + 2c\):

$$\begin{gathered} {{w}_{1}}(x,0) = - b, \\ {{w}_{2}}(x,0) = 2{v}(x,0) + b = 2a\sin \left( {\frac{{2\pi x}}{X} + \frac{\pi }{4}} \right) + b, \\ \end{gathered} $$

where \(c = \sqrt {gH} \), a = 2, \(b = 10,\) and X = 10.

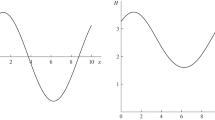
The exact solution of this problem was modeled by numerical computations based on the monotone DG1A1 method on a fine grid with the spatial step \(h = 0.0005\). The depth profiles obtained in these computations at the times T = 1 and T = 2.5 are shown by the solid curves in Fig. 1 on an interval of period length) and in Fig. 2 (near the shock front). The open circles in Figs. 1 and 2 depict the depth computed using to the modified scheme (see the description below) on a grid with the spatial step \(h = 0.05\). Figure 2 shows similar results produced by DG1 (squares), DG1A1 (crosses), and DG1A2 (triangles). In Fig. 2, we can see oscillations generated by the nonmonotone DG1 method near the shock front; they are smoothed by DG1A2 and are completely suppressed by DG1A1.

Fig. 1.
figure 1

Depth of fluid obtained according to the combined scheme (open circles) and the integral orders of convergence obtained according to the combined scheme (solid circles), the DG1 method (squares), the DG1A1 method (crosses), and the DG1A2 method (triangles). The solid line depicts the exact solution produced by the DG1A1 method on a fine grid.

Full size image
Fig. 2.
figure 2

Depth of fluid in the neighborhood of the shock front obtained according to the combined scheme (circles), the DG1 method (squares), the DG1A1 method (crosses), and the DG1A2 method (triangles). The solid line depicts the exact solution produced by the DG1A1 method on a fine grid.

Full size image

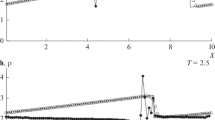
Figure 1 presents the orders of integral convergence \({{\rho }_{j}}\) of the discrete solutions on the intervals \([{{x}_{j}},X]\) as determined by the method proposed in [11], while Figs. 3 and 4 show the grid functions (ri)j = \({\text{log|}\delta}{{w}_{i}}({{x}_{j}}){\text{|}}\), where \(\delta {{w}_{i}}({{x}_{j}})\) are the relative local imbalances in the computed absolute values of the invariants \({{w}_{1}}\) and \({{w}_{2}}\) as obtained by the method described in [12]. The quantities \({{\rho }_{j}}\) and \({{({{r}_{i}})}_{j}}\) were computed on the baseline grid with the spatial step \(h = 0.005.\) They are shown for every 30th spatial node \(j = 30i\) in Fig. 1 and for every 35th node \(j = 35i\) in Figs. 3 and 4. These numerical results are presented for the combined scheme (circles), DG1 (squares), DG1A1 (crosses), and DG1A2 (triangles). The Courant number \(r = 0.5\) was used in all the computations.

Fig. 3.
figure 3

Graphs of the grid functions \({{({{r}_{i}})}_{j}}\) obtained at the time T = 1 according to the combined scheme (circles), the DG1 method (squares), the DG1A1 method (crosses), and the DG1A2 method (triangles).

Full size image
Fig. 4.
figure 4

Graphs of the grid functions \({{({{r}_{i}})}_{j}}\) obtained at the time T = 2.5 according to the combined scheme (circles), the DG1 method (squares), the DG1A1 method (crosses), and the DG1A2 method (triangles).

Full size image

5. Figure 1 suggests that the nonmonotone DG1 method, despite the noticeable oscillations at the shock front (Fig. 2), ensures the second order of integral convergence on the intervals \([{{x}_{j}},X]\), the left boundary of which lies within the domain of influence of the shock wave (this domain lies within the interval [4, 9] at the time T = 1 and occupies the entire computational domain at T = 2.5). Obtained by monotonizing the DG1 method, DG1A1 and DG1A2 (like finite-difference NFC schemes) reduce the rate of this convergence to the first order; as a result, their accuracy degrades noticeably (in comparison with DG1) when they are used to compute the invariants in the influence domain of the shock wave (Figs. 3 and 4).

Figure 1 shows that, in contrast to the DG1A1 method, DG1 and DG1A2 at T = 1 have the third order of integral convergence on the intervals \([{{x}_{j}},X]\), whose left boundary lies outside the domain of influence of the shock wave. On these intervals, DG1A1 has the second order of integral convergence. This result is explained by the fact that DG1 ensures the third order of local approximation for smooth solutions and the flux correction in DG1A2 preserves this order, while the stronger flux correction in DG1A1 reduces the accuracy of this approximation to the second order. As a result, outside the domain of influence of the shock wave, the invariants are computed using DG1A1 with a significantly lower accuracy than in the case of DG1 and DG1A2 (Fig. 3).

Relying on the presented accuracy analysis of the DG1 and DG1A1 methods, we can use them to construct a combined discontinuous Galerkin scheme that monotonically localizes shock fronts and simultaneously preserves increased accuracy in the domains of their influence. Such a combined scheme is constructed using the technique developed in [1, 2]. Specifically, the baseline scheme applied in the entire computational domain is specified as DG1, which preserves increased accuracy in the influence domain of the shock wave, while, as an internal scheme used in a grid neighborhood of the shock front, we choose DG1A1, which monotonically localizes this front. The resulting combined DG scheme combines the advantages of both methods, while being free from their shortcomings. This is illustrated by the numerical results produced by this scheme for the shock wave profile (open circles in Figs. 1 and 2), by the orders of its integral convergence (solid circles in Figs. 1 and 2), and by the accuracy of the invariants computed with the use of this scheme for the approximated solution (solid circles in Figs. 3 and 4).