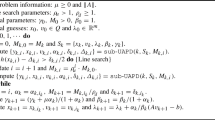In the late 1980s, A.S. Nemirovski showed that auxiliary low-dimensional optimization does not improve the theoretical worst-case rate of convergence of a first-order optimal gradient-type method for smooth convex minimization problems [1]. However, in practice, accelerated methods with linesearch (in particular, conjugate gradient methods) are usually more efficient than their fixed-stepsize counterparts in terms of the number of iterations. Moreover, such procedures have been successfully applied to nonconvex optimization problems [2]. Unfortunately, it is also well known that the gain in performance due to the use of linesearch is significantly reduced by the computational complexity of such procedures. It was noted in [3] that, for problems of a certain type frequently occurring in solving dual problems, the complexity of executing a linesearch step nearly coincides with the complexity of a usual gradient step. This fact motivates the study of methods with linesearch and their primal-dual properties [4–8].

Consider the minimization problem

$$f(x) \to \mathop {\min}\limits_{x \in {{\mathbb{R}}^{n}}} .$$

Its solution is denoted by \({{x}_{ * }}\). Assume that the objective function is differentiable and its gradient satisfies the Lipschitz condition with a constant L: for all x, \(y\, \in \,{{\mathbb{R}}^{n}}\),

$${\text{||}}\nabla f(y) - \nabla f(x){\text{|}}{{{\text{|}}}_{2}} \leqslant L{\text{||}}x - y{\text{|}}{{{\text{|}}}_{2}}.$$

We introduce an estimating sequence \({\text{\{ }}{{\psi }_{k}}(x){\text{\} }}\) [1, 4, 9, 10] and a sequence of coefficients \({\text{\{ }}{{A}_{k}}{\text{\} }}\):

$${{l}_{k}}(x) = \sum\limits_{i = 0}^k \,{{a}_{{i + 1}}}{\text{\{ }}f({{y}^{i}}) + \langle \nabla f({{y}^{i}}),x - {{y}^{i}}\rangle {\text{\} }},$$
$$\begin{gathered} {{\psi }_{{k + 1}}}(x) = {{l}_{k}}(x) + {{\psi }_{0}}(x) \\ = {{\psi }_{k}}(x) + {{a}_{{k + 1}}}{\text{\{ }}f({{y}^{k}}) + \langle \nabla f({{y}^{k}}),x - {{y}^{k}}\rangle {\text{\} }}{\text{,}} \\ \end{gathered} $$
$${{A}_{{k + 1}}} = {{A}_{k}} + {{a}_{{k + 1}}},\quad {{A}_{0}} = 0.$$

Let us describe an accelerated gradient method (AGM) with single linesearch.

Algorithm 1: AGM

Input: \({{x}^{0}} = {{{v}}^{0}}\), \(L\), \(N\)

Output: \({{x}^{N}}\)

 1: k = 0

 2: while\(k \leqslant N - 1\)do

 3: \({{\beta }_{k}} = \mathop {{\text{argmin}}}\limits_{\beta \in \left[ {0,1} \right]} f({{{v}}^{k}} + \beta ({{x}^{k}} - {{{v}}^{k}}))\)

 4: \({{y}^{k}} = {{{v}}^{k}} + {{\beta }_{k}}({{x}^{k}} - {{{v}}^{k}})\)

 5: \({{x}^{{k + 1}}} = {{y}^{k}} - \frac{1}{L}\nabla f({{y}^{k}})\)

 6: Choose \({{a}_{{k + 1}}}\) by solving \(\frac{{a_{{k + 1}}^{2}}}{{{{A}_{{k + 1}}}}} = \frac{1}{L}\)

 7: \({{{v}}^{{k + 1}}}\, = \,{{{v}}^{k}}\, - \,{{a}_{{k + 1}}}\nabla f({{y}^{k}})\)                            ▷\({{{v}}^{{k + 1}}}\, = \,\mathop {{\text{argmin}}}\limits_{x \in {{\mathbb{R}}^{n}}} {\kern 1pt} {{\psi }_{{k + 1}}}(x)\)

 8: \(k = k + 1\)

 9: end while

The main difference of this algorithm from well-known similar accelerated gradient methods [4, 10, 11] is the stepsize selection in line 3. The previous algorithms used a fixed stepsize (e.g., \({{\beta }_{k}} = \frac{k}{{k + 2}}\)).

Instead of Step 5, one can use different stepsize selection procedures, such as the Armijo rule [2] and its modern analogues (as in the universal fast gradient method [12]). The version of the method using exact linesearch for stepsize selection will be referred to as ALSM.

Algorithm 2: ALSM

Input: \({{x}^{0}} = {{{v}}^{0}}\)

Output: xN

 1: k = 0

 2: while\(k \leqslant N - 1\)do

 3: \({{\beta }_{k}} = \mathop {{\text{argmin}}}\limits_{\beta \in \left[ {0,1} \right]} f({{{v}}^{k}} + \beta ({{x}^{k}} - {{{v}}^{k}}))\)

 4: \({{y}^{k}} = {{{v}}^{k}} + {{\beta }_{k}}({{x}^{k}} - {{{v}}^{k}})\)

 5: \({{h}_{{k + 1}}} = \mathop {{\text{argmin}}}\limits_{h \geqslant 0} f({{y}^{k}} - h\nabla f({{y}^{k}}))\)

 6: \({{x}^{{k + 1}}} = {{y}^{k}} - {{h}_{{k + 1}}}\nabla f({{y}^{k}})\)

 7: Choose \({{a}_{{k + 1}}}\) by solving \(f({{y}^{k}}) - \frac{{a_{{k + 1}}^{2}}}{{2{{A}_{{k + 1}}}}}{\text{||}}\nabla f({{y}^{k}}){\text{||}}_{2}^{2} = f({{x}^{{k + 1}}})\)

    8: \({{{v}}^{{k + 1}}} = {{{v}}^{k}} - {{a}_{{k + 1}}}\nabla f({{y}^{k}})\)                            ▷ \({{{v}}^{{k + 1}}} = \mathop {{\text{argmin}}}\limits_{x \in {{\mathbb{R}}^{n}}} {{\psi }_{{k + 1}}}(x)\)

 9: \(k = k + 1\)

 10:    end while

Let us formulate the main theoretical results for these methods.

Theorem 1.For both AGM and ALSM,

$$\mathop {\min}\limits_{k = 0,...,N} {\text{||}}\nabla f({{y}^{k}}){\text{||}}_{2}^{2} \leqslant \frac{{2L(f({{x}^{0}}) - f({{x}_{ * }}))}}{N}.$$

If f(x) is convex, then, for both methods

$$\mathop {\min}\limits_{k = [N/2],...,N} {\text{||}}\nabla f({{y}^{k}}){\text{||}}_{2}^{2} \leqslant \frac{{32{{L}^{2}}{{R}^{2}}}}{{{{N}^{3}}}},$$
$$f({{x}^{N}}) - f({{x}_{ * }}) \leqslant \frac{{2L{{R}^{2}}}}{{{{N}^{2}}}},$$

where\(R = {\text{||}}{{x}_{ * }} - {{x}^{0}}{\text{|}}{{{\text{|}}}_{2}}\).

The function \(f(x)\) is called \(\gamma \)-weakly quasiconvex (where \(\gamma \in (0,1]\)) if, for all \(x \in {{\mathbb{R}}^{n}}\),

$$\gamma (f(x) - f({{x}_{ * }})) \leqslant \langle \nabla f(x),x - {{x}_{ * }}\rangle .$$

Note that γ-weakly quasiconvex functions are unimodal, but, in the general case, are not convex. If f(x) is γ-weakly quasiconvex, the AGM method can be considered with the following restarting procedure: as soon as

$$f(x_{i}^{N}) - f({{x}_{ * }}) \leqslant \left( {1 - \frac{\gamma }{2}} \right)(f(x_{i}^{0}) - f({{x}_{ * }})),$$

set \(x_{{i + 1}}^{0} = x_{i}^{N}\) and restart the method.

Theorem 2.If f(x) is γ-weakly quasiconvex, then, for the AGM and ALSM methods with the above-described restarting procedure,

$$f({{\tilde {x}}^{N}}) - f({{x}_{ * }}) = O\left( {\frac{{L{{R}^{2}}}}{{{{\gamma }^{3}}{{N}^{2}}}}} \right),$$

where\(R = \mathop {\max}\limits_{x:f(x) \leqslant f({{x}_{0}})} {\text{||}}x{\text{|}}{{{\text{|}}}_{2}}\)and\(\{ {{\tilde {x}}^{i}}\} \)is the sequence of points generated by the method in the course of all starts.

It can be shown that the SESOP method [3] can be applied to γ-weakly quasiconvex problems and has the convergence rate estimate

$$f({{\tilde {x}}^{N}}) - f({{x}_{ * }}) = O\left( {\frac{{L{{R}^{2}}}}{{{{\gamma }^{2}}{{N}^{2}}}}} \right)$$

with \(R = {\text{||}}{{x}^{0}} - {{x}_{ * }}{\text{|}}{{{\text{|}}}_{2}}\), but it requires solving a three-dimensional (possibly nonconvex) problem at every iteration step. On the contrary, the AGM method requires only solving a minimization problem on an interval.

Now we consider a convex optimization problem of the form

$$\phi (z) \to \mathop {\min}\limits_{Az = 0} .$$
((1))

In this case, a dual minimization problem can be constructed, namely,

$$\begin{gathered} f(x) = \mathop {\max}\limits_z \{ \langle x,Az\rangle - \phi (z)\} \\ = \langle x,Az(x)\rangle - \phi (z(x)) \to \mathop {\min}\limits_{x \in \mathbb{R}} . \\ \end{gathered} $$

According to the Demyanov–Danskin theorem, \(\nabla f(x)\) = Az(x). Assume that ϕ(z) is \(\mu \)-strongly convex. Then \(\nabla f(x)\) satisfies the Lipschitz condition with the constant \(L = \frac{{{{\lambda }_{{\max }}}(A)}}{\mu }\). Let us apply our methods to problem (1) with \({{x}^{0}} = {{{v}}^{0}} = 0\). Define

$$\mathop {\tilde {z}}\nolimits^N = \frac{1}{{{{A}_{N}}}}\sum\limits_{k = 0}^{N - 1} \,{{a}_{{k + 1}}}z({{y}^{k}}).$$

Theorem 3.For the AGM and ALSM methods,

$$f({{x}^{N}}) + \phi ({{\tilde {z}}^{N}}) \leqslant \frac{{16L{{R}^{2}}}}{{{{N}^{2}}}},$$
$$\mathop {{\text{||}}A{{{\tilde {z}}}^{N}}{\text{||}}}\nolimits_2 \leqslant \frac{{16LR}}{{{{N}^{2}}}},$$

where\(R = {\text{||}}{{x}_{ * }}{\text{|}}{{{\text{|}}}_{2}}\).

Consider a class of problems in which the objective function f(x) is not necessarily smooth. Let \(\nabla f(x)\) denote some subgradient of f(x). Assume that \(\nabla f(x)\) satisfies the Hölder condition: for all \(x,y \in {{\mathbb{R}}^{n}}\) and some \(u \in \left[ {0,1} \right]\),

$${\text{||}}\nabla f(y) - \nabla f(x){\text{|}}{{{\text{|}}}_{2}} \leqslant {{M}_{\nu }}{\text{||}}x - y{\text{||}}_{2}^{\nu }.$$

The following ULSM method can be proposed for solving problems of this class.

Algorithm 3: ULSM

Input: Initial point \({{x}^{0}} = {{{v}}^{0}}\), accuracy \(\varepsilon \)

Output: xN

 1: k = 0

 2: while\(k \leqslant N - 1\)do

 3: \({{\beta }_{k}} = \mathop {{\text{argmin}}}\limits_{\beta \in \left[ {0,1} \right]} f({{{v}}^{k}} + \beta ({{x}^{k}} - {{{v}}^{k}}))\)

 4: \({{y}^{k}} = {{{v}}^{k}} + {{\beta }_{k}}({{x}^{k}} - {{{v}}^{k}})\)

 5: \({{h}_{{k + 1}}} = \mathop {{\text{argmin}}}\limits_{h \geqslant 0} f({{y}^{k}} - h\nabla f({{y}^{k}}))\), where \(\langle \nabla f({{y}^{k}}),{{{v}}^{k}} - {{y}^{k}}\rangle \geqslant 0\)

 6: \({{x}^{{k + 1}}} = {{y}^{k}} - {{h}_{{k + 1}}}\nabla f({{y}^{k}})\)

      7: Choose \({{a}_{{k + 1}}}\) by solving \(f({{x}^{{k + 1}}}) = f({{y}^{k}}) - \frac{{a_{{k + 1}}^{2}}}{{2{{A}_{{k + 1}}}}}{\text{||}}\nabla f({{y}^{k}}){\text{||}}_{2}^{2} + \frac{{\varepsilon {{a}_{{k + 1}}}}}{{2{{A}_{{k + 1}}}}}\)

      8: \({{{v}}^{{k + 1}}} = {{{v}}^{k}} - {{a}_{{k + 1}}}\nabla f({{y}^{k}})\)                         ▷ \({{{v}}^{{k + 1}}} = \mathop {{\text{argmin}}}\limits_{x \in {{\mathbb{R}}^{n}}} {{\psi }_{{k + 1}}}(x)\)

      9:    k = k + 1

 10: end while

Note that, in contrast to other universal methods [12, 13], this one does not require estimating the necessary stepsize in an inner loop. This leads to a somewhat better estimate for the rate of convergence and, on average, to a smaller number of oracle calls per iteration step.

Theorem 4.If\(f(x)\)is convex and its subgradient satisfies the Hölder condition, then

$$f({{x}^{N}}) - f({{x}_{ * }})\frac{1}{{2{{A}_{N}}}}{\text{||}}{{x}_{ * }} - {{x}^{0}}{\text{||}}_{2}^{2} + \frac{\varepsilon }{2},$$

i.e., the method generates an ε-accurate solution after N iterations, where

$$N \leqslant \mathop {\inf}\limits_{\nu \in [0,1]} 2{{\left[ {\frac{{1 - \nu }}{{1 + \nu }}} \right]}^{{\frac{{1 - \nu }}{{1 + 3\nu }}}}}\mathop {\left[ {\frac{{{{M}_{\nu }}}}{\varepsilon }} \right]}\nolimits^{\frac{2}{{1 + 3\nu }}} {{R}^{{\frac{{2 + 2\nu }}{{1 + 3\nu }}}}}$$

with\(R = {\text{||}}{{x}_{0}} - x{\text{*|}}{{{\text{|}}}_{2}}\).

If the problem under consideration is strongly convex with a given constant \(\mu \), then use of the estimating sequence

$$\begin{gathered} {{\psi }_{{k + 1}}}(x) = {{l}_{k}}(x) + {{\psi }_{0}}(x) \\ = {{\psi }_{k}}(x) + {{a}_{{k + 1}}}\left\{ {f({{y}^{k}}) + \langle \nabla f({{y}^{k}}),x - {{y}^{k}}\rangle + \frac{\mu }{2}{\text{||}}x - {{y}^{k}}{\text{||}}_{2}^{2}} \right\} \\ \end{gathered} $$

leads to optimal (up to a multiplicative constant) analogues of the above-described methods in the class of strongly convex problems.