INTRODUCTION

Continuous phase modulation well known for its excellent spectral efficiency, low-energy consumption and constant envelope [1, 2], has been widely used in satellite communications [3, 4], fiber-optical communications [5] digital video broadcasting [6], telemetry [7] and so on. It could also be a potential candidate to multi-carrier waveforms for 5G as well as the Internet of Things (IoT) and wireless sensor networks [8]. Under low SNR scenario, the development of low complexity scheme of recovering CPM signals would render the CPM a more competitive alternative for these applications.

A wide array of techniques such as energy detection, matched filter detection, cyclostationary feature detection, covariance based detection and others have been developed [9–12]. However, under low-SNR scenario, these methods typically require to process a large number of samples, which could demand too long processing time to be feasible for many 5G or IoT applications. Furthermore, most of these schemes are only suitable for detecting the existence of the signals but not capable of recovering the IF of the signals. More interesting schemes which involve the IF estimation of the CPM signals proposed in [13] and further developed in [14], however, do not perform well under low SNR scenario.

In this paper, we develop a low computational complexity scheme to estimate the IF of CPM signals under low SNR scenario. The derivation of this IF estimator is based on the modified Wigner–Ville distribution (MWVD) where we choose a simple Chebyshev polynomial of order 5 as the kernel function for suppressing the cross-terms [15, 16]. Thus, this simplifies the computation of the MWVD which yields a novel estimator capable of recovering IF of CPM signals under low SNR scenario. The implementation of this estimator is then done through the Viterbi algorithm for further reducing computation complexity. As a comparison, we also employ the DFT-frequency extraction method as well as the non-coherent method proposed in [14]. The simulation results show that our scheme outperforms these methods under low SNR scenario.

The paper is organized as follows. In Section 1 we introduce the model of CPM signals. The algorithm for the IF estimation in a low SNR scenario is derived in Section 2. The simulation results are presented in Section 3.

1 PROBLEM FORMULATION

A CPM signal \(s(t,{\boldsymbol{\alpha }})\) is defined as

$$s(t,\boldsymbol{\alpha } ) = \sqrt[{}]{{{{2E} \mathord{\left/ {\vphantom {{2E} T}} \right. \kern-0em} T}}}{\text{cos}}(2\pi {{f}_{0}}t + \varphi (t,{\boldsymbol{\alpha }})),$$
(1)

where Ε and T represent the symbol energy and symbol period respectively, f0 denotes the carrier frequency. The information carrying phase is

$$\varphi (t,{\boldsymbol{\alpha }}) = 2\pi h\sum {{{\alpha }_{i}}q(t - iT)} ,$$
(2)

with \({\boldsymbol{\alpha }} = \{ \pm 1, \ldots , \pm (M - 1)\} \) representing the information symbol and h being the modulation index. The quantity q(t) is equal to

$$q(t) = \left\{ {\begin{array}{*{20}{l}} {0,\,\,\,\,t \leqslant 0,} \\ {\int\limits_{ - \infty }^t {g(\tau )} d(\tau ),\,\,\,\,0 < t \leqslant LT} \\ {\frac{1}{2},\,\,\,\,t > LT.} \end{array}} \right.{\mkern 1mu} ,$$
(3)

g(t) is frequency pulse with time duration LT. The model considered in this paper is

$$x(t) = s(t) + n(t) = A\exp [j2\pi \varphi (t)] + n(t){\mkern 1mu} ,$$
(4)

where x(t) is the observed signal x(t) and n(t) denotes white Gaussian noise, and the amplitude A as well as the information-carrying phase φ(t) defined in (2) is unknown to us. Thus, our goal in this paper is to develop a low computation scheme that is capable of recovering φ(t) of the CPM signal \(s(t) = A\exp [j2\pi \varphi (t)]\) from x(t) under low SNR scenario, and its derivative is just the IF of CPM signal.

2 MATERIALS AND METHODS

In this section, we first introduce the modified Wigner–Ville distribution which is exploited to reduce cross-term interference with the proper choice of the kernel function. Then, based on this MWVD, we develop a low computation complexity scheme to estimate the instantaneous frequency (IF) of CPM Signals. Finally, this scheme is implemented through the Viterbi algorithm.

2.1 The Modified Wigner–Ville Distribution

The modified Wigner–Ville distribution (MWVD) can be expressed as

$$\begin{gathered} {{D}_{x}}(t,f) \\ = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {{{A}_{x}}(\theta ,\tau )\Phi (\theta ,\tau )\exp ( - j2\pi \theta t - j2\pi f\tau )d\theta d\tau } } . \\ \end{gathered} $$
(5)

To simplify the estimator, we choose the kernel \(\Phi (\theta ,\tau )\) as

$$\Phi (\theta ,\tau ) = {1 \mathord{\left/ {\vphantom {1 {(1 + {{F}^{2}}(\theta ,\tau ))}}} \right. \kern-0em} {(1 + {{F}^{2}}(\theta ,\tau ))}},$$
(6)

where \(F(\theta ,\tau )\) is the Chebyshev polynomial of order 5, i.e.,

$$\begin{gathered} F(\theta ,\tau ) = 16{{\left( {\frac{{{{\theta }^{2}} + {{\tau }^{2}}}}{{2{{\sigma }^{2}}}}} \right)}^{5}} \\ - \,\,20{{\left( {\frac{{{{\theta }^{2}} + {{\tau }^{2}}}}{{2{{\sigma }^{2}}}}} \right)}^{3}} + 5\left( {\frac{{{{\theta }^{2}} + {{\tau }^{2}}}}{{2{{\sigma }^{2}}}}} \right). \\ \end{gathered} $$
(7)

The ambiguity function (AF) \({{A}_{x}}(\theta ,\tau )\) in (5) is defined as

$${{A}_{x}}(\theta ,\tau ) = \int\limits_{ - \infty }^{ + \infty } {x{\kern 1pt}^{ *}\left( {t - \frac{\tau }{2}} \right)} x\left( {t + \frac{\tau }{2}} \right)\exp (j2\pi \theta t)dt,$$
(8)

with τ and θ being the frequency and time shift. In order to obtain the parameters of the kernel function \(\Phi (\theta ,\tau )\) that can effectively suppress the cross-terms yielded from\({{A}_{x}}(\theta ,\tau )\,,\) we first transform \((\theta ,\tau )\) into the polar coordinate \((r,\psi )\) through

$$\begin{gathered} r = \sqrt {{{\theta }^{2}} + {{\tau }^{2}}} , \\ \psi = \arctan ({\tau \mathord{\left/ {\vphantom {\tau \theta }} \right. \kern-0em} \theta }) \\ \end{gathered} $$
(9)

and then solve the following optimization problem

$$\begin{gathered} \mathop {\max }\limits_\psi {\mkern 1mu} \int\limits_0^{2\pi } {\int\limits_0^{ + \infty } {{{{\left| {{{A}_{x}}(r,\psi )\Phi (r,\psi )} \right|}}^{2}}} } rdrd\psi , \\ {\text{s}}.{\text{t}}.\,\,{\kern 1pt} \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\int\limits_0^{ + \infty } {{{{\left| {\Phi (r,\psi )} \right|}}^{2}}} } drd\psi \leqslant \alpha ,\,\,\,\,\alpha \geqslant 0. \\ \end{gathered} $$
(10)

The solution of (10) yields the optimal kernel as

$$\begin{gathered} {{\Phi }_{{{\text{opt}}}}} = 16{{\left( {\frac{{{{r}^{2}}}}{{2{{\sigma }^{2}}({{\psi }_{{{\text{opt}}}}})}}} \right)}^{5}} \\ - \,\,20{{\left( {\frac{{{{r}^{2}}}}{{2{{\sigma }^{2}}({{\psi }_{{{\text{opt}}}}})}}} \right)}^{3}} + 5\left( {\frac{{{{r}^{2}}}}{{2{{\sigma }^{2}}({{\psi }_{{{\text{opt}}}}})}}} \right). \\ \end{gathered} $$
(11)

Substituting Φopt into (5), we obtain \({\mkern 1mu} D_{x}^{{{\text{opt}}}}(t,f)\) which leads to the IF estimator as

$${{\hat {f}}_{x}}(t) = \arg \mathop {\max }\limits_f \left[ {D_{x}^{{{\text{opt}}}}(t,f)} \right].$$
(12)

It is shown that under the low SNR situation the high noises could result in the estimation errors behaving dominantly impulsive [17]. Thus, we need to modify (12), which enables it to effectively extract the IF of CPM signals under the low SNR scenario.

2.2 Estimating IF of the Signals Based on the Viterbi Algorithm

In this section, we first modify the estimator of the IF of CPM signals given in (12) to ensure that the modified estimator can effectively extract the IF under the low SNR situation. Then the computation of the IF through the modified estimator is done by the Viterbi algorithm.

Throughout this paper, we assume that the IF of the given signal is continuous function of the time. We first discretize \(D_{x}^{{{\text{opt}}}}(t,f)\) of (12) which yields a \(M \times Q\) matrix

$${{\left[ {D_{x}^{{{\text{opt}}}}({{t}_{i}},{{f}_{j}})} \right]}_{{M \times Q}}},$$
(13)

with \(i = 1,2,...,M\) and \(j = 1,2,...,Q\).

Note that since the integral along the frequency axis is equal to the energy of the signal at time ti [18], the maximum value of \(D_{x}^{{{\text{opt}}}}({{t}_{i}},{{f}_{j}})\) at time ti is positive. Therefore, for each time instance n, we transfer (13) to optimize the summation of a set of sub-problems as suggested in [19]. That is, for the fixed time interval [n1, n2] with n1 and n2 being positive integers and each path k between n1 and n2, we compute the following optimization problem

$${{\hat {f}}_{x}}(n) = \arg \mathop {\max }\limits_{k \in K} \sum\limits_{n = {{n}_{1}}}^{{{n}_{2}}} {\left[ {D_{x}^{{{\text{opt}}}}(n,k(n))} \right]} .$$
(14)

Here K denotes the set comprised of all the paths between n1 and n2 and k(n) represents the path k at time n with \({{n}_{1}} \leqslant n \leqslant {{n}_{2}}\). On the other hand, under the low SNR scenario, [17] suggests that the estimation errors behave dominantly impulsive. To resolve this, we also need minimizing the distance between two adjacent time instance k(n) and k(n + 1) of path k from (14). That is, we simultaneously require to maximize the following equation

$$\sum\limits_{n = {{n}_{1}}}^{{{n}_{2}} - 1} {g(k(n),k(n + 1))} ,$$
(15)

where the exponential decay function g(x, y) is defined as

$${\mkern 1mu} g(x,y) = \left\{ \begin{gathered} 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {x - y} \right| \leqslant \Delta , \hfill \\ \exp \left[ { - c\left( {\left| {x - y} \right| - \Delta } \right)} \right],\,\,\,\,\left| {x - y} \right| > \Delta . \hfill \\ \end{gathered} \right.$$
(16)

Combing equation (14) and (15), we obtain the modified estimator of IF as

$${\mkern 1mu} \hat {f}(n) = \arg \mathop {\max }\limits_{k \in K} \left[ {\sum\limits_{n = {{n}_{1}}}^{{{n}_{2}}} {h\left( {D_{x}^{{{\text{opt}}}}(n,k(n))} \right) + \sum\limits_{n = {{n}_{1}}}^{{{n}_{2}} - 1} {g(k(n),k(n + 1))} } } \right],$$
(17)

where the non-decreasing function h(x) is introduced to assign a value for each element in (14) for simplifying the implementation of the Viterbi algorithm. To define h(x), without loss of generality we assume that the rows of the matrix (13) is sorted to satisfy

$$D_{x}^{{{\text{opt}}}}({{t}_{i}},{{f}_{1}}) \geqslant D_{x}^{{{\text{opt}}}}({{t}_{i}},{{f}_{2}}) \geqslant \ldots \geqslant D_{x}^{{{\text{opt}}}}({{t}_{i}},{{f}_{Q}}),$$
(18)

with \(i \in M\). Then the non-decreasing function h is defined as

$$h(D_{x}^{{{\text{opt}}}}({{t}_{i}},{{f}_{j}})) = \exp [ - (j - 1)].$$
(19)

The procedure computing the estimator (17) based on Viterbi algorithm proceeds as follows:

(i) Initialization: Define \({{L}_{{i,j}}}\) as the path metric from the starting point to point (i, j) and \({{P}_{{i,j}}}\) as the local optimal path composed of a set of points from the starting point to point (i, j). At time t1 choose \({{L}_{{1,l}}} = h(l)\) and set \({{P}_{{1,l}}} = l\) for \(l = 1,2,...,Q\).

(ii) At time ti for \(i \geqslant 2\), compute the path metric \({{L}_{{i,j}}}\) for each \(1 \leqslant j \leqslant Q\) and each \(1 \leqslant l \leqslant Q\) as follows

$${{L}_{{i,j}}} = {{L}_{{{{P}_{{i - 1,l}}}}}} + g(l,j) + h(j),$$
(20)

where \({{L}_{{{{P}_{{i - 1,l}}}}}}\) is the path metric of the local optimal path \({{P}_{{i - 1,l}}}\) which starts from the starting point to point (i – 1, l). The function g and h are defined in (16) and (19) respectively.

For each \(1 \leqslant j \leqslant Q\), the survival path at time ti is \(({{\hat {l}}_{j}},j)\) which maximizes the path metric (20), i.e.

$${{\hat {l}}_{j}} = \arg \mathop {\max }\limits_l \left[ {{{L}_{{{{P}_{{i - 1,l}}}}}} + g(l,j) + h(j)} \right].$$
(21)

The local optimal path \({{P}_{{i,{{{\hat {l}}}_{j}}}}}\) for \(2 \leqslant i \leqslant M - 1\) and \(1 \leqslant j \leqslant Q\) is therefore equal to

$${{P}_{{i,j}}} = \left[ {{{P}_{{i - 1,{{{\hat {l}}}_{j}}}}},j} \right].$$
(22)

(iii) If \(i \leqslant M - 1\), replace i with i + 1 and repeat step (2). Else, we have i = M which yields a set of the local optimal path \({{P}_{{M,\hat {j}}}}\) for \(1 \leqslant j \leqslant Q\). The optimal path is \({{\max }_{{1 \leqslant j \leqslant Q}}}\{ {{P}_{{M,\hat {j}}}}\} \).

3 RESULTS

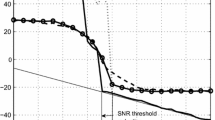
In this section, we utilize the scheme developed in the above section to extract the IF from a CPM signal. First, we deal with the raised cosine of LT (LRC) based CPM signal, which is easier to recovery with our method because of its continuous frequency. In order to compare the performance of our scheme with the frequency estimate method proposed in [14], we utilize the example of [14] in which the modulation index is chosen to be h = 0.29 together with the correlation length L = 1 and level number M = 4. Under SNR = 0 dB situation, Fig. 1 shows that the estimated the IF is depicted in the solid line while the actual IF is in the dotted line. The estimation results under SNR = –3 dB scenario are shown in Fig. 2 where the solid and dotted line represents the estimated and actual IF respectively. The BER curves of our scheme and the methods from [] are shown in Fig. 3 where line with Δ corresponds to the performance of our scheme while line with + or ○ represent the performances of DFT as well as non-coherent method respectively. Furthermore, we try to extract the frequency of the rectangular-based (LREC) CPM signal with frequency hopping, and successfully extract the signal IF under SNR = 0 dB scenario. Modulation index is chosen to be h = 0.4 together with the correlation length L =1 and level number M = 4. Figure 4 shows that the estimated IF is depicted in the solid line while the actual IF is in the dotted line.

Fig. 1.
figure 1

Estimated frequency and actual frequency of LRC-based CPM signal with SNR = 0 dB.

Full size image
Fig. 2.
figure 2

Estimated frequency and actual frequency of LRC-based CPM signal with SNR = –3 dB.

Full size image
Fig. 3.
figure 3

BER curves of several methods.

Full size image
Fig. 4.
figure 4

Estimated frequency and actual frequency of LEC-based CPM signal with SNR = 0 dB.

Full size image

CONCLUSIONS

A low computational complexity scheme based on the modified Wigner–Ville distribution (MWVD) is developed for estimating the instantaneous frequency (IF) of CPM signals under low SNR scenario. To simplify the computation of the MWVD, the Chebyshev polynomial of order 5 is chosen as the kernel function for suppressing the cross-terms. The implementation of this IF estimator is done through the Viterbi algorithm. The simulation results show that our scheme outperforms other estimating methods under low SNR scenario.