Plasmon Resonances in Square and Rectangular Noble Metal Nanoplates

Abstract—The article considers the two-dimensional diffraction problem of a TM-type plane electromagnetic wave on a cylindrical silver or gold structure, the contour of the cross section of which is a square or rectangle. In the wavelength range $300\,\,{\text{nm}} < \lambda < 900\,\,{\text{nm}}$ a rigorous numerical method is used calculate the spectra of the scattering cross section and scattering patterns. The influence of losses of the medium, the geometric dimensions of the structure, and the angle of incidence of a plane wave on the scattering cross section and scattering pattern is studied. It has been shown that the real losses of gold make it impossible for multipole resonances to exist at plate sizes substantially less than the wavelength. In the case of a silver plate, the position of the dipole and the presence of multipole resonances depends both on the length and thickness of the plate and on the angle of incidence of the plane wave.

INTRODUCTION

As is known, electromagnetic wave diffraction by noble metal nanostructures (silver, gold) in the visible wavelength range is accompanied both by the formation of surface waves (plasmon polaritons) and existence of their resonances. Moreover, interest in studying the properties of plasmon polaritons is mainly related to the high localization of the electromagnetic field near the surfaces of nanostructures, which allows their use in subwavelength and near-field probing. Thus, silver and gold nanowires are widely used as sensors [1]. Note that plasmon resonances in cylindrical nanostructures (filaments) with a circular cross section occur in the ultraviolet. Using nanotubes, plasmon resonance frequencies can be shifted to the visible region [2, 3]. In [4], plasmon resonances in quartz nanowires coated with a layer of gold with variable thickness were studied under the assumption that the shell boundaries are circular cylinders with displaced centers. Various geometries of silver and quartz shells, the cross-section contours of which are formed by circular or circular and elliptical cylinders, were considered in [5–7].

The aim of this work is to study the characteristics of plasmon resonances in 2D silver (gold) nanostructures in the case when the cross-sectional contours of the structure are square (rectangle) with different aspect ratios. Among related works, we mention [8‒11].

1 FORMULATION OF THE PROBLEM

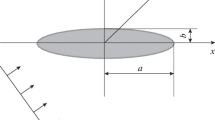
Let us consider the two-dimensional problem of diffraction of a plane electromagnetic linearly polarized wave by a two-dimensional cylindrical dielectric structure (plate), the cross section of which is square (Fig. 1a) or rectangular (Fig. 1b). A plane wave propagates in the direction of a unit vector ($\cos {{\varphi }_{0}},\sin {{\varphi }_{0}},0$) and is characterized by the following electromagnetic field components:

$$\begin{gathered} H_{z}^{0} = \exp ( - ikx\cos {{\varphi }_{0}} - iky\sin {{\varphi }_{0}}), \\ E_{x}^{0} = - \eta \sin {{\varphi }_{0}}\exp ( - ikx\cos {{\varphi }_{0}} - iky\sin {{\varphi }_{0}}), \\ E_{y}^{0} = \eta \cos {{\varphi }_{0}}\exp ( - ikx\cos {{\varphi }_{0}} - iky\sin {{\varphi }_{0}}). \\ \end{gathered} $$

(1)

Fig. 1.

Problem geometry for square (a) and rectangular (b) plate.

The time dependence is selected as $\exp (i\omega t),$ where $\omega = kc$ is the circular frequency, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ is the wavenumber of the free space, $c$ is speed of light in vacuum, $\lambda$ is the wavelength, and $\eta = 120\pi \,\,\Omega$ is the wave impedance of the vacuum.

For the structure shown in Fig. 1b , the contour of the cross section is described by the formula

$${{({x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a})}^{N}} + {{({y \mathord{\left/ {\vphantom {y b}} \right. \kern-0em} b})}^{N}} = 1,$$

(2)

where $N \gg 1$ (e.g., for $N = 18$) and $a \ne b.$ If in (2) we take $a = b,$ then formula (2) will describe the boundary of the structure (dielectric plate) with the contour of the square cross section (see Fig. 1a). We consider the medium of the structure to be silver (or gold). The frequency dependence of the relative dielectric permittivity ${{\varepsilon }_{{\text{s}}}}(\lambda ) = \varepsilon {\kern 1pt} '\,\, - i\varepsilon {\kern 1pt}^{"}$ ≡ $\operatorname{Re} ({{\varepsilon }_{{\text{s}}}}) - i\operatorname{Im} ({{\varepsilon }_{{\text{s}}}})$ of silver (or gold ${{\varepsilon }_{{\text{g}}}}(\lambda )$) was calculated by interpolating the experimental data of [12] using cubic splines. Figure 2a shows the dependence of the real and imaginary parts of the relative dielectric permittivity of silver. Similar dependences for gold are shown in Fig. 2b.

Fig. 2.

Dependence of real (1) and imaginary (2) parts of relative dielectric permittivity of silver (a) and gold (b) on wavelength.

The spatial distribution of the dielectric permittivity for the structures shown in Fig. 1 has the form

$$\bar {\varepsilon }(x,y) = \left\{ \begin{gathered} {{\varepsilon }_{{{\text{s}}{\text{,g}}}}},\,\,\,\,{{({x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a})}^{N}} + {{({y \mathord{\left/ {\vphantom {y b}} \right. \kern-0em} b})}^{N}} < 1. \hfill \\ 1,\,\,\,\,{{({x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a})}^{N}} + {{({y \mathord{\left/ {\vphantom {y b}} \right. \kern-0em} b})}^{N}} > 1. \hfill \\ \end{gathered} \right.$$

(3)

It is more convenient to study the formulated diffraction problem using the $z$ magnetic field component $U(x,y) = {{H}_{z}}(x,y)$, since the boundary value problem for the function $U(x,y)$ is scalar. The total field $U(x,y),$ i.e., the superposition of the incident and scattered fields in a piecewise constant medium (3), satisfies the Helmholtz equation

$$\frac{{{{\partial }^{2}}U(x,y)}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}U(x,y)}}{{\partial {{y}^{2}}}} + {{k}^{2}}\bar {\varepsilon }(x,y)U(x,y) = 0.$$

(4)

The electric field components can be expressed by the function $U(x,y)$

$$\begin{gathered} {{E}_{x}}(x,y) = \frac{\eta }{{ik\bar {\varepsilon }(x,y)}}\frac{{\partial U(x,y)}}{{\partial y}}, \\ {{E}_{y}}(x,y) = - \frac{\eta }{{ik\bar {\varepsilon }(x,y)}}\frac{{\partial U(x,y)}}{{\partial x}}. \\ \end{gathered} $$

(5)

At the boundaries of the structure there must be continuous values $U$ and $\frac{1}{{\bar {\varepsilon }}}\frac{{\partial U}}{{\partial N}},$ where $\frac{{\partial U}}{{\partial N}}$ is the derivative in the direction of the normal to the interface.

As already noted, the total field outside the plate consists of the incident (${{U}^{0}}$) and scattered (${{U}^{s}}$) fields. The incident field is given by the function

$${{U}^{0}} = \exp ( - ikx\cos {{\varphi }_{0}} - iky\sin {{\varphi }_{0}}).$$

(6)

The scattered field in a cylindrical coordinate system ($r,\varphi$), where $x = r\cos \varphi$ and $y = r\sin \varphi ,$ in the far field ($kr \to \infty$), must satisfy the radiation condition

$${{U}^{{\text{s}}}} = \Phi (\varphi )\sqrt {\frac{2}{{\pi kr}}} \exp \left( { - ikr + i\frac{\pi }{4}} \right),$$

(7)

where $\Phi (\varphi )$ is the scattering pattern.

Total scattering cross section ${{\sigma }_{{\text{S}}}}$ is determined by the formula

$${{\sigma }_{{\text{S}}}} = \frac{2}{{\pi k}}\int\limits_0^{2\pi } {{{{\left| {\Phi (\varphi )} \right|}}^{2}}} d\varphi .$$

(8)

2 NUMERICAL RESULTS

The formulated problem was numerically solved by the modified discrete sources method [13, 14]. Here, the accuracy in solving the problem was controlled by calculation of the residual $\delta$ of the boundary conditions in the linear norm at points at the middle between points where the boundary conditions are satisfied exactly (at such points, the boundary conditions are the most poorly met [13]). In all calculations below, the maximum residual of the boundary conditions does not exceed $\delta < {{10}^{{ - 3}}}.$Figure 3 shows an example of a typical distribution of the residual $\delta (n)$ along the contour (2) of a silver plate ($n$ is the number of the point on the contour) (the parameters of the contour (2) were considered to be as follows: $N = 18,\,\,a = 50\,\,{\text{nm}},$$b = 5\,\,{\text{nm}}$).

Fig. 3.

Distribution of absolute values of residual of boundary conditions along contour of silver plate for a = 50 and b = 5 nm.

Let us first consider the behavior of the normalized scattering cross section $k{{\sigma }_{{\text{S}}}}$ depending on the wavelength $\lambda$ (in all results presented below $\lambda$ varies within $300\,\,{\text{nm}} < \lambda < 600\,\,{\text{nm}}$ for silver and $300\,\,{\text{nm}} < \lambda < 900\,\,{\text{nm}}$ for gold) for the case of a silver plate at various angles of incidence ${{\varphi }_{0}}$ of the plane wave.

Figure 4 presents the results of calculating the normalized scattering cross section $k{{\sigma }_{{\text{S}}}}$ for an angle of incidence ${{\varphi }_{0}} = 0,$ i.e., when the plane wave hits (“illuminates”) a narrow part of the plate and propagates along its wide part. In this case, curve 1 corresponds to a square plate, and curves 2–5, to rectangular plate with $a = 50\,\,{\text{nm}}$ and b = 25, 125, 6.25, and 5 nm. From the figure it follows that in all cases, curves 1–5 contain two maxima, the amplitude ratio of which changes with decreasing plate thickness. In this case, the maxima lie in the wavelength range $320\,\,{\text{nm}} < \lambda < 360\,\,{\text{nm}}$ and hardly change their position at all.

Fig. 4.

Dependence of normalized scattering cross section on wavelength at angle of incidence ${{\varphi }_{0}} = 0$ of a plane wave for a silver plate with parameters of a = 50 nm and b = 50 (1), 25 (2), 12.5, (3), 6.25 (4), and 5 nm (5).

To understand the origin of these maxima, Fig. 5 shows the results of calculating the normalized scattering cross section $k{{\sigma }_{{\text{S}}}}$ for $a = b = 50\,\,{\text{nm}}{\text{,}}$${{\varphi }_{0}} = 0$ and various values of the imaginary part of the relative dielectric permittivity of silver, which determine the losses of the medium. It follows from this figure that for small values of the losses of the medium ($\operatorname{Im} (\varepsilon ) \leqslant \operatorname{Im} ({{\varepsilon }_{{\text{s}}}})$), both dipole and multipole resonances can be observed. In addition, it can be seen that for real values $\operatorname{Im} ({{\varepsilon }_{{\text{s}}}})$ such a silver plate has the first (right) maximum of the scattering cross section $k{{\sigma }_{{\text{S}}}}$ corresponds to a dipole resonance, and the second (left) maximum is the result of the merger of several multipole resonances.

Fig. 5.

Dependence of normalized scattering cross section on wavelength for ${{\varphi }_{0}} = 0,$$a = b = 50\,\,{\text{nm}}{\text{,}}$${{\varphi }_{0}} = 0$ and various losses for silver: $\operatorname{Im} (\varepsilon ) = 0$ (1), 0.1 Im (ε_s) (2) and 0.001 Im (ε_s) (3).

We note in passing that application of the technique and the results of [14] raise serious doubts for the case of thin nanoplates made from precious metals. On the one hand, this is because the plate thickness $2b$ should not be less than $2b \leqslant 10\,\,{\text{nm}}{\text{,}}$ since for a plate thickness of $2b < 10\,\,{\text{nm}}$, it is necessary to take into account the effects associated with spatial dispersion, and for $2b \leqslant 5\,\,{\text{nm}}$, it is necessary to apply quantum mechanics to describe the interaction of an electromagnetic wave with the plate [1]. On the other hand, for $2b > 10\,\,{\text{nm}}$, a fairly strong change in the field across the plate occurs, which is purposefully not taken into account in the methodology of [14]. In addition, we note that the reference to [13] as a test is incorrect, since it does not contain the corresponding calculations of the scattering cross section based on application of the method of surface integral equations that confirm the result of [14].

Figures 6a and 6b show the results of calculating the normalized scattering cross section $k{{\sigma }_{{\text{S}}}}$ for plane wave angles of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ and ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},$ i.e., when both sides of the plate are illuminated. The dimensions of the silver plate and numbering of the curves were assumed similar to the previous case. As follows from the figures, the scattering cross section $k{{\sigma }_{{\text{S}}}}$ has one maximum (right and main) associated with dipole resonance, and a second maximum (left with a significantly smaller level) resulting from the merging of multipole resonances. Note that the position of the main maximum $k{{\sigma }_{{\text{S}}}}$ depends on the thickness of the plate: with decreasing plate thickness, it shifts toward increased values of λ. In this case, the maxima of the scattering cross section $k{{\sigma }_{{\text{S}}}}$ lie in the wavelength range $320\,\,{\text{nm}} < \lambda < 550\,\,{\text{nm}}{\text{,}}$ which significantly exceeds the case of a plane wave incidence with an angle ${{\varphi }_{0}} = 0.$ In addition, comparison of the results presented in Figs. 6a and 6b shows that the positions of resonance of the scattering cross section $k{{\sigma }_{{\text{S}}}}$ for angles of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4},$${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ with the same plate thicknesses virtually coincide.

Fig. 6.

Dependence of normalized scattering cross section on wavelength at angles of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ (a) and ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (b) of plane wave for silver plate with parameters of a = 50 nm and b = 50 (1), 25 (2), 12.5 (3), 6.25 (4), and 5 nm (5).

Figures 7a and 7b show the results of calculating the normalized scattering cross section $k{{\sigma }_{{\text{S}}}}$ for a gold plate and plane wave angles of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ and ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$ The dimensions of the gold plates are the same as the silver ones. As we see, the frequency dependence of the scattering cross section $k{{\sigma }_{{\text{S}}}}$ has only one maximum determined by the dipole resonance. A decrease in plate thickness here, just like in the case of a silver plate, leads to a similar change in the position of the scattering cross section $k{{\sigma }_{{\text{S}}}}$: displacement to the large wavelength region. However, the wavelength range in which the maxima are located $k{{\sigma }_{{\text{S}}}}$ is $510\,\,{\text{nm}} < \lambda < 640\,\,{\text{nm}}{\text{,}}$ less than for a silver plate.

Fig. 7.

Dependence of normalized scattering cross section on wavelength an angle of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ (a) and ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ (b) of plane wave for gold plate with parameters of a = 50 nm and b = 50 (1), 25 (2), 12.5 (3), 6.25 (4), and 5 nm (5).

Figure 8 shows the influence of the plate material on the frequency dependence of the scattering cross section $k{{\sigma }_{{\text{S}}}}$. It shows the results of calculating the scattering cross section $k{{\sigma }_{{\text{S}}}}$ for silver and gold plates with the same dimensions $a = 100\,\,{\text{nm}},\,\,b = 5\,\,{\text{nm}}$ and the angle of incidence of the plane wave ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}.$ It follows from the figure that for a silver plate there are pronounced dipole and one multipole resonances. Moreover, the gold plate has only dipole resonance. Differences in the behavior of the frequency dependence of losses for silver and gold (see curves 2 in Figs. 2a, 2b) explain this behavior of the curves.

Fig. 8.

Dependence of normalized scattering cross section on wavelength for silver (1) and gold (2) plates with parameters $a = 100\,\,{\text{nm}},\,\,b = 5\,\,{\text{nm}}$ and plane wave angle of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}.$

In Fig. 9 shows the results of calculating the spatial distribution of the field $U = {{H}_{z}}(x = 0,y)$ along the $y$ axis for four wavelengths $\lambda$ = 367.27, 400, 539, and 600 nm. The geometric dimensions of the silver plate are $a = 50\,\,{\text{nm}}{\text{,}}$$b = 5\,\,{\text{nm;}}$ and the angle of incidence of a plane wave on the plate ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$ Note that for $\lambda \approx 400\,\,{\text{nm}}$ and $\lambda = 539\,\,{\text{nm}}$, there are local maxima of the scattering cross section. It follows from this figure that even in the case of a relatively thin plate ($2a = 10\,\,{\text{nm}}$), in the transverse direction, a sufficiently strong change in the field is observed, which cannot in any way be considered approximately constant. This also casts doubt on use of the integral equation obtained by the method of two-sided boundary conditions [14] to describe the interaction of electromagnetic waves with “thin plates” of precious metals.

Fig. 9.

Spatial distribution of field $U = {{H}_{z}}(x = 0,y)$ along $y$ axis for silver plate with parameters $a = 50\,\,{\text{nm}},$$b = 5\,\,{\text{nm}},$ plane angle of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ and fixed wavelength $\lambda$ = 367.27 (1), 400 (2), 539 (3), and 600 nm (4).

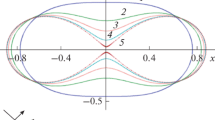
Lastly, let us discuss the results of calculating the scattering patterns. Figure 10 shows the calculation results illustrating the effect of losses for silver on the scattering pattern of a silver plate with parameters $a = 50\,\,{\text{nm}}{\text{,}}$ at a plane angle of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ at two wavelengths: 396 and 539 nm. As we see, the losses have a stronger effect on the scattering pattern for multipole resonance ($\lambda \approx 396\,\,{\text{nm}}$) than for dipole resonance ($\lambda \approx 539\,\,{\text{nm}}$).

Fig. 10.

Scattering pattern for silver plate with parameters $a = 50\,\,{\text{nm}}{\text{,}}$$b = 5\,\,{\text{nm}}$ and plane wave angle of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ for wavelength of $\lambda \approx 396\,\,{\text{nm}}$ (1, 2) and $\lambda \approx 539\,\,{\text{nm}}$ (3, 4) as function of loss of silver: curves 1 and 3, 0.001 Im (ε_s); curves 2 and 4, Im(ε_s).

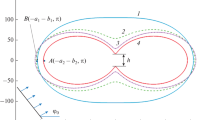
Figure 11 shows the effect of of the wavelength $\lambda$ on the scattering pattern of a silver plate with parameters $a = 100\,\,{\text{nm}}{\text{,}}$$b = 5\,\,{\text{nm}}$ at a plane wave angle of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$ at wavelengths of λ = 490, 750, 450, and 800 nm. Clearly, a change in wavelength λ yields scattering patterns with a different number of maxima.

Fig. 11.

Scattering pattern for silver plate with parameters $a = 100\,\,{\text{nm}}{\text{,}}$$b = 5\,\,{\text{nm}}$ at plane wave angle of incidence ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}$ as function of wavelength: λ = 490 (1), 750 (2), 450 (3), and 800 nm (4).

CONCLUSIONS

The diffraction of a plane wave by a cylindrical 2D structure—a square or rectangular silver (gold) plate—is considered. The spectral and spatial characteristics of the scattered field are calculated by rigorous numerical methods. It was shown that in real gold structures small in comparison to the wavelength, only dipole plasmon resonances are present. For silver plates, dipole and “aggregate” quadrupole resonances are observed only for a sufficiently large length. The influence of the geometric dimensions of the plate, the angle of incidence of the plane wave, and its wavelength on the positions of the maximum of the scattering cross section and the scattering pattern is demonstrated.