Fluctuation analysis, which includes the procedure of approximation and removal of low-frequency dynamics or trend (detrended fluctuation analysis, DFA) [1, 2], is a useful alternative to classical correlation analysis. It provides a more reliable estimation of long-range correlation characteristics than does the autocorrelation function, especially in the presence of noises and under nonstationary conditions. For stationary random processes, there exists an interrelation between the scaling exponent of the DFA method and characteristics describing the decrease of the autocorrelation function or the frequency dependence of the spectral power density function [1]; in spite of this fact, the presence of a more universal approach applicable both to stationary and nonstationary processes gave occasion to a wider use of the DFA method in investigations of the complex systems dynamics by experimental data [3–10]. Like any other method of digital signal processing, DFA has limitations, which have been discussed, e.g., in [11–14]. In [15], it was shown that different types of nonstationarity (trend, intermittent behavior, and variation of energy characteristics in time) had an effect on results of the DFA method and could lead to wrong interpretation of them. For this reason, reducing the signal to stationarity at the stage of preliminary processing (if possible) is a necessary procedure.

Under conditions of strong variation in characteristics of the system dynamics in time, e.g., during transition processes when properties of the signal under study are significantly different at different intervals, we proposed to use a modified DFA method [16], which includes calculation of an additional scaling exponent characterizing nonstationarity effects. This modified approach takes into account differences between local root-mean-square deviations of the signal profile from the piecewise linear approximation of the trend. In this work, further modification of the method is proposed to provide more stable results of the analysis.

The algorithm of the DFA method [2] includes the transition from the signal x(i), i = 1, …, N, to its profile within the framework of the generalized model of one-dimensional random walks

$$\begin{gathered} Y(k) = \sum\limits_{i = 1}^k {[x(i) - \langle x\rangle ],} \quad \langle x\rangle = \sum\limits_{i = 1}^N {x(i),} \\ k = 1,...,N, \\ \end{gathered} $$
(1)

segmentation of the profile Y(k) into nonoverlapping intervals with a length n, and linear approximation of the trend Yn(k) in each interval. The standard deviation of profile fluctuations relative to the trend

$$F(n) = \sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {{{{[Y(k) - {{Y}_{n}}(k)]}}^{2}}} } ,$$
(2)

is then calculated, and similar calculations are carried out in a wide range of n for analyzing the power-law behavior of dependence F(n) and estimating the scaling exponent α

$$F(n)\sim {{n}^{\alpha }}.$$
(3)

Such behavior is typical for many random processes, although the value of α can be different in different ranges of scales.

If the characteristics of nonstationary behavior strongly vary in time (for example, for transition processes or intermittence regimes), these changes have an effect on dependence (3). For this case, it was proposed in [16] to take into account local standard deviations of the profile from linear approximation Floc(n). They are calculated individually for each segment. Nonstationarity effects can be characterized using the measure

$$dF(n) = \max [{{F}_{{{\text{loc}}}}}(n)] - \min [{{F}_{{{\text{loc}}}}}(n)],$$
(4)

which takes small values for a homogeneous process and increases if nonstationarity properties change depending on the initial data segment.

Measure (4) is characterized by an increase with an increase in n; however, the power behavior of dF(n) is described by scaling exponent β:

$$dF(n)\sim {{n}^{\beta }},$$
(5)

which is different from α in the general case. This version of the DFA modification demonstrated the possibility of improving the diagnostics of structural changes in signals as compared to the standard algorithm in the analysis of physiological processes [17]. However, it has a substantial defect: there appears the sensitivity to individual artifacts having an effect on quantity max[Floc(n)] and, therefore, on the scaling exponent. To avoid this and to increase the algorithm stability, it is expedient to use statistical characteristics, e.g., to calculate the root-mean-square deviation of local values of Floc(n), i.e., to analyze the dependence

$$\sigma ({{F}_{{{\text{loc}}}}}(n))\sim {{n}^{\beta }}.$$
(6)

With allowance for differences in definitions, exponent β can be different when using formulas (5) and (6). In this case, we choose only one calculation variant that provides more stable results. In accordance with data of Fig. 1 for a random process with anticorrelations (α ≈ 0.04, Fig. 1a), the insignificant growth of logF(n) with an increase in the segment size is accompanied by a decrease in values of logdF and logσ (Floc), i.e., by negative scaling exponent β. The spread of values relative to the approximating straight line is less when dependence (6) is considered instead of (5). For white noise (α = 0.5, Fig. 1b) and the regime of intermittence between these random processes (Fig. 1c), approximate correspondence between the scaling exponents α and β is observed; for more stable calculations, however, it is also better to use σ(Floc(n)) instead of dF(n).

Fig. 1.
figure 1

Dependences (3), (5), and (6) presented in the double logarithmic scale for test signals: (a) anticorrelated random process (derivative of the 1/f noise), (b) white noise, and (c) periodic switchover between these processes.

Full size image

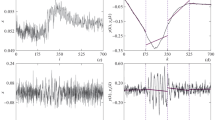
Figure 1 presents examples of analyzing signals whose scaling exponents are preserved with a change in the scale. As an example of an inhomogeneous process that demonstrates different scaling exponents for short- and long-range correlations, a 4-h electroencephalogram signal of a rat was considered. The signal included intervals of wakefulness and synchronized sleep. Figure 2 presents dependences described by formulas (3), (5), and (6) in the double logarithmic scale. Within the range 2.5 < logn < 3.5, the plot slopes are rather close; however, for long-range correlations (logn > 4.0), the behavior becomes essentially different and a positive α is in correspondence with negative exponent β. Using root-mean-square deviations of values of Floc(n) instead of the difference of extreme values (4) provides a decrease in the spread of the calculated values in all ranges of scales. The obtained results comfirm independence of the scaling exponents of the modified DFA method [16]. In addition, they testify that the further method modernization proposed in this work and using the statistics of local standard deviations of the signal profile from the linear approximation of the trend allows one to provide more stable calculation results achieved due to the decrease in the spread of values of logσ(Floc) as compared to logdF in the analysis of power regularities described by formulas (5) and (6). It is appropriate to take into account this fact when using the modified DFA method for solving problems of complex process diagnostics in the dynamics of systems with time-varying characteristics.

Fig. 2.
figure 2

Dependences (3), (5), and (6) presented in the double logarithmic scale for an electroencephalogram signal of a rat (the sampling frequency is 2 kHz).

Full size image