Supersonic Laminar Flow Past a Blunt Fin: Duality of the Numerical Solution

Abstract

The results of a numerical solution of the problem of supersonic flow past a blunt fin mounted on a plate with a developing boundary layer are presented. Generally, the case considered corresponds to the flow configuration used in the experimental and computational study by Tutty et al. (2013), in which the laminar air flow with the freestream Mach number of  6.7 is considered. The simulation was performed for different values of Reynolds number ranging from 5.0 × 10³ to 2.0 × 10⁴. Two stable solutions corresponding to metastable flow states with different configurations of the vortex structure were predicted within some range of Reynolds number. The bifurcation diagrams showing the main horseshoe vortex center location and the length of separation region versus the Reynolds number is presented, critical Reynolds number corresponding to occurrence of the second isolated solution is evaluated.

INTRODUCTION

A supersonic flow past an obstacle mounted on a streamlined surface results in a highly three-dimensional flow pattern, which includes an elongated flow separation region containing a set of horseshoe-shaped vortices and a complex shock-wave interaction [1–15]. The effects of the viscous–inviscid interaction are characterized by a strongly nonuniform distribution of the heat flux on the streamlined surface, the values of which can exceed by several times that values in the undisturbed boundary layer [4–7, 9, 13, 14]. The study of the flow structure of a similar configuration and the correct prediction of characteristics of heat transfer is important both for practical purposes, in particular, in the aerospace industry [16], and in fundamental and theoretical respects.

In the interaction of the boundary layer with the obstacle in the form of a blunt–fin body, the flow structure and pattern of local heat transfer depend on many parameters, such as the properties of a gas, characteristics of an incoming boundary layer, and the geometry of the considered configuration. Recently, the interest in this topic has again increased with a pronounced bias toward the use of computational fluid dynamics methods [4–8, 13, 14], which make it possible to study the flow structure for a wide range of parameters. Studies are performed for both laminar flow regimes [3–7, 12–15] and turbulent and transient regimes [8–11].

In this work, we present results of numerical simulation of supersonic laminar flow past a blunt fin mounted on a plate along which the boundary layer evolves. The formulation of the problem is based on the data of the calculation and experimental work [4], the authors of which studied the structure of the laminar flow in the front of a streamlined body at freestream Mach number M = 6.7 for three values of the Reynolds number based on the blunt diameter: Re_D = 1.25 × 10⁴, 2.50 × 10⁴, and 3.75 × 10⁴. The numerical solutions obtained in the cited work were interpreted by the authors as stationary and unique. Later, in a computational study [5], it was shown that, even at Re_D = 2.50 × 10⁴, the solution is unsteady.

Recently, we showed that [15], for the lowest of the aforementioned Reynolds numbers, Re_D = 1.25 × 10⁴, there are two stable stationary solutions with different configurations of vortices in the flow separation region. In fact, this can be considered as another case of the well-known feature of possible nonuniqueness of the supersonic flow past a body, system of bodies, or their separate parts (see, e.g., [17–21]). The physical aspect of this problem consists in strong nonlinearity of gas–dynamic processes. Under conditions of possible nonuniqueness, the realized flow pattern is determined not only by the geometric and physical parameters, but also by the prehistory of the flow formation; in other words, aerodynamic hysteresis occurs.

In this work, continuing the studies started in [15], we present the calculation results obtained for the Reynolds numbers varying in the range from 5.0 × 10³ to 2.0 × 10⁴. We study the duality of the solution by exceeding the Reynolds number of some critical value.

1. FORMULATION OF THE PROBLEM

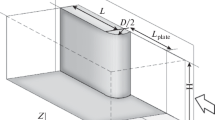
Figure 1 shows the computational domain of the considered problem of viscous perfect gas flow past a blunt fin mounted on a plate. The flow is assumed as symmetrical with respect to plane XZ; hence, the calculations are performed for half of the considered configuration.

Fig. 1.

Computational domain.

The simulated flow is determined by the following set of dimensionless parameters: free-stream Mach number M, Reynolds number Re_D, Prandtl number Pr, temperature factor T_w/T_∞, relative plate length L/D, and adiabatic exponent γ. The flow was calculated for the following fixed parameters corresponding to the data from [4]: M = 6.7, T_w/T_in = 4.75, Pr = 0.7, γ = 1.4, and L = 145 mm as the length of the plate to the junction. The calculations were performed at Reynolds numbers Re_D in the range from 5.0 × 10³ to 2.0 × 10⁴, with the Reynolds number being varied by changing blunt fin diameter D from 1 to 4 mm.

At the inlet boundary of the computational domain, a uniform flow is specified; the no-slip conditions are specified at the surface of the body and at the plate. The surfaces of the body and plate are maintained at constant temperature T_w. At the lateral and upper boundaries, the nonreflecting boundary conditions are specified, while the zero gradient condition for the calculated variables is specified at the outlet.

2. COMPUTATIONAL ASPECTS

In our calculations, we used the SINF/Flag-S finite-volume unstructured code developed at the Institute of Applied Mathematics and Mechanics of Peter the Great St. Petersburg Polytechnic University. We solved the complete 3D Navier–Stokes equations for a thermally and calorically perfect gas. The temperature dependence of viscosity was determined by the Sutherland formula.

To calculate the convective fluxes at the faces of control volumes, we used the AUSM scheme [22] of the second order of accuracy. The reconstruction of variables at the faces of control volumes of the unstructured grid was performed using the technique described in [23, 24]. To preserve the solution monotonicity, we used the TVD scheme [25]. A more detailed description of the numerical method is presented in [12].

We used a grid consisting of 10 million cells: as was shown in [15], such grid resolution is sufficient to resolve the key features of the flow. All calculations were performed for the nonstationary formulation. For time integration, we used the dual-step method with the three-layer approximation of the time derivative (“backward difference”) of the second order of accuracy. The dimensionless time step was given equal to ΔtU_∞/L = 3.67 × 10^–4, which ensures the Courant number of the order of unity in the most part of the computational domain.

3. CALCULATION RESULTS AND DISCUSSION

3.1. Duality of Solution at Re_D = 1.25 × 10⁴

It was shown in [15] that, for the considered configuration at Re_D = 1.25 × 10⁴ (D = 2.5 mm), there are two stable stationary solutions with different configurations of the vortex structure in the flow separation region.

The flow structure corresponding to one of the solutions previously obtained in [4, 15] and specified below as Solution I is shown in Fig. 2, where streamlines and the distribution of the relative heat flux on the surface of the body and plate are shown (q_w0 is the value of the heat flux in the undisturbed boundary layer on the flat plate at x = L). The main features of the considered flow are clearly seen, which consist in the formation of a flow separation region with a set of horseshoe-shaped vortices, influence of this region on the shock-wave pattern, along with the presence of the region of increased heat transfer.

Fig. 2.

Illustration of the three-dimensional flow structure, Re_D = 1.25 × 10⁴.

The duality of the solution for the considered Reynolds number is demonstrated in Fig. 3, where the flow structure in the symmetry plane for two different solutions (Solution I and Solution II) is shown. The solutions differ in the normalized length of the flow separation region (L_S/D) along with the location of the axis of the main horseshoe-shaped vortex (${{X}_{{v}}}$/D). In the first case, L_S/D = 6.50, ${{X}_{{v}}}$/D ≈ 1.8, and for the second solution L_S/D = 6.01, ${{X}_{{v}}}$/D ≈ 1.0. Figure 4 shows considerably different distributions of the non-dimensional heat flux, which were calculated for two solutions, as well as the surface streamlines.

Fig. 3.

Flow structure in the symmetry plane at Re_D = 1.25 × 10⁴: (a) Solution I and (b) Solution II.

Fig. 4.

Stanton number distributions and the surface streamlines at the plate at Re_D = 1.25 × 10⁴: (a) Solution I and (b) Solution II.

As was mentioned above, only one numerical solution (Solution I) and corresponding experimental data were presented in [4]. A comparison of the results of this work with that presented in [4] is shown in Fig. 5.

Fig. 5.

Comparison between the calculation results and the data [4] at Re_D = 1.25 × 10⁴: (a) the distribution of the non-dimensional heat flux and (b) the flow structure in the symmetry plane.

Figure 5a shows the distributions of the non-dimensional heat flux along the symmetry line on the plate (q_wp are corresponding values of heat flux in the undisturbed boundary layer). Clearly, the obtained solution with one global maximum and two local maxima is in good agreement with the data presented in [4]. Figure 5b shows the calculated flow structure in the symmetry plane; a good accordance of the results is also clearly seen.

3.2. Results of Parametric Calculations

For a more detailed study of duality of the numerical solution, for the considered problem, we performed calculations with “parameter continuation.” Actually, diameter D of the blunt fin was varied while the plate length and parameters of the free stream remained fixed. It should be noted that, in this case, the values of two key parameters of the problem—Reynolds number Re_D and relative plate length L/D—were being changed; consequently, relative thickness δ/D of the free-stream boundary layer is also changed.

By performing calculations at each given diameter value, the calculated flow fields corresponding to the first and second solutions for the nearest diameter value were used as the initial fields. Calculations were performed starting from the value D = 2.5 mm (Re_D = 1.25 × 10⁴) for the gradually decreasing and increasing fin diameter value.

In the case of D = 1.8 mm (Re_D = 9.0 × 10³), regardless of the initial field, the numerical solution is unique and stationary (Solution I). The second stationary solution occurs by exceedance of some critical Reynolds number value Re_{D, cr}. With a further increase in Reynolds number, the flow becomes unsteady. The Reynolds number values corresponding to the transition to the nonstationary flow regime are different for two solutions.

Figure 6 shows the Mach number fields in the symmetry plane for several cases (in the case of unsteady flow regimes, the time-averaged characteristics are presented). It is seen that the typical flow pattern inherent for the first and second solution persists with the increase in blunt fin diameter. In the first solution, the flow separation region is more extended and is more “pressed” to the plate; the main horseshoe-shaped vortex is elongated along the plate, and its center is located farther from the leading edge of the body, and an additional vortex occurs in the vicinity of the fin body. In the second solution, the flow separation region is shorter and the center of the main horseshoe-shaped vortex is located closer to the fin body.

Fig. 6.

The Mach number fields and streamlines in the symmetry plane for various diameters D (the dash-dotted curve indicates the sonic line): (a) Solution I and (b) Solution II.

The summary Table 1 contains the values of representative characteristics of the flow, which are the location of the center of the main horseshoe-shaped vortex (${{X}_{{v}}}$/D) and the length of the flow separation region (L_S/D) calculated as a function of the varying diameter of the fin body. Here also, for informational purposes, Reynolds number Re_D, relative plate length L/D, and relative thickness δ/D of the free-stream boundary layer are presented.

Table 1. Calculated parameters of the flow separation region for two solutions

Figure 7 shows the bifurcation diagrams obtained using the results of the parametric calculations, which show the dependence of the coordinate of the main horseshoe-shaped vortex center and dependence of the flow separation region length on the fin diameter (the Reynolds number). The obtained diagrams make it possible to conclude that critical diameter value D_cr lies between 1.8 and 1.85 mm. It is also clear that, with the increase in Re_D, the first solution changes evolutionarily, but the second solution looks as an isolated solution existing at Re_D > Re_{D, cr} ≈ 9.25 × 10³; in this case, point P is the bifurcation (transition) point isolated from the branch of Solution I.

Fig. 7.

Bifurcation diagrams: (a) the location of the center of the main horseshoe-shaped vortex and (b) the length of the flow separation region.

For the first solution, the length of the flow separation region, first, monotonically grows with the increase in the Reynolds number and, next, beginning from Re_D ≈ 1.5 × 10⁴, gradually decreases. For the second solution, the dependence is opposite: a decrease in the length of the flow separation region is observed up to Reynolds number Re_D ≈ 1.70 × 10⁴, from which the length increases. The changes in the pattern of the dependencies are determined by the transition to nonstationary flow regimes.

It should be emphasized once again that the presented bifurcation diagrams were obtained at the fixed location of the fin body with respect to the front edge of the plate (L = 145 mm). Therefore, relative thickness δ/D of the free-stream boundary layer, which is the key parameter of the problem, is changed by variation of D. Technically, the dependence of the critical Reynolds number on δ/D can be determined using similar calculations by variation of plate length L (which is a separate, extremely resource consuming problem).

3.3. Heat Transfer Characteristics

The pattern of local heat transfer on the plate surface is mainly determined by the configuration of vortices in the flow separation region, and this pattern can be considerably different for two branches of the solution. Figure 8 shows the distributions of the heat flux along the symmetry line for all cases considered. These distributions are presented as 3D diagrams, where the varying diameter is plotted over the third direction. Clearly, in the case of a small diameter, the solution exhibits only one local maximum of the heat flux; the increase in diameter results in the vortex structure in the front of the fin body becoming complicated and, consequently, the distribution of the heat flux being changed. For the first solution, in addition to the pronounced main maximum located near the body, two local maxima far away from the body are observed; for the second isolated solution, one local maximum is observed.

Fig. 8.

Distribution of the heat flux along the symmetry line for various diameters D: (a) Solution I and (b) Solution II.

Analysis of the heat flux values and of the intensity of oscillations (for nonstationary regimes) at several points on the plate were also performed (Fig. 9). The vertical lines indicate the root-mean-square deviations for unsteady regimes.

Fig. 9.

Heat flux values at several points on the plate along the symmetry line.

Figure 9 shows that the transition to the nonstationary flow regime occurs for two solutions at different Reynolds number values: for the first solution at 1.325 × 10⁴ (D = 2.65 mm), and for the second solution at a higher value of 1.70 × 10⁴ (D = 3.4 mm). More extended separation region in the Solution I probably causes the transition to non-stationary regime at lower value of the Reynolds number.

The presented diagrams clearly show differences in the general nature of the transition to the nonstationary regime: for the first solution, the intensity of oscillations is gradually increased starting from low values, whereas, for the second solution, occurring oscillations has considerable intensity right away.

CONCLUSIONS

The multivariate parametric calculations were performed for the three-dimensional problem of the interaction of the supersonic viscous gas flow with a blunt fin mounted on a plate with a developing boundary layer. The calculations were performed for the experimental conditions [4] at the fixed location of the body with respect to the leading edge of the plate.

The variation range of the Reynolds number was from 5.0 × 10³ to 2.0 × 10⁴, which includes the stationary and nonstationary flow regimes. The test calculations were performed for Re_D = 1.25 × 10⁴, which were in good agreement with the experimental and calculation data [4] for one of two possible stationary solutions of the problem.

The duality of the solution in the considered range of the Reynolds numbers were studied. The bifurcation diagrams were analyzed to estimate the critical value of the Reynolds number (Re_{D, cr} ≈ 9.25 × 10³), corresponding to occurrence of the second (isolated) solution. The main features of two solutions evolving with the increase in the Reynolds number were studied, values corresponding to the transition to the nonstationary flow regimes were estimated.

The changes in local heat transfer caused by the increase in the Reynolds number were studied. The characteristic features in the heat flux distributions were indicated for solutions of two types.