1 INTRODUCTION

Studying phase transitions (PT), critical, magnetic, and thermodynamic properties of magnets, which are described by the two-dimensional Izing and Potts lattice models, is of a great scientific interest, since it opens wide prospects for practical application [1–3]. Low-dimensional lattice models describe a wide class of real physical systems: layered magnets, liquid helium films, superconducting films, adsorbed films, etc. [1, 4, 5].

At the present time, the two-dimensional Izing model has been studied quite well and almost all its properties are known [6–10]. On the other hand, there are only a few facts established reliably for the two-dimensional Potts model with various numbers of the spin states q. Most avail the two-dimensional Potts model with various numbers of the spin states q able data were obtained for the two-dimensional Potts model with various numbers of the spin states q = 2 and q = 3 [11–14]. The two-dimensional Potts model with the number of spin states q = 4 is still scantily known. This model is interesting, since the value q = 4 is the boundary value of the range 2 ≤ q ≤ 4, where a second-order phase transition takes place, and the region of values q > 4, in which the phase transition occurs as a first-order PT [15]. According to [11–13], in the Potts model with the number of spin states q = 2, 3, and 4, a second-order PT is observed. However, at q = 4, this model demonstrated the peculiarities of the thermodynamic behavior. In this connection, in this work, we attempt to study PT and the thermodynamic properties of the two-dimensional ferromagnetic Potts model with the number of spin states q = 4 on a triangular lattice using the Monte Carlo (MC) method.

The PT character and the regularities of changing the thermodynamic behavior of this model cannot be unambiguously determined on the base of the data available now, and these problems remain open up to now. The study of the two-dimensional Potts model with the number of spin states q = 4 using modern methods and ideas will enable us to answer a number of questions related to PT and the thermodynamic properties of low-dimensional lattice systems.

2 MODEL AND METHOD OF STUDIES

The Hamiltonian of the Potts model with the number of spin states q = 4 can be represented as

$$H = - J\sum\limits_{i,j} {\cos {{\theta }_{{i,j}}},} $$
((1))

where J is the parameter of exchange ferromagnetic interactions for the nearest neighbors, θi, j is the angle between the interacting spins Si – Sj.

At the present time, such systems based on microscopic Hamiltonians are successfully studied using the MC method [6, 7, 16, 17]. Recently many new versions of the algorithms of the MC method have been developed. Among them, the Wang–Landau algorithm [14, 18, 19] is one of most efficient for studying similar system, in particular, at low temperatures. Thus, we use this algorithm in this work.

We introduce additions in the standard Wang–Landau algorithm, which enabled us to reveal the magnetic structure of the ground state of the system. This algorithm is a realization of the entropy simulating method and enables one to calculate the density-of-states function of the system. The Wang–Landau algorithm is based on the fact that we obtain a uniform energy distribution, executing a random walk in the energy space with the probabilities which are inversely proportional to the density of states g(E). Selecting the transition probabilities such that the visits of all energy states would become uniform, we can obtain initially unknown density of states g(E), knowing which we can calculate the values of required thermodynamic parameters at any temperature. Because density of states g(E) increases very fast with the sizes of the system under study, quantity lng(E) is used for convenience of storing and processing large numbers.

We used the Wang–Landau algorithm in the following form.

First, an arbitrary initial spin configuration is given. The start values of the density of states is g(E) = 1, the energy distribution histogram H(E) = 0, and the start modification factor is f = f0 = e1 ≈ 2.71828. We repeatedly execute steps in the phase space, until a relatively flat histogram H(E) will be obtained (i.e., until all possible energy states of the system will be visited approximately the same number of times). In this case, the transition probability from the state with energy E1 to the state with energy E2 is determined by formula p = g(E1)/g(E2). If the transition to the state with energy E2 took place, then g(E2) → f × g(E2), H(E2) → H(E2) + 1; in other cases, g(E1) → f × g(E1). If the histogram became “flat,” we performed the nulling of the histogram (H(E) → 0), decreased the modification factor f → \(\sqrt f \) and continued once again as long as f ≥ fmin. In our case, fmin = 1.0000000001. The Wang–Landau algorithm is described in more detail in [18, 19]. Thus, determining the density of states of the system, we can calculate the thermodynamic parameters at any temperature. In particular, internal energy U, free energy F, specific heat C and entropy S can be calculated using the following relationships:

$$U(T) = \frac{{\sum\limits_E {Eg(E){{e}^{{ - E/{{k}_{{\text{B}}}}T}}}} }}{{\sum\limits_E {f(E){{e}^{{ - E/{{k}_{{\text{B}}}}T}}}} }} \equiv {{\left\langle E \right\rangle }_{T}},$$
((2))
$$F(T) = - {{k}_{{\text{B}}}}T\ln \left( {\sum\limits_E {g(E){{e}^{{ - E/{{k}_{{\text{B}}}}T}}}} } \right),$$
((3))
$$C = (N{{K}^{2}})(\left\langle {{{U}^{2}}} \right\rangle - {{\left\langle U \right\rangle }^{2}}),$$
((4))
$$S(T) = \frac{{U(T) - F(T)}}{T},$$
((5))

where K = |J|/kBT, N is the number of particles, T is the temperature (here and further temperature is given in the |J|/kB units, and U is the internal energy (U is the normalized quantity).

We analyzed the PT character using the fourth-order Binder cumulant method and the histogram analysis of the data of the MK method [20, 21].

The calculations were performed for the systems with periodic boundary conditions and linear sizes L × L = N, L = 12–120, where L is measured in the unit cell sizes.

3 RESULTS AND DISCUSSIONS

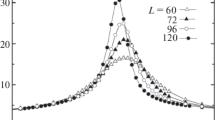
Figure 1 shows the characteristic temperature dependences of the specific heat C for the systems with linear sizes L = 60, 72, 96, and 120 (here and further the statistic errors are not larger than the sizes of the symbols used for constructing the dependences). Note that these dependences have pronounced maxima for all the systems near the critical temperature; the maxima increase with the number of spins in a system and they are at the same temperature within the limits of the error, even for the system with the least L. This fact shows, first, the high efficiency of using the method of adding the periodic boundary conditions and, second, that many parameters under study achieve saturation in N.

Fig. 1.
figure 1

Temperature dependences of specific heat C/kB.

Full size image

Figure 2 shows the temperature dependence of entropy S for the system with L = 120. It is seen that the entropy of the system tends to the value ln 4 predicted theoretically as temperature increases. At low temperatures close to the absolute zero of temperature, the entropy of the system tends to a zero. Similar dependences are observed for all values of L under consideration. This behavior of the entropy enables us to speak that there is no degeneracy of the ground state in this model.

Fig. 2.
figure 2

Temperature dependence of entropy S.

Full size image

The most efficient method of analyzing the PT character, the behavior of thermal characteristics near the critical point, and the determination of the critical temperature Tc is the method of the fourth-order Binder cumulants [21]:

$${{V}_{L}} = 1 - \frac{{\left\langle {{{U}^{4}}} \right\rangle }}{{3\left\langle {{{U}^{2}}} \right\rangle _{L}^{2}}},$$
((6))
$${{U}_{L}} = 1 - \frac{{\left\langle {{{m}^{4}}} \right\rangle }}{{3\left\langle {{{m}^{2}}} \right\rangle _{L}^{2}}},$$
((7))

where VL is the energy cumulant and UL is the magnetic cumulant.

Equations (6) and (7) enable one to determine the critical temperature Tc to a high accuracy for the first-order and second-order PTs, respectively. It should be noted that the application of the Binder cumulants allows one also to well test the PT type in a system. It is known that the first order PTs are characterized by that VL tends to some nontrivial value V* according to the relationship

$${{V}_{L}} = V{\text{*}} + b{{L}^{{ - d}}}$$
((8))

at L → ∞ and T = Tc(L), where V* differs from 2/3 and the minimum value ULmin(T = Tmin) diverges: ULmin(T = Tmin) → –∞ at L → ∞.

In the case of a second-order PT, the curves of the temperature dependence of the Binder cumulants UL have the pronounced intersection point [21].

Figure 3 shows the characteristic dependence of UL on temperature for various values of L. It is seen that there is no clear intersection point in the critical region, which favors the existence of a first-order PT in the system.

Fig. 3.
figure 3

Temperature dependences of the Binder magnetic cumulant UL.

Full size image

Figure 4 depicts the temperature dependence of the energy cumulant VL for various values of L. As is seen, the value of VL tends to 2/3, and V* = 2/3, which is characteristic of a second-order phase transition. This value was calculated using Eq. (8). It is seen from Fig. 4 that V* = 0.6660(1) in the model under study.

Fig. 4.
figure 4

Temperature dependences of the Binder energy cumulant VL.

Full size image

Thus, the more detailed analysis of the PT order was performed using the histogram analysis of the MC method data. This method enables us to reliably de-termine the PT order. The procedure of determining the PT order by this method is described in detail in [22, 23].

The results of this work obtained on the base of the histogram analysis show that PT in this model is a first-order transition. This result is demonstrated in Fig. 5, where histograms of the energy distribution are shown for the systems with linear sizes L = 60, 72, and L = 96. The plots were built near the critical temperature. It is seen from Fig. 5 that the dependences of probability W on energy E for all the systems have two maxima, which testify in favor of a first-order PT. The existence of the double peak in the energy distribution histograms is a sufficient condition of a first-order PT. Note that the double peaks are observed in this model only for the systems with big linear sizes (L > 60). In  addition, in this model, the double peaks are observed near the critical region only in a very narrow temperature range. This fact is shown in Fig. 6, where the energy distribution histograms are shown for the system with linear size L = 120. These plots were built at various temperatures close to the critical temperature. As is seen from Fig. 6, the double peaks are observed in a narrow temperature range 0.4438 K < T < 0.4450 K. At temperatures lower and higher this range, one peak disappears, with hampers the determination of the PT type in such systems. Such a behavior is characteristic of the systems, in which first-order phase transition close to second-order phase transitions occur.

Fig. 5.
figure 5

Energy distribution histograms for L = 60, 72, and 96.

Full size image
Fig. 6.
figure 6

Energy distribution histograms for L = 120 at various temperatures.

Full size image

4 CONCLUSIONS

The phase transitions and the thermodynamic properties of the two-dimensional ferromagnetic Potts model with the number of spin states q = 4 on a triangular lattice has been studied using the Wang–Landau algorithm of the Monte Carlo method. The analysis of the character of the phase transitions was performed based on the histogram method and the Binder cumulant method. It is shown that the system demonstrates a first-order phase transition.