Abstract—
Electrodynamic characteristics of a low-pressure (electron collision frequency much lower than the field frequency) capacitive HF discharge maintained by an electromagnetic field with a frequency between 13 and 900 MHz are studied analytically and numerically. It is demonstrated that the field of both the fundamental mode (the field in the metal–space-charge sheath–plasma–space-charge sheath–metal structure) and the field of the higher-order evanescent modes must be taken into account for correct calculation of discharge characteristics under such conditions in a wide range of electron densities. Expressions governing the amplitudes of excited waves, along with expressions governing the discharge impedance in the presence of these waves, are derived by using field expansion in eigenwaves of an empty waveguide and eigenmodes of the three-layer structure. The case in which the size of plasma is smaller than the size of the electrodes is analyzed in detail. In this case, excitation of higher-order types of waves in the plasma column is generated by axial plasma inhomogeneity and is not related to electrodynamic effects near the electrode boundaries. It is demonstrated that the positions of current and voltage resonances related to propagation of surface waves along the three-layer structure becomes substantially modified due to excitation of higher-order field modes of the same structure. In addition, resonances caused by excitation of standing surface waves near the lateral surface (resonances of higher-order modes of the three-layer structure and an empty waveguide) can take place. Variation of relative position of resonances caused by changes in the discharge chamber geometry is investigated. Obtained results qualitatively agree with the results of numerical calculation of the discharge impedance and field propagation in the discharge by COMSOL Multiphysics® software package.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
INTRODUCTION
High-frequency capacitive discharges sustained by electromagnetic fields form the foundation for a large class of technologies [1–4]. The necessity of increasing electron density in the discharge required sustaining discharges by fields of higher frequencies [5]. In this case, the discharge is maintained by the surface waves, propagating along the plasma–sheath–metal interface [6, 7]. The first models of the discharge describing its electrodynamic properties within the framework of the theory of long lines that predicted current and voltage resonances in the current-voltage characteristics were introduced after 2002 [8–12]. Experimental studies of field distribution confirmed that spatial inhomogeneities of the field and plasma density, existing in the discharge [13–17], can be explained within the framework of the model that takes into account excitation of the said waves. Energy in small-size discharges exhibiting a three-layer structure (metal–sheath–plasma–sheath–metal) was supplied by means of the higher-order modes [18]. Methods addressing possible plasma inhomogeneities upon excitation of a standing surface wave due to violation of plasma symmetry and phase matching of the waves propagating near different plasma boundaries were proposed [10]. Since spatial inhomogeneity of plasma in the discharge depends on radial structure of the field in the discharge [19], while the dependence of the discharge impedance on electron density determines stability of the former [20–24], so far, processes in such discharges were analyzed by means of numerical simulation. It was demonstrated [25–30] that nonlinearity of the sheath gives rise to harmonics of the electromagnetic field sustaining the discharge.
Despite an abundance of publications and obtained results, a large number of questions regarding theoretical and experimental investigation of the discharges remain unanswered. In particular, it is not clear what role in discharge excitation is played by the decaying and surface waves, and how the amplitudes of these waves are interrelated. In the first paper of this series [31], we demonstrated that the well-known geometric resonance in the plasma–space-charge sheath system [32, 33] does not take place for either surface or decaying waves taken separately. On the contrary, analysis distinguishing the decaying and surface waves in the driving electromagnetic field shows that the geometric resonance represents compensation of capacitive impedance introduced by the surface waves (for plasma of small size) and inductive impedance of the decaying waves.
In the present work, we calculated the amplitudes of various waves of the electromagnetic field and analyze types of possible resonances. We derived approximate expressions governing the discharge impedance taking into account excitation of various electromagnetic modes. The results of analysis are compared with numerical calculations of the discharge impedance and spatial distribution of the field by using the COMSOL Multiphysics® software package (the license belongs to Faculty of Physics of the Moscow State University). Numerical calculations carried out using analytical expressions and the results of numerical simulation are presented for the frequency of 137 MHz at which the discussed effects are most pronounced (we carried out similar calculations in a wider frequency range).
1 FIELD REPRESENTATION IN THE FORM OF EIGENFUNCTIONS INSIDE AND OUTSIDE OF PLASMA
It is well known that two types of resonances are possible in plasma of small size: the voltage resonance, called the geometric plasma—sheath resonance, mentioned earlier [32, 33], and the current resonance that is observed when the real part of dielectric permittivity becomes equal to zero. Calculations show that higher-order modes do not influence the discharge impedance as a whole much in a large area discharge in which major part of energy is transferred to the surface wave. Nevertheless, it was demonstrated in a phenomenological model proposed in [31] that both the surface waves and the higher order modes are essential for correct calculation of the impedance.
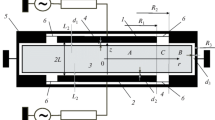
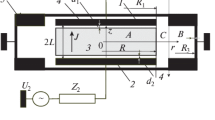
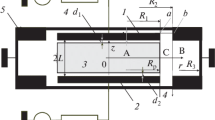
In this section, we will demonstrate calculation of field distribution and discharge impedance in the case of discharge confined in a finite space region r < R. The discharge chamber geometry for which calculation was carried out is illustrated in Fig. 1. We will demonstrate that the discharge impedance is determined by interaction of currents induced by three types of fields: the field of the surface wave, the field of evanescent modes in plasma, and the field of evanescent modes that concentrates outside of plasma. In a general case, the resonance occurs as a result of compensation voltages and currents induced by all types of fields. However, in some cases, individual types of the field can have no effect at certain plasma parameters. For example, geometric and current resonances analogous to those observed in a discharge of small size are caused by interaction of the field of the surface wave and the field of the higher-order modes of plasma column (the field of the first higher-order mode in the first place). In reality, compensation of impedances of the higher-order modes of plasma column and higher-order waveguide modes represents the resonance of the field of the surface wave propagating along the exterior plasma boundary that is readily observed in microwave plasma in a waveguide [34, 35]. Naturally, the resonance frequencies shift due to the presence of sheaths near the electrodes. The observed resonances are certainly affected by parameters of the external circuit as well [36]. In the present work, we will limit analysis to a discharge with identical sheaths. The case in which the size of plasma is smaller than the size of the electrodes will be analyzed. In this case, excitation of waves of higher-order types is caused by axial inhomogeneity of plasma and is unrelated to electrodynamic effects near the electrode boundaries.
Typical experimental arrangement: 1, 2—electrodes, 3—plasma, 4—space charge sheaths between plasma and the wall (electrodes), 5—discharge chamber, and 6—boundary of the area of calculation through which electromagnetic field is excited; 2L—distance between the electrodes; d1 and d2 thicknesses of the sheaths.
The field inside plasma can be represented in the form of a sum of eigenwaves of the three-layer system (TLS) metal–sheath–plasma–sheath–metal \(\left\{ {{{{\mathbf{e}}}_{{n{\mathbf{ + }}}}}(z),{{{\mathbf{h}}}_{{n{\mathbf{ + }}}}}(z)} \right\}\) [8, 19, 37–39]. In expressions (1), (2), and henceforth, only factors depending on z in the field representation that can be found in appendices to [31, 40] are understood in notations \({{{\mathbf{h}}}_{{{\boldsymbol{0\varphi + }}}}}\left( z \right) = {{{\boldsymbol{\varphi }}}_{{\mathbf{0}}}}{{h}_{{0\varphi + }}}\left( z \right)\) and \({{{\mathbf{e}}}_{{0z{\mathbf{ + }}}}}(z) = \) \({{{\mathbf{z}}}_{{\mathbf{0}}}}\rho {{h}_{{0{\boldsymbol{\varphi + }}}}}(z){{{{{{h}_{{0 + }}}} \mathord{\left/ {\vphantom {{{{h}_{{0 + }}}} k}} \right. \kern-0em} k}} \mathord{\left/ {\vphantom {{{{{{h}_{{0 + }}}} \mathord{\left/ {\vphantom {{{{h}_{{0 + }}}} k}} \right. \kern-0em} k}} {\varepsilon (z)}}} \right. \kern-0em} {\varepsilon (z)}}\), \({{{\mathbf{e}}}_{{nz{\mathbf{ + }}}}}(z) = {{{\mathbf{z}}}_{{\mathbf{0}}}}\rho {{h}_{{n{\boldsymbol{\varphi + }}}}}(z){{{{{{{\tilde {h}}}_{{n + }}}} \mathord{\left/ {\vphantom {{{{{\tilde {h}}}_{{n + }}}} k}} \right. \kern-0em} k}} \mathord{\left/ {\vphantom {{{{{{{\tilde {h}}}_{{n + }}}} \mathord{\left/ {\vphantom {{{{{\tilde {h}}}_{{n + }}}} k}} \right. \kern-0em} k}} {\varepsilon (z)}}} \right. \kern-0em} {\varepsilon (z)}}\); \(\rho = \sqrt {{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}} \) is the wave resistance of vacuum; \(k = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}\); ω is the circular frequency of the electromagnetic field; с is the speed of light; r0, φ0, and z0 are the unit vectors in the r, φ, and z directions, respectively. In plasma (|z| < L and r < R), \(\varepsilon (z) = {{\varepsilon }_{P}} = 1 - {{{{n}_{e}}} \mathord{\left/ {\vphantom {{{{n}_{e}}} {({{n}_{{\text{C}}}}(1 + i{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }))}}} \right. \kern-0em} {({{n}_{{\text{C}}}}(1 + i{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }))}}\); \({{n}_{{\text{C}}}} = {{m{{\omega }^{2}}{{\varepsilon }_{0}}} \mathord{\left/ {\vphantom {{m{{\omega }^{2}}{{\varepsilon }_{0}}} {{{e}^{2}}}}} \right. \kern-0em} {{{e}^{2}}}}\) is the critical electron concentration; e and m are the electron charge and mass, respectively; ne and ν are the electron density and collision frequency, respectively; \(\varepsilon \left( z \right) = {{\varepsilon }_{1}} = 1\) outside of plasma. Using the above expressions, the z-component of electric field Ez and azimuthal component of magnetic field Hφ at r < R can be expressed in the form
where the first term corresponds to excitation of a symmetric surface wave with radial propagation constant \({{h}_{{0 + }}}\), while the sum contains decaying modes (attenuation constant \({{\tilde {h}}_{{n + }}} = i{{h}_{{n + }}}\)). At low electron concentrations (ne < 2nC), similar to [31, 40], the field of the surface wave in (1) and henceforth is replaced by the field of the quasi-TEM wave, and the latter is excluded from the sum with respect to n. Outside of plasma, standard eigenfunctions for the field confined between two planes \(\left\{ {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}}_{{n{\mathbf{ + }}}}}\left( z \right),{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}}}_{{n{\mathbf{ + }}}}}\left( z \right)} \right\}\) are used [31]. In the region R < r < R1, we can write
The first term in (2) describes a TEM wave arriving from the peripheral region (R1 < r < R3) due to the field generated by the source in the excitation region (R1 < r < R2), while the second term describes a TEM wave scattered by the three-layer structure and propagating toward the peripheral region. For these waves, \({{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}_{{0{\mathbf{ + }}z}}}\left( z \right) = \rho {{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}}_{{0{\mathbf{ + }}\varphi }}}\left( z \right)\). The sum in (2) represents the sum of excited higher-order modes of the field for which \({{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}_{{nz{\mathbf{ + }}}}}\left( z \right) = {{{\mathbf{z}}}_{{\mathbf{0}}}}\rho {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_{{n{\boldsymbol{\varphi + }}}}}\left( z \right){{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}} \mathord{\left/ {\vphantom {{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}} k}} \right. \kern-0em} k}\), \({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_{{n + }}} = \sqrt {{{{\left( {{{n\pi } \mathord{\left/ {\vphantom {{n\pi } L}} \right. \kern-0em} L}} \right)}}^{2}} - {{k}^{2}}} \). In the process, we assumed that these waves decay in the radial direction relatively fast, so that their reflections from the electrode boundaries and the sidewall of the discharge chamber are negligibly small. So far, we did not take into account higher-order modes of the field in the plasma-free region that are excited at the electrode boundary. Expressions governing currents and voltages can be found in [31]. At r = R1, they yield
In the process, the discharge impedance at r = R1 is given by
Here and henceforth, voltage U of the electrode is assumed to be equal to the voltage between the electrode and the vacuum chamber. Therefore, the potential difference between the electrodes equals 2U. Relations (3) allow calculating electric and magnetic fields of the TEM waves at the plasma boundary (at point r = R):
Henceforth, it is convenient to use parameters \({{H}^{{{\text{ext}}}}}{\kern 1pt} \left( R \right)\) and \({{E}^{{{\text{ext}}}}}{\kern 1pt} \left( R \right)\) instead of amplitudes \({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }_{0}}\) and \({{A}^{{{\text{ext}}}}}\)of cylindrical waves. The requirement of tangential component of the electromagnetic field at the plasma lateral boundary being equal to each other leads to equation
When solving the latter, magnetic field amplitude Hext(kR) of the TEM waves can be considered to be given. The electric-field amplitude Eext(kR) can then be found from (6). Relations (5) allow calculating coefficients ATEM and Aext, while relations (3) and (4) allow calculating the discharge impedance. Limiting analysis to even waves, at r < R, we have
while, at r > R, we have
where
The obtained values coincide with each other at the plasma lateral boundary (r = R) due to (6). The fields of the higher-order waves decay at large distance from the boundary. Therefore, only the first term can be retained in the latter equation. The current resonance corresponds to denominator in the above expression becoming equal to zero, while the voltage resonance corresponds to the numerator in the above expression becoming equal to zero.
The necessity of calculating the fields of the higher-order modes is dictated by the fact that they participate in the development of local electron density perturbations in the regions where the shape of metallic elements of the setup drastically changes, e.g., at the electrode boundaries, in corners of the vacuum chamber, etc. The amplitude of such density perturbations can be comparable or even higher than the average electron density in the discharge. Therefore, the fields in this region of the discharge must be described as accurately as possible without limiting analysis to only one spatial mode (e.g., the surface wave). Hence, it is important to find expansion coefficients of the field in plasma in eigenfunctions of the three-layer waveguide. It should be noted that eigenfunctions in both the plasma-filled region, \(\left\{ {{{{\mathbf{e}}}_{n}},{{{\mathbf{h}}}_{n}}} \right\}\), and in the plasma-free region, \(\left\{ {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}}_{n}},{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}}}_{n}}} \right\}\), represent a complete system of functions. Both can be used for field presentation at the plasma boundary. For the sake of generality and convenience, let us introduce also the systems of eigenfunctions \(\left\{ {{\mathbf{e}}_{n}^{ + },{\mathbf{h}}_{n}^{ + }} \right\}\) and \(\left\{ {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{n}^{ + },{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{n}^{ + }} \right\}\) of an equation conjugate with respect to the Maxwell’s operator [37].
The system of equations, governing coefficients An+ and \({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }_{{n + }}}\), can be obtained it two ways: by using the biorthogonality condition of either the system of eigenfunctions \(\left\{ {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}}_{n}},{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}}}_{n}}} \right\}\) and \(\left\{ {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{n}^{ + },{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{n}^{ + }} \right\}\) or the system of eigenfunctions \(\left\{ {{{{\mathbf{e}}}_{n}},{{{\mathbf{h}}}_{n}}} \right\}\) and \(\left\{ {{\mathbf{e}}_{n}^{ + },{\mathbf{h}}_{n}^{ + }} \right\}\). Hence, Eq. (6) can be reduced to an infinite system of matrix equations. It can be solved after retaining a finite number of terms in the expansion of the field (the number of retained eigenfunctions inside and outside of plasma must be equal). As a result, the number of equations will be more than twice larger than the number of eigenfunctions.
Upon choosing a large number of eigenmodes, both methods should yield identical results. However, the rounding errors in calculation of individual terms of the series, ill-conditioned obtained matrix, and awkwardness of the obtained problem can play a role, too.
2 EXPANSION OF THE FIELD AT INTERFACE IN NATURAL WAVES OF AN EMPTY WAVEGUIDE
Let us choose functions from the \(\left\{ {{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}}}_{n}},{{{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}}}_{n}}} \right\}\) family. Note that axial dependences for these functions coincide completely. Let us multiply each of the equations governing electric field by \(\left\{ {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}_{{j + z}}^{ + }} \right\}\), multiply each of the equations governing magnetic field by \(\left\{ {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + \varphi }}^{ + }} \right\}\), and integrate the results from 0 to L. The resulting system of equations has the form
In the case under consideration, εP is the dielectric permittivity in the center of plasma column (z = 0). Equations (7) are written in such a way that the third and subsequent equations transform into equations describing a surface wave propagating along the lateral surface at d → 0. Due to their awkwardness, expressions for coefficients \({{C}_{{Bnj + }}}\) and \({{C}_{{Enj + }}}\) taking into account analytical formulas for the fields [40] are presented in Appendix A. Second powers of the norms of the waves in an empty waveguide are calculated in a standard way: \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{0 + }}^{2} = L\), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{j + }}^{2} = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}\). Sometimes, we will also need the norm of the eigenfunction of the electric field: \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{0 + }}^{E} = \rho \sqrt L \), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} _{{j + }}^{E} = \rho {{{{{\tilde {h}}}_{{n + }}}} \mathord{\left/ {\vphantom {{{{{\tilde {h}}}_{{n + }}}} k}} \right. \kern-0em} k}\sqrt {{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} \). Note that coefficients \({{C}_{{E00 + }}}\), \({{C}_{{Ej0 + }}}\), \({{C}_{{E0n + }}}\), and \({{C}_{{Enj + }}}\) are defined by different expressions. The first two equations in system (7) stand out since they allow calculating the amplitude of the surface wave and electric field of the TEM wave at the interface as a function of magnetic field. The rest of the equations allow finding the amplitudes of the higher-order waves as a function of the surface-wave amplitude. The discussed equations yield the following general relations:
where matrix S is determined by expression \({\mathbf{S}} = {{{\mathbf{\hat {S}}}}^{{ - 1}}}\), \({{\hat {S}}_{{ji}}}\;\, = \;\,\left( {\frac{{{{{\tilde {h}}}_{{i + }}}}}{{k{{\varepsilon }_{P}}}}{{I}_{0}}\left( {{{{\tilde {h}}}_{{i + }}}R} \right){{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right){{C}_{{Eij + }}} + } \right.\;\,\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}}}{k}{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{j + }}}R} \right)\;\, \times \) \(\left. {\mathop {{{I}_{1}}\left( {{{{\tilde {h}}}_{{i + }}}R} \right){{C}_{{Bij + }}}}\limits_{} } \right)\). Substituting the values of coefficients into the first two equations in (7), we have:
The latter expression shows that the presence of higher-order modes can substantially influence position of resonances. Averaged over height electric field at the plasma boundary in an empty part of the discharge chamber can be used to find the discharge impedance:
Hence, in agreement with general relations, excitation of higher-order field modes changes position of both the current resonances (points at which the denominator becomes equal to zero) and the voltage resonances (point in which the numerator equals zero). According to general expressions (2), we see that the amplitudes of higher-order waves depend both on the fundamental mode’s voltage (the term containing \({{J}_{0}}({{h}_{{0 + }}}R)\)) and its current (\({{J}_{1}}({{h}_{{0 + }}}R)\)). At first sight, it follows from (8) that the impedance of the line when its characteristics are varied will be equal to zero, on average, i.e., segments exhibiting capacitive and inductive impedance along the electron-density axis will occupy approximately equal areas, because all terms depend on Bessel functions, one way or another. Therefore, it is of interest to recast expression (8) separating components that depend on the relation between the wavelength of the radial surface wave and plasma radius (i.e., ultimately, on the electron density) relatively weakly and those that depend on it strongly:
where
An expression governing discharge conductivity can be obtained analogously:
It follows from (10) that two terms can be distinguished in the expression for impedance upon excitation of a surface wave. At fixed phase of the current, the first term describes impedance introduced by the radial surface waves and higher-order modes of the field excitation of which is related to voltage across the line, i.e., their phase changes according to the phase of voltage. The second term describes excitation of higher-order waves by current flowing in the line; their phase is related to the phase of current, and this term introduces an inductive impedance. Similar analysis can be conducted for conductivity (10), the only difference being that it is more convenient to have the phase matched to that of voltage.
3 EXPANSION OF THE FIELD AT INTERFACE IN NATURAL WAVES OF THE THREE-LAYER PLASMA STRUCTURE
Let us choose functions from the \(\left\{ {{{{\mathbf{e}}}_{n}},{{{\mathbf{h}}}_{n}}} \right\}\) and \(\left\{ {{\mathbf{e}}_{n}^{ + },{\mathbf{h}}_{n}^{ + }} \right\}\) families. The orthogonality conditions for these functions were analyzed and norms squared \(N_{{j + }}^{2}\) for all waves were calculated in [40]. An analog of equations (7) has the form
Expressions for coefficients \(D_{{jn}}^{B}\) and \(D_{{jn}}^{E}\) can be found in Appendix A. Comparison of matrices of equations (7) and (11) shows that their elements for electric and magnetic fields interchange. General formulas governing the amplitudes of the corresponding modes and impedances can be obtained by repeating the steps described in the previous section. The discharge impedance and amplitudes of different modes are determined by expressions
where \({{P}_{{ji}}} = \left( {\frac{{{{{\tilde {h}}}_{{j + }}}}}{{k{{\varepsilon }_{P}}}}{{I}_{0}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right){{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{i + }}}R} \right)D_{{jn + }}^{B} + } \right.{{I}_{1}}\left( {{{{\tilde {h}}}_{{j + }}}R} \right) \times \) \({{\left. {\frac{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{i + }}}}}{k}{{K}_{0}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{i + }}}R} \right)D_{{ji + }}^{E}} \right)}^{{ - 1}}}\). Amplitudes of higher-order modes of the field outside of plasma can be calculated by using expression
The amplitude of the surface wave driven in plasma is given by \({{A}_{{0 + }}}{{J}_{1}}\left( {{{h}_{ + }}R} \right)N_{{0 + }}^{2} = {{H}^{{{\text{ext}}}}}\left( {kR} \right)D_{{00 + }}^{B} - \) \(\sum\nolimits_{n = 1}^K {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}_{{n + }}}} {{K}_{1}}\left( {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }}_{{n + }}}R} \right)D_{{0n + }}^{B}\). Note that both expressions yield the same result for the impedance when only one mode is taken into account. As we mentioned above, the system of equations contains an infinite number of equations, in a general case. Taking into consideration possible errors in calculation of coefficients, numerical solution of this system of equations can be more time consuming than straightforward solution of Maxwell’s equations by means of the finite element or finite difference methods. Nevertheless, the discussed system turns out to be very convenient for classification of resonance states, because the number of coefficients can be considerably reduced near the resonance when conducting a qualitative analysis. Let us discuss classification of possible resonances.
4 A SIMPLIFIED EQUATION GOVERNING THE DISCHARGE IMPEDANCE
Formula (8) (or (12)) represents the general expression governing the discharge impedance. However, it should be simplified for understanding the results. Suppose that the influence of sheaths in the equations governing higher-order modes in equations (7) is small. Therefore, the axial propagation constants of the higher-order waves in plasma and outside of plasma are close to each other. In this case, only one diagonal term can be retained in (8) and (12). Matrices Sij and Pij become diagonal, and solutions obtained in the previous section become greatly simplified. Equations (7) yield the following expressions for the matrix elements:
It should be noted that the validity of this approximation needs additional investigation. However, analysis turn out to be cumbersome and can be the subject of a separate publication. The fact that contributions of perturbations with a smaller wavenumber and those with a large wavenumber will have opposite signs and partially compensate each other works in favor of this approximation. Nevertheless, a transition from general expressions of Section 3 to those obtained in the present section means a transition from quantitative analysis to a qualitative one. Using expressions for various field components [31, 40], we can obtain the following expression governing the discharge impedance:
Analogous expression in the case of low densities corresponding to the absence of a surface wave has the form
where index 0 denotes a quasi-TEM mode that transforms into the first evanescent mode at Re ε < 0 rather than the surface wave. Coefficients in the equation are calculated using the same formulas provided in Appendix A as in the case of propagation of surface waves. Analogous expressions can also be obtained by using system of equations (12). Assuming that
we arrive to the following result:
Let us analyze various types of resonances that can be observed in the discharge.
4.1 Resonance of Surface Waves Near the Lateral Surface
Let us analyze resonances related to excitation of standing surface waves along the lateral surface first. Impedance introduced by surface waves is separated out in formula (13) (the first term) (as well as in (14)), along with impedance introduced by the higher-order evanescent modes. In the process, the amplitudes of the higher-order modes can experience resonance enhancement upon fulfillment of the resonance condition that corresponds to excitation of surface waves propagating along the lateral surface and takes into account cylindric symmetry of the system (Bessel functions of imaginary argument and Macdonald functions), along with the influence of the sheaths (coefficients \(C_{{jj}}^{E}\) and \(C_{{jj}}^{B}\) in (13) or \(D_{{jj}}^{E}\) and \(D_{{jj}}^{B}\) in (14)):
The latter expression represents a simplified dispersion relation for the surface waves. The influence of these modes is substantial in both the numerator (the influence on the resonance in voltages) and in the denominator (the influence on the resonance in currents). The discussed resonance can be clearly seen in the curve representing the dependence of impedance on electron density, provided that not only the mode under consideration but also at least one of the other waves is taken into consideration in the numerator or the denominator. It is in this case that the resonances in currents shift relative to the resonances in voltages, and we see the corresponding spikes in the current-voltage characteristic in the discharge impedance dependence on electron density. The amplitude of the surface wave is relatively high. Therefore, the phase of voltage or the phase of current of the surface wave in a certain region changes within the (0, π) interval. Correspondingly, the amplitude of voltage or the amplitude of current exceeds the amplitude of the fundamental mode. This specificity reveals itself as the resonance in current or the resonance in voltage in the dependence of impedance on electron density.
Alternatively, when both amplitudes (the amplitudes of voltage and current) of the resonance mode exceed the amplitude of the fundamental mode, the impedance calculated by using expression (13) temporarily transforms to that determined by the discussed mode which is very close to the impedance in the single-mode regime [31]:
4.2 Resonances of Radial Surface Waves and Geometric Resonance in the Plasma–Space-Charge Sheath System
Two more types of resonances can take place in the discharge in addition to resonances related to excitation of surface waves near the lateral surface. All these resonances are described by zeros of the numerator (resonance in voltages) or denominator (resonance in currents) in expressions (8), (12), (13), or (14).
First, these are the resonances related to excitation of radial surface waves that are mathematically described by Bessel functions and are related to zeros of the latter.
Second, physically, these are resonances related to global distribution of currents and voltages in the discharge among which we can identify a current resonance that is observed upon fulfillment of condition
and a voltage resonance that was named the geometric resonance in the plasma–sheath system [32, 33]. In the latter case, an inductive impedance introduced by the higher-order modes is compensated by the impedance of a short open line, which has a capacitive character. This resonance is observed at high plasma densities when plasma radius is smaller than the wavelength of the surface wave. The resonance condition, taking into account the inductive impedance introduced by modes of higher types (at electron densities exceeding the resonance density for the lateral surface wave) is given by the following relation:
Using approximate expression (13), we find that
For small size discharge we have \({{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)} \mathord{\left/ {\vphantom {{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)} {{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}}} \right. \kern-0em} {{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}} = \) \({{\left( {{{{{h}_{{0 + }}}R} \mathord{\left/ {\vphantom {{{{h}_{{0 + }}}R} 2}} \right. \kern-0em} 2}} \right)}^{{ - 1}}}\). The capacitive impedance is replaced by an inductive one with decrease in electron density at the point of the geometric resonance. Penetration depth of the higher-order modes into plasma increases with further decrease in electron density, and inductive impedance introduced by the second term increases. Oscillations of the first term in the last expression give rise to spikes in the amplitude of absorption related to excitation of surface waves or to the appearance of new current and voltage resonances if absorption of surface waves is weak and the amplitude of the wave reflected from the center of the discharge is low. In the opposite case, if the reactive part of the impedance introduced by the surface waves exceeds inductive impedance of the fundamental mode, not only additional spikes but also new current and voltage resonances can appear.
The results obtained when using expression (13) to calculate the impedance for plasma radii of 2, 5 10, 15, and 20 cm with the length of the plasma column set equal to 8 cm are presented in Fig. 2. The ratio of the effective collision frequency to the field frequency was assumed to be equal to 0.1, while the sheaths thickness was set equal to 3 mm. Excitation of a surface wave and two higher-order modes was taken into account in the calculations. The results show that the discharge, in general, is characterized by an inductive impedance in the region of excitation of surface waves, because impedance introduced by the latter is purely active almost everywhere due to their strong absorption. The presence of the surface wave reflected from the center of the discharge reveals itself in spikes of absorption in the curve depicting impedance only at high electron densities. These spikes can be seen in Fig. 2 at discharge radius equal to 5 cm and larger. They are marked by thin vertical lines and a stars. The spikes become more evident with increase in the electron density, because this leads to a decrease in surface wave attenuation and a decrease in the inductive impedance of the higher-order modes that play the role of a background for the spikes.
Discharge impedance (1—Re Z, 2—Im Z, Ω) (results of analytical calculation) for symmetric discharge under in-phase excitation; plasma radius is R = 2 (a), 5 (b), 10 (c), 15 (d), and 20 (e) cm; field frequency is 135.6 MHz; sheaths’ thicknesses are d1 = d2 = 3 mm. Collision frequency is assumed to be equal to 0.1 of the field frequency. The scale is decreased by a factor of 20 in the region where no surface waves are propagating (3—Re Z/20, 4—Im Z/20, Ω). Stars and black vertical lines denote the positions of resonances related to excitation of surface waves.
Resonances in currents at density equal to critical and a geometric resonance that shifts toward higher electron densities with increase in radius can be seen in all diagrams, which is related to a decrease in the \({{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)} \mathord{\left/ {\vphantom {{{{J}_{0}}\left( {{{h}_{{0 + }}}R} \right)} {{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}}} \right. \kern-0em} {{{J}_{1}}\left( {{{h}_{{0 + }}}R} \right)}}\) ratio.
5 THE INFLUENCE OF THE EXTERIOR PART OF THE DISCHARGE CHAMBER ON DISCHARGE IMPEDANCE
Before comparing the results of analytical calculations with those, obtained by numerical solution of Maxwell’s equations, let us investigate the influence of the exterior part of the chamber on discharge impedance as a whole. In the geometry under investigation, the influence of the exterior part of the electrodes, the region of excitation, the working chamber periphery, and the line connecting the chamber with the source of the field should be taken into consideration. Let us analyze these processes step-by-step.
5.1 The Influence of Capacitance of the Exterior Part of the Electrodes
In the previous sections, we calculated discharge impedance Z0 on cylindrical surface r = R limiting the area, occupied by the discharge. Nevertheless, it was assumed that the size of the electrodes did not coincide with the size of plasma (Fig. 1). In the simplest case, when the difference in radii is much smaller than the wavelength of the TEM wave, impedance at point R = R1 is given by (see Appendix D for more general formulas)
Here, \(\tilde {C}\Delta r\) and \(\tilde {L}\Delta r\) are the capacitance (2–10 pF) and inductance (less than 0.01 µH) introduced by the peripheral region, respectively, while \(\Delta r = {{R}_{1}} - R\). The influence of inductance can be neglected under the conditions discussed in the present work.
5.2 The Influence of Impedance of the Exterior Part of the Working Chamber and Higher-Order Modes of the Field Driven Near the Point of Power Deposition
In the previous subsection, we analyzed the influence of an extra area of the electrodes adjacent to the discharge. Let us now investigate the influence of the exterior part of the chamber (Fig. 1). Impedance can be calculated similar to the case of discharge chamber completely filled with plasma [40], except eigenwaves of the three-layer structure should be replaced with eigenwaves of the external waveguide (Appendix E):
Here, \({{Z}_{{D1}}}\) is determined by expressions from subsection 5.1 or Appendix D, and \(z = {{\rho L} \mathord{\left/ {\vphantom {{\rho L} {\left( {2\pi R} \right)}}} \right. \kern-0em} {\left( {2\pi R} \right)}}\). An equivalent scheme of the discharge for the geometry under consideration is illustrated in Fig. 3. In the scheme, Z0 is the impedance of plasma (calculated by using expressions from Section 2, taking into account higher-order modes), and Line 1 is the energy transmission line from the plane of excitation to the discharge boundary. The line is formed by the exterior part of the electrodes. The size of this area is usually small relative to the wavelength of the HF wave in vacuum. Therefore, this impedance represents capacitance connected to the discharge in parallel. A closed line (Line 3), formed by the empty exterior part of the vacuum chamber, is connected with this line in series. Concentrated elements representing contribution of the fields of the higher-order waves of an empty waveguide, initiated in the excitation region, are connected to this line in parallel. It should be noted that, in contrast to the case of a chamber completely filled with plasma, excitation of higher-order modes in an empty waveguide introduces an additional capacitive impedance. In the process, impedances introduced by higher-order modes at r < R and r > R are also connected in series, in agreement with the expression above. Other notations in the figure are as follows: ZS is the internal resistance of the power source; US is its electromotive force; \(Z_{e}^{j}\) and \(Z_{i}^{j}\) are impedances introduced by the higher-order modes driven inside and outside of plasma.
An equivalent circuit of the discharge. Line 1—open long line describing a surface wave at r < R1; line 3—closed line in the peripheral region describing propagation of the TEM wave at r > R2; Zji and Zje are concentrated impedances describing higher-order modes of the field in the interior (r < R) and exterior (r > R) regions that are connected in series. Line 2—the supply line delivering energy from the source; ZS is the internal resistance of the source.
Two obvious conclusions follow from the derived expressions:
(1) Excitation of higher-order modes of the field gives rise to the appearance of additional currents that shift position of the current resonances.
(2) The field of the TEM wave in the exterior part of the chamber can also substantially influence excitation of the field in the discharge. In the process, the impedance of the exterior part of the chamber turns out to be connected with the impedance of the interior part in series (for each wave). This means that it will not influence position of current resonances but can substantially change the values of electron density at which the voltage resonance takes place. For small sizes, impedance introduced by this part of the chamber will be inductive. If this impedance is large, the geometric resonance in the plasma–sheath system can disappear. On the other hand, compensation of reactive part of the impedance of the central part can result in sharp increase in the magnitude of the field in the discharge center. The field amplitude in the plasma region turns out to be very low if the impedance of the exterior part at the point of energy deposition is very large, so that \(H_{0}^{{{\text{ext}}}}{\kern 1pt} \left( {{{R}_{3}}} \right) \to 0\) (a quarter-wave piston), and the discharge becomes unsustainable under such conditions.
The results of impedance calculation by using analytical formulas are presented in Fig. 4. The ratio of capacitance connected to the discharge in parallel to discharge capacitance at low currents decreases with increase in the discharge radius. Therefore, the largest shift in the position of the resonance in currents toward higher values of electron concentration is achieved for a discharge with a diameter of 2 cm and monotonically decreases with increase in its radius. Due to small value of inductance introduced by the exterior parts, position of the geometric resonance remains largely unchanged (see Figs. 2 and 4). Therefore, the values of electron density at which the resonance in currents and the resonance in voltages are observed are relatively close to each other in a discharge of small size. The corresponding values of density differ by a factor of 3–10 in other cases.
The influence of impedance introduced by the peripheral part of the working chamber on discharge impedance (1—Re Z, 2—Im Z, Ω) (results of analytical calculation) for a symmetric discharge under in-phase excitation. Plasma radius is equal to R = 2 (a), 5 (b), 10 (c), 15 (d), and 20 cm (e); field frequency is 135.6 MHz; thicknesses of sheaths are d1 = d2 = 3 mm. Collision frequency is assumed to be equal to 0.1 of the field frequency.
Similar to the case of discharge chamber completely filled with plasma, the current resonance takes place when inductive current through plasma and capacitive current flowing through the plasma-free region compensate each other. The discharge has inductive impedance, on average, at densities lower than that, corresponding to the geometric resonance, and higher than that, corresponding to the current resonance. Weak resonances related to surface-wave reflection from the center of the discharge can be seen on the background of a relatively slowly varying inductive impedance. Small influence of these resonances is explained by strong absorption of the surface wave. These resonances become more pronounced than in Fig. 2 when additional capacitance is taken into account, because part of the inductive impedance introduced by the higher-order modes is compensated by capacitance of the exterior part of the chamber.
6 NUMERICAL SIMULATION OF A SYMMETRICALLY DRIVEN DISCHARGE
Analytical results, obtained in the previous subsections, were compared with the results of numerical calculations, carried out by using the COMSOL Multiphysics® software package. Similar to [40], Maxwell equations were solved in the space region including the central part of the chamber (0 < r < R3, –L < z < L) and the space between the electrodes (R1 < r < R2, –L < |z| < L + L2), see Fig. 1. Zero boundary conditions for tangential component of the electric field were imposed at the electrodes and the vacuum chamber wall. A symmetrically driven discharge for which current I, flowing in through the lower electrode, was assumed to be equal to current, flowing out through the upper electrode, was analyzed. The azimuthal magnetic field at the exterior boundary 6 (R1 < r < R2, –|z| = L + L2) was assumed given: \({{H}_{\varphi }}\left( {r, \pm \left( {L + {{L}_{2}}} \right)} \right) = {I \mathord{\left/ {\vphantom {I {2\pi r}}} \right. \kern-0em} {2\pi r}}\).
Impedance was calculated at several points. First, at the discharge boundary (r = R). In this case, according to general expressions obtained in [31],
It was assumed here that current is determined by the magnetic field magnitude averaged over height (different relations between electrode currents that were used for calculation of impedance and spatial field distribution were discussed in [31]).
Second, in the case under consideration, expressions governing impedance at boundary 6 of the area of calculation coincide with those derived in [40]:
Electron-density distribution in plasma was assumed to be uniform, while dielectric permittivity was defined using the cold-plasma model. The discharge region was limited by a dielectric (ε = 1) from the exterior-wall side.
The results of impedance calculation at the discharge boundary are illustrated in Fig. 5 (1, r = R). Since the values of impedance substantially decrease when electron density changes by three orders of magnitude, the curves were plotted on two scales (diagrams on the left- and right-hand side), which allowed demonstrating the behavior of impedance at low and high plasma densities. Comparison with analytical calculations (Fig. 2) shows that they agree with each other qualitatively. At low densities (less than 5–6 times the critical density), the results agree also quantitatively. However, deviation of numerically calculated curve from that calculated analytically increases with increase in electron density. Numerical calculations predict the occurrence of geometric resonance in the plasma–sheath system at lower values of electron density. This mismatch can be related to the approximations used in the analytical calculations, namely, the diagonal approximation in the matrix and the fact that only two higher-order modes were considered. However, the presence of spikes in the impedance (both in analytical and numerical calculations) indicates substantial changes in the relation between the field amplitudes of the surface wave and evanescent modes.
Discharge impedance (1—Re Z, 2—Im Z, Ω) (results of numerical simulations) for a symmetric discharge under in-phase excitation. The diagram on the right-hand side represents the same curves as in figures above but on a larger scale. Parameters are the same as in Fig. 4. Impedance was calculated at the exterior plasma boundary.
Calculation of the impedance at the boundary of the calculation region were carried out at distance L2 = 1 cm (2, Fig. 6) and L2 = 10 cm (3, not shown in the paper) from the discharge chamber boundary. Estimates and numerical calculations conducted using the COMSOL Multiphysics® software package showed that the influence of peripheral part of the working-chamber is not critical when the difference in radii R3–R2 is smaller than 5 cm and at frequency of 135.6 MHz, because inductance introduced by the exterior part of the chamber is smaller than 0.01 µH. On the contrary, capacitance of the peripheral part of the electrodes and the external supply line substantially shift position of resonance in currents toward higher electron densities, while position of geometric resonances in the plasma–sheath system remains largely unchanged (Fig. 6). Resonances related to excitation of surface waves reveal themselves more clearly when part of inductive impedance of the higher-order modes is compensated by capacitance of the supply line.
Same as in Fig. 5. The influence of the exterior part of the discharge chamber was excluded because R3 = R2, but the capacitance of the supply line was taken into account.
Since calculations showed that the influence of resonances in the current-voltage curves related to excitation of standing surface waves was weak, when the ratio of the electron collision frequency to the field frequency was set equal to ν/ω = 0.1, we carried out calculations also for ν/ω = 0.01 (Fig. 7), although this value of collision frequency is too low for typical HF discharges. A jump in the impedance, related to the appearance of traveling radial surface waves, can be clearly seen in Fig. 7 (A). This jump is observed at electron densities slightly lower than twice the critical density, which can be caused by the influence of the sheath. However, additional calculations are needed for determining exact reason for this shift, including direct calculation of dispersion of eigenwaves of the three-layer system taking into account collisions but without using the perturbation-theory approach. Further increase in the electron density leads to the appearance of spikes in absorption and oscillations in the curve representing imaginary part of the impedance which correspond to excitation of standing surface waves. The values of electron density at which excitation of standing surface waves near the lateral surface takes place do not change upon variation of discharge radius (B). At the same time, resonances related to excitation of radial standing surface waves shift toward higher electron densities with increase in plasma radius (C). Geometric resonance in the plasma–sheath system is marked separately (D).
Discharge impedance (1—Re Z, 2—Im Z, Ω) (results of numerical simulation) for a symmetric discharge under in-phase excitation. All calculations are the asme as in Fig. 5 but collision frequency is set equal to 0.01 of the field frequency.
Note that variation of parameters of external circuit strongly impacts position of the current resonances that we referred to as the global resonances along the electron-concentration axis, because compensation of voltages and currents occurs in the discharge as a whole, currents and voltages changing gradually upon variation of plasma parameters. At the same time, position (but not the amplitude) of the interior resonances (excitation of surface waves) is determined by internal properties of the system and weakly depends on parameters of the external circuit. Their amplitude can sharply increase if position of this resonance is close to that of the global resonance.
It should be noted that, when calculating discharge characteristics in the present work, we assumed that the radius of electrodes exceeds the plasma radius, and the surface waves, along with the higher-order types of modes, were thus driven after the field of the source transformed into a TEM wave rather than by the source field directly. We will analyze the other case in one of the forthcoming works, simultaneously with analytical calculations.
Calculated spatial distributions of magnetic field in plasma are illustrated in Figs. 8–10. Since impedance dependences on electron density do not change much qualitatively for all values of plasma radius (2, 5, 10, 15, and 20 cm), in contrast to the case of a discharge chamber completely filled with plasma [40], here we will compare distributions of the azimuthal magnetic field in discharges of different radius that have plasma densities corresponding to identical characteristic points in the dependence of impedance on electron density. Since the exterior part of the discharge chamber had the same configuration in all cases, comparison of spatial distribution of the fields allows estimating the influence of changes in the size of plasma on spatial distribution of the field. Field distributions for a discharge of 2-cm radius are presented in Figs. 8a, 8b, 9a, 9b, 10a, and 10b; those for a discharge of 5-cm radius are presented in Figs. 8c, 8d, 9c, 9d, 10c, and 10d; distributions for a discharge of 10-cm radius are depicted in Figs. 8e, 8f, 9e, 9f, 10e, and 10f; distributions for a discharge of 15-cm radius are presented in Figs. 8g, 8g, 9g, 9h, 10g, and 10h; distributions for a discharge of 20-cm radius are illustrated in Figs. 8i, 8j, 9i, 9j, 10i, and 10j. Resonances related to excitation of a standing surface wave at the dielectric sidewall of the discharge chamber take place in a discharge of small radius upon increase in electron density above twice the critical density. Excitation of a surface wave propagating along the electrode starts playing an important role with increase in discharge radius. Since absorption coefficient of this wave is substantially larger than that of the wave propagating along the lateral surface, its presence leads to redistribution of current into this wave, and the surface wave at the lateral surface becomes less prominent.
Spatial distribution of magnetic field upon excitation of a surface wave near the lateral surface of the discharge for several values of plasma and working-chamber radii. Conditions are the same as in Fig. 2. The real component of magnetic field is shown on the left-hand side, while its imaginary component is shown on the right-hand side, A/m. Plasma radius is set equal to 2 (a, b), 5 (c, d), 10 (e, f), 15 (g, h), and 20 cm (i, j).
Figure 9 corresponds to a resonance in currents. In this case, the current in regions outside of plasma is compensated by the current flowing through the plasma column. Density of current flowing through plasma should decrease with increase in plasma radius. As a result, electron density corresponding to resonance decreases. Due to low plasma density and large penetration depth of the field of the higher-order mode, current is mainly carried by the higher-order modes of the field. Since discharge radius increases simultaneously, condition for excitation of the radial surface wave that can be seen in Figs. 9e, 9f improve. However, the amplitude of this wave is much lower than that of the field of the higher-order mode.
Finally, Fig. 10 illustrates the field distribution corresponding to a geometric resonance in the plasma–sheath system. The energy transferred to the surface wave and that transferred to higher-order modes of the field are approximately equal to each other at the point of resonance. The wavelength of the surface wave at high electron densities turns out to be larger than the size of the system. Therefore, its current is distributed uniformly over the electrode area. At the same time, the current of the higher-order modes concentrates near the plasma boundary, i.e., flows through a smaller area. Therefore, the magnitude of magnetic field induced by the higher-order modes turns out to be larger than that induced by the surface wave, although by a small amount. Hence, analysis of spatial structure of the high-frequency field by means of numerical simulation corroborates the qualitative picture obtained by using analytical calculations.
Let us compare the curves representing impedance that were obtained in the present work with those obtained in the previous work of this series ([40], Fig. 2) for the same values of the plasma radius. First, the global resonance in currents in the circuit under consideration which is caused by the resonance in current flowing though plasma and current flowing though additional capacitance of the exterior region of the chamber, along with capacitance of the supply line, shifts toward higher electron densities. This difference agrees well with expression (15) and is related to additional capacitance introduced by part of the electrodes not covered by plasma.
Second, resonances related to excitation of surface waves are less pronounced in the case under consideration relative to analogous resonances in a chamber completely filled with plasma. Apparently, this difference is related to field configuration of the source maintaining plasma. In [40], this field was concentrated in the region near the electrode (a δ-shaped source was used in the model). The field of the surface wave attained maximum, while, on the contrary, the field of the higher-order modes attained minimum in that region. In the present work, both the surface waves and higher-order types of waves are excited by a TEM wave, which has uniform field distribution along the axis. This fact should facilitate predominant excitation of higher-order field modes that attain maximum in the center (z = 0).
Third, a resonance related to compensation of higher-order fields modes currents outside and inside plasma, which corresponds to resonance excitation of the surface waves near the lateral surface, can occur in the geometry considered in the present work.
Note that, in general, there is a possibility to influence the fields of the two components, the field of the surface wave and the field of the higher order modes, in the discussed geometry. At the same time, there are three components in a completely filled chamber: the surface wave in the central region, the surface wave in the peripheral region, and the higher-order modes in the vicinity of the excitation region, which offers advantages from the point of view of controlling the spatial distribution of electron density. However, this fact can also create additional problems.
There are no propagating waves in the plasma-free region in a discharge chamber with a design under consideration under anti-phase discharge excitation, at least, if the distance between the plates is smaller than the wavelength in vacuum. Therefore, the current to the sidewall under anti-phase excitation must flow through a very small capacitance between plasma and the wall. Hence, excitation of antisymmetric waves in a symmetric discharge in the discussed geometry is problematic. However, these waves can be generated upon violation of symmetry (e.g., in the sheaths sizes is different or electron density distribution is not symmetric), especially, taking into account that such symmetry violation can occur spontaneously [34, 35, 41]. Calculation of dispersion curves [31] shows that the length of antisymmetric waves is much shorter than that of symmetric ones in a wide range of electron densities. Therefore, resonances related to excitation of such waves are observed at higher electron densities. This conclusion is confirmed by calculations for a discharge chamber completely filled with plasma [40]. Asymmetry of the discharge in a partially filled vacuum discharge chamber can lead to excitation of antisymmetric waves and appearance of new resonances. This problem needs additional investigation, which will be the subject of future work.
7 MAIN RESULTS OF THE PRESENT WORK
The main results of this work can be summarized as follows:
(i) Analytical calculations of the field in a capacitive low pressure high frequency discharge revealed that, with high degree of accuracy, the field in plasma can be presented as a sum of surface waves and evanescent eigenmodes of E-waves in a three-layer sheath–plasma–sheath structure surrounded my metallic electrodes. Both the surface waves and higher-order evanescent field modes must be taken into account for correct calculation of the discharge impedance.
(ii) The main current resonance observed in the discharge that we refer to as the «global resonance» is related to compensation of capacitive impedance of the exterior part of the chamber and inductive impedance of the discharge. Since this resonance in the geometry under consideration is observed under the same conditions as resonances associated with the multiplicity of the plasma dimensions and the surface wavelength, the latter are masked by the discussed resonance.
(iii) The main voltage resonance observed in the system represents a geometric resonance in the plasma–sheath system. In the range of parameters typical for plasma reactors and field frequency considered in the problem, this resonance occurs in plasma with radial size being smaller than 15 cm. In the case of larger plasma dimensions, the line along which the surface waves propagate is often characterized by an inductive impedance or its capacitive impedance is insufficient for compensation of the inductive impedance introduced by the higher order modes.
(iv) The higher-order field modes have larger amplitude and play a more important role in sustaining the discharge than in the case of the discharge completely filling the discharge chamber [36].
(v) The perturbation theory approach with respect to parameter ν/ω is insufficient for correct analytical description of properties of the discharge with density in the range between critical and twice the critical d-ensities.
(vi) Capacitance of the circuit connecting plasma with generator and inductance introduced by an empty part of the chamber can substantially influence discharge characteristics or even the possibility of sustaining it. The role of these effects increases with increase in frequency of the field sustaining the discharge.
(vii) Comparison of the results of analytical calculations and numerical simulation of discharge properties by using the COMSOL Multiphysics® software package showed their satisfactory qualitative agreement.
Research reported in this series of works (including [31, 40]) revealed that the higher-order evanescent field modes and the surface waves propagating along the plasma–sheath–metal interfaces play equally important role, determining impedance of the high-frequency low-pressure capacitive discharge as a whole and spatial distribution of the field. Higher-order modes are excited at all sharp inhomogeneities of the working chamber, such as boundaries (and ribs) of the electrodes, corners of vacuum chamber, and in the region of energy deposition. In the process, the relation between the amplitudes of different types of the waves can vary substantially depending on plasma density and the working-chamber geometry. Therefore, the probability to obtain universal recommendations that would create conditions required for realization of existing (and, possibly, new) technological processes for all possible regimes of the discharge is low. Nevertheless, calculations allow estimating the efficiency of energy deposition into a given field mode, finding under what conditions and what influence does one or another type of the field has on the impedance and spatial distribution of plasma density. Our analysis clearly demonstrates the possibility of choosing and investigating a wide range of setups not only based on the results of experiments conducted in previous setups but also based on theoretical analysis of electrodynamic properties of the system.
REFERENCES
M. A. Lieberman and A. J. Lichtenberg, Principles of Plasma Discharges and Materials Processing (Wiley, New York, 2005).
J. Perrin, J. Schmitt, C. Hollenstein, A. Howling, and L. Sansonnens, Plasma Phys. Control. Fusion 42, B353 (2000).
J. P. M. Schmitt, M. Elyaakoubi, and L. Sansonnens, Plasma Sources Sci. Technol. 11, A206 (2002).
A. E. Park, B. U. Cho, and J. K. Lee, IEEE Trans. Plasma Sci. 31, 628 (2003).
S. Samukawa, M. Hori, S. Raul, K. Tachibana, P. Bruggeman, G. Kroesen, J. C. Whitehead, A. B. Mur-phy, A. F. Gutsol, S. Starikovskaia, U. Kortshagen, J.‑P. Boeuf, T. J. Sommerer, M. J. Kushner, U. Czarnetzki, et al., J. Phys. D: Appl. Phys. 45, 253001 (2012).
D. J. Cooperberg, Phys Plasmas 5, 862 (1998).
D. J. Cooperberg and C. K. Birdsall, Plasma Sources Sci. Technol. 7, 41 (1998).
M. A. Liberman, J. P. Booth, P. Chabert, J.-M. Rax, and M. M. Turner, Plasma Sources Sci. Technol. 11, 283 (2002).
P. Chabert, J.-L. Ramimbault, J.-M. Rax, and M. A. Lieberman, Phys. Plasmas 11, 1175 (2004).
P. Chabert, J.-L. Ramimbault, J.-M. Rax, and A. Pepper, Phys. Plasmas 11, 4081 (2004).
L. Sansonnens, A. A. Howling, and Ch. Hollenstein, Plasma Sources Sci. Technol. 15, 302 (2006).
P. Chabert, J. Phys. D: Appl. Phys. 40, R63 (2007).
G. A. Hebner, E. V. Barnat, P. A. Miller, A. M. Paterson, and J. P. Holland, Plasma Source Sci. Technol. 15, 889 (2006).
W. Gekelman, M. Barnes, S. Vincena, and P. Pribyl, Phys. Rev. Lett. 103, 045003 (2009).
D. Eremin, R. P. Brinkman, and T. Mussenbrock, Plasma Processes Polym. 14, 1600164 (2017).
K. Zhao, Y.-X. Liu, E. Kawamura, De-Qi Wen, M. A. Lieberman, and Y.-N. Wang, Plasma Sources Sci. Technol. 27, 055017 (2018).
K. Zhao, De-Qi Wen, Y.-X. Liu, M. A. Lieberman, D. J. Economou, and Y.-N. Wang, Phys. Rev. Lett. 122, 185002 (2019).
T. Mussenbrock, T. Hemke, D. Ziegler, R. P. Brinkman, and M. Klick, Plasma Sources Sci. Technol. 17, 025018 (2008).
L. Sansonnens, A. A. Howling, and Ch. Hollenstein, Plasma Sources Sci. Technol. 15, 302 (2006).
P. Leprince, G. Mattieussent, and W. P. Allis, J. Appl. Phys. 42, 4 (1971).
I. Lee, D. B. Graves, and M. A. Lieberman, Plasma Sources Sci. Technol. 17, 015018 (2008).
D. Eremin, T. Hemke, R. P. Brinkmann, and T. Mussenbrock, J. Phys. D: Appl. Phys. 46, 084017 (2013).
D. Eremin, IEEE Trans. Plasma Sci. 45, 527 (2017).
De-Qi Wen, E. Kawamura, M. A. Lieberman, A. J. Lichtenberg, and Y.-N. Wang, Plasma Sources Sci. Technol. 26, 015007 (2017).
M. A. Lieberman, IEEE Trans. Plasma Sci. 16, 638 (1998).
M. A. Lieberman, IEEE Trans. Plasma Sci. 17, 338 (1989).
T. Mussenbrock and R. P. Brinkman, Plasma Sources Sci. Technol. 16, 377 (2007).
T. Mussenbrock, R. P. Brinkman, M. A. Lieberman, A. J. Lichtenberg, and E. Kawamura, Phys. Rev. Lett. 101, 085004 (2008).
Y. Yamazawa, Appl. Phys. Lett. 95, 191504 (2009).
M. A. Lieberman, A. J. Lichtenberg, E. Kawamura, and A. M. Marakhtanov, Plasma Sources Sci. Technol. 24, 055011 (2015).
S. A. Dvinin, O. A. Sinkevich, Z. A. Kodirzoda, and D. K. Solikhov, Plasma Phys. Rep. 46, 1181 (2020).
J. Taillet, Am. J. Phys. 37, 423 (1969).
V. A. Godyak, Sov. J. Plasma Phys. 2, 78 (1976).
S. A. Dvinin, V. A. Dovzhenko, and G. S. Solntsev, Sov. J. Plasma Phys. 8, 698 (1982).
S. A. Dvinin, S. A. Postnikov, G. S. Solntsev, and L. I. Tsvetkova, Sov. J. Plasma Phys. 9, 749 (1983).
S. Rauf, Z. Chen, and K. Collins, J. Appl. Phys. 107, 093302 (2010).
L. B. Felsen and N. Marcuvitz, Radiation and Scattering of Waves (Prentice-Hall, Englewood Cliffs, 1973).
V. V. Nikol’skii and T. I. Nikol’skaya, Electrodynamics and Radio Wave Propagation (Nauka, Moscow, 1989) [in Russian].
L. A. Vainshtein, Electromagnetic Waves (Radio i Svyaz’, Moscow, 1990) [in Russian].
S. A. Dvinin, O. A. Sinkevich, Z. A. Kodirzoda, and D. K. Solikhov, Plasma Phys. Rep., 47, 28 (2021).
E. Kawamura, M. A. Lieberman, and A. J. Lichtenberg, Phys. Plasmas 25, 093517 (2018).
Author information
Authors and Affiliations
Corresponding authors
Appendices
APPENDIX A
Calculation of Coefficients in Equations
Norms of eigenfunctions were calculated in [40]. Expressions governing coefficients in systems of equations (7) and (11) (the first index denotes the number of the wave in the three-layer system, while the second index denotes that in the empty space) have the form
The following notations were used in the above expressions: \({{a}_{{0 + }}} = \sqrt {h_{{0 + }}^{2} - {{k}^{2}}{{\varepsilon }_{1}}} \); \({{p}_{{0 + }}} = \sqrt {h_{{0 + }}^{2} - {{k}^{2}}{{\varepsilon }_{P}}} \); \({{\tilde {a}}_{{n + }}} = \sqrt {{{k}^{2}}{{\varepsilon }_{1}} - h_{{n + }}^{2}} \); \({{\tilde {p}}_{{n + }}} = \sqrt {{{k}^{2}}{{\varepsilon }_{P}} - h_{{n + }}^{2}} \); \({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} }_{{n + }}} = {{n\pi } \mathord{\left/ {\vphantom {{n\pi } L}} \right. \kern-0em} L}\); εP and ε1 are the dielectric permittivities of plasma and sheath, respectively. All coefficients (C, D) have the dimension of length. Note also that, for convenience of conducting numerical calculations, \({{\varepsilon }_{{\text{p}}}}\) enters in expressions for different coefficients in different ways.
APPENDIX B
Calculation of Amplitudes of Different Types of Waves in the Diagonal Representation. Expansion in Waveguide Modes
Using the assumption of predominant role played by the diagonal terms, we can write expressions governing different components of the electric field. The amplitudes of the fields of higher-order types of waves have the following form inside plasma (r < R)
and outside of plasma (r > R):
The term in the denominator in the previous two expressions is the same, meaning that the fields of the higher-order modes grow simultaneously both outside and inside plasma, and plasma densities at which a resonance is observed are also the same. This resonance can be interpreted as the resonance related to excitation of surface waves at the plasma-column lateral surface. The amplitude of the surface wave propagating along the sheath can be calculated by using expression
APPENDIX C
Calculation of Amplitudes of Different Types of Waves in the Diagonal Approximation. Expansion in Modes of the Three-Layer Structure
Using general formulas, we find that the amplitude of the higher-order modes of the field in the diagonal approximation can be calculated by using the following expression:
where \({{E}^{{{\text{ext}}}}}\left( {kR} \right) = \rho {{H}^{{{\text{ext}}}}}\left( {kR} \right){{Z\pi R} \mathord{\left/ {\vphantom {{Z\pi R} L}} \right. \kern-0em} L}\). The amplitude of the surface wave propagating along the sheath satisfies expression
while the field of the higher-order modes inside plasma is given by
APPENDIX D
Calculation of Impedance Introduced by the Exterior Part of the Electrodes
Let the discharge impedance calculated according to any expression in (10)–(12) is equal to ZD. Distribution of potential and current in the R < r < R1 region satisfies the telegraph equations [37–39]:
where \({{\tilde {C}r} \mathord{\left/ {\vphantom {{\tilde {C}r} R}} \right. \kern-0em} R}\) and \({{\tilde {L}R} \mathord{\left/ {\vphantom {{\tilde {L}R} r}} \right. \kern-0em} r}\) are the capacitance and inductance of the line per unit length, respectively; \(\tilde {C} = {{{{\varepsilon }_{0}}2\pi R} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}2\pi R} L}} \right. \kern-0em} L}\); \(\tilde {L} = {{{{\mu }_{0}}L} \mathord{\left/ {\vphantom {{{{\mu }_{0}}L} {\left( {2\pi R} \right)}}} \right. \kern-0em} {\left( {2\pi R} \right)}}\). Introducing resistance of the line \(z = {{\rho L} \mathord{\left/ {\vphantom {{\rho L} {\left( {2\pi R} \right)}}} \right. \kern-0em} {\left( {2\pi R} \right)}}\) and substituting voltage and current in the form of a sum of Bessel and Neumann functions,
we find that the impedance at point r > R is given by
In the case of small difference of radii (\(k(r-R) \ll 1\)), it is easier to find the correction to the impedance directly from expression (D.1):
\(\Delta r = r - R\). Under the conditions of the present study, the influence of inductance of the line can be neglected in most cases.
APPENDIX E
Calculation of Impedance Introduced by the Peripheral Region of the Working Chamber
The conditions of tangential components of the electric field being equal to each other at the surface at which external energy is deposited into the discharge leads to relation (\({{U}_{{D1}}}\) is the voltage of the fundamental mode, and \({{Z}_{{D1}}}\) is the impedance of the interior transmission line at the electrode boundary calculated in the previous subsection)
Here, the first term in the left-hand side corresponds to the field of the TEM wave in the interior region calculated in Appendix D; two sums correspond to the fields of the higher-order modes in the interior and exterior regions, respectively (\({{B}_{{n + }}}\) and \({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }_{{n + }}}\) are the wave amplitudes); the last term represents the field of the TEM wave with amplitude \({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }_{{0 + }}}\) in the interior region representing a closed transmission line; the term in the right-hand side represents the external source of the field. Since the lateral surface of the chamber is made of metal, \({{Q}_{0}}\left( {k{{R}_{3}}} \right) = 0\). In the geometry under consideration (Fig. 1), we can write:
Similar to [36], we will assume that the region of energy deposition is small, so that \({{R}_{2}}-{{R}_{1}} \ll {{R}_{1}}\). The condition of currents at r = R1 and r = R2 being equal to each other means that HS = 0. Voltage equal to U is applied at the boundary points z = ±L: \({{E}^{S}} = \) \( - U\delta \left( {z - L} \right)\). Amplitudes of the fields can be calculated similar to [40] by replacing eigenwaves of the three-layer structure by eigenwaves of an empty waveguide. In the discussed case, (E.1) yields
Knowing amplitudes of all waves, we can find the source current (by using relation \({{i}_{n}} = 2\pi r{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }_{{\varphi n + }}}(L)\)):
and impedance at the point of excitation (16).
Rights and permissions
About this article
Cite this article
Dvinin, S.A., Sinkevich, O.A., Kodirzoda, Z.A. et al. Specificities of Electromagnetic Field Excitation in a Capacitive HF Discharge. III. Symmetric Discharge Partially Filling the Discharge Chamber. Plasma Phys. Rep. 47, 211–234 (2021). https://doi.org/10.1134/S1063780X2102001X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1063780X2102001X