Investigation of Shock Waves in Nonextensive Electron–Positron–Ion Plasma with Relativistic Ions

Abstract

Nonlinear propagation of ion-acoustic (IA) shock wave in a nonextensive and relativistic plasma is investigated by deriving space fractional Korteweg–de Vries–Burgers (SFKB) equation. This unmagnetized and collisionless plasma contains relativistic thermal ions, q-distributed electrons, and positrons. A modified tanh-function method is presented to solve the obtained SFKB equation taking space fractional and relativistic parameters, electrons nonextensivity, positrons nonextensivity, and electron-to-positron temperature ratio. It is observed that the structure of the IA shock wave can be modified by space fractional parameters. On the other hand, the IA shock wave shape can be modulated using the space fractional parameter. Our results can help understand the astrophysical environments such as pulsar magnetospheres, quasars, and collimated jets.

1 INTRODUCTION

Relativistic electron–positron–ion (e–p–i) plasma is of considerable interest in several areas such as astrophysics environments, gamma-ray bursts (GRB) [1], pulsars, and quasars [2]. There are signs of the existence of relativistic e–p–i plasma in nature. In the early universe, such plasma is generated when radiation and relativistic particles are more important than ordinary matter. It happens when the temperature is approximately above 10⁹ K. Several theories of quasars jets, supernova explosions, and galaxy formations are based on relativistic models [3–5]. Due to the interaction of intense electromagnetic waves or intense laser pulses with a solid target, the relativistic effects can appear in the laboratory and natural plasma [6–9]. In cosmology and astrophysics, the intense electromagnetic waves come from the light emitted from pulsars, or radiation emitted from black holes that caused the generation of relativistic plasma [7–10].

Furthermore, the shock wave and pulsar wind are also observed in the interaction of relativistic electrons or ions with plasma. Shock waves are an important feature in several phenomena occurring in the cosmology and astrophysical environments such as galactic nuclei [11], galaxies [12], neutron stars, and solar flares [13]. For example, the stars’ luminosity can be increased by an increase in the total light emitted from the galaxy. For this reason, an explosion can occur in the stars. Several mechanisms are proposed to explain the energy emitted from the explosion [14]. One of the probable mechanisms is the formation of shock waves, which propagate outward. On the other hands, the formation and observation of the shock structures is often occurs in dissipative plasmas, when the dissipation property is dominant over the dispersion property in such plasma [15–18]. The existence of the nonextensive and superthermal electrons, nonextensive positrons in space and astrophysical plasma, solar wind, and magnetosphere environment is reported [19, 20] as causing dissipative plasma and shock formation. However, generated shock waves are able to penetrate into the interplanetary space, galaxy, and solar flares, where they appear as interplanetary shock [21]. Thus, it is essential to investigate the shock wave propagation in relativistic plasmas. Recently, several authors have studied the shock wave propagation in plasmas [22–27]. In paper [24], the effects of isothermal electrons and relativistic ions on the structure of IA shock waves in a relativistic e–p–i plasma were studied. It was found that the structure of ion-acoustic shock waves depends on the temperature, the relativistic streaming factor, and the relative velocity. Oblique IA shock waves propagation in relativistic e–p–i plasmas with nonthermal electrons and relativistic ions has been studied in [25]. It was shown that the propagation of ion-acoustic shock waves depends significantly on the nonthermal and the relativistic parameters. In [26], the nonlinear propagation of IA shock wave in a dissipative relativistic plasma was investigated. The results show that as the relativistic parameter, temperature ratio, and positron concentration increase, the amplitude of IA shock wave decreases. The collisions effect on the structure of IA shock waves in a relativistic regime was studied in [27] and it was revealed that by an increase in relativistic and superthermal parameters, the structure of IA shock wave is modified.

Fractional calculus has many applications in various fields of science, engineering, and economics [28–34]. Fractional partial differential equations (PDEs) have attracted much interest in applied physics and conceptual modeling to describe various phenomena arising in real-world systems. Thus, the solution to this type of equation is essential. We focus on a class of analytical methods to solve them. Some of these methods are Lindstedt–Poincaré method [35, 36], Adomian decomposition method [37–39], Jacobi elliptic function method [40], spectral method [41], and differential transform method [42]. In this manuscript, using Agrawal method [43, 44], the SFKB equation is first derived to study the nonlinear propagation of IA shock waves in a relativistic and nonextensive plasma. Then, we propose a modified ta-nh‑function method to solve the obtained SFKB equation.

2 BASIC EQUATIONS

We consider an unmagnetized, fully ionized, and collisionless plasma that consists of relativistic thermal ions, nonextensive positrons, and nonextensive electrons with concentrations ${{N}_{i}}$, ${{N}_{p}}$, and ${{N}_{e}}$, respectively. The hydrodynamics fluid equations that concern the nonlinear propagation of IA waves in a relativistic plasma can be written as [26, 45]:

$$\frac{{\partial {{N}_{i}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {{{N}_{i}}{\kern 1pt} {{U}_{i}}} \right) = 0,~$$

(1)

$$\frac{{\partial \left( {\eta {{U}_{i}}} \right)}}{{\partial t}} + {{U}_{i}}\frac{{\partial \left( {\eta {{U}_{i}}} \right)}}{{\partial x}} + \frac{{\partial {\Phi }}}{{\partial x}} - \rho \frac{{{{\partial }^{2}}{{U}_{i}}}}{{\partial {{x}^{2}}}} = 0,$$

(2)

$$\frac{{{{\partial }^{2}}{\Phi }}}{{\partial {{x}^{2}}}} = {{\gamma }_{e}}{{N}_{e}} - {{N}_{i}} - {{\gamma }_{p}}{{N}_{p}},$$

(3)

where parameters are given by

$$\begin{gathered} {{N}_{e}} = {{[1 + (q - 1){\kern 1pt} \Phi ]}^{{(q + 1)/[2(q - 1)]}}}, \\ {{N}_{p}} = {{[1 - (q - 1)g\Phi ]}^{{(q + 1)/[2(q - 1)]}}}, \\ {{N}_{{e0}}} = {{N}_{{p0}}} + {{N}_{{i0}}},\quad g = \frac{{{{T}_{e}}}}{{{{T}_{p}}}},\quad {{\gamma }_{e}} = \frac{1}{{1 - f}}, \\ {{\gamma }_{p}} = \frac{f}{{1 - f}},\quad f = \frac{{{{N}_{{p0}}}}}{{{{N}_{{e0}}}}}, \\ \end{gathered} $$

(4)

where g is the electron-to-positron temperature ratio, f  is the relative concentration of positron to electron in equilibrium, q is the nonextensivity parameter; the subscript $k = i,e,~p$ stands for the ions, electrons, and positrons, respectively; ${{N}_{i}} = {{N}_{{i0}}}{\text{/}}{{N}_{{e0}}}$, ${{U}_{i}} = {{U}_{{i0}}}{\text{/}}\sqrt {{{{{T}_{e}}} \mathord{\left/ {\vphantom {{{{T}_{e}}} {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}}}$; ${{N}_{i}}$, ${{U}_{i}}$, and ρ are the normalized ion concentration, ion fluid speed, and ion viscosity, respectively; ${{m}_{k}}$ and ${{T}_{k}}$  are masses and temperatures, respectively; and Φ is the potential normalized by ${{T}_{e}}{\text{/}}e$. The time and space variables are normalized by the plasma period $\omega _{{pe}}^{{ - 1}} =$${{({{m}_{e}}{\text{/}}4\pi {{n}_{{e0}}}{{e}^{2}})}^{{1/2}}}$, and the Debye length λ_De = ${{({{T}_{e}}{\text{/}}4\pi {{n}_{{e0}}}{{e}^{2}})}^{{1/2}}}$, respectively. The relativistic parameter is defined as $\eta = 1 + {{U}_{i}}^{2}{\text{/}}2{{c}^{2}} + 3{{U}_{i}}^{4}{\text{/}}8{{c}^{2}}$, where $c$ is the speed of light. We applied the reductive perturbation technique [46] to study the IA shock waves’ structure. We introduce the stretched coordinates as follows:

$$\begin{gathered} \xi = \varepsilon \left( {x - {{u}_{0}}t} \right),~\quad \tau = {{\varepsilon }^{3}}~t, \\ \rho = {{\rho }_{0}}\varepsilon , \\ \end{gathered} $$

(5)

where ${{\rho }_{0}}$ is the normalized ion viscosity, the expansion factor measuring the nonlinearity is given by ε, and the IA wave speed ${{u}_{0}}$, normalized by $\sqrt {{{{{T}_{e}}} \mathord{\left/ {\vphantom {{{{T}_{e}}} {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}}}$.

The dimensionless variables ${{N}_{i}}$, ${{U}_{i}}$, and Φ are expanded in the following manner:

$$\begin{gathered} {{N}_{i}} = 1 + {{\varepsilon }^{2}}{{N}_{{i1}}} + {{\varepsilon }^{4}}{{N}_{{i2}}} + \ldots , \\ {\Phi } = {{\varepsilon }^{2}}{{{\Phi }}_{1}} + {{\varepsilon }^{4}}{{{\Phi }}_{2}} + \ldots , \\ {{U}_{i}} = {{U}_{{i0}}} + {{\varepsilon }^{2}}{{U}_{{i1}}} + {{\varepsilon }^{4}}{{U}_{{i2}}} + \ldots . \\ \end{gathered} $$

(6)

Substituting Eqs. (5) and Eqs. (6) into Eqs. (1)–(3), the lowest order in ε, yields

$${{N}_{{i1}}} = \frac{{{{U}_{{i1}}}}}{{{{u}_{0}} - {{U}_{{i0}}}}},\quad {{U}_{{i1}}} = \frac{{{{{\Phi }}_{1}}}}{{{{\eta }_{1}}\left( {{{u}_{0}} - {{U}_{{i0}}}} \right)}}~,$$

(7)

$$\begin{gathered} {{N}_{{i1}}} = \frac{{\left( {q + 1} \right)\left( {1 + fg} \right)}}{{2\left( {1 - f} \right)}}~{{{\Phi }}_{1}}, \\ {{\eta }_{1}} = 1 + \frac{3}{2}{{\alpha }^{2}} + \frac{{15}}{8}{{\alpha }^{4}}, \\ \alpha = \frac{{{{U}_{{i0}}}}}{c}. \\ \end{gathered} $$

In the next order in ε, using Eqs. (7), finally, the KdV‒Burgers equation can be achieved as:

$$\frac{{\partial {{{\Phi }}_{1}}}}{{\partial \tau }} + {{C}_{1}}{{{\Phi }}_{1}}\frac{{\partial {{{\Phi }}_{1}}}}{{\partial \xi }} + {{C}_{2}}\frac{{{{\partial }^{3}}{{{\Phi }}_{1}}}}{{\partial {{\xi }^{3}}}} - {{C}_{3}}\frac{{{{\partial }^{2}}{{{\Phi }}_{1}}}}{{\partial {{\xi }^{2}}}} = 0,$$

(8)

$$\begin{gathered} {{N}_{{i1}}} = \frac{{\left( {q + 1} \right)\left( {1 + fg} \right)}}{{2\left( {1 - f} \right)}}~{{{\Phi }}_{1}}, \\ {{\eta }_{1}} = 1 + \frac{3}{2}{{\alpha }^{2}} + \frac{{15}}{8}{{\alpha }^{4}}, \\ \end{gathered} $$

$$\alpha = \frac{{{{U}_{{i0}}}}}{c},$$

$$\begin{gathered} {{C}_{1}} = \left( {{{\eta }_{1}} - \frac{{{{\eta }_{2}}\left( {{{u}_{0}} - {{U}_{{i0}}}} \right)}}{{{{U}_{{i0}}}}}} \right)\left( {\frac{1}{{2{{\eta }_{1}}^{2}\left( {{{u}_{0}} - {{U}_{{i0}}}} \right)}}} \right) \\ + \;\frac{1}{{{{\eta }_{1}}\left( {{{u}_{0}} - {{U}_{{i0}}}} \right)}} + \frac{{\left( {q - 3} \right)\left( {1 - f{{g}^{2}}} \right)\left( {{{u}_{0}} - {{U}_{{i0}}}} \right)}}{{4\left( {1 + fg} \right)}}, \\ \end{gathered} $$

$$\begin{gathered} {{C}_{2}} = \frac{{{{\eta }_{1}}{{{\left( {{{u}_{0}} - {{U}_{{i0}}}} \right)}}^{3}}}}{2}, \\ {{C}_{3}} = \frac{{{{\rho }_{0}}}}{{2{{\eta }_{1}}}}. \\ \end{gathered} $$

The SFKB equation is derived as (see Appendix A)

$$\begin{gathered} \frac{{\partial {{{\Phi }}_{1}}}}{{\partial \tau }} + {{C}_{1}}{{{\Phi }}_{{10}}}D_{\xi }^{\gamma }{{{\Phi }}_{1}} + {{C}_{{20}}}D_{\xi }^{{\gamma \gamma \gamma }}{{{\Phi }}_{1}} - {{C}_{{30}}}D_{\xi }^{{\gamma \gamma }}{{{\Phi }}_{1}} = 0, \\ 0 < \gamma \leqslant 1. \\ \end{gathered} $$

(9)

Equation (9) represents the SFKB equation describing the propagation of IA shock waves in the relativistic plasma with the electrons and positrons’ nonextensivity.

3 DERIVATION OF THE SAGDEEV POTENTIAL [47–51]

To study the arbitrary amplitude of ion-acoustic shock waves, we introduce $\chi = \xi - M\tau ,$ where M is the  Mach number, viz., the velocity of shock. By t-ransforming Eq. (8) into the χ coordinate, it can be written as

$$ - M\frac{{d{{{\Phi }}_{1}}}}{{d\chi }} + {{C}_{1}}{{{\Phi }}_{1}}\frac{{d{{{\Phi }}_{1}}}}{{d\chi }} + {{C}_{2}}\frac{{{{d}^{3}}{{{\Phi }}_{1}}}}{{d{{\chi }^{3}}}} - {{C}_{3}}\frac{{{{d}^{2}}{{{\Phi }}_{1}}}}{{d{{\chi }^{2}}}} = 0.$$

(10)

Integrating Eq. (10) we find

$$\frac{{{{d}^{2}}{{{\Phi }}_{1}}}}{{d{{\chi }^{2}}}} = \frac{M}{{{{C}_{2}}}}{{{\Phi }}_{1}} - \frac{{{{C}_{1}}}}{{2{{C}_{2}}}}{{{\Phi }}_{1}}^{2} + \frac{{{{C}_{3}}}}{{{{C}_{2}}}}\frac{{d{{{\Phi }}_{1}}}}{{d\chi }}.$$

(11)

We have assumed the integration constant to be zero. To derive the Sagdeev potential, we set

$$\begin{gathered} \frac{{{{d}^{2}}{{{\Phi }}_{1}}}}{{d{{\chi }^{2}}}} = - \frac{{dV({{{\Phi }}_{1}})}}{{d{{{\Phi }}_{1}}}}, \\ - \frac{{dV({{{\Phi }}_{1}})}}{{d{{{\Phi }}_{1}}}} = \frac{M}{{{{C}_{2}}}}{{{\Phi }}_{1}} - \frac{{{{C}_{1}}}}{{2{{C}_{2}}}}{{{\Phi }}_{1}}^{2} + \frac{{{{C}_{3}}}}{{{{C}_{2}}}}\frac{{d{{{\Phi }}_{1}}}}{{d\chi }}. \\ \end{gathered} $$

(12)

Multiplying both sides of Eq. (12) by $\partial {{{\Phi }}_{1}}{\text{/}}\partial \chi$, we obtain

$$\begin{gathered} \frac{1}{2}{{\left( {\frac{{d{{{\Phi }}_{1}}}}{{d\chi }}} \right)}^{2}} + V({{{\Phi }}_{1}}) = W({{{\Phi }}_{1}}), \\ V({{{\Phi }}_{1}}) = - \frac{M}{{2{{C}_{2}}}}{\Phi }_{1}^{2} + \frac{{{{C}_{1}}}}{{6{{C}_{2}}}}{\Phi }_{1}^{3}, \\ W({{{\Phi }}_{1}}) = \frac{{{{C}_{3}}}}{{{{C}_{2}}}}\int {\frac{{d{{{\Phi }}_{1}}}}{{d\chi }}} d{{{\Phi }}_{1}}. \\ \end{gathered} $$

(13)

Equation (13) is the energy equation, $W({{{\Phi }}_{1}})$ and $V({{{\Phi }}_{1}})$ are the variable energy of a particle and Sagdeev potential, respectively [52, 53].

4 SOLUTION OF SFKB EQUATION

Modified tanh-function method [54] is used to obtain the exact analytical solution to the SFKB equation. For this purpose, we propose and apply transformation ${{{\Phi }}_{1}}\left( {\xi ,\tau } \right) = {{{\Phi }}_{1}}\left( \chi \right)$, $\chi = {{f}_{1}}{{\xi }^{\gamma }}{\text{/}}\Gamma \left( {1 + \gamma } \right) - {{f}_{2}}\tau$ to Eq. (9) and convert it into the following form

$$\begin{gathered} - {{f}_{2}}\frac{{\partial {{{\Phi }}_{1}}}}{{\partial \chi }} + {{C}_{1}}{{f}_{1}}{{{\Phi }}_{1}}\frac{{\partial {{{\Phi }}_{1}}}}{{\partial \chi }} + {{C}_{2}}{{f}_{1}}^{3}\frac{{{{\partial }^{3}}{{{\Phi }}_{1}}}}{{\partial {{\chi }^{3}}}} \\ - \;{{C}_{3}}{{f}_{1}}^{2}\frac{{{{\partial }^{2}}{{{\Phi }}_{1}}}}{{\partial {{\chi }^{2}}}} = 0. \\ \end{gathered} $$

(14)

By integrating Eq. (10) once, we obtain

$$ - {{f}_{2}}{{{\Phi }}_{1}} + \frac{1}{2}{{C}_{1}}{{f}_{1}}{{{\Phi }}_{1}}^{2} + {{C}_{2}}{{f}_{1}}^{3}\frac{{{{\partial }^{2}}{{{\Phi }}_{1}}}}{{\partial {{\chi }^{2}}}} - {{C}_{3}}{{f}_{1}}^{2}\frac{{\partial {{{\Phi }}_{1}}}}{{\partial \chi }} = 0.$$

(15)

Balancing $\Phi _{1}^{2}$ with ${{{{\partial }^{2}}{{{\Phi }}_{1}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{{\Phi }}_{1}}} {\partial {{\chi }^{2}}}}} \right. \kern-0em} {\partial {{\chi }^{2}}}}$ in Eq. (15) give

$$m + 2 = 2m\,\,\, \Rightarrow \,m = 2.$$

(16)

By applying the modified tanh-function method to Eq. (15) and using Eq. (16), the exact analytical solution of Eq. (15) is given by

$$\begin{gathered} {{{\Phi }}_{1}} = {{a}_{0}} + {{a}_{1}}\varphi \left( \chi \right) + {{a}_{2}}{{\varphi }^{2}}\left( \chi \right) + {{a}_{{ - 1}}}{{\varphi }^{{ - 1}}}\left( \chi \right) \\ + \;{{a}_{{ - 2}}}{{\varphi }^{{ - 2}}}\left( \chi \right),\quad {{a}_{2}}\;\;{\text{or}}\;\;\,{{a}_{{ - 2}}} \ne {\text{0,}} \\ \end{gathered} $$

(17)

where ${{a}_{0}}$ and ${{a}_{{ \pm i}}}$ ($i = 1,2$) are undetermined constants to be calculated, and $\varphi \left( \chi \right)$ satisfies the Riccati equation

$$\frac{{\partial \varphi \left( \chi \right)}}{{\partial \chi }} = b + {{\varphi }^{2}}\left( \chi \right).$$

(18)

Equation (18) has three types of solutions as

$$\begin{gathered} b < 0\, \Rightarrow \varphi \left( \chi \right) = - \sqrt { - b} \tanh \left( {\sqrt { - b} \chi } \right), \\ b > 0\, \Rightarrow \varphi \left( \chi \right) = \sqrt b \tan \left( {\sqrt b \chi } \right), \\ b = 0\, \Rightarrow \varphi \left( \chi \right) = - \frac{1}{\chi }. \\ \end{gathered} $$

(19)

Using Eqs. (17) and (18), we calculate the ${{{{\partial }^{2}}{{{\Phi }}_{1}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{{\Phi }}_{1}}} {\partial {{\chi }^{2}}}}} \right. \kern-0em} {\partial {{\chi }^{2}}}}$ and $\Phi _{1}^{2}$ parameters. Then, substituting these parameters and Eq. (19) into Eq. (15), a set of equations can be derived in the following forms by collecting the powers of $\varphi \left( \chi \right)$:

$$\begin{gathered} 6{\kern 1pt} {\kern 1pt} {{C}_{2}}{{f}_{1}}^{3}{{a}_{2}} + \frac{1}{2}{{C}_{1}}{{f}_{1}}a_{2}^{2} = 0, \\ 2{\kern 1pt} {{C}_{2}}{{f}_{1}}^{3}{{a}_{1}} + {{C}_{1}}{{f}_{1}}{{a}_{2}}{{a}_{1}} - 2{{C}_{3}}{{f}_{1}}^{2}{{a}_{2}} = 0, \\ \end{gathered} $$

$$\begin{gathered} - {{f}_{2}}{{a}_{2}} + 8{{C}_{2}}{{f}_{1}}^{3}{{a}_{2}}b + \frac{1}{2}{{C}_{1}}{{f}_{1}}\left( {2{{a}_{2}}{{a}_{0}} + a_{1}^{2}} \right) \\ - \;{{C}_{3}}{{f}_{1}}^{2}{{a}_{1}} = 0, \\ - {{f}_{2}}{{a}_{1}} + 2{{C}_{2}}{{f}_{1}}^{3}{{a}_{1}}b + {{C}_{1}}{{f}_{1}}\left( {{{a}_{2}}{{a}_{{ - 1}}} + {{a}_{0}}{{a}_{1}}} \right) \\ - \;2{{C}_{3}}{{f}_{1}}^{2}{{a}_{2}}b = 0, \\ \end{gathered} $$

$$\begin{gathered} \frac{1}{2}{{C}_{1}}{{f}_{1}}\left( {2{{a}_{2}}{{a}_{{ - 2}}} + 2{{a}_{1}}{{a}_{{ - 1}}} + a_{0}^{2}} \right) - {{C}_{3}}{{f}_{1}}^{2}\left( {{{a}_{1}}b - {{a}_{{ - 1}}}} \right) \\ - \;{{f}_{2}}{{a}_{0}} + 2{{C}_{2}}{{f}_{1}}^{3}\left( {{{a}_{{ - 2}}} + {{a}_{2}}{{b}^{2}}} \right) = 0, \\ \end{gathered} $$

(20)

$$\begin{gathered} 2{{C}_{2}}{{f}_{1}}^{3}{{a}_{{ - 1}}}b + {{C}_{1}}{{f}_{1}}\left( {{{a}_{{ - 2}}}{{a}_{1}} + {{a}_{{ - 1}}}{{a}_{0}}} \right) \\ + \;2{{C}_{3}}{{f}_{1}}^{2}{{a}_{{ - 2}}} - {{a}_{{ - 1}}}{{f}_{2}} = 0, \\ - {{f}_{2}}{{a}_{{ - 2}}} + 8{{C}_{2}}{{f}_{1}}^{3}{{a}_{{ - 2}}}b + \frac{1}{2}{{C}_{1}}{{f}_{1}}\left( {2{{a}_{{ - 2}}}{{a}_{0}} + a_{{ - 1}}^{2}} \right) \\ - \;{{C}_{3}}{{f}_{1}}^{2}{{a}_{{ - 1}}}b = 0, \\ \end{gathered} $$

$$\begin{gathered} 2{{C}_{2}}{{f}_{1}}^{3}{{a}_{{ - 1}}}{{b}^{2}} + {{C}_{1}}{{f}_{1}}{{a}_{{ - 2}}}{{a}_{{ - 1}}} + 2{{C}_{3}}{{f}_{1}}^{2}{{a}_{{ - 2}}}b = 0, \\ 6{{C}_{2}}{{f}_{1}}^{3}{{a}_{{ - 2}}}{{b}^{2}} + \frac{1}{2}{{C}_{1}}{{f}_{1}}a_{{ - 2}}^{2} = 0. \\ \end{gathered} $$

Using the Maple software, the solution of Eqs. (20) is obtained as

$$\begin{gathered} {{a}_{0}} = \frac{{9C_{3}^{2}}}{{25{{C}_{1}}{{C}_{2}}}},\quad {{a}_{1}} = \frac{{10{{C}_{2}}{{f}_{2}}}}{{{{C}_{1}}{{C}_{3}}}}, \\ {{a}_{2}} = - \frac{{625C_{2}^{3}f_{2}^{2}}}{{3{{C}_{1}}C_{3}^{4}}},\quad b = - \frac{{9C_{3}^{6}}}{{15{\kern 1pt} {\kern 1pt} 625f_{2}^{2}C_{2}^{4}}}, \\ {{a}_{{ - 1}}} = 0,\quad {{f}_{1}} = \frac{{25{{C}_{2}}{{f}_{2}}}}{{6C_{3}^{2}}},\quad {{a}_{{ - 2}}} = 0, \\ \end{gathered} $$

(21)

where ${{f}_{2}}$ is an arbitrary constant.

Using Eqs. (19) and (21), the shock wave solution of the SFKB equation, Eq. (9), can be obtained as follows

$$\begin{gathered} {{{\Phi }}_{1}} = \frac{{3C_{3}^{2}}}{{25{{C}_{1}}{{C}_{2}}}} \\ \times \;\left( {3 - 2\tanh \left( {\frac{{3C_{3}^{3}}}{{125{{f}_{2}}C_{2}^{2}}}\chi } \right) - {{{\tanh }}^{2}}\left( {\frac{{3C_{3}^{3}}}{{125{{f}_{2}}C_{2}^{2}}}\chi } \right)} \right), \\ \chi = \frac{{25{{C}_{2}}{{f}_{2}}{{\xi }^{\gamma }}}}{{6C_{3}^{2}\Gamma \left( {1 + \gamma } \right)}} - {{f}_{2}}\tau . \\ \end{gathered} $$

(22)

5 RESULTS AND DISCUSSIONS

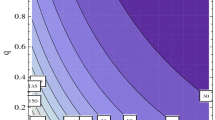
According to our knowledge, there is no investigation of the effect of the space fractional parameter on the behavior of IA shock wave in relativistic plasma including electrons, positrons, and relativistic thermal ions. Thus, our aim is to investigate the behavior of IA shock waves in such plasma. For this purpose, we have first derived the SFKB equation using a semi-inverse technique for an unmagnetized, collisionless, and relativistic plasma. This plasma contains relativistic thermal ions, q-distributed electrons, and positrons. Then, we propose a modified tanh-function method considering a fractional complex transform to solve the obtained SFKB equation. Moreover, our goal is to show how the features of shock waves solutions can be affected by the plasma parameters such as space fractional and relativistic parameters, electrons to positrons nonextensivity, and electron-to-positron temperature ratio. We have chosen the numerical quantities for the Figs. 1–6 as $f = 0.3$, ${{\rho }_{0}} = 0.5$, ${{U}_{{i0}}} = 0.9$, and ${{f}_{2}} = 0.3$. Figure 1 shows the relation between the amplitude of the IA shock wave ${{{\Phi }}_{1}}$ and space fractional parameter γ for different values of electron nonextensivity $q = 3.5$, 4, and 4.5. It illustrates that the amplitude of the IA shock wave decreases with an increase in space fractional parameter and electron nonextensivity. Therefore, for increasing the IA shock wave’s amplitude, we can increase the space fractional parameter γ instead of electron nonextensivity q.

Fig. 1.

The shock wave amplitude versus γ with $\tau = 0.5$, $g = 1$, $\eta = 0.1$, and $\xi = 2$ for different values of $q = 3.5$ (solid curve), 4 (dashed curve) and 4.5 (long dashed curve).

Fig. 2.

The shock wave amplitude versus γ for different values of $\xi = 1.5$ (solid curve), 2 (dashed curve), and 2.5 (long dashed curve). The remaining parameters are the same as in Fig. 1, $q = 4$.

Fig. 3.

The shock wave amplitude versus ξ for different values of $q = 3.5$ (solid curve), 4 (dashed curve), and 4.5 (long dashed curve). The remaining parameters are the same as on Fig. 1, $\gamma = 1$.

Fig. 4.

The shock wave amplitude versus ξ for different values of $g = 1$ (solid curve), 4 (dashed curve), and 7 (long dashed curve); $\tau = 0.5$, $q = 4$, $\eta = 0.1$, and $\gamma = 1$.

Fig. 5.

The shock wave amplitude versus ξ with $\tau = 0.5$, $g = 1$, $q = 4$, and $\gamma = 1$ for different values of $\eta = 0.05$ (solid curve), 0.2 (dashed curve), and 0.35 (long dashed curve).

Fig. 6.

The shock wave amplitude versus γ with $\tau = 0.5$, $g = 1$, $q = 4$, $\xi = 2$ for different values of $\eta = 0.05$ (solid curve), 0.2 (dashed curve), and 0.35 (long dashed curve).

The influence of space fractional parameter γ for different values of spatial $\xi = 1.5$, 2, and 2.5 on the IA shock wave is represented in Fig. 2. It is shown that as space fractional parameter and spatial parameter decrease, the amplitude of the shock wave increases. Therefore, the shock wave feature can be modulated using the fractional parameter. The behaviors of the shocks for different values of electron nonextensivity q, relativistic parameter η, and electron-to-positron temperature ratio g are displayed in Figs. 3–5. It is clear that the IA shock wave’s amplitude is increasing by an increase in q and g (represented in Figs. 3 and 4) while this trend is vice-versa for η as shown in Fig. 5. By the other word, with an increase in relativistic parameter from $\eta = 0.05$ to 0.35 the amplitude of the IA shock wave is decreased. The IA shock wave’s amplitude ${{{\Phi }}_{1}}$ versus space fractional parameter γ for different relativistic parameter $\eta = 0.05$, 0.2, and 0.35 is shown in Fig. 6. It is depicted that as relativistic and space fractional parameters increase, the amplitude of the IA shock wave decreases.

6 CONCLUSIONS

Using the semi-inverse technique, SFKB equation for an unmagnetized and collisionless e–p–i plasma containing relativistic thermal ions, q-distributed electrons, and positrons is derived to investigate the structure of IA shock waves. The modified tanh-function method is presented to solve the obtained SFKB equation. We investigated the effects of different parameters on the structure of relativistic plasma. Our results show that increase in the electron nonextensivity q and the electron-to-positron temperature ratio g leads to increase in shock amplitude while this trend is inversed for the space fractional parameter γ and the relativistic parameter η. Our results may help to understand the astrophysical environments such as pulsar magnetospheres, quasars, and collimated jets.

DERIVATION OF SFKB EQUATION

To formulate the space fractional Korteweg–de Vries–Burgers (SFKB) equation, let’s us introduce a potential function $\varphi \left( {\xi ,\tau } \right)$ as ${{{\Phi }}_{1}}\left( {\xi ,\tau } \right) = {{\varphi }_{\xi }}\left( {\xi ,\tau } \right) = {{\varphi }_{\xi }}$, and substituting it into Eq. (8), we obtain the Korteweg–de Vries–Burgers (KB) equation as

$${{\varphi }_{{\xi \tau }}} + {{C}_{1}}{{\varphi }_{\xi }}{{\varphi }_{{\xi \xi }}} + {{C}_{2}}{{\varphi }_{{\xi \xi \xi \xi }}} - {{C}_{3}}{{{\Phi }}_{{1\xi \xi }}} = 0,$$

(A.1)

The functional of Eq. (A.1) is given by

$$\begin{gathered} J\left( \varphi \right) = \mathop \smallint \nolimits^ d\xi \mathop \smallint \nolimits^ d\tau \varphi \\ \times \;[{{a}_{1}}{{\varphi }_{{\xi \tau }}} + {{a}_{2}}{{C}_{1}}{{\varphi }_{\xi }}{{\varphi }_{{\xi \xi }}} + {{a}_{3}}{{C}_{2}}{{\varphi }_{{\xi \xi \xi \xi }}} - {{a}_{4}}{{C}_{3}}{{{\Phi }}_{{1\xi \xi }}}], \\ \end{gathered} $$

(A.2)

where ${{a}_{1}}$, ${{a}_{2}}$, ${{a}_{3}}$, and ${{a}_{4}}$ are constants.

Integrating Eq. (A.2) by parts using ${{\left. {{{\varphi }_{\xi }}} \right|}_{R}} =$${{\left. {{{\varphi }_{{\xi \xi }}}} \right|}_{R}} = {{\left. {{{\varphi }_{{\xi \xi \xi }}}} \right|}_{R}} = {{\left. {{{\varphi }_{\xi }}} \right|}_{T}} = 0$, we obtain

$$\begin{gathered} J\left( \varphi \right) = \mathop \smallint \nolimits^ d\xi \mathop \smallint \nolimits^ d\tau \\ \times \;\;[ - {{a}_{1}}{{\varphi }_{\xi }}{{\varphi }_{\tau }} - \frac{1}{2}{{a}_{2}}{{C}_{1}}\varphi _{\xi }^{3} + {{a}_{3}}{{C}_{2}}\varphi _{{\xi \xi }}^{2} - {{a}_{4}}{{C}_{3}}\varphi {{{\Phi }}_{{1\xi \xi }}}]. \\ \end{gathered} $$

(A.3)

The first variation of Eq. (A.3) gives us the constants as: ${{a}_{1}} = 1{\text{/}}2$, ${{a}_{2}} = 1{\text{/}}3$, ${{a}_{4}} = 1$.

Therefore, the Lagrangian of KB equation can be written as

$$\begin{gathered} F1\left( {{{\varphi }_{\tau }},{{\varphi }_{\xi }},{{\varphi }_{{\xi \xi }}}} \right) \\ = - \frac{1}{2}{{\varphi }_{\xi }}{{\varphi }_{\tau }} - \frac{1}{6}{{C}_{1}}\varphi _{\xi }^{3} + \frac{{{{C}_{2}}}}{2}\varphi _{{\xi \xi }}^{2} - {{C}_{3}}\varphi {{{\Phi }}_{{1\xi \xi }}}. \\ \end{gathered} $$

(A.4)

Similarly, the space fractional Lagrangian of the KB equation can be written as

$$\begin{gathered} F2\left( {\varphi ,{{\varphi }_{\tau }},{}_{0}D_{\xi }^{\gamma }\varphi ,{}_{0}D_{\xi }^{{\gamma \gamma }}\varphi } \right) = - \frac{1}{2}{{\varphi }_{\tau }}{}_{0}D_{\xi }^{\gamma }\varphi \\ - \;\frac{1}{6}{{C}_{1}}{{\left( {{}_{0}D_{\xi }^{\gamma }\varphi } \right)}^{3}} + \frac{{{{C}_{2}}}}{2}{{\left( {{}_{0}D_{\xi }^{{\gamma \gamma }}\varphi } \right)}^{2}} - {{C}_{3}}\varphi {}_{0}D_{\xi }^{{\gamma \gamma }}{{{\Phi }}_{1}}, \\ 0 < \gamma \leqslant 1. \\ \end{gathered} $$

(A.5)

In Eq. (A.5), ${}_{0}^{{}}D_{\xi }^{\gamma }$ denotes the Riemann–Liouville (RL) fractional derivative as follows [55, 56]:

$$\begin{gathered} {}_{a}^{{}}D_{\xi }^{\gamma }f\left( \xi \right) = \frac{1}{{\Gamma \left( {\lambda - \gamma } \right)}} \\ \times \;\frac{{{{d}^{\lambda }}}}{{d{{\xi }^{\lambda }}}}\left( {\int\limits_a^\xi {dx{{{\left( {\xi - x} \right)}}^{{\lambda - \gamma - 1}}}f\left( x \right)} } \right), \\ \lambda - 1 < \gamma \leqslant \lambda ,\quad \xi \in \left[ {a,b} \right]. \\ \end{gathered} $$

(A.6)

Thus, the functional of SFKB equation can be presented as

$$J\left( \varphi \right) = \mathop \smallint \limits_R^{} d\xi \mathop \smallint \limits_T^{} d\tau F2\left( {\varphi ,{{\varphi }_{\tau }},{}_{0}^{{}}D_{\xi }^{\gamma }\varphi ,{}_{0}^{{}}D_{\xi }^{{\gamma \gamma }}\varphi } \right),$$

(A.7)

According to semi-inverse technique [43, 44, 57], taking the first variations of Eq. (A.7) with respect to φ, $\delta J\left( \varphi \right)$, and optimizing it, $\delta J\left( \varphi \right) = 0$, leads to

$$\begin{gathered} \frac{{\partial F2}}{{\partial \varphi }} - \frac{\partial }{{\partial \tau }}\left( {\frac{{\partial F2}}{{\partial {{\varphi }_{\tau }}}}} \right) - {}_{0}^{{}}D_{\xi }^{\gamma }\left( {\frac{{\partial F2}}{{\partial {}_{0}^{{}}D_{\xi }^{\gamma }\varphi }}} \right) \\ + \;{}_{0}^{{}}D_{\xi }^{{\gamma \gamma }}\left( {\frac{{\partial F2}}{{\partial {}_{0}^{{}}D_{\xi }^{{\gamma \gamma }}\varphi }}} \right) = 0. \\ \end{gathered} $$

(A.8)

Substituting Eq. (A.5) into Eq. (A.8) and applying ${{{\Phi }}_{1}} = {}_{0}^{{}}D_{\xi }^{\gamma }\varphi$, we obtain

$$\begin{gathered} \frac{{\partial {{{\Phi }}_{1}}}}{{\partial \tau }} + {{C}_{1}}{{{\Phi }}_{{10}}}D_{\xi }^{\gamma }{{{\Phi }}_{1}} + {{C}_{{20}}}D_{\xi }^{{\gamma \gamma \gamma }}{{{\Phi }}_{1}} - {{C}_{{30}}}D_{\xi }^{{\gamma \gamma }}{{{\Phi }}_{1}} = 0, \\ 0 < \gamma \leqslant 1. \\ \end{gathered} $$

(A.9)