Screw Theory: From Mechanical Engineering to Twistors

Abstract

In a brief review, the development of the concept of screws is outlined, which ultimately influenced the creation of the twistor calculus.

1 INTRODUCTION

The advancement of technology in the 19th century motivated the development of statics and computational kinematics. The problem of composition of forces acting along skew lines led to the appearance of concepts of sliding vectors and screws and to the comprehension of a force as a screw, while the description of a set of forces acting on a rigid body led to the concept of a Grassmannian. A century later, the analysis on Grassmannians served as a basis for creating the twistor calculus, since the possibility to interpret the complexified Minkowski space as a Grassmannian in a 4-dimensional linear space over the complex number field (as the twistor space) was revealed. The twistor technique has been successfully used to classify instantons in the Yang–Mills theory and to find some solutions to the Einstein equations.

Mathematical constructions used in this development direction of physics have not gained due attention in educational programs. In this work, an attempt is made to give a simple and visual description of screws and Grassmannians. The “engineering” origin of the mentioned mathematical objects, having a reputation for being complex and abstract, is emphasized.

2 THE PROBLEM OF COMPOSITION OF FORCES AND THE SLIDNG VECTORS

The concept of a screw arose in applied mechanics during calculations that require considering a large number of forces acting in complex mechanisms [1, 2]. The problem of the composition of forces in statics can be formulated as follows: it is required to find the resultant force acting on a rigid body so that a torque of this resultant force about any point be equal to a sum of the respective torques.

In statics, a force acting on a rigid body is characterized by a sliding vector, since it is characterized not only by a magnitude and direction, but also by a line of action.

The difference between fixed, free, and sliding vectors is as follows: a free vector is defined with an accuracy of any parallel translations; a sliding vector, with an accuracy of parallel translations along its direction; a fixed vector is in one-to-one correspondence with a directed segment that specifies it. More strictly, a sliding vector is the class of equivalence of directed segments if the directed segments lying on the same line are considered equivalent.

It is possible to define the operation of composition of sliding vectors. The problem of the composition of forces requires the introduction of a more general mathematical concept than a vector for describing a force acting on a rigid body.

A sum of two sliding vectors $\overleftarrow {AB}$ and $\overleftarrow {CD}$, acting along the lines $(AB)$ and $(CD)$, is found as follows: first, we add $\overleftarrow {AB}$ and $\overleftarrow {CD}$ as free vectors $\overleftarrow {AB} + \overleftarrow {CD} = \overleftarrow {MG}$, then we reduce the arbitrariness in choosing an origin of the resulting vector (point $M$):

● If $(AB)$ and $(CD)$ intersect at the point $P$, then $M = P$ (i.e., the line of action of the resulting vector passes through $P$).

● If the added vectors are codirectional: $\overleftarrow {AB} \uparrow \uparrow \overleftarrow {CD}$, then $M$ is selected on the segment $[AC]$ so that

$$\frac{{\left| {AM} \right|}}{{\left| {MC} \right|}} = \frac{{\left| {CD} \right|}}{{\left| {AB} \right|}}.$$

(1)

● If the added vectors are oppositely oriented: $\overleftarrow {AB} \uparrow \downarrow \overleftarrow {CD}$ and $\left| {AB} \right| > \left| {CD} \right|$ $(\left| {AB} \right| < \left| {CD} \right|)$, the point $M$ is chosen on the part of the ray $\left[ {CA} \right)~\left( {\left[ {AC} \right)} \right)$ outside the segment $[AC]$ so that Eq. (1) is satisfied.

● Degenerate case: $\overleftarrow {AB} \uparrow \downarrow \overleftarrow {CD}$ and $\left| {AB} \right| = \left| {CD} \right|$; the passage to the limit $\left| {AB} \right| \to \left| {CD} \right|$ leads to $M \to \infty$and $|MG| \to 0$, moreover, $\left| {\overleftarrow {MG} \times \overleftarrow {AM} } \right| \to \left| {\overleftarrow {AC} \times \overleftarrow {AB} } \right|$. The resulting force tends to zero in magnitude, its line of action tends to an infinitely distant straight line, moreover, its moment relative to any point in the plane tends to the moment of a couple of forces $\overleftarrow {AB}$ and $\overleftarrow {CD}$. The concept of “couple of forces” (i.e., a pure moment) in statics is used to describe this situation [3].

● If $(AB)$ and $(CD)$ intersect, we decompose each of the added vectors into components as follows: $\overleftarrow {AB} = \overleftarrow {AE} + \overleftarrow {EB}$, $\overleftarrow {CD} = \overleftarrow {CF} + \overleftarrow {FD}$, where $\overleftarrow {AE}$ and $\overleftarrow {CF}$ are parallel to $\overleftarrow {MG}$, $\overleftarrow {EB}$ and $\overleftarrow {FD}$ are perpendicular to $\overleftarrow {MG}$; in this case $\overleftarrow {EB} + \overleftarrow {FD} = 0$, consequently, $\overleftarrow {EB}$ and $\overleftarrow {FD}$ represent a pure moment parallel to $\overleftarrow {MG}$. A position of the point $M$ is determined by composition of parallel vectors $\overleftarrow {AE}$ and $\overleftarrow {CF}$ as sliding ones: $\overleftarrow {AE} + \overleftarrow {CF} = \overleftarrow {MG}$.

3 SCREWS AND GRASSMANN MANIFOLDS

A sliding vector $\overleftarrow {AB}$ (a force) in 3-dimensional affine space can be represented by a bivector $f = \overleftarrow {OA} \wedge \overleftarrow {OB}$ in the extended 4-dimensional space ${\text{T}}$:

$$\left( {\begin{array}{*{20}{c}} {\overleftarrow {OA} } \\ {\overleftarrow {OB} } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {1,}&{{{x}_{A}},}&{{{y}_{A}},}&{{{z}_{A}}} \\ {1,}&{{{x}_{B}},}&{{{y}_{B}},}&{{{z}_{B}}} \end{array}} \right),$$

where $O$ is the origin of coordinates in ${\text{T}}$, while $({{x}_{A}},{{y}_{A}},{{z}_{A}})$ and $({{x}_{B}},{{y}_{B}},{{z}_{B}})$ are the coordinates of $A$ and $B$, respectively. Plücker coordinates of a bivector $\overleftarrow {OA} \wedge \overleftarrow {OB}$

$${{p}_{{01}}} = \left| {\begin{array}{*{20}{c}} 1&{{{x}_{A}}} \\ 1&{{{x}_{B}}} \end{array}} \right|\,\,\,\,{{p}_{{02}}} = \left| {\begin{array}{*{20}{c}} 1&{{{y}_{A}}} \\ 1&{{{y}_{B}}} \end{array}} \right|\,\,\,\,{{p}_{{03}}} = \left| {\begin{array}{*{20}{c}} 1&{{{z}_{A}}} \\ 1&{{{z}_{B}}} \end{array}} \right|$$

$${{p}_{{12}}} = \left| {\begin{array}{*{20}{c}} {{{x}_{A}}}&{{{y}_{A}}} \\ {{{x}_{B}}}&{{{y}_{B}}} \end{array}} \right|\,\,\,\,{{p}_{{13}}} = \left| {\begin{array}{*{20}{c}} {{{x}_{A}}}&{{{z}_{A}}} \\ {{{x}_{B}}}&{{{z}_{B}}} \end{array}} \right|\,\,\,\,{{p}_{{23}}} = \left| {\begin{array}{*{20}{c}} {{{y}_{A}}}&{{{z}_{A}}} \\ {{{y}_{B}}}&{{{z}_{B}}} \end{array}} \right|$$

contain information about both the force vector ${{F}_{i}} = {{p}_{{0i}}}$ and its torque about the origin of coordinates ${{M}_{i}} = {{\epsilon }_{{ijk}}}{{p}_{{jk}}}$.

Thus, we obtained a one-to-one correspondence between sliding vectors in the 3-dimensional space and decomposable external forms (bivectors) in the 4‑dimensional space, which contain among the factors at least one vector with a nonzero $t$-component.

Since a sum of two bivectors is not always a decomposable form, a sum of forces cannot always be described by a sliding vector.

However, an indecomposable form of the kind ${{f}_{1}} \wedge {{g}_{1}} + {{f}_{2}} \wedge {{g}_{2}}$ (the linear independence of ${{f}_{1}},{{g}_{1}},{{f}_{2}}$, and ${{g}_{2}}$ results from the indecomposability) can always be represented as a sum $f_{1}^{'} \wedge g_{1}^{'} + f_{2}^{'} \wedge g_{2}^{'}$, where $f_{1}^{'} = (0,\vec {f}_{1}^{'})$, $g_{1}^{'} = (1,\vec {g}_{1}^{'})$, $f_{2}^{'} = (0,\vec {f}_{2}^{'})$, $g_{2}^{'} = (0,\vec {g}_{2}^{'})$; in this case, $f_{1}^{'},g_{1}^{'},f_{2}^{'},g_{2}^{'}$ are obtained from ${{f}_{1}},{{g}_{1}},{{f}_{2}},{{g}_{2}}$ using the symplectic transformation. Moreover, the symplectic transformation can be selected in such a way that ${{\overrightarrow {\tilde {f}} }_{2}} \times \left. {{{{\overrightarrow {\tilde {g}} }}_{2}}} \right\|\vec {f}_{1}^{'}$. The bivectors $f_{2}^{'} \wedge g_{2}^{'}$, in which $g_{2}^{{'(0)}} = f_{2}^{{'(0)}} = 0$, correspond to a force couple (i.e., a pure moment). Thus, a sum of arbitrary forces can be resolved into a combination of a force (a sliding vector) and a pure moment (or force couple) parallel to it (a free vector). This assertion was first proved by L. Poinsot [3]. This combination was called a screw, a sum of two screws is again a screw; it is possible to define the concept of an angle between screws, a scalar product of screws and other operations with screws.

Thus, the adequate description of an action of several forces on a rigid body is given in terms of screws, not vectors. In this case, the representation of screws by 2-forms ${{p}_{{ij}}}{{e}^{i}} \wedge {{e}^{j}}$ in an extended 4-dimensional space is of particular importance. Forces (i.e., sliding vectors) are represented by 2-forms that satisfy the Plücker relation:

$${{p}_{{01}}}{{p}_{{23}}} - {{p}_{{02}}}{{p}_{{13}}} + {{p}_{{03}}}{{p}_{{12}}} = 0,$$

(2)

which is the condition of orthogonality of the force and its moment relative to the origin of coordinates.

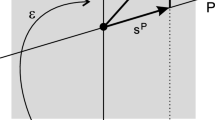
A screw, i.e., an equivalent of the action of an arbitrary number of forces on a rigid body, is uniquely given by a couple $(\vec {F},\vec {M})$, where $\vec {F}$ is the sum of all these forces, represented by a sliding vector with an arbitrarily chosen line of action $\left\| {\vec {F}} \right.$, while $\vec {M}$ is the sum of the moments of all forces relative to some point $O$ on this line. It can be shown that the screw depends neither on the choice of a two-parameter arbitrariness in the choice of the line of action $\vec {F}$, nor on the choice of the point $\mathcal{O}$: $\vec {M}$ depends on the point $\mathcal{O}$ in such a way that the combined effect of the action of $\vec {F}$and $\vec {M}$ on the body remains unchanged. In this case, there is such a line of action that $\vec {M} = p\vec {F}$, this line of action is called the axis of the screw.

In addition to screws that describe the effect of a system of forces on a rigid body (called the force or dynamic screws), the screws can be considered, which describe the movement of a rigid body: kinematic screws. A kinematic screw is a pair $(\vec {\Omega },\vec {v})$, where $\vec {\Omega }$ is the sliding vector of angular velocity, the line of action of which is the instantaneous axis of rotation, while $\vec {v}$ is the free vector of velocity.

The concept of screws and the screw calculus have proven to be extremely useful in engineering mechanics [4] and robotics [5] for the calculation of various mechanisms. A detailed presentation of the theory with examples of the practical application can be found in [2].

4 SCREWS AND TWISTORS

However, it makes sense to consider a screw which in some sense is dual to a kinematic one: the motion of a rigid body can also be characterized by a screw $(\vec {p},\vec {J})$, where $\vec {p}$ is a sliding vector of momentum, a line of which is such that the angular momentum relative to the points of this axis is parallel to the momentum, while $\vec {J}$ is a free vector of angular momentum. We will call this screw a momentum screw. A sum of these two screws corresponds to the momentum screw of the composite system, a difference conforms to the relative motion. In the limiting case, when a rigid body becomes a material point, but its angular momentum retains a nonzero value, we can speak of a material point with a spin. Operations with momentum screws correspond to the description of the dynamics of a system consisting of material points with a spin (elementary particles in the classical nonrelativistic approximation). However, the momentum screw is remarkable for the fact that is naturally generalized for the relativistic case: the 3-vector $\vec {p}$ is replaced by a 4-vector ${{p}_{\mu }}$, while the ordinary moment $\vec {J}$ is replaced by the form corresponding to the generators of the Lorentz group ${{J}_{{\mu \nu }}}$ (by the form of the relativistic angular momentum). As in the case of a force screw, a change in the line of action of the momentum vector leads to a change in the angular momentum according to the formula:

$${{J}_{{\mu \nu }}} \to {{J}_{{\mu \nu }}} + {{x}_{\mu }}{{p}_{\nu }} - {{p}_{\mu }}{{x}_{\nu }}.$$

(3)

Among the set of relativistic screws of momentum, a 7-dimensional subset of screws is especially distinguished, whose momenta lie on the light cone. In this case, the tensor quantities ${{J}_{{\mu \nu }}}$ and ${{p}_{\mu }}$ can be expressed in terms of two Weyl 2-spinors ${{\omega }_{A}}$ and ${{\pi }_{{\dot {A}}}}$

$$\begin{gathered} {{p}_{\mu }}\sigma _{{A\dot {A}}}^{\mu } = {{{\bar {\pi }}}_{A}}{{\pi }_{{\dot {A}}}},\,\,\,\,{{J}_{{\mu \nu }}}\sigma _{{A\dot {A}}}^{\mu }\sigma _{{B\dot {B}}}^{\nu } \\ = \imath ({{\omega }^{A}}{{\pi }^{B}} + {{\omega }^{B}}{{\pi }^{A}}){{\epsilon }^{{\dot {A}\dot {B}}}} - \imath {{\epsilon }^{{AB}}}({{\omega }^{{\dot {A}}}}{{\pi }^{{\dot {B}}}} + {{\omega }^{{\dot {B}}}}{{\pi }^{{\dot {A}}}}). \\ \end{gathered} $$

(4)

In this case, Eq. (3) entails the dependence of the spinor $\omega$ on $x$:

$${{\omega }^{A}} = {{\omega }^{A}} + {{x}^{{A\dot {A}}}},{{\pi }_{{\dot {A}}}},$$

(5)

where

$${{x}^{{A\dot {A}}}} = \sigma _{\mu }^{{A\dot {A}}}{{x}^{\mu }} = \left( {\begin{array}{*{20}{c}} {{{x}^{0}} + {{x}^{3}}}&{{{x}^{1}} - \imath {{x}^{2}}} \\ {{{x}^{1}} + \imath {{x}^{2}}}&{{{x}^{0}} - {{x}^{3}}} \end{array}} \right).$$

A pair of spinors $({{\omega }_{A}},{{\pi }_{{\dot {A}}}})$, satisfying Eq. (5), was named the twistor [6, 7].

Another approach leading to the concept of twistors arises from the description of a set of light rays in four-dimensional space-time [8]. Using the Plücker coordinates $\left( {{{v}_{\mu }},{{M}_{{\mu \nu }}} = {{v}_{\mu }}{{l}_{\nu }} - {{l}_{\mu }}{{v}_{\nu }}} \right)$ to describe a light ray in a general position, where the 4-vector $v$ is along the light ray, while a lightlike vector $l$ connects the origin of coordinates with the light ray under consideration, is quite similar to the above-discussed consideration of dynamic screws and momentum screws. The lightlike vectors $v$ and $l$ can be expressed in terms of 2-spinors:

$${{v}_{\mu }}\sigma _{{A\dot {A}}}^{\mu } = {{\bar {\upsilon }}_{A}}{{\upsilon }_{{\dot {A}}}},\,\,\,\,{{l}_{\mu }}\sigma _{{A\dot {A}}}^{\mu } = {{\bar {\lambda }}_{A}}{{\lambda }_{{\dot {A}}}}.$$

(6)

The 5-dimensional manifold of light rays is naturally nested into the real 8-dimensional space of twistors ${{Z}_{\alpha }} = ({{\lambda }^{{\dot {A}}}},{{\upsilon }_{A}})$, where ${{\lambda }^{{\dot {A}}}} = \frac{{{{{\bar {\upsilon }}}_{A}}{{l}^{{A\dot {A}}}}}}{{{{{\bar {\upsilon }}}_{A}}{{{\bar {\lambda }}}^{A}}}}$.

The twistor concept can also be approached from the other side, starting not from the construction of twistor analogs of any objects in the Minkowski space, but from the representation of points in the Minkowski space by planes in ${{{\mathbf{C}}}^{4}}$. Namely, to each point $x$ we put into correspondence the matrix (${{x}^{\mu }}$ are considered complex-valued)

$$X = \left( {I,\sigma _{\mu }^{{A\dot {A}}}{{x}^{\mu }}} \right) = \left( {\begin{array}{*{20}{c}} {{{x}^{0}} + {{x}^{3}}}&{{{x}^{1}} - \imath {{x}^{2}}}&1&0 \\ {{{x}^{1}} + \imath {{x}^{2}}}&{{{x}^{0}} - {{x}^{3}}}&0&1 \end{array}} \right).$$

and consider the plane in ${{{\mathbf{C}}}^{4}}$ spanned by the rows of this matrix. This is how the implementation of the Minkowski space as a large Schubert cell of the Grassmannian $G{{r}_{2}}({{{\mathbf{C}}}^{4}})$ arises; this approach is studied in detail in [9].

5 CONCLUSIONS

The concept of Grassmannian arises quite naturally when solving the problem of the composition of forces acting on a rigid body. An arbitrary system of these forces can be represented as a screw: a superposition of a force and a couple. The space of screws is isomorphic to the space of external forms in ${{{\mathbf{R}}}^{4}}$, in which the hyperplane ${{x}^{0}} = 0$ is a 3‑dimensional space of forces. Decomposable forms correspond to “primary” quantities: forces or pure moments (force couples). Thus, the set of forces and couples of forces presents a Grassmannian cone whose projectivization is the Grassmannian $G{{r}_{2}}({{{\mathbf{R}}}^{4}})$. This approach allows us to consider forces and force couples as quantities of the same nature.

The further attention to the theory of Grassmann manifolds led to the observation that the manifold $G{{r}_{2}}({{{\mathbf{C}}}^{4}})$ can be identified with the complexified compactified Minkowski space, which makes it possible to express mathematical objects in the Minkowski space in terms of those in the original twistor space ${{{\mathbf{C}}}^{4}}$.

On the other hand, the twistor space arises in a natural way if the angular momentum and four-momentum of the relativistic system, considered as a screw, are expressed in terms of Weyl spinors: a pair of spinors forming the twistor has the same dependence on coordinates as a couple of vectors forming the screw.

Thus, the concepts of screws and Grassmann manifolds, which were formed in the epoch of a tremendous upgrowth of applied mechanics, played a significant role in the development of the theory of twistors.